Professor Diminoi
UNIDADES DE MEDIDAS
Regra de tres – Comprimento – Capacidade – Massa - Tempo
As unidades de medida são siglas utilizadas para representar quantidades específicas de determinadas grandezas físicas.
As unidades de medida são representações das grandezas físicas utilizadas em diversas áreas do conhecimento com o intuito de quantificar uma matéria, uma sensação, o tempo ou o tamanho de algo, por exemplo.
Em todo o mundo as unidades de medida seguem um padrão determinado pelo Sistema Internacional de
Unidaders (SI). A partir da unidade-padrão estabelecida pelo Sistema Internacional, podemos ainda utilizar outras unidades derivadas dela, o que permite compararmos e ampliarmos a noção quantitativa da grandeza.
O Sistema Internacional adota a unidade kelvin, por exemplo, como padrão para a grandeza temperatura. Essa unidade é muito utilizada em experimentos laboratoriais, mas, no dia a dia, a maioria dos países utiliza a unidade graus Celsius, que é derivada da unidade kelvin.
Unidades de massa
As unidades mais utilizadas para o trabalho com a massa de uma matéria são:
Tonelada (t)
Quilograma (kg) [unidade-padrão de massa segundo o SI];
Grama (g)
Miligrama (mg)
Para converter uma unidade em outra, basta seguir estas relações:
1 t = 1000 Kg
1 kg = 1000 g
1 g = 1000 mg
Relação entre as unidades de massa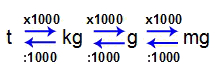
01) Transformar 2,5 kg em gramas.
Resolucao
Como 1 kg equivale a 1000 gramas, podemos montar a seguinte regra de três:
1 kg --------- 1000 g
2,5 Kg---------- x
x . 1 = 2,5.1000
x = 2500 g
02) Transformar 4 mg em kg.
Resolucao
Como 1 kg equivale a 1000000 de mg (resultado da multiplicação 1000 x1000 da diferença entre a unidade kg e a mg), podemos montar a seguinte regra de três:
1 kg --------- 1000000 mg
x---------- 4 mg
1000000.x = 4.1
x = 4
10000000
x = 0,000004 Kg
Unidades de volume
Metro cúbico (m3) [unidade-padrão de volume segundo o SI];
Litro (L) ou decímetro cúbico (dm3);
Mililitro (mL) ou centímetro cúbico (cm3).
Para converter uma unidade na outra, basta seguir estas relações:
1 m3 = 1000 L
1L = 1 dm3
1L = 1000 mL
1dm3 = 1000 cm3
1cm3 = 1mL
Relação entre as unidades de volume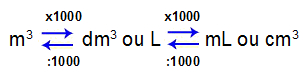 Como podemos acompanhar no esquema acima, uma unidade de volume é sempre 1000 vezes maior que a outra. Quando comparamos a unidade maior (m3) com a unidade menor (mL ou cm3), a diferença é de 1000000 de vezes.
Como podemos acompanhar no esquema acima, uma unidade de volume é sempre 1000 vezes maior que a outra. Quando comparamos a unidade maior (m3) com a unidade menor (mL ou cm3), a diferença é de 1000000 de vezes.
Conversão de unidades de volume
03) Transformar 4,5 m3 em dm3.
Resolucao
Como 1 m3 equivale a 1000 dm3, podemos montar a seguinte regra de três:
1m3 --------- 1000 dm3
4,5 m3---------- x
x.1 = 4,5.1000
x = 4500 dm3
04) Transformar 300 cm3 em L.
Resolucao
Como 1 L equivale a 1000 de cm3, podemos montar a seguinte regra de três:
1L --------- 1000 cm3
x---------- 300 cm3
1000.x = 300.1
x = 300
1000
x = 0,3 dm3
Unidades de pressão
As unidades mais utilizadas para o trabalho com a pressaosão:
Atmosfera (atm)
Milímetro de mercúrio (mmHg)
Centímetro de mercúrio (cmHg)
(Pa) ou quilopascal (KPa = 1000 Pa) [unidade-padrão de pressão segundo o SI].
Para converter uma unidade na outra, basta seguir estas relações:
1 atm = 101,325 kPa
1 atm = 101325 Pa
1 atm = 760 mmHg
1 atm = 76 cmHg
OBS.: Foram utilizadas relações partindo do atm porque os valores utilizados são numericamente mais simples de trabalhar e/ou memorizar (caso necessário).
Conversão de unidades de pressão
05) Transformar 2 atm em KPa.
Resolucao
Como 1 atm equivale a 101,325 KPa, basta montar a seguinte regra de três:
1atm --------- 101,325 KPa
2 atm ---------- x
x.1 = 2.101,325
x = 202, 650 KPa
06) Transformar 200 mmHg em cmHg.
Utilizando as relações fornecidas acima, inicialmente devemos converter 200 mmHg para atm por meio da seguinte regra de três:
Resolucao
1 atm --------- 760 mmHg
x ---------- 200 mmHg
x.760 = 200.1
x = 200
760
x = 0,26 atm
Em seguida, transformamos o resultado em atm para cmHg na regra de três a seguir:
1 atm --------- 76 cmHg
0,26 atm ----------y
y.1 = 0,26.76
y = 19,76 cmHg
07) Transformar 500 cmHg em KPa.
Utilizando as relações fornecidas acima, inicialmente devemos converter 500 cmHg para atm por meio da seguinte regra de três:
Resolucao
1 atm --------- 76 cmHg
x ---------- 500 cmHg
x.76 = 500.1
x = 500
76
x = 6,57 atm
Em seguida, transformamos o resultado em atm para cmHg na regra de três a seguir:
1 atm --------- 101,325 KPa
6,57 atm ----------y
y.1 = 6,57.101,325
y = 665,70 KPa
Unidades de temperatura
As unidades mais utilizadas para o trabalho com temperaturasão:
Graus Celsius (oC)
Graus Fahrenheit (oF)
Kelvin (K) [unidade-padrão de temperatura segundo o SI].
Para converter uma unidade de temperatura em outra, podemos utilizar as fórmulas a seguir:
De graus Celsius para Kelvin:
TK = ToC + 273
De graus Celsius para Fahrenheit:
ToC = ToF-32
5 9
Conversão de unidades de temperatura
01) Transformar 45 oC para oF.
Resolaucao
Para realizar a transformação, basta colocar os dados na fórmula abaixo:
ToC = ToF-32
5 9
45 = ToF-32
5 9
5.(ToF-32) = 45.9
5ToF - 160 = 405
5ToF = 405 + 160
ToF = 565
5
ToF = 113 oF
02) Transformar 200 K para oC.
esolucao
Para realizar a transformação, basta colocar os dados na fórmula a seguir:
TK = ToC + 273
200 = ToC + 273
ToC = 200 – 273
ToC = - 73 oC
Unidades de comprimento
As unidades mais utilizadas para o trabalho com comprimentosão:
Quilômetro (km)
Metro (m) [unidade-padrão de comprimento segundo o SI]
Centímetro (cm)
Decímetro (dm)
Milímetro (mm).
Para converter uma unidade na outra, basta seguir estas relações:
1 km = 1000 m
1 m = 100 cm
1 dm = 10 cm
1 cm = 10 mm
Conversão de unidades de comprimento
03) Transforme 5 km em dm.
Resolucao
Analisando o esquema, a diferença entre km e dm é da ordem de 100000, assim, basta montar a seguinte regra de três:
1 Km --------- 100000 dm
5 Km ---------- x
x.1 = 5.100000
x = 500000 dm
04) Transformar 500 mm em cm.
Resolucao
Como 1 cm equivale a 10 mm, basta utilizar a seguinte regra de três:
1 cm --------- 10 mm
x ---------- 500 mm
x.10 = 500.1
x = 500
10
x = 50 cm
Unidades de energia na forma de calor
As unidades mais utilizadas para o trabalho com a energia na forma de calorsão:
Joule (J) ou quilojoule (KJ = 1000 J) [o joule é a unidade-padrão estabelecida pelo SI];
Calorias (cal) ou quilocalorias (Kcal = 1000 cal).
Resolucao
Para converter uma unidade na outra, basta seguir esta seguinte relação:
1 cal = 4,18 J
1Kcal = 4,18 KJ
05) Transforme 2600 Kcal em KJ.
Resolucao
Como 1 Kcal equivale a 4,18 KJ, basta utilizar a seguinte regra de três:
1 Kcal --------- 4,18 KJ
2600 Kcal ---------- x
x.1 = 2600.4,18
x = 10868 KJ
Unidades de tempo
Hora (h)
Minuto (min)
Segundo (s) [unidade]padrão de tempo estabelecida pelo SI].
Para converter uma unidade na outra, basta seguir estas relações:
1h = 60 min
1 min = 60 s
Conversão de unidades de tempo
06) Transforme 6 h em segundos.
Resolucao
Como 1 hora equivale a 3600 segundos (resultado da multiplicação 60x60 da diferença entre horas e segundos), basta montar a seguinte regra de três:
1 h --------- 3600 s
6h ---------- x
x.1 = 6.3600
x = 21600 s
07) Transformar 600 s em minutos.
Resolucao
Como 1 minuto equivale a 60 s, basta utilizar a seguinte regra de três:
1 min --------- 60 s
x ---------- 600 s
x.60 = 600
x = 600
x = 600
60
x = 10 min
Mol (quantidade de matéria)
É a unidade que estabelece a quantidade de entidades (átomos, íons, elétrons, nêutrons, moléculas) que formam uma determinada matéria.
Segundo Amedeo Avogrado, 1 mol de qualquer matéria contém 6,02.1023 entidades.
Exemplo:
1 mol de H2O.
Um mol da substância água apresenta:
6,02.1023 moléculas de água;
3.6,02.1023 átomos (o 3 é resultado da soma de 1 oxigênio com 2 hidrogênios);
2.6,02.1023 átomos de hidrogênio;
1.6,02.1023 átomos de oxigênio.
As unidades de medida são modelos estabelecidos para medir diferentes grandezas, tais como comprimento, capacidade, massa, tempo e volume.
Sitema Internacional
O Sistema Internacional de Unidades (SI) define a unidade padrão de cada grandeza. Baseado no sistema métrico decimal, o SI surgiu da necessidade de uniformizar as unidades que são utilizadas na maior parte dos países.
Medidas de Comprimento
Existem várias medidas de comprimento, como por exemplo a jarda, a polegada e o pé.
No SI a unidade padrão de comprimento é o metro (m). Atualmente ele é definido como o comprimento da distância percorrida pela luz no vácuo durante um intervalo de tempo de 1/299.792.458 de um segundo.
Os múltiplos e submúltiplos do metro são: quilômetro (km), hectômetro (hm), decâmetro (dam), decímetro (dm), centímetro (cm) e milímetro (mm).
Medidas de Capacidade
A unidade de medida de capacidade mais utilizada é o litro (l). São ainda usadas o galão, o barril, o quarto, entre outras.
Os múltiplos e submúltiplos do litro são: quilolitro (kl), hectolitro (hl), decalitro (dal), decilitro (dl), centilitro (cl), mililitro (ml).
Medidas de Massa
No Sistema Internacional de unidades a medida de massa é o quilograma (kg). Um cilindro de platina e irídio é usado como o padrão universal do quilograma.
As unidades de massa são: quilograma (kg), hectograma (hg), decagrama (dag), grama (g), decigrama (dg), centigrama (cg) e miligrama (mg).
São ainda exemplos de medidas de massa a arroba, a libra, a onça e a tonelada. Sendo 1 tonelada equivalente a 1000 kg.
Medidas de Volume
No SI a unidade de volume é o metro cúbico (m3). Os múltiplos e submúltiplos do m3 são: quilômetro cúbico (km3), hectômetro cúbico (hm3), decâmetro cúbico (dam3), decímetro cúbico (dm3), centímetro cúbico (cm3) e milímetro cúbico (mm3).
Podemos transformar uma medida de capacidade em volume, pois os líquidos assumem a forma do recipiente que os contém. Para isso usamos a seguinte relação:
1 l = 1 dm3
Tabela de conversão de Medidas
O mesmo método pode ser utilizado para calcular várias grandezas.
Primeiro, vamos desenhar uma tabela e colocar no seu centro as unidades de medidas bases das grandezas que queremos converter, por exemplo:
Capacidade = litro (l)
Comprimento = metro (m)
Massa = grama (g)
Volume = metro cúbico (m3)
Observação: tudo o que estiver do lado direito da medida base são chamados submúltiplos. Os prefixos deci, centi e mili correspondem respectivamente à décima, centésima e milésima parte da unidade fundamental.
Do lado esquerdo estão os múltiplos. Os prefixos deca, hecto e quilo correspondem respectivamente a dez, cem e mil vezes a unidade fundamental.
E o Tempo?
A unidade de medida base do tempo no SI é o segundo (s). Atualmente o segundo é definido como o tempo de duração de 9.192.631.770 vibrações da radiação emitida pela transição eletrônica entre os níveis hiperfinos do estado fundamental do átomo de césio 133.
Os múltiplos do segundo são o minuto, a hora e o dia. Essas medidas não são decimais, por isso usa-se as seguintes relações:
1 minuto (min) = 60 segundos (s)
1 hora = 3 600 segundos (s)
60 minutos (min) = 1 hora (h)
24 horas (h) = 1 dia (d)
Os submúltiplos do segundo são:
Décimo de segundo = 0,1 s ou 1/10 s
Centésimo de segundo = 0,01 s ou 1/100 s
Milésimo de segundo = 0,001 s ou 1/1000 s
Questões resolvidas
08) (PM Acre) Determine o valor em decímetros de 0,375 dam.
(A) 3,75 dm
(B) 0,0375 dm
(C) 3750 dm
(D) 37,5 dm
(E) 375 dm
Resolução:
Temos que 1 dam (decâmetro) equivale a 10 metros, e 1 metro equivale a 10 dm (decímetros), ou seja, 1 dam = 100 dm.
Daí, 0,375 dam = 37,5 dm
Alternativa D
09) (Vunesp) Em um elevador, estão uma quantidade de pacotes com diferentes pesos, totalizando 222,8 kg. Se cada um desses pacotes tivesse 750 gramas a mais, a soma de todos esses pesos seria igual a 438,8 kg. A quantidade de pacotes é igual a
(A) 288
(B) 410
(C) 375
(D) 425
(E) 256
Resolução
O peso total equivale a 222,8 kg, porém com o acréscimo de 750 g (0,75 kg) em cada pacote, o peso total passaria a ser de 438,8 kg.
Calculando a diferença:
438,8 – 222,8 = 216 kg
Dividindo este valor pelo peso, em quilos, acrescentado a cada pacote:
216 / 0,75 = 288
Alternativa A
10) (Vunesp) Analise as seguintes igualdades.
I. 178 litros = 17,8 m3.
II. 0,8 km = 800000 mm.
III. 8,15h = 8h9min.
IV. 47500 cm2= 475 m2
As duas únicas afirmações verdadeiras são
(A) II e III.
(B) I e III.
(C) I e IV.
(D) I e II.
(E) II
Resolução
Analisando cada uma das afirmações:
I) 1 m³ equivale a 1000 litros (errado).
II) 0,8 km = 800 m = 800000 mm (certo).
III) 0,15h = 1/4 h = 15 min (errado).
IV) 475 m² = 4750000 cm² (errado)
Alternativa E
11) (EDUCA) Uma caixa d’água em forma de paralelepípedo reto tem 2,5 metros de comprimento e 1,5 metro de largura. Nessas condições, a altura necessária dessa caixa d’água para que ela possua capacidade total de 18750 litros será:
(A) 5 metros
(B) 4,5 metros
(C) 3,75 metros
(D) 6 metros
(E) 5,25 metros
Resolução
Sabendo que 1 m³ equivale a 1000 litros, para que a capacidade total da caixa seja de 18750 litros, o volume deverá ser de 18,75 m³.
Sendo h a altura da caixa, temos:
2,5 . 1,5 . h = 18,75
3,75 . h = 18,75
h = 18,75 / 3,75
h = 5 m
Alternativa A
12) (CONSCAM) A respeito de unidades de medida do sistema métrico, identifique como verdadeiras “V” ou falsas “F” as seguintes afirmativas:
( ) 1 cm² = 0,0001 m²
( ) 1 m3 = 1 litro.
( ) 6 m2 = 60 dm2.
Assinale a alternativa que apresenta a sequência correta, de cima para baixo.
(A) VVF
(B) VFV
(C) VFF
(D) FVV
(E) FVF
Resolução
1 cm² = 0,0001 m² (V)
1 m³ = 1000 litros (F)
6 m² = 600 dm² (F)
Alternativa C
13) A mais antiga das funções do Instituto Médico Legal (IML) é a necropsia. Num determinado período, do total de atendimentos do IML, 30% foram necropsias. Do restante dos atendimentos, todos feitos a indivíduos vivos, 14% procediam de acidentes no trânsito, correspondendo a 588. Pode-se concluir que o total de necropsias feitas pelo IML, nesse período, foi
(A) 2 500.
(B) 1 600.
(C) 2 200.
(D) 3 200.
(E) 1 800.
Resolucao
30% de atendimentos de necrópsias
70% de atendimentos a indivíduos vivos
Considerando apenas os atendimentos a indivíduos vivos, 14% (588) se referem a acidentes no trânsito. Assim, podemos calcular quantos atendimentos a indivíduos vivos (x):
14% de x = 588
14x/100 = 588
x = 588.100/14
x = 4200
Sabendo disto, temos que 4200 equivale a 70% do total de atendimentos (y):
70% de y = 4200
70y/100 = 4200
y = 4200.100/70
y = 6000
O total de atendimentos foi de 6000.
Como as necrópsias corresponderam a 30%:
30% de 6000 = 6000.30/100 = 1800
Alternativa E
14) Em uma empresa com 5 funcionários, a soma dos dois menores salários é R$ 4.000,00, e a soma dos três maiores salários é R$ 12.000,00. Excluindo-se o menor e o maior desses cinco salários, a média dos 3 restantes é R$ 3.000,00, podendo-se concluir que a média aritmética entre o menor e o maior desses salários é igual a
(A) R$ 3.500,00.
(B) R$ 3.400,00.
(C) R$ 3.050,00.
(D) R$ 2.800,00.
(E) R$ 2.500,00.
Resolucao
Sejam os salários em ordem crescente: x, y, z, w, k
Temos:
x + y = 4000
z + w + k = 12000
(y + z + w)/3 = 3000, ou seja, y + z + w = 9000
Somando as duas primeiras equações:
x + y + z + w + k = 16000
Subtraindo a terceira equação da soma acima:
x + y + z + w + k – y – z – w = 16000 – 9000
x + k = 7000
Como x é o menor e k é o maior salário, concluímos que a média é 3500.
Alternatia A
15) Dez funcionários de uma repartição trabalham 8 horas por dia, durante 27 dias, para atender certo número de pessoas. Se um funcionário doente foi afastado por tempo indeterminado e outro se aposentou, o total de dias que os funcionários restantes levarão para atender o mesmo número de pessoas, trabalhando uma hora a mais por dia, no mesmo ritmo de trabalho, será
(A) 29.
(B) 30.
(C) 33.
(D) 28.
(E) 31.
Resolucao
Vamos resolver utilizando a regra de três composta:
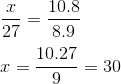
Alternativa B
16) Uma pessoa pegou emprestada certa quantia por dez meses,à taxa de juros simples de 4% ao mês. O valor do empréstimo, acrescido dos juros, deverá ser pago em 10 parcelas iguais de R$ 1.260,00. Nesse caso, o juro total desse empréstimo será
(A) R$ 4.800,00.
(B) R$ 3.800,00.
(C) R$ 4.600,00.
(D) R$ 3.600,00.
(E) R$ 4.200,00.
Resolucao
Calculando o valor final:
10.1260 = 12600,00
Como os juros são simples e de 4% ao mês, em 10 vezes, o valor subiu 40%. Podemos então calcular o valor emprestado (x):
x + 40% de x = 12600
1,4x = 12600
x = 12600/1,4 = 9000
Calculando o total de juros:
12600 – 9000 = 3600
Alternativa D
17) Foram construídos dois reservatórios de água. A razão entre os volumes internos do primeiro e do segundo é de 2 para 5, e a soma desses volumes é 14 m³. Assim, o valor absoluto da diferença entre as capacidades desses dois reservatórios, em litros, é igual a
(A) 8 000.
(B) 6 000.
(C) 4 000.
(D) 6 500.
(E) 9 000.
Resolucao
Sejam:
x = volume do primeiro reservatório
y = volume do segundo reservatório
x/y = 2/5, ou seja, x = 2y/5
x + y = 14
Temos um sistema de equações. Substituindo a primeira na segunda equação: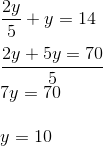
Vamos calcular o valor de x:
x = 2y/5 = 2.10/5 = 4
MEDIDAS DE COMPRIMENTO
19) (Basa-Cesgranrio) O comprimento de um grande fio corresponde à soma dos comprimentos de 24 fios menores. São eles:
- 12 fios, cada um dos quais com comprimento que mede 14,7 cm;
- 4 fios, cada um dos quais com comprimento que mede 0,3765 km;
- 8 fios, cada um dos quais com comprimento que mede 13,125 dam.
Esse grande fio foi dividido em 3 fios de igual comprimento, chamados de unidade modelo. Qual é a medida, em metros, do comprimento de uma unidade modelo?
(A) 6385,500
(B) 2557,764
(C) 852,588
(D) 94,302
(E) 31,434
Resolução
12 fios de comprimento 14,7 cm:
12 . 14,7 = 176,4 cm = 1,764 m
4 fios de comprimento 0,3765 km:
4 . 0,3765 = 1,506 km = 1506 m
8 fios de comprimento 13,125 dam:
8 . 13,125 = 105 dam = 1050 m
Total:
1,764 + 1506 + 1050 = 2557,764 m
Dividindo o fio grande por 3:
2557,764 = 852,588
Alternativa C
20) (PM AC) Determine o valor em decímetros de 0,375 dam.
(A) 3,75 dm
(B) 0,0375 dm
(C) 3750 dm
(D) 37,5 dm
(E) 375 dm
Resolução
Temos que:
1 dam (decâmetro) = 10 m
1 m = 10 dm (decímetros)
Logo, 1 dam = 100 dm
Daí, 0,375 dam = 37,5 dm
Alternativa D
21) (Correios) Nos Correios, são utilizados vários tipos de caixas para o envio de encomendas, entre elas, a caixa do tipo 4B, um paralelepípedo retângulo, em papel ondulado, com arestas medindo 360 mm, 270 mm e 180 mm. O volume dessa caixa, em dm³, é:
(A) superior a 18 e inferior a 21.
(B) superior a 21 e inferior a 24.
(C) superior a 24.
(D) inferior a 15.
(E) superior a 15 e inferior a 18.
Resolução
Veja em nossa sessão unidades e medidas que:
1 m = 10 dm (decímetros)
1 m = 1.000 mm (milímetros)
Primeiramente, transformaremos as medidas das arestas para dm:
360 mm = 3,6 dm
270 mm = 2,7 dm
180 mm = 1,8 dm
Para calcular o volume de um paralelepípedo retângulo, basta efetuarmos a multiplicação:
V = base . comprimento . altura
V = 3,6 . 2,7 . 1,8
V = 17,496 dm³
Alternativa E
MEDIDAS DE TEMPO
22) (TJ PE – FCC) Eram 22 horas e em uma festa estavam 243 mulheres e 448 homens. Verificou-se que, continuadamente a cada nove minutos, metade dos homens ainda presentes na festa ia embora. Também se verificou que, continuadamente a cada 15 minutos, a terça parte das mulheres ainda presentes na festa ia embora. Desta forma, após a debandada das 22 horas e 45 minutos, a diferença entre o número de mulheres e do número de homens é
(A) 14.
(B) 28.
(C) 36.
(D) 44.
(E) 58.
Resolução
Quantidade de homens:
22h: 448
22h 09min: 224
22h 18min: 112
22h 27min: 56
22h 36min: 28
22h 45min: 14
Quantidade de mulheres:
22h: 243
22h 15min: 162
22h 30min: 108
22h 45min: 72
Diferença:
72 – 14 = 58
Alternativa E
23) (IBGE – FGV) Quando era jovem, Arquimedes corria 15 km em 1h45min. Agora que é idoso, ele caminha 8 km em 1h20min.
Para percorrer 1 km agora que é idoso, comparando com a época em que era jovem, Arquimedes precisa de mais:
(A) 10 minutos
(B) 7 minutos
(C) 5 minutos
(D) 3 minutos
(E) 2 minutos
Resolução
Quando era jovem ele corria 15 km em 105 minutos.
105 / 15 = 7
Daí, Arquimedes percorria 1 km em 7 minutos.
Agora que é idoso ele caminha 8 km em 80 minutos.
80 / 8 = 10
Daí, Arquimedes percorre 1 km em 10 minutos.
Conclusão: Arquimedes precisa de mais 3 minutos.
Alternativa D
24) (PM AP – FCC) Os meses de março, abril e maio têm, respectivamente, 31, 30 e 31 dias. Sabendo que o dia 1° de março de 2018 cairá em uma quinta feira, o dia 31 de maio de 2018 cairá em uma
(A) 3a feira.
(B) 2a feira.
(C) 4a feira.
(D) 6a feira.
(E) 5a feira.
Resolução
Estando no dia 01/03, após 30 dias será 31/03.
Sabendo que abril possui 30 dias e que maio possui 31 dias, podemos concluir que passaram-se 91 (30 + 30 + 31) dias de 01/03 a 31/05.
Observe que a divisão de 91 dias por 7 (quantidade de dias por semana) é exatamente igual a 13, ou seja, se 01/03 foi uma quinta-feira, podemos concluir que, passadas exatas 13 semanas, o dia 31/05 também será em uma quinta.
Alternativa E
25) (PM AC – IBADE) Duas patrulhas A e B, de um mesmo Batalhão de Polícia Militar fazem ronda em diferentes bairros da cidade. A patrulha A efetua a ronda no bairro da Sorte e, caso não atenda a nenhuma ocorrência, retorna ao Batalhão em exatos 35 minutos, saindo em seguida para a próxima ronda. A patrulha B efetua a ronda no Bairro Esperança e, não atendendo a nenhuma ocorrência, retorna ao Batalhão em exatos 40 minutos, saindo em seguida para a próxima ronda.
Considerando que, no último domingo, as duas patrulhas saíram juntas do Batalhão às 14 horas e 50 minutos, se não houve ocorrências para ambas, em que horário elas voltaram a se encontrar no Batalhão?
(A) 18h e 55min
(B) 19h e 25min
(C) 18h e 50min
(D) 19h e 30min
(E) 18h e 20min
Resolução
A patrulha A retorna a cada 35 minutos, enquanto a patrulha B retorna a cada 40 minutos.
Como não existiram ocorrências, basta calcularmos o MMC de 35 e 40.
Temos:
35 = 5.7
40 = 2³.5
Daí, MMC(35, 40) = 280, ou seja, as patrulhas se encontrarão a cada 280 minutos, que equivale a 4 horas e 40 minutos.
Como as patrulhas saíram juntas às 14:50, podemos concluir que se encontrarão às 19:30.
Al;ternativa D
26) (PM PE) Três ciclistas A, B e C treinam em uma pista. Eles partem de um ponto P da pista e completam uma volta na pista ao passarem novamente pelo mesmo ponto P. O ciclista A gasta 30 seg , o ciclista B, 45 seg, e o ciclista C, 40 seg, para dar uma volta completa na pista. Após quanto tempo, os três ciclistas passam juntos, no ponto P, pela terceira vez consecutiva?
(A) 18 min.
(B) 25 min.
(C) 30 min.
(D) 15 min.
(E) 20 min.
Resolucao
O encontro acontece em um múltiplo comum de 30, 45 e 40.
Como MMC( 30, 45, 40) = 360, o primeiro encontro ocorrerá com 360 segundos, o segundo encontro com 720 segundos e o terceiro encontro com 1080 segundos.
Transformando para minutos:
1080 seg / 60 = 18 min
Alternativa A
27) (PM TO – Consulplan) Cássio é dentista e atende, em média, um paciente a cada 20 minutos. Num certo dia, Cássio conseguiu atender 16 pessoas num intervalo de 4 horas e 16 minutos. Quantos minutos ele conseguiu economizar, em média, em cada atendimento?
(A) 2 minutos
(B) 3 minutos
(C) 4 minutos
(D) 6 minutos
Resolucao
Para calcularmos a média no dia citado, basta dividirmos o tempo gasto pela quantidade de atendimentos.
Vamos então transformar 4 horas e 16 minutos em uma fração, para que possamos efetuar a divisão:
4 + 16/60
4 + 4/15
(60 + 4)/15
64/15
Agora podemos dividir por 16 para calcularmos a média:
(64/15) / 16 = 64/15.16 = 64/240 = 16/60
Poderíamos ter simplificado a fração, porém nosso objetivo é calcular o tempo médio em horas de cada atendimento, por isso deixamos o denominador ser igual a 60. Podemos então dizer que o mesmo é 16/60 horas ou 16 minutos.
Tempo médio economizado por atendimento: 20 – 16 = 4
Alternativa C
28) (TJ PR – UFPR) Um tanque é abastecido com água por três torneiras, cada uma com uma vazão diferente, que podem ser abertas e fechadas individualmente. Quando o tanque se encontra vazio, cada uma delas é capaz de enchê-lo em 2, 5 e 10 horas individualmente. Se as três torneiras forem abertas simultaneamente, no momento em que o tanque está vazio, quanto tempo será necessário para enchê-lo?
(A) 1 hora e 15 minutos.
(B) 1 hora e 48 minutos.
(C) 3 horas e 20 minutos.
(D) 7 horas e 12 minutos.
Resolução
Sendo x o tempo total, considerando que 2, 5 e 10 são inversamente proporcionais a vazão das torneiras, e que 1 representa o tanque cheio, temos a seguinte equação:
x/2 + x/5 + x/10 = 1
(5x + 2x + x)/10 = 1
8x/10 =1
x = 10/8 = 1,25
Convertendo para horas, 1,25 corresponde a 1 hora e 15 minutos
Alternativa A
29) (PM SP – Vunesp) Um escritório de advocacia precisa imprimir duas cópias de um mesmo documento, e a impressora disponível para realizar o serviço leva 12 segundos para imprimir cada uma das 50 páginas desse documento. Após imprimir a primeira cópia, com 50 páginas, foram feitos alguns ajustes e reparos nessa impressora, que passou a imprimir cada página desse documento em 9 segundos, o que fez com que o tempo gasto para imprimir as 50 páginas da segunda cópia desse documento fosse reduzido em
(A) 2 minutos e 50 segundos.
(B) 2 minutos e 30 segundos.
(C) 3 minutos e 30 segundos.
(D) 2 minutos e 05 segundos.
(E) 3 minutos e 50 segundos.
Resolução
Vamos calcular em quanto tempo a impressora imprimiu o primeiro documento:
(50 pág) x (12 seg) = 600 seg = 10 min
Agora basta notar que na segunda cópia, a impressora passou a imprimir uma folha em 9 segundos e não mais em 12.
A velocidade aumentou em 3/12 = 0,25 = 25%
Então, o tempo de impressão da segunda cópia reduziu em 25%:
25% de 10 minutos = 10.25/100 = 2,5 minutos = 2 minutos e 30 segundos
Alternativa B
30) (Sejus ES) Para ir de casa ao trabalho, de porta a porta, Elis percorre de bicicleta 3600 metros a uma velocidade média de 300 metros por minuto. Se esse mesmo percurso fosse efetuado utilizando-se uma moto a uma velocidade média de 30 quilômetros por hora, levaria a menos que de bicicleta
(A) 4 min 48 s.
(B) 4 min 8 s.
(C) 5 min 18 s.
(D) 6 min 8 s.
(E) 7 min 2 s.
Resolução
Com a bicicleta ele percorre 3600 metros a 300 metros por minuto, ele gasta:
3600/300 = 12 minutos
Com a moto sua velocidade é de 30 km por hora, como 1 hora = 60 minutos:
Sua velocidade em metros por minuto é 30000/60 = 500
Como são 3600 metros, 3600/500 = 7,2 minutos
Diferença:
12 – 7,2 = 4,8 minutos = 4 minutos e 48 segundos
Alternativa A
31) (GCM SP – IBADE) Leonardo acordou atrasado e, ao verificar o relógio, percebeu que o tempo decorrido do dia era igual a dois quintos do tempo até o final do dia. O horário, aproximado, em que Leonardo acordou foi:
(A) 17h e 9min.
(B) 6h e 51min.
(C) 15h e 33min.
(D) 6h e 22min.
(E) 9h e 10min.
Resolução
Considere que, quando Leonardo acordou, faltavam x horas para o final do dia.
Como “o tempo decorrido do dia era igual a dois quintos do tempo até o final do dia”, podemos concluir que havia se passado 2x/5.
Considerando que um dia possui 24 horas, temos que:
x + 2x/5 = 24
5(x + 2x/5) = 5.24
5x + 2x = 120
7x = 120
x = 120/7
Como 119/7 = 17, vamos considerar que:
x = 17 + 1/7
Como um dia possui 24 horas, Leonardo acordou:
24 – (17 + 1/7) = 6 + 6/7 horas
Vamos calcular quantos minutos equivalem a 6/7 horas?
60 minutos . 6/7 = 360/7 = 51,4
Conclusão: Leonardo acordou as 6 horas e 51 minutos.
Alternativa B
MEDIDA DE MASSA
32) (Banestes – FGV) 1 cm³ de gesso tem 1,4 g de massa.
A massa de 1 m³ de gesso é:
(A) 1,4 kg
(B) 14 kg
(C) 140 kg
(D) 1400 kg
(E) 14000 kg
Resolução
Calculando quantos cm³ existem em 1 m³:
100.100.100 = 1000000 cm³
Usando a proporção informada:
1000000 . 1,4 = 1400000 g
Como 1 kg equivale a 1000 gramas:
1400000 = 1400 kg
Alternativa D
33) (TJ CE – ESAF) Se uma solução contém 2 mg/ml de uma substância dissolvida, quanto da substância existe em um litro da solução?
(A) 200 mg
(B) 2 g
(C) 20 g
(D) 200 g
(E) 2 kg
Resolução
Como a proporção é de 2mg/ml e 1 litro corresponde a 1000 ml, basta multiplicarmos por 1 mil:
2mg x 1000 = 2000 mg
Como 1 g corresponde a 1000 mg, então existem 2 g da substância em 1 litro.
Alternativa B
34) (ENEM) A bula de um antibiótico infantil, fabricado na forma de xarope, recomenda que sejam ministrados, diariamente, no máximo 500 mg desse medicamento para cada quilograma de massa do paciente. Um pediatra prescreveu a dosagem máxima desse antibiótico para ser ministrada diariamente a uma criança de 20 kg pelo período de 5 dias. Esse medicamento pode ser comprado em frascos de 10 mL, 50 mL, 100 mL, 250 mL e 500 mL. Os pais dessa criança decidiram comprar a quantidade exata de medicamento que precisará ser ministrada no tratamento, evitando a sobra de medicamento. Considere que 1 g desse medicamento ocupe um volume de 1 cm³.
A capacidade do frasco, em mililitro, que esses pais deverão comprar é
(A) 10.
(B) 50.
(C) 100.
(D) 250.
(E) 500.
Resolução
A criança possui 20 kg e a dose diária máxima é de 0,5 gramas (500 mg) por quilo de massa do paciente.
20 . 0,5 = 10 gramas por dia
A questão informa que o pediatra prescreveu o remédio por 5 dias:
5 . 10 = 50 gramas
Considerando que 1 g desse medicamento ocupa um volume de 1 cm³, é fácil concluir que 50 gramas ocuparão um volume de 50 cm³.
Finalizando, o aluno deveria ter o conhecimento prévio de que 1 cm³ equivale a 1 mL, ou seja, o paciente deverá tomar 50 mL do medicamento.
Alternativa B
35) (ESAF) Se uma solução contém 2 mg/ml de uma substância dissolvida, quanto da substância existe em um litro da solução?
(A) 200 mg
(B) 2 g
(C) 20 g
(D) 200 g
(E) 2 kg
Resolução
Como a proporção é de 2mg/ml e 1 litro corresponde a 1000 ml, basta multiplicarmos por 1 mil:
2.1000 = 2000 mg
Como 1 g corresponde a 1000 mg, existem 2g da substância em 1 litro de solução.
Alternativa B
MEDIDAS DE ÁREAS
36) (PM RN – Consultec) Sabe-se que 1 hectare é equivalente a 10.000m², ou seja, a um quadrado de lado 100m. Se os 800.000 habitantes da cidade de Natal fossem uniformemente distribuídos nos 172km² da área da cidade, então é correto afirmar que, em cada hectare, deveriam morar, aproximadamente,
01) 4600 pessoas.
02) 480 pessoas.
03) 460 pessoas.
04) 48 pessoas.
05) 46 pessoas.
Resolução
Temos que 1 hectare é equivalente a 0,01 km².
Calculando a quantidade de hectares da cidade:
172 / 0,01 = 17200 hectares
Quantidade de habitantes por hectare:
800000 / 17200 = 46,5 pessoas
Resposta: 05
37) (PM PI – Nucepe) José comprou um sítio de 14 hectares, reservando, para a construção da casa e área de lazer, 1/4 do terreno. O restante, José usou para plantar arroz, milho e feijão. Se a área plantada tem 2/7 de arroz e 3/5 de milho, quantos metros quadrados do terreno foram ocupados com a plantação de feijão?
Dado: 1 hectare = 10000 m²
(A) 140.000 m²
(B) 72.000 m²
(C) 105.000 m²
(D) 12.000 m²
(E) 25.000 m²
Resolução
Se ele reservou 1/4 para a construção, então restaram 3/4 para a plantação:
14 hectares x 3/4 = 14.3/4 = 42/4 = 10,5 hectares
Desses 10,5 hectares ele plantou 2/7 de arroz, 3/5 de milho e feijão no restante:
2/7 + 3/5 = (10 + 21)/35 = 31/35
Logo, sobraram 4/35 para o feijão.
10,5 hectares x 4/35 = 10,5.4/35 = 42/35 = 6/5 hectares.
Como 1 hectare = 10000 m²:
10000.6/5 = 60000/5 = 12000 m²
Alternativa D
38) (TJ RG – FAURGS) Se a área do desenho de um retângulo na escala 1:200 é de 50 cm², então a área real desse retângulo é de
(A) 1 m²
(B) 5 m²
(C) 20 m²
(D) 100 m²
(E) 200 m²
Resolução
Se os lados do desenho são x e y, e a escala é 1:200, podemos concluir que os lados do retângulo são 200x e 200y.
Calculando a área:
200x.200y = 40000xy
Daí, temos que a área real é 40000 vezes maior do que a área do desenho:
50.40000 = 2.000.000 cm² = 200 m²
Alternativa E
MEDIDAS DE VOLUME
39) (TJ CE – ESAF) Quantos cm³ existem em 10 litros?
(A) 10
(B) 100
(C) 1.000
(D) 10.000
(E) 100.000
Resolução
Para resolver a questão, o candidato deverá ter conhecimento de que em 10cm³ cabe exatamente 1 litro.
Imagine 10 caixas de 10 cm³ cada uma, lado a lado. O volume, se considerarmos que são apenas um sólido é:
10 cm x 10 cm x 100 cm = 10.000 cm³
Alternativa D
40) (ENEM) Uma empresa especializada em conservação de piscinas utiliza um produto para tratamento da água cujas especificações técnicas sugerem que seja adicionado 1,5 ml desse produto para cada 1000 l de água da piscina. Essa empresa foi contratada para cuidar de uma piscina de base retangular, de profundidade constante igual a 1,7 m, com largura e comprimento iguais a 3 m e 5 m, respectivamente. O nível da lâmina d’água dessa piscina é mantido a 50 cm da borda da piscina.
A quantidade desse produto, em mililitro, que deve ser adicionada a essa piscina de modo a atender às suas especificações técnicas é :
(A) 11,25
(B) 27,00
(C) 28,80
(D) 32,25
(E) 49,50
Resolução
A piscina possui uma profundidade de 1,7 m. Como o nível da água é mantido a 50 cm da borda, podemos concluir que a altura da água é de 1,2 m, ou seja, a água ocupa um paralelepípedo reto de medidas 1,2, 3 e 5 metros.
Calculando o volume:
1,2 . 3 . 5 = 18 m³
Sabendo que a proporção é de 1 m³ de volume para 1000 litros de água, podemos calcular a quantidade de litros de água da piscina:
18 . 1000 = 18.000 litros
Calculando a quantidade de produto:
18 . 1,5 = 27ml
Alternativa B
41) (PM Pará – Fadesp) Sabendo-se que uma pessoa consome aproximadamente 800 metros cúbicos de água por ano e que o planeta dispõe de, no máximo, 9000 quilômetros cúbicos de água para o consumo por ano, pode-se afirmar que a capacidade máxima de habitantes que o planeta suporta, considerando-se apenas a disponibilidade de água
para consumo, é aproximadamente:
(A) 11.100.000.000.
(B) 11.150.000.000.
(C) 11.250.000.000.
(D) 11.350.000.000.
Resolução
Sabe-se que 1 km³ corresponde a 1.000.000.000 m³, daí 9.000 km³ correspondem a 9.000.000.000.000 m³.
9.000.000.000.000 / 800 = 11.250.000.000
Alternativa C
42) (PM RN – Consultec) Um reservatório, inicialmente vazio, com capacidade para 8000 litros, recebe água à razão de 1600cm³ por segundo.
O tempo decorrido para que ele fique totalmente cheio é de
01) 1h 20min 40s
02) 1h 21min 30s
03) 1h 22min
04) 1h 23min 20s
05) 1h 24min 40s
Resolução
Para resolvermos a questão, é necessário sabermos que:
– 1 m³ equivale a 1000 litros.
– 0,0016 m³ equivale a 1600 cm³.
O objetivo da questão é encher um reservatório de 8 m³ a uma taxa de 0,0016 m³ por segundo.
8 / 0,0016 = 5000 segundos
Efetuando as devidas transformações, temos que 5000 segundos é equivalente a 1h 23min 20s.
Resposta 04
43) (Correios – Cespe) Nos Correios, são utilizados vários tipos de caixas para o envio de encomendas, entre elas, a caixa do tipo 4B, um paralelepípedo retângulo, em papel ondulado, com arestas medindo 360 mm, 270 mm e 180 mm. O volume dessa caixa, em dm³, é:
(A) superior a 18 e inferior a 21.
(B) superior a 21 e inferior a 24.
(C) superior a 24.
(D) inferior a 15.
(E) superior a 15 e inferior a 18.
Resolução
Veja em nossa página sobre unidades e medidas que:
1 m = 10 dm (decímetros)
1 m = 1.000 mm (milímetros)
Transformando as medidas das arestas para dm:
360 mm = 3,6 dm
270 mm = 2,7 dm
180 mm = 1,8 dm
Calculando o volume do paralelepípedo retângulo:
Volume = base x comprimento x altura.
Volume = 3,6 x 2,7 x 1,8
Volume = 17,496dm³
Alternativa E
44) (PM RN – Consultec) Na saída da cidade de Mossoró (RN), uma blitz intercepta um caminhão- baú lotado de caixas retangulares, cada uma com 12 garrafas de mel. O comandante da operação ordenou que o soldado contasse quantas garrafas de mel havia no caminhão. O soldado, inteligentemente, simplesmente verificou que o volume interno do baú era igual a 36m³ e que o volume de cada caixa era igual a 36000cm³. Voltou-se ao comandante e disse, com toda certeza, que o número de garrafas era x.
Se o baú estava com a maior quantidade possível de caixas e se a resposta do soldado está correta, 15% de x é igual a
01) 2800
02) 2400
03) 1800
04) 1600
05) 1500
Resolução
Temos que 36000cm³ = 0,036m³. Como a capacidade do baú é de 36m³, podemos concluir que o número de caixas de mel é:
36 / 0,036 = 1000 caixas
Como cada caixa possui 12 garrafas, podemos concluir que existem 12000 garrafas.
15% . 12000 = 1800
Resposta: 03
Continua...





