Professor Diminoi
RAIZ QUADERADA & RAIZ CÚBICA
A raiz quadrada é um caso particular e comum de radiciação.
Calcular a raiz quadrada de um número x é procurar qual número elevado a dois resulta em x.
Raiz quadrada é uma operação básica da Matemática.
A raiz quadrada é uma operação básica e importante da matematica. Se trata da operação inversa da potenciacao. Assim, calcular a raiz quadrada de um número n é descobrir qual número elevado ao quadrado resulta em n.
Por exemplo, a raiz quadrada de 9 é igual a 3, pois, 3² é 9.
Uma raiz quadrada pode ser exata, gerando um número chamado de quadrado perfeito, ou pode ser não exata.
Radiciação
Na raiz quadrada, o índice da raiz é 2. Ela é a mais comum entre as radiciações, mas também é possível calcular raiz cúbica, raiz quarta, entre outras raízes.
A radiciação é o inverso da potenciação. Por exemplo, se eu pedir a raiz quinta de um número n, estamos procurando qual é o número que, multiplicado por ele 5 vezes, resulta em n.
Elementos da radiciação
A raiz quadrada é uma radiciação que possui o índice igual a 2.
Ela é a operação inversa de uma potência de expoente 2.
Seus elementos fundamentais são: índice, radical, radicando e raiz.
A raiz quadrada de um número aé representada por √a.
Pode ser exata ou não exata.

Quando os índices são diferentes
Para realizar uma multiplicação ou uma divisão entre raízes que apresentam índices distintos, precisamos modificá-las para que todas tenham o mesmo índice. Para tanto, podemos aplicar a 2ª propriedade da radiciação, que afirma que
Exemplos 1:
a) √9 + √4 = 5
b) √25 - √16 = 1
c) √49 + √16 = 11
d) √100 - √36 = 4
f) √25 - ³√8 = 3
g) ³√27 + ⁴√16 = 5
h) ³√125 - ³√8 = 3
i) √25 - √4 + √16 = 7
j) √49 + √25 - ³√64 = 8
Exemplos 2:
a) 5√2 + 3√2 = (5+3)√2 = 8√2
b) 6³√5 - 2³√5 = (6 – 2) ³√5 = 4³√5
c) 2√7 - 6√7 + √7 = (2 – 6 +1) √7 = -3√7
Exemplos 3:
a) 2√7 + 3√7 = 5√7
b) 5√11 - 2√11 = 3√11
c) 8√3 - 10√3 = -2√3
d) ⁴√5 + 2⁴√5 = 3⁴√5
e) 4³√5 - 6³√5 = -2³√5
f) √7 + √7 = 2√7
g) √10 + √10 = 2√10
h) 9√5 + √5 = 10√5
i) ⁵√2 – 8.³√2 = -5.³√2
j) ³√7 – 13.³√7 = -5.³√7
k) 7√2 - 3√2 +2√2 = 6√2
l) 5√3 - 2√3 - 6√3 = -3√3
m) 9√5 - √5 + 2√5 = 10√5
n) 7√7 - 2√7 - 3√7 = 2√7
o) 8. ³√6 - ³√6 – 9. ³√6 = -2. ³√6
p) ⁴√8 + ⁴√8 – 4. ⁴√8 = -2. ⁴√8
Como se calcula raiz quadrada "na mão"?
O melhor método para calcular a raiz quadrada é decompor o número em seus fatores primos.
Exemplo
Raiz de 64.
Decompomos o 64 seus fatores primos:
64 | 2
32 | 2
16 | 2
8 | 2
4 | 2
2 | 2
1
Logo 64 é igual a 26.
Dividimos o expoente 6 pelo expoente da raiz quadrada (que é 2), e retiramos o número da raiz.
Exemplos
6 dividido por 2 é igual a 3, então a resposta é 23, ou seja, 8.
![]()
Tipos de raiz quadrada
Uma raiz quadrada pode ser exata ou não. Para que a gente consiga classificar, precisamos levar em consideração se a resposta é um número racional ou um número irracional.
Raiz quadrada exata
Uma raiz quadrada é exata quando resulta em um numero racional, como uma fracao, um número inteiro, um número decimal, desde que, ao multiplicar esse número por ele mesmo, encontremos exatamente o radicando.
Exemplos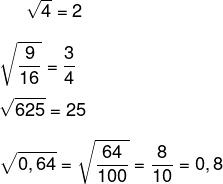
Quando o número para o qual desejamos calcular a raiz quadrada exata é muito grande, o ideal é recorrer à fatoração desse número. Como estamos calculando a raiz quadrada, vamos agrupar essa fatoração como potências de dois conforme o exemplo a seguir.
Exemplo
Calcule a raiz quadrada de 3600.
Agora que realizamos a fatoração, vamos calcular a raiz de 3600 na forma fatorada.
Podemos perceber que a raiz de um número ao quadrado é igual ao próprio número. Por exemplo, sabemos que 3 ao quadrado é 9 e que a raiz de 9 é igual ao próprio 3.
Então podemos simplificar o expoente 2 com o radical.
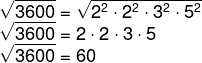
Na raiz exata, quando a resposta é um número natural, ele é conhecido como quadrado perfeito. Veja todos os quadrados perfeitos de 0 até 100.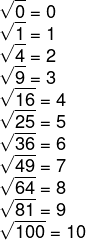
Os quadrados perfeitos de 0 até 100 são 0, 1, 4, 9, 16, 25, 36, 49, 64, 81 e 100.
Raiz quadrada não exata
Existem casos em que a raiz não é exata. Quando isso acontece, podemos encontrar a melhor aproximação possível para a raiz desse número, já que a resposta é um número irracional. Para essa aproximação, vamos utilizar os quadrados perfeitos que já conhecemos.
Exemplo
Para encontrar a raiz de 40, vamos compará-la com as raízes exatas que conhecemos. Analisando os quadrados perfeitos, sabemos que 40 está entre 36 e 49.
![]()
Agora vamos encontrar o número decimal entre 6 e 7 que está mais próximo de 40.
6,1² = 37,21
6,2²= 38,44
6,3²=39,69
6,4²=40,96 → passou de 40, então vamos usar o número decimal anterior para a aproximação.
![]()
Perceba que 6,32 não dá exatamente 40, mas chega próximo, por isso essa raiz quadrada não é exata.
Interpretação geométrica da raiz quadrada
Alguns livros de história da matemática dizem que a raiz quadrada surgiu para resolver problemas de áreas de quadrdado. Suponha que queiramos achar o lado de um terreno que tem formato de um quadrado e que sua área seja igual a 169 m².
Como a area do quadadro é calculada por l², então calcular a raiz de 169, geometricamente, é encontrar o lado do quadrado que possui essa área.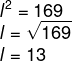
O lado do quadrado é de 13 metros.
QUESTOES RESOLVIDAS – RAIZ QUADRDADA
01) Qual é a melhor aproximação para a raiz quadrada de 72?
(A) 8,1
(B) 8,2
(C) 8,3
(D) 8,4
(E) 8,5
Resolução
Sabemos que 72 está entre os quadrados perfeitos 64 e 81, então temos que:![]()
8,1² = 65,61
8,2² = 67,24
8,3² = 68,89
8,4² = 70,56
8,5² = 72,25 → passou, então a melhor aproximação é a anterior, 8,4.
Alternativa D
02) Qual das raízes abaixo não é exata?
(A) √121
(B) √1,69
(C) √5
(D) √1/4
(E) √1
Resolução
a) Possui raiz exata igual a 11, pois 11² =121.
b) Possui raiz exata igual a 1,3, pois 1,3² = 1,69.
c) Não possui raiz exata
d) Possui raiz exata, pois o numerador 1²=1 e o denominador 22 = 4, logo a raiz dessa fração é igual a 1/2.
e) Possui raiz exata igual a 1.
Alternativa C
Raiz quadrada não exata
Em muitos casos, o número pode não possuir uma raiz quadrada exata, ou seja, a solução da raiz quadrada é um numero irrracional. Para calcular uma raiz quadrada não exata, utilizamos aproximações, ou seja, números que quando elevamos ao quadrado chegam bem próximo do resultado desejado.
03) Calcule o valor da √60.
Resolução:
Sabemos que essa raiz não é exata, então, primeiramente, identificaremos qual é o número anterior a 60 que possui raiz exata, que é 49, e também o número posterior a 60 que possui raiz exata, que é 64.
√49 < √60 < √64
Calculando as raízes de 49 e 64:
7 < √60 < 8
Note que 60 está próximo de 64, então a √60 estará próxima de 8. Calcularemos, assim, o quadrado dos números próximos a 8.
7,9² = 62,41
7,8² = 60,84
7,7² = 59,29
Descobrimos que a √60 está entre 7,7 e 7,8.
Portanto, dizemos que a √60 = 7,7 por falta ou que a √60 = 7,8 por excesso.
EXERCIOS RESOLVIDOS
02) Sobre a raiz quadrada, julgue as afirmativas a seguir:
I → É possível calcular a raiz quadrada de número negativo.
II → Os números 0, 1, 4, 9 e 16 são todos quadrados perfeitos menores que 20.
III → A raiz quadrada de 6 é igual a 3.
As afirmativas são, respectivamente:
(A) V, V e V.
(B) F, F e F.
(C) F, F e V.
(D) F, V e F.
(E) V, F e V.
Resolução:
I → Falsa
A potência de dois possui resultado somente positivo, logo, não é possível calcular a raiz quadrada de um número negativo.
II → Verdadeira
Os números listados são os únicos que possuem raiz exata menores que 30.
III → Falsa
3² = 9, logo, a raiz quadrada de 9 é 3, e não a de 6.
Alternativa D
06) (PM Piauí – Nucepe) A expressão √18 + √50 é equivalente:
(A) 2√2
(B) 3√2
(C) 8√2
(D) 15√2
(E) 8√3
Resolução
Vamos fatorar os números dentro dos radicais:
18 = 2.3²
50 = 2.5²
Resolvendo a expressão:
√18 + √50 = √(2.3²) + √(2.5²) = 3√2 + 5√2 = 8√2
Alternativa C
07) (Ethos concursos) A raiz quadrada de um número é uma importante operação matemática, assim como a adição, a subtração, a multiplicação e a divisão. Somente alguns números possuem raiz quadrada, aqueles considerados quadrados perfeitos. Sendo assim, calcule a raiz quadrada de 625 e assinale a alternativa CORRETA.
(A) 35
(B) 24
(C) 25
(D) 17
(E) 49
Resolução
Inicialmente, realizaremos a fatoração do número: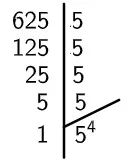
Dessa forma, temos:
√625 = √54
√625 = 5²
√625 = 25
Alternativa C
08) Sobre a raiz quadrada, julgue as afirmativas a seguir:
I → É possível calcular a raiz quadrada de número negativo.
II → Os números 0, 1, 4, 9 e 16 são todos quadrados perfeitos menores que 20.
III → A raiz quadrada de 6 é igual a 3.
As afirmativas são, respectivamente:
(A) V, V e V.
(B) F, F e F.
(C) F, F e V.
(D) F, V e F.
(E) V, F e V.
Resolução
I → Falsa
A potência de dois possui resultado somente positivo, logo, não é possível calcular a raiz quadrada de um número negativo.
II → Verdadeira
Os números listados são os únicos que possuem raiz exata menores que 30.
III → Falsa
3² = 9, logo, a raiz quadrada de 9 é 3, e não a de 6.
Alternativa D
09) Determine a raiz quadrada do número 1024.
√1024
Para determinar a raiz de 1024, vamos fazer a decomposição em primos:
1024 = 22 . 22 . 22 . 22 . 22
Então,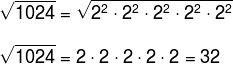
10) Um terreno possui área igual a 196 m². Sabendo que esse terreno tem formato de um quadrado, então os seus lados possuem medida igual a:
(A) 12 m.
(B) 13 m.
(C) 14 m.
(D) 15 m.
Resolucao
A área de um quadrada é igual ao lado ao quadrado, então, para encontrar o valor do lado, vamos calcular a raiz quadrada da área do terreno.
Para calcular a raiz quadrdada de 196, vamos fatorar esse número: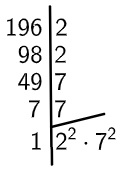
Então, temos que:![]()
Alternativa C
11) Dos números abaixo, marque aquele que possui uma raiz quadrada exata.
(A) 600
(B) 215
(C) 144
(D) 110
(E) 70
Resolucao
Analisando as alternativas, a única que é formada por um quadrado perfeito é a alternativa “c”, pois temos que 12² = 144, ou seja, √144 = 12. As demais alternativas não são raízes exatas.
Alternativa C
12) O valor da expressão algébrica √4 + √16 – √25 . √9
(A) – 9.
(B) – 6.
(C) – 5.
(D) – 4.
(E) – 2.
Resolucao
Resolvendo a expressão, temos que:
√4+√16 – √25 ×√9
2 + 4 – 5 × 3
6 – 15
– 9
Alternativa A
13) (Cefet/RJ) Por qual número devemos multiplicar o número 0,75 de modo que a raiz quadrada do produto obtido seja igual a 45?
(A) 2700
(B) 2800
(C) 2900
(D) 3000
Resolucao
Seja x o número procurado, temos que: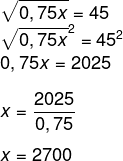
Alternativa: A
14) O valor da expressão numérica a seguir é:
(A) 2
(B) 3
(C) 4
(D) 5
(E) 6
Resolucao
Realizando o produto, temos que: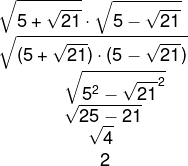
Alternativa A
15) Qual é a raiz quadrada de 5184?
(A) 42
(B) 58
(C) 68
(D) 72
(E) 88
Resolucao
Fatorando 5184, temos que:
Então, podemos fazer o seguinte cálculo: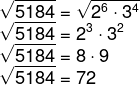
Alternativa D
16) Analise as afirmativas a seguir:
I - A raiz quadrada de 1500 é menor que 38.
II – A raiz quadrada de 190 é maior que 13.
III – A raiz quadrada de 0 é igual a 0.
Marque a alternativa correta.
(A) Somente a afirmativa I é verdadeira.
(B) Somente a afirmativa II é verdadeira.
(C) Somente a afirmativa III é verdadeira.
(D) Somente as afirmativas I e II são verdadeiras.
(E) Somente as afirmativas II e III são verdadeiras.
Resolucao
I → Falsa, pois sabemos que 38 · 38 = 1.444, logo a raiz de 1500 é maior que 38.
II → Verdadeira, pois sabemos que 13 · 13 = 169, logo a raiz de 190 é maior que 13.
III → Verdadeira, pois a raiz de 0 é 0.
Alternativa E
17) (Ethos concursos) A raiz quadrada de um número é uma importante operação matemática, assim como a adição, a subtração, a multiplicação e a divisão. Somente alguns números possuem raiz quadrada, são aqueles considerados quadrados perfeitos. Sendo assim, calcule a raiz quadrada de 625 e assinale a alternativa CORRETA.
(A) 35
(B) 24
(C) 25
(D) 17
(E) 49
Resolucao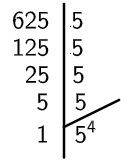
Então, temos que:
√625 = √54
√625 = 5²
√625 = 25
Alternativa C
18) Qual é o valor da simplificação da expressão a seguir?![]()
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
Resolucao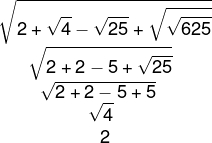
Alternativa C
19) Sabendo que √x = 9, então o valor da terça parte de x é:
(A) 81
(B) 72
(C) 36
(D) 27
(E) 9
Resolucao
√x = 9
√x² = 9²
x = 81
Como queremos a terça parte de x então 81: 3 = 27.
Alternativa D
20) Sobre a raiz quadrada, julgue as afirmativas a seguir.
I → Não é possível calcular a raiz quadrada de número negativo.
II → Os números 0, 1, 4, 9 e 16 são todos os quadrados perfeitos menores que 20.
III → A raiz quadrada de 8 é igual a 4.
As afirmativas são, respectivamente:
(A) V, V e V.
(B) F, F e F.
(C) F, F e V.
(D) V, V e F.
(E) V, F e V.
Resolucao
I → Verdadeira.
II → Verdadeira.
II → Falsa, pois 4 é raiz quadrada de 16, e não de 8.
Alternativa D
21) (IFG) Os babilônicos talvez tenham usado a fórmula abaixo para obter aproximações interessantes de raízes quadradas de números não quadrados perfeitos.
Atribuindo a = 4/3 e b = 2/9 nessa fórmula, é correto afirmar que obtemos a aproximação: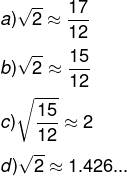
Resolucao
Vamos substituir o valor de a e b: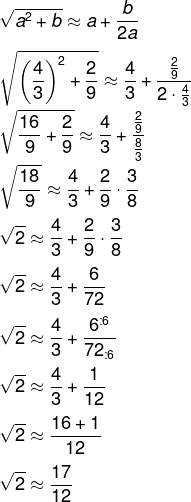
Alternativa A
22) (Guarda Civil SP) Qual o valor da expressão √(0,0016) : √(0,000064) ?
(A) 0,0005
(B) 0,005
(C) 0,5
(D) 5
(E) 50
Resolução
Vamos resolver por partes:
√(0,0016) = √(0,0016) = √(16/10000) = 4/100
√(0,000064) = √(0,000064) = √(64/1000000) = 8/1000
Fazendo a divisão: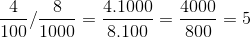
Alternativa D
23) (Guarda Civil SP) Qual o valor de x na expressão abaixo?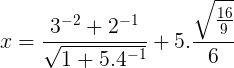
(A) 1/27
(B) 41/27
(C) 1/17
(D) 11/18
(E) 41/17
Resolução
Vamos calcular por partes:
3-² + 2-¹ = 1/9 + 1/2 = (2 + 9)/18 = 11/18
√(1 + 5.4-¹) = √(1 + 5/4) = √[(4 + 5)/4] = √(9/4) = 3/2
5.√(16/9)/6 = 5.(4/3)/6 = 5 . 4/6 . 3 = 20/18 = 10/9
(11/18) / (3/2) = 11. 2/18 . 3 = 22/54 = 11/27
11/27 + 10/9 = (11 + 30)/27 = 41/27
Alternativa E
24) (PM Piauí – Nucepe) A expressão √18 + √50 é equivalente:
(A) 2√2
(B) 3√2
(C) 8√2
(D) 15√2
(E) 8√3
Resolução
Vamos fatorar os números dentro dos radicais:
18 = 2.3²
50 = 2.5²
Resolvendo a expressão:
√18 + √50 = √(2.3²) + √(2.5²) = 3√2 + 5√2 = 8√2
Alternatiova C
25) (DNIT ESAF) Qual o valor da expressão?![]()
(A) 3
(B) √3
(C) 5
(D) √5
(E) 4
Resolução
Vamos resolver utilizando as propriedades da radiciação: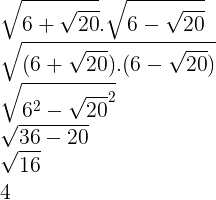
26) Quala raiz quadrada do número 256?
O seguinte resultado foi obtido:
27) Qual a raiz dadrada vde 512?
Resolucao 
Fatoração 512.
Após a simplificação obtemos o resultado:
RAIZ CUBICA
Como calcular raiz cúbica?
Existem várias maneiras de calcular a raiz cúbica, mas quais são elas? Aqui, entenderemos, junto aos exemplos, as formas de se calcular a raiz cúbica de um número.
Confira: Relacionadas
MMC e MDC
O MDC e o MMC são essenciais para tornar mais fáceis alguns tipos de conta, além de serem importantes para o estudo da matemática.
Equação de Segundo Grau
As equações de segundo grau fazem parte da matemática, e podem ter suas raízes encontradas por meio da fórmula de Bhaskara.
Função exponencial
Uma planta crescendo, a população de uma cidade diminuindo e outros exemplos podem ser explicados matematicamente pela função exponencial.
Por fatoração
A fatoração nos ajuda em muitos momentos no mundo da matemática e, com o cálculo de raiz cúbica, não seria diferente. Para se calcular a raiz cúbica de um número por fatoração, são necessários os seguintes passos:
Primeiro, devemos fatorar o número em questão. Vamos tomar como exemplo o número 125;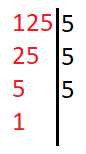
Em seguida, colocamos o número fatorado dentro da raiz cúbica;![]()
Por fim, elevamos o número fatorado pelas vezes que ele se repete e obtemos o resultado.![]()
Alguns exemplos do cálculo de raiz cúbica por fatoração: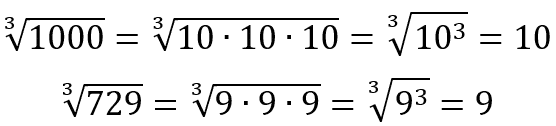
Raízes cúbicas por estimação repetida
Esse método é utilizado para obter a raiz cúbica de qualquer número. Para esse exemplo, vamos tentar descobrir a raiz cúbica de 600. Dessa forma, vamos começar a entender o método.
Primeiro, devemos escolher dois limites: um inferior e um superior. Em outras palavras, precisamos saber dois cubos perfeitos entre os quais o 600 esteja. Sabe-se que 8³=512 e 9³=729. Assim, a solução para a raiz cúbica de 600 está entre 8 e 9;
O segundo passo é escolher um segundo digito. Como o resultado está entre 8 e 9, podemos escolher o segundo digito como sendo 5. Assim, nosso possível resultado é 8,5. Vamos testar a estimativa elevando-a ao cubo. Dessa forma, 8,5³ = 614,1;
No passo anterior, obtivemos um resultado maior que 600. Vamos então ajustar nossa estimativa. Assim, vamos reduzir o segundo digito para 4, assim a estimativa fica 8,4. Elevando-a ao cubo, obtemos 8,4³ = 592,7;
O próximo passo é ajustar a estimativa novamente até se obter um resultado que seja o mais próximo possível do verdadeiro. Se fizermos 8,43 ao cubo, vamos obter como resultado o valor 599,07, mas ainda não é um resultado que queremos. Se fizermos 8,434 ao cubo, teremos o resultado de 599,93, que é muito próximo de 600. Portanto, o resultado da raiz cúbica de 600, de uma forma aproximada, é 8,434.
Esse método, como podemos ver, é uma forma de tentativa e erro. Em outras palavras, você tem que ir tentando ajustar a estimativa até chegar próximo do resultado.
QUESTOES RESOLVIDAS – RAIZ CUBICA
01) Qual é a raiz cúbica de 3375?
(A) 12
(B) 13
(C) 14
(D) 15
(E) 16
Resolucao
Para calcular essa raiz, utilizaremos o metodo da fatoracao:
Em vez de multiplicar todos os fatores obtidos, como é feito para encontrar o mínimo múltiplo comum, reescreva esses fatores agrupando-os em potências de 3 sempre que possível, como foi feito acima.
Para finalizar, substitua 3375 por 33·53 no radical para obter a seguinte raiz e prossiga utilizando as propriedades dos radicais![]()
Alternqativa D
02) Em função de √2, qual é o resultado da expressão a seguir?![]()
(A) 22√2
(B) 16√2
(C) 32√2
(D) 21√2
(E) 18√2
Resolucao
Primeiramente, decomponha 2048 e 512. Após isso, reescreva os fatores primos em potências de 2, se possível.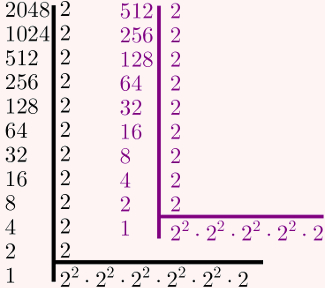
Por fim, utilize as mesmas propriedades do exercício anterior para simplificar os cálculos e subtraia os resultados. Observe: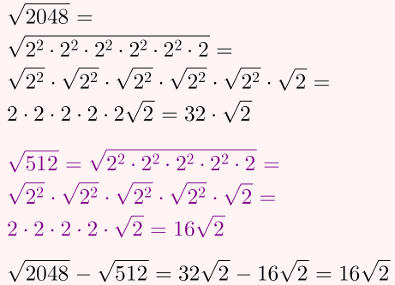
Alternativa B
03) Quais são as raízes da equação x2 + 16x – 36 = 0?
(A) 2 e 3
(B) 20 e 20
(C) 2 e 20
(D) 20 e – 20
(E) 2 e – 18
Resolucao
Utilizando o método de Bhaskara, calcularemos o discriminante: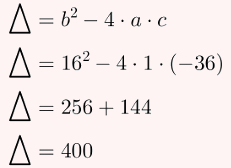
Tendo em vista que precisaremos calcular a raiz de 400 para usar seu resultado na fórmula de Bhaskara, seguem os respectivos cálculos: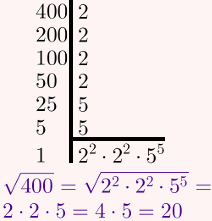
Agora resta apenas calcular as raízes: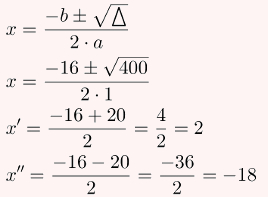
Dessa maneira, as raízes são 2 e –18.
Alternativa E
04) Um lote quadrado possui 1600 m2 de área. Qual é a medida do comprimento desse lote quadrado?
(A) 40 m
(B) 42 m
(C) 44 m
(D) 46 m
(E) 48 m
Resolucao
A medida do lado de um quadrado sempre pode ser obtida a partir da raiz quadrada de sua área. Portanto, basta calcular a raiz quadrada de 1600 para obter a medida em questão. Utilizando o método da fatoração, teremos: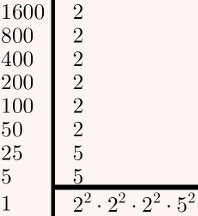
Para finalizar, substitua 1600 no radical pelo produto encontrado na fatoração anterior, como ilustrado na imagem seguinte:
Portanto, o comprimento do lote é 40 m.
Alternativa A
Contunuacao ...






