Professor Diminoi
O que é o módulo ou valor absoluto de um número?
O módulo ou valor absoluto de um número corresponde à distância que esse número está da origem na reta numérica.
O conjunto dos números inteiros, representado por , inclui os números naturais e exclui os números exclusivamente racionais ou irracionais. Portanto, dentro dos inteiros, há todos os números positivos e negativos desde que não sejam decimais. Para demonstrar a distribuição dos números inteiros, nós utilizamos a reta numérica: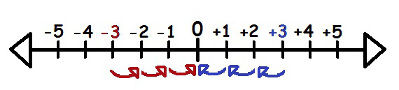 O (+3) e o (-3) possuem o mesmo módulo, pois ambos estão três unidades distantes da origem
O (+3) e o (-3) possuem o mesmo módulo, pois ambos estão três unidades distantes da origem
Nessa reta estão destacados os números – 3 e +3. Queremos verificar a distância desses números em relação ao ponto zero, que podemos chamar de origem. Se considerarmos que os espaços entre um número e outro possuem o mesmo tamanho, podemos chamar essa distância de “uma unidade”. Logo, no desenho, cada seta representa uma unidade.
Analisando a imagem, vemos que o – 3 está a três unidades da origem, e que o +3 também está a três unidades da origem, mas em sentido oposto ao – 3.
Essa distância de um número à origem é chamada de módulo ou valor absoluto de um número e é representada da seguinte forma:
módulo de – a = |– a| = a
O módulo de um número sempre será positivo, pois ele representa uma distância variável positiva.
Exemplos de alguns exemplos de módulos:
|– 3| = 3
|+ 2| = 2
| 0 | = 0
|– 9| = 9
|+10| = 10
|– a| = a
|+ a| = a
Chamamos por números opostos ou simétricos aqueles números que possuem mesmo módulo ou valor absoluto, isto é, aqueles números que estão a mesma distância da origem, porém em sentidos opostos. Sendo assim, podemos afirmar que:
– 2 e + 2 são opostos ou simétricos
– 3 e + 3 são opostos ou simétricos
+ 4 e – 4 são opostos ou simétricos
+a e – a são opostos ou simétricos
E o que acontece quando operamos números opostos ou simétricos?
|- 4| + |+ 3| = 4 + 3 = 7
|+ 1| – |- 5| = 1 – 5 = – 4
|- 5|+|+7|-|-10| = 5 + 7 – 10 = + 2
(+4) + (– 4) = 0
(– 2) + (+ 2) = 0
Se nós estivermos realizando operações com o módulo ou o valor absoluto dos números, basta que nós façamos o cálculo independente do valor do número dentro do módulo. Agora, se somarmos números que se diferenciam apenas pelo sinal, uma vez que são simétricos, nossa soma sempre resultará em zero.
Exemplos:
a) | 34 | = 34
b) | -5 | = 5
c) | 0 | = 0
d) | -13 | = 13
e) |-√2|= √2
01) Observe a definição de módulo:
|-3| = 3
|5| = 5
|0| = 0
|-10| = 10
|π| = π
|-π| = π
|-√2| = √2
|√2| = √2
|√2 – 3| = 3 – √2
|3 – √2| = 3 – √2
02) Observe a definição de módulo:
a) |-13| = 13
b) |50| = 50
c) |0| = 0
d) |-1| = 1
e)|-π| = π
f) |-√3| = √3
g) |√3| = √3
03) Ache os valores de:
a) |-3 + 4| = |1| = 1
b) |5 – 16| = |-11| = 11
c) |1,3 – 4,5| = |-3,2| = 3,2
d) |√3 – 1| = √3 – 1
e)|2 – π| = π – 2
f) |1 – √3| = √3 – 1
04) Calcula, analiticamente, os seguintes módulos:
a) | 3 – 7| = 4
b) | -3 + 53| = 50
c) | -100 + 234| = 134
d) | – 5,8 + 3,0125| = 1,7875
05) Qual é o valor de y = |√2 – 1| – |1 – √2|?
Resolucao
Promeira vamos resolver por partes:
|√2 – 1| = √2 – 1
|1 – √2| = √2 – 1
Daí,
√2 – 1 – (√2 – 1) = 0
OBSERVACAO:
Identidade importante:![]()
06) Calcule o valor da expressão |5 – 12,3|
Resolucao
|5 – 12,3| = | - 7,3 | = 7,3
EQUACAO MODULAR
Equação modular é uma equação que, no primeiro ou no segundo membro, tem termos em módulo. Para resolver problemas de equação modular, devemos aplicar a definição de módulo. A equação modular é uma quacao que, no primeiro ou no segundo membro, possui termos em módulo. O módulo, conhecido também como valor absoluto, está ligado à distância que um número tem até o zero. Como estamos falando de distância, o módulo de um número é sempre positivo.
A equação modular é uma quacao que, no primeiro ou no segundo membro, possui termos em módulo. O módulo, conhecido também como valor absoluto, está ligado à distância que um número tem até o zero. Como estamos falando de distância, o módulo de um número é sempre positivo.
Módulo de um número real Módulo de x
Módulo de x
Para conseguir resolver problemas de equação modular, torna-se necessário relembrar a definição de módulo. O módulo é sempre igual à distância que um número tem até o zero, e, para representar o módulo de um número n, utilizamos a barra reta da seguinte forma: |n|. Para calcular o |n|, dividimos em dois casos:![]() Sendo assim, podemos dizer que |n| é igual ao próprio n quando ele for um número positivo ou igual a zero, e, no segundo caso, |n| é igual ao oposto de n se ele for negativo. Lembre-se de que o oposto de um número negativo é sempre positivo, sendo assim, o |n| tem sempre um resultado igual a um número positivo.
Sendo assim, podemos dizer que |n| é igual ao próprio n quando ele for um número positivo ou igual a zero, e, no segundo caso, |n| é igual ao oposto de n se ele for negativo. Lembre-se de que o oposto de um número negativo é sempre positivo, sendo assim, o |n| tem sempre um resultado igual a um número positivo.
Exemplos:
a) |2| = 2
b) |-1| = -(-1) = 1![]()
Como resolver uma equação modular?
Para encontrar a solução de uma equação modular, é necessário analisar cada uma das possibilidades, ou seja, dividir, sempre em dois casos, cada um dos módulos. Além de saber a definição de módulo, para resolver equações modulares, é fundamental que se saiba resolver equacoes polinominal.
Exemplo 1
|x – 3| = 5
Para encontrar a solução dessa equação, é importante relembrar que existem dois resultados possíveis que faz com que |n| = 5, são eles, n = -5, pois |-5| = 5, e também n = 5, pois |5| = 5. Então, usando essa mesma ideia, temos que:
I → x – 3 = 5
ou
II → x – 3 = -5
Resolvendo uma das equações separadamente:
Resolução (1ª)
x – 3 = 5
x = 5 + 3
x = 8
Resolução (2ª)
x – 3 = -5
x = -5 + 3
x = -2
Então existem duas soluções: S = {-2, 8}.
Note que, se x = 8, a equação é verdadeira, pois:
|x – 3| = 5
|8 – 3| = 5
|5| = 5
Note também que, se x = -2, a equação também é verdadeira:
|-2 – 3| = 5
|-5| = 5
Exemplo 2
|2x + 3| = 5
Assim como no exemplo 1, para encontrar a solução, é necessário dividir em dois casos, de acordo com a definição de módulo.
I → 2x + 3 = 5
II → 2x + 3 = -5
Resolução (1ª)
2x + 3 = 5
2x = 5 – 3
2x = 2
x = 2/2
x = 1
Resolução (2ª)
2x + 3 = -5
2x = -5 – 3
2x = -8
x = -8/2
x = -4
Então, o conjunto de soluções é: S = {1, -4}.
Exemplo 3
|x + 3| = |2x – 1|
Quando temos a igualdade de dois módulos, precisamos dividir em dois casos:
1º caso, primeiro e segundo membro de mesmo sinal.
2º caso, primeiro e segundo membro de sinais opostos.
Resolução (1ª)
Faremos com os dois lados maiores que zero, ou seja, simplesmente tiraremos o módulo. Podemos fazer também com ambos negativos, porém o resultado será o mesmo.
X + 3 ≥ 0 → |x + 3| = x + 3
2x – 1 ≥ 0 → |2x – 1| = 2x – 1
x + 3 = 2x – 1
x – 2x = -1 – 3
x = -4 (-1)
x = 4
Resolução (2ª)
Lados de sinais opostos. Escolheremos um lado para ser positivo, e o outro, negativo.
Escolhendo:
|x + 3| ≥ 0 → |x + 3| = x + 3
|2x – 1| < 0 → |2x –1| = – (2x – 1)
Então, temos que:
x + 3 = – (2x – 1)
x + 3 = – 2x + 1
x + 2x = - 3 + 1
3x = -2
x = -2/3
Conjunto de soluções S = {4, -2/3}.
QUESTOES RESOLVIDAS
01) (UFJF) O número de soluções negativas da equação modular |5x – 6| = x² é:
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
Resolução
Queremos resolver a equação modular:
|5x – 6| = x²
Então, vamos separar em dois casos:
Resolução (1ª)
5x – 6 > 0 → |5x – 6| = 5x – 6
Então, temos que:
5x – 6 = x²
-x² + 5x – 6 = 0
Vale lembrar que o valor do delta nos diz quantas soluções a equação quadrática possui:
a = -1
b = 5
c = -6
Δ = b² – 4ac
Δ = 5² – 4 · (-1) · (-6)
Δ = 25 – 24
Δ = 1
Como 1 é positivo, então, nesse caso, existem duas soluções reais.
Resolução (2ª)
|5x – 6| < 0 → |5x – 6| = – (5x – 6)
– (5x – 6) = x²
– 5x + 6 = x²
– x² – 5x + 6 = 0
Δ = b² – 4ac
Δ = (-5)² – 4 · (-1) · (+6)
Δ = 25 + 24
Δ = 49
Como Δ é positivo nesse caso também, então há duas soluções reais, logo, o total de soluções reais é 4.
Alternativa E
02) (PUC SP) O conjunto solução S da equação |2x – 1| = x – 1 é:
(A) S = {0, 2/3}
(B) S = {0, 1/3}
(C) S = Ø
(D) S = {0, -1}
(E) S = {0, 4/3}
Resolução (1ª)
|2x – 1| = 2x – 1
Então, temos que:
2x – 1 = x – 1
2x – x = – 1 + 1
x = 0
Resolução (2ª)
|2x – 1| = – (2x – 1)
– (2x – 1) = x – 1
-2x + 1 = x – 1
-2x – x = -1 – 1
-3x = -2 (-1)
3x = 2
x = 2/3
Alternativa A
03) Resolva as seguintes equações modulares:
a) | x + 3 | = 7
b) |3x - 8 | = 13
Resolucao .gif)
04) Encontre o conjunto solução da equação | 3x+2 | = x + 1
Resolucao .gif)
05) Resolva a equação | 3x+1 | = | x-3 |
Resolucao .gif)
06) (U.F. Juiz de Fora-MG) O número de soluções negativas da equação | 5x-6 | = x2 é:
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
Resolucao .gif)
07) (U. Tuiuti – PR) As raízes reais da equação |xl 2 + |x| - 6 = 0 são tais que:
(A) a soma delas é – 1.
(B) o produto delas é – 6.
(C) ambas são positivas.
(D) o produto delas é – 4.
(E) n.d.a.
Resolucao .gif)
08) Simplifique a fração:![]() Resolucao
Resolucao
x + 5 |= x + 5, se x + 5 ≥ 0, ou x ≥ - 5.
Ou
| x + 5 | = - (x+5), se x + 5 < 0 ou x < -5.
Assim, teremos duas possibilidades: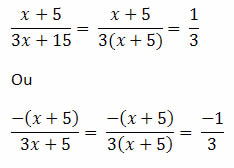
09) Resolva a equação![]()
Resolucao![]() Sendo assim,
Sendo assim,
| x | = 36 que é uma equação modular.
De uma forma geral, se k é um número real positivo, temos:
| x| = k
x = k
ou
x = - k
Sendo assim,
| x | = 36
x = 36
ou
x = -36
Portanto, S = {-36, 36}
10) Resolva a equação |x + 5| = 12
Resolucao
|x + 5| = 12
x + 5 = 12
ou
x + 5 = - 12
Segue que
x + 5 = 12
x = 12 – 5
x = 7
ou
x + 5 = - 12
x = -12 – 5
x = - 17
Portanto, S = {-17, 7}
11) Simplifique a fração abaixo:![]() Resolucao
Resolucao
Pela definição de módulo, temos que:
|x – 2| = x – 2, se x ≥ 2
|x – 2| = -(x – 2), se x < 2
Para resolver o exercício temos dois casos a considerar:
Se x ≥ 2![]() Se x < 0
Se x < 0![]()
Continua ...





