Professor Diminoi
ETEC
001) (ETEC) O Quadrado Mágico é uma tabela quadrada composta por números inteiros consecutivos a partir do 1, em que a soma de cada coluna, de cada linha e de cada diagonal são iguais. Essa soma é chamada de número mágico. Aprenda a encontrar o número mágico de um quadrado 3 x 3, como o da figura. O quadrado mágico 3 x 3 possui 9 posições, portanto deve ser preenchido com os números de 1 até 9, sem repetição. O número mágico pode ser encontrado seguindo dois passos.
O quadrado mágico 3 x 3 possui 9 posições, portanto deve ser preenchido com os números de 1 até 9, sem repetição. O número mágico pode ser encontrado seguindo dois passos.
Passo 1 – Encontrar a soma total dos números: 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45
Passo 2 – Dividir a soma encontrada pelo número de colunas existentes no quadrado. No caso do quadrado mágico 3 x 3, os 9 números estão agrupados em 3 colunas. Logo o número mágico será 45:3 = 15
Em condições semelhantes, o número mágico de um quadrado 4 x 4 será
(A) 16.
(B) 24.
(C) 34.
(D) 64.
(E) 136.
Resolução:
Quadrado Mágico 4 x 4 ou de ordem 4 é um quadrado quadriculado formado por 4 linhas e 4 colunas perfazendo um total de 16 células. Ou seja, o quadrado mágico de ordem 4, Normal ou Puro tem como formação os 16 primeiros números naturais:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 +13 + 14 + 15 + 16 = 136
136 : 4 = 34
Alternativa: C
002) (ETEC) No século XVI, divertidos duelos intelectuais entre professores das academias contribuíram para o avanço da Matemática. Motivado por um desses duelos, o matemático italiano Niccólo Fontana (Tartaglia) (1500 – 1557) encontrou uma fórmula para resolver equações polinomiais de terceiro grau. No entanto, os outros matemáticos da época não tinham acesso a tal descoberta, tendo que encontrar formas alternativas para resolver aqueles problemas. Uma dessas formas alternativas é a fatoração, que facilita a observação das raízes (soluções), pois transforma a adição dos termos da equação em uma multiplicação igualada a zero. Veja o exemplo.
x³ + 6x² + 5x – 12 = 0 <=> (x – 1) ∙ (x + 3) ∙ (x + 4) = 0
Analisando o exemplo dado, é correto afirmar que essa equação
(A) possui três raízes naturais distintas.
(B) possui três raízes inteiras distintas.
(C) possui duas raízes naturais distintas e uma raiz irracional.
(D) possui duas raízes irracionais distintas e uma raiz inteira.
(E) não possui raízes reais.
Resolução:
Cubo da soma
Com a propriedade distributiva, é possível criar uma “fórmula” também para produtos com o seguinte formato:
(x + a)(x + a)(x + a)
Na notação de potência, ele é escrito da seguinte maneira:
(x + a)3
Por meio da propriedade distributiva e simplificando o resultado, encontraremos o seguinte para esse produto notável:
(x + a)3 = x3 + 3x2a + 3xa2 + a3
Alternativa: B
003) (ETEC) Marcelo decidiu construir uma gangorra para poder brincar com seu filho. Sobre um cavalete, ele apoiou uma tábua de modo que, quando ambos se sentassem, estando cada um em um dos extremos da tábua e sem tocar os pés no chão, a gangorra pudesse ficar equilibrada horizontalmente, sem pender para nenhum dos lados. Considerou também o fato de que seu peso era três vezes maior que o de seu filho, e que a distância entre os locais onde ele e o filho deveriam se sentar era de 3,2 m. De acordo com essas considerações, a distância entre o ponto onde o filho de Marcelo deve se sentar e o ponto de apoio da tábua no cavalete é, aproximadamente, de
Observação: Despreze o peso da tábua, bem como as dimensões dos corpos de Marcelo e de seu filho
(A) 0,8 m.
(B) 1,2 m.
(C) 1,6 m.
(D) 2,0 m.
(E) 2,4 m.
Resolução: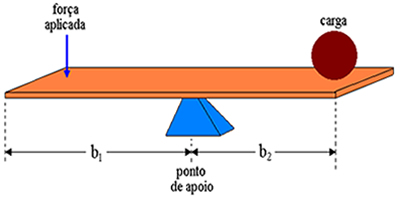 Fa = Cg
Fa = Cg
Pp = 3x
Pf = x
b1 = 2,4
b2 = 0,4
Resolução direta: sabendo-se que a distância entre elas deves er 3,4 e que o peso do pai e três vezes mior que o do filho. Basta dividir 3,3/3 = 0,8.
Distância do filho ao ponto de apoio é de 0,8
Distância do pai ao ponto de apoio é de 2,4
Alternativa: E
005) (ETEC) Produzir sombras na parede é uma brincadeira simples. Para brincar, basta que você providencie uma vela e um ambiente escuro. Em certa noite, quando a luz havia acabado, Fernando e seu irmãozinho, aproveitaram a luz de uma vela acesa deixada sobre a mesa para brincarem com sombras. Posicionou, cuidadosamente, sua mão espalmada entre a chama e a parede, de forma que a palma da mão estivesse paralela à parede. A ação assustou seu irmãozinho, uma vez que a sombra projetada na parede tinha cinco vezes a largura da mão espalmada de Fernando. Sabendo que a distância da mão de Fernando até a chama da vela era de 0,5 m e que a largura de sua mão quando espalmada é de 20 cm, a distância entre a parede e a chama da vela (considerada puntiforme), era de
(A) 0,5 m.
(B) 1,0 m.
(C) 2,0 m.
(D) 2,5 m.
(E) 5,0 m.
Resolução: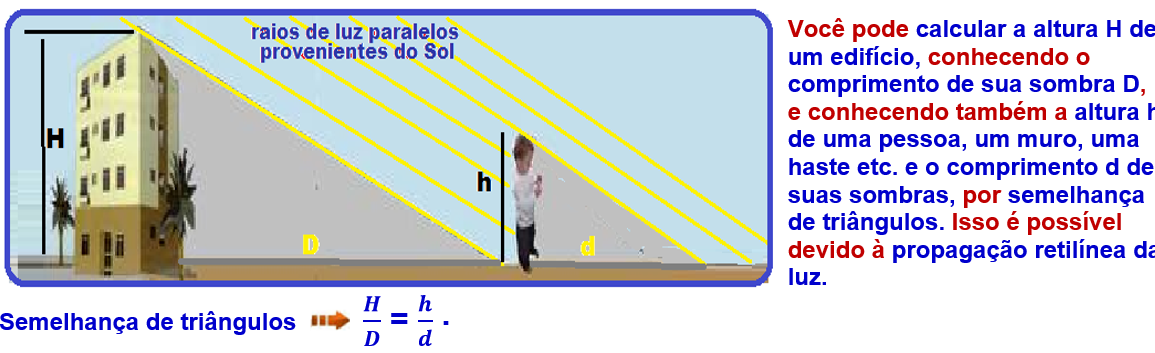 H = largura da mão de Fernando = 20cm = 0,2m
H = largura da mão de Fernando = 20cm = 0,2m
h = largura da mão do irmãozinho de Fernando = 1m
D = distância da mão de Fernando até a chama = 0,5
d = distância da mão do irmãozinho de Fernando a parede =
H/D = h/d
0,2/0,5 = 1/d
0,2d = 0,5
d = 0,5/0,2
d = 2,5
Alternativa: D
006) (ETEC) Observe o Tangram, em uma possível disposição de suas peças. Na figura, tem-se que:
Na figura, tem-se que:
l QS é paralelo a BD ;
l os polígonos ABCD e OPQR são quadrados;
l S é ponto médio de CD ;
l P é ponto médio de OB ;
l O é ponto médio de BD .
Se a área do triângulo ABO é 16 cm², a área do quadrado OPQR é, em centímetros quadrados,
(A) 2.
(B) 4.
(C) 6.
(D) 8.
(E) 10.
Resolução:
Se você prolongar o segmento AO, você terá um triângulo BOC = ABO. Analisando o polígono OPQR você perceberá que é a metade do triângulo ABO, ou seja 8 cm2
Alternativa: D
008) (ETEC) A utilização de números inteiros faz parte do nosso dia a dia. Como exemplo, considere o seguinte problema: Maria está organizando o seu guarda-roupa e dispõe de N gavetas para guardar sua coleção de camisetas. Se, em cada uma dessas gavetas, colocar exatamente 10 camisetas, restam 4 camisetas; se colocar exatamente 9 camisetas, restam 7 camisetas.
Nessas condições, pode-se afirmar que o número de camisetas da coleção de Maria é
(A) 31.
(B) 32.
(C) 33.
(D) 34.
(E) 35.
Resolução:
Chamando as gavetas de x igualando a equação temos:
10x + 4 = 9x + 7
10x – 9x = 7 -4
x = 3
Usando o enunciado:
Quando a Maria coloca 10 camisetas em cada gaveta
10 . 3 = 30 (sobra 4) = 34
Quando a Maria coloca 10 camisetas em cada gaveta
7 . 3 = 27 (sobra 7) = 34
Alternativa: D
009) (ETEC) No texto, o pai de Santos Dumont refere-se às “imagens em movimento daqueles franceses, os irmãos Lumière”. Para dar a noção de movimento, o cinema utiliza o efeito da “persistência da visão”, isto é, ao visualizar-se determinado objeto, a imagem persiste na retina por uma fração de segundo. Imagens projetadas a um ritmo superior ou igual a 16 vezes por segundo associam-se na retina sem interrupção, dando a impressão de movimento. Dessa forma, o número de imagens de um filme com duração de 1 hora e 30 minutos, projetado a 16 imagens por segundo, é
(A) 21 600.
(B) 43 200.
(C) 57 600.
(D) 86 400.
(E) 90 200.
Resolução:
1,5h = 90minutos
90 . 60 = 5400
5400 . 16 = 86400
Alternativa: D
010) (ETEC) O Teorema de Pitágoras, provavelmente a relação mais conhecida da Matemática, afirma que em todo triângulo retângulo, o quadrado da hipotenusa é igual à soma dos quadrados dos catetos. Atribui-se a Pitágoras, matemático grego do século VI a.C., a primeira demonstração desse teorema, embora essa relação já fosse aplicada pelo menos mil anos antes. Pensando nisso, analise a seguinte situação: um helicóptero, para sobrevoar uma região, parte do ponto A do solo e sobe verticalmente 250 m; em seguida, voa horizontalmente 160 m para o leste; finalmente, desce verticalmente 130 m até o ponto B.
Nessas condições, a distância entre os pontos A e B é, em metros,
(A) 120.
(B) 180.
(C) 200.
(D) 260.
(E) 280.
Resolução:
Fórmula de Pitágoras:
Substituindo os valores no segundo triângulo retângulo cujas medidas são: a = 120, b =160 e a hipotenusa valendo x
Pitágoras
h2 = a2 + b2
h2 = 1202 + 1602
h2 = 14400 + 25600
h2 = 40000
h = √40000
h = 200
Alternativa: C
011) (ETEC) Em uma comunidade será implantada uma horta coletiva. Para preparar o solo, o técnico agrícola recomendou 400 g de calcário para cada metro quadrado da superfície dos canteiros. Sabendo que a horta terá quatro canteiros retangulares de dimensões 1,0 m x 1,5 m, então a quantidade de calcário necessária para o preparo desses canteiros será, em quilogramas,
(A) 1,6.
(B) 1,8.
(C) 2,0.
(D) 2,2.
(E) 2,4.
Resolução:
Área do de retângulo:
A = 1, 0
B = 1,5
Àrea = a . b
A = 1 . 15
A = 1,5m2
Àrea total = 1,5 . 4
Área total = 6m2
Para cada metro quadrado recomenda-se 40g = 0,4 kg.
6 . 0,4 = 2,4
Alternativa: E
012) (ETEC) A equipe de logística de uma transportadora, após definir o roteiro mais viável para a realização da entrega de mercadorias, determinou que um dos motoristas deveria fazer oito entregas pela manhã, gastando entre deslocamento, descarga e assinatura de documentos exatos 30 minutos para cada uma das entregas.
Tudo transcorria de acordo com as especificações, porém, na sétima entrega, houve um atraso de 10 minutos.
Sabe-se que a distância entre o sétimo e o oitavo ponto de entrega é de 15 km e que o motorista conseguirá manter a velocidade média de 60 km/h para percorrer esse trajeto. Sendo assim, é correto afirmar que, para cumprir o prazo estipulado pela equipe de logística, esse motorista terá disponível, para a descarga e a assinatura de documentos, o tempo de
(A) 1 minuto.
(B) 5 minutos.
(C) 10 minutos.
(D) 15 minutos.
(E) 20 minutos.
Resolução:
Vm = 60m/s
S = 15 km
T =
Vm = s/t
60 = 15/tt = 15/10
t = 025 h = 15min
como ele perdeu 10 minutos fica, 15 – 10 = 5
Alternativa: B
014) (ETEC) (questão de física mas podemos existe uma fórmula básica de velocidade média e a interpretação de gráfico) Uma das formas de mobilidade urbana sustentável é o uso de bicicletas. O aumento da autonomia das bicicletas elétricas tem chamado a atenção do mercado, que observa a crescente procura. Um ciclista, movendo-se em um solo plano, sai de casa com sua bicicleta elétrica, desenvolvendo as velocidades indicadas no gráfico. Admita que a autonomia dessa bicicleta é de 60 km, que a bateria encontrava-se completamente carregada e que a breve aceleração, no início do movimento, pode ser desconsiderada. Nessas condições, após 45 minutos de passeio, a distância que ainda será possível percorrer sem realizar a recarga da bateria é, em km,
Admita que a autonomia dessa bicicleta é de 60 km, que a bateria encontrava-se completamente carregada e que a breve aceleração, no início do movimento, pode ser desconsiderada. Nessas condições, após 45 minutos de passeio, a distância que ainda será possível percorrer sem realizar a recarga da bateria é, em km,
(A) 25.
(B) 30.
(C) 35.
(D) 40.
(E) 45.
Resolução:
Velocidade média = distância / tempo
Vm = 20
d =
t = 45minutos que corresponde a 0.75h
Vm = d/t
20 = d / 0,75
D = 20 . 0,75
D = 15
Pelo gráfico o ciclista percorreu 15km e ainda te pode percorrer 45km sem carregar a bateria.
Alternativa: E
015) (ETEC) Em uma comunidade será implantada uma horta coletiva. Para preparar o solo, o técnico agrícola recomendou 400 g de calcário para cada metro quadrado da superfície dos canteiros. Sabendo que a horta terá quatro canteiros retangulares de dimensões 1,0 m x 1,5 m, então a quantidade de calcário necessária para o preparo desses canteiros será, em quilogramas,
(A) 1,6.
(B) 1,8.
(C) 2,0.
(D) 2,2.
(E) 2,4.
Resolução:
Área do de retângulo:
A = 1, 0
B = 1,5
Àrea = a . b
A = 1 . 15
A = 1,5m2
Àrea total = 1,5 . 4
Área total = 6m2
Para cada metro quadrado recomenda-se 40g = 0,4 kg.
6 . 0,4 = 2,4
Alternativa: E
016) (ETEC) No texto, o pai de Santos Dumont refere-se às “imagens em movimento daqueles franceses, os irmãos Lumière”. Para dar a noção de movimento, o cinema utiliza o efeito da “persistência da visão”, isto é, ao visualizar-se determinado objeto, a imagem persiste na retina por uma fração de segundo. Imagens projetadas a um ritmo superior ou igual a 16 vezes por segundo associam-se na retina sem interrupção, dando a impressão de movimento. Dessa forma, o número de imagens de um filme com duração de 1 hora e 30 minutos, projetado a 16 imagens por segundo, é
(A) 21 600.
(B) 43 200.
(C) 57 600.
(D) 86 400.
(E) 90 200.
Resolução:
1,5h = 90minutos
90 . 60 = 5400
5400 . 16 = 86400
Alternativa: D
017) (ETEC) Suponha que um terreno retangular de área 4225km2 será delimitado para se tornar uma nova Reserva Extrativista. Se o comprimento do terreno excede em 100km sua largura (x), uma equação que permite determinar essa largura (x) é
(A) x2 + 100 x + 4 225 = 0
(B) x2 − 100 x + 4 225 = 0
(C) x2 + 100 x – 4 225 = 0
(D) x2 + 4 225 x − 100 = 0
(E) x2 – 4 225 x + 100 = 0
Resolução:
Área = b . h
4225 = x . (x + 100)
4225 = x2 + 100x
x2 + 100x – 4225
Alternativa: C
018) (ETEC) (Questão de Física/Proporcionalidade e interpretação de texto) É surpreendente como a vida pode ocorrer mesmo em locais inóspitos como, por exemplo, nas fossas das Marianas, grande depressão oceânica localizada na fronteira entre as placas tectônicas do Pacífico e das Filipinas. Nesse local, o leito oceânico atinge cerca de 11 000 metros de profundidade. A pressão é tão grande que os seres que lá habitam tiveram de desenvolver condições especiais para sua sobrevivência, o que torna impossível trazê-los vivos para a superfície.
Considerando que para cada 10 metros de profundidade sob a água, a pressão é acrescida de 1 atm, é correto afirmar que a pressão total suportada pelos seres que vivem no fundo das fossas das Marianas equivale a
(A) 110 atm.
(B) 111 atm.
(C) 1 100 atm.
(D) 1 101 atm.
(E) 1 110 atm.
Resolução:
10m ----- 1
11000 ------- x
10x = 11000
x = 11000/10
x = 1100
Observação: da superfície ate os primeiros 10m temos 1 atm. Portanto, devemos somar 1100 + 1 =11001
Alternativa: D
Leia o texto para responder as questões 19 e 20.
VOCÊ SABIA?
O Sistema Métrico é um sistema de medição reconhecido internacionalmente. Ele surgiu durante a Revolução Francesa em virtude da existência de diversos padrões de medida que dificultavam o funcionamento do comércio e da indústria.
A légua é uma unidade de comprimento que não pertence ao Sistema Métrico, cuja ideia base era de que corresponderia aproximadamente ao caminho percorrido por um homem caminhando a pé durante uma hora. No Brasil, de acordo com o dicionário Houaiss, uma légua equivale a 6,6 km.
As Botas de Sete Léguas, da fábula, permitem à pessoa que as usa conseguir dar passos que valem sete léguas cada um. 019) (ETEC) O Sistema Métrico é um sistema de medição reconhecido internacionalmente. Ele surgiu durante a Revolução Francesa em virtude da existência de diversos padrões de medida que dificultavam o funcionamento do comércio e da indústria. A légua é uma unidade de comprimento que não pertence ao Sistema Métrico, cuja ideia base era de que corresponderia aproximadamente ao caminho percorrido por um homem caminhando a pé durante uma hora. No Brasil, de acordo com o dicionário Houaiss, uma légua equivale a 6,6 km. As Botas de Sete Léguas, da fábula, permitem à pessoa que as usa conseguir dar passos que valem sete léguas cada um.
019) (ETEC) O Sistema Métrico é um sistema de medição reconhecido internacionalmente. Ele surgiu durante a Revolução Francesa em virtude da existência de diversos padrões de medida que dificultavam o funcionamento do comércio e da indústria. A légua é uma unidade de comprimento que não pertence ao Sistema Métrico, cuja ideia base era de que corresponderia aproximadamente ao caminho percorrido por um homem caminhando a pé durante uma hora. No Brasil, de acordo com o dicionário Houaiss, uma légua equivale a 6,6 km. As Botas de Sete Léguas, da fábula, permitem à pessoa que as usa conseguir dar passos que valem sete léguas cada um.
Admita que a menina dos quadrinhos esteja visitando a avó que mora em outra cidade. A fim de voltar da casa de sua avó para o prédio onde mora, usando a bota de 7 léguas da história, a menina dá 3 passos para leste e 4 passos para o norte. A figura representa de modo esquemático esse trajeto realizado pela garota. A distância entre a casa da avó e o prédio no qual a menina mora é, em quilômetros, igual a
A distância entre a casa da avó e o prédio no qual a menina mora é, em quilômetros, igual a
(A) 323,4
(B) 231,0
(C) 142,6
(D) 46,2
(E) 35,0
Resolução:
A menina estava calçada com uma bota 7 léguas. Isso quer dizer que a cada passo ela caminhava 7 léguas.
Para o leste ela caminhou 3 . 7 = 21 léguas
Para o norte ela caminhou 4 . 7 = 28 léguas
Olhando o desenho podemos aplicar Pitágoras:
h2 = a2 + b3
h2 = 212 + 493
h2 = 441 + 784
h2 = 1225
h = √1225
h = 35 légua
Uma légua tem 6600m = 6,6km
Para transforma léguas 35 em km basta multiplicar 35 . 6,6 = 231
Alternativa: B
020) (ETEC) A légua é uma medida de comprimento que varia de acordo com o período histórico e o país em que é usada. Segundo o dicionário Priberam, por exemplo, ela equivale a 5 km em Portugal. Pode-se, portanto, estimar que a légua brasileira é maior que a portuguesa em cerca de
(A) 76%.
(B) 68%.
(C) 32%.
(D) 24%.
(E) 13%.
Resolução:
Alternativa: C
021) (ETEC) A Estrela da Morte é uma arma ícone da série cinematográfica Star Wars. De formato esférico ela era considerada similar a uma Lua. Essa arma/estação espacial podia se locomover pelo espaço na velocidade da luz, ou seja, 3,0 ×105 km/s. Admita que a Estrela da Morte precisasse se posicionar de maneira a realizar um ataque de máxima eficiência ao Planeta C. Inicialmente, a estação espacial encontrava-se no ponto A e, entre ela e o Planeta C, havia um grande asteroide, por isso necessitou ir para o ponto B, de modo a poder visualizar perfeitamente o Planeta C, conforme a figura. Assinale a alternativa que contém o tempo que a Estrela da Morte demorou para se locomover do ponto A para o B.
Assinale a alternativa que contém o tempo que a Estrela da Morte demorou para se locomover do ponto A para o B.
(A) 5,0 ×104 s
(B) 15,0 ×104 s
(C) 45,0 ×104 s
(D) √353 x 104s
(E) √353/3 x 104s
Resolução:
h2 = a2 + b2
(1,7.10¹⁰)² = AB² + (8,0.10⁹)²
2,89.10²⁰ = AB² + 64.10¹⁸
289.10¹⁸ = AB² + 64.10¹⁸
AB² = 289.10¹⁸ - 64.10¹⁸
AB² = 10¹⁸(289 - 64)
AB² = (√225.10¹⁸)
AB = 15 . 10⁹ km.
Velocidade média:
Vm = ∆S / ∆t
3,0.10⁵ = 15.10⁹/t
t = 15.10⁹/3,0.10⁵
t = 5.10⁴ segundos.
Alternativa: A
022) (ETEC) O empreendedorismo é, para muitos, uma oportunidade, assim como para ilda Regina que decidiu investir em uma agência de publicidade. Nesse mercado competitivo, entre seus diferenciais, a empresária decidiu desenvolver um cartão de visita que tem a forma de um polígono convexo com todos os lados de mesma medida, e apenas quatro ângulos internos, sendo dois deles agudos e dois obtusos. A figura matemática que é descrita tendo, obrigatoriamente, todos os elementos do cartão de visita citado é o
(A) losango.
(B) pentágono.
(C) quadrado.
(D) retângulo.
(E) triângulo.
Alternativa: A
Leia o texto para responder às questões 002e 003
A Feira do Peixe Vivo, em Caxias do Sul, visa promover uma melhor qualidade de vida à população ao estimular o consumo de peixes. A feira ocorre uma vez ao mês e comercializa espécies como carpa capim (11 reais o quilograma), carpa húngara (9 reais o quilograma) e o bagre (X reais o quilograma).
023) (ETEC) Em sua barraca, um piscicultor comercializava bagres, cujas massas variavam de 1,3 kg a 1,6 kg. Um freguês comprou o bagre de maior massa por R$ 25,00. De acordo com as informações do texto, é correto afirmar que
(A) X < 15.
(B) 15 < X < 20.
(C) 15 > X > 20.
(D) 15 < X > 20.
(E) X > 20.
Alternativa: B
024) (ETEC) Carlos Rogério, empresário do ramo de festas e eventos, decidiu oferecer a seus clientes embalagens diferenciadas para as populares lembrancinhas. Segundo o empresário, a introdução de uma embalagem em formato de poliedro convexo regular (apresentada na imagem, com sua planificação) aumentou seu faturamento no último mês. Sabendo que todas as faces da embalagem de Carlos Rogério são polígonos regulares, pode-se afirmar que um ângulo interno de uma dessas faces mede
Segundo o empresário, a introdução de uma embalagem em formato de poliedro convexo regular (apresentada na imagem, com sua planificação) aumentou seu faturamento no último mês. Sabendo que todas as faces da embalagem de Carlos Rogério são polígonos regulares, pode-se afirmar que um ângulo interno de uma dessas faces mede
Lembre-se de que: Um poliedro convexo é chamado de regular se suas faces são polígonos regulares, e cada um desses polígonos regulares tem o mesmo número de lados.
(A) 108°
(B) 180°
(C) 360°
(D) 405°
(E) 540°
Alternativa: A
Leia o texto para responder às questões 025 e 026.
Em suas últimas viagens o programa Apollo levou um veículo capaz de mover-se sobre a superfície lunar com uma velocidade máxima de 13 km/h. As baterias desse veículo permitiam uma autonomia para 92 km. O veículo era muito leve. Na Terra, seu peso era aproximadamente 2 100 N, enquanto que, na Lua, pesava cerca de 350 N.
025) (ETEC) Admita que os astronautas, ao utilizarem o veículo lunar, mantiveram velocidade constante igual à velocidade máxima. Assim sendo, a expectativa do tempo de uso do veículo, até o total esgotamento de suas baterias, seria de aproximadamente
(A) 3 h.
(B) 5 h.
(C) 6 h.
(D) 7 h.
(E) 9 h.
Alternativa: D
026) (ETEC) A força gravitacional, quando nos referimos a objetos próximos à superfície de corpos celestes, recebe o nome de força peso. A força peso é calculada pelo produto da massa do objeto, cujo peso se deseja conhecer, pelo valor da aceleração da gravidade do local em que esse objeto se encontra. Considerando que o valor da aceleração da gravidade no planeta Terra seja 10 m/s2, o valor da aceleração da gravidade na Lua corresponde à
(A) metade do valor da aceleração da gravidade da Terra.
(B) terça parte do valor da aceleração da gravidade da Terra.
(C) quarta parte do valor da aceleração da gravidade da Terra.
(D) quinta parte do valor da aceleração da gravidade da Terra.
(E) sexta parte do valor da aceleração da gravidade da Terra.
Alternativa: E
Leia o texto para responder à questão a seguir
O soro fisiológico é uma solução utilizada para diversos fins, dentre os quais: limpar olhos e nariz, lavar queimaduras e feridas, hidratações e nebulizações. É uma solução de cloreto de sódio de concentração 0,9% (massa/volume). Essa concentração corresponde à razão entre à massa de cloreto de sódio, em gramas, e o volume de 100 mL da solução.
027) (ETEC) Um paciente desidratado, em que é administrado 500 mL de soro na veia, receberá uma massa de sal correspondente a
(A) 0,45 g.
(B) 4,50 g.
(C) 45,00 g.
(D) 9,00 g.
(E) 0,90 g.
Alternativa: B
028) (ETEC) Os morcegos não enxergam muito bem, entretanto, são mamíferos capazes de ouvir sons cujas frequências vão de 1 000 Hz a 120 000 Hz.
Observação:
Lembre-se que:
v = λ ∙ f
v = velocidade de propagação do som no ar, de valor 340 m/s;
λ = comprimento de onda, em m;
f = frequência da onda, em Hz.
O maior comprimento de onda das ondas sonoras audíveis por morcegos é de
(A) 0,12 m.
(B) 0,34 m.
(C) 1,2 m.
(D) 120 m.
(E) 350 m.
Alternativa: B
029) (ETEC) Suponha que um terreno retangular de área 4 225 km2 será delimitado para se tornar uma nova Reserva Extrativista. Se o comprimento do terreno excede em 100 km sua largura (x), uma equação que permite determinar essa largura (x) é
(A) x2 + 100 x + 4 225 = 0
(B) x2 − 100 x + 4 225 = 0
(C) x2 + 100 x – 4 225 = 0
(D) x2 + 4 225 x − 100 = 0
(E) x2 – 4 225 x + 100 = 0
Alternativa: C
030) (ETEC) Considere o quadro que apresenta dados do Projeto de Monitoramento do Desmatamento dos Biomas Brasileiros por Satélite, em seu relatório de 2009. A partir da definição de hotspot apresentada no texto e dos dados do quadro, e considerando apenas a porcentagem de área desmatada até 2009, o Bioma Extra-amazônico que pode ser classificado como hotspot é
A partir da definição de hotspot apresentada no texto e dos dados do quadro, e considerando apenas a porcentagem de área desmatada até 2009, o Bioma Extra-amazônico que pode ser classificado como hotspot é
(A) o Cerrado.
(B) a Mata Atlântica.
(C) a Caatinga.
(D) o Pampa.
(E) o Pantanal.
Alternativa: B
031) ((ETEC) Admita que a área da superfície do planeta Terra seja de 500 milhões de km2 . Logo, pode-se estimar que o tamanho médio de cada hotspot identificado em 1999 seria, em km2 ,
(A) 28 × 106
(B) 28 × 104
(C) 28 × 103
(D) 28 × 101
(E) 28 × 100
Alternativa: B
032) (ETEC) O agulhão bandeira é um recordista em velocidade, podendo chegar a surpreendentes 110 km/h devido a sua forma hidrodinâmica e força física. Observação: Lembre-se de que velocidade escalar média é a razão entre distância percorrida e tempo necessário para se percorrer tal distância.
Observação: Lembre-se de que velocidade escalar média é a razão entre distância percorrida e tempo necessário para se percorrer tal distância.
Considerando essa velocidade escalar média constante durante 3 minutos, a distância que esse peixe é capaz de se deslocar é, em metros, de
(A) 180.
(B) 330.
(C) 1 800.
(D) 2 000.
(E) 5 500.
Alternativa: E
033) (ETEC) A Mata Atlântica é uma série de ecossistemas de florestas tropicais da América do Sul que abriga uma diversidade de espécies endêmicas. Estudos estimam que haja um total de 8 732 espécies entre plantas e vertebrados endêmicos nesse bioma, e que a diferença entre a quantidade daquelas plantas e a quantidade destes vertebrados, nessa ordem, seja de 7 268 espécies.
Nessas condições, a quantidade de plantas endêmicas nesse bioma é
(A) 732.
(B) 1 464.
(C) 5 813.
(D) 8 000.
(E) 16 000.
Alternativa: D
034) (ETEC) O papel das doenças na conservação da vida selvagem é por vezes subestimado. Durante expedições no Polo Sul, acredita-se que os cães utilizados para o transporte de trenós tenham transmitido o vírus da cinomose canina a uma espécie de foca que habitava essa região, levando à ocorrência de extensa mortalidade desses animais. Suponha que, em determinado período de uma expedição esse vírus tenha se propagado na região delimitada pelo triângulo ABC, da figura, em que:
Suponha que, em determinado período de uma expedição esse vírus tenha se propagado na região delimitada pelo triângulo ABC, da figura, em que:
- a medida de AC é igual a 70 km;
- o ângulo BAC é reto;
- o ângulo ABC mede 45º. Após um mês, essa doença atingiu a área correspondente ao triângulo DEF, em que:
- a medida de DF é igual a 140 km;
- o ângulo EDF é reto;
- o ângulo DEF mede 45º. Sobre a área do triângulo DEF, é correto afirmar que ela é
(A) a metade da área ABC.
(B) a quarta parte da área ABC.
(C) o dobro da área ABC.
(D) o quádruplo da área ABC.
(E) o sétuplo da área ABC.
Alternativa: D
036) ((ETEC) Segundo pesquisas, na história do planeta Terra, houve cinco grandes eventos cujos impactos sobre a biodiversidade foram tão devastadores que acarretaram extinções em massa, como a dos dinossauros.
Suponha que um desses episódios foi causado por um impacto com um asteroide de 15 km de diâmetro, o que deixou em nosso planeta uma cratera de 200 km de diâmetro. Considere que a energia liberada pelo impacto de um asteroide é diretamente proporcional apenas ao cubo do diâmetro da cratera formada.
Assinale a expressão que relaciona corretamente a energia liberada E, no fenômeno descrito, com o diâmetro do asteroide, na qual k representa a constante de proporcionalidade.
(A) E = k ∙15
(B) E = k ∙ 200
(C) E = k ∙ 3 000
(D) E = k ∙ 3 3750
(E) E = k ∙ 8 000 000
Alternativa: E
037) (ETEC) Uma questão ambiental relevante, na atualidade, remete ao acúmulo e ao descarte de resíduos sólidos. A indústria nuclear é responsável pelo armazenamento e controle dos rejeitos que produz.
Suponha que uma indústria nuclear armazene seus resíduos em recipientes cilíndricos, cuja altura é igual a 4 m e o diâmetro da base igual a 12 m.
Observação:
V = πr2 . h
V = volume do cilindro;
r = raio do círculo da base;
h = altura do cilindro.
Contudo, devido a mudanças operacionais, decide-se alterar a altura e o raio destes recipientes cilíndricos de tal maneira que o novo recipiente:
- tenha volume igual a 62,5% do volume do recipiente anterior;
- e possua raio da base igual à metade do raio da base do recipiente anterior; Desta forma, a altura do novo recipiente cilíndrico deve ser, em metros, igual a
(A) 8.
(B) 10.
(C) 16.
(D) 20.
(E) 40.
Alternativa: B
Leia o texto para responder às questões de números 038 e 039
Para reduzir o consumo de derivados de petróleo, os fabricantes de produtos de plásticos iniciaram a produção de suas peças utilizando bioplástico, material biodegradável e/ou produzido a partir de fontes renováveis. A Xplástico, indústria há 20 anos no mercado, usa 6 000 toneladas de plástico comum para fabricar 20 bilhões de peças todos os anos. Essa empresa, no início do ano de 2018, começou a produzir a linha eco-copos com bioplástico. Essa linha representa algo em torno de 2% do número total de peças plásticas produzidas por ano nessa empresa.
038) (ETEC) Suponha que a razão anual entre as quantidades de eco-copos e o total de peças plásticas produzidas seja constante até 2030, e que a quantidade de massa plástica utilizada na confecção de cada peça seja sempre igual. O número de toneladas de plástico comum que deixarão de ser utilizadas pela Xplástico, de 2 018 a 2 030, ao produzir as peças de eco-copos, é
(A) 10.
(B) 120.
(C) 1 320.
(D) 1 440.
(E) 1 560.
Alternativa: E
039) (ETEC) De acordo com o texto, pode-se concluir corretamente que o número de peças produzidas pela X plástico por hora, em média, está mais próximo de
(A) 2,0 × 1012.
(B) 2,0 × 109 .
(C) 2,0 × 106 .
(D) 2,0 × 103 .
(E) 2,0 × 100 .
Alternativa: C
040) (ETEC) Um técnico em edificações irá acompanhar a instalação de painéis solares em uma laje plana e horizontal. Após os cálculos necessários, ele determina que, para ocupar menos espaço nos telhados e obter melhor ângulo solar:
cada painel deve ter uma inclinação constante e igual a 20º;
a distância entre os dois painéis deve ser 3,5 vezes a altura h dos painéis.
 Dado:
Dado:
- sen 20º = 0,34
- cos 20º = 0,94
- tg 20º = 0,36
Sabendo que cada placa solar é quadrada e tem 1 m2 de superfície, a distância entre dois painéis é, em metros, de
(A) 0,34.
(B) 0,36.
(C) 0,94.
(D) 1,19.
(E) 1,26.
Alternativa: D
041) (ETEC) A matéria orgânica, quando decomposta, torna-se um excelente adubo. Na compostagem, a matéria orgânica é empilhada em grandes montes. Com a decomposição, a temperatura no interior desses montes aumenta, podendo matar organismos importantes para a própria decomposição. Por esse motivo, a temperatura deve ser monitorada. O ideal é que, na compostagem, a temperatura permaneça entre 50 ºC e 60 ºC.
Observação:
0F/5 = 0F - 32/9
Considere que: em que é a temperatura medida na escala Celsius e é a temperatura medida na escala Fahrenheit
Essas temperaturas, escritas em Fahrenheit, são, respectivamente,
(A) 58 ºF e 68 ºF.
(B) 58 ºF e 76 ºF.
(C) 122 ºF e 132 ºF.
(D) 122 ºF e 140 ºF.
(E) 132 ºF e 140 ºF.
Alternativa: D
042) (ETEC) O vidro das embalagens é um material 100% reciclável, ou seja, 1 kg de vidro pode ser reciclado várias vezes. Uma empresa de reciclagem de vidro transforma 50 kg de vidro em 125 garrafas iguais e o material utilizado para fazer 5 destas garrafas pode ser transformado em 40 copos de licor, também iguais entre si. Assim sendo, o número de copos de licor que seria possível reciclar, com 50 kg de vidro, é
(A) 15 625.
(B) 1 600.
(C) 1 000.
(D) 160.
(E) 100.
Alternativa: C
043) (ETEC) Entre as formas mais comuns de coleta seletiva existentes no Brasil, existe aquela realizada porta a porta por associações ou cooperativas de catadores de materiais recicláveis. Suponha que um caminhão, pertencente a uma dessas cooperativas, faça diariamente um percurso de 630 km com mesma velocidade média. Excepcionalmente, em um determinado dia, o motorista aumenta sua velocidade média em 10 km/h, economizando 4 h em seu percurso habitual. Logo, o número de horas gastos, diariamente, no percurso habitual, é de
(A) 14.
(B) 15.
(C) 16.
(D) 17.
(E) 18.
Alternativa: E
044) (ETEC) Suponha que l não ocorra, no mundo, o desperdício anual de alimento divulgado pela FAO, isto é, que todo esse alimento possa ser tratado e conservado para a alimentação humana; e l todo esse alimento seja destinado a todas as pessoas subnutridas do mundo, de acordo com os dados da ONU. Nessas condições, em 2015 (ano que teve 365 dias), a quantidade de alimento, em quilogramas, destinada, em média, por pessoa, por dia, estaria mais próxima de
(A) 8.
(B) 6.
(C) 4.
(D) 2.
(E) 1.
Alternativa: C
Leia o texto para responder às questões de números 045 e 046.
Um painel fotovoltaico converte energia solar em energia elétrica de forma sustentável. Suponha que, em uma região plana, será instalado um sistema de painéis fotovoltaicos para suprir uma comunidade com energia elétrica. Segue a descrição de alguns itens do projeto: Segue a descrição de alguns itens do projeto:
Segue a descrição de alguns itens do projeto:
- l instalação de 5 filas paralelas entre si; cada fila contendo 10 painéis;
- l cada painel foi montado com 4 módulos fotovoltaicos congruentes entre si, conforme figura;
- l em cada módulo fotovoltaico, a superfície de captação da energia solar é de forma retangular, com dimensões de 65 cm por 150 cm;
- l os painéis deverão estar separados, de modo que um não faça sombra sobre o outro e, também, não sejam encobertos pela sombra de qualquer outro objeto;
- l os painéis são idênticos entre si e estão apoiados sobre o solo
045) (ETEC) No projeto descrito, a área total da superfície de captação de energia solar é, em metros quadrados,
(A) 195.
(B) 185.
(C) 175.
(D) 165.
(E) 155.
Alternativa: A
046) (ETEC) A figura apresenta o modelo matemático para a determinação da distância mínima entre dois painéis de filas paralelas e adjacentes do projeto descrito.
Na figura, tem-se que:
- l A: ponto que representa o topo do painel;
- l B: representa o ponto de apoio do painel no solo;
- l o segmento AB representa o painel;
- l C: representa o ponto de apoio no solo do painel paralelo e mais próximo;
- l o segmento AH representa a distância do topo do painel ao solo;
- l β representa a medida do ângulo de incidência dos raios do Sol em relação ao solo *;
- l d = BC é a distância entre os pontos B e C.
*A distância mínima entre dois painéis que estão em filas paralelas e adjacentes depende do ângulo (β) de incidência solar às 12 h do dia do solstício de inverno, momento em que o Sol atinge a maior declinação em latitude, medida a partir da linha do equador.
Dados:
sen 21,80° = 0,3714
cos 21,80° = 0,9285
tg 21,80° = 0,40
Na figura, sabendo que BH = 120 cm e que, no local de instalação dos painéis, β = 21,80°, a distância mínima (d) entre dois painéis que estão em filas paralelas e adjacentes é, em metros,
(A) 2,35.
(B) 2,45.
(C) 2,55.
(D) 2,65.
(E) 2,75.
Alternativa: B
Leia os trechos para responder à questão.
Os benefícios da reciclagem do papel incluem a redução no consumo de água e energia utilizadas na produção. Mas é fato que, com a reciclagem de papel, deixa-se de cortar árvores: calcula-se que, para cada 1 tonelada de papel reciclado, salvam-se de 15 a 20 árvores.
Em 2015, 46,3% do papel produzido e comercializado no Brasil foi reciclado e voltou para a cadeia produtiva.
048) (ETEC) No Brasil, em 2015, considerando uma produção e comercialização total de 10 milhões de toneladas de papel, de acordo com os dados dos trechos, podem-se salvar até N árvores. O valor de N é
(A) 2,315 . 104 .
(B) 2,315 . 105 .
(C) 9,260 . 106 .
(D) 9,260 . 107 .
(E) 9,260 . 108 .
Alternativa: D
Leia o texto e a tabela para responder às questões de números 049 e 050.
O aleitamento materno é a mais sábia estratégia natural de vínculo, afeto, proteção e nutrição para a criança e constitui a mais sensível, econômica e eficaz intervenção para redução da morbimortalidade infantil. Permite ainda um grandioso impacto na promoção da saúde integral da dupla mãe/bebê. Nos primeiros dias após o nascimento, o leite materno é chamado de colostro. O leite de mães de recém-nascidos prematuros é diferente do de mães de bebês a termo. A principal proteína do leite materno é a lactoalbumina e a do leite de vaca é a caseína, de difícil digestão para a espécie humana. A tabela apresenta as diferenças entre o colostro e o leite maduro, entre o leite de mães de bebês a pré-termo e de bebês a termo e entre o leite materno e o leite de vaca (1) Bebê a termo: gestação de 39 a 40 semanas.
(1) Bebê a termo: gestação de 39 a 40 semanas.
(2) Bebê a pré-termo: gestação de 37 a 38 semanas.
Acesso em: 01.09.2016. Adaptado.
049) (1º SEM/17) De acordo com o texto e a tabela, pode-se afirmar que
(A) um bebê a termo de 27 dias, ao ser amamentado, ingere 7,0 g/dL de lactose.
(B) a lactoalbumina, a principal proteína do leite de vaca, é de fácil digestão para o bebê.
(C) o leite de vaca, por ter mais proteína que o colostro e que o leite maduro, é mais adequado para a criança.
(D) o leite maduro consumido pelo bebê a pré-termo contém mais lactose que o leite de vaca e menos proteína que o colostro.
(E) o colostro apresenta mais lipídios, menos proteína e menos lactose do que o leite maduro, independentemente dos dias de vida do bebê.
Alternativa: D
050) (ETEC) A quantidade de lactose que um bebê a pré-termo de 4 dias ingere ao ser amamentado com 80 mL de leite materno é, em gramas,
(A) 0,04.
(B) 0,4.
(C) 4,0.
(D) 40,0.
(E) 400,0.
Alternativa: C
Leia o texto e analise a figura para responder às questões de números 051 e 052
No mundo de hoje a acessibilidade é um direito e, para garanti-lo, são necessárias algumas adaptações, como as rampas em locais públicos, conforme mostra a figura.
051) (ETEC) Suponha que a rampa desenhada na figura tenha 6 m de comprimento. Se, sobre a rampa, um cadeirante mover sua cadeira com velocidade constante de 0,2 m/s, o tempo necessário para conseguir vencer o desnível do ponto mais baixo ao mais alto é, em segundos,
(A) 12.
(B) 15.
(C) 20.
(D) 30.
(E) 45.
Alternativa: D
052) (ETEC) Considere que:
- l uma rampa é um exemplo de máquina simples, oferecendo uma vantagem mecânica para quem a utiliza;
- l uma pessoa, subindo pela escada ou pela rampa, tem que realizar o mesmo trabalho contra a força peso;
- l essa mesma pessoa suba pela escada em um tempo menor que o necessário para subir pela rampa.
A vantagem do uso da rampa para realizar o trabalho contra a força peso, em comparação com o uso da escada, se deve ao fato de que, pela rampa,
(A) a potência empregada é menor. (B) a potência empregada é maior.
(C) a potência empregada é a mesma.
(D) a energia potencial gravitacional é menor.
(E) a energia potencial gravitacional é maior.
Alternativa: A
053) (ETEC) A caminho da erradicação da pobreza, para poder contemplar a todos com o direito à habitação, as novas edificações devem ser construídas com o menor custo e demandar cuidados mínimos de manutenção. Um acontecimento sempre presente em edificações, e que torna necessária a manutenção, é o surgimento de rachaduras. Há muitas formas de surgirem rachaduras como, por exemplo, pela acomodação do terreno ou ocorrência de terremotos. Algumas rachaduras, ainda, ocorrem devido à dilatação térmica. A dilatação térmica é um fenômeno que depende diretamente do material do qual o objeto é feito, de suas dimensões originais e da variação de temperatura a que ele é submetido.
∆S = S0 . ∆β . ∆Ɵ
Para um objeto como um muro, o acréscimo ou decréscimo da área da superfície do muro é calculado pela expressão: Em que:
∆S = representa a variação (acréscimo ou diminuição) da área da superfície que o muro apresentará;
S0 = é a área original da superfície do muro, antes de ocorrer a dilatação térmica;
β = é uma constante que está relacionada com o material que foi utilizado em sua construção;
∆Ɵ = é a variação de temperatura à qual o muro é submetido
Considere dois muros feitos com o mesmo material, sendo que o menor deles possui uma área de superfície igual a 100 m2 , enquanto que o maior tem 200 m2 . Se o muro menor sofrer uma variação de temperatura de +20 ºC e o maior sofrer uma variação de +40 ºC, a variação da área da superfície do muro maior em relação à variação da área da superfície do muro menor, é
(A) quatro vezes menor.
(B) duas vezes menor.
(C) a mesma.
(D) duas vezes maior.
(E) quatro vezes maior.
Alternativa: E
054) (ETEC) Por ser um consumidor voraz de chocolate, João estabeleceu que, para não exagerar, sempre comerá exatamente 1 kg de chocolate a cada 5 dias. Ao estudar o conceito de pegada hídrica em sua aula de Ciências, João calculou que, após um ano, a pegada hídrica do seu consumo de chocolate será de N metros cúbicos de água, considerando a média mundial. Assim sendo, o valor de N está mais próximo de
(A) 10.
(B) 100.
(C) 600.
(D) 1 200.
(E) 6 200.
Alternativa: D
055) (ETEC) No lanche da tarde, João comeu um pão com queijo, de massa total de 200 g. Curioso como sempre, determinou que, considerando só a produção dos dois ingredientes desse lanche (o pão e o queijo), o consumo de água foi de 830 litros. Sabendo que, em média, a pegada hídrica do pão é de 1,6 L/g e a do queijo é de 5,0 L/g, pode-se concluir corretamente que, em relação a esse consumo,
(A) a quantidade de pão é igual à quantidade de queijo.
(B) a quantidade de pão é o dobro da quantidade de queijo.
(C) a quantidade de pão é o triplo da quantidade de queijo.
(D) a quantidade de queijo é o dobro da quantidade de pão.
(E) a quantidade de queijo é o triplo da quantidade de pão.
Alternativa: E
056) (ETEC) Um avião, com a finalidade de abastecer uma região que se encontra isolada, voa em linha reta horizontalmente, com velocidade constante em relação ao solo, quando abandona uma caixa com alimentos, conforme a imagem. Desprezando a resistência do ar, a trajetória descrita pela caixa de alimentos terá a forma de uma
Desprezando a resistência do ar, a trajetória descrita pela caixa de alimentos terá a forma de uma
(A) parábola, do ponto de vista de um observador que estiver no avião.
(B) linha reta vertical, do ponto de vista de um observador que estiver no avião.
(C) linha reta vertical, do ponto de vista de um observador que estiver na Terra.
(D) linha reta horizontal, do ponto de vista de um observador que estiver no avião.
(E) mesma figura para qualquer observador, pois a trajetória independe do referencial.
Alternativa: B
057) (ETEC) Um aluno deseja calcular a energia envolvida no cozimento de um certo alimento. Para isso, verifica que a potência do forno que utilizará é de 1 000 W. Ao colocar o alimento no forno e marcar o tempo (∆t) gasto até o seu cozimento, ele concluiu que 3 minutos eram o bastante.
Lembre-se que:
P = E/∆t
P = potência (W)
E = energia (J) e
∆t = variação de tempo (s)
Dessa maneira, a energia (E) necessária para cozinhar o alimento é de
(A) 180 000 J.
(B) 55 000 J.
(C) 18 000 J.
(D) 5 500 J.
(E) 1 800 J.
Alternativa: A
Leia o texto para responder a questão 058.
Há mais de um tipo de bafômetro, mas todos são baseados em reações químicas envolvendo o álcool etílico presente na baforada e um reagente – por isso, o nome técnico desses aparelhos é etilômetro. Nos dois mais comuns são utilizados dicromato de potássio (que muda de cor na presença do álcool) e célula de combustível (que gera uma corrente elétrica). Este último é o mais usado entre os policiais no Brasil. Com a nova legislação, o motorista que for flagrado com nível alcoólico acima do permitido (0,1 mg/L de sangue) terá que pagar uma multa de R$ 955,00, além de ter o carro apreendido e perder a habilitação. Se estiver embriagado (níveis acima de 0,3 mg/L de sangue), ainda corre o risco de ficar preso por 6 meses a 1 ano.
058) (ETEC) Um adulto de 75 kg possui, em média, 5 litros de sangue. Esse adulto foi flagrado, no teste do bafômetro, com nível alcoólico exatamente igual ao limite máximo permitido. A massa de álcool contida no sangue desse adulto, em mg, é igual a
(A) 0,1.
(B) 0,2.
(C) 0,3.
(D) 0,4.
(E) 0,5.
Alternativa: E
059) (ETEC) Para exemplificar uma aplicação do conceito de velocidade média, um professor de Ciências explica aos seus alunos como é medida a velocidade de um veículo quando passa por um radar. Os radares usam a tecnologia dos sensores magnéticos. Geralmente são três sensores instalados no asfalto alguns metros antes do radar. Esse equipamento mede quanto tempo o veículo demora para ir de um sensor ao outro, calculando a partir daí, a velocidade média do veículo. Considere um veículo trafegando numa pista cuja velocidade máxima permitida seja de 40 km/h (aproximadamente 11 m/s) e a distância média entre os sensores consecutivos seja de 2 metros.
Considere um veículo trafegando numa pista cuja velocidade máxima permitida seja de 40 km/h (aproximadamente 11 m/s) e a distância média entre os sensores consecutivos seja de 2 metros.
O mínimo intervalo de tempo que o veículo leva para percorrer a distância entre um sensor e outro consecutivo, a fim de não ultrapassar o limite de velocidade é, aproximadamente, de
(A) 0,10 s.
(B) 0,18 s.
(C) 0,20 s.
(D) 0,22 s.
(E) 1,00 s.
Alternativa: B
060) (ETEC) Leia os textos e considere o infográfico. - Mata ciliar é a formação vegetal às margens dos rios, córregos, lagos, represas e nascentes. É considerada pelo Código Florestal Federal como Área de Preservação Permanente (APP), com diversas funções ambientais. De acordo com o artigo 2o desse Código, a largura da faixa de mata ciliar a ser preservada está relacionada com a largura dos rios, córregos, lagos, represas e nascentes, conforme mostra a figura.
- Mata ciliar é a formação vegetal às margens dos rios, córregos, lagos, represas e nascentes. É considerada pelo Código Florestal Federal como Área de Preservação Permanente (APP), com diversas funções ambientais. De acordo com o artigo 2o desse Código, a largura da faixa de mata ciliar a ser preservada está relacionada com a largura dos rios, córregos, lagos, represas e nascentes, conforme mostra a figura.
- Fora do estuário, o trecho mais largo do rio Amazonas, não interrompido por ilhas, fica a cerca de 20 km da foz do rio Xingu, onde tem 13 km de largura.
De acordo com o Código Florestal Federal, para o trecho de um rio cuja largura é 4% da largura do rio Amazonas (citada no texto), a largura da faixa de mata ciliar deve ser, em metros, igual a
(A) 500.
(B) 200.
(C) 100.
(D) 50.
(E) 30.
Alternativa: B
063) (ETEC) Para demonstrar a quantidade de calor envolvida em um processo físico, uma professora de Ciências propõe o seguinte experimento a seus alunos. Em um recipiente de vidro deve-se colocar 100 g de água destilada e medir a temperatura da mesma. Posteriormente, o recipiente é aquecido até o início da ebulição, quando se mede novamente a temperatura da água, obtendo-se o valor de 100 °C. A professora apresenta a equação que permite calcular a quantidade de calor envolvida no experimento:
Q = m . c . ∆t
Lembre-se que:
Q = quantidade de calor (em cal)
m = massa (em g)
c = calor especifico da água (c = 1 cal/g °C)
∆T = variação de temperatura (em °C)
Supondo que um grupo constatou que a temperatura inicial era de 20 °C, a quantidade de calor necessária para aquecer somente a referida massa de água deve ser de
(A) 1 000 cal.
(B) 2 000 cal.
(C) 4 000 cal.
(D) 6 000 cal.
(E) 8 000 cal.
Alternativa: E
064) (ETEC) Um especialista, ao fazer um levantamento hidrográfico de uma região marítima, representou no plano cartesiano os dados obtidos. Ao terminar a sua tarefa observou que, em particular, as ilhas A, B e C formavam um triângulo conforme a figura. Sabendo que as coordenadas dos pontos que representam as ilhas são A(2; 3), B(18; 15) e C(18; 3), pode-se concluir que a tangente do ângulo BAC é
Sabendo que as coordenadas dos pontos que representam as ilhas são A(2; 3), B(18; 15) e C(18; 3), pode-se concluir que a tangente do ângulo BAC é
(A) 3/5
(B) 3/4
(C) 4/5
(D) 5/4
(E) 4/3
Alternitiva: B
065) (ETEC) Vinícius observa duas crianças, Caio e João, empurrando uma caixa de brinquedos. Relembrando a aula de Ciências que teve pela manhã, ele observa o deslocamento da caixa e faz um desenho representando as forças envolvidas nesse processo, conforme a figura. Considerando que a caixa esteja submetida a duas forças horizontais, nos sentidos representados na figura, de intensidades F1 = 100 N e F2 = 75 N, ficou pensando em como poderia evitar o deslocamento da caixa, fazendo com que ela ficasse em equilíbrio (parada).
Considerando que a caixa esteja submetida a duas forças horizontais, nos sentidos representados na figura, de intensidades F1 = 100 N e F2 = 75 N, ficou pensando em como poderia evitar o deslocamento da caixa, fazendo com que ela ficasse em equilíbrio (parada).
Concluiu, então, que para isso ocorrer, uma outra criança deveria exercer uma força de intensidade igual a
(A) 100 N, junto com João.
(B) 100 N, junto com Caio.
(C) 75 N, junto com João.
(D) 25 N, junto com Caio.
(E) 25 N, junto com João.
Alternativa: E
066) (ETEC) O cartum brinca com a palavra parábola, que tem diferentes significados de acordo com o contexto em que é empregada. Em Matemática, no estudo de funções, a parábola é uma curva que representa uma função polinomial
Em Matemática, no estudo de funções, a parábola é uma curva que representa uma função polinomial
(A) constante e sua expressão geral é dada por f(x) = a, com a ≠ 0.
(B) de 1º grau e sua expressão geral é dada por f(x) = ax + b, com a ≠ 0.
(C) de 1º grau e sua expressão geral é dada por f(x) = ax2 + bx + c, com a ≠ 0.
(D) de 2º grau e sua expressão geral é dada por f(x) = ax + b, com a ≠ 0.
(E) de 2º grau e sua expressão geral é dada por f(x) = ax2 + bx + c, com a ≠ 0.
Alternativa: E
067) (ETEC) Um escritório utiliza uma fragmentadora de papéis, que corta em tiras muito finas documentos cujo conteúdo não se deseja tornar público. Suponha que a fragmentadora desse escritório só aceite uma folha por vez, sendo capaz de fazer sua função a uma velocidade de 3 metros por minuto. Sendo assim, para que um documento com 25 folhas seja fragmentado, levando em consideração que cada folha desse documento tem comprimento de 30 cm, o tempo mínimo para realizar a completa fragmentação desse documento é de
(A) 1 min 40 s.
(B) 2 min 20 s.
(C) 2 min 30 s.
(D) 3 min 50 s.
(E) 3 min 40 s.
Alternativa: C
068) (ETEC) O gráfico indica como varia a intensidade de uma força aplicada ininterruptamente sobre um corpo enquanto é realizado um deslocamento na mesma direção e no mesmo sentido das forças aplicadas. Na Física, existe uma grandeza denominada trabalho. O trabalho de uma força, durante a realização de um deslocamento, é determinado pelo produto entre essas duas grandezas quando ambas têm a mesma direção e sentido Considerando o gráfico dado, o trabalho total realizado no deslocamento de 8 m, em joules, corresponde a
Considerando o gráfico dado, o trabalho total realizado no deslocamento de 8 m, em joules, corresponde a
(A) 160.
(B) 240.
(C) 280.
(D) 320.
(E) 520.
Alternativa: D
069) (ETEC) Um estudante avaliou o tempo diário do uso do chuveiro em sua casa no decorrer de trinta dias consecutivos, o que permitiu a construção do quadro. Sabendo que o chuveiro de sua casa tem potência de 2 800 W, o estudante calculou que, no período avaliado, o consumo de energia em sua casa, devido ao uso do chuveiro, foi, aproximadamente, de
Sabendo que o chuveiro de sua casa tem potência de 2 800 W, o estudante calculou que, no período avaliado, o consumo de energia em sua casa, devido ao uso do chuveiro, foi, aproximadamente, de
(A) 90 kWh.
(B) 105 kWh.
(C) 125 kWh.
(D) 140 kWh.
(E) 155 kWh.
Alternativa: C
070) (ETEC) No munícipio de São Paulo, segundo dados do Instituto Brasileiro de Geografia e Estatística (IBGE), existem 12 milhões de habitantes e, segundo o Repositório de Dados Eleitorais do Tribunal Superior Eleitoral (TSE), no mesmo município, existem 9 milhões de eleitores registrados. Nessas condições, pode-se afirmar que, no munícipio de São Paulo, para cada 3 eleitores registrados, existem
(A) 75 habitantes.
(B) 40 habitantes.
(C) 30 habitantes.
(D) 4 habitantes.
(E) 3 habitantes.
Alternativa: D
071) (ETEC) Em uma Zona Eleitoral, há 6 seções, cada uma com uma urna eletrônica. Considere que o tempo médio que uma pessoa leva no processo de votação é de 3 minutos e cada seção atende o mesmo número de pessoas. Admita, ainda, que compareceram para votar 450 eleitores nessa Zona Eleitoral. Assinale a alternativa que apresenta o tempo mínimo e necessário para que todo o processo de votação seja finalizado nessa Zona Eleitoral.
(A) 3 h 55 min
(B) 3 h 45 min
(C) 2 h 40 min
(D) 2 h 25 min
(E) 1 h 15 min
Alterntiva: B
072) (ETEC) Sem dispor de uma trena de comprimento suficiente, um pedreiro determinou a medida do desnível (d) de um terreno, valendo-se da propriedade da propagação retilínea da luz. Observou que, em determinado momento do dia, um muro vertical de 1,5 m de altura, construído na parte alta do terreno, projetava uma sombra de 0,4 m sobre a parte superior do terreno, que era plana e horizontal. No mesmo instante, o desnível do terreno projetava sobre a parte mais baixa, igualmente horizontal, uma sombra de 1,6 m, conforme a figura. Com suas observações, foi capaz de deduzir corretamente que o desnível do terreno era de
Com suas observações, foi capaz de deduzir corretamente que o desnível do terreno era de
(A) 6,0 m.
(B) 8,0 m.
(C) 10,0 m.
(D) 12,0 m.
(E) 14,0 m.
Alternativa: A
073) (ETEC) Considerando y o valor do prêmio em 2017 e x o valor do prêmio em 2016, assinale a alternativa que apresenta a relação correta entre os dois valores.
(A) y = x + 0,12
(B) y = 1,12 x
(C) y = 12 x
(D) x = 1,12 y
(E) x = y + 0,12
Alternativa: B
074) (ETEC) Com base nas informações contidas no texto e assumindo que, em 2016, uma coroa sueca era equivalente a R$ 0,42, pode-se afirmar que o valor aproximado do Prêmio Nobel, para cada modalidade de premiação, em 2016 era, em milhões de reais, de cerca de
(A) 3,33
(B) 3,66
(C) 3,78
(D) 5,04
(E) 7,92
Alternativa: A
075) (ETEC) Um vencedor do Prêmio Nobel deseja encomendar a construção de uma caixa para acomodar a medalha que recebeu como parte da premiação. A caixa terá a forma de um paralelepípedo de base quadrada, sobre a qual sabe-se que:
A caixa terá a forma de um paralelepípedo de base quadrada, sobre a qual sabe-se que:
- a medida do lado da base é 4 mm maior do que o diâmetro da medalha;
- o volume total é igual a 147 cm3 ;
- o material do qual a caixa será feita tem espessura desprezível.
A altura da caixa, em centímetros, será igual a
(A) 2,0
(B) 2,3
(C) 3,0
(D) 3,3
(E) 4,0
Alternativa: C
076) (ETEC) Para transportar terra adubada retirada da compostagem, um agricultor enche um carrinho de mão e o leva até o local de plantio aplicando uma força horizontal, constante e de intensidade igual a 200 N. Se durante esse transporte, a força resultante aplicada foi capaz de realizar um trabalho de 1 800 J, então, a distância entre o monte de compostagem e o local de plantio foi, em metros
Observação: Lembre-se de que o trabalho realizado por uma força, durante a realização de um deslocamento, é o produto da intensidade dessa força pelo deslocamento.
(A) 6.
(B) 9.
(C) 12.
(D) 16.
(E) 18.
Alternativa: B
077) (ETEC) O gráfico apresenta os valores médios dos preços de terras agrícolas da cidade de Andradina (SP), no período de 2004 a 2014, de acordo com o Instituto de Economia Agrícola (IEA). Com base no gráfico, pode-se afirmar corretamente que,
Com base no gráfico, pode-se afirmar corretamente que,
(A) em 2010, por hectare, a diferença entre o valor médio da terra de cultura de segunda e o valor da terra para pastagem foi maior que R$ 2.000,00.
(B) em 2011, por 10 hectares de terra para pastagem, se pagava, em média, cerca de R$ 120.500,00.
(C) em 2013, por hectare, o valor médio da terra de cultura de segunda era maior que o valor médio da terra para pastagem.
(D) em cada ano do período de 2004 a 2014, o valor médio da terra de cultura de primeira por hectare não ultrapassou R$ 20.000,00.
(E) em cada ano do período de 2012 a 2014, os quatro tipos de terras tinham valor médio por hectare maior que R$ 10.000,00.
Alternativa: E
078) (ETEC) Suponha que uma semeadeira é arrastada sobre o solo com velocidade constante de 4 km/h, depositando um único grão de milho e o adubo necessário a cada 20 cm de distância. Após a semeadeira ter trabalhado por 15 minutos, o número de grãos de milho plantados será de, aproximadamente,
(A) 1 200.
(B) 2 400.
(C) 3 800.
(D) 5 000.
(E) 7 500.
Alternativa: D
079) (ETEC) Todos aqueles que tiveram oportunidade de lidar com imóveis rurais se depararam com uma unidade de medida de terras denominada alqueire, o que usualmente vem seguido de uma dúvida: será o alqueire mineiro, com seus 4,84 ha, o paulista, equivalente a 2,42 ha, ou até mesmo o chamado alqueirão, com 19,36 ha?
O Sr. João tem terras produtivas e sabe que pode colher 48 sacas de soja por hectare de plantação. Em sua fazenda, ele plantou 5 alqueires paulistas de soja. Assim sendo, o número de sacas que o Sr. João espera colher é mais próximo de
(A) 250.
(B) 580.
(C) 840.
(D) 1 160.
(E) 4 640.
Alternativa: B
080) (ETEC) A criação de área de preservação permanente e reservas legais são medidas importantes de proteção ambiental para a conservação do solo e da água, elementos essenciais para a vida na Terra. Uma fazenda apresenta as seguintes características:
Lembre-se que:
- 1 are (a) equivale a 100 m2
- 1 hectare (ha) equivale a 100 a
- área total: 80 ha;
- área para lavoura: 28 ha;
- área para plantação de eucalipto: 15 ha;
- área ocupada por benfeitoria/desmatada: 12 ha;
- a área restante é destinada à preservação ambiental/ reserva legal. Se a região destinada à preservação ambiental/reserva legal dessa fazenda tem forma retangular, as dimensões desse retângulo podem ser
(A) 50 m x 50 m.
(B) 50 m x 500 m.
(C) 500 m x 500 m.
(D) 500 m x 5 000 m.
(E) 5 000 m x 5 000 m.
Alternativa: C
081) (ETEC) Segundo um pesquisador da Empresa Brasileira de Pesquisa Agropecuária (EMBRAPA), a maioria das terras suscetíveis à desertifi cação no Brasil encontra-se nas áreas semiáridas e subúmidas do Nordeste. A quantificação dessas áreas mostra que cerca de 181 000 km2 encontram-se em processo de desertificação, o que corresponde a 20% da área semiárida da região Nordeste, aproximadamente.
De acordo com o texto, a área da região semiárida do Nordeste é, aproximadamente, em quilômetros quadrados,
(A) 181 000.
(B) 217 200
(C) 362 000.
(D) 582 400.
(E) 905 000.
Alternativa: E
088) (ETEC) Apenas 11% dos solos terrestres são agricultáveis e até mesmo esse pequeno espaço é constantemente agredido com o uso de práticas nocivas. De acordo com a Organização das Nações Unidas (ONU), aproximadamente 75 milhões de toneladas de solos férteis se perdem todos os anos no mundo. Essas perdas acontecem fundamentalmente pela ação dos processos erosivos, que agem de três formas distintas. Assinale a alternativa que apresenta a sequência correta da ação dos processos erosivos.
(A) Transporte, desagregação e deposição.
(B) Deposição, transporte e desagregação.
(C) Transporte, deposição e desagregação.
(D) Deposição, desagregação e transporte.
(E) Desagregação, transporte e deposição
Alternativa: E
083) (ETEC) A erosão é o processo de desgaste, transporte e sedimentação das rochas e, principalmente, dos solos. Ela pode ocorrer por ação de fenômenos da natureza ou do ser humano. A imagem mostra uma fenda no solo, proveniente de erosão. Para determinar a distância entre os pontos A e B da fenda, pode-se utilizar o modelo matemático da fi gura
Para determinar a distância entre os pontos A e B da fenda, pode-se utilizar o modelo matemático da fi gura Na figura, tem-se:
Na figura, tem-se:
- os triângulos AFC e EFD ;
- o ponto E pertencente ao segmento AF ;
- o ponto D pertencente ao segmento CF ;
- os pontos C, D e F pertencentes ao terreno plano que margeia a borda da fenda; e
- as retas AC e ED que são paralelas entre si.
Sabendo-se que BC = 5 m, CD = 3 m, DF = 2 m e ED = 4,5 m, então, a distância entre os pontos A e B é, em metros,
(A) 6,25.
(B) 6,50.
(C) 6,75.
(D) 7,25.
(E) 7,75.
Alternativa: A
085) (ETEC) A Faculdade de Matemática da Universidade Federal do Pará, Campus de Castanhal, realizou uma pesquisa sobre a variação da cobertura vegetal ao longo do Eixo da BR-316. A pesquisa analisou imagens de satélite de 1999 a 2008. Em relação à área estudada, entre os dados levantados, obteve-se: ... em 1999, 61% da área era preenchida por fl oresta, 20% por plantações, 13% por campos abertos, 5% por áreas urbanizadas e 1% por água. Nove anos depois, esses índices são de 46% de fl orestas, 25% de plantações, 20% de campos abertos, 8% de áreas urbanizadas e apenas a presença de água se mostrou constante, permanecendo em 1%. Acesso em: 26.07.2015. Adaptado.
De acordo com o texto, de 1999 a 2008,
(A) a variação da área estudada ocupada pela fl oresta aumentou 15%.
(B) a variação da área estudada ocupada pela presença de água diminuiu 10%.
(C) a variação da área estudada ocupada pelas plantações diminuiu em mais de 25%.
(D) a área ocupada pelos campos abertos aumentou mais de 50%.
(E) a área ocupada pelas áreas urbanizadas aumentou mais de 80%.
Alternativa: D
086) (ETEC) Um terreno inclinado traz dificuldades para a construção civil, para a agricultura e para um caminhante aventureiro. Seja α a medida do ângulo que a superfície do terreno faz com o plano horizontal, conforme a figura.
Seja α a medida do ângulo que a superfície do terreno faz com o plano horizontal, conforme a figura.
A taxa de declividade, ou apenas declividade, de um terreno é a tangente desse ângulo α.
A declividade de um terreno é, normalmente, expressa em porcentagem, por exemplo, se tg α = 0,23, então, a taxa de declividade é 23%. Um excursionista sobe uma montanha que tem declividade de 50%.
Considere que, do ponto que o excursionista partiu até o topo da montanha, o desnível vencido foi de 1 000 metros. Nessas condições, a menor distância percorrida pelo excursionista até o topo da montanha é, em quilômetros,
(A) √ 2
(B) √ 3
(C) √ 4
(D) √ 5
(E) √ 6
Alternativa: D
087) (ETEC) ) Leia o texto e assinale a alternativa que completa correta e respectivamente suas lacunas. Na construção civil, o termo recalque se refere à acomodação do solo, após a construção de uma edificação. O recalque uniforme costuma ser previsto. Porém, quando ele não é uniforme, pode até causar o desabamento de construções. Observe o que ocorreu com um prédio, quando o recalque não foi uniforme Se o prédio inclinado fosse considerado um bloco retangular, inicialmente com sua base apoiada sobre o solo horizontal, haveria uma inclinação limite, a partir da qual ele tombaria, situação que seria causada no momento em que a projeção __________________ de seu centro de gravidade estivesse __________________ da base de sustentação.
Se o prédio inclinado fosse considerado um bloco retangular, inicialmente com sua base apoiada sobre o solo horizontal, haveria uma inclinação limite, a partir da qual ele tombaria, situação que seria causada no momento em que a projeção __________________ de seu centro de gravidade estivesse __________________ da base de sustentação.
(A) horizontal, fora
(B) horizontal, dentro
(C) transversal, fora
(D) vertical, dentro
(E) vertical, fora
Alternativa: E
090) (ETEC) A Companhia do Latão é um grupo de teatro influenciado pela obra de Bertolt Brecht cujas peças criticam a sociedade atual. Os cenários são simples e despojados e dão margem à imaginação da plateia, fazendo-a cúmplice dos atores e, em muitas ocasiões, parte do espetáculo. Na criação da atmosfera cênica na peça Ópera dos Vivos, a Companhia utilizou 8 baldes plásticos vermelhos, cada um deles com uma lâmpada de 150 W em seu interior.
Se todas essas lâmpadas fossem mantidas acesas durante meia hora, ao longo da apresentação, a energia utilizada por elas seria, em watt-hora,
(A) 600.
(B) 800.
(C) 900.
(D) 1 200.
(E) 1 500
Alternativa: A
091) (ETEC) Para causar a impressão de continuidade, esses fotogramas eram projetados um por um, a uma velocidade de 24 fotogramas por segundo. Se a cada 30 mm da fita de um filme existe um único fotograma, em uma animação de 3 minutos de duração, a fita terá um comprimento aproximado, em metros, de
(A) 70.
(B) 90.
(C) 130.
(D) 150.
(E) 220.
Alternativa: C
Lei o texto a seguir.
Em um antigo projetor de cinema, o filme a ser projetado deixa o carretel F, seguindo um caminho que o leva ao carretel R, onde será rebobinado. Os carretéis são idênticos e se diferenciam apenas pelas funções que realizam. Pouco depois do início da projeção, os carretéis apresentam-se como mostrado na figura, na qual observamos o sentido de rotação que o aparelho imprime ao carretel R.Nesse momento, considerando as quantidades de filme que os carretéis contêm e o tempo necessário para que o carretel R dê uma volta completa, é correto concluir que o carretel F gira em sentido
(A) anti-horário e dá mais voltas que o carretel R.
(B) anti-horário e dá menos voltas que o carretel R.
(C) horário e dá mais voltas que o carretel R.
(D) horário e dá menos voltas que o carretel R.
(E) horário e dá o mesmo número de voltas que o carretel R
Alternativa: D
Considere o texto e as figuras para responder às questões de números 092 e 093.
O circo é uma expressão artística, parte da cultura popular, que traz diversão e entretenimento. É um lugar onde as pessoas têm a oportunidade de ver apresentações de vários artistas como mágicos, palhaços, malabaristas, contorcionistas e muito mais. Mas antes que a magia desse mundo se realize, há muito trabalho na montagem da estrutura do circo. A tenda de um circo deve ser montada em um terreno plano e para isso deve ser construída uma estrutura, conforme a sequência de figuras.
Nas figuras, considere que:
- foram colocadas 8 estacas congruentes perpendiculares ao plano do chão;
- cada estaca tem 4 m acima do solo;
- as estacas estão igualmente distribuídas, sendo que suas bases formam um octógono regular;
- os topos das estacas consecutivas estão ligados por varas de 12 m de comprimento;
- para imobilizar as estacas, do topo de cada uma delas até o chão há um único cabo esticado que forma um ângulo de 45° com o solo (a figura mostra apenas alguns desses cabos). Todos os cabos têm a mesma medida;
- no centro do octógono regular é colocado o mastro central da estrutura, que é vertical;
- do topo de cada estaca até o topo do mastro é colocada uma outra vara. Todas essas varas têm a mesma medida;
- na estrutura superior, são formados triângulos isósceles congruentes entre si; e
- em cada um desses triângulos isósceles, a altura relativa à base é de 15 m.
092) (ETEC) A cobertura e as laterais da tenda descrita serão totalmente revestidas por lona. Para que isso ocorra, a quantidade mínima de lona que deverá ser usada é, em metros quadrados, igual a
(A) 138.
(B) 384.
(C) 720.
(D) 1 104.
(E) 1 200.
Alternativa: D
093) (ETEC) A quantidade de cabo utilizada para imobilizar as oito estacas, é, em metros,
Observação: Para o cálculo, considere apenas a quantidade de cabo do topo de cada estaca até o solo. Despreze as amarras.
(A) 16√2 .
(B) 24√2 .
(C) 32√2 .
(D) 40√2 .
(E) 48√ 2 .
Alternativa: C
093) (ETEC) A apresentação de motociclistas, dentro do globo da morte, é sempre um momento empolgante de uma sessão de circo, pois, ao atingir o ponto mais alto do globo, eles ficam de ponta cabeça. Para que, nesse momento, o motociclista não caia, é necessário que ele esteja a uma velocidade mínima (v) que se relaciona com o raio do globo (R) e a aceleração da gravidade (g) pela expressão: V = √R . d com R dado em metros.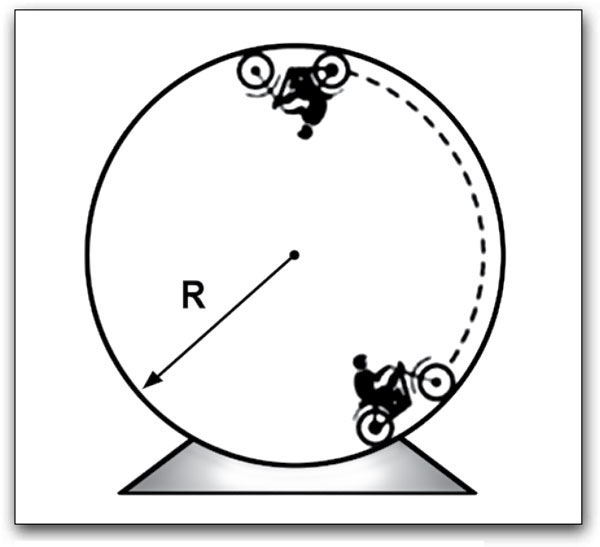 Considere que no ponto mais alto de um globo da morte, um motociclista não caiu, pois estava com a velocidade mínima de 27 km/h. Assim sendo, o raio do globo é, aproximadamente, em metros, adote g = 10m/s2
Considere que no ponto mais alto de um globo da morte, um motociclista não caiu, pois estava com a velocidade mínima de 27 km/h. Assim sendo, o raio do globo é, aproximadamente, em metros, adote g = 10m/s2
(A) 5,6.
(B) 6,3.
(C) 7,5.
(D) 8,2.
(E) 9,8.
Alternativa: A
094) (ETEC) A mostra “Castelo Rá-Tim-Bum – A exposição” recriou o famoso castelo, em homenagem ao programa infantil da TV Cultura o qual completou 20 anos do início de sua veiculação em 2014. Essa mostra foi inaugurada em julho, no Museu da Imagem e do Som (MIS), localizado na cidade de São Paulo, obtendo enorme sucesso de público. Os ingressos, vendidos na bilheteria do Museu, são de R$ 10,00 (inteira) e R$ 5,00 (meia). Para menores de cinco anos, o ingresso é gratuito.
Admita que no dia da inauguração da exposição:
- ingressaram 1 700 visitantes;
- entre esses visitantes, 150 eram menores de cinco anos;
- a arrecadação total foi de R$ 12.500,00;
- todos os visitantes pagantes adquiriram os ingressos exclusivamente na bilheteria do MIS; e
- com exceção das crianças menores de 5 anos, os demais visitantes pagaram ingresso.
Assim sendo, pode-se concluir que a quantidade de visitantes que pagou meia entrada nesse dia foi de
(A) 600 pessoas.
(B) 650 pessoas.
(C) 700 pessoas.
(D) 750 pessoas.
(E) 800 pessoas.
Alternativa: A
095) (ETEC) No Monumento às Bandeiras, situado no Parque do Ibirapuera em São Paulo, o escultor Victor Brecheret representou a ação de escravos e portugueses empenhados em transportar uma enorme canoa, arrastando-a pela mata. Admita que, numa situação real, todos os homens que estão a pé exercem forças de iguais intensidades entre si e que as forças exercidas pelos cavalos também tenham as mesmas intensidades entre si. Na malha quadriculada, estão representados o sentido e a direção dos vetores força de um homem, de um cavalo e do atrito da canoa com o chão. Como a malha é constituída de quadrados, também é possível verificar que as intensidades da força de um cavalo e do atrito são múltiplos da intensidade da força de um homem.
Admita que, numa situação real, todos os homens que estão a pé exercem forças de iguais intensidades entre si e que as forças exercidas pelos cavalos também tenham as mesmas intensidades entre si. Na malha quadriculada, estão representados o sentido e a direção dos vetores força de um homem, de um cavalo e do atrito da canoa com o chão. Como a malha é constituída de quadrados, também é possível verificar que as intensidades da força de um cavalo e do atrito são múltiplos da intensidade da força de um homem.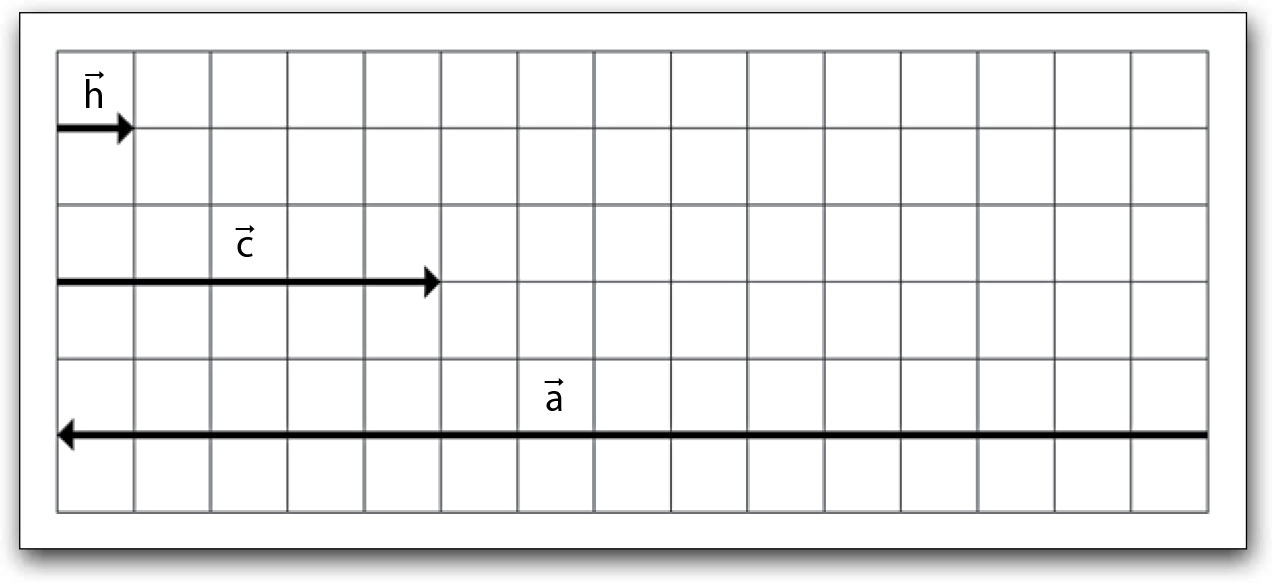 Imagine que, em determinado momento, as forças horizontais sobre a canoa sejam unicamente a de sete homens, dois cavalos e do atrito da canoa com o chão. A canoa tem massa igual a 1 200 kg e, devido às forças aplicadas, ela é movimentada com aceleração de 0,4 m/s2 . Com base nessas informações, é correto afirmar que a intensidade da força exercida por um único homem é, em newtons,
Imagine que, em determinado momento, as forças horizontais sobre a canoa sejam unicamente a de sete homens, dois cavalos e do atrito da canoa com o chão. A canoa tem massa igual a 1 200 kg e, devido às forças aplicadas, ela é movimentada com aceleração de 0,4 m/s2 . Com base nessas informações, é correto afirmar que a intensidade da força exercida por um único homem é, em newtons,
(A) 180.
(B) 240.
(C) 360.
(D) 480.
(E) 500.
Alternativa: B
097) (ETEC) Sacolas imensas são usadas para o transporte de minérios, sucatas e entulhos. Elas são feitas de plástico reciclável e têm quatro alças, conforme mostra a figura. São facilmente movimentadas encaixando-se suas quatro alças no gancho de pequenos guindastes. Suponha que em uma dessas sacolas sejam colocados 1 200 kg de entulho e que todos os pontos de fixação de cada alça na sacola sofram trações de mesma intensidade, quando a sacola é erguida.
Lembre-se que: o peso de um corpo é calculado pela expressão
P = m · g
P = peso do corpo (N);
m = massa do corpo (kg),
g = aceleração da gravidade, de valor 10 m/s2 .Nessas condições, a componente vertical da tração a que cada ponto de fixação das alças é submetido será, em newtons,
(A) 120.
(B) 150.
(C) 1 200.
(D) 1 500.
(E) 3 000.
Alternativa: D
098) (ETEC) O transporte de areia apresenta uma característica própria: o caminhão é carregado e, durante o transporte, devido ao movimento e trepidação, a areia se adensa e, além do mais, a carga perde água diminuindo o volume físico. Assim, para evitar dúvidas, quando o caminhão de areia chega à obra, o volume da areia deve ser calculado. Como calcular o volume de areia em um caminhão? Primeiro, obtém-se a altura da areia em cinco pontos estratégicos, a saber: no centro do monte (parte mais alta) e em cada um dos cantos da caçamba, conforme figura. Depois, deve-se medir as dimensões internas da caçamba (comprimento e largura). Finalmente, o volume (V) será a média aritmética das cinco alturas, multiplicada pela largura (L) e pelo comprimento (C) da caçamba, isto é:Observações:
- A figura é meramente ilustrativa.
- M1 , além de representar o ponto onde foi feita a medida, também representa a altura da areia nesse mesmo ponto. As especificações para M1 valem para M2 , M3 , M4 e M5 .
Um caminhão carregado de areia chega a uma determinada obra e tomam-se as medidas necessárias para o cálculo do volume, de acordo com o processo descrito no texto.
As alturas obtidas são 0,8 m; 0,7 m; 0,9 m; 0,8 m e 1,2 m.
O comprimento e a largura internos da caçamba são 5,0 m e 2,4 m, respectivamente.
Assim sendo, o volume de areia, em metros cúbicos, é
(A) 9,44.
(B) 9,82.
(C) 10,24.
(D) 10,56.
(E) 10,78.
Alternativa: D
099) (ETEC) Uma empresa de transporte de areia cobra R$ 75,00 por metro cúbico de areia fina. O valor do frete da carga, entre o ponto de distribuição de areia e o local da entrega, é de R$ 5,00 por metro cúbico de areia por quilômetro rodado. Considere que uma encomenda de 2 metros cúbicos de areia fina foi orçada em R$ 450,00. Nessas condições, a distância entre o ponto de distribuição de areia e o local da entrega é, em quilômetros,
(A) 15.
(B) 30.
(C) 45.
(D) 60.
(E) 75.
Alternativa: B
Leia o texto para responder às questões de números 100 e 101.
Acidentes acontecem com frequência no Brasil, país que utiliza principalmente o transporte rodoviário para fazer a conexão entre produtores, distribuidores e consumidores.
Associação Brasileira da Indústria Química mantém o Pró-Química, um serviço de informações via telefone para auxiliar as autoridades rodoviárias, o corpo de bombeiros, os produtores e os transportadores a lidar com as ocorrências envolvendo substâncias químicas nas estradas brasileiras.
No âmbito do Estado de São Paulo, o DER disponibiliza o Sistema de Informações de Produtos Perigosos e a Companhia
Ambiental do Estado de São Paulo (CETESB) também mantém equipes em plantão todos os dias do ano no Centro de Controle de Desastres e Emergências Químicas.
Para prevenir os acidentes e minimizar os riscos, o Brasil vem adotando uma legislação específica e rigorosa em relação ao transporte de produtos químicos por via rodoviária.
Para poderem trafegar, os caminhões que transportam produtos ou resíduos químicos perigosos são obrigados a adotar uma série de medidas de segurança.
O caminhão tem de estar em boas condições de manutenção e portar placas indicativas para mostrar o que carrega e seus riscos.
A indicação dos perigos é feita por painéis de segurança retangulares e duas linhas com números em preto. A linha superior indica o número de risco, e a linha inferior traz o número ONU, ou seja, o número que identifica o produto de acordo com a listagem de produtos perigosos utilizada internacionalmente.
Os rótulos de risco trazem números e símbolos indicando a classificação dos produtos transportados e seu enquadramento em uma das classes ou subclasses especificadas na Resolução da Agência Nacional de Transportes Terrestres.
Existem cerca de 3 500 números ONU relacionando os produtos perigosos. A Organização das Nações Unidas (ONU) possui um comitê específico para legislar sobre esse assunto.
100) (ETEC) De acordo com o texto, é correto afirmar que
(A) a ocorrência de acidentes no Brasil é muito rara porque foi adotada uma legislação específica e rigorosa.
(B) o Brasil adotou uma legislação moderada emrelação ao transporte de produtos químicos por via rodoviária.
(C) os rótulos de risco trazem os números ONU na linha superior, que identificam o produto de acordo com a listagem de produtos perigosos.
(D) a CETESB mantém um serviço de informações via telefone para auxiliar nas ocorrências envolvendo substâncias químicas nas estradas brasileiras.
(E) a ONU legisla sobre o transporte de produtos perigosos por meio de um comitê que relaciona os produtos perigosos à números, denominados número ONU.
Alternativa: E
101) (ETEC) Pela análise do texto e dos painéis de segurança representados no caminhão, conclui-se corretamente que os números ONU
(A) 30 e 33 significam que o veículo transporta um único produto químico.
(B) 30 e 33 significam que o veículo transporta produtos químicos diferentes.
(C) 30 e 1993 significam que o veículo transporta produtos químicos diferentes.
(D) 1993 e 1999 significam que o veículo transporta um único produto químico.
(E) 1993 e 1999 significam que o veículo transporta produtos químicos diferentes.
Alternativa: E
102) (ETEC) O Exército Brasileiro possui unidades em todos os estados da federação, podendo realizar, por via aérea, o transporte de soldados ou equipamentos de um local a outro do país.
Nas figuras 1 e 2 foram traçadas malhas quadriculadas idênticas. Sobre a malha quadriculada da figura 1, está desenhado o mapa do Brasil. Na malha quadriculada da figura 2, estão representados os possíveis vetores deslocamento a serem realizados. Suponha que uma aeronave decole do ponto destacado na figura 1 pelo símbolo situado na divisa entre o Mato Grosso do Sul e o Paraná, e siga sucessivamente os deslocamentos indicados pelos vetores a, b, c e d, nessa ordem. Completado o plano de voo, a aeronave estará sobre o estado
(A) da Bahia.
(B) de São Paulo.
(C) de Tocantins.
(D) de Minas Gerais.
(E) do Rio Grande do Sul.
Alternativa: A
103) (ETEC) Alguns meios de transporte são realmente especiais como o veículo chamado Fênix 2, uma cápsula de aço criada para resgatar, um a um, 33 mineiros chilenos que ficaram presos a 700 metros abaixo da superfície. Primeiramente foi perfurado um túnel até a câmara onde se encontravam os mineiros. Em seguida, a Fênix 2 foi levada até essa câmara. Lá embaixo, a partir do instante em que um mineiro já estava posicionado dentro da cápsula, a subida da Fênix 2 pelo túnel demorava 16 minutos. É correto afirmar que, durante a subida da cápsula da câmara até a superfície, a velocidade média da Fênix 2 foi, aproximadamente,
(A) 0,7 km/h.
(B) 2,6 km/h.
(C) 3,4 km/h.
(D) 3,6 km/h.
(E) 4,4 km/h.
Alternativa: B
104) (ETEC) A necessidade de abastecimento de água levou os romanos a construírem a maior rede hídrica da Antiguidade. Eles conheciam o sistema de transporte por canalização subterrânea e o de aquedutos por arcos suspensos. A água, proveniente de locais mais elevados, era conduzida por canais ligeiramente inclinados e que terminavam em reservatórios de onde era distribuída para o consumo. A figura representa um aqueduto que ligava o nível do lago de onde era retirada a água até o reservatório de uma cidade
Admita que o desnível entre a entrada da água no aqueduto e sua saída no reservatório era de 20 metros. Considere que entraram 100 kg da água do lago no aqueduto.
Lembre que: a energia potencial gravitacional de um corpo é calculada pela expressão
EP = m · g · h
EP = a energia potencial gravitacional (J);
m = a massa do corpo (kg);
g = a aceleração da gravidade, de valor 10 m/s2, e
h = a medida do desnível (m).
Para a situação descrita, suponha que há conservação da energia mecânica
Após essa massa de água ter percorrido o aqueduto, a energia cinética com que ela chegou ao reservatório foi, em joules, de
(A) 100.
(B) 200.
(C) 1 000.
(D) 2 000.
(E) 20 000.
Alternativa: E
106) (ETEC) Carlos Frederico, aluno de uma ETEC do estado de São Paulo, foi selecionado para fazer intercâmbio na área técnica em uma instituição situada em Londres. O aluno embarcou para Londres às 6 horas do dia 26 de fevereiro de 2014, no Aeroporto Internacional de Guarulhos. O tempo de voo entre Guarulhos e Londres foi exatamente 11 horas. Sabendo que Guarulhos segue o horário de Brasília (GMT –3, ou seja, menos três horas em relação ao meridiano central Greenwich), quando Carlos Frederico desembarcou em Londres, os relógios dessa cidade marcavam
Observação: Desconsidere a existência do horário de verão.
(A) 6 horas.
(B) 9 horas.
(C) 11 horas.
(D) 17 horas.
(E) 20 horas.
Alternativa: E
107) (ETEC) Uma pessoa viajará para o exterior e levará dois mil dólares para suas despesas. No dia em que comprou essa quantia no banco, a cotação do dólar era de R$ 2,10. Além de pagar pela compra de dólares, também pagou o Imposto sobre Operações Financeiras (IOF), que corresponde a 0,38% do valor pago pela compra. Assim sendo, para efetuar o total da compra, essa pessoa gastou
(A) R$ 3.043,48.
(B) R$ 3.546,54.
(C) R$ 4.035,42.
(D) R$ 4.215,96.
(E) R$ 4.796,00.
Alternativa: D
108) (ETEC) Nos versos de Mar Portuguez, o poeta Fernando Pessoa homenageia seus compatriotas que participaram das viagens dos descobrimentos.
Observação: Ó mar salgado, Quanto do teu sal são lágrimas de Portugal
A água do mar apresenta diversos sais que lhe conferem a salinidade, pois, em cada quilograma de água do mar, estão dissolvidos, em média, cerca de 35 g de sais. (spq.pt/boletim/docs/boletimSPQ_101_056_24.pdf
Baseando-se na concentração de sais descrita no texto, para a obtenção de 1 kg de sais, a massa de água do mar necessária será, em kg, aproximadamente de
(A) 1.
(B) 5.
(C) 20.
(D) 29.
(E) 35.
Alternativa: D
109) (ETEC) A Jornada Mundial da Juventude (JMJ) aconteceu no Rio de Janeiro, em julho de 2013, e atraiu visitantes do Brasil e de vários outros países.
Segundo a Prefeitura do Rio, 3,2 milhões de pessoas compareceram à cerimônia de encerramento da JMJ, que ocorreu na Praia de Copacabana.
A área da superfície ocupada pelas pessoas que compareceram à cerimônia de encerramento da JMJ equivale à área da superfície de cerca de N campos de futebol do estádio do Maracanã. Sabendo-se que o campo de futebol do Maracanã tem forma retangular com dimensões de 105 metros por 68 metros e adotando-se que, em uma concentração de grande porte como essa, um metro quadrado é ocupado por 4 pessoas, em média; então, considerando os dados apresentados, o número inteiro positivo mais próximo de N será
(A) 45.
(B) 57.
(C) 112.
(D) 136.
(E) 144.
Alternativa: C
110) (ETEC) O passeio em teleférico é uma opção turística em várias cidades do mundo. O teleférico mais alto e o segundo mais longo do mundo fica na cidade de Mérida, Venezuela, unindo a cidade ao Pico Espejo, cujo topo está a uma altura de 4 765 metros acima do nível do mar.
O teleférico sai da estação de Barinitas, a 1 577 metros acima do nível do mar, na cidade de Mérida e, depois de se deslocar 12,5 km, atinge o topo do Pico Espejo. Considere que o cabo do teleférico seja completamente esticado e que q seja o ângulo, com vértice na estação de Barinitas, formado pelo cabo do teleférico e a horizontal, conforme a figura. Nessas condições, o valor aproximado do ângulo q é
Nessas condições, o valor aproximado do ângulo q é
(A) 11º.
(B) 15º.
(C) 18º.
(D) 22º.
(E) 25º.
Alternativa: B
111) (ETEC) Um atrativo da cidade de Santos é subir de bondinho até o topo do Monte Serrat, que se localiza a aproximadamente 150 m do nível do mar. O funicular é um sistema engenhoso de transporte de pessoas que liga dois bondinhos idênticos por meio de um único cabo, fazendo com que o peso do bonde que desce o monte auxilie a subida do outro bonde. Nesse sistema, se os atritos forem desprezíveis, o esforço da máquina que movimenta o cabo se resumirá apenas ao esforço de transportar passageiros. Considere que, em uma viagem,
Considere que, em uma viagem,
- os passageiros no bonde, que se encontra no alto do monte, somam a massa de 600 kg;
- os passageiros no bonde, que se encontra ao pé do monte, somam a massa de 1 000 kg;
- a aceleração da gravidade tem valor 10 m/s2 ;
- cada bonde se move comvelocida de constante.
Observação: Para responder a essa questão, lembre-se de que a energia potencial gravitacional é calculada pela relação:
Epot = massa x aceleração da gravidade x altura
Conclui-se corretamente que a energia empregada pelo motor, que movimenta o sistema funicular para levar os passageiros a seus destinos, deve ser, em joules,
(A) 40 000.
(B) 150 000.
(C) 600 000.
(D) 900 000.
(E) 1 000 000.
Alternativa: C
112) (ETEC) Algumas cidades têm implantado corredores exclusivos para ônibus a fim de diminuir o tempo das viagens urbanas. Suponha que, antes da existência dos corredores, um ônibus demorasse 2 horas e 30 minutos para percorrer todo o trajeto de sua linha, desenvolvendo uma velocidade média de 6 km/h. Se os corredores conseguirem garantir que a velocidade média dessa viagem aumente para 20 km/h, o tempo para que um ônibus percorra todo o trajeto dessa mesma linha será
Se os corredores conseguirem garantir que a velocidade média dessa viagem aumente para 20 km/h, o tempo para que um ônibus percorra todo o trajeto dessa mesma linha será
(A) 30 minutos.
(B) 45 minutos.
(C) 1 hora.
(D) 1 hora e 15 minutos.
(E) 1 hora e 30 minutos.
Alternativa: B
113) (ETEC) Um grupo de amigos, em visita a Aracaju, alugou um carro por dois dias. A locação do carro foi feita nas seguintes condições: R$ 40,00 por dia e R$ 0,45 por quilômetro rodado. No primeiro dia, saíram de Aracaju e rodaram 68 km para chegar à Praia do Saco, no sul de Sergipe. No segundo dia, também partiram de Aracaju e foram até Pirambu, no norte do estado, para conhecer o Projeto Tamar. Por uma questão de controle de gastos, o grupo de amigos restringiu o uso do carro apenas para ir e voltar desses lugares ao hotel onde estavam hospedados em Aracaju, fazendo exatamente o mesmo percurso de ida e volta. Nas condições dadas, sabendo que foram pagos R$ 171,80 pela locação do carro, então o número de quilômetros percorrido para ir do hotel em Aracaju a Pirambu foi
(A) 68.
(B) 61.
(C) 50.
(D) 46.
(E) 34.
Alternativa: E
114) (ETEC) Em uma comunidade será implantada uma horta coletiva. Para preparar o solo, o técnico agrícola recomendou 400 g de calcário para cada metro quadrado da superfície dos canteiros. Sabendo que a horta terá quatro canteiros retangulares de dimensões 1,0 m x 1,5 m, então a quantidade de calcário necessária para o preparo desses canteiros será, em quilogramas,
(A) 1,6.
(B) 1,8.
(C) 2,0.
(D) 2,2.
(E) 2,4.
Alternativa: E
115) (ETEC) Na Estatística da Produção Agrícola, publicada em outubro de 2013, pelo Instituto Brasileiro de Geografia e Estatística (IBGE), a estimativa para a safra nacional de cereais, leguminosas e oleaginosas de 2013 era cerca de 187 milhões de toneladas, valor superior à safra obtida em 2012 que foi de 162 milhões de toneladas aproximadamente. Em relação à safra de 2012, a estimativa para a safra nacional de cereais, leguminosas e oleaginosas de 2013 teve um aumento percentual aproximado de
(A) 13,3%.
(B) 14,7%.
(C) 15,4%.
(D) 16,5%.
(E) 17,6%.
Alternativa: C
116) (ETEC) A equipe de logística de uma transportadora, após definir o roteiro mais viável para a realização da entrega de mercadorias, determinou que um dos motoristas deveria fazer oito entregas pela manhã, gastando entre deslocamento, descarga e assinatura de documentos exatos 30 minutos para cada uma das entregas. Tudo transcorria de acordo com as especificações, porém, na sétima entrega, houve um atraso de 10 minutos. Sabe-se que a distância entre o sétimo e o oitavo ponto de entrega é de 15 km e que o motorista conseguirá manter a velocidade média de 60 km/h para percorrer esse trajeto. Sendo assim, é correto afirmar que, para cumprir o prazo estipulado pela equipe de logística, esse motorista terá disponível, para a descarga e a assinatura de documentos, o tempo de
(A) 1 minuto.
(B) 5 minutos.
(C) 10 minutos.
(D) 15 minutos.
(E) 20 minutos.
Alternativa: B
117) (ETEC) Durante a colocação dos contêineres em um navio de carga, o operador do guindaste de uma ponte móvel teve de interromper o traslado de um deles para aguardar a orientação do técnico portuário sobre o local exato em que o contêiner deveria ser baixado. O contêiner e sua carga interna somam juntos a massa de 100 000 kg, e o operador o manteve suspenso e em repouso até segunda ordem. Adote: g = 10 m/s2 para o valor da aceleração da gravidade.
Adote: g = 10 m/s2 para o valor da aceleração da gravidade.
Considerando o esquema de roldanas montado na ponte móvel, a intensidade da força F que deve ser mantida no ponto P do cabo de aço, para garantir a permanência do contêiner em repouso, será, em newtons,
(A) 100 000.
(B) 200 000.
(C) 500 000.
(D) 1 000 000.
(E) 2 000 000.
Alternativa: C
Leia o texto para responder às questões de números 118 a 119.
Do you speak english? “Hey, man!”, gritam duas crianças, enquanto atravessam a rua Sergipe, em São Paulo. Em um período de dez minutos, outras sete pessoas, em carros e motos, passam soltando cumprimentos em inglês. Elas se dirigem ao vendedor de balas que trabalha naquele ponto há 21 anos. Não é um vendedor qualquer. É “Joseph Robert” da Silva, 46, “nickname”1 Bob Chiclete, que só vende suas balas de eucalipto e hortelã falando “in English”. E onde ele aprendeu a falar? “It’s easy. Here, at the corner”, responde dizendo que é fácil, aprendeu nas esquinas. “Um dia, perguntei a um estudante como se dizia ´bom-dia` em inglês. Depois, soube o que era ´my friend`. E assim fui engrenando e melhorando a abordagem.” Com o tempo, alguns conhecidos lhe deram livros didáticos que ele estuda com afinco durante a tarde, ao chegar em casa, em Embu, depois de vender balas das 9h às 14h. “I study a lot”2 , afiança. Além de livros, ele também ganha roupas de presente dos clientes que, em sua maioria, viraram amigos do popular vendedor. Na quinta-feira passada, vestia um sapato de couro preto com bico fino, calça de linho verde-musgo, camisa mostarda, gravata e blazer grafite. Mesmo tão bem-vestido, diz que já sofreu preconceito de quem acha absurdo ele saber inglês. O vendedor brinca que só faz negócio com quem corresponde. E por que tudo isso, afinal? “É meu marketing.” Vende mais? “Of course!” – diz, dando certeza. Mas em seguida relativiza “I hope”, isto é, “espero que sim”. Mas parece que é verdade. Na mesma hora uma moça buzina para ele se aproximar e leva dois pacotes de balas. É a bancária Bruna L., 21, que “sempre compra” de Bob Chiclete, ela própria falando inglês com ele. No período da tarde, Bob costuma ter vendido tudo. Quem não entende a língua se cativa com a simpatia: “Ele está sempre aqui, bonitão assim, é um barato”, diz o fotógrafo Waldir G., 53, em outro carro. “Não sei inglês, mas me divirto.”
(Cristina Moreno de Castro, Folha de S. Paulo, 09.05.2011. Adaptado)
118) (ETEC) Assinale a alternativa correta de acordo com a leitura do texto.
(A) Com o dinheiro da venda de balas e chicletes, Joseph Robert pretende, no futuro, frequentar um curso regular de língua inglesa.
(B) Utilizar frases em inglês, ter simpatia e um visual diferenciado são estratégias de que Bob Chiclete se serve para fazer seu marketing pessoal.
(C) Alguns estudantes do bairro tomaram a iniciativa de ensinar a língua inglesa ao vendedor e também lhe atribuíram o apelido de Bob Chiclete.
(D) Graças ao bom humor e às brincadeiras em inglês, Bob Chiclete assegura que passou a vender mais mercadoria, o que o obrigou a ampliar o horário de trabalho.
(E) Apesar da popularidade, o vendedor comenta que já sofreu discriminação, especialmente por parte de pessoas mais jovens que consideram absurdo ele saber inglês.
Alternativa: B
119) (ETEC) Leia as alternativas reescritas a partir das ideias do 6o parágrafo e assinale aquela em que todos os termos em destaque mantêm o sentido original do texto.
(A) Com os livros didáticos cedidos, ele estuda com dificuldade durante a tarde, pois vendeu balas das 9h às 14h.
(B) Com os livros didáticos coletados, ele estuda com interesse durante a tarde, porque vendeu balas das 9h às 14h.
(C) Com os livros didáticos presenteados, ele estuda com empenho durante a tarde, após ter vendido balas das 9h às 14h.
(D) Com os livros didáticos disponibilizados, ele estuda prazerosamente durante a tarde, apesar de ter vendido balas das 9h às 14h.
(E) Com os livros didáticos adquiridos, ele estuda brevemente durante a tarde, mesmo tendo vendido balas das 9h às 14h.
Alternativa: C
120) (ETEC) Em uma empresa distribuidora de mala direta, João, Marcelo e Pedro são responsáveis por ensacar e etiquetar revistas. Certa vez, receberam um lote de 6 120 revistas e, ao terminarem a tarefa, perceberam que o lote de revistas havia sido dividido em partes diretamente proporcionais ao respectivo tempo de trabalho de cada um deles na empresa. Sabendo que João trabalha há 9 meses na empresa, Marcelo, há 12 meses e Pedro, há 15 meses; o número de revistas que João ensacou e etiquetou foi
(A) 1 360.
(B) 1 530.
(C) 1 890.
(D) 2 040.
(E) 2 550.
Alternativa: B
121) (ETEC) O planeta encolheu! Desde o século XIX, início da era das telecomunicações, as grandes distâncias vêm sendo superadas pela rapidez com que as mensagens são enviadas. Considere o gráco Analisando o gráco, pode-se armar corretamente que,
Analisando o gráco, pode-se armar corretamente que,
(A) em junho de 2012, o número de usuários ativos de internet em domicílio, no Brasil, era de 41 483.
(B) de junho de 2011 a junho de 2012, o número de usuários ativos de internet em domicílio com conexão de até 512 Kb diminuiu cerca de 2,7 milhões.
(C) de outubro de 2011 a maio de 2012, os números de usuários ativos de internet em domicílio com conexão de 512 Kb a 2 Mb formam uma sequência crescente.
(D) de junho a julho de 2011, o número de usuários ativos de internet em domicílio com conexão de até 512 Kb foi superior ao número de usuários com conexão acima de 2 Mb.
(E) em março de 2012, o número de usuários ativos de internet em domicílio com conexão de 512 Kb a 2 Mb correspondeu ao dobro do número dos que se conectavam com até 512 Kb.
Alternativa: D
122) (ETEC) Agora, veja esta outra situação em que se utiliza a linguagem matemática. Uma operação é uma regra que associa a cada par de elementos de um conjunto A um único elemento de A
Seja o símbolo que representa uma operação, no conjunto dos números inteiros, de nida por x@y = x . y + 1.
Exemplo: 2@3 = 2 . 3 + 1 = 7
Considerando a operação de nida acima, 145 pode ser representado por
(A) 12@12.
(B) 13@12.
(C) 14@12.
(D) 15@12.
(E) 16@12.
Alternativa: A
123) (ETEC) Até o nal do século XVIII, a falta de uma linguagem comum para a medição de grandezas foi um problema na comunicação de informações, entre elas as cientí cas, por isso se criou um sistema de unidades chamado Sistema Internacional. A implantação desse sistema de medida ainda passa por uma fase de adaptação. É o caso da unidade de energia que nos moldes antigos era a caloria (cal) e, no Sistema Internacional, a mesma grandeza atualmente se mede em joule (J).
Observação: Considere 1 cal = 4,2 J
Assim sendo, se a embalagem de determinado alimento indica que o valor energético desse alimento é de 340 000 cal, também deverá informar que a energia é, em joules, aproximadamente,
(A) 1 400 000.
(B) 3 400 000.
(C) 4 200 000.
(D) 6 300 000.
(E) 8 100 000.
Alternativa: A
124) (ETEC) A fotografia a é uma modalidade de comunicação. De suas origens até hoje, o princípio da captura de uma imagem é o mesmo, diferenciado apenas por melhorias como uso de lentes e de sensores de luz. A forma mais primitiva de máquina fotográ ca é a conhecida por câmara escura de orifício. Um estudante, curioso para observar como a imagem em uma dessas câmaras é obtida, escurece o interior de uma latinha de ervilhas, faz um furo central no fundo da lata e, do outro lado, onde havia a tampa, cola um disco de papel translúcido. Ao apontar sua câmara escura de orifício para uma vela acesa, distante 30 cm do orifício da latinha, vê a projeção da imagem da vela sobre o papel, conforme mostra a gura. Observando as dimensões da latinha, a distância da vela ao orifício e o tamanho da imagem obtida, pode-se determinar que o tamanho da vela utilizada é de
Observando as dimensões da latinha, a distância da vela ao orifício e o tamanho da imagem obtida, pode-se determinar que o tamanho da vela utilizada é de
(A) 2 cm.
(B) 4 cm.
(C) 8 cm.
(D) 10 cm.
(E) 12 cm.
Alternativa: D
Considere as informações para responder às questões de números 125 e 126.
As órbitas dos satélites de comunicação são geoestacionárias e devem ser equatoriais, isto é, estar no plano da linha do Equador terrestre. Como o nome sugere, um satélite geoestacionário (geo = Terra, estacionário = parado) deve acompanhar a rotação do planeta de forma a car sempre parado em relação a um ponto xo na superfície da Terra. A gura 1 ilustra a ideia do “campo de visão” de um satélite geoestacionário, ou seja, mostra a região do planeta que o satélite é capaz de cobrir, “enxergar”. O satélite envia sinais eletromagnéticos para a Terra, e o que delimita a região coberta pelos sinais é o fato de o planeta ser esférico. Desta forma, os sinais recebidos ou transmitidos, entre o satélite e a Terra, cam con nados num cone cuja intersecção com a superfície da Terra determina a área de cobertura do satélite. É nesta região da superfície da Terra que podemos colocar antenas capazes de trocar sinais eletromagnéticos com o satélite. No exemplo da figura 1, os sinais emitidos pelo satélite, no limite, “tocam” o planeta nos pontos T1 e T2 .
No exemplo da figura 1, os sinais emitidos pelo satélite, no limite, “tocam” o planeta nos pontos T1 e T2 .
Na figura 2, apresenta-se um modelo matemático simplicado da posição do satélite S em relação à Terra.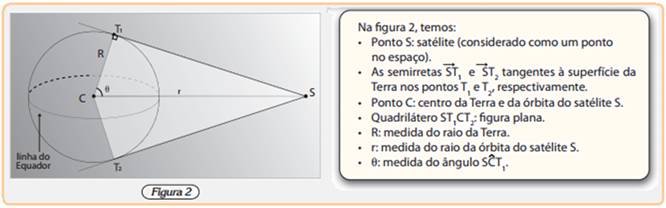 Note que u corresponde à latitude máxima que o sinal do satélite pode alcançar. Considerando os valores aproximados de 6 400 km para o raio da Terra e 42 000 km para o raio da órbita do satélite geoestacionário S, determina-se que u = 81,2°. Conclusão: um satélite geoestacionário cobre uma região entre as latitudes 81,2° N e 81,2° S. Essa região não chega aos polos geográ cos da Terra. Mas chega quase lá. E isso não é nenhum problema porque ninguém, aparentemente, vai querer transmitir sinais de TV ou internet para ursos polares ou pinguins, vai?!
Note que u corresponde à latitude máxima que o sinal do satélite pode alcançar. Considerando os valores aproximados de 6 400 km para o raio da Terra e 42 000 km para o raio da órbita do satélite geoestacionário S, determina-se que u = 81,2°. Conclusão: um satélite geoestacionário cobre uma região entre as latitudes 81,2° N e 81,2° S. Essa região não chega aos polos geográ cos da Terra. Mas chega quase lá. E isso não é nenhum problema porque ninguém, aparentemente, vai querer transmitir sinais de TV ou internet para ursos polares ou pinguins, vai?!
125) (ETEC) De acordo com o texto, conclui-se que a medida do ângulo é
(A) 8,8°.
(B) 13,2°.
(C) 17,6°.
(D) 22,0°.
(E) 26,4°.
Alternativa: C
126) (ETEC) No Brasil, o rádio completou 90 anos em 2012 e mostra que permanece como um poderoso veículo de comunicação, por meio do qual são passadas informações, notícias e entretenimento. Sobrevivente da ascensão da televisão na década de 1950, o rádio resiste, agora, à popularização da internet, fazendo da rede uma plataforma para a ampliação da sua audiência. O Target Group Index, do IBOPE Media, em uma pesquisa sobre o uso do rádio, estudou um universo que representava N milhões de pessoas e constatou que 8% desse universo, ou seja, 4,2 milhões dessas pessoas, a rmavam ter escutado rádio pela internet nos últimos trinta dias.
(www.ibope.com.br/pt-br/noticias/Paginas/Radio-completa-90-anos-e-mantem-sua-popularidade-atraves-de-outras-midias.aspx Acesso em: 15.08.2012. Adaptado)
De acordo com o texto, N é igual a
(A) 33,6.
(B) 48,7.
(C) 52,5.
(D) 65,3.
(E) 76,2
Alternativa: C
127) (ETEC) A informação da velocidade máxima permitida nas estradas é feita por placas espalhadas no acostamento. Um motorista, apesar de ter pressa, não deseja ultrapassar o limite máximo de velocidade de 80 km/h estabelecido para a estrada em que viaja.
Observação: Considere que o trajeto entre esses marcos é retilíneo
Considerando que o motorista dirigiu do marco 65 km até o marco 345 km, mantendo a velocidade máxima em todo o trajeto, o tempo necessário para completar sua viagem, no percurso entre esses marcos quilométricos, foi, em horas,
(A) 1,3.
(B) 2,0.
(C) 2,5.
(D) 3,3.
(E) 3,5.
Alternativa: E
128) (ETEC) Em agosto de 1888, inseguro do sucesso de seu invento, Karl Benz pensava em desistir de expor seu veículo a motor, em Munique. Percebendo a insegurança do marido, Bertha Benz tomou a iniciativa: sem ele perceber, saiu com o carro de 2,5 HP e dirigiu por 106 km até a casa de sua mãe, tornando-se a primeira mulher automobilista e promovendo, assim, o invento do marido.
No meio automobilístico, é comum referir-se à potência de um motor na unidade HP (Horse Power). Em Ciências, seguindo as normas do Sistema Internacional de Unidades (SI), essa grandeza deve ser medida na unidade W (watt). Sendo assim, a potência do motor do automóvel dirigido por Bertha Benz, em watt, era de
Dado: 1 HP = 746 W
(A) 298.
(B) 1 490.
(C) 1 865.
(D) 5 124.
(E) 18 900.
Alternativa: C
129) (ETEC) ) Chiquinha Gonzaga, a primeira mulher a reger uma orquestra no Brasil, foi também excelente pianista. Embora um piano possua cordas, ele é classificado como um instrumento de percussão, já que cada corda é golpeada por um pequeno martelo. Individualmente cada tecla é uma alavanca apoiada entre os extremos, portanto, enquanto a pianista pressiona com o dedo um dos extremos da alavanca, o outro extremo exerce força sobre o mecanismo que aciona o pequeno martelo, como mostra a figura. Considerando-se as dimensões indicadas na tecla representada na figura, ao se aplicar com o dedo uma força vertical de intensidade 2 N, transfere-se ao mecanismo do martelo uma força vertical, voltada para cima, de intensidade
Considerando-se as dimensões indicadas na tecla representada na figura, ao se aplicar com o dedo uma força vertical de intensidade 2 N, transfere-se ao mecanismo do martelo uma força vertical, voltada para cima, de intensidade
Observação: Lembre que, nesse tipo de alavanca, multiplicando-se a intensidade da força aplicada em uma extremidade pela distância que separa o ponto de aplicação dessa força até o ponto de apoio da alavanca, o resultado é sempre constante.
(A) 1 N.
(B) 2 N.
(C) 3 N.
(D) 6 N.
(E) 8 N.
Alternativa: C
130) (ETEC) De acordo com as companhias de seguro, por serem consideradas mais cautelosas e terem um comportamento mais disciplinado no trânsito, as mulheres pagam menos pelo seguro de seu automóvel. Suponha que um homem e uma mulher possuam o mesmo modelo de automóvel e, além disso, que esses motoristas tenham a mesma idade, o mesmo tempo de habilitação e usem o veículo nas mesmas condições. Pelo seguro de seu automóvel, o homem paga R$ 2.400,00 e a mulher, R$ 1.680,00. Assim sendo, em relação a esse homem, essa mulher paga X% a menos de seguro. O valor de X é
(A) 17.
(B) 27.
(C) 30.
(D) 63.
(E) 70.
Alternativa: C
131) (ETEC) Uma organização internacional de ajuda humanitária é formada apenas por mulheres, sendo 20 brasileiras e 16 não brasileiras. Após a formação de uma comissão para organizar uma festa beneficente, percebeu-se que a comissão era composta por dois quintos do total das brasileiras e por um quarto do total das não brasileiras. Assim sendo, o número de integrantes da comissão era
(A) 6.
(B) 8.
(C) 10.
(D) 12.
(E) 16
Alternativa: D
132) (ETEC) Você já deve ter visto em seu bairro pessoas que vieram diretamente da roça e, munidas de carrinhos de mão e uma simples balança, vendem mandiocas de casa em casa. A balança mais usada nessas situações é a apresentada na figura a seguir. A balança representada está em equilíbrio, pois o produto da massa do massor pela distância que o separa do ponto P é igual ao produto da massa que se deseja medir pela distância que separa o ponto em que os cordames do prato são amarrados na haste até o ponto P. Considere que no prato dessa balança haja 3 kg de mandiocas e que essa balança tenha um massor de 0,6 kg. Para que se atinja o equilíbrio, a distância d do massor em relação ao ponto P deverá ser, em cm,
A balança representada está em equilíbrio, pois o produto da massa do massor pela distância que o separa do ponto P é igual ao produto da massa que se deseja medir pela distância que separa o ponto em que os cordames do prato são amarrados na haste até o ponto P. Considere que no prato dessa balança haja 3 kg de mandiocas e que essa balança tenha um massor de 0,6 kg. Para que se atinja o equilíbrio, a distância d do massor em relação ao ponto P deverá ser, em cm,
(A) 16.
(B) 20.
(C) 24.
(D) 36.
(E) 40.
Alternativa: E
133) (ETEC) Para preparar biscoitos circulares, após abrir a massa formando um retângulo de 20 cm de largura por 40 cm de comprimento, dona Maria usou um cortador circular de 4 cm de diâmetro, dispondo-o lado a lado várias vezes sobre toda a massa para cortar os biscoitos, conforme a figura. Com a sobra de massa, dona Maria abre um novo retângulo, de mesma espessura que o anterior, para cortar mais biscoitos.
Com a sobra de massa, dona Maria abre um novo retângulo, de mesma espessura que o anterior, para cortar mais biscoitos.
Observação: Área do círculo de raio r
A = πr2
Adote: π = 3
Assim sendo, desconsiderando a espessura da massa, as dimensões desse novo retângulo podem ser
(A) 8 cm x 30 cm.
(B) 8 cm x 25 cm.
(C) 9 cm x 24 cm.
(D) 10 cm x 22 cm.
(E) 10 cm x 21 cm.
Alternativa: B
134) (ETEC) A hidroponia consiste em um método de plantio fora do solo em que as plantas recebem seus nutrientes de uma solução, que flui em canaletas, e é absorvida pelas raízes. Por meio de uma bomba hidráulica, em determinada horta hidropônica, a solução é elevada até uma altura de 80 cm, sendo vertida na canaleta onde estão presas as mudas. Devido a uma ligeira inclinação da canaleta, a solução se move para o outro extremo, lá sendo recolhida e direcionada ao reservatório do qual a bomba reimpulsiona o líquido, como mostra a figura. Suponha que nessa horta hidropônica foi empregada uma bomba com potência de 20 W. Se toda a potência dessa bomba pudesse ser empregada para elevar a água até a canaleta, a cada um segundo (1 s), o volume de água que fluiria seria, em litros,
Suponha que nessa horta hidropônica foi empregada uma bomba com potência de 20 W. Se toda a potência dessa bomba pudesse ser empregada para elevar a água até a canaleta, a cada um segundo (1 s), o volume de água que fluiria seria, em litros,
(A) 2,0.
(B) 2,5.
(C) 3,0.
(D) 3,5.
(E) 4,0.
Alternativa: B
135) (ETEC) O gráfico apresenta uma comparação entre as porções que os alunos pesquisados consomem dos grupos alimentares citados bem como as porções recomendadas por nutricionistas. A partir da análise dos dados do gráfico, pode-se concluir que
A partir da análise dos dados do gráfico, pode-se concluir que
(A) o número de porções consumidas de óleo e gorduras é o triplo do número recomendado.
(B) o número de porções consumidas de leite, queijo e iogurte está acima do número recomendado.
(C) os alunos consomem doze porções de açúcares e doces para cada porção de verduras e legumes consumida.
(D) os adolescentes consomem, em quatro dos oito grupos alimentares citados, mais do que o dobro do recomendado pelos nutricionistas.
(E) o número de porções consumidas de carnes e ovos e de feijões e leguminosas supera o número de porções consumidas de arroz, pães, massa, batata e mandioca.
Alternativa: D
136) (ETEC) Considere os seguintes dados obtidos na pesquisa que envolveu um grupo de 1167 alunos de Etecs. Do total de alunos pesquisados, 40% substituem o almoço por lanche e, destes, 72% estão no peso normal. Assim sendo, pode-se concluir que o número de alunos que substituem o almoço por lanche e que estão no peso normal é, aproximadamente,
(A) 131.
(B) 248.
(C) 336.
(D) 433.
(E) 657.
Alternativa: C
137) (ETEC) O café é consumido há séculos por vários povos não apenas como bebida, mas também como alimento. Descoberto na Etiópia, o café foi levado para a Península Arábica e dali para a Europa, chegando ao Brasil posteriormente.Dado: aceleração da gravidade g = 10m/s2
No Brasil, algumas fazendas mantêm antigas técnicas para a colheita de café. Uma delas é a de separação do grão e da palha que são depositados em uma peneira e lançados para cima. Diferentemente da palha, que é levada pelo ar, os grãos, devido à sua massa e forma, atravessam o ar sem impedimentos alcançando uma altura máxima e voltando à peneira. Um grão de café, após ter parado de subir, inicia uma queda que demora 0,3 s, chegando à peneira com velocidade de intensidade, em m/s,
(A) 1.
(B) 3.
(C) 9.
(D) 10.
(E) 30.
Alternativa: B
139) (ETEC) Para prevenir a anemia por deficiência de ferro, deve haver um consumo equilibrado de alimentos ricos desse elemento químico. Observe a tabela que apresenta a quantidade de ferro na composição de 100 g de alimentos.Em uma refeição, Pedro consumiu 6,0 mg de ferro ao ingerir apenas espinafre cozido e carne bovina assada. Sabendo que a quantidade de carne bovina ingerida foi o dobro da quantidade de espinafre ingerida, conclui-se que a quantidade de carne bovina ingerida foi, aproximadamente, em gramas,
(A) 130.
(B) 140.
(C) 150.
(D) 160.
(E) 170.
Alternativa: A
140) (ETEC) Para melhorar a qualidade do solo, aumentando a produtividade do milho e da soja, em uma fazenda é feito o rodízio entre essas culturas e a área destinada ao pasto. Com essa finalidade, a área produtiva da fazenda foi dividida em três partes conforme a figura.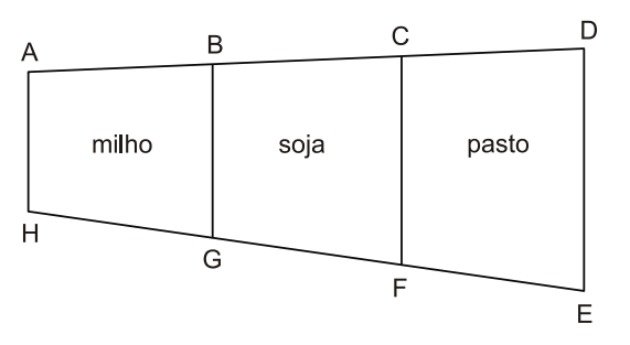 Considere que
Considere que
os pontos A, B, Ce Destão alinhados;
os pontos H,G, Fe E estão alinhados;
os segmentos AH, BG, CFe DEsão, dois a dois, paralelos entre si;
AB = 500 m, BC = 600 m, CD = 700 me HE = 1 980 m.
Nessas condições, a medida do segmento GF é, em metros,
(A) 665.
(B) 660.
(C) 655.
(D) 650.
(E) 645.
Alternativa: B
141) (ETEC) Assinale a alternativa que preenche, corretamente, o texto. Sem considerar as capitais, as 106 cidades brasileiras com mais de 200 000 habitantes que ofereciam aos moradores vários benefícios da urbanização correspondiam, aproximadamente, a ____% do total de cidades brasileiras.
(A) 0,36.
(B) 0,75.
(C) 2,00.
(D) 5,00.
(E) 8,00.
Alternativa: C
142) (2º SEM/12) Em algumas cidades brasileiras encontramos, em vias de grande circulação, termômetros que indicam a temperatura local medida na escala Celsius. Por causa dos jogos da Copa, no Brasil, os termômetros deverão passar por modificações que permitam a informação da temperatura também na escala Fahrenheit, utilizada por alguns países. Portanto, após essa adaptação, um desses termômetros que indique, por exemplo, 25 ºC, também apontará a temperatura de (A) 44 ºF.
(A) 44 ºF.
(B) 58 ºF.
(C) 64 ºF.
(D) 77 ºF.
(E) 86 ºF.
Alternativa: D





