ESTATISTICA GERAL

ONLINE

ESTATISTICA GERAL

Professor Diminoi

Crise da estatística e a era da incerteza. Em que acreditar? | VEJA

ESTATÍSTICA

A estatística é o campo da matemática que relaciona fatos e números em que há um conjunto de métodos que nos possibilita coletar dados e analisá-los, assim sendo possível realizar alguma interpretação deles.

Para que serve a estatística?

A estatística está relacionada a problemas de contagem ou organização de dados. Além disso, ela tem um importante papel no desenvolvimento de ferramentas que possibilitam o processo de organização de dados, com em tabelas. A estatística está presente também em diversos campos da ciência, com base na coleta de dados e em seu tratamento, é possível trabalhar modelos matemáticos que permitem maior desenvolvimento na área estudada.

Alguns campos em que a estatística é fundamental:

- Economia,

- Meteorologia,

- Marketing,

- Esportes,

- Sociologia

- Geociências.

Divisões da estatística

A estatística é dividida em duas partes, descritiva e inferencial. A primeira está relacionada à contagem dos elementos envolvidos na pesquisa, esses elementos são contados um a um. Na estatística descritiva, temos como principais ferramentas as medidas de posição, como média, mediana e moda, assim como as medidas de dispersão, como variância e desvio-padrão, temos também tabelas de frequências e gráficos.

Estatística Descritiva

Ainda na estatística descritiva, temos uma metodologia muito bem definida para uma apresentação de dados com grau considerável de confiabilidade que passa por organização e coleta, resumo, interpretação e representação e, por fim, análise de dados. Um exemplo clássico da utilização da estatística descritiva ocorre na realização do censo populacional (de 10 em 10 anos) pelo Instituto Brasileiro de Geografia e Estatística (IBGE).

Estatística Inferencial

A estatística inferencial, por sua vez, é caracterizada não por coletar dados dos elementos de uma população um a um, e sim por realizar a análise de uma amostra dessa população, tirando conclusões sobre ela. Na estatística inferencial, deve-se tomar cuidado na escolha da amostra, pois ela deve representar muito bem a população.

A estatística inferencial é utilizada, por exemplo, nas pesquisas eleitorais. Escolhe-se uma amostra da população, de forma que a represente, e assim é realizada a pesquisa. Na escolha de uma amostra que não represente muito bem essa população, dizemos que a pesquisa é tendenciosa e, por consequência, não confiável.

Dado estatístico

O dado estatístico é um elemento que pertence ao conjunto da população, obviamente esse dado deve estar envolvido com o tema da pesquisa.

Amostra

Chamamos de amostra o subconjunto formado com base no universo estatístico. Uma amostra é utilizada quando a população é muito grande ou infinita. Em casos em que coletar todas as informações do universo estatístico é inviável por motivos financeiros ou logísticos, também se faz necessário a utilização de amostras.

A escolha de uma amostra é de extrema importância para uma pesquisa, e ela deve representar de maneira fidedigna a população. Um exemplo clássico da utilização das amostras em uma pesquisa é na realização do censo demográfico do nosso país.

Variável

Em estatística, a variável é o objeto de estudo, isto é, o tema que a pesquisa pretende estudar. Por exemplo, ao estudar-se as características de uma cidade, o número de habitantes pode ser uma variável, assim como o volume de chuva em determinado período ou até mesmo a quantidade de ônibus para o transporte público.

Mediana são medidas de tendência central utilizadas em estatística são:

- Média,

- Moda

- Média

Média

A média (M_e) é calculada somando todos os valores de um conjunto de dados e dividindo este valor pelo número de elementos deste conjunto.

Fórmula para cálculo da média simples

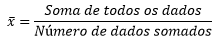
Exemplo 1: Os jogadores de uma equipe de basquete apresentam as seguintes idades: 28, 27, 19, 23 e 21 anos.

Qual a média de idade desta equipe?

Resolução

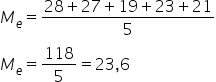
Moda

A Moda (M_o) representa o valor mais frequente de um conjunto de dados, sendo assim, para defini-la, basta observar a frequência com que os valores aparecem.

Um conjunto de dados é chamado de bimodal quando apresenta duas modas, ou seja, dois valores são mais frequentes.

Exemplo 2: Em uma sapataria durante um dia foram vendidos os seguintes números de sapato:

34, 39, 36, 35, 37, 40, 36, 38, 36, 38 e 41.

Qual o valor da moda desta amostra?

Resolução
Observando os números vendidos notamos que o número 36 foi o que apresentou maior frequência (3 pares), portanto, a moda é igual a:

M_o = 36

Mediana

A Mediana (M_d) representa o valor central de um conjunto de dados. Para encontrar o valor da mediana é necessário colocar os valores em ordem crescente ou decrescente (rol)

Observação importante: quando o número de elementos de um conjunto é par, a mediana é encontrada pela média dos dois valores centrais. Assim, esses valores são somados e divididos por dois.

Exemplo 3: Em uma escola, o professor de educação física anotou a altura de um grupo de alunos. Considerando que os valores medidos foram:

1,54 m; 1,67 m, 1,50 m; 1,65 m; 1,75 m; 1,69 m; 1,60 m; 1,55 m e 1,78 m

Qual o valor da mediana das alturas dos alunos?

Resolução
Primeiro devemos colocar os valores em ordem (rol). Neste caso, colocaremos em ordem crescente. Assim, o conjunto de dados ficará:

1,50; 1,54; 1,55; 1,60; 1,65; 1,67; 1,69; 1,75; 1,78

Como o conjunto é formado por 9 elementos, sendo um número ímpar, a mediana será igual ao 5º elemento, ou seja:

M_d = 1,65 m

Exemplo 4: Calcule o valor da mediana da seguinte amostra de dados:

(32, 27, 15, 44, 15, 32)

Resolução
Primeiro precisamos colocar os dados em ordem, assim temos:

15, 15, 27, 32, 32, 44

Como essa amostra é formada por 6 elementos, sendo um número par, a mediana será igual à média dos elementos centrais, ou seja:

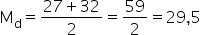
Medidas de dispersão

Amplitude
Subtração entre o maior valor e o menor valor dos elementos do conjunto.

A amplitude (H) ou intervalo total é calculada pegando os valores extremos do conjunto de dados.

H = x₁ – x_n

H = é a amplitude;

x_{1 =} é o primeiro valor;

x_{n =} é o último valor.

Variância
Dispersão dos dados variáveis em relação à média.
Estatística Básica - Variância

V = é a variância

x_{i =} é um valor qualquer no conjunto de dados não posição i

M_{A =} é a média aritmética

N = é o total dos dados do conjunto

Desvio
Os desvio serve para medir a dispersão entre uma variável em relação a medida de tendência central.

D_i = x_i – M_A

D_{i =} é o desvio

x_{i =} é uma variável qualquer

M_{A =} é a média aritmética dos dados

Desvio Médio
O desvio médio é calculado fazendo a diferença entre uma variável pela média. O desvio médio serve para indicar a distância de cada elemento da amostra e o seu valor médio.
Prof. André Aparecido da Silva - ppt carregar

D_{M =} é o desvio médio
x_{i =} é um valor qualquer no conjunto de dados não posição i
M_{A =} é a média aritmética
N = é o total dos dados do conjunto

Desvio Padrão
O desvio padrão serve para calcular a uniformidade do conjunto de dados. Assim, quanto mais próximo de 0 (zero), mais próximo da média estão os dados do conjunto.
Desvio Padrão | Educa Mais Brasil D_{P =} é o desvio padrão

x_{i =} é um valor qualquer no conjunto de dados não posição i

M_{A =} é a média aritmética

N = é a quantidade total dos dados do conjunto

Exemplo

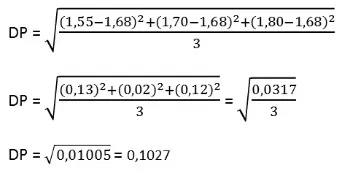
Em uma equipe de remo os atletas possuem as seguintes alturas: 1,55 m ; 1,70 m e 1,80 m. Qual é o valor da média e do desvio padrão da altura desta equipe?

Cálculo da média, sendo n = 3

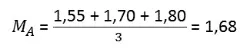
Resolução:

Cálculo do desvio padrão

QUESTÕES RESOLVIDAS

01) O treinador de um time de futebol anotou o número de gols marcados pela sua equipe durante as últimas partidas de um campeonato e obteve o seguinte conjunto:

{0, 2, 3, 1, 0, 2, 1, 0, 1, 2, 1, 3, 1, 0, 4, 1, 2, 1}

Qual é a moda desse conjunto?

Resolução
Analisando esse conjunto, podemos verificar que a sua moda é 1.

{0, 2, 3, 1, 0, 2, 1, 0, 1, 2, 1, 3, 1, 0, 4, 1, 2, 1}

Por mais que outros resultados se repitam bastante, como 0 (ou seja, nenhum gol marcado), aquele que mais se repete é 1, o que faz com que ele seja a única moda do conjunto. Então, representamos a moda por:
M_o = {1}

02) Para presentear suas funcionárias com pares de sapatos, o dono de uma empresa anotou a numeração calçada por cada uma delas e obteve a seguinte lista:

{37, 35, 36, 34, 37, 35, 38, 35, 37, 33, 39, 37, 37, 36, 36, 38, 34, 39, 36}

Quais são os valores que mais se repetem nesse conjunto?
Resolução
Analisando esse conjunto, encontraremos os valores que mais se repetem:
{37, 35, 36, 34, 37, 35, 38, 35, 37, 33, 39, 37, 35, 36, 36, 38, 34, 39, 36}
Note que tanto 37 quanto 36 aparecem 4 vezes, sendo os valores mais frequentes. Dessa forma, o conjunto possui duas modas:
M_o = {36, 37}

Média aritmética simples
Para calcular a média aritmética simples, é preciso realizar:
- a soma de todos os elementos do conjunto;
- a divisao desse conjunto, após a soma, pela quantidade de valores.
Exemplo

03) Se a média aritmética entre n, n – 1, 2n + 1 e 4 é 10, determine o valor de n.
Resolucao
Se para calcular a média aritmética entre n, n – 1, 2n + 1 e 4, somamos todos esses termos e dividimo-los por 4, expressaremos esse cálculo como uma equação cujo resultado será 10:

n + (n – 1) + (2n + 1) + 4 = 10
4

n + n – 1 + 2n + 1 + 4 = 10 · 4
4n + 4 = 40
4n = 40 – 4
4n = 36
n = 36
4
n = 9
Portanto, para que a média aritmética entre n, n – 1, 2n + 1 e 4 seja 10, devemos ter n = 9.

04) No segundo bimestre, João alcançou as seguintes médias:

Matemática: 8,5

Português: 7,3

História: 7,0

Geografia: 7,5

Inglês: 9,2

Espanhol: 8,4

Física: 9,0

Química: 7,2

Biologia: 8,0

Educação Física: 9,5

01) Determine a média aritmética bimestral de João.
Resolucao
Considerando que João possui 10 matérias, para determinar a média aritmética delas, devemos somá-las e dividi-las por 10:

Me = 8,5 + 7,3 + 7,0 + 7,5 + 9,2 + 8,4 + 9,0 + 7,2 + 8,0 + 9,5
10

Me = 81,6
10
Me = 8,16
Me ≈ 8,2
Portanto, João alcançou a média de 8,2 aproximadamente.

05) (UFC) A média aritmética das notas dos alunos de uma turma formada por 25 meninas e 5 meninos é igual a 7. Se a média aritmética das notas dos meninos é igual a 6, a média aritmética das notas das meninas é igual a:

(A) 6,5

(B) 7,2

(D) 7,8

(E) 8,0
Resolucao
Primeiramente vamos identificar a soma das notas dos meninos por x e a nota das meninas por y. Se a turma tem 5 meninos e a média aritmética de suas notas é igual a 6, então a soma das notas dos meninos (x) dividida pela quantidade de meninos (5) deve ser igual a 6, isto é:
x = 6
5
x = 6 . 5
x = 30
Do mesmo modo, se a turma tem 25 meninas (Me é a média aritmética de suas notas), o quociente da soma das notas das meninas (y) e a quantidade de meninas (25) deve ser igual a Me, isto é:
y = Me
25
y = Me . 25
y = 25 . Me
Para calcular a média da turma, devemos somar as notas dos meninos (30) às notas das meninas (y) e dividir pela quantidade de alunos (25 + 5 = 30). O resultado deverá ser 7. Sendo assim, temos:

x + y = 7
25 + 5

30 + 25 . Me = 7
30

30 + 25 . Me = 7 . 30
30 + 25 . Me = 210
25 . Me = 210 – 30
25 . Me = 180

Me = 180
25

Me = 7,2

Portanto, a média aritmética das notas das meninas é 7,2.
Alternativa B

06) (Mackenzie – SP) A média aritmética de n números positivos é 7. Retirando-se do conjunto desses números o número 5, a média aritmética dos números que restam passa a ser 8. O valor de n é:

(A) 2

(B) 3

(D) 6

(E) 9
Resolucao
Seja S a soma dos n números positivos. Portanto, o cálculo de sua média aritmética pode ser dado por:
S = 7
n
S = 7n
Se retiramos o número 5 do conjunto de números, a soma será S – 5 e a quantidade de números será n – 1. Se a média aritmética é igual a 8, temos:
S – 5 = 8
n – 1
Substituindo S por S = 7n, que encontramos anteriormente, teremos a seguinte equação:
7n – 5 = 8
n – 1
7n – 5 = 8 . (n – 1)
7n – 5 = 8n – 8
7n – 8n = – 8 + 5
– n = – 3
n = 3
Portanto, o valor de n é 3.
Alternativa B

07) (Fuvest-SP) A distribuição das idades dos alunos de uma classe é dada pelo seguinte gráfico: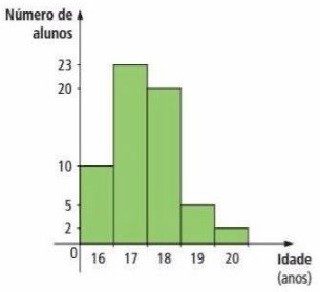
Qual das alternativas representa melhor a média de idade dos alunos?

(A) 16 anos e 10 meses

(B) 17 anos e 1 mês

(D) 18 anos e 6 meses

(E) 19 anos e 2 meses
Resolucao
Observando o gráfico, note que existem repetições nas idades, para isso basta observar o eixo da frequência (eixo vertical). Assim, para calcular a média da idade, vamos utilizar a ideia de média ponderada.

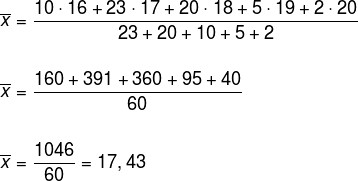Portanto, a média de idade dessa amostra é de 17 anos e 5 meses.
Alternativa C

08) Uma pesquisa foi realizada com 250 pessoas em um restaurante. A pessoa deveria apenas dar uma nota de 0 a 10 para o atendimento que recebeu. Os resultados obtidos foram organizados em uma tabela. Observe: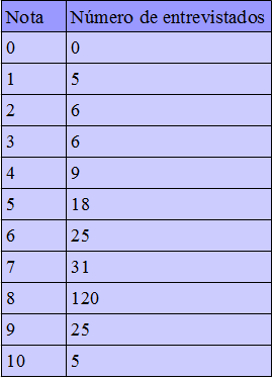
Qual é a nota média dada pelos frequentadores desse restaurante para o serviço prestado?

(A) 8,0

(B) 7,9

(D) 7,0

(E) 7,1
Resolucao
Esse tipo de exercício deve ser resolvido por meio de uma média ponderada, na qual o número de entrevistados é o peso. Como o número de entrevistados é 250, então, já é conhecido o resultado da soma dos pesos. Observe:
M = 0·0 + 1·5 + 2·6 + 3·6 + 4·9 + 5·18 + 6·25 + 7·31 + 8·120 + 9·25 + 10·5
250
M = 0 + 5 + 12 + 18 + 36 + 90 + 150 + 217 + 960 + 225 + 50
250
M = 1763
250
M ≈ 7,05
Alternativa D

09) A seguir são apresentadas duas listas com números e pesos. Qual das médias ponderadas é a maior e quais seus respectivos resultados?
→ MP1 de 5, 6, 7, 8 e 9, com os pesos 5, 6, 7, 8 e 9, respectivamente
→ MP2 de 5, 6, 7, 8 e 9 com os pesos 9, 8, 7, 6 e 5, respectivamente

(A) MP1 < MP2 e seus resultados são 7,3 e 6,7

(B) MP2 > MP1 e seus resultados são 7,3 e 6,7

(D) MP1 = MP2 e seus resultados são 7,3 e 7,3

(E) MP1 = MP2 e seus resultados são 6,7 e 6,7
Resolucao

MP1 = 5·5 + 6·6 + 7·7 + 8·8 + 9·9
5 + 6 + 7 + 8 + 9

MP1 = 25 + 36 + 49 + 64 + 81
35

MP1 = 255
35

MP1 ≈ 7,3

MP2 = 5·9 + 6·8 + 7·7 + 8·6 + 9·5
9 + 8 + 7 + 6 + 5

MP2 = 45 + 48 + 49 + 48 + 45
35

MP2 = 235
35

MP2 ≈ 6,7
Logo, MP1 > MP2 e seus resultados são 7,3 e 6,7
Alternativa C

10) (UNCISAL) Em cada bimestre, uma faculdade exige a realização de quatro tipos de avaliação, calculando a nota bimestral pela média ponderada dessas avaliações. Se a tabela apresenta as notas obtidas por uma aluna nos quatro tipos de avaliações realizadas e os pesos dessas avaliações,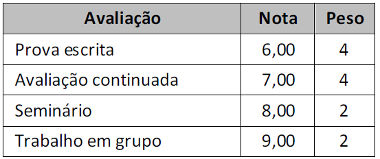
sua nota bimestral foi aproximadamente igual a

(A) 8,6.

(B) 8,0.

(D) 7,2.

(E) 6,8.
Resolucao
A média ponderada é a soma dos produtos das notas pelos pesos dividida pela soma dos pesos. Considerando PE = Prova escrita, AC = avaliação contínua, S = Seminário e TG = trabalho em grupo, a solução desse exercício é:

Média Ponderada = PE·4 + AC·4 + S·2 + TG·2
4 + 4 + 2 + 2

Média Ponderada = 6·4 + 7·4 + 8·2 + 9·2
4 + 4 + 2 + 2

Média Ponderada = 24 + 28 + 16 + 18
12

Média Ponderada = 86
12

Média Ponderada = 7,2
Alternativa D

11) (UFT TO) A nota final para uma disciplina de uma instituição de ensino superior é a média ponderada das notas A, B e C , cujos pesos são 1, 2 e 3, respectivamente. Paulo obteve A = 3,0 e B = 6,0 . Quanto ele deve obter em C para que sua nota final seja 6,0 ?

(A) 7,0

(B) 9,0

(D) 10,0
Resolucao
Escreveremos a fórmula da média ponderada substituindo os valores conhecidos nela. Substituiremos também a nota final pelo resultado (média ponderada) e calcularemos a nota que falta. Observe:

MP = A·1 + B·2 + C·3
1 + 2 + 3

6,0 = 3,0·1 + 6,0·2 + C·3
1 + 2 + 3

6,0 = 3,0 + 12,0 + C·3
6

6·6,0 = 3,0 + 12,0 + C·3
36,0 = 15,0 + 3C
36,0 – 15,0 = 3C
21,0 = 3C

C = 21,0
3

C = 7,0
Alternativa A

12) (PM ES-Exatus) Um veículo com motor flex pode ser abastecido com álcool e/ou gasolina. Caso seja abastecido com 30 litros de gasolina, ao preço de R$ 2,90 o litro, e 20 litros de álcool, a R$ 1,80 o litro, o preço médio do litro de combustível utilizado nesse abastecimento é igual a:
(A) R$ 2,35

(B) R$ 2,38

(D) R$ 2,43

(E) R$ 2,46
Resolução
Basta calcularmos a média ponderada:
M = (30.2,90 + 20.1,80)/50
M = (87 + 36)/50
M = 123/50
M = 2,46
Alternativa E

15) Na escola de Gabriel, a média anual de cada matéria é calculada de acordo com os princípios da média ponderada. Considerando que o peso das notas esteja relacionado com o bimestre em questão, determine a média anual de Gabriel sabendo que as notas em Matemática foram iguais a:
Resolucao
1º Bimestre: 7,0
2º Bimestre: 6,0
3º Bimestre: 8,0
4º Bimestre: 7,5

Mp = 7,0 . 1 + 6,0 . 2 + 8,0 . 3 + 7,5·4
1 + 2 + 3 + 4

Mp = 7,0 + 12,0 + 24,0 + 30,0
10
Mp = 73,0
10

Mp = 7,3
Resposta: a média anual de Gabriel é correspondente a 7,3.

13) Buscando melhorar o atendimento ao usuário do sistema de saúde de um município, a Prefeitura realizou uma pesquisa de rendimento satisfatório com 500 pessoas. As notas disponibilizadas aos entrevistados no intuito de avaliar o nível de satisfação compreendem as notas inteiras de 1 a 10.
Resolucao
Observe os resultados na tabela a seguir: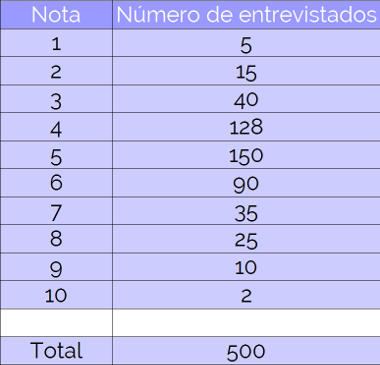

Mp = 1 . 5 + 2 . 15 + 3 . 40 + 4 . 128 + 5 . 150 + 6 . 90 + 7 . 35 + 8 . 25 + 9 . 10 + 10 . 2
5 + 15 + 40 + 128 + 150+ 90 + 35 + 25 + 10 + 2

Resposta: a média de satisfação dos usuários do sistema de saúde do município em questão foi igual a 5,0."

16) A lista a seguir contém o peso de alguns funcionários de uma determinada empresa:

{65, 92, 80, 74, 105, 85, 68, 85, 79}

Note que nesse conjunto há 9 elementos, então existe uma quantidade ímpar de valores no conjunto. Qual é a mediana do conjunto?
Resolução
Primeiramente, colocaremos esses dados em ordem crescente:

65, 68, 74, 79, 80, 85, 85, 92, 105

Agora, analisando o conjunto, basta encontrar o valor que está posicionado no meio do conjunto. Como há 9 valores, o termo central será o 5º, que no caso é 80 kg.

65, 68, 74, 79, 80, 85, 85, 92, 105

Logo, dizemos que:
M_e = 80

17) Qual é a mediana do conjunto a seguir? {5, 1, 8, 6, 4, 1, 2, 10}
Resolução
De início, colocaremos os dados em ordem crescente:

{1, 1, 2, 3, 5, 6, 8, 10}

Note que há 8 elementos nesse conjunto, sendo 3 e 5 os termos centrais:

{1, 1, 2, 3, 5, 6, 8, 10}

Calculando a média entre eles, temos:

Me = 3 + 52 = 82 = 4Me = 3 + 52 = 82 = 4

A mediana desse conjunto é, portanto, 4.

18) Um professor de matemática costuma verificar a aprendizagem de seus alunos através da mediana das notas obtidas pela turma. Considere que a turma de 2014 obteve as seguintes notas no 2° bimestre:
Qual é a mediana das notas? Considerando que a média escolar é 7,0, a mediana está acima ou abaixo dessa média?
Resolucao
Para verificar a mediana das notas, é fundamental ordená-las. Para isso, vamos organizá-las em ordem crescente:
Ordenando as notas, podemos observar que os valores centrais dessa sequência são 7,5 e 7,6, portanto a mediana será dada pela média aritmética desses valores:

M.A. = 7,5 + 7,6
2

M.A. = 15,1
2

M.A. = 7,55
A mediana das notas obtidas pela turma é de 7,55. Essa nota está acima da média escolar 7,0.

19) Confira na tabela a seguir as medalhas conquistadas pelo Brasil nas Olimpíadas de 1968 a 2012:
Encontre a mediana do total de medalhas conquistadas pelo Brasil nesses anos.
Resolucao
Primeiramente, devemos descobrir o total de medalhas conquistadas a cada ano:
Basta agora organizar as quantidades de medalhas em ordem crescente:
Os valores centrais dessa sequência numérica são 6 e 8. Para encontrar a mediana, calcularemos a média aritmética desses dois valores:

M.A. = 6 + 8
2

M.A. = 14
2

M.A. = 7

Portanto, a mediana do total de medalhas conquistadas pelo Brasil nas Olimpíadas de 1968 a 2012 é igual a sete medalhas.

20) (FGV) Sejam os números 7, 8, 3, 5, 9 e 5 seis números de uma lista de nove números inteiros. O maior valor possível para a mediana dos nove números da lista é

(A) 5

(B) 6

(D) 8

(E) 9
Resolucao
Como se trata da mediana, organizaremos esses números em ordem crescente:
Mas o enunciado do exercício informou que na lista constam nove números, portanto, restam ainda três valores que não conhecemos. Todavia, como a mediana deve ser a maior possível, devemos considerar que esses números desconhecidos são x, y e z e que eles são maiores que nove. Agora basta acrescentar esses números à sequência:
Considerando os números desconhecidos maiores que nove, a mediana é dada pelo número central da sequência, ou seja, o número 8.
Alternativa D

21) (Enem – 2010) Suponha que a etapa final de uma gincana escolar consista em um desafio de conhecimentos. Cada equipe escolheria 10 alunos para realizar uma prova objetiva, e a pontuação da equipe seria dada pela mediana das notas obtidas pelos alunos. As provas valiam, no máximo, 10 pontos cada. Ao final, a vencedora foi a equipe Ômega, com 7,8 pontos, seguida pela equipe Delta, com 7,6 pontos. Um dos alunos da equipe Gama, a qual ficou na terceira e última colocação, não pôde comparecer, tendo recebido nota zero na prova. As notas obtidas pelos 10 alunos da equipe Gama foram 10; 6,5; 8; 10; 7; 6,5; 7; 8; 6; 0. Se o aluno da equipe Gama que faltou tivesse comparecido, essa equipe

(A) teria a pontuação igual a 6,5 se ele obtivesse nota 0.

(B) seria a vencedora se ele obtivesse nota 10.

(E) empataria com a equipe Ômega na primeira colocação se o aluno obtivesse nota 9.
Resolucao
Já sabemos as notas obtidas pelas duas primeiras equipes: a equipe Ômega obteve 7,8 pontos e a equipe Delta obteve 7,6 pontos. Vamos organizar as notas da equipe Gama em ordem crescente:
De acordo com as notas obtidas pelos alunos, a mediana é dada pela média aritmética dos elementos centrais da sequência, portanto:

M.A. = 7 + 7
2

M.A. = 14
2

M.A. = 7
Para que a nota subisse, o aluno faltoso deveria obter uma nota x superior a oito. A ordenação das notas ficaria da seguinte forma:
Nesse caso, não faz diferença se a nota x for 8,1 ou até mesmo 10,0, pois a mediana é dada pela média aritmética das notas 7 e 8:

M.A. = 7 + 8
2

M.A. = 15
2

M.A. = 7,5

Ainda que o aluno faltoso tirasse uma nota superior a 8, a nota máxima que a equipe Gama poderia obter seria 7,5. Dessa forma, mesmo assim a equipe permaneceria no terceiro lugar.
Alternativa D

22) (TJ SP-Vunesp) Certa competição tem 6 etapas eliminatórias. Sabe-se que a média aritmética do número de pessoas que participaram da primeira e da segunda etapa é igual ao quádruplo da média aritmética do número de pessoas que participaram de cada uma das quatro etapas seguintes.
Desse modo, a razão entre o número de pessoas que participaram da primeira e da segunda etapa e o número total de pessoas que participaram dessa competição é de

(A) 1/2

(B) 1/3

(D) 2/3

(E) 3/4
Resolução
Vamos representar cada etapa pelas letras a, b, c, d, e, f, nesta ordem.
Utilizando o conceito de média aritmética, temos pelo enunciado que:

(a + b)/2 = 4.(c + d + e + f)/4

(a + b)/2 = (c + d + e + f)

Somando (a + b) em ambos os lados temos:

(a + b)/2 + (a + b) = (c + d + e + f) + (a + b)

(a + b)/2 + 2(a + b)/2 = (a + b + c + d + e + f)

(a + b)3/2 = (a + b + c + d + e + f)

(a + b) = (a + b + c + d + e + f)2/3

Logo, a quantidade de participantes das duas primeiras etapas representa 2/3 do total.
Alternativa D

23) (BB-Fundação Carlos Chagas) Nos quatro primeiros dias úteis de uma semana o gerente de uma agência bancária atendeu 19, 15, 17 e 21 clientes. No quinto dia útil dessa semana esse gerente atendeu n clientes. Se a média do número diário de clientes atendidos por esse gerente nos cinco dias úteis dessa semana foi 19, a mediana foi
(A) 21.

(B) 19.

(D) 20.

(E) 23.
Resolução
Para calcularmos a média aritmética, somamos os valores e dividimos pela quantidade de termos:

Média = (19 + 15 + 17 + 21 + n) / 5 = 19

19 + 15 + 17 + 21 + n = 19 x 5

72 + n = 95

n= 95 – 72 = 23

Nossa sequencia ordenada é então: 15, 17, 19, 21, 23
Como a mediana é o termo do meio quando ordenados, a resposta é 19.
Alternativa B

24) (PM ES-Exatus) A tabela que segue é demonstrativa do levantamento realizado por determinado batalhão de Polícia Militar, no que se refere às idades dos policiais integrantes do grupo especial desse batalhão:
Idade Nr. de Policiais
25 12
28 15
30 25
33 15
35 10
40 8
A moda, média e mediana dessa distribuição são, respectivamente, iguais a:

(A) 30, 31, 30

(B) 30, 31, 31

(D) 31, 30, 31

(E) 31, 31, 30
Resolução
Moda é o valor que aparece com mais frequência: 30.

Média: Temos que somar todas as idades e dividir pela quantidade de policiais:
(25×12 + 28×15 + 30×25 + 33×15 + 35×10 + 40×8)/85
= (300 + 420 + 750 + 495 + 350 + 320)/85
= 2635/85 = 31

Mediana é o termo do meio quando colocamos todos em ordem:
São 85 termos, o do meio é o termo de número 43, ou seja, 30 anos.
Alternativa A

25) (Prova Resolvida PM ES-Funcab) A tabela abaixo representa os dados dos balanços das operações do Batalhão de Polícia de Trânsito (BPTran) da Polícia Militar – ES em três grandes feriados nacionais do ano de 2012.
Dia do trabalho: 220 acidentes, 2 mortos, 78 feridos
Dia de finados: 186 acidentes, 2 mortos, 54 feridos
Dia do trabalho: 219 acidentes, 1 mortos, 51 feridos
O valor que melhor representa a média do número de feridos, de acordo com a tabela acima, é:
(A) 57
(B) 59
(C) 61
(D) 63
(E) 65
Resolução
Calculando a média aritmética:
(78 + 54 + 51)/3 = 183/3 = 61
Alternativa C

26) (Prova Resolvida Sejus ES-Vunesp) A média aritmética dos salários de 4 funcionários de uma empresa é R$ 2.500,00. A média aritmética dos salários dos dois primeiros é R$ 3.000,00, o quarto ganha R$ 500,00 a mais que o terceiro. Nesse caso, o salário do quarto empregado é igual a

(A) R$ 2.350,00.

(B) R$ 2.750,00.

(D) R$ 2.250,00.

(E) R$ 3.250,00.
Resolução
Vamos chamar de x, y, z, w o salário de cada funcionários.
Como a média dos salários dos 4 é 2500:
(x + y + z + w)/4 = 2500
x + y + z + w = 4.2500
x + y + z + w = 10000 (1)
Como a média dos salários dos dois primeiros é 3000:
(x + y)/2 = 3000
x + y = 2.3000
x + y = 6000 (2)
Como o quarto ganha 500 a mais que o terceiro:
w – z = 500 (3)
Fazendo (1) – (2):
z + w = 4000 (4)
Fazendo (3) + (4):
2w = 4500
w = 4500/2 = 2250
Alternativa D

27) (Prova Resolvida PM SP) João tem 5 filhos, sendo que dois deles são gêmeos. A média das idades deles é 8,6 anos. Porém, se não forem contadas as idades dos gêmeos, a média dos demais passa a ser de 9 anos. Pode-se concluir que a idade dos gêmeos, em anos, é

(A) 6,5.

(B) 7,0.

(D) 8,0.

(E) 8,5.
Resolução
Seja x a idade de cada um dos gêmeos.
Como a média das idades dos 3 filhos que não são gêmeos é 9, a soma das idades dos 3 é 27 anos.
Sabendo que a média dos 5 filhos é 8,6 temos:
(27 + 2x)/5 = 8,6
27 + 2x = 8,6.5
2x = 43 – 27
2x = 16
x = 16/2
x = 8 anos
Alternativa D

28) (Prova Resolvida RFB-Esaf) Considere a seguinte amostra aleatória das idades em anos completos dos alunos em um curso preparatório. Com relação a essa amostra, marque a única opção correta:
29, 27, 25, 39, 29, 27, 41, 31, 25, 33, 27, 25, 25, 23, 27, 27, 32, 26, 24, 36, 32, 26, 28, 24, 28, 27, 24, 26, 30, 26, 35, 26, 28, 34, 29, 23, 28.

(A) A média e a mediana das idades são iguais a 27.

(B) A moda e a média das idades são iguais a 27.

(D) A média das idades é 27 e o desvio-padrão é 1,074.

(E) A moda e a mediana das idades são iguais a 27.
Resolução
Primeiramente vamos colocar as 37 idades em ordem crescente:
23, 23, 24, 24, 24, 25, 25, 25, 25, 26, 26, 26, 26, 26, 27, 27, 27, 27, 27, 27, 28, 28, 28, 28, 29, 29, 29, 30, 31, 32, 32, 33, 34, 35, 36, 39, 41.
A moda é o valor que aparece com mais frequência. Note que o 27 aparece 6 vezes e nenhum outro aparece com tanta frequência.
A mediana é o valor que, após ordenar todos os valores, se encontra no centro. Note que o 27 se encontra na posição 19º, ou seja, exatamente no meio.
Alternativa E

29) (BASA-Cesgranrio) Sabe-se que 30% dos clientes de um banco são do sexo masculino e os 70% restantes são do sexo feminino. Entre os clientes do sexo masculino, a média do tempo de vínculo com o banco é igual a 4 anos e, entre os clientes do sexo feminino, é igual a 6 anos.
Considerando-se todos os clientes, de ambos os sexos, qual é a média do tempo de vínculo de cada um com o banco?

(A) 5 anos

(B) 5,3 anos

(D) 5,4 anos

(E) 5,7 anos
Resolução
Neste caso devemos calcular a média ponderada. Veja:
Média = (4.30 + 6.70)/100
Média = (120 + 420)/100
Média = 540/100
Média = 5,4 anos
Alternativa D

30) (Enem) Uma grande rede de supermercados adota um sistema de avaliação dos faturamentos de suas filiais considerando a média de faturamento mensal em milhão. A matriz da rede paga uma comissão para os representantes dos supermercados que atingirem uma média de faturamento mensal (M), conforme apresentado no quadro.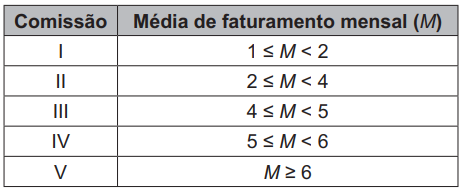
Um supermercado da rede obteve os faturamentos num dado ano, conforme apresentado no quadro.
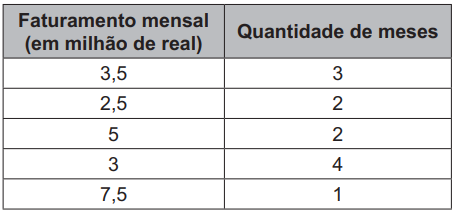Nas condições apresentadas, os representantes desse supermercado avaliam que receberão, no ano seguinte, a comissão de tipo

(A) I.

(B) II.

(D) IV.

(E) V.
Resolução:
Inicialmente, calcularemos a média aritmética ponderada:
M = 3,5 . 3+2,5 . 2+5 . 2+3 . 4+7,5 . 13+2+2+4+1M = 3,5 . 3+2,5 . 2+5 . 2+3 . 4+7,5 . 13+2+2+4+1
M = 10,5 + 5 + 10 + 12 + 7,512M = 10,5 + 5 + 10 + 12 + 7,512
M = 4512M = 4512
M = 3,75M = 3,75
A média está entre 2 e 4, então a comissão será do tipo II.
Alternativa B

31) (Enem) O quadro apresenta o número de terremotos de magnitude maior ou igual a 7, na escala Richter, ocorridos em nosso planeta nos anos de 2000 a 2011.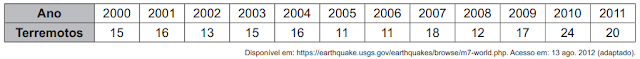
Um pesquisador acredita que a mediana representa bem o número anual típico de terremotos em um período. Segundo esse pesquisador, o número anual típico de terremotos de magnitude maior ou igual a 7 é

(A) 11.

(B) 15.

(D) 15,7.

(E) 17,5.
Resolução:
Para encontrar a mediana, primeiramente colocaremos esses dados em ordem:

11, 11, 12, 13, 15, 15, 16, 16, 17, 18, 20, 24

Agora, encontraremos os dois termos centrais do conjunto:

11, 11, 12, 13, 15, 15, 16, 16, 17, 18, 20, 24

Calculando a média entre eles, temos:
Me = 15 + 162 = 312 = 15,5Me = 15 + 162 = 312 = 15,5
Alternativa C

32) (Enem) O gráfico apresenta o comportamento de emprego formal surgido, segundo o CAGED, no período de janeiro de 2010 a outubro de 2010.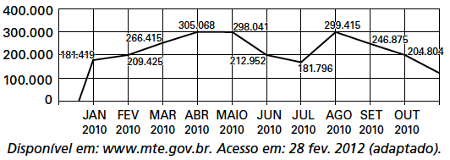
Com base no gráfico, o valor da parte inteira da mediana dos empregos formais surgidos no período é

(A) 212.952

(B) 229.913

(D) 255.496

(E) 298.041
Resolucao
Para calcular a mediana, devemos escrever todos os números referentes ao comportamento de emprego formal em ordem crescente:
181.419
181.719
204.804
209.425
212.952
246.875
266.415
298.041
299.415
305.068
Observe que os valores centrais dessa lista são: 212.952 e 246.875. A média entre eles é:

Mediana = 212.952 + 246.875
2

Mediana = 459.827
2

Mediana = 229.913,05
A parte inteira desse resultado é 229.913.
Alternativa B

34) Quais valores são, respectivamente, a moda, média e mediana dos números da lista a seguir?
133, 425, 244, 385, 236, 236, 328, 1000, 299, 325

(A) 236; 361,1 e 312

(D) 244; 361 e 312

(D) 236; 361,1 e 310

(E) 236; 361,1 e 299
Resolução
A moda é o número que aparece com maior frequência. Observe que todos os números aparecem apenas uma vez na lista, exceto 236, que aparece duas vezes. Assim, a moda é 236.
A média é obtida pela soma de todos os números e dividindo o resultado pela quantidade de números somados:

M = 133 + 425 + 244 + 385 + 236 + 236 + 328 + 1000 + 299 + 325
10

M = 3611
10

M = 361,1

A mediana é o número central de uma lista em ordem crescente. Caso a lista tenha um número par de elementos, é a média entre os dois números centrais.
133, 236, 236, 244, 299, 325, 328, 385, 425, 1000
299 + 325 = 624 = 312
2 2
Assim, moda, média e mediana são: 236; 361,1 e 312.
Alternativa A

35) Dois alunos apostaram qual deles terminaria o ano com a maior média. As notas deles foram:
Entre as alternativas a seguir, assinale aquela que for correta.

(A) O aluno 1 conseguiu a melhor média, pois possui as melhores notas iniciais.

(B) O aluno 2 conseguiu a melhor média, pois manteve as notas próximas umas das outras.

(D) O aluno 2 venceu a aposta, pois sua média foi 7,0.

(E) Nenhum aluno venceu a aposta, pois suas médias foram iguais.
Resolucao
Para resolver esse exercício, calcule a média dos dois alunos em primeiro lugar.

Aluno 1:

10 + 9 + 5 + 4 = 28 = 7
4 4

Aluno 2:

6 + 6,5 + 7,5 + 8 = 28 = 7
4 4

As médias dos alunos são iguais, por isso, nenhum deles venceu a aposta.
Alternativa E

36) Nesta etapa, os alunos terão a oportunidade de trabalhar os conhecimentos elaborados, fazendo a aplicação do conteúdo. Proponha as questões a seguir.
Determine a moda, a mediana e a média do conjunto de dados: 3, 10, 9, 8, 7, 6, 3

Resolucao
Moda: 3; média: 6,57; mediana: 7.

GRÁFICOS E TABELAS
Gráfico é uma representação geométrica de um conjunto de dados usada para facilitar a compreensão das informações apresentadas nesse conjunto. Gráficos ajudam a identificar padrões, verificar resultados e comparar medidas de forma ágil. Além disso, eles podem ser usados de diversas formas e em diferentes áreas do conhecimento.

Elementos dos gráficos
Alguns elementos estão presentes em todos os tipos de gráficos. São eles:

Título: frases curtas com a palavra-chave do assunto apresentado.

Fonte: parte importante para dar credibilidade ao gráfico. Identificação da fonte (estudos científicos, órgãos públicos, instituições privadas, economistas, etc.) no qual a informação foi retirada.

Números: valores que são essenciais para a comparação dos fatos. Eles são organizados em ordem crescente e apontam quantidades e períodos (mês, semestre, ano).

Legendas: pequeno resumo das informações analisadas no gráfico. Podem ser colocadas em qualquer parte e destacadas por cores.

Tipos de Gráficos
Existem variados tipos de gráficos, que atuam conforme os dados coletados, e como serão transmitidos. Por esse motivo, nem todos eles são adequados em certas situações.

A escolha incorreta pode comprometer a análise dos números e a autenticidade da informação. Conheça a utilidade de cada um deles:

Gráfico de Colunas
O gráfico de colunas, também chamado de gráfico de barra, são usados na comparação dos quantitativos em setores, espaços de tempo ou lugares. Os dados são colocados na posição vertical e as categorias qualitativas na horizontal.

Serve para informações simples e valores em duração (crescente ou decrescente). Podem ser projetados em barras agrupadas, barras empilhadas, cones, cilindros e pirâmides.

Gráfico de Linhas
Também conhecido como gráfico de segmento, é utilizado para exemplificar parâmetros de evolução e regressão. Ou seja, sequências numéricas presentes em certos espaços de tempo.

Considere a sua aplicação caso não seja necessário discutir a continuidade das variações. São projetados das seguintes maneiras:

Linha com marcadores

Linha empilhada

Linha empilhada com marcadores

Linha 3D

Gráfico de Pizza

O gráfico de pizza ou gráfico de setores é adequado para estatísticas e percentuais (porcentagens). As partes, quando somadas, devem resultar no todo (100%). É viável para série de dados, valores positivos e diferentes de zero, menos de sete categorias avaliadas. Podem aparecer em 3D, pizza de pizza e barra de pizza.

Gráfico de Área
Semelhante ao gráfico de linhas com marcadores, destaca as alterações e compara as variáveis em relação ao tempo. Assim como o de pizza, representa partes de um todo e as categorias em duas ou mais dimensões.
Os tipos são: área 3D, área empilhada, área 3D empilhada e porcentual de área empilhada.

Gráfico de Dispersão
Também conhecido como gráfico de Scatter, esse tipo mostra a relação entre diferentes variáveis e seus resultados.

O uso desse modelo é aconselhado em trabalhos que destacam as semelhanças entre os valores sem o auxílio do tempo. Quanto mais dados forem incluídos, melhores serão as análises.
Podem ser elaborados de tais formas:

Dispersão com linhas suaves

Dispersão com linhas suaves e marcadores

Dispersão com linhas retas

Dispersão com linhas retas e marcadores

Gráfico de Rede
Tipos de gráficos: rede. (Foto: Pixabay)

Fluxograma com sequências interligadas para determinar os dados que ainda não foram concluídos e as suas dependências. Desenhos com nós e flechas são os mais usados.

Histogramas
Assim como o gráfico de colunas, utiliza a distribuição e análise de dados estatísticos. A altura dos desenhos é proporcional a frequência dos acontecimentos e as barras são separadas entre si.
Modelo de histograma. (Foto: Educa Mais Brasil)

A variável precisa ser quantitativa e o valores de forma contínua. A depender da sua estética, são classificadas em:

Histograma simétrico

Histograma assimétrico

Histograma Despenhadeiro

Histograma com Dois Picos

Histograma Platô

Histograma Retângulos Isolados

Infográficos

Entre os tipos de gráficos, essa categoria explora é a que mais explora imagens, desenhos e variados elementos visuais, tornando-os altamente atrativos ao público leitor. Por isso, é comum a aparição em matérias jornalísticas, livros didáticos e campanhas publicitárias.

ESTATISTICA- GRAFICOS E TABELAS RESOLVIDOS
37) (Fuvest) A distribuição das idades dos alunos de uma classe é dada pelo seguinte gráfico: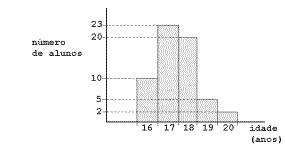
Qual das alternativas representa melhor a média de idade dos alunos?

(A) 16 anos e 10 meses

(B) 17 anos e 1 mês

(D) 18 anos e 6 meses

(E) 19 anos e 2 meses
Resolucao
Note que o eixo x do gráfico fornece-nos a idade dos alunos e o eixo y fornece-nos a frequência de cada uma das idades, ou seja, a quantidade de vezes que a idade aparece. Assim, devemos utilizar a média ponderada para calcular a média das idades.

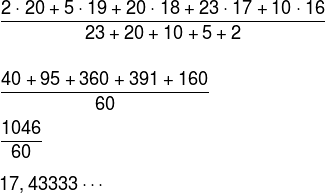Sabemos que 17,43333… = 17 + 0,4333… . Para transformar 0,43333… em meses devemos multiplicá-lo por 12, logo:
0,4333 · 12 = 5 meses
Portanto, a média de idade desses alunos é de 17 anos e 5 meses."
Alternativa C

38) (UCB - DF)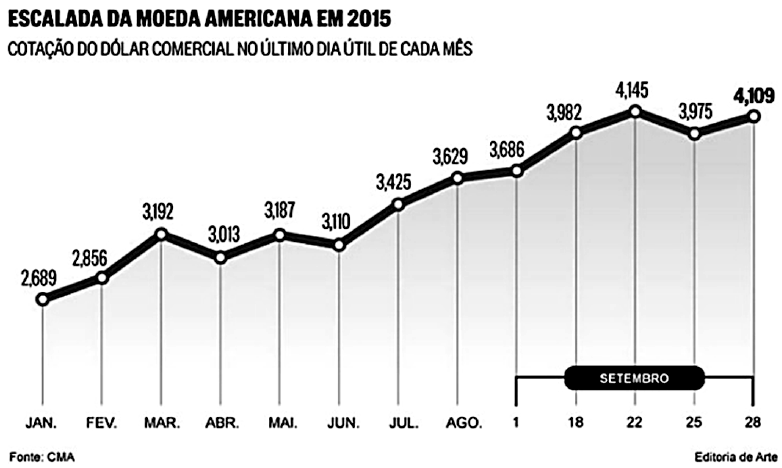
Com base exclusivamente nos dados apresentados no gráfico quanto à cotação do dólar comercial no último dia útil de cada mês de 2015, assinale a alternativa correta.

(A) Em dezembro de 2014, a cotação do dólar comercial foi menor que 2,689.

(B) O maior valor para a cotação do dólar comercial foi verificado em 28 de setembro.

(C) A função que representa o valor da cotação do dólar comercial em relação ao tempo é crescente, no intervalo apresentado no gráfico.

(D) A diferença entre os valores da cotação do dólar comercial de maio e de março foi menor que um centavo de real.

(E) Em 15 de agosto, o valor da moeda foi menor que 3,629.
Resolucao
a) Incorreta!
O texto do exercício diz que as respostas devem ter como base exclusivamente os dados apresentados no gráfico. Como ele é referente apenas ao ano de 2015, não é possível garantir que a cotação do dólar em 2014 seguiu o mesmo padrão de 2015.
b) Incorreta!
Em 22 de setembro, a cotação do dólar foi a maior: 4,145. No dia 28 de setembro, a cotação foi de 4,109.
c) Incorreta!
A função apresenta alguns intervalos decrescentes, embora pareça ser crescente em um sentido geral. Por exemplo, do mês de março para abril, a função é decrescente.
d) Correta!
e) Incorreta!
Os valores presentes na tabela são referentes ao último dia do mês. A linha que liga esses valores não é exata, pois indica um “progresso médio” da cotação do dólar. Assim, do mês de julho para o mês de agosto, em média, a cotação do dólar aumentou, mas nada garante que exatamente no dia 15 de agosto ela tenha sido maior que 3,629.
Alternativa D

39) (UCB - DF)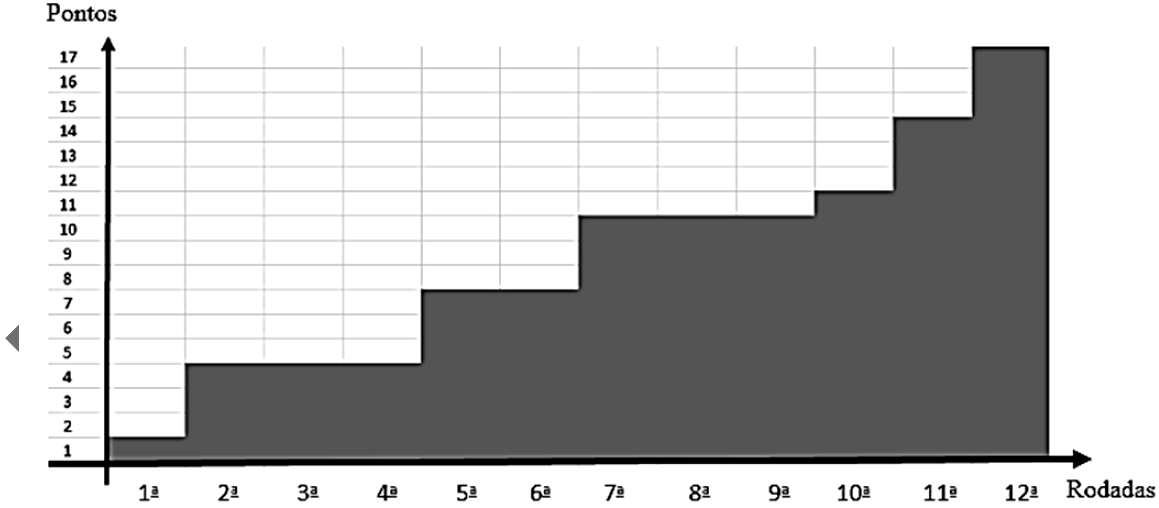
O gráfico mostra o número de pontos de uma equipe de futebol nas 12 primeiras rodadas de um campeonato. Sabendo que, nesse campeonato, em caso de vitória a equipe soma três pontos, em caso de empate soma um ponto e em caso de derrota não soma ponto, assinale a alternativa correta.

(A) A equipe perdeu os jogos da segunda, terceira e quarta rodadas.

(B) Nas doze rodadas, o número de vitórias foi igual ao número de derrotas.

(D) A equipe conseguiu dois empates entre a sétima e a nona rodadas.

(E) Nas doze rodadas, a equipe empatou três vezes.
Resolucao
a) Incorreta!
Na segunda rodada, a equipe venceu o jogo, subindo seu ranking para 4 pontos.
b) Correta!
c) Incorreto!
A média dos pontos obtidos por rodada é a soma de todos os pontos obtidos, dividida pelo número de rodadas jogadas. Pela tabela, o time alcançou 17 pontos em 12 rodadas:
17/12 = 1,42 aproximadamente.
d) Incorreta!
A equipe venceu o jogo da sétima rodada e perdeu os jogos da oitava e nona.
e) Incorreta!
A equipe empatou em duas rodadas: primeira e décima.
Alternativa B

40) Para construir um gráfico de setores, representando alguma estatística a respeito de sua turma, um estudante fez a divisão ilustrada na imagem e colocou nele um número referente a um dos setores do gráfico. A respeito dessa construção, assinale a alternativa correta.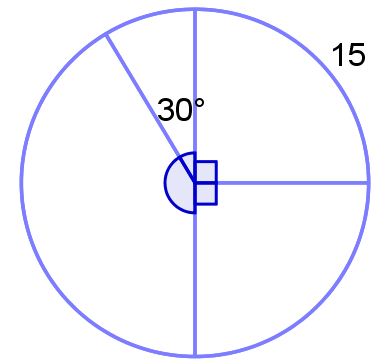
(A) O maior ângulo central nesse gráfico mede 150°.

(B) O número total de alunos nessa turma é 62.

(D) Não é possível garantir que os setores são proporcionais aos números que representam.

(E) O maior setor desse gráfico representa 20 alunos.
Resolucao
Observe que as medidas do lado direito desse gráfico são ambas com 90°, totalizando 180°. Para os dois outros ângulos, sobram apenas 180°. Como 30° é a medida do ângulo do menor setor, então 150° é a medida do ângulo do maior setor. Portanto, a alternativa correta é a letra A.
Para mostrar que as outras alternativas estão erradas, basta usar regra de três e descobrir os valores específicos de cada parte do gráfico.
Alternativa A

41) O gráfico a seguir diz respeito aos resultados obtidos por uma turma de alunos de um curso preparatório específico para professor de educação básica.
Resultados dos professores no curso preparatório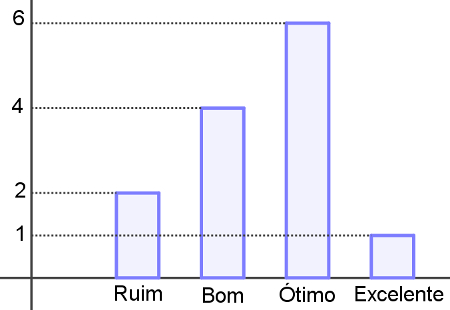
Para continuar no mercado, é necessário que esse curso aprove pelo menos 70% de seus alunos, que, por sua vez, são professores especializando-se. Sabendo que os aprovados são apenas aqueles que obtiveram resultado ótimo ou excelente, pode-se afirmar que esse curso continuará no mercado?

(A) Sim, pois o percentual de professores aprovados foi, aproximadamente, 70%

(B) Sim, pois o percentual de professores aprovados foi, aproximadamente, 80%

(D) Não, pois o percentual de professores aprovados foi, aproximadamente, 40%

(E) Sim, pois o percentual de professores aprovados foi, aproximadamente, 90%
Resolucao
Para calcular o percentual de professores aprovados, primeiro vamos encontrar quantos professores obtiveram o resultado como ótimo ou excelente. Analisando o gráfico é possível observar que 6 professores atingiram o resultado ótimo e 1 atingiu o resultado excelente, tendo um total de 7 aprovados. Note também que 6 professores foram reprovados com resultados bom ou ruim, totalizando (6 reprovados + 7 aprovados) 13 professores. Então para calcular a porcentagem de aprovados temos que dividir 6 por 13.
6 : 13 = 0,53 à 53% de aprovados.
Alternativa C

42) (ENEM) O dono de uma farmácia resolveu colocar à vista do público o gráfico mostrado a seguir, que apresenta a evolução do total de vendas (em reais) de certo medicamento ao longo do ano de 2011.
De acordo com o gráfico, os meses em que ocorreram, respectivamente, a maior e a menor venda absolutas em 2011 foram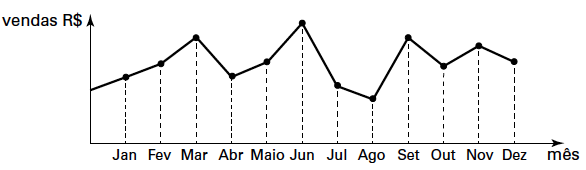
(A) março e abril.

(B) março e agosto.

(D) junho e setembro.

(E) junho e agosto.
Resolucao
Qual questão você marcaria?
Talvez seja óbvio demais. Você pode marcar na prova uma questão e chegue no cartão resposta, dá aquela balançada e marca outra. Mas é isso mesmo:
Alternativa: E

43) (ENEM) O gráfico expõe alguns números da gripe A-H1N1. Entre as categorias que estão em processo de imunização, uma já está completamente imunizada, a dos trabalhadores da saúde.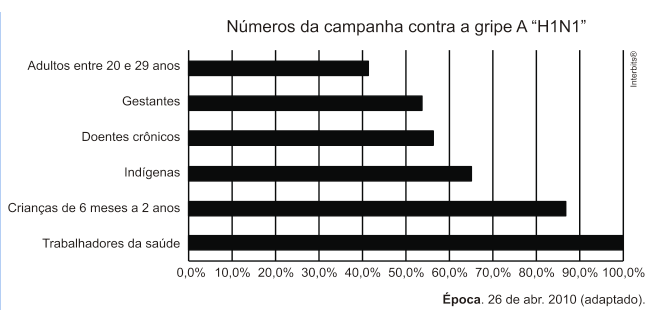
De acordo com o gráfico, entre as demais categorias, a que está mais exposta ao vírus da gripe A-H1N1 é a categoria de

(A) indígenas.

(B) gestantes.

(D) adultos entre 20 e 29 anos.

(E) crianças de 6 meses a 2 anos.
Resolucao
E aí, o que você acha? Os adultos estão mais suscetíveis à doença já que é o menor grupo imunizado, com 40% no total.
Alternativa: D

44) (ENEM) O procedimento de perda rápida de “peso” é comum entre os atletas dos esportes de combate. Para participar de um torneio, quatro atletas da categoria até 66 kg, Peso-Pena, foram submetidos a dietas balanceadas e atividades físicas. Realizaram três “pesagens” antes do início do torneio. Pelo regulamento do torneio, a primeira luta deverá ocorrer entre o atleta mais regular e o menos regular quanto aos “pesos”. As informações com base nas pesagens dos atletas estão no quadro.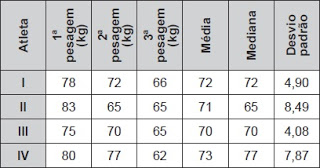
Após as três “pesagens”, os organizadores do torneio informaram aos atletas quais deles se enfrentariam na primeira luta. A primeira luta foi entre os atletas

(A) I e III.

(B) I e IV.

(D) II e IV.

(E) III e IV.
Resolução:
Em casos de empate, o atleta de melhor desempenho e mais regular é aquele que não se afasta da média ou seja o de menor desvio padrão. O Atleta III é o mais regular (menor desvio padrão) e o Atleta II é o menos regular (maior desvio padrão). Na terceira pesagem todos bateram o peso de 66kg e portanto aptos para lutar.
Alternativa: C

45) (ENEM) A figura a seguir apresenta dois gráficos com informações sobre as reclamações diárias recebidas e resolvidas pelo Setor de Atendimento ao Cliente (SAC) de uma empresa, em uma dada semana. O gráfico de linha tracejada informa o número de reclamações recebidas no dia, o de linha contínua é o número de reclamações resolvidas no dia. As reclamações podem ser resolvidas no mesmo dia ou demorarem mais de um dia para serem resolvidas.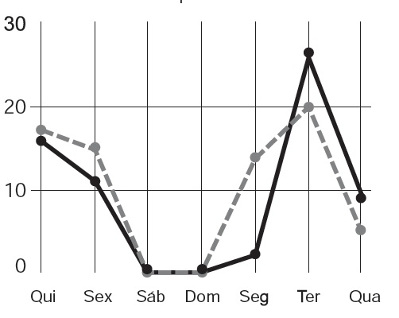
O gerente de atendimento deseja identificar os dias da semana em que o nível de eficiência pode ser considerado muito bom, ou seja, os dias em que o número de reclamações resolvidas excede o número de reclamações recebidas.
O gerente de atendimento pôde concluir, baseado no conceito de eficiência utilizado na empresa e nas informações do gráfico, que o nível de eficiência foi muito bom na

(A) segunda e na terça-feira.

(B) terça e na quarta-feira.

(D) quinta-feira, no sábado e no domingo.

(E) segunda, na quinta e na sexta-feira.
Resolução:
Analisando o enunciado do problema e o gráfico, observamos que a linha tracejada representa as reclamações recebidas e a linha contínua representa as reclamações resolvidas. Se nós desejamos identificar os dias em que o número de reclamações resolvidas excedeu as reclamações recebidas, basta procurar no gráfico os dias em que a linha contínua atingiu maiores picos em relação à linha tracejada. No gráfico, podemos constatar que tal fato ocorreu apenas na terça e na quarta. Portanto, são esses os dias em que o nível de eficiência foi muito bom.
Alternativa: B

46) (ENEM) Em um blog de variedades, músicas, mantras e informações diversas, foram postados “Contos de Halloween”. Após a leitura, os visitantes poderiam opinar, assinalando suas reações em: “Divertido”, “Assustador” ou “Chato”. Ao final de uma semana, o blog registrou que 500 visitantes distintos acessaram esta postagem.
O gráfico a seguir apresenta o resultado da enquete.
O administrador do blog irá sortear um livro entre os visitantes que opinaram na postagem “Contos de Halloween”. Sabendo que nenhum visitante votou mais de uma vez, a probabilidade de uma pessoa escolhida ao acaso entre as que opinaram ter assinalado que o conto “Contos de Halloween” é “Chato” é mais aproximada por

(A) 0,09.

(B) 0,12.

(D) 0,15.

(E) 0,18.
Resolução:
Vemos que nesta questão foram cobrados, além da habilidade em leitura de gráfico, também o de cálculo de probabilidades. Como o sorteio foi entre os que opinaram, vemos que o 21% não opinou, sobrando então 79% de opinantes.
Número total de opinantes = 0,79 x 500 =395
Número de opinantes que votou “chato” = 0,12×500 = 60
Assim sendo, a probabilidade de uma pessoa escolhida ao acaso dentre as que opinaram, ter assinalado “chato” será:

Alternativa: D

47) (ENEM) O gráfico mostra a variação da extensão média de gelo marítimo, em milhões de quilômetros quadrados, comparando dados dos anos 1995, 1998, 2000, 2005 e 2007.
Os dados correspondem aos meses de junho a setembro. O Ártico começa a recobrar o gelo quando termina o verão, em meados de setembro. O gelo do mar atua como o sistema de resfriamento da Terra, refletindo quase toda a luz solar de volta ao espaço. Águas de oceanos escuros, por sua vez, absorvem a luz solar e reforçam o aquecimento do Ártico, ocasionando derretimento crescente do gelo.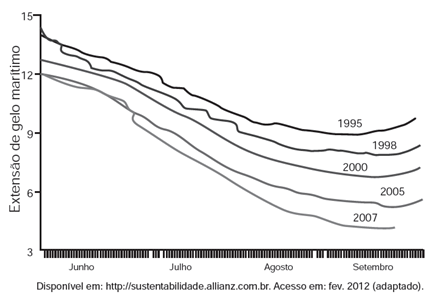
Com base no gráfico e nas informações do texto, é possível inferir que houve maior aquecimento global em

(A) 1995.

(B) 1998.

(D) 2005.

(E) 2007.
Alternativa: E

48) (ENEM) Uma enquete, realizada em março de 2010, perguntava aos internautas se eles acreditavam que as atividades humanas provocam o aquecimento global. Eram três as alternativas possíveis e 279 internautas responderam à enquete, como mostra o gráfico.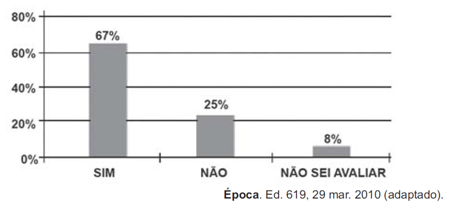
Analisando os dados do gráfico, quantos internautas responderam “NÃO” à enquete?

(A) Menos de 23.

(B) Mais de 23 e menos de 25.

(D) Mais de 100 e menos de 190.

(E) Mais
Alternativa: C

(ENEM) Texto para as questões 49 e 50.

49) (ENEM) Nos últimos anos, ocorreu redução gradativa da taxa de crescimento populacional em quase todos os continentes. A seguir, são apresentados dados relativos aos países mais populosos em 2000 e também as projeções para 2050.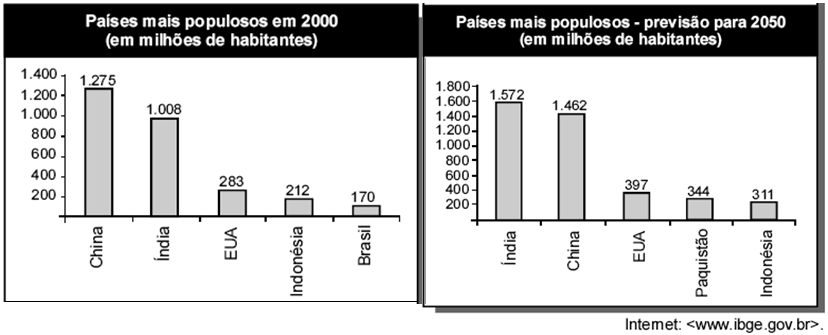
Com base nas informações acima, é correto afirmar que, no período de 2000 a 2050:

(A) a taxa de crescimento populacional da China será negativa.

(B) a população do Brasil duplicara.

(D) a população do Paquistão crescerá mais de 100%.

(E) a China será o país com a maior taxa de crescimento populacional do mundo.
Resolução:
a) Falsa!
A taxa de crescimento é o percentual de pessoas a mais em 2050. Assim:

1462 – 1275 = 187 = 0,146 = 14,6%
1275 1275

Essa é uma taxa de crescimento positiva.
b) Falsa!
A população brasileira, em 2000, era de 170 milhões. Se duplicasse, partiria para 340 milhões e apareceria em quinto lugar no gráfico referente a 2050, no lugar da Indonésia.
c) Falsa!

As referidas taxas de crescimento são:
Indonésia:
311 – 212 = 99 = 0,467
212 212

EUA:
397 – 283 = 114 = 0,403
283 283
Portanto, a taxa de crescimento da Indonésia é maior que a dos EUA.
d) Verdadeira!
A população do Paquistão era menor que a do Brasil e, por isso, sequer aparecia no gráfico referente a 2000. Em 2050, a população do Paquistão será de 344 milhões, mais que o dobro da população do Brasil em 2000. O dobro significa um acréscimo de exatamente 100%. Mais que o dobro indica mais que 100%.
e) Falsa!
Pelos cálculos feitos nas alternativas a e c, as taxas da Indonésia e dos EUA serão maiores que as da China.
Alternativa: D

50) (ENEM) Com base nas informações dos gráficos mostrados, suponha que, no período 2050-2100, a taxa de crescimento populacional da Índia seja a mesma projetada para o período 2000-2050. Sendo assim, no início do século XXII, a população da Índia, em bilhões de habitantes, será:

(A) inferior a 2,0

(B) superior a 2,0 e inferior a 2,1

(D) superior a 2,2 e inferior a 2,3

(E) superior a 2,3
Resolução:
A taxa de crescimento populacional da Índia, em 2050, é de:
1572 – 1008 = 564 = 0,559 = 55,9%
1008 1008
Dessa maneira, a população em 2100 será de:
1572·(1 + 0,559) = 1572·1,559 = 2450
A Índia terá 2450 milhões de habitantes aproximadamente, o que é um número superior a 2,3 bilhões de habitantes.
Alternativa: E

51) (BB – Fundação Carlos Chagas) O supervisor de uma agência bancária obteve dois gráficos que mostravam o número de atendimentos realizados por funcionários. O Gráfico I mostra o número de atendimentos realizados pelos funcionários A e B, durante 2 horas e meia, e o Gráfico II mostra o número de atendimentos realizados pelos funcionários C, D e E, durante 3 horas e meia.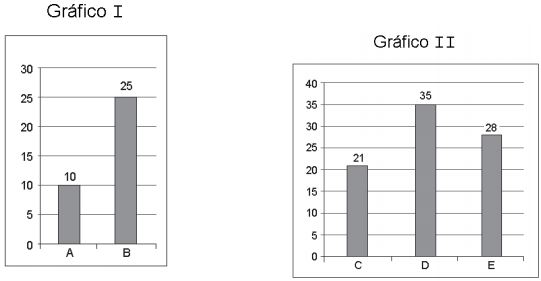
Observando os dois gráficos, o supervisor desses funcionários calculou o número de atendimentos, por hora, que cada um deles executou. O número de atendimentos, por hora, que o funcionário B realizou a mais que o funcionário C é:

(A) 4.

(B) 3.

(D) 5.

(E) 6.
Resolução:
Funcionário B:
25 atendimentos / 2,5 horas = 10 clientes por hora
Funcionário C:
21 atendimentos / 3,5 horas = 6 clientes por hora
Diferença: 10 – 6 = 4
Alternativa: A

52) (Sejus ES – Vunesp) Observe os gráficos e analise as afirmações I, II e III.
Procura por graduação aumenta ano a ano
Explosão do número de inscritos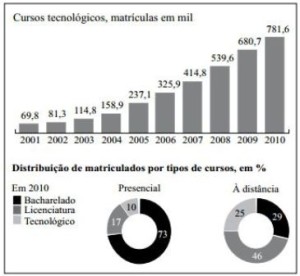
Em 2010, o aumento percentual de matrículas em cursos tecnológicos, comparado com 2001, foi maior que 1000%.
Em 2010, houve 100,9 mil matrículas a mais em cursos tecnológicos que no ano anterior.
III. Em 2010, a razão entre a distribuição de matrículas no curso tecnológico presencial e à distância foi de 2 para 5.
É correto o que se afirma em

(A) I e II, apenas.

(B) II, apenas.

(D) II e III, apenas.

(E) I, II e III.
Resolução:
CERTO
Matrículas em 2001: 69800;
Matrículas em 2010: 781600;
Crescimento: 781600 – 69800 = 711800
Crescimento em porcentagem: 711800/69800 = 10,19 ou 1019%
CERTO
Matrículas em 2010: 781600
Crescimento: 781600 – 680700 = 100900
III. CERTO
Em 2010 tivemos 10 matrículas presenciais e 25 à distância:
10/25 = 2/5
Alternativa: E

53) (PM SP) Para uma festa junina, foi contratada uma barraca de pastéis, que levou os seguintes tipos de recheios: carne, queijo e palmito. A tabela a seguir mostra a quantidade de pastéis vendidos na festa.
Recheios Número de pastéis vendidos
Carne —— 56
Queijo —– 72
Palmito —- 32
Em relação ao número total de pastéis vendidos na festa, o gráfico que representa essas informações, em porcentagem, é: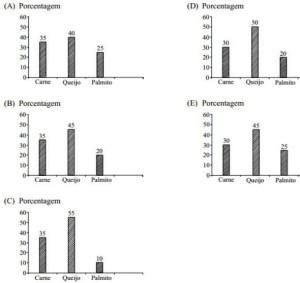

Em relação ao número total de pastéis vendidos na festa, o gráfico que representa essas informações, em porcentagem, é:
Resolução:
Total de pastéis vendidos: 56 + 72 + 32 = 160
Carne: 56/160 = 0,35 = 35%
Queijo: 72/160 = 0,45 = 45%
Palmito: 0,20 = 20%
Alternativa: B

54) (BB – Cesgranrio) Os gráficos abaixo apresentam dados sobre a produção e a reciclagem de lixo em algumas regiões do planeta.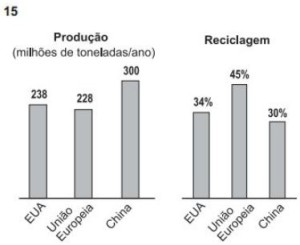
Baseando-se nos dados apresentados, qual é, em milhões de toneladas, a diferença entre as quantidades de lixo recicladas na China e nos EUA em um ano?

(A) 9,08

(B) 10,92

(D) 21,68

(E) 24,80
Resolução:
A China produz 300 milhões e recicla 30%, ou seja, recicla 90 milhões.
Os EUA produzem 238 milhões e recicla 34%, ou seja, reciclam 80,92 milhões.
China – EUA = 90 – 80,92 = 9,08 milhões de toneladas.
Alternativa: A

55) (INSS – Cespe) A tabela abaixo mostra, em porcentagens, a distribuição relativa da população brasileira por grupos etários, de acordo com dados dos censos demográficos de 1940 a 2000.
Com base nos dados acerca da evolução da população brasileira apresentados na tabela acima, julgue a afirmação abaixo:
“O gráfico a seguir ilustra corretamente as informações apresentadas na tabela.”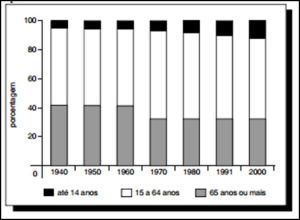
Resolução:
Observe que o gráfico estaria certo se as cores de “até 14 anos” e “65 anos ou mais” fossem invertidas.
Resposta: Errado

56) (PM Pará) O gráfico abaixo mostra a produção diária de lixo orgânico de duas pessoas. O dia da semana que o gráfico mostra que as produções de lixo das duas pessoas foram iguais é: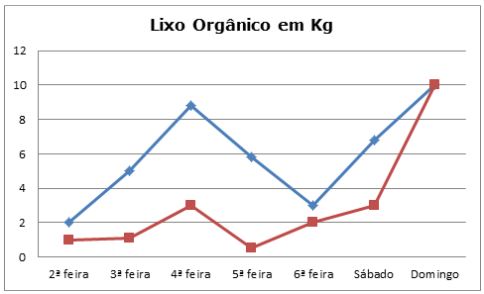
(A) 2ª feira

(B) 4ª feira

(D) Sábado

(E) Domingo
Resolução:
Repare que existe interseção das linhas azul e vermelha apenas no Domingo, onde cada uma produziu 10 kg de lixo orgânico.
Alternativa: E

57) (PM Pará) O gráfico abaixo mostra que no período de 94 a 95 houve um grande aumento no desmatamento da Amazônia. O aumento aproximado, em porcentagem, desse desmatamento no período de 94 a 95 foi de: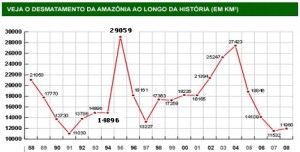
(A) 95

(B) 92

(D) 88

(E) 85
Resolução:
Calculando o crescimento do desmatamento:
29059 – 14896 = 14163
Para calcularmos a porcentagem, basta dividir pelo desmatamento de 94:
14163/14896 = 0,95 = 95%
Alternativa: A

58) (PM MG) O 150º Batalhão é responsável pela 301ª CIA PM, 302ª CIA PM, 303ª CIA PM e 304ª CIA PM. Nesse Batalhão, no ano de 2017, todas as CIAS PM obtiveram redução percentual (%) nos crimes em relação ao ano de 2016. Com base nas informações contidas no gráfico abaixo, marque a alternativa CORRETA.
GRÁFICO: crimes na área do 150º BPM, por CIA PM – 2016 a 2017: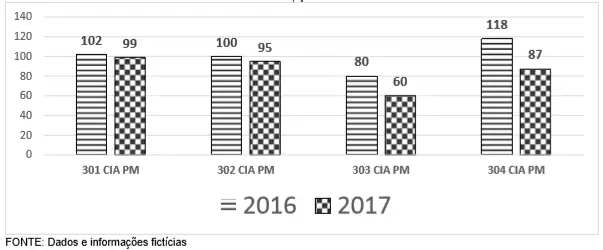

( ) A 301ª CIA PM obteve maior redução percentual que a 304ª CIA PM.

( ) A 303ª CIA PM conseguiu reduzir os crimes em 25%.

( ) A 303ª CIA PM obteve menor redução percentual que a 302ª CIA PM.

( ) A 302ª CIA PM conseguiu reduzir os crimes em 12%.
Resolução:
Calculando o percentual de redução de cada CIA:
301ª CIA: 3/102 = 2,94%
302ª CIA: 5/100 = 5%
303ª CIA: 20/80 = 25%
304ª CIA: 31/118 = 26,2%
Alternativa: B

59) (Detran SP – Vunesp) O gráfico apresenta a distribuição de vítimas de trânsito no mês de julho de 2013, segundo o tipo de usuário da via pública em uma determinada cidade brasileira.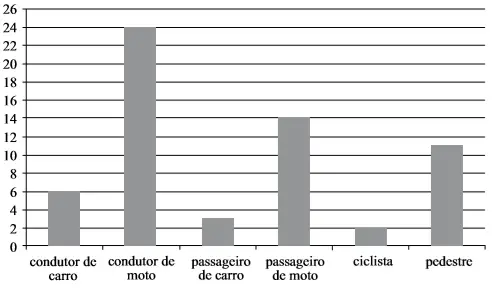
O grupo que corresponde a 2/5 do total de vítimas é o de

(A) passageiro de carro.

(B) condutor de carro.

(D) pedestre.

(E) condutor de moto.
Resolução
Analisando o gráfico, a quantidade de vítimas em cada grupo foi:
condutor de carro: 6
condutor de moto: 24
passageiro de carro: 3
passageiro de moto: 14
ciclista: 2
pedestre: 11
Total de vítimas: 6 + 24 + 3 + 14 + 2 + 11 = 60
60 . 2/5 = 120/5 = 24
Alternativa: E

POPULAÇÃO E AMOSTRA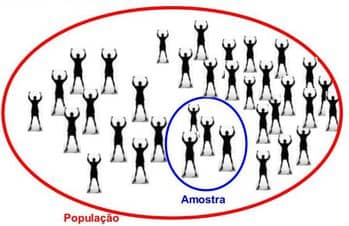

Populacao
A população de pesquisa é um conjunto completo de elementos que têm um parâmetro comum entre si
É importante mencionar que todos sabemos o que a palavra “população” significa em nossas vidas diárias. É frequentemente usada para descrever a população humana ou o número total de pessoas que vivem em uma área geográfica de um país ou estado.

Exemplo: o número todas as lojas de roupa em uma cidade.

Amostra
Uma amostra é a menor parte do total, ou seja, um subconjunto de toda a população. Quando são realizadas pesquisas, a amostra são os membros da população convidados a participar da pesquisa.

Simplificando, uma amostra é um subgrupo ou subconjunto da população, que pode ser estudado para investigar as características ou o comportamento dos dados da população.

Exemplo 1: geralmente, as amostragens são grupos de pessoas, mas isso varia com a população. No exemplo acima, onde a população era o número total de lojas de roupa de uma cidade, a amostra poderia ser apenas as lojas de roupas para bebês dessa cidade.

Exemplo 2: Uma empresa de comida para gatos gostaria de conhecer todas as lojas de animais em que pode vender. A empresa possui dados da população sobre o número total de lojas de animais em uma cidade específica.

POPULACAO E AMOSTRA – RESOLVIDOS
60) (PM MG) O gerente de uma empresa, com um total de 150 funcionários, realizou um experimento com o objetivo de verificar o consumo de água dos funcionários durante o turno de trabalho. Foram selecionados, aleatoriamente, 50 funcionários e mensurada a quantidade de litros de água consumida por cada um, no período de 30 dias. Sabe-se, também, que cada funcionário teve a mesma probabilidade de ser incluído na seleção. Com base nestas informações, relacione a segunda coluna de acordo com a primeira:
COLUNA 1
(1) Quantidade total de funcionários da empresa.
(2) Consumo de litros de água por funcionário.
(3) 50 funcionários selecionados aleatoriamente.
(4) Técnica utilizada para seleção da amostra.
COLUNA 2
( ) Variável contínua.
( ) Amostra.
( ) Amostragem aleatória simples.
( ) População.
Marque a alternativa que contém a sequência CORRETA de respostas, na ordem de cima para baixo:
( ) 4, 2, 3, 1.
( ) 2, 1, 4, 3. ) 3, 2, 1, 4. ) 2, 3, 4, 1.
Resolução
A população é o conjunto estudado, ou seja, todos os funcionários da empresa.
Consumo de litros de água por funcionário é uma variável contínua.
Os 50 funcionários selecionados são uma amostra.
A técnica utilizada é a amostragem aleatória simples.
Resposta: D

61) (TSE) Para uma população de 10 indivíduos é retirada uma amostra de 3 indivíduos, sem reposição. Assim, o número de amostras possíveis é
(A) 80.
(B) 120.

(D) 720.
Resolução
A questão informa o tamanho da população (10 pessoas) e o tamanho da amostra (3 pessoas).
Como precisamos calcular a quantidade de amostras possíveis, basta calcularmos a quantidade de combinações de 10 pessoas, tomadas 3 a 3.
C_3,3 = 10! / 7!.3! = 10.9.8/3.2.1 = 120
Alternativa B

MEDIDA DE DISPERSAO:
Amplitude / Desviao padrao / Variancia
As medidas de dispersão são usadas para obter o grau de variabilidade dos elementos de um conjunto de informações. Amplitude e desvio são os mais fundamentais desses cálculos.

São elas: amplitude, desvio, variancia ou desvio padrao. Essas últimas são chamadas medidas de dispersão.

A média é uma medida de tendência central usada para representar os números de um conjunto utilizando apenas um número. No entanto, imagine que um professor precisa descobrir quais dos seus alunos tiveram melhor desempenho durante o ano letivo.

Dois desses alunos tiveram a mesma média: 6,0.
Notas do primeiro foram 6,5; 6,5; 6,0 e 5,0
Notas do segundo foram 1,0; 4,0; 9,0 e 10,0

Pode-se concluir que esse aluno empenhou-se mais no processo de aprendizagem.

Assim, a média por si só não é suficiente para mostrar o desenvolvimento dos alunos desse professor, ela é uma espécie de meta que o aluno deve alcançar para ser aprovado.

Para analisar o progresso de um aluno, podemos usar as medidas de dispersão, que indicam o quão distante está cada uma das notas desses alunos da média obtida.

Amplitude
A primeira medida de dispersão é conhecida como amplitude e determina a diferença entre o maior e o menor elemento de uma lista.

Usando o mesmo exemplo utilizado acima, das notas dos dois alunos, observe a amplitude das notas deles:

Primeiro: Média 6,0; amplitude = 6,5 – 5,5 = 1,0

Segundo: Média 6,0; amplitude = 10,0 – 1,0 = 9,0

Observando apenas esses números, é possível perceber que o primeiro aluno estabilizou as notas de suas provas e o segundo, não. Para concluir que o segundo aluno teve melhor desenvolvimento, ainda precisamos ver o restante de suas notas.

Desvio padrao
O desvio é a diferença entre uma informação individual de um conjunto e a média desse conjunto. Em outras palavras, é a diferença que cada informação tem com a média. Dessa maneira, é possível calcular o desvio de cada elemento de um conjunto.

Assim, os desvios devem ser calculados para cada elemento desse conjunto. No exemplo dado acima, seriam quatro desvios para o primeiro aluno e outros quatro desvios para o segundo aluno.

Notas do primeiro aluno: 6,5 6,5; 6,0 e 5,0.

Média = 6,0.
Desvios

d₁ = 6,5 – 6,0 = 0,5

d₂ = 6,5 – 6,0 = 0,5

d₃ = 6,0 – 6,0 = 0

d₄ = 5,0 – 6,0 = – 1,0

Observe que o sinal nos desvios é importante. É ele que determina, por meio do desvio, se a nota tirada é maior ou menor que a média.

Notas do segundo aluno: 1,0; 4,0; 9,0 e 10,0.
Média: 6,0

Desvios:

d₁ = 1,0 – 6,0 = – 5,0

d₂ = 4,0 – 6,0 = – 2,0

d₃ = 9,0 – 6,0 = 3,0

d₄ = 10,0 – 6,0 = 4,0

EXERCÍCIOS SOBRE AS MEDIDAS DE DISPERSÃO AMPLITUDE E DESVIO
62) A respeito das medidas estatísticas denominadas amplitude e desvio, assinale a alternativa correta:

(A) Em estatística, não existem diferenças entre desvio e desvio padrão, exceto pelo nome.

(B) A amplitude é uma medida de tendência central usada para encontrar um único valor que representa todos os valores de um conjunto.

(D) A amplitude é uma medida de dispersão calculada sobre cada um dos valores de um conjunto de informações.

(E) O desvio é uma medida de dispersão calculada sobre cada um dos valores de um conjunto de informações.
Resolucao
a) Incorreta!
O desvio é a medida relacionada à dispersão de cada um dos valores de um conjunto. O desvio padrão é uma medida relacionada à dispersão geral de um conjunto.
b) Incorreta!
A amplitude é a diferença entre o maior e o menor valor de um conjunto. Portanto, ela é uma medida de dispersão e não uma medida de tendência central.
c) Incorreta!
O desvio é uma medida de dispersão relacionada a cada um dos valores de um conjunto e não à sua dispersão total.
d) Incorreta!
A amplitude é a diferença entre o maior e o menor valor de um conjunto. Portanto, ela não é calculada sobre todos os valores do conjunto.
e) Correta!
Alternativa E

63) Qual é a soma dos desvios dos seguintes números: 10, 15, 25 e 10.

(A) 0

(B) 10

(D) -5

(E) -10
Resolucao
Sabendo que cada desvio é a diferença entre um dos valores do conjunto e a média desse conjunto, calcularemos a média e depois subtrairemos esse valor obtido de cada um dos números dados. Observe que o número a ser subtraído é a média. Essa ordem é importante para a resolução do exercício.
M = 10 + 15 + 25 + 10
4
M = 60
4
M = 15
Desvios:
10 – 15 = – 5
15 – 15 = 0
25 – 15 = 10
10 – 15 = – 5
A soma desses desvios, portanto, será:
– 5 + 0 + 10 + (– 5) = 10 – 10 = 0
Alternativa A

64) Um professor fez uma pesquisa de idades em uma turma do ensino médio, composta por 15 alunos, e obteve os seguintes resultados:
15, 15, 15, 15, 16, 16, 16, 14, 16, 16, 16, 17, 17, 18, 18
Qual é a amplitude das idades dos alunos dessa sala de aula?

(A) 1

(B) 2

(D) 4

(E) 5
Resolucao
Para encontrar a amplitude de um conjunto, basta calcular a diferença entre o maior e o menor valor da lista:
18 – 14 = 4
Então, as idades dos alunos dessa turma têm uma amplitude de 4 anos.
Alternativa D

65) O treinador de um time de futebol resolveu dispensar os dois jogadores mais velhos e os dois jogadores mais jovens de seu time. Feito isso, determinou a amplitude das idades dos jogadores restantes. A lista com as idades de todos os jogadores é a seguinte:
14, 14, 16, 16, 16, 16, 17, 17, 17, 18, 19, 25, 16, 19, 30, 31, 32, 32, 33, 35, 36, 37, 39, 39, 40, 41
Qual foi a amplitude encontrada por esse treinador?

(A) 20 anos

(B) 23 anos

(D) 30 anos

(E) 35 anos
Resolucao
Os jogadores mais jovens têm idades iguais a 14 anos. Os dois jogadores mais velhos têm 40 e 41 anos. Excluindo esses jogadores, no novo time o mais jovem terá 16 anos e o mais velho terá 39 anos. A amplitude das idades é dada considerando esses dois valores:
39 – 16 = 23
A amplitude encontrada pelo treinador foi de 23 anos.
Alternativa B

66) (CONSULPLAN) Considerando as medidas de posição e as medidas de dispersão usadas na bioestatística, relacione adequadamente as colunas a seguir.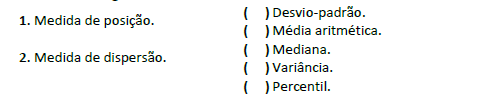

(A) 1, 2, 2, 1, 2.

(B) 1, 1, 2, 1, 2.

(D) 2, 2, 1, 2, 1.
Resolução
As medidas de dispersão apresentadas na segunda coluna são o desvio padrão e a variância.
Alternativa C

67) (IBFC) São consideradas Medidas de Dispersão na análise estatística:

(A) A Variância e o Desvio Padrão.

(B) A Média, a Moda e a Mediana.

(D) A Moda e a Média.
Resolução
Conforme visto na questão 1, a variância e o desvio padrão são medidas de dispersão.
Média, moda e mediana são consideradas medidas de posição.
Alternativa A

67) (IBFC) A alternativa que apresenta uma série de valores cuja dispersão ou variabilidade seja maior é:

(A) 33, 33, 33, 33, 33

(B) 33, 32, 34, 32, 34

(D) 30, 35, 35, 33, 32

(E) 10, 20, 30, 40, 65
Resolução
Os valores que apresentam maior dispersão ou variabilidade são aqueles que, no geral, possuem elementos mais distantes da média aritmética.
Alternativa E

68) (IBFC) Em um hospital foram registrados os “pesos” em Kg, das crianças atendidas, em um mesmo dia, conforme lista abaixo:

O desvio médio referente ao “peso”, em Kg, das crianças atendidas nesse dia no hospital foi de:

(A) 0,4

(B) 0,4

(D) 0

(E) 0,5
Resolução
Calculando a média dos “pesos” das crianças: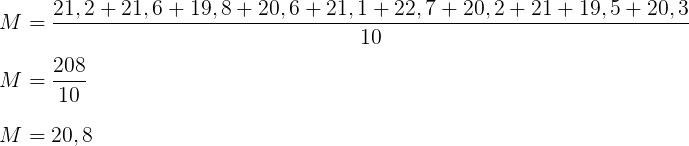

Calculando os desvios:
21,2 – 20,8 = 0,4
21,6 – 20,8 = 0,8
19,8 – 20,8 = -1,0
20,6 – 20,8 = -0,2
21,1 – 20,8 = 0,3
22,7 – 20,8 = 1,9
20,2 – 20,8 = -0,6
21,0 – 20,8 = 0,2
19,5 – 20,8 = -1,3
20,3 – 20,8 = -0,5
Desvio médio: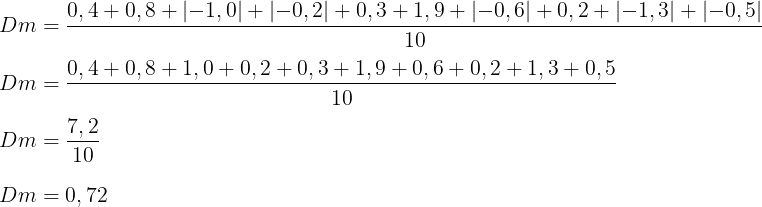

Alternatiava D

69) (IBFC) São consideradas Medidas de Dispersão na análise estatística:

(A) A Variância e o Desvio Padrão.

(B) A Média, a Moda e a Mediana.

(D) A Moda e a Média.
Resolução
Conforme visto na questão 1, a variância e o desvio padrão são medidas de dispersão.
Média, moda e mediana são consideradas medidas de posição.
Alternativa A

70) (IBFC) A alternativa que apresenta uma série de valores cuja dispersão ou variabilidade seja maior é:

(A) 33, 33, 33, 33, 33

(B) 33, 32, 34, 32, 34

(D) 30, 35, 35, 33, 32

TABELA DE DISTRIBUIÇÃO DE FREQUÊNCIA
Uma Distribuição de Frequência é um um tipo de tabela que condensa uma coleção de dados conforme as frequências (repetições de seus valores). Esta ferramenta é de muita importância num estudo estatistica. Estes dados podem ser brutos ou organizados em rol.

Os dados brutos são aqueles que ainda não foram numericamente organizados, como exemplifica a tabela abaixo:
Um rol é um arranjo de dados numéricos brutos em ordem crescente ou decrescente de grandeza. Na Figura abaixo apresentamos os dados da tabela anterior em em rol crescente. A diferença entre o maior e menor dado do rol é chamado de amplitude total dos dados.

No nosso exemplo da tabela anterior a amplitude total dos dados é de 23 cm

Quando se resumem grandes massas de dados brutos, costuma-se frequentemente distribuí-los em classe ou categorias e determinar o número de indivíduos que pertencem a cada classe. Um arranjo tabulado dos dados por classe, juntamente com as frequências correspondentes, é denominado distribuição de frequência.

Usando as tabelas mostradas anteriormente podemos dizer que a tabela abaixo é uma distribuição de frequência das alturas de 40 estudantes da Universidade XYZ.

Vamos explicar como chegamos nessa distribuição de frequência como se fosse um exercício resolvido passo a passo. A primeira classe ou categoria na tabela representada na tabela acima contem alturas que variam de 150 cm a 154 cm.

Amplitude

A amplitude do intervalo de uma classe é a diferença entre os limites reais superior e inferior dessa classe e é referida, também como a amplitude, o tamanho ou o comprimento da classe. Na nossa tabela acima, das distribuições de frequências todas as classes possuem amplitudes igual a 4 cm.

Advertisement
O ponto médio de uma classe é o ponto intermediário do intervalo classe que é obtido somando o limite inferior da classe ao limite superior da classe e dividindo por 2.
No intervalo de classe “150 |—– 154”, por exemplo, é o ponto médio é dado por (154 + 150)/2 = 152.

Distribuicao de frequencia
Uma distribuição de frequência é uma série estatística na qual os dados estão organizados em grupos de classes ou categorias estabelecidas convenientemente.

Para que serve a tabela de frequência?
A tabela de frequências é uma forma de representação da frequência de cada valor distinto da variável. Juntamente com as frequências, esta poderá incluir frequências relativas, frequências acumuladas e frequências relativas acumuladas.

Como se calcula a distribuição de frequência?
Voltando ao exemplo, se quisermos calcular a frequência relativa do teremos: Frequência acumulada é o total acumulado (soma) de todas as frequências absolutas anteriores até a frequência absoluta do valor atual. Frequência acumulada relativa é você ir dividindo o valor da frequência acumulada pelo total de valores

Como calcular a frequência de uma tabela?
Para calcular a frequência relativa, precisamos encontrar a frequência absoluta, que é o número de vezes que um dado apareceu, e dividi-la pelo total de dados obtidos.

Como calcular a frequência simples?
Para encontrar a frequência absoluta de um dado, basta contar quantas vezes ele se repetiu no conjunto, cada valor de variável possui a sua frequência absoluta dentro do conjunto.

Como saber o intervalo de classe?
Amplitude de uma classe, ou seja, diferença entre o maior valor (limite superior) e o menor valor (limite inferior) de uma classe. Em uma distribuição de freqüências que apresente classes de mesma largura, é a diferença entre quaisquer dois valores médios consecutivos.

Qual e a amplitude da amostra?
A amplitude de uma amostra é a diferença entre o valor máximo e o valor mínimo observados na amostra.

Questões resolvidas:
71) (MPE BA – FGV) A distribuição de frequências do número de apreensões de valores (em milhões R$) realizadas pela Polícia Federal, em determinado período, é conforme a seguir: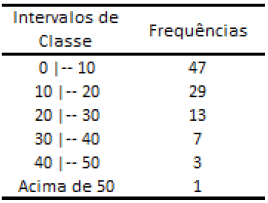
Assim sendo, é correto afirmar que:

(A) o último Decil está na penúltima classe;

(B) a mediana da distribuição está na 2ª classe;

(D) a moda exata da distribuição está na 1ª classe;

(E) a distribuição é assimétrica à esquerda.
Resolução
Analisando a tabela de distribuição de frequências, podemos constatar que existiram 100 apreensões no período em questão.
Quando ordenamos os valores, a mediana é o termo central. Se na primeira classe já temos 47 termos, e a segunda classe possui 29, é fácil concluir que a mediana está na segunda classe.
Alternativa B

72) (SUDAM AM – IADES) Em 20 dias de aula, um professor de estatística anotou o número de alunos ausentes. Depois, fez a seguinte tabela de frequências: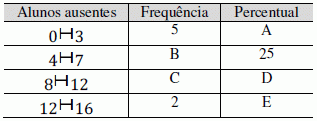
A letra B representa o número

(A) 5.

(B) 6.

(D) 8.

(E) 9.
Resolução
Analisando a segunda classe, temos que B representa 25% da quantidade de dias de aula.
Como o professor fez a pesquisa durante 20 dias, temos que B = 5.
Alternativa A

73) (INEP – IBFC) Seja x a variável discreta “número de carros” de 20 pessoas e considerando a distribuição abaixo: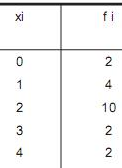
A média contínua do número de carros é:

(A) 1,8

(B) 1,9

(D) 3,0

(E) 3,6
Resolução
Calculando a média, que pode ser encarada como uma média ponderada:
0 . 2 = 0
1 . 4 = 4
2 . 10 = 20
3 . 2 = 6
4 . 2 = 8
(0 + 4 + 20 + 6 + 8)/20 = 1,9
Alternativa B

74) (PM MG) Analise a tabela de distribuição de frequência abaixo:
TABELA: anos de serviço na PM, militares do 185º BPM, dezembro de 2017: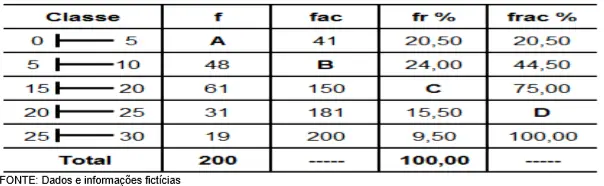
Sabe-se que f é a frequência absoluta, fac é a frequência absoluta acumulada, fr% é a frequência relativa (percentual) e frac% é a frequência relativa (percentual) acumulada. Considerando as informações da tabela, é CORRETO afirmar que os valores de A, B, C, D, são respectivamente:

(A) 41; 89; 30,50; 90,50.

(B) 48; 89; 30,50; 25,00.

(C ) 41; 61; 25,00; 90,50.

(D) 48; 79; 44,50; 90,50.
Resolução
Na coluna 2, que apresenta a frequência absoluta f, podemos verificar que a frequência absoluta total é igual a 200. Temos:
A + 48 + 61 + 31 + 19 = 200
A + 159 = 200
A = 200 – 159
A = 41
Podemos calcular o valor de B através da soma das frequências absolutas das duas primeiras classes.
B = 41 + 48 = 89
C é o percentual da terceira classe.
61 / 200 = 0,305 = 30,5%
D é o percentual acumulado nas 4 primeiras classes, ou seja, basta subtrair de 100% o percentual da última classe.
100% – 9,5% = 90,5%.
Alternativa A

75) Uma pesquisa foi realizada sobre a quantidade de acessos aos sites A, B, C e D, de segunda-feira até sexta-feira:
Site A
Segunda-feira: 80 acessos
Terça-feira: 60 acessos
Quarta-feira: 40 acessos
Quinta-feira: 100 acessos
Sexta-feira: 50 acessos

Site B
Segunda-feira: 100 acessos
Terça-feira: 50 acessos
Quarta-feira: 60 acessos
Quinta-feira: 20 acessos
Sexta-feira: 80 acessos

Site C
Segunda-feira: 30 acessos
Terça-feira: 100 acessos
Quarta-feira: 70 acessos
Quinta-feira: 40 acessos
Sexta-feira: 60 acessos

Site D
Segunda-feira: 40 acessos
Terça-feira: 60 acessos
Quarta-feira: 30 acessos
Quinta-feira: 40 acessos
Sexta-feira: 80 acessos

Analisando esses dados coletados, podemos afirmar que:
I → A frequência absoluta de acessos a todos os sites na segunda feira é de 250.
II → A frequência absoluta de acessos ao site D é de 220.
III → A frequência absoluta de acessos na sexta feira é de 270.
Marque alternativa correta:

(A) Somente a I é verdadeira.

(B) Somente a II é verdadeira.

(D) Somente a II é falsa.

(E) Somente a III é falsa.
Resolucao
I → Verdadeira
Realizando a soma dos acessos na segunda-feira, temos:
80 + 100 + 30 + 40 = 250
II → Falsa
Somando o total de acessos, de segunda até sexta, ao site D:
40 + 60 + 30 + 40 + 80 = 250
III → Verdadeira
Somando o total de acessos, na sexta-feira, aos sites A, B, C e D:
50 + 80 + 60 + 80 = 270
Alternativa D

76) A estatura dos estudantes da 2ª série do Ensino Médio de uma escola está descrita na lista a seguir:
1,66     1,60     1,61    1,50    1,62     1,60     1,65
1,67     1,64     1,60    1,62    1,61     1,68     1,63
1,56     1,73     1,60    1,55    1,64     1,68     1,55
1,52     1,59     1,63    1,60    1,55     1,55     1,69
1,51     1,66     1,70    1,64    1,54     1,61     1,56
1,72     1,53     1,57    1,56    1,58     1,58     1,61
De acordo com os dados encontrados, podemos afirmar que:

(A) Há 7 pessoas com altura superior a 1,67.

(B) A frequência absoluta da altura de 1,55 é 4.

(D) A frequência absoluta de alturas menores que 1,60 é 14.
Resolucao
Para resolver, primeiro colocaremos os dados em ordem para facilitar a análise das alternativas:
1,50     1,51    1,52    1,53    1,54     1,55     1,55
1,55     1,55    1,56    1,56    156      1,57     1,58
1,58     1,59    1,60    1,60    1,60     1,60     1,60
1,61     1,61    1,61    1,61    1,62     1,62     1,63
1,63     1,64    1,64    1,64    1,65     1,66     1,66
1,67     1,68    1,68    1,69    1,70     1,72     1,73
Com os dados em ordem, é mais fácil verificar que a frequência absoluta da altura de 1,55 é igual a 4, pois esse dado se repete 4 vezes.
Alternativa B

77) (Enem) Uma enquete, realizada em março de 2010, perguntava aos internautas se eles acreditavam que as atividades humanas provocam o aquecimento global. Eram três alternativas possíveis, e 279 internautas responderam à enquete, como mostra o gráfico: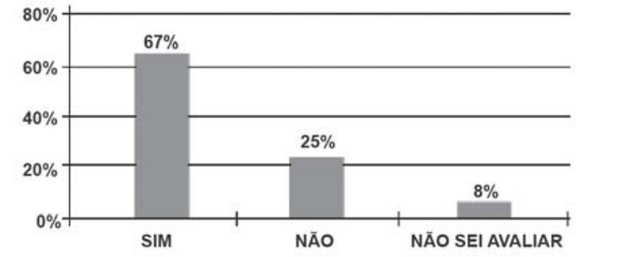
Analisando os dados do gráfico, quantos internautas responderam “NÃO” à enquete?

(A) Menos de 23.

(B) Mais de 23 e menos de 25.

(D) Mais de 100 e menos de 190.

(E) Mais de 200.
Resolucao
Para calcular a frequência absoluta dos que responderam “não”, basta calcular 25% de 279.
0,25 · 279 = 69,75
Analisando as alternativas, esse número é maior que 50 e menor que 75.
Alternativa C

78) Marque a alternativa que contém a definição correta da frequência absoluta:

(A) A frequência absoluta é uma frequência utilizada na probabilidade e que estuda a chance de um determinado evento acontecer.

(B) A frequência absoluta é uma porcentagem, utilizamo-la para saber qual é a porcentagem que aquele valor representa em relação ao todo.

(C) A frequência absoluta é o valor que mais se repetiu dentro de um conjunto de dados estatísticos. Para encontrá-la, contamos quantas vezes cada valor apareceu em um conjunto, e aquele valor mais frequente é conhecido como frequência absoluta.

(D) A frequência absoluta de um conjunto é uma frequência utilizada na estatística para a tomada de decisões. Para encontrar a frequência absoluta de um dado, basta contar quantas vezes ele se repetiu no conjunto. Cada valor de variável possui a sua frequência absoluta dentro do conjunto.

(E) A frequência absoluta é o valor absoluto de um conjunto de dados, representado pelo termo central desse conjunto. Utilizamos a frequência absoluta para tomar decisões na estatística.
Resolucao
A alternativa que descreve de forma correta o que é a frequência absoluta.
Alternativa D

79) (EEAR) A tabela apresenta as frequências acumuladas das notas de 70 alunos, obtidas em uma avaliação. A frequência absoluta da 2ª classe é: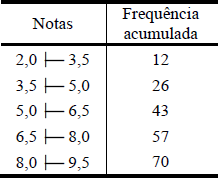
(A) 14

(B) 15

(D) 17
Resolucao
Para encontrar a frequência acumulada da 2ª classe, basta realizar a subtração entre a frequência acumulada da 2ª e da 1ª classe: 26 – 12 = 14.
Alternativa A

DIAGRAMA DE RAMOS E FOLHAS
Confira como fazer diagrama de Pareto em 5 passos:

- Defina seu objetivo.
- O primeiro passo para que se alcance bons resultados ao aplicar a metodologia de Pareto é definir claramente seu objetivo com ela. ...
- Faça o levantamento de dados. ...
- Categorize os problemas. ...
- Faça uma tabela com os dados.

O que significa ramos de folhas?
O ramo tem um significado de prosperidade, começo, novo e fases de mudanças. Em algumas estações do ano, os ramos ficam secos, mas todos sabem que meses após essa fase seca, novas folhas e flores irão surgir, trazendo um renascimento da vida.

Como criar caule?
Como criar um diagrama de caule e folhas O caule é tudo que está antes do último algarismo, e a folha é o algarismo final. Escreva os caules em uma coluna vertical e não pule os caules só porque eles não têm nenhum dado.

Como funciona o diagrama de Dispersão?
Esse tipo de diagrama traz números simultâneos das duas variáveis, deixando visível se o que acontece em uma variável causou interferência na outra. ... Ao estudar a correlação, você tem uma variável dependente Y (efeito), que se relaciona a variáveis independentes X (causas).

O que é um diagrama de caule e folhas?
Um diagrama de caule e folhas é uma tabela utilizada para organizar dados. O 'caule' está à esquerda e contém o primeiro algarismo ou os primeiros algarismos. A 'folha' está à direita e contém o último algarismo. Por exemplo, 5 podem ser representados juntos num diagrama de caule e folhas como 54 | 3,8.

Como funciona o caule?
O caule possui duas funções principais: suporte e condução de substâncias, mas também pode servir como reserva nutritiva. Condução: as substâncias produzidas nas folhas (seiva elaborada) são transportadas pelo caule, através do floema. Esses compostos são levados para todas as partes da planta, onde serão consumidos.

Como fazer um diagrama deramos e folhas?
Um diagrama de ramos e folhas é um dispositivo para apresentação de dados quantitativos em um formato gráfico, semelhante a um histograma, que ajuda a visual...

Qual a unidade de folha do diagrama?
Este diagrama ramo-e-folhas mostra os tempos de espera do cliente para um chat de serviço ao cliente on-line com um representante. A primeira linha tem um valor de ramo 8 e contém os valores de folha 0, 2 e 3. A unidade de folha é 1. Assim, a primeira linha do gráfico representa os valores de amostra de aproximadamente 80, 82 e 83.

Qual a diferença entre histograma e diagrama de Ramos?
Diferentemente dos histogramas, diagramas de ramos e folhas retêm os dados originais até no mínimo dois dígitos significantes e põem os dados em ordem, facilitando assim a inferência baseada em ordem e a estatística não paramétrica . Uma diagrama de ramos e folhas básico contém duas colunas separadas por uma linha vertical.

Qual é o nosso ramo de folhas?
Esse é o nosso gráfico Ramo-Folha! Se a gente tiver números muito grandes, os valores dos dados podem ser arredondados a uma casa que será usada para as folhas. Os dígitos que sobrarem à esquerda da casa à qual se arredondou são usados como o ramo.

Exemplo 1

Exemplo 2

QUESTOES RESOLVIDAS
80) (ABIN – CESPE) Considerando que o diagrama de ramos e folhas acima mostra a distribuição das idades (em anos) dos servidores de determinada repartição pública, julgue os itens subsequentes.
a) O primeiro quartil e o terceiro quartil são, respectivamente, 34 e 46 anos de idade.
Resolução
Temos aqui um diagrama de ramos e folhas onde os ramos representam as dezenas e as folhas representam as unidades das idades dos servidores.
As idades, em ordem crescente, são:
21, 22, 23, 26, 33, 34, 35, 37, 38, 41, 42, 46, 46, 49, 50, 52, 54, 55
Os quartis Q₁, Q₂ e Q₃ dividem os valores em quatro partes iguais:
Q₁ = 33
Q₂ = (38 + 41) / 2 = 39,5
Q₃ = 49
Resposta errada

b) A mediana das idades dos servidores é igual a 39,5 anos.
Resolução
A mediana é exatamente o valor do meio, quando todos os valores estão em ordem alfabética, ou a média dos dois valores do meio, quando a quantidade de termos é par.
Veja que a mediana já foi calculada é igual a Q₂ = 39,5 anos.
Resposta certa

81) (TJ AP – FCC) O diagrama de ramo e folhas a seguir corresponde às idades dos 40 funcionários de um setor de um órgão público em uma determinada data.
A soma da mediana e da moda destas idades é igual a

(A) 67,0

(B) 66,5

(D) 65,5

(E) 65,0
Resolução
Observe que o os ramos representam as dezenas e as folhas representam as unidades das idades dos 40 funcionários.
A mediana é o termo central. Como existem 40 idades, ela será a média dos 20º e 21º termos:
(34 + 34) / 2 = 34
A moda é a idade que aparece com maior frequência. Temos 4 funcionários com 33 anos.
Somando a mediana com a moda:
34 + 33 = 67
Alternativa A

82) (TRE PI – FCC) O diagrama de ramo e folhas abaixo corresponde às observações das idades de 50 eleitores escolhidos aleatoriamente em uma determinada zona eleitoral:

O valor do módulo da diferença entre a mediana e a moda destas idades observadas é

(A) 0

(B) 3

(D) 14

(E) 16
Resolução
Temos um diagrama de ramos e folhas que representa a idade de 50 pessoas.
Dispostas em ordem crescente, a mediana das idades é a média dos 25º e 26º termos:
(32 + 32) / 2 = 32
A moda é a idade que aparece com maior frequência. Temos 4 eleitores com 46 anos.
Calculando o módulo da diferença (o maior pelo menor):
46 – 32 = 14
Alternativa D

ANOVA
Análise da Variância (ANOVA) é um método para testar a igualdade de três ou mais médias populacionais, baseado na análise das variâncias amostrais. Os dados amostrais são separados em grupos segundo uma característica (fator).

Para que serve a tabela ANOVA?
A Análise de Variância ( ANOVA ) é uma fórmula estatística usada para comparar as variâncias entre as medianas (ou médias) de grupos diferentes. Diversos cenários usam ANOVA para determinar se há alguma diferença entre as medianas dos diferentes grupos

Como interpretar a tabela da ANOVA?
Um nível de significância de 0,05 indica que o risco de se concluir que existe uma diferença, quando, na verdade, não existe nenhuma diferença real, é de 5%. Se o valor-p for menor ou igual ao nível de significância, rejeite a hipótese nula e conclua que nem todas as médias da população são iguais.

Para que fins e utilizado um teste de Análise de Variância?
Análise de variância é a técnica estatística que permite avaliar afirmações sobre as médias de populações. A análise visa, fundamentalmente, verificar se existe uma diferença significativa entre as médias e se os fatores exercem influência em alguma variável dependente.

O que preciso ter para usar ANOVA
Os resíduos (observação menos a média) devem ser normais ou próximos da normalidade. Para verificar se suas dados são normais, clique aqui.

- As variâncias de cada amostra devem ser iguais. ...
- As amostras devem ser independentes.

O que significa valor de p menor que 0 05?
Na maioria das análises, um alfa de 0.05 é usado como ponto de corte para significância. Se o valor-p for menor que 0.05, devemos rejeitar a hipótese nula de que não há diferença entre as médias e concluir que existe uma diferença significativos.

Como interpretar os resultados da ANOVA?
Tomando como base a tabela anterior, pode-se concluir que existe pelo menos dois professores com alunos com desempenho significativamente diferentes ao avaliar o valor-p = 0,010 (menor que o nível de significância estabelecido de 0,05).

RESOLVIDOS SOBRE ANOVA
83) (CESPE-ABIN) Julgue o próximo item, acerca de análise de variância ANOVA.
A ANOVA consiste em teste de hipótese para avaliar se os diferentes tratamentos de um experimento produzem as mesmas variâncias com relação a determinada variável resposta Y.
Resolução
A ANOVA testa média e não variância. O teste verifica se as médias as médias de duas ou mais populações são iguais. A hipótese nula afirma que todas as médias de população são iguais, enquanto a hipótese alternativa afirma que pelo menos uma é diferente.
Resposta Errada

84) (CESPE – ABIN) Julgue o próximo item, acerca de análise de variância ANOVA.
A ANOVA consiste em teste de hipótese para avaliar se os diferentes tratamentos de um experimento produzem as mesmas variâncias com relação a determinada variável resposta Y.
Resolucao
A ANOVA testa média e não variância. O teste verifica se as médias as médias de duas ou mais populações são iguais. A hipótese nula afirma que todas as médias de população são iguais, enquanto a hipótese alternativa afirma que pelo menos uma é diferente.
Resposta errada

DISTRIBUIÇÃO DE POISSON
A distribuição de Poisson é utilizada para descrever a probabilidade do número de ocorrências em um intervalo contínuo (de tempo ou espaço). No caso da distribuição binomial, a variável de interesse era o número de sucessos em um intervalo discreto (n ensaios de Bernoulli). Ela descreve resultados de experiências nos quais contamos acontecimentos que ocorrem aleatoriamente mas a uma taxa média definida.

85) (RFB – Esaf) O número de petroleiros que chegam a uma refinaria ocorre segundo uma distribuição de Poisson, com média de dois petroleiros por dia. Desse modo, a probabilidade de a refinaria receber no máximo três petroleiros em dois dias é igual a: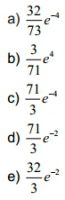

Resolução
Observe abaixo a fórmula para se determinar a probabilidade de um dado número X de sucessos em uma distribuição de Poisson. Onde e = 2,71828… é a constante de Euler.

A média é de dois petroleiros por dia. Obviamente, a cada dois dias, teremos uma média de 4 petroleiros, logo λ=4.
Calculando a probabilidade da plataforma receber no máximo 3 petroleiros em 2 dias:
P(X ≤ 3) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)

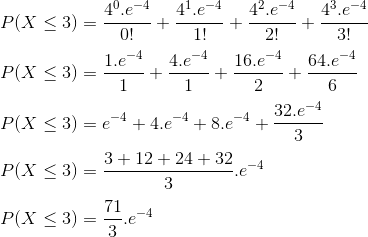
Alternativa C

86) (ANAC – Esaf) Uma distribuição Binomial pode ser aproximada por uma distribuição de Poisson, quando a probabilidade do evento é pequena de ocorrer e a população considerada é relativamente grande. Assuma esta aproximação para o problema descrito a seguir. Considere que passageiros chegam a um aeroporto a uma taxa média de três passageiros por segundo. Pede-se para determinar, com uma boa aproximação, qual a probabilidade (P) de que não mais de dois passageiros chegarão ao aeroporto em um intervalo de um segundo (caso seja necessário, use o valor de e = exp(1) = 2,72).

(A) P = 0,28.

(B) P = 0,22.

(D) P = 0,25.

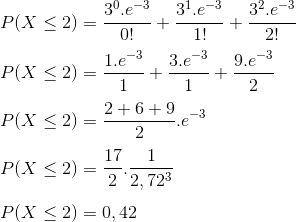Alternativa E

87) (SEFAZ PI – FCC) O número de falhas mensais de um computador é uma variável que tem distribuição de Poisson com média λ. Sabe-se que λ é igual à média de uma distribuição uniforme no intervalo [2, 4]. Nessas condições, a probabilidade de o computador apresentar exatamente duas falhas no período de 15 dias é igual a:
Dados: e^-3 = 0,05; e^-1,5 = 0,22.

(A) 22,50%

(B) 12,50%

(D) 15,25%

(E) 24,75%
Resolução
A média de uma distribuição uniforme no intervalo [a, b] é a média aritmética dos valores a e b. Assim, a média da distribuição uniforme no intervalo [2, 4] é dada por:
(2 + 4)/2 = 3
Veja que o valor encontrado corresponde ao período de um mês, ou seja, a média de falhas a cada 15 dias é igual a 1,5.
Como a questão pede a probabilidade do computador apresentar exatamente duas falhas no período de 15 dias, utilizaremos a fórmula da distribuição de Poisson, onde λ = 1,5 e X = 2:

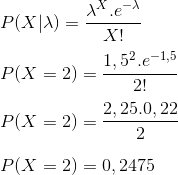Alternativa E

88) (SEFAZ PE – FCC) Para resolver a questão abaixo, considere as informações a seguir:
Se Z tem distribuição normal padrão, então:
P(Z < 1,64) = 0,950; P(Z < 2,05) = 0,98; P(Z < 2,24) = 0,987; P(Z < 2,40) = 0,992.
Suponha que o número de pedidos de empréstimos que um banco recebe por dia seja uma variável com distribuição de Poisson com média de λ pedidos por dia. Sabe-se que o parâmetro λ satisfaz à equação P(X < λ) = 0,008, onde X é uma variável aleatória que tem distribuição normal com média 15 e variância 25. Nessas condições, a probabilidade de o banco receber, em um dia qualquer, exatamente 4 pedidos de empréstimo
Dados: e^-3 = 0.05; e^-4 = 0,018

(A) está compreendida entre 20% (inclusive) e 22% (exclusive).

(B) é maior do que 25%.

(D) está compreendida entre 16% (inclusive) e 18% (exclusive).

(E) está compreendida entre 18% (inclusive) e 20% (exclusive).
Resolução
Sabendo que temos uma distribuição normal padrão, com P(Z < 2,40) = 0,992, podemos concluir que P(Z < -2,40) = 0,008).
Como a variância é igual a 25, podemos concluir que o desvio padrão é igual a 5.
Z = (λ – μ)/σ
-2,40 = (λ – 15)/5
-12 = λ – 15
λ = 3

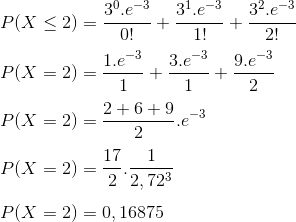Alternativa D

89) (ANAC-Esaf) Uma distribuição Binomial pode ser aproximada por uma distribuição de Poisson, quando a probabilidade do evento é pequena de ocorrer e a população considerada é relativamente grande. Assuma esta aproximação para o problema descrito a seguir. Considere que passageiros chegam a um aeroporto a uma taxa média de três passageiros por segundo. Pede-se para determinar, com uma boa aproximação, qual a probabilidade (P) de que não mais de dois passageiros chegarão ao aeroporto em um intervalo de um segundo (caso seja necessário, use o valor de e = exp(1) = 2,72).

(A) P = 0,28.

(B) P = 0,22.

(D) P = 0,25.

(E) P = 0,42.
Resolução
A questão pede a probabilidade de chegarem não mais de 2 passageiros em um intervalo de um segundo, assim, utilizaremos a fórmula da distribuição de Poisson para calcular a probabilidade de chegarem até 2 passageiros em um intervalo de um segundo.
P(X ≤ 2) = P(X = 0) + P(X = 1) + P(X = 2)
Alternativa E

90) (CESPE - Analista de Correios – Estatístico) Uma cadeia de Markov é denominada irredutível (ou ergódica) caso qualquer estado possa ser transformado em qualquer outro estado, não necessariamente em um único passo. Uma cadeia de Markov com matriz de transição P é regular caso exista um número inteiro positivo n tal que todos os elementos da matriz potência Pⁿ sejam estritamente positivos.
Julgue o seguinte item a respeito desses conceitos.
“O dígrafo abaixo representa uma cadeia de Markov regular.”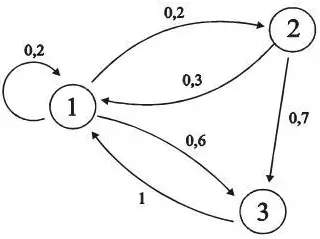
Resolução
O dígrafo pode ser representado pela seguinte matriz de transição:
Tem dúvidas acerca da formação da matriz de transição?
Note que o elemento p₂₃ é igual a probabilidade de chegar em 3, saindo de 2.
Por definição, uma cadeia de Markov é regular se existe um natural r₀ tal que para todo r ≥ r_0, (p_ij)^r > 0, ∀i,j∈S. Ou seja, se existe uma potência de P com todas as entradas positivas.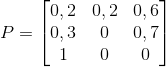

Resposta certao

91) (CNJ – CESPE – Analista Judiciário) A população de um país é dividida em classes alta (A), média (M) e baixa (B). Um estudo estatístico mostra que, atualmente, 10% da população pertence à classe A, 40% à classe M e 50% à classe B. Considera-se um modelo simplificado para as mudanças de classes, na forma de uma cadeia de Markov, em que as mudanças de uma geração para a próxima acontecem de acordo com a seguinte matriz de transição: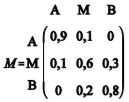
Assim, por exemplo, as probabilidades dos filhos de uma família da classe M pertencerem às classes A, M ou B são iguais a 10%, 60% e 30%, respectivamente.
Com base nessa situação hipotética, julgue os itens subsequentes.

a) Se o modelo descrito valer por tempo indeterminado, então as proporções das classes A, M e B tenderão para as probabilidades estacionárias 2/7, 2/7 e 3/7, respectivamente.
Resolução
Sejam a, m e b as probabilidades estacionárias referentes as classes A, M e B.
As probabilidades dos filhos de uma família da classe A pertencerem às classes A, M ou B são iguais a 90%, 10% e 0%, respectivamente.
a = 0,9a + 0,1m
As probabilidades dos filhos de uma família da classe M pertencerem às classes A, M ou B são iguais a 10%, 60% e 30%, respectivamente.
m = 0,1a + 0,6m + 0,2b
As probabilidades dos filhos de uma família da classe B pertencerem às classes A, M ou B são iguais a 0%, 30% e 80%, respectivamente.
b = 0,3m + 0,8b
Temos também que:
a + m + b = 1
O nosso objetivo será resolver o sistema de equações abaixo:
a = 0,9a + 0,1m (I)
m = 0,1a + 0,6m + 0,2b (II)
b = 0,3m + 0,8b (III)
a + m + b = 1 (IV)
Manipulando as equações I, II e III:
a – m = 0
a – 4m + 2b = 0
3m – 2b = 0
a + b + m = 1
Como o nosso objetivo é estudar as Cadeias de Markov, a resolução do sistema linear será omitida.
Temos:
a = 2/7
m = 2/7
b = 3/7
Resposta certa

b) Na próxima geração, 13% da população pertencerá à classe A, 35% à classe M e 52% à classe B.
Resolução
Resolveremos a questão analisando agora as colunas da matriz de transição.
As colunas 1, 2 e 3 nos informam as chances de um indivíduo da próxima geração pertencer às classes A, M e B. Utilizaremos a informação do enunciado, que diz “atualmente, 10% da população pertence à classe A, 40% à classe M e 50% à classe B”
Classe A (coluna 1):
0,9 . 10% + 0,1 . 40% + 0 . 50% = 9% + 4% + 0% = 13%
Classe M (coluna 2):
0,1 . 10% + 0,6 . 40% + 0,2 . 50% = 1% + 24% + 10% = 35%
Classe B (coluna 3):
0 . 10% + 0,3 . 40% + 0,8 . 50% = 0% + 12% + 40% = 52%
Resposta certa

c) Na hipótese de que o modelo tenha sido válido para a formação da geração atual, então as classes A, M e B na geração anterior eram formadas por 5%, 30% e 65% da população, respectivamente.
Resolução
A resolução do item c é praticamente igual ao item b, a diferença é que agora nós queremos saber a geração anterior, e não a próxima.
Sejam x, y e z os valores referentes as classes A, M e B na geração anterior, e 0,1, 0,4 e 0,5 os valores referentes a geração atual.Classe A (coluna 1):
0,9x + 0,1y + 0z = 0,1
Classe M (coluna 2):
0,1x + 0,6y + 0,2z = 0,4
Classe B (coluna 3):
0x + 0,3y + 0,8z = 0,5
O nosso objetivo será verificar se {5%, 30%, 65%} é a solução do sistema abaixo.
0,9x + 0,1y = 0,1
0,1x + 0,6y + 0,2z = 0,4
0,3y + 0,8z = 0,5
Basta analisarmos a primeira equação para termos certeza que {5%, 30%, 65%} não é o conjunto solução.
Resposta errada

92) O Procedimento de perda rápida de "peso" é comum entre os atletas dos esportes de combate. Para participar de um torneio, quatro atletas da categoria até 66 kg, Peso-Pena, foram submetidos a dietas balanceadas e atividades físicas. Realizaram três "pesagens" antes do início do torneio. Pelo regulamento do torneio, a primeira luta deverá ocorrer entre o atleta mais regular e o menos regular quanto aos "pesos". As informações com base nas pesagens dos atletas estão no quadro.

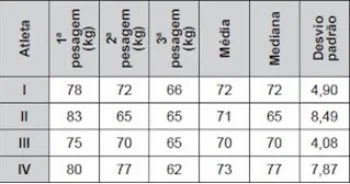
Após as três "pesagens", os organizadores do torneio informaram aos atletas quais deles se enfrentariam na primeira luta.

A primeira luta foi entre os atletas

(A) I e III.

(B) I e IV.

(D) II e IV.

(E) III e IV

Resolução:

Para encontrar os atletas mais regulares usaremos o desvio padrão, pois essa medida indica o quanto que o valor desviou da média.

O atleta III é o com menor desvio padrão (4,08), logo é o mais regular. O menos regular é o atleta II com maior desvio padrão (8,49).

Alternativa: C

93) (ENEM – 2012) Um produtor de café irrigado em Minas Gerais recebeu um relatório de consultoria estatística, constando, entre outras informações, o desvio padrão das produções de uma safra dos talhões de sua propriedade. Os talhões têm a mesma área de 30 000 m² e o valor obtido para o desvio padrão foi de 90 kg/talhão. O produtor deve apresentar as informações sobre a produção e a variância dessas produções em sacas de 60 kg por hectare (10 000 m²). A variância das produções dos talhões expressa em (sacas/hectare)² é:

(A) 20,25

(B) 4,50

(D) 0,50

(E) 0,25.

Resolução:

Como a variância deve estar em (sacas/hectare)² , precisamos transformas as unidades de medidas.

Cada talhão tem 30 000 m² e cada hectare tem 10 000 m², assim devemos dividir o desvio padrão por 3. Encontramos o valor de 30 kg/hectare. Como a variância é dada em sacas de 60 kg por hectare então temos que o desvio padrão será de 0,5 sacas/hectare. A variância será igual a (0,5)² .

Alternativa: E

94) (ENEM – 2010 - Marco e Paulo foram classificados em um concurso. Para classificação no concurso o candidato deveria obter média aritmética na pontuação igual ou superior a 14. Em caso de empate na média, o desempate seria em favor da pontuação mais regular. No quadro a seguir são apresentados os pontos obtidos nas provas de Matemática, Português e Conhecimentos Gerais, a média, a mediana e o desvio padrão dos dois candidatos.
Dados dos candidatos no concurso

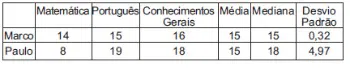
O candidato com pontuação mais regular, portanto mais bem classificado no concurso, é

(A) Marco, pois a média e a mediana são iguais.

(B) Marco, pois obteve menor desvio padrão.

(D) Paulo, pois obteve maior mediana.

(E) Paulo, pois obteve maior desvio padrão.

Resolução:

Como a média de Marco e Paulo foram iguais, o desempate será feito pelo menor valor do desvio padrão, pois é o que indica pontuação mais regular.

Alternativa: B

Continua...

topo