EM - NUMEROS COMPLEXOS

Professor Diminoi

NUMEROS COMPLEXOS

Introducao
Vamos considerar a equação x² - 2x + 5 = 0:
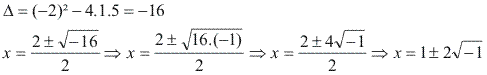
Sabemos que o número √-1não pertence ao conjunto dos números reais, pois não existe nenhum número que elevado ao quadrado resulte em -1.

Para que a equação acima tenha solução, temos que estender o conjunto dos números reais para obter um novo conjunto, chamado de conjunto dos números complexos e representado por C.
O número √-1, foi denominado unidade imaginária e criou-se o número i, de modo que:
i² = -1
Logo, i = √-1, p-rtanto, as soluções da equação x² - 2x + 5 = 0 em C são 1 - 2i e 1 + 2i.

Forma algébrica de um número complexo
Todo número complexo z pode ser escrito na forma:
z =  a + bi, com a, b (pertente aos reais)

Essa forma é chamada forma algébrica do número complexo.
Observe que um número complexo nesse formato tem duas partes:
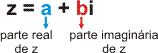Indicamos:
Re(z) = a
Im(z) = b

Exemplos
z =  3 + 5i             Re(z) = 3 e Im(z) = 5
z = -7 +18i            Re(z) = -7 e Im(z) = 18
z = 53 – 25i          Re(z) = 53 e Im(z) = -25

Se a parte real do número complexo é nula, então o número é imaginário puro.

Exemplo: z = 3i    Re(z) = 0 e Im(z) = 3

Exemplo
Determine o valor de k para que o número complexo z = (k – 4) +3i seja imaginário puro:
Resolução
Para que o número seja imaginário puro, a parte real deve ser nula:
k – 4 = 0 
k = 4
Se a parte imaginária do número complexo é nula, então o número é real.

Exemplo: z = 10   Re(z) = 10 e Im(z) = 0
Exemplo
Determine o valor de k para que o número complexo z = 3 + (k² – 4)i seja um número real:
Resolução
Para que o número seja real, a parte imaginária deve ser nula:
k² – 4 = 0   k² = 4 
k = -2 ou k = 2

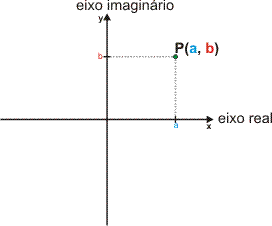
Podemos associar  qualquer número complexo z = a + bi a um ponto no plano de Argand-Gauss. No eixo das abscissas (eixo real,) representa-se a parte real, e, no eixo das ordenadas (eixo imaginário), a parte imáginária do número complexo.

O ponto P é o afixo ou imagem geométrica de z.
Exemplo
Represente no plano de Argand-Gauss os números complexos:
Resolução
Cada complexo será um ponto no plano cuja abscissa é a parte real e a ordenada é a parte imaginária:
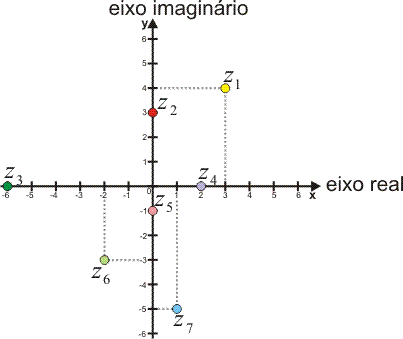
Note que os números reais estão localizados sobre o eixo real, assim como os números imaginários puros estão sobre o eixo imaginário.

Observação: Não é definida para o campo dos números complexos a relação de ordem, isto é, não existe um número complexo maior ou menor que outro.

Igualdade de números complexos
Dois números complexos são iguais quando suas partes reais e imaginárias forem respectivamente iguais.

Exemplo
Determine x e y, de modo que: (2x + y) + 6i = 5 + (x + 4y)i.
Resolução


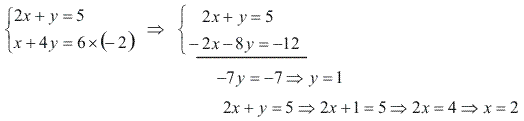
Conjugado de um número complexo
Sendo z = a + bi, define-se como conjugado de z o complexo z = a – bi, ou seja:
z = a + bi 
z = a – bi

Na prática, para se obter o conjugado de um número complexo, trocamos o sinal do coeficiente da parte imaginária.

Exemplos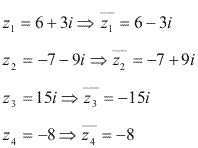


 

 

 

 

Geometricamente, podemos observar que dois números complexos conjugados têm, respectivamente, partes reais iguais e partes imaginárias simétricas.

Exemplo
z = 5 + 2i e seu conjugado z= 5 -2i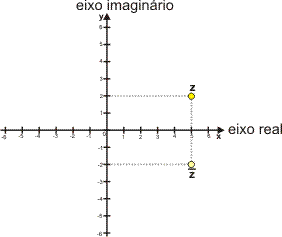

Adição e subtração de números complexos na forma algébrica

Adição
Considerando-se os complexos: z₁ = a + bi e z₂ = c + di, a soma, a soma z₁ + z₂ é obtida somando-se suas partes reais e imaginárias separadamente:
z1 + z₂ = (a + c) + (b + d)

Exemplos
a) (2 + 3i) + (5 + 4i) = (2+5) + (3 + 4)i = 7 + 7i
b) 2i + (6 + 9i) = (0 + 6) + (2 + 9)i = 6 + 11i
c) (5 + 3i) + 3 = (5 + 3) + (3 + 0)i = 8 + 3i

Subtração
Dados os complexos z₁ = a + bi e z₂ = c + di, a diferença z₁ – x₂ é obtida subtraindo-se suas partes reais e imaginárias separadamente:
Z₁ – z₂ = (a – c) + (d – b)

Exemplos
a) (2 + 3i) - (5 + 4i) = (2 - 5) + (3 - 4)i = -3 - i
b) 2i - (6 - 9i) = (0 - 6) + (2 -(-9))i = -6 + 11i
c) (5 + 3i) - 3 = (5 - 3) + (3 - 0)i = 2 + 3i

Multiplicação e divisão de números complexos na forma algébrica

Multiplicação
Dados os complexos: z₁ = a + bi e z₂ = c + di o produto z₁ . z₂  é obtido de acordo com a regra da multiplicação de binômios e sabendo-se que i² = -1:
z₁ . z₂ = (ac – bd) + (ad + bc)i


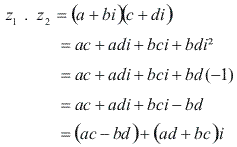
Exemplos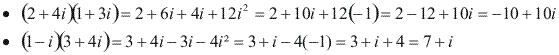


Divisão
Dados os complexos z₁ = a + bi e z₂ = c + di, o quociente
E obtido multiplicando-se ambos os termos da fração pelo conjugado do denominador.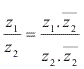
Justificativa:
Multiplicando o numerador e o denominador pelo mesmo número complexo, o valor de
Não se altera. Além disso, note que o denominador
E um número real:
Desta maneira, podemos obter a forma algébrica de
Exemplos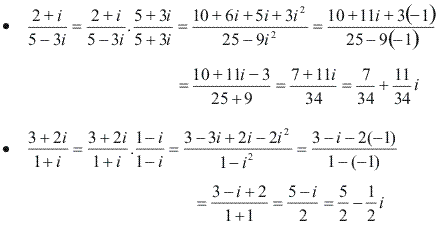


 

 

 

 

 

 


Potências de i
Vamos calcular algumas potências de i:

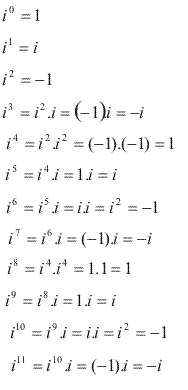
Note que os resultados repetem-se de 4 em 4. Então podemos escrever: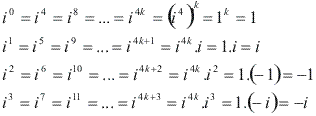

Portanto, para calcular potências de i, basta dividir o expoente de i por 4 e considerar apenas i elevado ao resto dessa divisão.

Exemplos


 

 

 

 

 

 

 

 

 

 

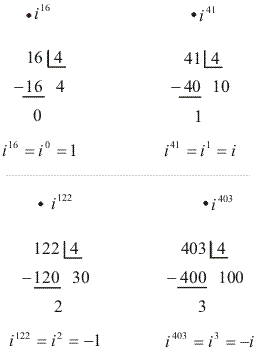
Módulo e argumento de um número complexo
Considere o número complexo z = a + bi e o ponto P que o representa.
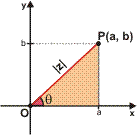
A distância de P até a origem é denominada módulo de z, e representada por [z]. Do triângulo retângulo destacado temos:
A medida do ângulo  , formado por OP com o eixo das abscissas, medido no sentido anti-horário, é denominada argumento do complexo z. Note que
Indica-se:
= arg(z)
 Note que:
 e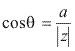 
Exemplo
Determine o módulo e o argumento de z = √3 +i
Resolução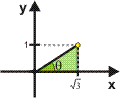
Módulo
Argumento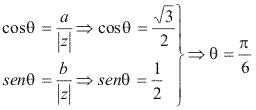


Forma trigonométrica ou polar
Considere o número complexo z = a + bi, de módulo [z] e argumento  .
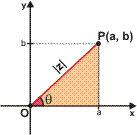Temos que: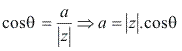
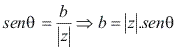Substituindo em z = a + bi, temos:
Essa expressão é denominada forma trigonométrica ou polar do complexo z.

Exemplo
Escreva na forma trigonométrica o número complexo z = 1 + i:
Resolução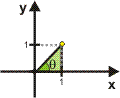



Módulo:

Argumento:


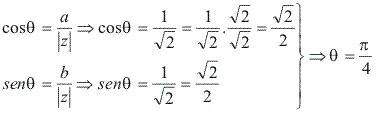
Portanto, z pode ser escrito na forma trigonométrica:
Exemplo
Escreva na forma trigonométrica o número complexo z = 8i:
Resolução

Módulo:
Argumento: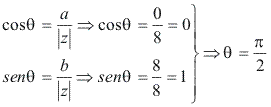

Portanto, z pode ser escrito na forma trigonométrica:

Exemplo 3
Escreva na forma algébrica o número complexo
Resolução
Essa transformação é imediata, pois basta substituir
e
Pelos respectivos valores: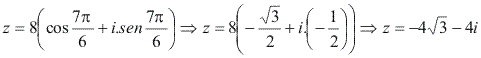


Multiplicação e divisão de números complexos na forma trigonométrica
Algumas operações com números complexos são mais facilmente efetuadas quando os números estão na forma trigonométrica.
Acompanhe a seguir como funcionam as operações de multiplicação de divisão.

Multiplicação
Considere dois números complexos na forma trigonométrica
O produto z₁ . z₂ é dado por:


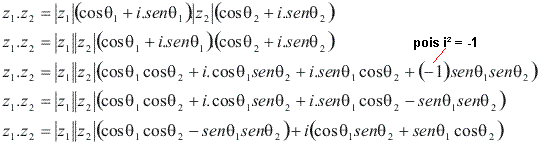
Lembrando das fórmulas de adição de arcos:

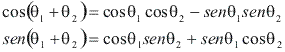
Assim:
Observe que o produto z₁ . z₂   é um número complexo cujo módulo é o produto dos módulos dos fatores e cujo argumento é a soma dos argumentos dos fatores.

Exemplo
Calcule o produto z₁ . z₂  , com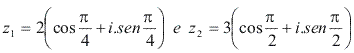
Resolução
O módulo de z₁ . z₂  é  produto 
O argumento de z₁ . z₂   é dado pela soma
Assim:

Divisão
Considere dois números complexos na forma trigonométrica:
O quociente
E dado por:

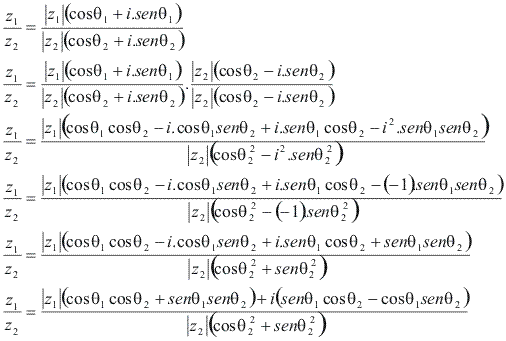
Lembrando das fórmulas de diferença de arcos:
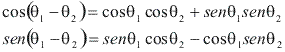
E da relação trigonométrica fundamental:
Assim:
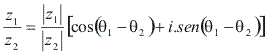Observe que o quociente

E um número complexo cujo módulo é o quociente dos módulos do dividendo e do divisor, e cujo argumento é a diferença  dos argumentos do dividendo e do divisor.

Exemplo
Calcule o quociente
Com
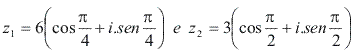Resolução
O módulo de
E o quociente
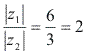O argumento de
E dado pela diferença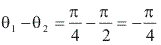

Como

Fazemos:

Assim: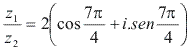


 
Potenciação e radiciação de números complexos na forma trigonométrica
Potenciação
Sendo
E n um número inteiro maior que 1, temos: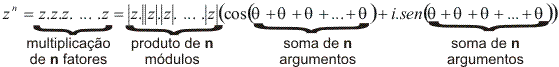
Assim:
Essa fórmula é conhecida como 1ª fórmula de Moivre.

Exemplo
Calcule
Vamos considerar
Para posteriormente calcularmos z⁶. Para aplicar a 1ª fórmula de Moivre, precisamos calcular o módulo e o argumento de z.

Módulo
Argumento

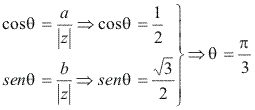
Calculando z⁶: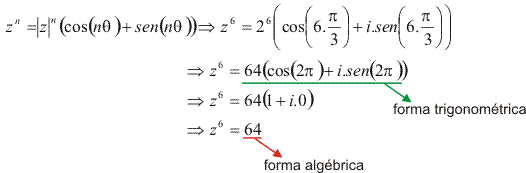


Radiciação
Se
Suas raízes enésimas são dadas por: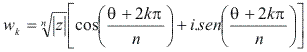
Essa expressão é conhecida como 2ª fórmula de Moivre.

Exemplo
Determine as raízes cúbicas de z = 8.
Resolução
Vamos calcular o módulo e o argumento de z para a aplicação da 2ª fórmula de Moivre:
Módulo:
Argumento: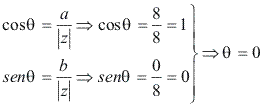 

As raízes cúbicas de 8 são dadas por:
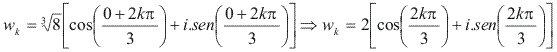
O número k pode assumir os valores 0, 1 e 2:

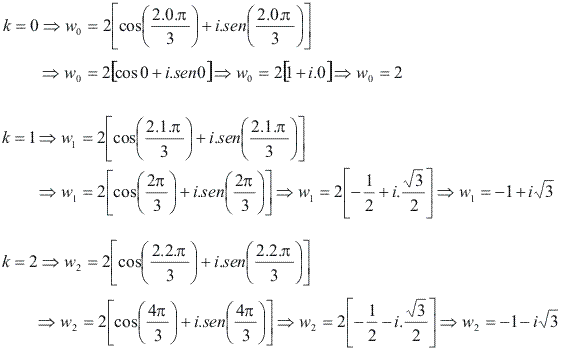
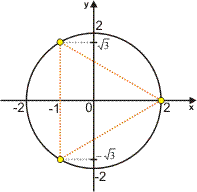
Geometricamente, note que as três raízes estão sobre uma circunferência de raio 2 e são vértices de um triângulo equilátero; seus argumentos formam uma PA, cujo primeiro termo é 0 e a razão é


Continua ...