Professor Diminoi

NÚMEROS NATURAIS

O conjunto dos Números Naturais é um conjunto numérico formado por 0, 1, 2, 3, 4, 5, …

Dizemos que esse conjunto é infinito positivamente, pois não há números negativos, decimais ou fracionários.

Esse conjunto é representado pelos símbolos.

Utilizamos a seguinte notação para representar o conjunto dos Números Naturais:

N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …}

Dentro do conjunto dos números naturais há subconjuntos tais como:

Conjunto dos números naturais não nulos:

N* = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …}

Conjunto dos números naturais pares:

P = {0 , 2, 4, 6, 8, 10, …}

Conjunto dos números naturais ímpares:

I = {1, 3, 5, 7, 9, 11, ...}"

Observação: se um número é inteiro e positivo, podemos dizer que é um número natural.

Quando o zero não faz parte do conjunto, é representado com um asterisco ao lado da letra N e, nesse caso, esse conjunto é denominado de Conjunto dos Números Naturais Não-Nulos: N* = {1, 2, 3, 4, 5, 6, 7, 8, 9...}.

Conjunto dos Números Naturais Pares = {0, 2, 4, 6, 8...}

Conjunto dos Números Naturais Ímpares = {1, 3, 5, 7, 9...}

Antecessor e sucessor

O conjunto de números naturais é infinito. Todos possuem um antecessor (número anterior) e um sucessor (número posterior), exceto o número zero (0).

Temos:

O antecessor de 1 é 0 e seu sucessor é o 2;

O antecessor de 2 é 1 e seu sucessor é o 3;

O antecessor de 3 é 2 e seu sucessor é o 4;

O antecessor de 4 é 3 e seu sucessor é o 5.

Cada elemento é igual ao número antecessor mais um, exceptuando-se o zero.

Assim, podemos notar que:

O número 1 é igual ao anterior (0) + 1 = 1;

O número 2 é igual ao anterior (1) + 1 = 2;

O número 3 é igual ao anterior (2) + 1 = 3;

O número 4 é igual ao anterior (3) + 1 = 4.

Número oposto ou simétrico

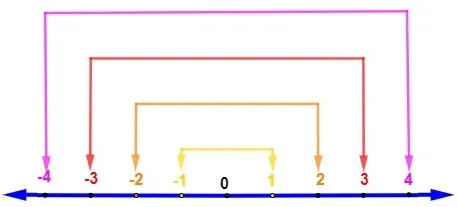
O número que está na mesma distância da origem da reta numérica é conhecido como oposto ou simétrico de um número. Seja n um número inteiro, o posto de n é igual a –n.

Módulo ou valor absoluto

O módulo ou valor absoluto de um número n, representado por |n|, é a distância que esse número tem até a origem, ou seja, a distância do número até o zero.

Na prática, podemos separar em dois casos:

Se n for positivo ou igual a zero, ou seja, n > 0 ou n = 0, então |n| é o próprio n.

Se n for negativo, ou seja, n < 0, então |n| é igual a –n.

Em resumo, se o número for negativo, o módulo será esse número só que positivo, e se ele for positivo, o módulo será o próprio número.

De modo geral, temos que:

|n| = n → se n for positivo.

|n|= –n → se n for negativo.

Exemplos

Quando n for positivo:

|0| = 0

|23| = 23

|5| = 5

|0,3| = 0,3

Quando n for negativo (aqui será feito de forma detalhada, para deixar claro a definição de módulo, mas esse calculo normalmente é feito de forma direta):

|–1| = – (–1) = 1

|–3| = – (–3) = 3

|–0,3| = – (–0,3) = 0,3

É importante entendermos a definição de módulo, porém, para calcular-se o módulo de um número negativo, esse cálculo pode ser feito de forma direta, apenas trocando-se o sinal do número.

Assim: |–2| = 2.

A função dos números naturais é contar e ordenar.

Nesse sentido, vale lembrar que os homens, antes de inventarem os números, tinham muita dificuldade em realizar a contagem e ordenação das coisas.

Segundo a história, essa necessidade começou com a dificuldade apresentada pelos pastores dos rebanhos em contarem suas ovelhas.

Assim, alguns povos antigos, desde os egípcios e babilônios, utilizaram diversos métodos, desde acumular pedrinhas ou marcar as ovelhas.

Exemplos de algumas propriedades dos números naturais:

Ordem: Os números naturais são ordenados, o que significa que podemos compará-los entre si.

Exemplo: 5 é maior que 3.

Adição: A adição de números naturais é sempre um número natural.

Exemplo: 5 + 3 = 8

Multiplicação: A multiplicação de números naturais é sempre um número natural.

Exemplo: 5 x 3 = 15

Primo e composto: um número natural é primo se tiver apenas dois divisores: 1 e ele mesmo. Caso contrário, é composto.

Comparação de dois números inteiros

Quando comparamos dois números inteiros, podemos separar quatro casos:

1. Comparando um número inteiro com o zero, sabemos que o zero é maior que qualquer número positivo e menor que qualquer número negativo.

0 > – 5 (Zero é maior que menos cinco)

–2 < 0 (Menos dois é menor que zero)

25 > 0 (Vinte e cinco é maior que zero)

0 < 10 (Zero é menor que dez)

2. Um número positivo é sempre maior que um número negativo, e um número negativo é sempre menor que um número positivo. 

Exemplos:

5 > – 8 (Cinco é maior que menos oito)

12 > – 4 (Doze é maior que menos quatro)

– 1 < 1 (Menos um é menor que um)

– 9 < 4 (Menos nove é menor que quatro)

3. Quando comparamos dois números positivos, o maior deles é o que está mais distante do zero.

Exemplos:

5 > 3 (Cinco é maior que três)

3 > 2 (Três é maior que dois)

4 < 9 (Quatro é menor do que nove)

20 < 50 (Vinte é menor que cinquenta.)

4. Quando comparamos dois números negativos, o maior deles é o que está mais próximo do zero.

Exemplos:

–12 < – 9 (Menos doze é menor que menos nove)

– 42 < – 30 (Menos quarenta e dois é menor que menos trinta)

– 1 > – 5 (Menos um é maior que menos cinco)

– 16 > – 20 (Menos dezesseis é maior que menos vinte)

QUESTÕES RESOLVIDAS

01) Sobre os números naturais, julgue as afirmativas a seguir:

I. Todo número natural possui sucessor.

II. Todo número natural possui antecessor.

III. O conjunto dos números naturais é infinito.

Marque a alternativa correta.

(A) Somente a afirmativa I é verdadeira.

(B) Somente a afirmativa II é verdadeira.

(C) Somente a afirmativa III é verdadeira.

(D) Somente a afirmativa I é falsa.

(E) Somente a afirmativa II é falsa.

Resolução:

I → Verdadeira. Para encontrar o sucessor de um número, basta somar 1 a ele.

II → Falsa, pois 0 é um  número natural e não possui antecessor.

III → Verdadeira. Como todo número possui sucessor, então, dado um número n, sempre existirá o número n + 1.

Alternativa: E

02) Analise os conjuntos a seguir e os relacione com os conjuntos descritos nas sentenças I, II e III.

A = {0,2,4,6,8,10…}

B = {1,3,5,7,9,11…}

C = {1,2,4,8}

I – Conjunto dos números ímpares

II – Conjunto dos divisores de 8

III – Conjunto dos números pares

Ao relacionar o conjunto com as sentenças, temos que:

(A) A – I; B – II; C – III.

(B) A – III; B – II; C – I.

(C) A – I; B – III ; C – II.

(D) A – III; B – I; C – II.

(E) A – II; B – I; C – III.

Resolução:

A – III. Note que o conjunto A é composto por todos os números pares.

B – I. Já o conjunto B é composto por todos os números ímpares.

C – II. Os números que compõem o conjunto C são os divisores de 8.

Alternativa: D

03) Lais é uma aluna muito dedicada e gosta muito de estudar Matemática. Durante a aula de operações básicas, ela decidiu criar a expressão numérica a seguir:

[2 × ( 6 – 2) + 10 ] – 15

Ao resolver a expressão, a resposta encontrada foi:

(A) 3, que é um número natural.

(B) 3, que não é um número natural.

(C) – 3, que é um número natural.

(D) – 3, que não é um número natural.

Resolução:

 [2 × ( 6 – 2) + 10 ] – 15

[2 × 4 + 10 ] – 15

[8 + 10 ] – 15

18 – 15

3

Alternativa: A

04) A quantidade de números naturais de três algarismos que podemos formar usando os algarismos 1, 2 e 3, sem repeti-los, é:

(A) 6 números.

(B) 5 números.

(C) 10 números.

(D) 4 números.

(E) 3 números.

Escrevendo todas as possibilidades, os números que podemos formar são:

123

132

213

231

312

321

Há seis possibilidades.

Alternativa: A

05) (Enem 2016) O ábaco é um antigo instrumento de cálculo que usa notação posicional de base dez para representar números naturais. Ele pode ser apresentado em vários modelos, um deles é formado por hastes apoiadas em uma base. Cada haste corresponde a uma posição no sistema decimal e nelas são colocadas argolas; a quantidade de argolas na haste representa o algarismo daquela posição. Em geral, colocam-se adesivos abaixo das hastes com os símbolos U, D, C, M, DM e CM que correspondem, respectivamente, a unidades, dezenas, centenas, unidades de milhar, dezenas de milhar e centenas de milhar, sempre começando com a unidade na haste da direita e as demais ordens do número no sistema decimal nas hastes subsequentes (da direita para esquerda), até a haste que se encontra mais à esquerda.

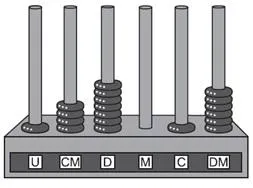
Entretanto, no ábaco da figura, os adesivos não seguiram a disposição usual.

Nessa disposição, o número que está representado na figura é:

(A) 46 171.

(B) 147 016.

(C) 171 064.

(D) 460 171.

(E) 610 741.

Resolução:

A ordem correta da direita para a esquerda seria:

Unidades (U) → 1

Dezenas (D) → 7

Centenas (C) → 1

Unidade de milhar (M) → 0

Dezenas de milhar (DM) → 6

Centenas de milhar (CM) → 4

Então, o número representado no ábaco é 460 171.

Alternativa: D

06) Dado o número 1000, o seu antecessor e o seu sucessor são, respectivamente:

(A) 900 e 1100.

(B) 990 e 1010.

(C) 1001 e 900.

(D) 999 e 1001.

(E) 1001 e 999.

Resolução:

O antecessor de 1000 é 1000 – 1 = 999.

O sucessor de 1000 é 1000 + 1 = 1001.

Alterntiva: D

07) A soma do sucessor de um número n com o antecessor de 35 é igual a 60. Então, podemos afirmar que o valor de  n é:

(A) 27.

(B) 26.

(C) 25.

(D) 24.

(E) 23.

Resolução:

O antecessor de 35 é 35 – 1 = 34.

Sabemos que 34 + n = 60, então n tem que ser igual a 26, pois 34 + 26 = 60. Como a questão quer o valor de n, então 26 – 1 = 25.

Alternativa: C

08) (FGV) Para motivar os alunos no aprendizado das operações com números naturais, o professor propôs aos alunos a seguinte brincadeira: ele escolhe um dos alunos voluntários para a brincadeira e pede que o aluno pense em um número natural de 10 a 99. A seguir, o professor pede para o aluno fazer, sucessivamente, as seguintes operações:

Somar 6 ao número pensado;

Multiplicar o resultado por 2;

Subtrair 10 do resultado obtido; e

Informar ao professor o valor encontrado.

Alguns segundos após, o professor “adivinha" o número pensado pelo aluno.

Mariana participa da brincadeira e, após efetuar as operações pedidas pelo professor, informa ter encontrado o número 62.

A soma dos algarismos do número pensado por Mariana é:

(A) 12

(B) 9

(C) 7

(D) 5

(E) 3

Resolução:

Para encontrar o número que a Mariana pensou inicialmente, basta realizar os passos feitos, mas fazendo a operação inversa.

O terceiro passo era subtrair 10 do resultado obtido. Vamos realizar a operação contrária, ou seja, somar 10 a 62.

62 + 10 = 72

O segundo passo era multiplicar por 2, logo vamos realizar a operação contrária, ou seja, dividir por 2.

72 : 2 = 36

O primeiro passo era somar 6, então, realizando a operação inversa, vamos subtrair 6.

36 – 6 = 30

O número pensado por Mariana foi 30. A soma dos seus algarismos é 3 + 0 = 3.

Alternativa: E

09) Sobre as operações com os números naturais, julgue as afirmativas a seguir:

I – A soma de dois números naturais sempre será um número natural.

II – A multiplicação entre dois números naturais sempre será um número natural.

III – A subtração entre dois números naturais sempre será um número natural.

IV – A divisão entre dois números naturais sempre será um número natural.

As afirmativas são, respectivamente:

(A) V, V, V, V.

(B) V, F, F, V.

(C) F, V, F, V.

(D) V, V, F, F.

(E) F, F, V, F.

Resolução:

I → Verdadeira.

II → Verdadeira.

III → Falsa, pois a subtração pode gerar um número inteiro como resposta, quando o minuendo é maior que o subtraendo.

IV → Falsa, pois a divisão pode não ser exata, gerando um número decimal como resposta.

Alternativa: D

10) As idades de Mariana, Maria Alice e Marcela são três números consecutivos. Sabendo que a soma desses números é igual a 48, qual é a idade da mais velha?

(A) 14

(B) 15

(C) 16

(D) 17

(E) 18

Resolução:

Seja n a idade da mais nova, sabemos que três idades consecutivas são n, n + 1 e n + 2, então:

n + n + 1 + n + 2 = 48

3n + 3 = 48

3n = 48 – 3

3n = 45

n = 45/3

n = 15

A mais nova possui 15 anos, e a mais velha, 15 + 2 = 17 anos.

Alternativa: D

11) Analise as afirmativas a seguir:

I – O conjunto {0,3,5,7,9,12} é composto somente por números naturais.

II – O conjunto { – 2, – 1, 0, 2, 3, 4} possui números naturais e números que não são naturais.

III – Todo número natural possui antecessor.

Marque a alternativa correta:

(A) Somente a I é verdadeira.

(B) Somente a II é verdadeira.

(C) Somente a III é verdadeira.

(D) Somente a I e III são verdadeiras.

(E) Somente a I e II são verdadeiras.

Resolução:

I → Verdadeira, pois todos os elementos do conjunto são números naturais.

II → Verdadeira, pois há números naturais e números que não são naturais no conjunto.

III → Falsa, pois zero é um número natural e não possui antecessor.

Alternativa: E

12) No dia 05, Kárita recebeu o seu salário, de R$ 3500,00. Nesse mesmo dia, ela pagou a escola do seu filho, que lhe custa R$ 615,00. Posteriormente, ela fez as compras do supermercado e gastou um total de R$ 555,00. Depois disso, no dia 10, ela pagou o condomínio, que custa R$ 310,00. Quanto ainda resta do seu salário?

(A) R$ 3000,00

(B) R$ 2020,00

(C) R$ 1950,00

(D) R$ 1860,00

(E) R$ 1710,00

Resolução:

3500 – 615 – 555 – 310 = 2020

Alternativa: B

13) Analise as expressões numéricas a seguir que envolvem números inteiros:

I. (– 3 + 4) × 2

II. (– 6 – 4) : 5

III. – 3 × (– 5) + 4

IV. 8 : (-2) – 1

Tem como resultado um número inteiro negativo:

(A) somente I.

(B) somente II.

(C) somente I e II.

(D) somente II e IV.

(E) somente III e IV.

Resolução:

I. (– 3 + 4) × 2 = 1× 2 = 2

II. (– 6 – 4) : 5 = – 10 : 5 = – 2

III. – 3 × (– 5) + 4 = +15 + 4 = 19

IV. 8 : (-2) – 1 = – 4 – 1 = – 5"

Alternativa: D

13) O senhor Venâncio tinha 230 ovelhas. O seu tio ofereceu-lhe mais 70 ovelhas. No total, quantas ovelhas o senhor Venâncio tem?

Resolução:

Já que o senhor Venâncio tinha 230 ovelhas e foram-lhe oferecidas 70 ovelhas. Neste caso, temos de somar as duas quantidades. Assim, temos:

230+70=300

Portanto, o senhor Venâncio tem 300 ovelhas.

14) O pai do José tem 43 anos e a mãe tem 34 anos. Qual é a diferença entre as idades dos pais?

Resolução:

Para determinar a diferença do pai e da mãe, basta subtrair as duas idades. Neste caso, temos:

43-34=9

Portanto, a diferença das idades é de 9 anos.

15) Na quadra festiva um avicultor vendeu no primeiro dia 3 centenas de ovos, no dia seguinte vendeu 7 dezenas e por fim vendeu 3 dezenas. Quantas centenas de ovos vendeu?

Resolução:

Primeiramente, vendeu-se 3 centenas de ovos: centena corresponde a 100. Logo, temos de calcular o produto de 3 x 100 = 300. Sendo assim , teremos 300 ovos;

Posteriormente, vendeu-se 7 dezenas de ovos: dezena corresponde a 10. Portanto, temos de calcular o produto de 7 x 10 = 70. Sendo assim, temos 70 ovos.

Finalmente, vendeu-se 3 dezenas de ovos que corresponde a 30 ovos.

Somando os ovos que foram vendidos, temos:

300+70+30=400

Logo, temos 400 ovo que corresponde a 4 centenas de ovos.

16) Denise colheu 28 maçãs e quer guarda-las em cesto. Se em cada cesto colocar 4 maçãs, de quantos cestos vai precisar?

Resolução:

Para saber o número de cesto que vai precisar. Basta, dividir o numero de maçãs que colheu (28) pelo numero de maçãs que vai colocar em cada cestos (4). Assim, temos:

28:4 = 7

Portanto, a Denise precisará de 7 cestos.

17) A Ana tem 14 rebuçados e a Eva tem 17. Quantos rebuçados têm as duas meninas?

Resolução:

Para determinar o total de rebuçados, devemos adicionar as duas quantidades. Assim, temos: 14+17=31

Portanto, as duas meninas têm 31 rebuçados.

18) A mãe do Ivo comprou 18 bananas. Ao almoço, os filhos comeram 7. Quantas bananas restaram?

Resolução:

Compraram 18 bananas e comeram 7 bananas. Neste caso, temos de subtrair as duas quantidades para encontrarmos o resto. Assim, temos:

18-7=11

Portanto, restaram 11 bananas.

19) Efetue a multiplicação dos seguintes números naturais:

a) 2534 x 453 =

b) 123 x 764 5=

c) 98 x 43 =

Resolução:

a). Para determinar o produto de : 2534 x 453, temos de aplicar o algoritmo da multiplicação. Sendo assim , temos: 2534 x 453=1147902.

b). Para determinar o produto de : 123 x 7645 =, temos de aplicar o algoritmo da multiplicação. Sendo assim , temos: 123 x 7645 = 940335

c). Para determinar o produto de : 98 x 43, temos de aplicar o algoritmo da multiplicação. Sendo assim , temos: 98 x 43 =4 214

20) Uma escola recebeu 650 livros de Matemática da 2ª classe e 234 livros de Língua portuguesa. Outra recebeu 150 livros de matemática da 2ª classe e 690 de língua portuguesa.

a) Quantos livros de matemática receberam no total as escolas?

b) Quantos livros de língua portuguesa receberam no total as escolas?

Resolução:

a). Na primeira escola tem 650 livros de matemática e na segunda escola temos 150 livros de matemática. Adicionando os livros das duas escolas, temos:

650+150=800

Portanto, as duas escolas receberam 800 livros de matemática.

b). Na primeira escola temos 234 livros de língua portuguesa e na segunda escola temos 690 livros de língua portuguesa. Adicionando os livros das duas escolas, temos:

234+690=924

Portanto, as duas escolas receberam 924 livros de língua portuguesa.

22) Quanto ao domínio dos números naturais, resolve:

a) 16-23=

b) 23-12=

c) 23:45=

Resolução:

a). Não tem solução, porque no domínio dos números naturais o aditivo não deve ser menor que o subtrativo.

b). 11

c). Não tem solução, porque no domínio dos números naturais o divisor não pode ser maior que o dividendo.

23) Considerando o conjunto A = {-10, -9, -3, 1, 12, 30} indique neste conjuntos quais números são pertencentes ao conjunto dos números naturais.

Resolução:

O conjunto dos naturais é definido por N = {x ∈ N | x ≥ 0}

Então, os números negativos não pertencem aos naturais.

Portanto, somente os números 1, 12 e 30 são naturais.

24) A diferença entre os números naturais 20010 e 3291 é igual a:

Resolução:

20010 – 3291 = 16719

25) Realize a diferença entre o conjunto dos naturais não-nulos e o conjunto dos números naturais.

Resolução:

O conjunto dos números naturais não-nulos é representado por N* = {1, 2, 3, 4, 5, 6, …}

Portanto, N – N* = {0}

26) Escreva o sucessor e o antecessor dos números naturais abaixo:

a) 23

b) 1092

c) 18

d) 92

e) 1

Resolução:

O sucessor de um número é dado por x + 1, onde x é o número que queremos saber o seu sucessor.

O antecessor de um número é dado por x – 1. Nos números naturais o zero não possui antecessor.

a) antecessor: x – 1 = 23 – 1 = 22 e sucessor: x + 1 = 23 + 1 = 24

b) antecessor: x – 1 = 1092 – 1 = 1091 e sucessor: x + 1 = 1092 + 1 = 1093

c) antecessor: x – 1 = 18 – 1 = 17 e sucessor: x + 1 = 18 + 1 = 19

d) antecessor: x – 1 = 92 – 1 = 91 e sucessor: x + 1 = 92 + 1 = 93

e) antecessor: x – 1 = 1 – 1 = 0 e sucessor: x + 1 = 1+ 1 = 2