Professor Diminoi
QUESTÕES DO SARESP
3ª SÉRIE ENSINO MÉDIO
01) (SIMULADO SARESP – 3ªEM/Médio) Sendo dada a equação 𝑥2 + 𝐵𝑥 + 𝐶 = 0 e sabendo que 4 e −5 são as raízes dessa equação, então, temos que:
(A) B = 1 e C = −9.
(B) B = 1 e C = −20.
(C) B = 9 e C = 20.
(D) B = 20 e C = −20.
Resolução:
Da equação algébrica: x
2 + a ∙ x + b = 0 , tem-se que as raízes são: x1 = 4 e x2 = - 5.
Os coeficientes dos termos da equação são: a = 1, b = B e c = C.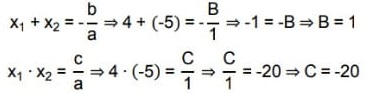
Utilizando as relações entre a soma e produto de raízes com os coeficientes da equação temos: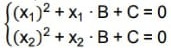
Outra forma de se resolver:
Temos duas raízes (x1 e x2) e duas incógnitas (os coeficientes B e C).
A partir destes dados, obtém se o sistema de equações lineares: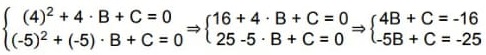
Substituindo os valores das raízes, temos que:
Na primeira linha temos que: C = −16 – 4∙B (I).
Substituindo este resultado na equação da 2ª linha temos que:
-5B - 16 - 4B = -25 ⇒ -9B = -25 + 16 ⇒ -9B = -9 ⇒ B = 1
e
C = -16 - 4 ∙ 1 ⇒ C = -20
Alternativa: B
02) (SIMULADO SARESP – 3ªEM/Fácil) A forma fatorada da equação x2 - 10x + 24 = 0 é
(A) (x + 4) . (x - 6) = 0
(B) (x -4) . (x + 6) = 0
(C) ( x + 4) . (x + 6) = 0
(D) (x - 4) . (x - 6) =0
Resolução:
Uma equação do 2º grau com uma raiz igual a p e outra igual a m pode ser escrita como (x − p) . (x − m) = 0. Escrita dessa maneira, dizemos que está em sua forma fatorada. De acordo com o enunciado, deve-se encontrar as raízes da equação e utilizá-las para escrever na forma fatorada.
Dada a equação: x2- 10x + 24 = 0 determinando suas raízes pelo método de Bháskara, temos que: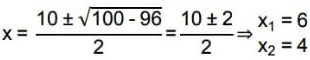
Então a equação na forma fatorada fica como:
(x − 4) . (x − 6) = 0
Alternativa: D
03) (SIMULADO SARESP – 3ªEM/Médio) Uma equação de 3º grau pode ser escrita: ax³ + bx² + cx + d = 0, (com
A ≠ 0). A equação polinomial cujas raízes são −1, 1 e 2 deve ser escrita como:
(A) x3 + 2x2- x + 2 = 0
(B) 2x2+ x + 2 = 0
(C) x3 − 2x2 - x + 2 = 0
(D) 2x2- x - 2 = 0
Resolução:
Conhecendo as raízes r1 = -1, r2 = 1 e r3 = 2 e conhecendo-se a forma fatorada de
uma equação de 3º grau, (x - r1) . (x - r2) . (x - r3) = 0, temos que:
(x -(-1)) . (x - 1) . (x - 2) = 0
(x + 1) . (x - 1) . (x - 2) = 0
(x2- 1) ∙ (x - 2) = 0
x3- 2x2- x + 2 = 0
Alternativa: C
04) (SIMULADO SARESP – 3ªEM/Fácil) A soma das raízes da equação x3- 7x2+ 12x = 0 é:
(A) 5.
(B) 6.
(C) 7.
(D) 12.
Resolução:
Uma equação de terceiro grau pode ser escrita na forma: x3- S1x2 + S2x - S3 = 0, de tal forma que S1 = r1 + r2 + r3. Na equação polinomial dada, x3- 7x2+ 12x = 0 , o coeficiente da variável de grau 2 é 7, desta forma, temos que a soma das raízes da equação polinomial é 7.
Alternativa: C
05) (SIMULADO SARESP – 3ªEM/Fácil) Na figura a seguir o quadrado ABCD foi dividido em dois quadrados e dois retângulos.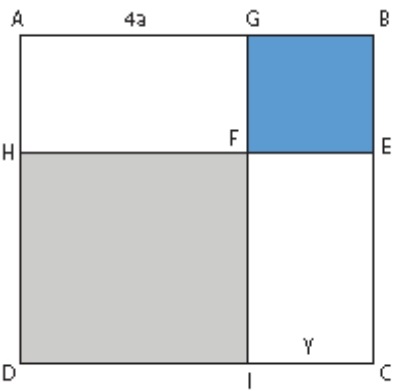 O polinômio que representa a área do quadrado ABCD é:
O polinômio que representa a área do quadrado ABCD é:
(A) AABCD = 16 ∙ a2 + 4 ∙ a ∙ y
(B) AABCD = 4 ∙ a ∙ y + y2
(C) AABCD = 16 ∙ a + 4 ∙ y
(D) AABCD = 16 ∙ a2 + 8ay + y2
Resolução:
As relações entre o conhecimento relativo às grandezas e medidas, notadamente no conhecimento da área do quadrado e retângulo, para uma representação algébrica, visando especificamente as operações, entre monômios e binômios. Desta forma, a resolução da questão consiste basicamente em estabelecer as medidas não informadas na figura e estabelecer a área do quadrado ABCD, conforme segue: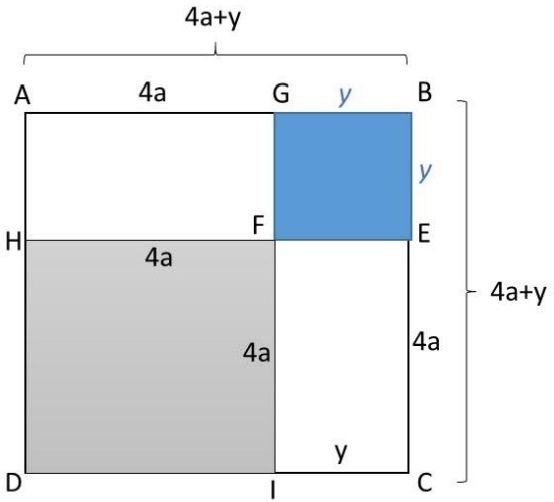
Então a área do quadrado ABCD será dada por:
(4a + y) . (4a + y) =
((4a + y))2 =
16 . a2 + 8 . a . y + y2
Alternativa: D
06) (SIMULADO SARESP – 3ªEM/Médio) Um engenheiro foi contratado para construir um tanque de concreto para mistura de argila e água em uma indústria de cerâmica. Para isso, ele definiu as medidas internas do tanque como x, (x + 1) e (2x +1), conforme a figura. Dessa forma poderia atender diversas demandas de volume e de espaço físico para construção.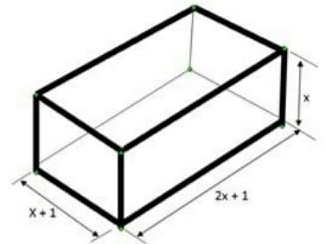 Nessas condições, a equação que fornece o valor de x para um volume de 30 m3 é:
Nessas condições, a equação que fornece o valor de x para um volume de 30 m3 é:
(A) 2x2 + x + 2x + 1 = 30
(B) 2x3 + 3x2 + x - 30 = 0
(C) x3 + 2x2 + x - 30 = 0
(D) x3 + x2 + x = 30
Resolução:
(x + 1) . (2x + 1) . x = 30
(2x2 + x + 2x + 1) . x = 30
2x3 + x2 + 2x2 + x – 30 = 0
2x3 + 3x2 + x - 30 = 0
Alternativa: B
07) (SIMULADO SARESP – 3ªEM/Difícil) A divisão do polinômio p(x) = x5- 2x4- x + m por q(x) = x - 1 é exata.
O valor de m é
(A) −2.
(B) −1.
(C) 0.
(D) 2.
Resolução:
o Teorema do Resto, ou Teorema de D’Alembert, cujo enunciado é:
“Um polinômio P(x) é divisível por (x − a) se e somente se P(a) = 0”
Temos
De acordo com os dados da questão, temos que p(x) é divisível por q(x), pois a divisão é exata, então de acordo com o teorema do resto, temos que: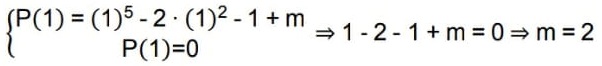
Alternativa: D
08) (SIMULADO SARESP – 3ªEM/Difícil) O quociente e o resto da divisão do polinômio P(x)= x3 + 2x + 1 por (x + 2) são, respectivamente,
(A) x2- 2x + 6 e -11
(B) -2x + 6 e -11
(C) x2- 2x e -13
(D) x2- 2x + 6 e 11
Resolução:
O resto será o valor de P(−2), ou seja:
R = (-2)3 + 2 . (-2) + 1 = -8 - 4 + 1 = -11
O cálculo quociente da divisão pode ser encontrado por meio do algoritmo de Briot– Ruffini:
Portanto o quociente da divisão de P(x) por (x + 2) será: x2- 2x + 6
Alternativa: A
09) (SIMULADO SARESP – 3ªEM/Médio) Utilizando o dispositivo prático de Briot-Ruffini, a divisão do polinômio P(x) 2x4 + 4x3 - 7x2 + 12 por D(x) = (x−1) tem quociente igual a:
(A) Q(x) = 2x3 + 6x2- x - 1
(B) Q(x) = x3 + x2- x - 1
(C) Q(x) = 2x2 + 6x3 - x - 1
(D) Q(x) = -2x2 + 6x3 - x - 1
Resolução:
Utilização do dispositivo prático de Briot-Ruffini. Ao aplica-lo o aluno deverá chegar ao seguinte resultado.
Assim temos: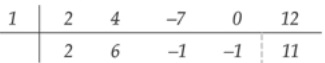
Q(x) = 2x3 + 6x2- x - 1 e R(x) = 11
Alternativa: A
10) (SIMULADO SARESP – 3ªEM/Fácil) Considere a região do plano complexo indicado a seguir. Cada ponto da região é a imagem de um complexo e foi objeto de uma transformação da figura pintada em vermelho nas figuras a, b e c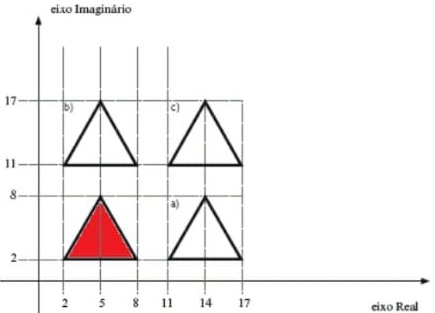 Pode-se afirmar que a representação c) é o resultado
Pode-se afirmar que a representação c) é o resultado
(A) da soma com o número complexo 9 + 9i.
(B) do produto pelo número imaginário 2i.
(C) da soma ao número complexo 9i.
(D) do produto pelo número real 2.
Resolução:
Ao desenvolver a habilidade de realizar transformações no plano, referentes a operações com números complexos.
Na questão, a região triangular hachurada para atingir a posição indicada em C será deslocada para a direita de 9 unidades, em seguida, para cima, de 9 unidades, e depois para a direita de 9 unidades, que corresponde ao complexo: 9 + 9i.
Alternativa: A
11) (SIMULADO SARESP – 3ªEM/Médio) Considere a região do plano complexo indicada na figura a seguir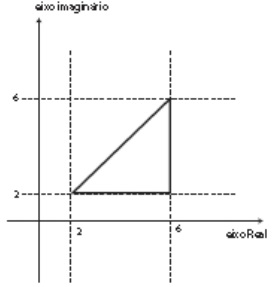 Cada ponto da região é a imagem de um complexo e será objeto de uma transformação somado a 3i, que será representado graficamente por:
Cada ponto da região é a imagem de um complexo e será objeto de uma transformação somado a 3i, que será representado graficamente por: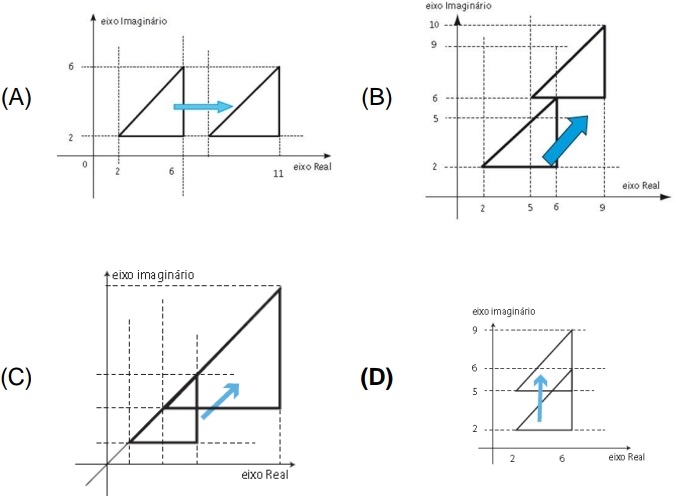
Resolução:
Ao realizar transformações no plano, referentes a operações com números complexos. Na questão, cada ponto da região será deslocado na direção do eixo imaginário de 3 unidades, a região transformada será um triângulo de vértices nas imagens dos complexos: 2 + 5i, 6 + 5i e 6 + 9i.
Alternativa: D
12) (SIMULADO SARESP – 3ªEM/Média) A relação entre a pressão e a temperatura de um gás quando este é mantido em um recipiente de volume constante é uma função linear definida pela relação P/T= a, ou seja, a razão entre a pressão e a temperatura é constante. A tabela seguinte mostra, para um determinado gás, a evolução da pressão em relação à temperatura. O valor que está faltando na tabela é
O valor que está faltando na tabela é
(A) 100.
(B) 140.
(C) 150.
(D) 170.
(E) 180.
Resolução:
Em relação de proporcionalidade direta entre as variáveis do problema, Temperatura e Pressão e o coeficiente de proporcionalidade a que pode ser obtido da tabela, observando que: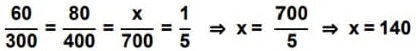
Alternativa: B
13) (SIMULADO SARESP – 3ªEM/Médio) O retângulo representado na figura tem 35 m2 de área.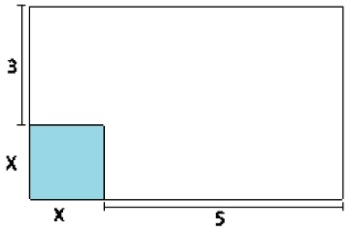 A área do quadrado sombreado é, em m2, igual a
A área do quadrado sombreado é, em m2, igual a
(A) 3.
(B) 4.
(C) 9.
(D) 16.
(E) 18.
Resolução:
Resolver o problema fazendo uso de produtos notáveis particionando a figura adequadamente.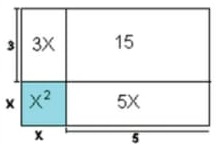
Então, sabendo que a área de todo o retângulo é 35 m2, a soma das áreas particionadas deverá resultar no mesmo valor, ou seja
x2 + 3x + 5x + 15 = 35
que pode ser ajustada para a seguinte equação do 2º grau
x2 + 8x - 20 = 0
Resolvendo a equação, obtém-se x = -10 ou x = 2.
Como o valor de x se refere a uma medida, apenas a segunda solução (x = 2) é cabível.
Logo, x2 = 4.
Também seria possível equacionar o problema com auxílio da linguagem algébrica. Como a área é igual a 35 m2 e a figura corresponde a um retângulo, sua área é dada pelo produto dos seus lados que medem (x + 3) e (x + 5). Portanto, (x + 3) . (x + 5) = 35 que resulta na mesma equação descrita no outro método.
Alternativa: B
14) (SIMULADO SARESP – 3ªEM/Médio) Considere a dízima periódica 0,99999.... Representado na reta numérica, este número estará
(A) à direita do número 1.
(B) à esquerda do número 1.
(C) sobre o número 1.
(D) sobre o número 0.
(E) sobre o número 9.
Resolução:
Para o aluno transformar a dízima periódica numa fração irredutível, usando as regras, deverá fazer 9/9, obtendo assim o número 1.
Alternativa: C
15) (SIMULADO SARESP – 3ªEM/Médio) Um jovem avista o topo de uma torre segundo um ângulo de 45º, conforme a ilustração.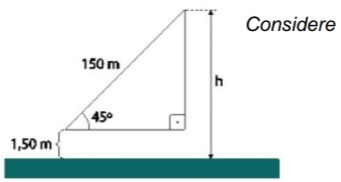 Sabe-se que a distância dos seus olhos ao topo da torre é 150m e, ainda, que a distância dos seus olhos ao solo é 1,50 m. A altura aproximada h da torre é
Sabe-se que a distância dos seus olhos ao topo da torre é 150m e, ainda, que a distância dos seus olhos ao solo é 1,50 m. A altura aproximada h da torre é
(A) 77 m.
(B) 100 m.
(C) 107 m.
(D) 150 m.
Resolução:
Esse problema aborta a aplicação da relação trigonométrica seno. Nesse caso, além de aplicar a devida relação trigonométrica, é necessário acrescentar a medida 1,50 m ao resultado. Assim,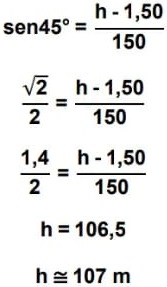
Alternativa: C
1ª SÉRIE ENSINO MÉDIO
16) (SIMULADO SARESP – 3ªEM/Fácil) A tabela a seguir informa a vazão de uma torneira aberta em relação ao tempo: A expressão que representa a vazão em função do tempo é
A expressão que representa a vazão em função do tempo é
(A) y = x . 20
(B) y = x + 100
(C) y = x - 200
(D) y = 5x . 400
Resolução:
É necessário compreender a função como expressão de uma proporcionalidade. Nota-se pela tabela que a cada unidade de tempo (x) corresponde a vazão (y) da torneira igual a 20. Assim, quando x é igual a 1, y é igual a vinte (y=1 . 20); quando x = 5, y = 5 . 20 e assim sucessivamente (y = 20 . x ou y = x . 20). Dessa forma, a vazão se mantém, proporcionalmente crescente de 20 unidades à medida que o tempo passa. Logo, a expressão que representa a vazão em função do tempo é y = x . 20.
Alternativa: A
17) (SIMULADO SARESP – 3ªEM/Fácil) O comprimento C de uma circunferência é uma função do diâmetro d, no caso, C é diretamente proporcional a d, e temos C = f(d) = π . d. Então, a constante de proporcionalidade (k) é:
(A) k = 2d
(B) k = π
(C) k = 2/π
(D) k = 2 π
Resolução:
Adotando a constante de proporcionalidade. A proposta expressa no problema atende o conceito de função linear, y = kx e y/x = k. Uma função que estabelece entre c e d uma relação tal que c/d é constante é chamada linear. Expressamos a relação por C = π . d, “π” constante e dizemos que a variação de “C” é diretamente proporcional a variação de “d”
C = 2πr
c = π2r
c = πd
c/d = π
Assim, k = π, que é a constante de proporcionalidade entre o comprimento da circunferência e o seu diâmetro
Alternativa: B
18) (SIMULADO SARESP – 3ªEM/Fácil) Existe uma relação de proporcionalidade direta entre duas grandezas x e y. Se x é diretamente proporcional a y, então, também y será diretamente proporcional a x.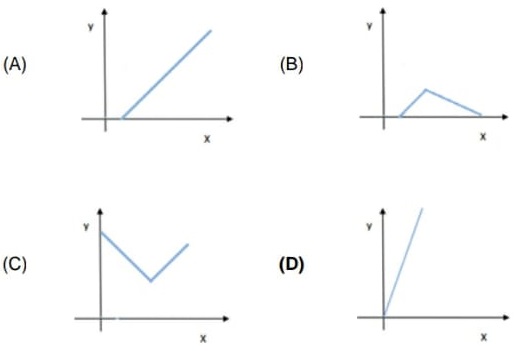
O gráfico que representa uma relação de proporcionalidade direta entre as duas grandezas é:
Resolução:
Dado que, só existe uma relação de proporcionalidade direta entre as grandezas x e y. Se x é diretamente proporcional a y, então também y é diretamente proporcional a x. Quando existe proporcionalidade direta entre duas grandezas, o gráfico que une os pontos correspondentes é uma reta que contém a origem do referencial.
Dos gráficos apresentados, o único que atende essa premissa é o da alternativa D.
Alternativa: D
19) (SIMULADO SARESP – 3ªEM/Médio) Considere os gráficos a seguir: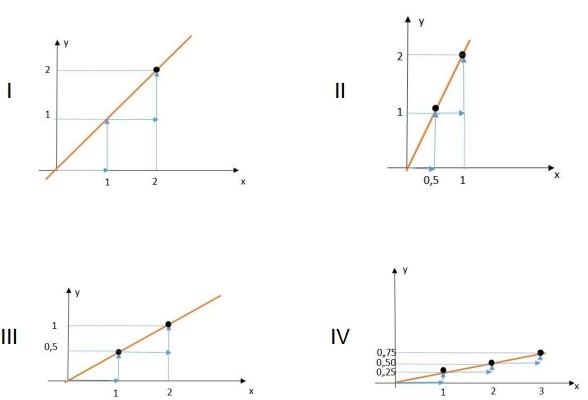 Considerando as constantes de proporcionalidade encontradas em cada uma das funções e organizando-as em ordem crescente, obtemos a seguinte sequência:
Considerando as constantes de proporcionalidade encontradas em cada uma das funções e organizando-as em ordem crescente, obtemos a seguinte sequência:
(A) IV, III, I e II.
(B) II, I, III e IV.
(C) III, IV, I e II.
(D) I, II, III e IV.
Resolução:
Em todos os gráficos verifica-se que as constantes de proporcionalidade são positivas, isto indica existe uma relação de interdependência envolvendo grandezas diretamente proporcionais, graficamente a constante de proporcionalidade indica a inclinação da reta e é calculada através da relação: 𝛼 =∆𝑦/∆𝑥.
A seguir apresentamos o valor de a, para cada reta apresentada nos gráficos.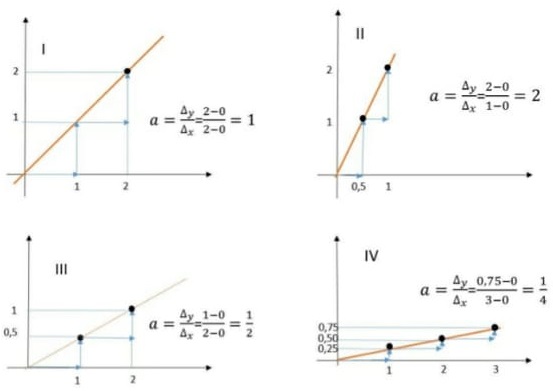
Portanto a sequência em ordem crescente das constantes de proporcionalidade dos gráficos apresentados na questão será: IV, III, I e II, que atende a alternativa A da questão.
Alternativa: A
20) (SIMULADO SARESP – 3ªEM/Fácil) O valor a ser pago por uma pessoa para abastecer seu automóvel varia proporcionalmente em função da quantidade de litros de combustível utilizado. Tal função trata-se de uma relação de proporcionalidade direta.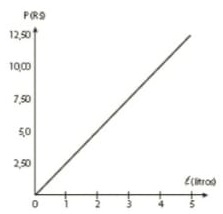 A partir das informações apresentadas no gráfico, pode-se afirmar que:
A partir das informações apresentadas no gráfico, pode-se afirmar que:
(A) a relação de litros (L) e Preço (P) é decrescente, ou seja, quanto maior a quantidade de litros, menor o valor a ser pago.
(B) a relação de litros (L) e Preço (P) é crescente, ou seja, quanto maior a quantidade de litros, maior o valor a ser pago.
(C) a relação de litros (L) e Preço (P) é crescente e sua constante de proporcionalidade é k = 3,5.
(D) a relação de litros (L) e Preço (P) é decrescente e sua constante de proporcionalidade é k = −3,5.
Resolução:
No gráfico a relação de crescimento entre as grandezas envolvidas. Do gráfico, tem-se que a relação litros e preço é direta, e que o valor do litro do combustível em questão é R$ 2,50. Então a constante k de proporcionalidade é k = 2,5. Assim, P = k . L ou P = 2,5 . L e, portanto, quanto maior a quantidade de litros de combustível, maior o valor a ser pago.
Alternativa: B
21) (SIMULADO SARESP – 3ªEM/Difícil) O preço (P) a ser cobrado em uma corrida de taxi é composto por uma quantia fixa (bandeirada), igual para todas as corridas, mais uma parcela variável, que é diretamente proporcional ao número de quilômetros rodados: P = a + b.x (b é o custo de cada quilometro rodado).
Em certa cidade, temos P = 15 + 0,8x (P em reais e x em quilômetros).
O gráfico de P em função de x que atende a proposição é: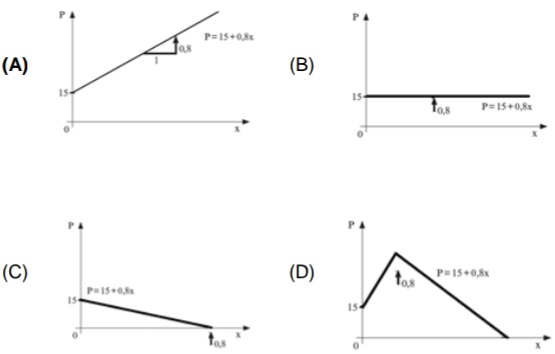
Resolução:
Este problema é uma situação em que a proporcionalidade direta existe apenas no cálculo da parcela variável da corrida, existindo outra parcela fixa, independente dos quilômetros rodados.
O gráfico que atende ao solicitado no problema é o da alternativa A.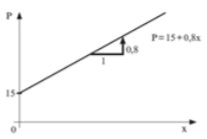
Alternativa: A
22) (SIMULADO SARESP – 3ªEM/Fácil) Indique qual dos gráficos abaixo expressa uma proporcionalidade
direta entre uma grandeza e o quadrado da outra, considerando as grandezas x e y, em que 𝑦 = 𝑥2.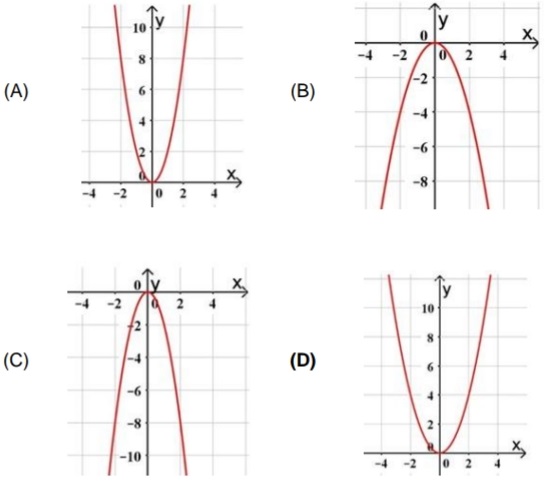
Resolução:
Esta questão tem por objetivo tornar evidente a habilidade do aluno na identificação por gráfico de características referentes à proporcionalidade direta entre uma grandeza e o quadrado da outra. Neste caso o gráfico da alternativa D é o correspondente à função y = x2, em que y é expresso pelo quadrado de x. De forma que, para cada x real do domínio há um y real na imagem correspondente ao quadrado de x. Graficamente, isso se expressa por um acréscimo (ou decréscimo) constante em y, a cada unidade que se avança em x, no gráfico a seguir, esta afirmação fica evidente.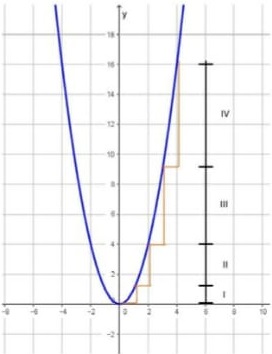
A variação em y, é calculada através da taxa média de variação, conforme a razão: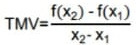
Para exemplificar, calcularemos a taxa de variação média, nos intervalos representados por I, II, III e IV, na figura.
No intervalo I, temos que: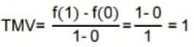
No intervalo II, temos que:
No intervalo III, temos que: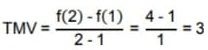
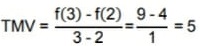
No intervalo IV, temos que: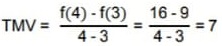
Estes resultados comprovam as demarcações representadas no segmento de reta, que representa a variação no eixo y.
Alternativa: D
23) (SIMULADO SARESP – 3ªEM/Médio) Dada a função: y = 0,25x2 + 2x + 10. O gráfico que representa corretamente a proporcionalidade direta entre uma grandeza e o quadrado de outra é: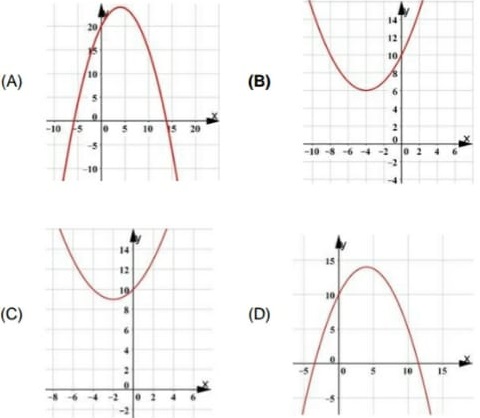
Resolução:
Identifica algumas características importantes da função polinomial de 2º grau, por meio das características de seus coeficientes e também pelas coordenadas do vértice da parábola. Então temos que:
Os dados acima, são condições suficientes para o esboço do seguinte gráfico: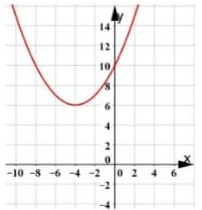
Portanto, o gráfico da função: C = 0,25 . x2 + 2 . x + 10, será representado pelo gráfico indicado na alternativa B.
Alternativa: B
24) (SIMULADO SARESP – 3ªEM/Difícil) A tabela mostra a proporcionalidade direta entre a grandeza x e seu quadrado. A função que representa a variação das grandezas será:
A função que representa a variação das grandezas será:
(A) y =1/8 . x
(B) y = 4x2
(C) y = 1/8 . x2
(D) y = 8x2
Resolução:
Verificar a regularidade encontrada na variação das grandezas x e y, informadas na tabela e generalizar estes dados em uma função que expresse a proporcionalidade direta da grandeza x com o seu quadrado.
De acordo com a variação das grandezas apresentadas na tabela, nota-se que a constante de proporcionalidade (k) varia de acordo com o quadrado do valor de x na razão de 1/8, conforme a tabela abaixo: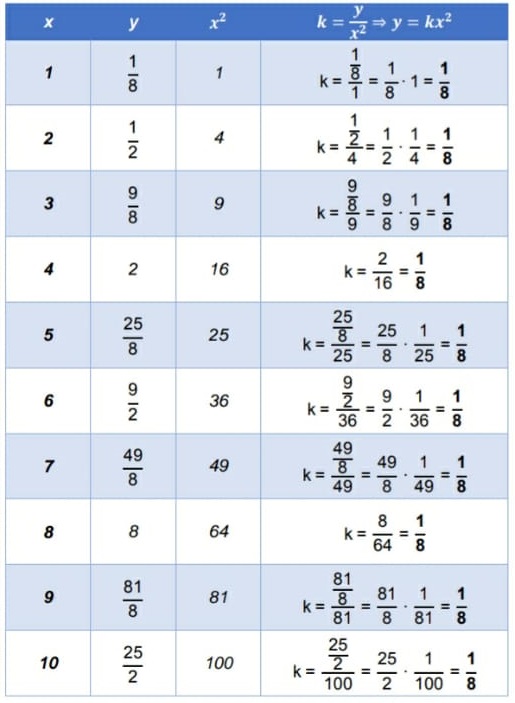
Então a função que representa as grandezas x e y da tabela será:
y = 1/8 . x2
Alternativa: C
25) (SIMULADO SARESP – 3ªEM/Médio) A área de um celular (retangular) é de 121,5 cm2 tendo de altura (C) uma vez e meia a sua largura (L).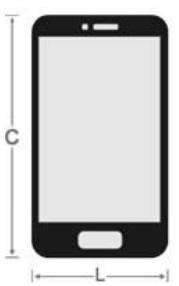 Sabendo-se que a área de uma figura retangular é calculada multiplicando-se a medida da sua largura pela medida de sua altura, a expressão matemática que representa a área desse celular é:
Sabendo-se que a área de uma figura retangular é calculada multiplicando-se a medida da sua largura pela medida de sua altura, a expressão matemática que representa a área desse celular é:
(A) −121,5 = 1,5L2.
(B) 1,5L2−121,5 = 0.
(C) C = 1,5L2.
(D) L = 1,5C2.
Resolução:
Se chamarmos de C a altura da tela, e L a largura, temos que 1,5L é a medida da altura da tela.
Sabemos que a área de uma figura geométrica retangular é calculada multiplicandose a medida da sua largura pela medida da sua altura. Escrevendo o enunciado na forma de uma sentença matemática, temos que: L . 1,5L = 121,5, ou 1,5L2−121,5 = 0
Alternativa: B
26) (SIMULADO SARESP – 3ªEM/Médio) Em um jogo de futebol, um chute durante um passe de bola descreve uma trajetória em formato de um arco de uma parábola de acordo com a seguinte função y = -x2 + 7x. Determine a altura máxima atingida pela bola.
Em um jogo de futebol, um chute durante um passe de bola descreve uma trajetória em formato de um arco de uma parábola de acordo com a seguinte função y = -x2 + 7x. Determine a altura máxima atingida pela bola.
(A) 7 m.
(B) 12 m.
(C) 12,25 m.
(D) 14,0 m.
Resolução:
Dada a função que estabelece a trajetória da bola: 𝑦 = −𝑥2 + 7𝑥, temos que:
- coeficientes da função: a = −1, b = 7 e c = 0
- a parábola tem concavidade voltada para baixo (a < 0);
- a parábola não intercepta o eixo y, pois não existe o termo independente da função.
Desta forma, calcularemos as coordenadas do vértice da parábola: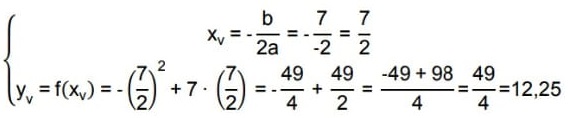
Outra maneira de se estabelecer as coordenadas do vértice: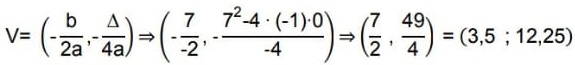
Conclui-se que a altura máxima, da bola será de 12,25 metros percorridos em 3,5 segundos.
Alternativa: C
27) (SIMULADO SARESP – 3ªEM/Difícil) Deseja-se cercar com muros um terreno retangular utilizando-se de uma parede já existente. Sabe-se que o comprimento do muro que será construído para cercar os outros três lados do terreno deverá ter 36 m de comprimento, conforme mostra a figura a seguir. De acordo com as indicações propostas no enunciado, a área máxima do terreno cercado será de:
De acordo com as indicações propostas no enunciado, a área máxima do terreno cercado será de:
(A) 72 m2
(B) 108 m2
(C) 144 m2
(D) 162 m2
Resolução:
Da figura apresentada, temos que: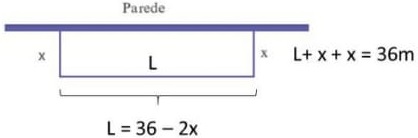
Desta forma a área do terreno será dada por: A(x) = x . (36 - 2x) = -2x2 + 36x
Verificando as características da função A(x), temos:
- coeficientes da função: a = −2, b = 36 e c = 0
- a parábola tem concavidade voltada para baixo (a < 0);
- a parábola não intercepta o eixo y, pois não existe o termo independente da função.
Desta forma, calcularemos as coordenadas do vértice da parábola: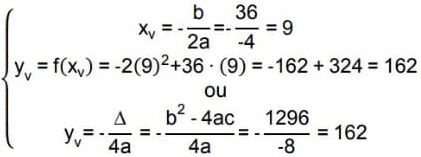
Representando graficamente A(x), temos que: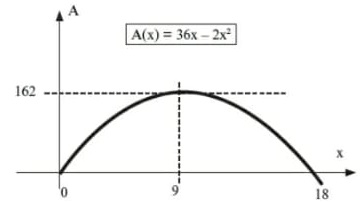
Então a área máxima a ser cercada corresponde à ordenada do vértice (𝑦𝑣) que equivale a 162 m, que satisfaz a alternativa D da questão.
Alternativa: D
28) (SIMULADO SARESP – 3ªEM/Fácil) As variáveis x e n assumem valores conforme tabela abaixo. A relação entre x e n é dada pela expressão
A relação entre x e n é dada pela expressão
(A) n = x + 2.
(B) n = 2x.
(C) n = 2x + 2.
(D) n = x + 4.
Resolução:
Para isso, deverá perceber que o padrão apresentado é que os valores de n sempre são o dobro do valor correspondente x que matematicamente é descrito por n = 2x.
Alternativa: B
29) (SIMULADO SARESP – 3ªEM/Médio) Os veículos são as principais fontes de poluição por partículas finas nas grandes cidades. O quadro compara os níveis de emissão desses poluentes por parte de caminhões, motos e carros.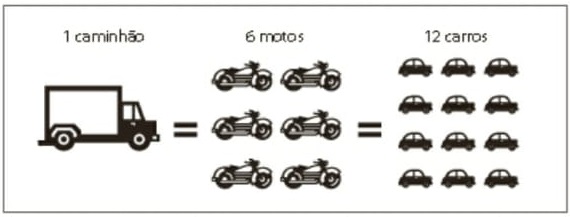 No caso específico das partículas finas, é correto afirmar, de acordo com o quadro, que:
No caso específico das partículas finas, é correto afirmar, de acordo com o quadro, que:
(A) carros são duas vezes mais poluentes do que motos.
(B) dois carros juntos emitem 1/6 das partículas emitidas por um caminhão.
(C) motos são seis vezes menos poluentes que carros.
(D) caminhões emitem 1/6 das partículas emitidas por motos.
Resolução:
A resolução do problema sugere a análise das relações de proporcionalidade entre os níveis de emissão de poluentes por parte de caminhões, motos e carros. Dessa análise é possível verificar que uma moto emite 1/6 das partículas emitidas pelos caminhões e que um carro emite 1/12 das partículas emitidas pelos caminhões.
Assim, dois carros emitem 2x1/12 = 1/6 das partículas emitidas por um caminhão.
Alternativa: B
30) (SIMULADO SARESP – 3ªEM/Médio) Para sustentar o telhado de um galpão cuja parede tem 3 metros de altura, João colocou um conjunto de vigas, medindo, cada viga, 10 metros de comprimento. Na figura, uma delas aparece apoiada nos pontos B e C. A altura máxima do telhado, isto é, a distância AB é igual a 9 metros.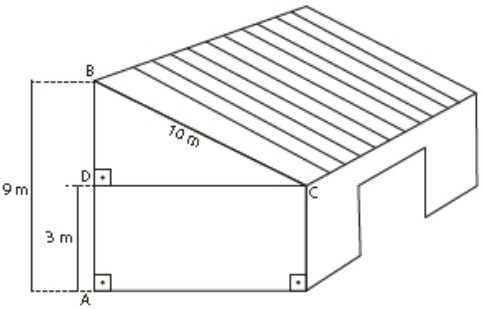 Pode-se concluir que a medida CD da parede do galpão mede, em metros,
Pode-se concluir que a medida CD da parede do galpão mede, em metros,
(A) 6.
(B) 8.
(C) 10.
(D) 12.
Resolução:
Para a resolução do problema, o estudante explora três momentos de percepção geométrica:
I) conceber o segmento CD como parte do triângulo BCD para obtenção de sua medida;
II) deduzir que a medida do segmento BD é igual a 6 m, mesmo que isso confronte a perspectiva do desenho, afinal se BA = 9 m e DA = 3 m, então BD deve equivaler a medida faltante para completar os 9 m, ou seja, BD = 6 m.
III) calcular a medida do segmento DC por meio do Teorema de Pitágoras, já que o triângulo BCD é retângulo.
Assim, (BC)2 = (DC)2 + (BD)2
Logo, (DC)2 = 100 – 36
Então (DC) = 8 m.
Alternativa: B





