Professor Diminoi
PROPRIEDADES DA POTENCIAÇÃO
Radiciação
Radiciação é a operação inversa da potenciação, logo, todas as propriedades da radiciação são derivadas da potenciação.![]()
Representação da radiciação
A radiciação é uma operação em que buscamos um número que satisfaz determinada potência. Considere os números a e b números reais e n um número racional, definimos a raiz n-ésima de a como sendo um número que, quando elevado a n, seja igual ao número a, nesse caso, representado por b, ou seja:
Exemplos
a) A raiz quadrada de 36 é igual a 6, pois 62 = 36.
![]()
Observe que, para determinar a raiz quadrada de 36, devemos buscar um número que, quando elevamos ao quadrado, seja igual a 36. Logicamente, esse número é o 6.
b) A raiz cúbica de 125 é igual 5, pois 53 = 125.
![]()
c) Agora vejamos a raiz décima de 1024. Como não se trata de um número trivial, a melhor saída é realizar a decomposição em fatores primos do 1024 e, em seguida, escrevê-lo na forma de potência.

Veja que o número 1024 = 210, assim o número que, elevado a 10º potência, resulta em 1024 é o número 2, ou seja:![]()
Nomenclatura da radiciação
Considerando a raiz n-ésima anterior, temos a seguinte nomenclatura:
a = Radicando
n = índice
b = raiz
√ = Radical
Propriedades da radiciação
Assim como na potenciação, temos algumas propriedades na radiciação. Nesta a história é a mesma, uma vez que ambas são operações inversas.
Propriedade 1: Raiz em que o expoente do radicando é igual ao índice
![]()
A propriedade 1 afirma que, sempre que o índice for igual ao expoente do radicando, o resultado da raiz n-ésima é a própria base.
Exemplos
Propriedade 2: Potência de expoente radical![]()
A propriedade 2, na verdade, é uma propriedade de potenciação em que o expoente é uma fração. O numerador da fração passa a ser o expoente do radicando, e o denominador passa a ser o índice da raiz.
Exemplo
Propriedade 3: Produto de raízes de índices iguais
![]()
A propriedade 3 afirma que o produto entre duas raízes com índices iguais é igual à raiz de mesmo índice do produto dos radicandos.
Exemplo
Propriedade 4: Quociente de raízes de índices iguais
De maneira análoga à propriedade 3, a propriedade 4 afirma que a divisão entre duas raízes de índices iguais é igual à raiz de mesmo índice da divisão dos quocientes.
Exemplos:
Propriedade 5: Potência de uma raiz![]()
A propriedade 5 diz-nos que uma raiz n-ésima elevada a um determinado expoente m é igual à raiz n-ésima do radicando elevado ao expoente.
Exemplos:
Propriedade 6: Raiz de outra raiz![]()
Quando nos depararmos com uma raiz de outra raiz, basta conservar o radicando e multiplicar os índices das raízes.
Exemplos:
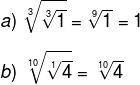
Propriedade 7: Simplificação de raízes
![]()
A propriedade 7 afirma que, em uma raiz n-ésima de uma potência, podemos multiplicar o índice e o expoente do radicando por qualquer número desde que seja diferente de 0.






