GEOMETRIA PLANA E CONCEITOS

Professor Diminoi

GEOMETRIA PLANA

A geometria plana é a área da matemática que estuda as figuras planas, iniciando-se nos conceitos primitivos de ponto, reta e plano, e, com base neles, desenvolvendo-se até a construção das figuras planas, com o cálculo de suas respectivas áreas e perímetros.

Os conceitos da geometria plana têm grande incidência no Enem, com recorrência de questões que exigem o conceito de área ou até mesmo noções básicas de ângulos. Além disso, ela é base para a geometria espacial, porém, a diferença entre ambas é que a primeira é bidimensional, e a segunda, tridimensional.

Os conceitos de comprimento e largura permanecem indefinidos, e frequentemente se classificam como conceitos primitivos.

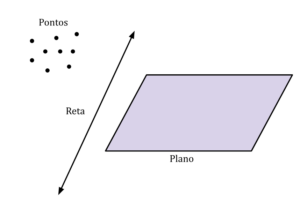
Pontos

Um ponto, no sentido matemático, é uma abstração de nosso senso comum de indivisibilidade. É um objeto que não pode ser decomposto em outros menores e no qual não existe qualquer extensão, isto é, não podemos “nos deslocar” dentro de um ponto.

Dizemos que um ponto é um objeto de dimensão zero, ou ainda que um ponto não possui graus de liberdade. Geralmente o denotamos por letras maiúsculas:

Reta, semirreta e segmento de reta

Agora, falando sobre objetos de uma dimensão temos as retas, as semirretas e os segmentos de retas, um conjunto de pontos com algumas características específicas.

Reta: figura geométrica unidimensional que se estende indefinidamente em ambas as direções. Uma reta possui sequência infinita de pontos alinhados e, geralmente, a denotamos por letras minúsculas:

A seta representa uma extensão infinita na direção a qual ela indica.

Semirreta: conceito geométrico que se assemelha a uma reta, mas tem ponto de partida específico chamado de origem e continua indefinidamente em uma única direção.

Semirreta r com origem em A.

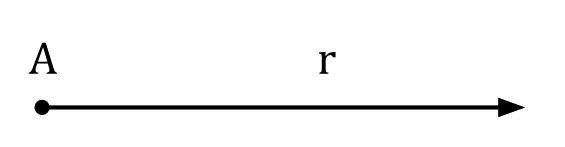
Segmento de reta: um segmento de reta é uma parte limitada de uma reta que consiste em dois pontos extremos e em todos os pontos que estão entre esses extremos.

Segmento de reta AB

Cada um destes objetos apresentados possui uma notação específica quando se trata dos seus pontos

Planos

Os planos são uma superfície bidimensional que se estende infinitamente em todas as direções. Um plano é completamente plano, não tem espessura e é composto por uma infinidade de pontos que estão alinhados em uma única superfície. Não importa em que direção você se mova dentro de um plano, você permanecerá dentro desse plano. Geralmente o denotamos por uma letra grega minúscula:

Plano π

Um plano é descrito como sendo infinito em extensão nas direções horizontal e vertical, mas ainda assim é uma superfície plana, sem profundidade. Pode ser representado graficamente como uma folha de papel ou um quadro bidimensional, mas, na realidade, um plano não tem bordas ou limites.

Ângulos

De forma geral, definimos ângulos por semirretas concorrentes e de mesma origem. Em geometria plana, associamos um valor numérico, medido em graus, para indicar quão "aberto" estão esses dois segmentos. Esse valor também indica a orientação de abertura. Essas linhas ou segmentos são chamados de lados do ângulo, e o ponto comum é chamado de vértice do ângulo.

Ângulo definido pelas semirretas OA e OB

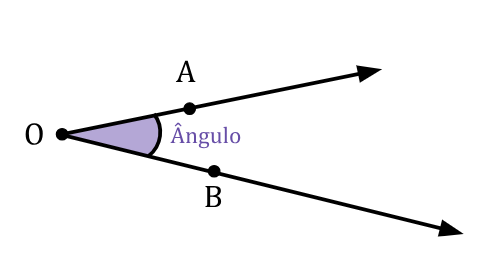
E como podemos referenciar um ângulo específico? Há duas formas de realizarmos esse processo.

A primeira é utilizar os pontos que definem os segmentos: observe a imagem acima, temos duas semirretas definidas pelos pontos A, O e B, então chamaremos esse ângulo de BÔA (usaremos sempre o sentido anti-horário).

A segunda forma é associar ao ângulo, uma letra grega minúscula, como α ou β (alpha ou beta). A medida de um ângulo geralmente é expressa em graus (°). No entanto, os ângulos também podem ser medidos em radianos, grados e outros sistemas de medida.

Existem vários tipos de ângulos com base em suas medidas:

Ângulo agudo: tem medida menor que 90 graus.

Representação de ângulo agudo

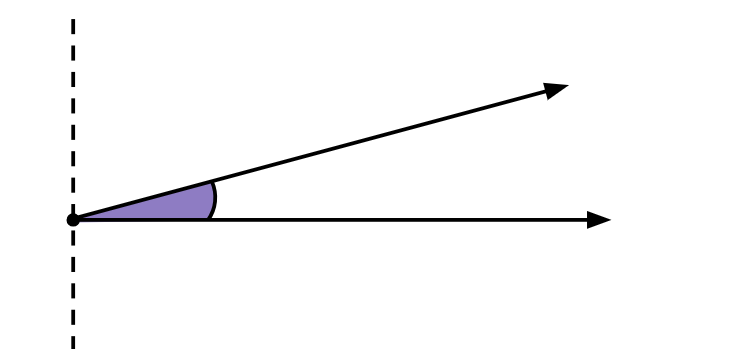
Ângulo reto: tem medida exatamente igual a 90 graus. É uma interseção de duas linhas que forma um canto de 90 graus, como o canto de uma folha de papel.

Ângulo obtuso: tem medida entre 90 e 180 graus.

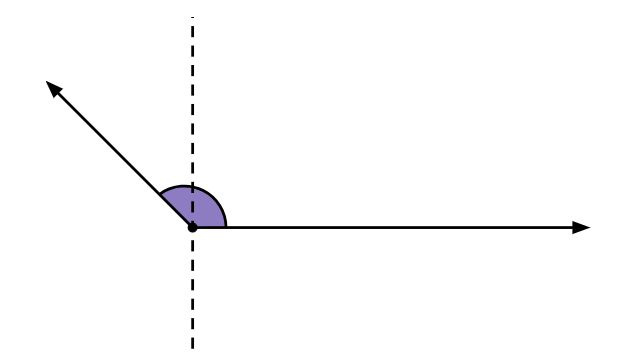
Ângulo raso: tem medida exatamente igual a 180 graus. Nesse caso, os lados são uma extensão direta um do outro.

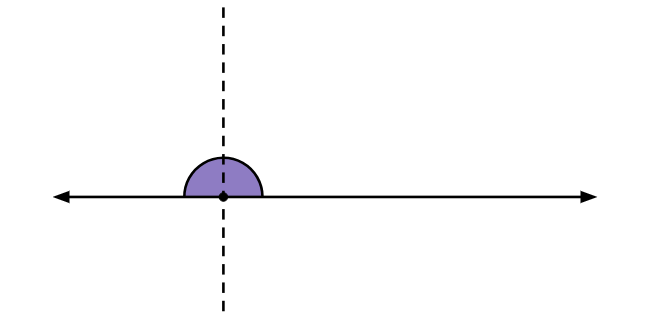
Note que no ângulo raso as semirretas que o delimitam formam uma reta.

Área

Área é uma medida que descreve a extensão ou a superfície de uma figura plana ou tridimensional. Sua quantidade nos diz quanto espaço uma forma geométrica ocupa em um plano ou no espaço. O cálculo da área depende do tipo de figura ou forma que estamos medindo.

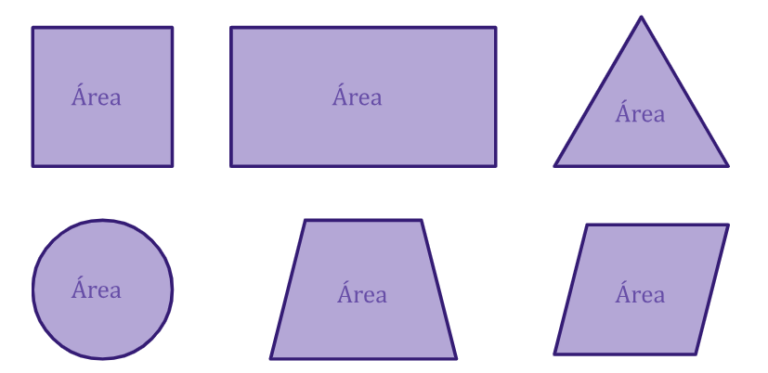
A medida da área vai depender das medidas utilizadas na figura. Por exemplo, um quadrado com lado em centímetros vai ter sua área em cm² .

Perímetros

O perímetro é uma medida que descreve o comprimento total de uma figura ou forma, que geralmente se refere à soma das medidas dos lados de uma figura geométrica. O cálculo do perímetro depende do tipo de figura que estamos considerando.

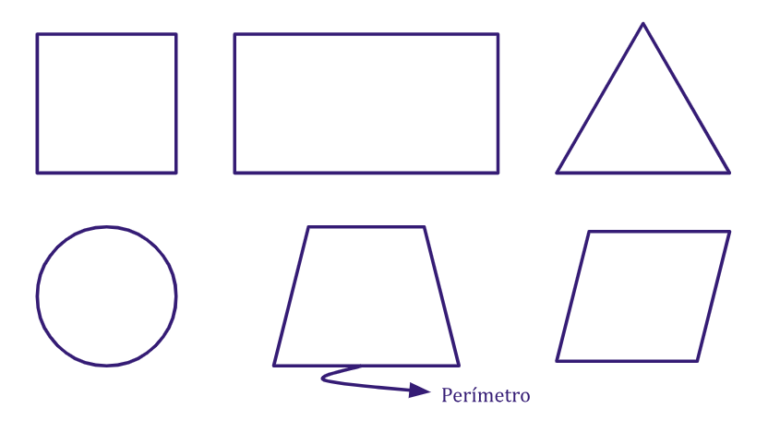
Conheça as principais figuras planas, conceitos e fórmulas

Na geometria plana, encontramos um fascinante mundo de formas e estruturas que desempenham papel fundamental em nossa compreensão do espaço e das relações entre diferentes elementos geométricos.

Triângulo

Um triângulo é uma figura geométrica plana composta por três lados e três ângulos. Os triângulos são uma das formas mais simples e fundamentais da geometria plana, além de estarem presentes em diversos ramos da Matemática e outras ciências.

Classificação de triângulos

Triângulo equilátero: todos os lados desse triângulo possuem comprimento igual e ângulos com a mesma medida.

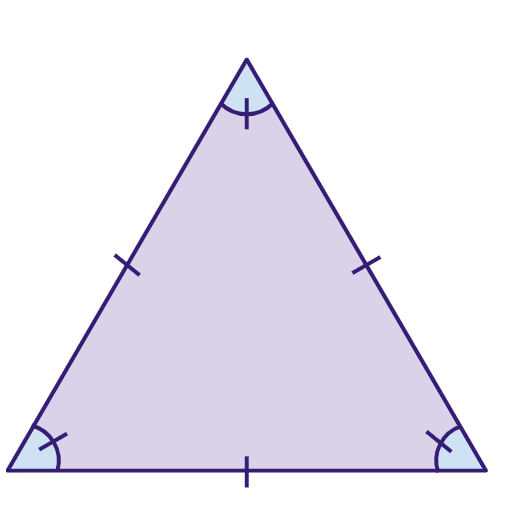
Triângulo isósceles: possui dois lados de comprimento iguais e ângulos da base com mesma medida.

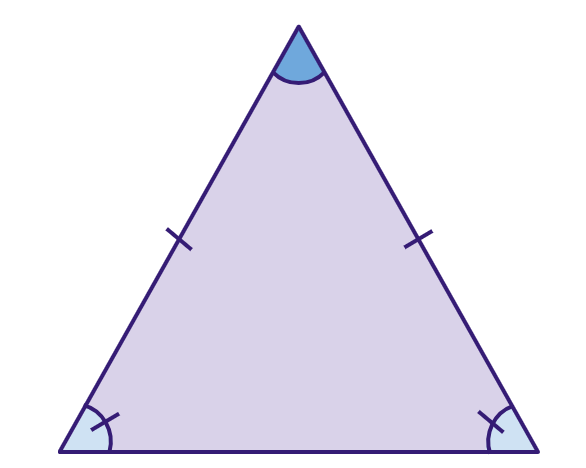
Triângulo escaleno: um triângulo em que todos os lados têm comprimentos diferentes.

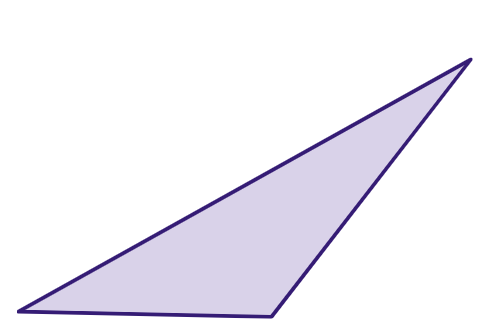
Classificação de triângulos por ângulos

Triângulo retângulo: um triângulo que tem um ângulo reto (90 graus).

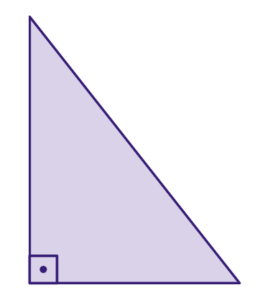
Triângulo acutângulo: todos os ângulos são agudos (menos de 90 graus).

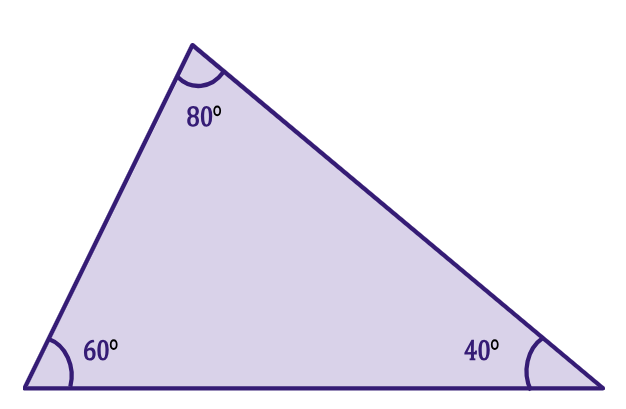
Triângulo obtusângulo: possui um ângulo obtuso (mais de 90 graus).

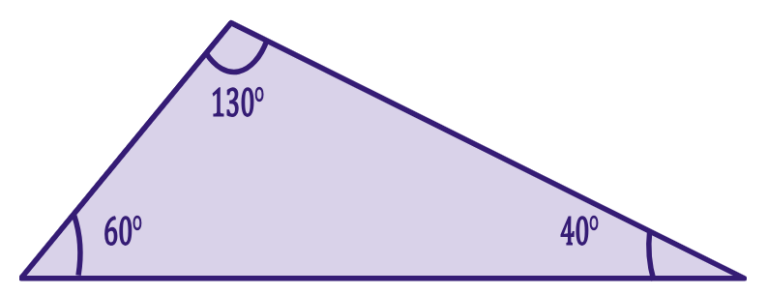
Propriedades importantes do triângulo

A soma dos ângulos internos de um triângulo sempre totaliza 180 graus.

Teorema de Pitágoras

O teorema de Pitágoras é aplicável a triângulos retângulos e estabelece a relação entre os lados de um triângulo retângulo: c² + b² = a², onde "c" e "b" são os comprimentos dos catetos e "a" é o comprimento da hipotenusa.

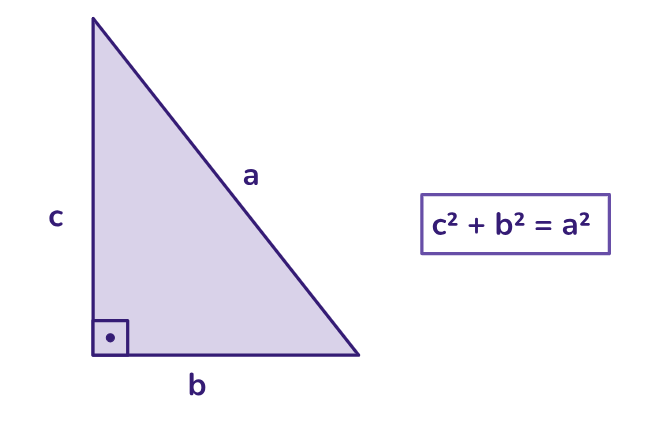
A desigualdade triangular afirma que a soma de quaisquer dois lados de um triângulo deve ser maior que o terceiro lado.

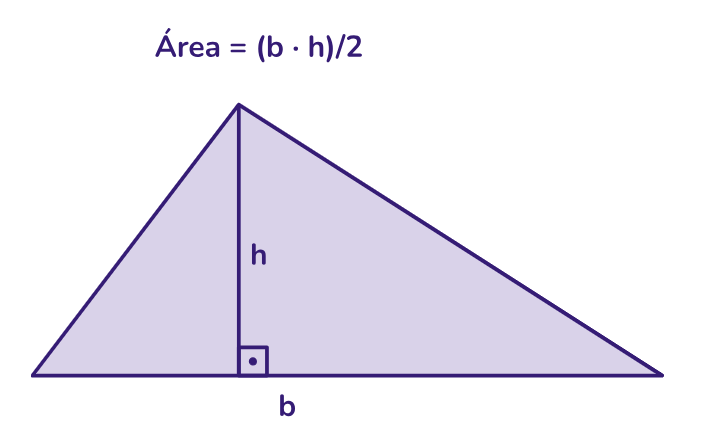
Área do triângulo

A fórmula básica para calcular a área de um triângulo é (base x altura) / 2, onde a base é o comprimento de um dos lados do triângulo e a altura é a distância perpendicular entre a base e o vértice oposto.

Quadrado

O quadrado é uma figura geométrica bidimensional que possui quatro lados de igual comprimento e quatro ângulos retos (90 graus). Isso significa que todos os lados do quadrado têm o mesmo comprimento e que seus ângulos internos medem exatamente 90 graus.

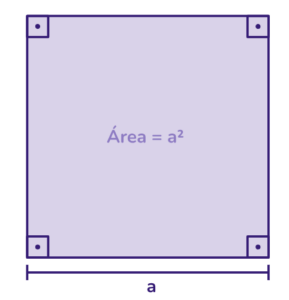
Área do quadrado: pode ser calculada multiplicando o comprimento de um de seus lados pelo próprio lado, sendo (a) o lado do quadrado temos que sua área é a².

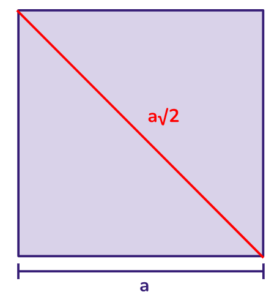
Diagonal do quadrado: um quadrado possui duas diagonais que conectam os vértices opostos. As diagonais de um quadrado também têm o mesmo comprimento e dividem o quadrado em dois triângulos retângulos idênticos. Seu comprimento é sempre a multiplicação do seu lado por √2.

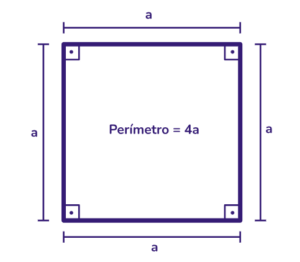
Perímetro do quadrado: o perímetro de um quadrado é a soma dos comprimentos de seus quatro lados: Perímetro = 4 . a.

Retângulo

Um retângulo é uma figura geométrica bidimensional que possui quatro lados e quatro ângulos retos (de 90 graus). Essa característica o torna um tipo específico de quadrilátero.

Propriedades fundamentais dos retângulos:

Os lados opostos de um retângulo têm o mesmo comprimento, o que significa que os lados adjacentes são iguais em pares.

Os diagonais de um retângulo têm o mesmo comprimento e se cruzam no centro do retângulo em ângulos retos.

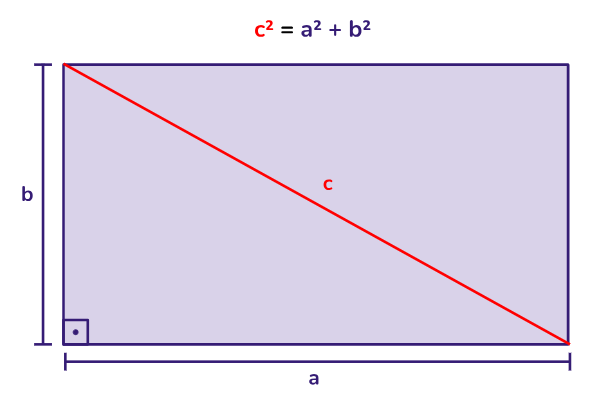
Área do retângulo: a área de um retângulo pode ser calculada multiplicando seu comprimento e largura: Área = Comprimento x Largura

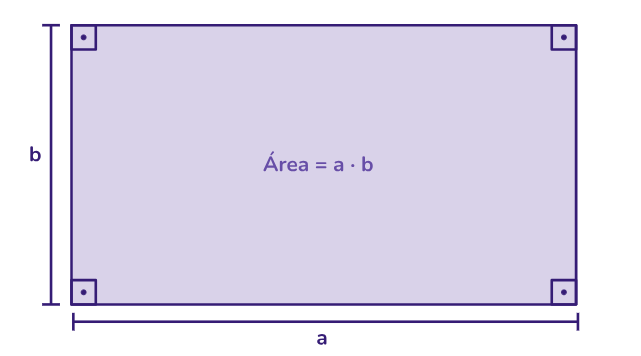
Perímetro do retângulo: o perímetro de um retângulo é a soma dos comprimentos de todos os seus lados: Perímetro = 2 x (comprimento + largura).

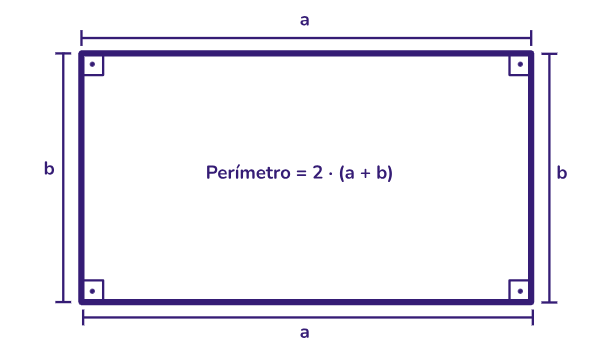
Observação: todo quadrado é um retângulo, porém nem todo retângulo é um quadrado.

Círculo

Um círculo é uma figura geométrica bidimensional que consiste em todos os pontos que estão a uma distância constante (raio) de um ponto central (centro). Essa distância é chamada de raio e é igual em todas as direções.

Elementos de um círculo

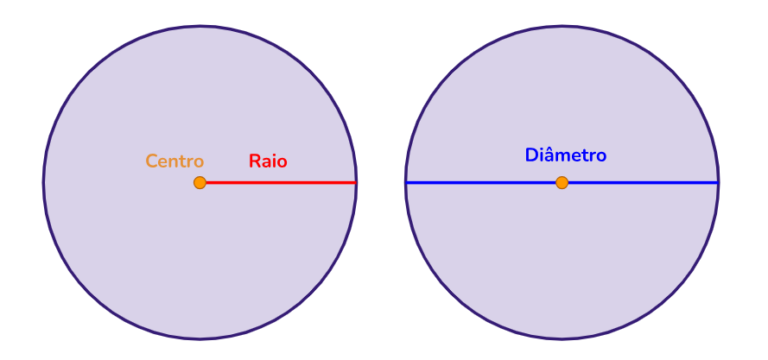
Centro: o ponto central do círculo a partir do qual todas as distâncias (raios) são medidas.

Raio: a distância do centro de um círculo a qualquer ponto na circunferência.

Circunferência: a linha curva que forma a fronteira do círculo, composta por todos os pontos a uma distância igual do centro.

Diâmetro: é dobro do raio. Ou seja, o diâmetro é uma linha que atravessa o centro do círculo e liga dois pontos opostos da circunferência.

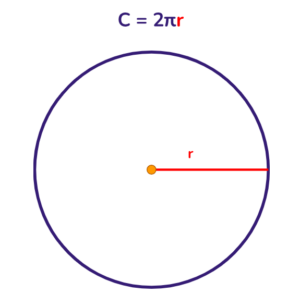
Perímetro do círculo: corresponde ao comprimento da circunferência de mesmo raio.

A medida do comprimento C de uma circunferência de raio r é dada por:

Comprimento de uma circunferência

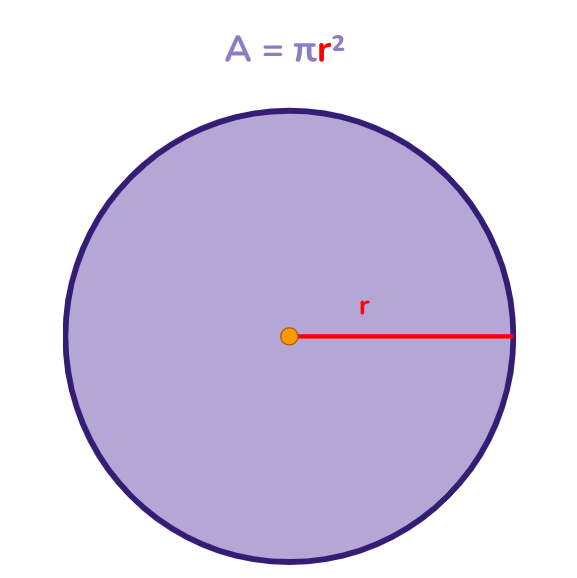
Área do círculo: é a medida de sua região interior. Em um círculo de raio r, sua área A é dada por

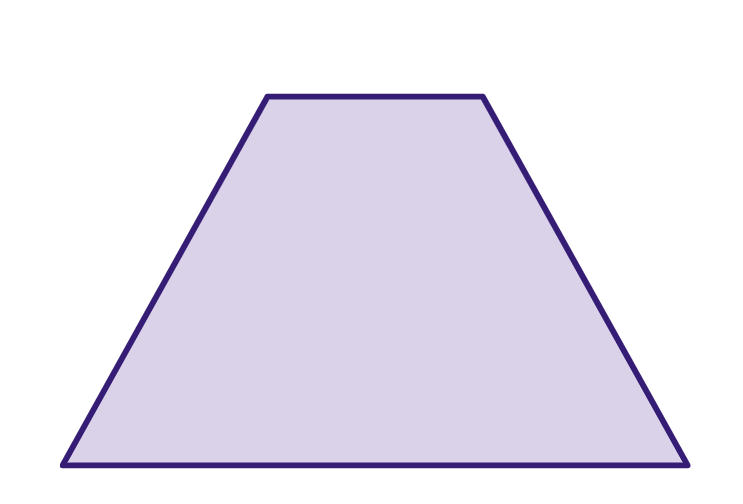
Trapézio

Um trapézio é um polígono de quatro lados em que pelo menos um par de lados é paralelo, mas os outros dois lados não são.

Lados e ângulos: um trapézio tem quatro lados e quatro ângulos. Os dois lados que são paralelos são chamados de bases, enquanto os outros dois lados são chamados de pernas ou não paralelos. As bases podem ter diferentes comprimentos, e as pernas também podem ter diferentes comprimentos.

Bases: as bases de um trapézio são as linhas paralelas que estão opostas uma à outra.

A base mais longa é chamada de "base maior", e a base mais curta é chamada de "base menor".

Altura: a altura de um trapézio é a distância perpendicular entre as duas bases. A altura é sempre medida entre as bases paralelas.

Os trapézios podem ser classificados em diferentes tipos, dependendo de suas características.

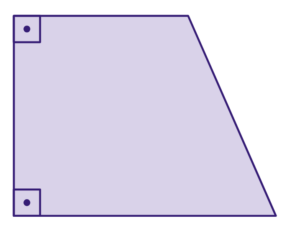
Trapézio retângulo: tem um ângulo reto (90 graus)

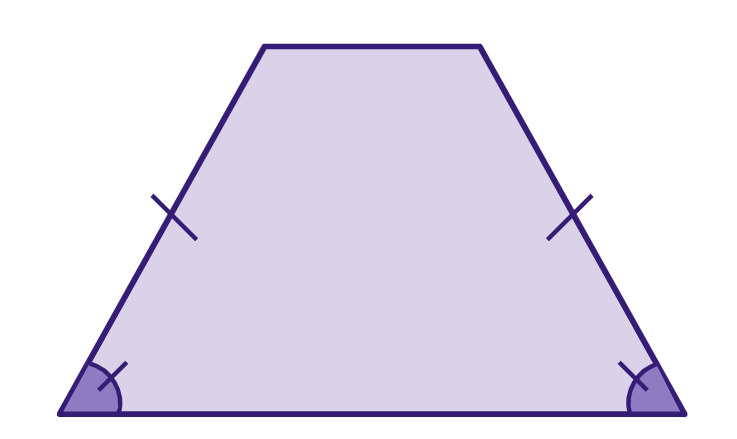
Trapézio isósceles: tem dois lados congruentes

Trapézio escaleno: tem lados de diferentes comprimentos

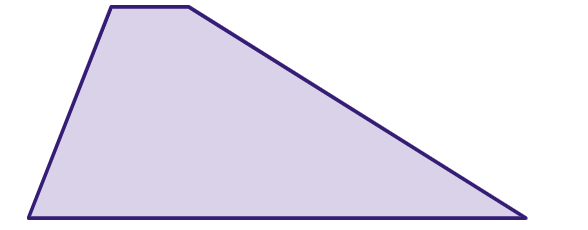
Perímetro do trapézio: é a soma dos comprimentos dos seus quatro lados.

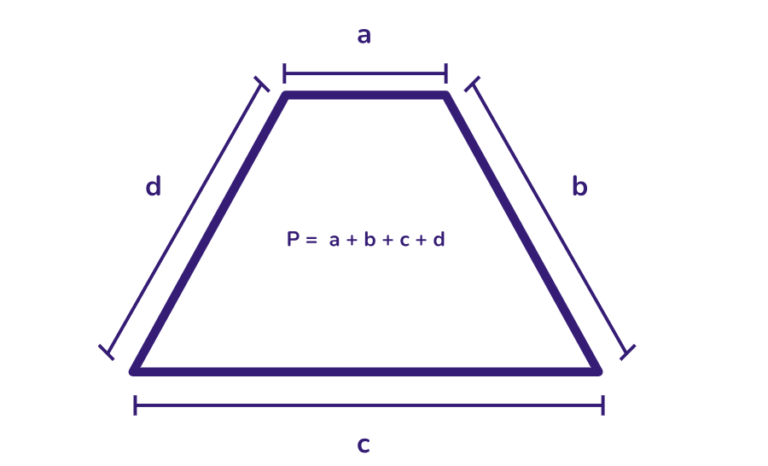
Área do trapézio: pode ser calculada usando a fórmula A = (1/2) . (soma das bases) . altura.

A altura é uma linha perpendicular às bases, que liga as duas bases paralelas.

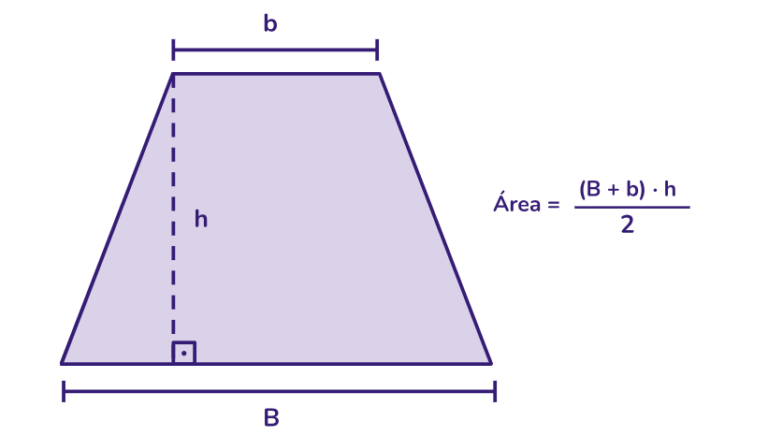
Área de um trapézio

Losango

Um losango é um quadrilátero (um polígono com quatro lados) que tem lados congruentes (todos os lados têm o mesmo comprimento) e ângulos opostos congruentes (todos os ângulos opostos têm o mesmo tamanho).

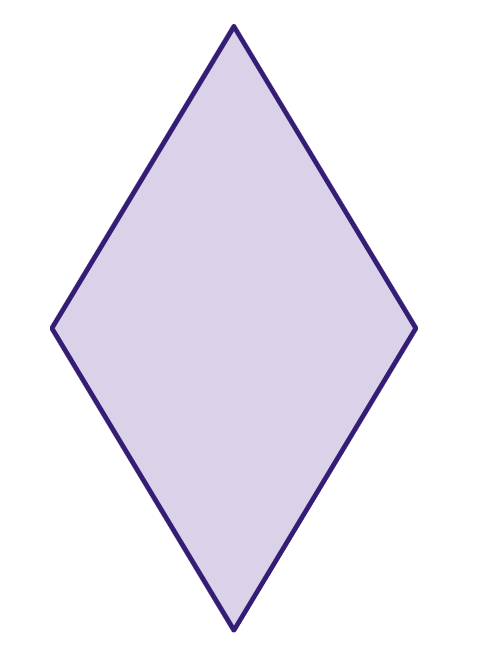
Área do losango: pode ser calculada usando a fórmula A = (diagonal maior * diagonal menor) / 2, onde "A" é a área, e as diagonais são as medidas das duas diagonais do losango.

Em um losango, as diagonais são sempre perpendiculares uma à outra.

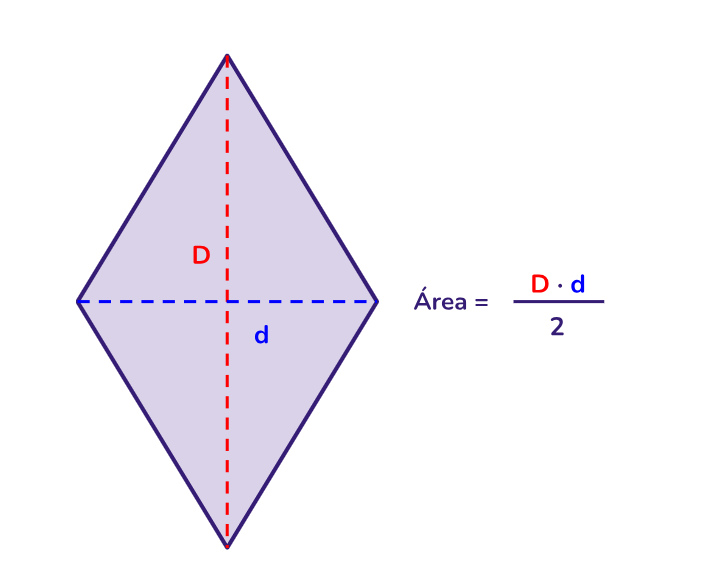
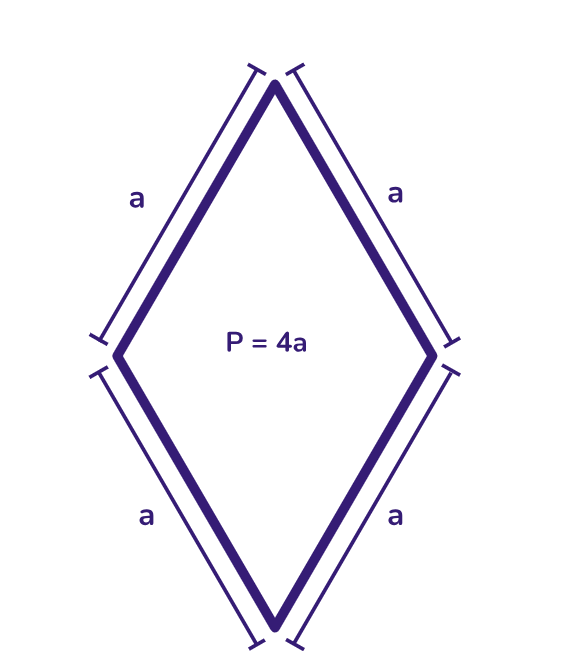
Perímetro: é a soma dos comprimentos de seus quatro lados.

QUESTÕES DE VESTIBULAR A ENEM

01) (Cefet/MG - 2016) A área quadrada de um sítio deve ser dividida em quatro partes iguais, também quadradas, e, em uma delas, deverá ser mantida uma reserva de mata nativa (área hachurada), conforme mostra a figura a seguir.

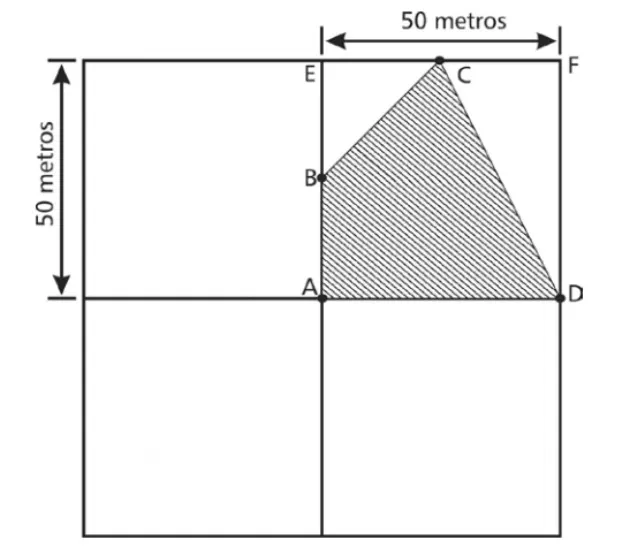
Sabendo-se que B é o ponto médio do segmento AE e C é o ponto médio do segmento EF, a área hachurada, em m², mede

(A) 625,0.

(B) 925,5.

(D) 2500,0.

Resolução:

Observando a figura, notamos que a área hachurada corresponde à área do quadrado de lado 50 m menos a área dos triângulos BEC e CFD.

A medida do lado BE, do triângulo BEC, é igual a 25 m, pois o ponto B divide o lado em dois segmentos congruentes (ponto médio do segmento).

O mesmo acontece com os lados EC e CF, ou seja, suas medidas também são iguais a 25 m, pois o ponto C é o ponto médio do segmento EF.

Assim, podemos calcular a área dos triângulos BEC e CFD. Considerando um dois lados conhecidos como a base, o outro lado será igual a altura, pois os triângulos são retângulos.

Calculando a área do quadrado e dos triângulos BEC e CFD, temos:

Portanto, a área hachurada, em m², mede 1562,5.

Alternativa: C

02) (IFSP - 2016) Uma praça pública em forma de circunferência tem raio de 18 metros. Diante do exposto, assinale a alternativa que apresenta sua área.

(A) 1.017,36 m²

(B) 1.254,98 m²

(D) 1.698,44 m²

(E) 1.710,34 m²

Resolução:

Para encontrar a área da praça, devemos utilizar a fórmula da área do círculo:

A = π.R²

Substituindo o valor do raio e considerando π = 3,14, encontramos:

A = 3,14 . 18² = 3,14 . 324 = 1 017, 36 m²

Portanto, a área da praça é de 1 017, 36 m².

Alternativa: A

03) (IFRS - 2016) Um retângulo tem dimensões x e y, que são expressas pelas equações x²= 12 e (y - 1)² = 3.

O perímetro e a área deste retângulo são, respectivamente

(A) 6√3 + 2 e 2 + 6√3
(B) 6√3 e 1 + 2√3
(C) 6√3 + 2 e 12
(D) 6 e 2√3
(E) 6√3 + 2 e 2√3 + 6

Resolução:

Primeiro vamos resolver as equações, para encontrar os valores de x e y:

x²= 12

x = √12

√4.3

2√3

(y - 1) ²= 3 ⇒ y = √3 + 1

O perímetro do retângulo será igual a soma de todos os lados:

P = 2.2√3 + 2. (√3 + 1) = 4√3 + 2√3 + 2 = 6√3 + 2

Para encontrar a área, basta multiplicar x.y:

A = 2√3 . (√3 + 1) = 2√3 + 6

Portanto, o perímetro e a área do retângulo são, respectivamente, 6√3 + 2 e 2√3 + 6.

Alternativa: E

04) (Aprendiz de Marinheiro - 2016) Analise a figura a seguir:

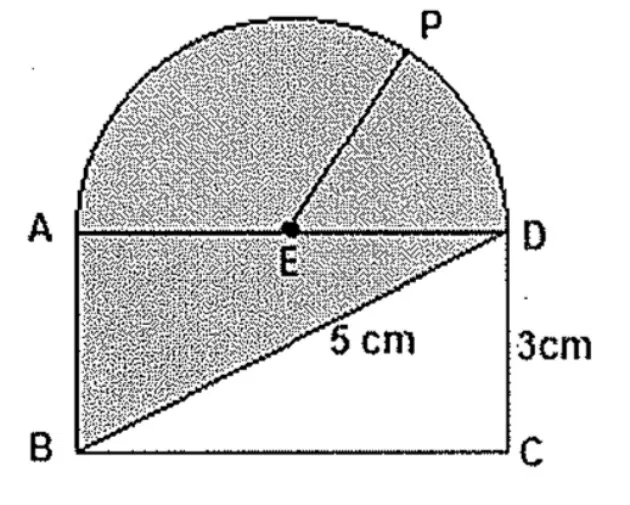
Sabendo que EP é o raio da semicircunferência de centro em E, como mostra a figura acima, determine o valor da área mais escura e assinale a opção correta. Dado: número π=3

(A) 10 cm²

(B) 12 cm²

(D) 10 cm²

(E) 24 cm²

Resolução:

A área mais escura é encontrada somando-se a área da semicircunferência com a área do triângulo ABD. Vamos começar calculando a área do triângulo, para isso, note que o triângulo é retângulo.

Vamos chamar o lado AD de x e calcular a sua medida através do teorema de Pitágoras, conforme indicado abaixo:

5²= x² + 3²
x² = 25 - 9
x = √16
x = 4

Conhecendo a medida do lado AD, podemos calcular a área do triângulo:

Precisamos ainda, calcular a área da semicircunferência. Note que o seu raio será igual a metade da medida do lado AD, assim, r = 2 cm. A área da semicircunferência será igual a:

A área mais escura será encontrada fazendo-se: A_T= 6 + 6 = 12 cm²

Portanto, o valor da área mais escura é 12 cm².

Alternativa: B

05) (Enem - 2016) Um senhor, pai de dois filhos, deseja comprar dois terrenos, com áreas de mesma medida, um para cada filho. Um dos terrenos visitados já está demarcado e, embora não tenha um formato convencional (como se observa na Figura B), agradou ao filho mais velho e, por isso, foi comprado. O filho mais novo possui um projeto arquitetônico de uma casa que quer construir, mas, para isso, precisa de um terreno na forma retangular (como mostrado na Figura A) cujo comprimento seja 7 m maior do que a largura.

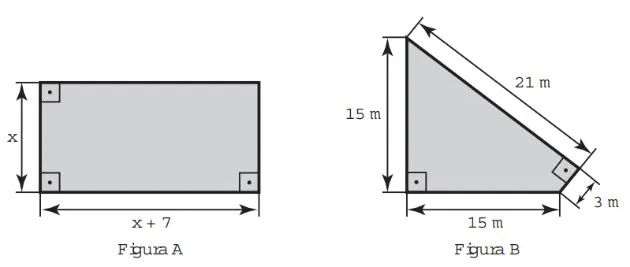Para satisfazer o filho mais novo, esse senhor precisa encontrar um terreno retangular cujas medidas, em metro, do comprimento e da largura sejam iguais, respectivamente, a

(A) 7,5 e 14,5

(B) 9,0 e 16,0

(D) 10,0 e 17,0

(E) 13,5 e 20,5

Resolução:

Como a área da figura A é igual a área da figura B, vamos primeiro calcular esta área. Para isso, vamos dividir a figura B, conforme imagem abaixo:

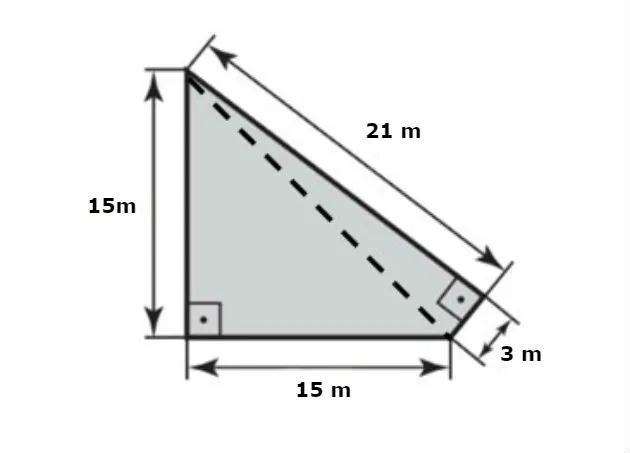Note que ao dividir a figura, temos dois triângulos retângulos. Sendo assim, a área da figura B será igual a soma das áreas desse triângulos. Calculando essas áreas, temos:

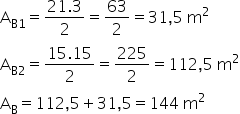
Sendo a figura A um retângulo, sua área é encontrada fazendo-se:

A_A = x . (x + 7)= x²+ 7x

Igualando a área da figura A com o valor encontrado para a área da figura B, encontramos:

x² + 7x = 144
x² + 7x - 144 = 0

Vamos resolver a equação do 2º grau, usando a fórmula de Bhaskara:

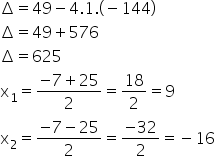
Como uma medida não pode ser negativa, vamos considerar apenas o valor igual a 9. Portanto, a largura do terreno da figura A será igual a 9 m e o comprimento será igual a 16 m (9+7).

Portanto, as medidas do comprimento e da largura devem ser iguais, respectivamente, a 9,0 e 16,0.

Alternativa: B

06) (Enem - 2015) Uma empresa de telefonia celular possui duas antenas que serão substituídas por uma nova, mais potente. As áreas de cobertura das antenas que serão substituídas são círculos de raio 2 km, cujas circunferências se tangenciam no ponto O, como mostra a figura.

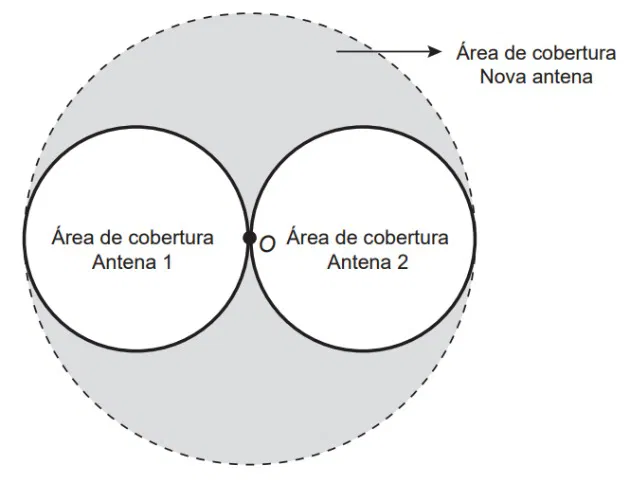
O ponto O indica a posição da nova antena, e sua região de cobertura será um círculo cuja circunferência tangenciará externamente as circunferências das áreas de cobertura menores. Com a instalação da nova antena, a medida da área de cobertura, em quilômetros quadrados, foi ampliada em

(A) 8 π

(B) 12 π

(D) 32 π

(E) 64 π

Resolução:

A ampliação da medida da área de cobertura será encontrada diminuindo-se as áreas dos círculos menores do círculo maior (referente a nova antena).

Como a circunferência da nova região de cobertura tangencia externamente as circunferências menores, seu raio será igual a 4 km, conforme indicado na figura abaixo:

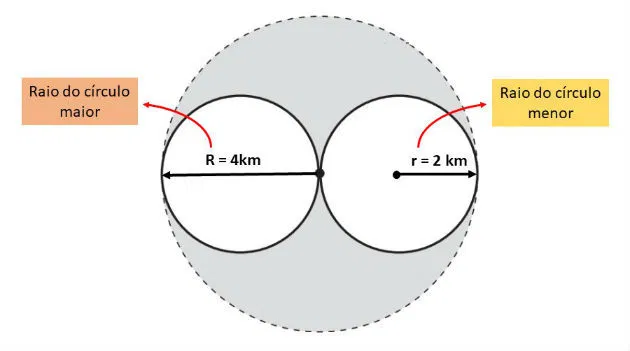Vamos calcular as áreas A₁ e A₂dos círculos menores e a área A₃ do círculo maior:

A₁= A₂ = 2² . π = 4 π
A₃ = 4².π = 16 π

A medida da área ampliada será encontrada fazendo-se:

A = 16 π - 4 π - 4 π = 8 π

Portanto, com a instalação da nova antena, a medida da área de cobertura, em quilômetros quadrados, foi ampliada em 8 π.

Alternativa: A

07) (Enem - 2015) O esquema I mostra a configuração de uma quadra de basquete. Os trapézios em cinza, chamados de garrafões, correspondem a áreas restritivas.

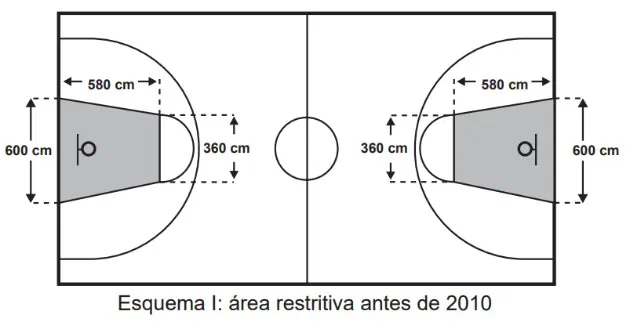Visando atender as orientações do Comitê Central da Federação Internacional de Basquete (Fiba) em 2010, que unificou as marcações das diferentes ligas, foi prevista uma modificação nos garrafões das quadras, que passariam a ser retângulos, como mostra o Esquema II.

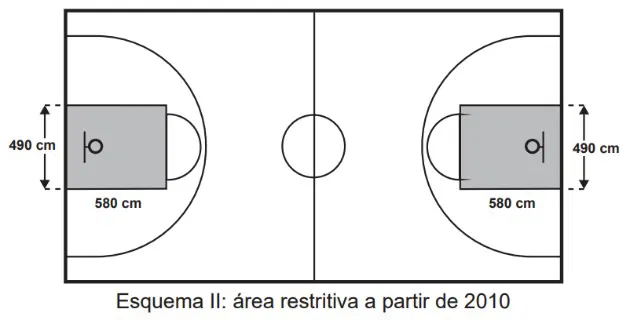Após executadas as modificações previstas, houve uma alteração na área ocupada por cada garrafão, que corresponde a um(a)

(A) aumento de 5 800 cm².

(B) aumento de 75 400 cm².

(D) diminuição de 63 800 cm².

(E) diminuição de 272 600 cm².

Resolução:

Para descobrir qual foi a alteração na área ocupada, vamos calcular a área antes e depois da alteração.

No cálculo do esquema I, utilizaremos a fórmula da área do trapézio. Já no esquema II, usaremos a fórmula da área do retângulo.

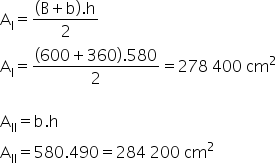
A alteração da área será então:

A = A_II- A_I
A = 284 200 - 278 400 = 5 800 cm²

Portanto, após executadas as modificações previstas, houve uma alteração na área ocupada por cada garrafão, que corresponde a um aumento de 5 800 cm².

Alternativa: A

08) Ana decidiu construir uma piscina retangular em sua casa com as medidas 8 m de base por 5 m de altura. Ao redor dela, em forma de trapézio, foi preenchido com grama.

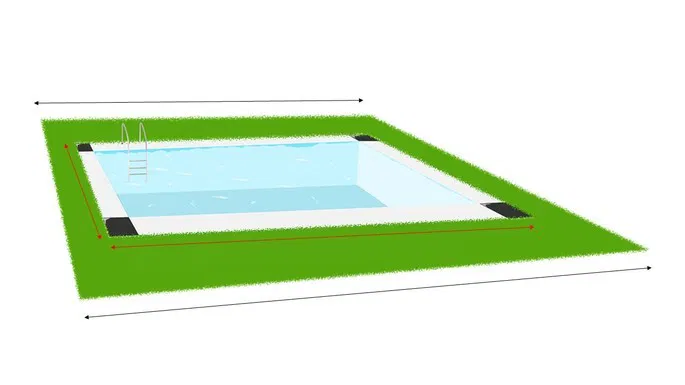Sabendo que a altura do trapézio é 11 m e as suas bases são 20 m e 14 m, qual a área da parte que foi preenchida com grama?

(A) 294 m²

(B) 153 m²

(D) 216 m²

Resolução:

Como o retângulo, que representa a piscina, está inserido dentro de uma figura maior, o trapézio, vamos iniciar calculando a área da figura externa.

A área do trapézio é calculada pela fórmula:

Onde,

B é a medida da base maior;
b é a medida da base menor;
h é a altura.

Substituindo na fórmula os dados do enunciado, temos:

Agora, vamos calcular a área do retângulo. Para isso, precisamos apenas multiplicar a base pela altura.

A = b . h

A = 8 . 5

A = 40m²

Para encontrar a área coberta por grama, precisamos subtrair da área do trapézio o espaço ocupado pela piscina.

187 m² – 40km² = 147m²

Portanto, a área preenchida com grama foi de 147 m².

Alternativa: C

09) Para reformar o telhado de seu armazém, Carlos decidiu comprar telhas colonial. Utilizando este tipo de cobertura são necessárias 20 peças para cada metro quadrado de telhado.

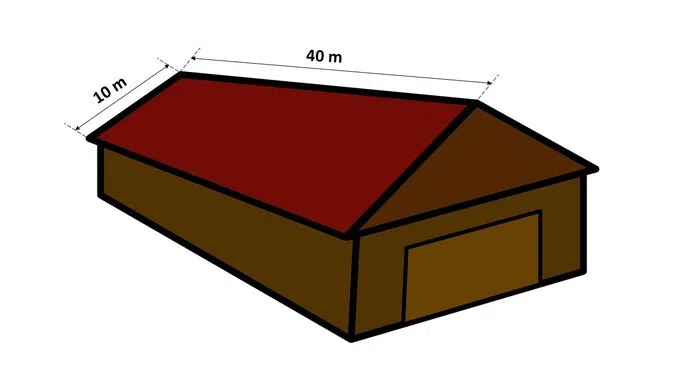
Se a cobertura do local é formada por duas placas retangulares, como na figura acima, quantas telhas Carlos precisa comprar?

(A) 12000 telhas

(B) 16000 telhas

(D) 9600 telhas

Resolução:

A cobertura do armazém é feita por duas placas retangulares. Portanto, devemos calcular a área de um retângulo e multiplicar por 2.

A = b . h

A = 40 . 10

A = 400m²

2 . 400 = 800m²

Sendo assim, a área total do telhado é 800 m². Se cada metro quadrado necessita de 20 telhas, através de uma regra de três simples calculamos quantas telhas preenchem o teto de todo armazém.

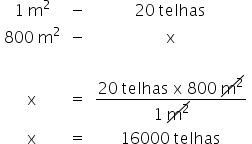
Portanto, será necessário comprar 16 mil telhas.

Alternativa: B

10) Márcia gostaria de dois vasos de madeira idênticos para decorar a entrada da sua casa. Por só conseguir comprar um do que mais gostou, ela decidiu contratar um marceneiro para construir outro vaso com as mesmas dimensões. O vaso deve ter as quatro faces laterais em forma de trapézio isósceles e a base é um quadrado.

Sem levar em consideração a espessura da madeira, quantos metros quadrados de madeira serão necessários para reproduzir a peça?

(A) 0,2131 m²

(B) 0,1311 m²

(D) 0,3121 m²

Resolução:

Um trapézio isósceles é o tipo que possui os lados iguais e bases com medidas diferentes. Pela imagem, temos as seguintes medidas do trapézio de cada lateral do vaso:

Base menor (b): 19 cm;
Base maior (B): 27 cm;
Altura (h): 30 cm.

De posse dos valores, calculamos a área do trapézio:

Como o vaso é formado por quatro trapézios precisamos multiplicar por quatro a área encontrada.

4 . 690m² = 2760m²

Agora, precisamos calcular a base do vaso, que é formada por um quadrado de lado 19 cm.

A = L . L

A = 19 . 19

A = 362cm²

Somando-se as áreas calculadas chegamos a área total de madeira a ser utilizada para construir.

A_t = 2760 + 361

A_t = 3121cm²

Entretanto, a área precisa ser apresentada em metros quadrado.

3121 : 10000 = 0,3121m²

Portanto, sem levar em consideração a espessura da madeira, foram necessários 0,3121 m² de material para fabricar o vaso.

Alternativa: D

11) Qual é a área de um losango que possui diagonal menor medindo 5 centímetros, sabendo que a diagonal maior é o triplo da diagonal maior:

(A) 35 cm²

(B) 37,5 cm²

(D) 70 cm²

(E) 45 cm²

Resolução

d = comprimento da diagonal menor

D = comprimento da diagonal maior

Sabendo que a diagonal menor mede 5 cm e que a diagonal maior mede o triplo da menor, então, temos que:

d = 5 e D = 5 · 3 = 15

Agora calculando a área, temos que:

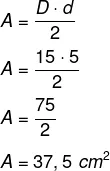
Alternativa: B

12) (IFG 2012) Em um retângulo, a razão entre a medida da altura e a medida da base é de 2/5, e o perímetro desse retângulo mede 42 cm. A área desse retângulo em cm² é igual a:

(A) 88

(B) 90

(D) 94

(E) 96

Resolução

Seja 2x a altura e 5x a base, temos que:

P = 2 (2x + 5x) = 42

4x + 10x = 42

14x = 42

x = 42/14

x = 3

Então, os lados medem:

2x = 2 . 3 = 6

5x = 5 . 3 = 15

Agora, basta calcular a sua área:

A = 6 . 15 = 90

Alternativa: B

13) (Enem 2016) Um senhor, pai de dois filhos, deseja comprar dois terrenos, com áreas de mesma medida, um para cada filho. Um dos terrenos visitados já está demarcado e, embora não tenha um formato convencional (como se observa na Figura B), agradou ao filho mais velho e, por isso, foi comprado. O filho mais novo possui um projeto arquitetônico de uma casa que quer construir, mas, para isso, precisa de um terreno na forma retangular (como mostrado na Figura A) cujo comprimento seja 7 m maior do que a largura.

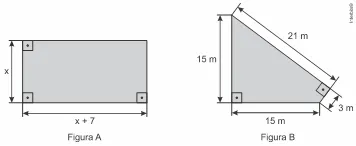
Para satisfazer o filho mais novo, esse senhor precisa encontrar um terreno retangular cujas medidas, em metro, do comprimento e da largura sejam iguais, respectivamente, a

(A) 7,5 e 14,5.

(B) 9,0 e 16,0.

(D) 10,0 e 17,0.

(E) 13,5 e 20,5.

Resolução:

Primeiro calcularemos a área da figura B. Podemos dividir essa área em dois triângulos retângulos, o primeiro com base igual a 3 m e altura igual a 21 m e o segundo com base e altura iguais a 15 m, então, temos que:

A = (15 ⸳ 15) : 2 + (3 ⸳ 21) : 2 = 112,5 + 31,5 = 144

Por outro lado, sabemos que as áreas são as mesmas, então, temos que:

x (x + 7) = 144

Analisando os divisores de 144, temos que 9 ⸳ (9 + 7) = 9 ⸳ 16 = 144.

Nesse caso, temos que x = 9 e x + 7 = 16.

Alternativa: B

14) (Enem 2020 - digital) Uma empresa deseja construir um edifício residencial de 12 pavimentos, num lote retangular de lados medindo 22 e 26 m. Em 3 dos lados do lote serão construídos muros. A frente do prédio será sobre o lado do lote de menor comprimento. Sabe-se que em cada pavimento 32 m² serão destinados à área comum (hall de entrada, elevadores e escada), e o restante da área será destinado às unidades habitacionais. A legislação vigente exige que prédios sejam construídos mantendo distâncias mínimas dos limites dos lotes onde se encontram. Em obediência à legislação, o prédio ficará 5 m afastado da rua onde terá sua entrada, 3 m de distância do muro no fundo do lote e 4 m de distância dos muros nas laterais do lote, como mostra a figura.

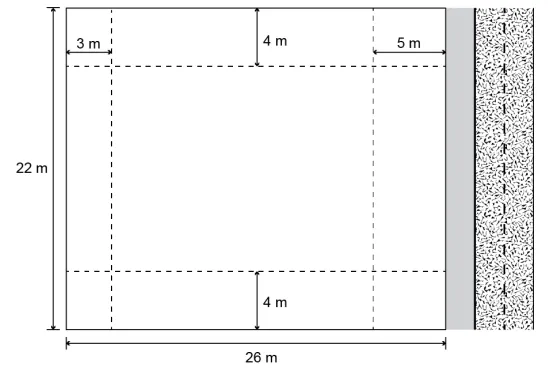
A área total, em metro quadrado, destinada às unidades habitacionais desse edifício será de

(A) 2640.

(B) 3024.

(D) 6480.

(E) 6864.

Resolução:

Para encontrar as medidas do retângulo central, na altura de 22 metros, é necessário subtrair o espaço que não será utilizado. Esse espaço é de 4 metros, tanto em cima quanto em baixo, então, temos que 22 – 4 – 4 = 14 m. Analisando a base do retângulo que mede 26 metros, é necessário subtrair 3 m e 5 m, então, 26 – 3 – 5 = 18 m. Assim, área construída é de 18 ⸳ 14 = 252 m.

Nessa área de 252 m², serão retirados 32 m² para a área de convivência, então, 252 – 32 = 220. Agora, multiplicando pelos 12 pavimentos, temos que 220 ⸳ 12 = 2640.

Alternativa: A

15) (Enem) João tem uma loja onde fabrica e vende moedas de chocolate com diâmetro de 4 cm e preço de R$ 1,50 a unidade. Pedro vai a essa loja e, após comer várias moedas de chocolate, sugere ao João que ele faça moedas com 8 cm de diâmetro e mesma espessura e cobre R$ 3 a unidade. Considerando que o preço da moeda depende apenas da quantidade de chocolate, João

(A) aceita a proposta de Pedro, pois, se dobra o diâmetro, o preço também deve dobrar.

(B) rejeita a proposta de Pedro, pois o preço correto seria R$ 12.

(D) rejeita a proposta de Pedro, pois o preço correto seria R$ 6.

(E) rejeita a proposta de Pedro, pois o preço correto seria R$ 4,50.

Resolução:

Calcularemos a área em cada um dos casos:

r1 = 4 cm

A1 = πr² = π4² = 16π

r2 = 8

A2 = πr² = π8² = 64π

Ao dividir 64π por 16π, temos como resposta 4, o que significa que o gasto com a moeda maior é 4 vezes maior, logo, o valor ideal de venda seria 1,50 ⸳ 4 = 6,00.

Alternativa: D

16) (Enem - PPL) A logomarca de uma empresa de computação é um quadrado, AEFG, com partes pintadas como mostra a figura. Sabe-se que todos os ângulos agudos presentes na figura medem 45° e que AB = BC = CD = DE. A fim de divulgar a marca entre os empregados, a gerência decidiu que fossem pintadas logomarcas de diversos tamanhos nas portas, paredes e fachada da empresa. Pintadas as partes cinzas de todas as logomarcas, sem desperdício e sem sobras, já foram gastos R$ 320.

O preço das tintas cinza, preta e branca é o mesmo.

Considerando que não haja desperdício e sobras, o custo para pintar as partes pretas e o custo para pintar as partes brancas serão, respectivamente,

(A) R$ 320 e R$ 640.

(B) R$ 640 e R$ 960.

(D) R$ 1280 e R$ 2240.

(E) R$ 2240 e R$ 2560.

Resolução:

Analisando a imagem, sabemos que a área do logotipo todo é igual a 8 vezes as áreas pintadas de cinza, logo, o custo com o todo será de 320 ⸳ 8 = R$ 2560.

Sabemos que a área da parte branca é metade da área total:

R$ 2560 : 2 = R$ 1280

Para pintar a área preta, o custo será de 2560 – 320 – 1280 = R$ 960.

Então, os custos das partes preta e branca serão de, respectivamente, R$ 960 e R$ 1280.

Alternativa: C

17) (Enem - PPL) Na zona rural, a utilização de unidades de medida como o hectare é bastante comum. O hectare equivale à área de um quadrado de lado igual a 100 metros. Na figura, há a representação de um terreno por meio da área em destaque. Nesta figura, cada quadrado que compõe esta malha representa uma área de 1 hectare.

O terreno em destaque foi comercializado pelo valor R$ 3.600.000. O valor do metro quadrado desse terreno foi de

(A) R$ 30.

(B) R$ 300.

(D) R$ 3600.

(E) R$ 300.000.

Resolução:

Primeiro calcularemos a área do quadrado:

A = l²

A = 100² = 10.000

Há 12 quadrados na área, então 12 ⸳ 10.000 = 120.000 m². Para saber o custo de cada quadrado, basta dividir o valor pago pelo terreno pela sua área:

3.600.000 : 120.000 = R$ 30

Alternativa: A

18) (Enem) Para decorar a fachada de um edifício, um arquiteto projetou a colocação de vitrais compostos de quadrados de lado medindo 1 m, conforme a figura a seguir.

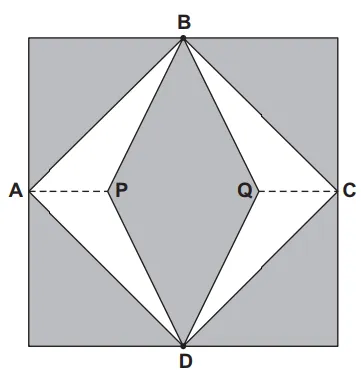
Nesta figura, os pontos A, B, C e D são pontos médios dos lados do quadrado e os segmentos AP e QC medem 1/4 da medida do lado do quadrado. Para confeccionar um vitral, são usados dois tipos de materiais: um para a parte sombreada da figura, que custa R$ 30 o m², e outro para a parte mais clara (regiões ABPDA e BCDQB), que custa R$ 50 o m².

De acordo com esses dados, qual é o custo dos materiais usados na fabricação de um vitral?

(A) R$ 22,50

(B) R$ 35

(D) R$ 42,50

(E) R$ 45

Resolução:

A área da região branca é igual a 4 vezes a área dos triângulos, pois ela é formada por 4 triângulos congruentes.

A área de um dos triângulos brancos possui base igual a 1/4 = 0,25 metro, e altura igual a 1/2 = 0,5 metro, então, a área de 4 desses triângulos é igual a:

A = 4 (0,25 ⸳ 0,5) : 2

A = 2 (0,25 ⸳ 0,5)

A = 0,25 m²

A área escura é a diferença entre a área do quadrado e a área branca.

Área do quadrado = 1² = 1

1 – 0,25 = 0,75

Calcula-se o preço do vitral por meio do produto da área de cada região pelo valor do m²:

V = 0,25 ⸳ 50 + 0,75 ⸳ 30

V = 12,5 + 22,5 = 35 reais

Alternativa: B

19) (Enem) Jorge quer instalar aquecedores no seu salão de beleza para melhorar o conforto dos seus clientes no inverno. Ele estuda a compra de unidades de dois tipos de aquecedores: modelo A, que consome 600 g/h (gramas por hora) de gás propano e cobre 35 m² de área, ou modelo B, que consome 750 g/h de gás propano e cobre 45 m² de área. O fabricante indica que o aquecedor deve ser instalado em um ambiente com área menor do que a da sua cobertura. Jorge vai instalar uma unidade por ambiente e quer gastar o mínimo possível com gás. A área do salão que deve ser climatizada encontra-se na planta seguinte (ambientes representados por três retângulos e um trapézio).

Avaliando-se todas as informações, serão necessários

(A) quatro unidades do tipo A e nenhuma unidade do tipo B.

(B) três unidades do tipo A e uma unidade do tipo B.

(D) uma unidade do tipo A e três unidades do tipo B.

(E) nenhuma unidade do tipo A e quatro unidades do tipo B.

Resolução:

É necessário calcular cada uma das áreas. As figuras I, II e III são retângulos, então, para calcular suas áreas, basta multiplicar suas bases e suas alturas.

A_I = 8 ⸳ 6 = 40 m²

A_II = 6 ⸳ 5 = 30 m²

A_III = 4 ⸳ 6 = 24 m²

A área IV possui formato de um trapézio, então, temos que:

Assim, atendendo as recomendações, será utilizado o modelo A nos ambientes II e III, e o modelo B nos ambientes I e IV.

Alternativa: C

20) (Enem - PPL) Uma escola tem um terreno vazio no formato retangular cujo perímetro é 40 m, onde se pretende realizar uma única construção que aproveite o máximo de área possível.

Após a análise realizada por um engenheiro, este concluiu que, para atingir o máximo de área do terreno com uma única construção, a obra ideal seria

(A) um banheiro com 8 m².

(B) uma sala de aula com 16 m².

(D) um pátio com 100 m².

(E) uma quadra com 160 m².

Resolução:

Para encontrar a área desse terreno, basta supor que ele seja um quadrado (a figura mais simples na qual podemos pensar) com o perímetro igual a 40. Assim, temos que:

40 : 4 = 10 metros

A área de um quadrado de 10 metros é igual a 10² = 100 m.

Como a área máxima desse terreno é de 100 metros quadrados, então podemos construir um pátio com 100 m².

Alternativa: D

21) (Enem) O prefeito de uma cidade deseja promover uma festa popular no parque municipal para comemorar o aniversário de fundação do município. Sabe-se que esse parque possui formato retangular, com 120 m de comprimento por 150 m de largura. Além disso, para segurança das pessoas presentes no local, a polícia recomenda que a densidade média, num evento dessa natureza, não supere quatro pessoas por metro quadrado.

Seguindo as recomendações de segurança estabelecidas pela polícia, qual é o número máximo de pessoas que poderão estar presentes na festa?

(A) 1000

(B) 4500

(D) 72.000

(E) 120.000

Resolução:

Calculando a área do terreno, temos que A = 120 ⸳ 150 = 18.000.

Há 4 pessoas por m², então, para seguir a recomendação, o número máximo de pessoas nesse evento é dado por 4 ⸳ 18.000 = 720.000.

Alternativa: D

22) (Enem 2020) Um fazendeiro possui uma cisterna com capacidade de 10.000 litros para coletar a água da chuva. Ele resolveu ampliar a área de captação da água da chuva e consultou um engenheiro que lhe deu a seguinte explicação: “Nesta região, o índice pluviométrico anual médio é de 400 milímetros. Como a área de captação da água da chuva de sua casa é um retângulo de 3 m de largura por 7 m de comprimento, sugiro que aumente essa área para que, em um ano, com esse índice pluviométrico, o senhor consiga encher a cisterna, estando ela inicialmente vazia”.

Sabe-se que o índice pluviométrico de um milímetro corresponde a um litro de água por metro quadrado. Considere que as previsões pluviométricas são cumpridas e que não há perda, por nenhum meio, no armazenamento da água.

Em quantos metros quadrados, no mínimo, o fazendeiro deve aumentar a área de captação para encher a cisterna em um ano?

(A) 1,6

(B) 2,0

(D) 15,0

(E) 25,0

Resolução:

A área de captação de chuva da casa do fazendeiro é retangular, então, é calculada pela multiplicação 7 ⸳ 3 = 21 m². Sabemos que o volume anual de água captada, dado que está na cisterna, é de 10.000 e que o índice pluviométrico anual é de 400, então, a razão entre 10.000 e 400 é igual a 25 m². Calculando a diferença entre a área da fazenda e a área de captação, 25 – 21 = 4 m².

Alternativa: C

23) (Omini 2021 - adaptada) Wilson tem um terreno retangular e desejando plantar uma horta, colocou dois irrigadores nesse terreno, ambos com alcance circular de raio igual a 4 metros, como na figura abaixo.

A área que os irrigadores não alcançam será uma parte do terreno em que Wilson não fará a horta. Qual o valor dessa área? Utilize π = 3,14.

(A) 100,48 m²

(B) 36,48 m²

(D) 27,52 m²

(E) 22,32 m²

Resolução:

Como o raio é de 4 metros, esse terreno possui 4 ⸳ 4 = 16 metros de comprimento e 4 ⸳ 2 = 8 metros de largura, então, sua área é igual a 16 ⸳ 8 = 128 m².

Agora, calcularemos a área das circunferências, A = π r².

A = 3,14 ⸳ 4 ²

A = 3,14 ⸳ 16

A = 50,24

Assim, a área que queremos é a diferença entre a área do retângulo e a área dos dois círculos:

128 – 2 ⸳ 50,24
128 – 100,48 = 27,52 m²

Alternativa: D

24) (Enem - segunda aplicação) O banheiro de uma escola pública, com paredes e piso em formato retangular, medindo 5 metros de largura, 4 metros de comprimento e 3 metros de altura, precisa de revestimento no piso e nas paredes internas, excluindo a área da porta, que mede 1 metro de largura por 2 metros de altura. Após uma tomada de preços com cinco fornecedores, foram verificadas as seguintes combinações de azulejos para as paredes e de lajotas para o piso, com os preços dados em reais por metro quadrado, conforme a tabela.

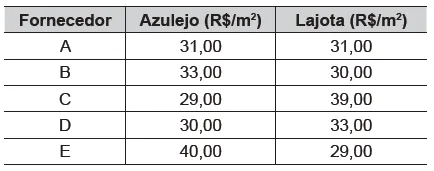
Desejando-se efetuar a menor despesa total, deverá ser escolhido o fornecedor:

(A) A

(B) B

(D) D

(E) E

Resolução:

Primeiro calcularemos a área de cada uma das dimensões do banheiro:

Área da parede:

2 (5 ⸳ 3) + 2 ⸳ (4 ⸳ 3) = 30 + 24 = 54 m²

É necessário retirar a área da porta e as áreas da parede.

Área da porta:

2 ⸳ 1 = 2 m²

54 – 2 = 52 m².

A área da lajota é igual a 5 ⸳ 4 = 20 m².

Agora encontraremos o valor gasto em cada caso:

A: (52 × 31,00) + (20 × 31,00) = 1612 + 620 = R$ 2232

B: (52 × 33,00) + (20 × 30,00) = 1716 + 600 = R$ 2316

C: (52 × 29,00) + (20 × 39,00) = 1508 + 780 = R$ 2288

D: (52 × 30,00) + (20 × 33,00) = 1560 + 660 = R$ 2220

E: (52 × 40,00) + (20 × 29,00) = 1716 + 600 = R$ 2316

Então, a melhor opção é o fornecedor D.

25) (IFG 2017 - adaptada) A área de lazer da fazenda da Dona Helena tem o formato retangular com 15 m de comprimento e 12 m de largura. Existe uma piscina de adulto e uma infantil com o formato circular de raios 3 m e 2 m respectivamente. Helena pretende pintar o chão de toda a área de lazer no tom de verde. Um galão de tinta é recomendável para pintar 11 m². Quantos galões de tinta Dona Helena deve comprar para pintar a área desejada sabendo que as piscinas não serão pintadas? (Dado π = 3)

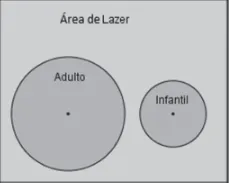
(A) 14 galões

(B) 13 galões

(D) 11 galões

(E) 10 galões

Resolução:

Primeiro encontraremos a área do terreno:

A_T= 15 ⸳ 12 = 180 m²

Agora calcularemos a área de cada uma das piscinas.

Área da piscina adulto A₁

A₁ = π ⸳ 3² = 3 ⸳ 3² = 27 m²

Área piscina infantil A₂

A₂ = π ⸳ 2² = 3 ⸳ 2² = 12 m²

Então, a área de lazer A:

A = A_T – A₁ – A₂ = 180 – 27 – 12 = 141 m²

Sabemos que um galão pinta 11 m², então vamos dividir 141 por 11 para encontrar o número de galões.

141 : 11 = 12,82

Assim, o número de galões necessários é de 13 m².

Alternativa: B

26) (G1 - IFAL) Julgue as afirmativas abaixo e assinale a alternativa correta.

I. Todo paralelogramo é losango.

II. Se um quadrilátero tem todos os lados com a mesma medida, então esse quadrilátero é um quadrado.

III. As diagonais de um quadrado são perpendiculares entre si.

(A) Só I é verdadeira.

(B) Só II é verdadeira.

(D) I e III são verdadeiras.

(E) II e III são verdadeiras.

Resolução

I) Falsa. Um losango é um paralelogramo de lados todos com a mesma medida.
II) Falsa. Um quadrado deve ter todos os lados com a mesma medida e além disto todos os ângulos devem ser retos.
III) Verdadeira. As diagonais de um quadrado são sempre perpendiculares entre si.

Alternativa: C

27) (Ufrgs) Assinale a alternativa que apresenta corretamente os valores, na mesma unidade de medida, que podem representar as medidas dos lados de um triângulo.

(A) 1 – 2 – 4

(B) 3 – 2 – 6

(D) 3 – 9 – 4

(E) 6 – 4 – 5

Resolução:

Condições para representar um triângulo: “qualquer um dos lados é menor que a soma dos outros dois e maior que o valor absoluto da diferença entre esses lados”. Assim, conseguimos escrever uma expressão matemática da seguinte maneira: "se somar dois lados não pode ser menor que o lado restante".

|4−5| < 6 < 4 + 5
|4−6| < 5 < 4 + 6
|5−6| < 4 < 5 + 6

A única opção que tal condição satisfaz é 6 - 4 - 5.

Alternativa: E

28) (Enem) Para garantir a segurança de um grande evento público que terá início às 4 h da tarde, um organizador precisa monitorar a quantidade de pessoas presentes em cada instante. Para cada 2.000 pessoas se faz necessária a presença de um policial. Além disso, estima-se uma densidade de quatro pessoas por metro quadrado de área de terreno ocupado. Às 10 h da manhã, o organizador verifica que a área de terreno já ocupada equivale a um quadrado com lados medindo 500m. Porém, nas horas seguintes, espera-se que o público aumente a uma taxa de 120.000 pessoas por hora até o início do evento, quando não será mais permitida a entrada de público.

Quantos policiais serão necessários no início do evento para garantir a segurança?

(A) 360

(B) 485

(D) 740

(E) 860

Resolução:

A área do terreno quadrado de lado 500 m é igual a 500² = 250.000 m². Logo, segue que inicialmente estão presentes 250.000 ⋅ 4 = 1.000.000 de pessoas. Ademais, em 16 − 10 = 6 horas, chegarão mais 120.000 ⋅ 6 = 720.000 pessoas. Portanto, a resposta é (1.720.000)/(2.000) = 860

Alternativa: E

Continua...

topo