Professor Diminoi
Resumo sobre números decimais
Os números decimais são aqueles que possuem uma parte não inteira, representados com vírgulas.
Podem ser representados como fração.
Utilizamos os números decimais em diversas medidas, como as de comprimento, de massa e monetárias.
Quando a divisão não é exata, encontramos como resposta um número decimal.
O que são números decimais
Os números decimais são aqueles que possuem vírgula, sendo na maioria das vezes resultado de divisões não exatas ou de medições. Quando realizamos a medição de comprimentos, por exemplo, utilizamos como medida o metro. Porém, quando aquilo que estamos medindo possui uma parte que não forma um metro, representamos a parte decimal (centímetros) utilizando a vírgula.
É comum ouvir que a altura de uma pessoa é 1,82 metro, por exemplo. Existem várias outras situações em que o número decimal é utilizado: no valor de determinado produto, que pode ser R$ 2,50, ou no resultado da divisão de 15 por 4, que é igual a 3,75.
Números decimais por extenso
Para fazer a leitura de um número decimal, é importante saber que ele é composto por uma parte inteira, que vem antes da vírgula, e por uma parte decimal, que vem depois da vírgula. Por exemplo, no número 3,12, 3 é a parte inteira e 12 é a parte decimal.
Exemplos de como se lê os números decimais:
Quando há apenas um número depois da vírgula, a parte decimal é chamada de décimo:
0,3 → três décimos.
2,1 → dois inteiros e um décimo.
3,5 → três inteiros e cinco décimos ou três inteiros e meio.
14,2 → catorze inteiros e dois décimos.
Quando há dois números depois da vírgula, a parte decimal é chamada de centésimo:
0,36 → trinta e seis centésimos.
2,52 → dois inteiros e cinquenta e dois centésimos.
30,27 → trinta inteiros e vinte e sete centésimos.
23,06 → vinte e três inteiros e seis centésimos.
Quando há três números depois da vírgula, a parte decimal é chamada de milésimo:
0,102 → cento e dois milésimos.
1,325 → um inteiro e trezentos e vinte e cinco milésimos.
10,017 → dez inteiros e dezessete milésimos.
92,001 → noventa e dois inteiros e um milésimo.
11) Resolva as somas abaixo:
a) 0,02+3,12 =
b) 4,54+2,15 =
c) 3,001+0,143 =
d) 75,2+0,01 =
e) 0,8+0,3 =
f) 5,4+2,32 =
g) 0,003+0,12 =
h) 0,03+17,8+9,2 =
i) 80,2+36,8+125,1 =
j) 58,2+80,6+120,8 =
k) 45,7+1,37+2,01 =
l) 1,5+2,05+8,13 =
02) Resolva as subtrações abaixo:
a) 49,7-13,2 =
b) 75,2-8,8 =
c) 128,3-1,05 =
d) 138,2-2,05 =
e) 4,3-0,8 =
f) 989,8-63,47 =
g) 4,35-3,852 =
h) 2,135-1,78 =
i) 9,031-8,35 =
Operações com números decimais
Os números decimais são aqueles que pertencem ao conjunto dos números racionais (Q) e são escritos com a utilização de uma vírgula. Esses números são formados por uma parte inteira e uma parte decimal, que se apresenta à direita da vírgula.
Nomenclatura de um número decimal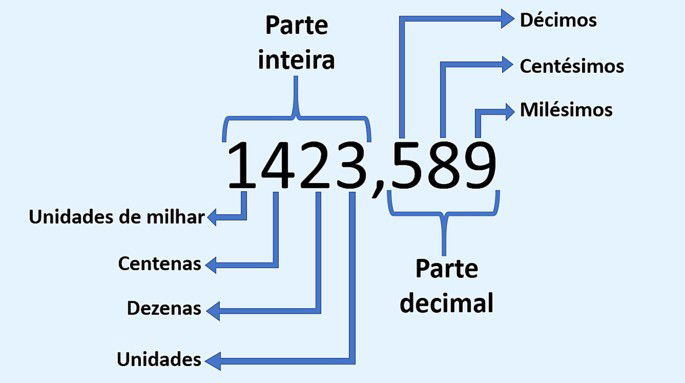

As operações matemáticas básicas
Adição
Subtração
Multiplicação
Divisão
Adição e subtração de decimais usando usando algoritmo prático
Exemplo
13,5 + 2,8
Resolução:
Primeiramente, montamos o algoritmo: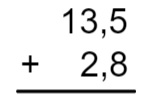
Agora, realizamos a adição normalmente, da direita para a esquerda, e na soma será colocada a vírgula na mesma posição em que ela estava nas parcelas.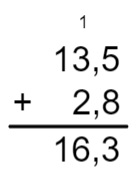
Então, temos:
13,5 + 2,8 = 16,3
Exemplo:
3,75 + 10,8
Note que a primeira parcela possui duas casas decimais, e a segunda, apenas uma. Quando isso acontece, para igualar as casas decimais, é acrescentado um zero ao final da segunda parcela. Dessa forma, somamos:
3,75 + 10,80
Resolução: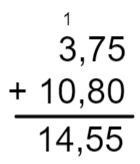
Subtração de números decimais
Para calcular a subtração de dois números decimais, posicionamos os números com as vírgulas sempre embaixo da outra vírgula no algoritmo. O detalhe na subtração, que não consta na adição, é que o maior número deve ficar sempre acima.
Exemplo:
12,5 – 9,22
Resolução:
Para que a quantidade de números após a vírgula seja igual, calcularemos 12,50 – 9,22. Se posicionarmos corretamente os números, realizar a subtração de dois números decimais será igual a realizar a subtracao de dois números inteiros.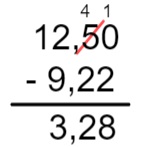
Multiplicação de números decimais
A multiplicacao de numeros decimais é feita normalmente, porém, ao final, é necessário acrescentar a vírgula no produto, de modo que o número de casas decimais seja igual à soma das casas decimais de cada um dos fatores.
Exemplo
12,3 · 4
Resolução:
Montando a multiplicação, temos: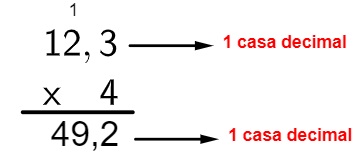
Exemplo
32,90 · 1,5
Resolução:
Divisão de números decimais
Para realizar a divisao entre numeros decimais, primeiramente igualamos as casas depois da vírgula de cada um dos números e depois podemos remover a vírgula e dividir normalmente.
Aprenda a dividir qualquer tipo de número, seja ele inteiro ou decimal
Ao aprender sobre a operação da divisão, sabemos que existem divisões exatas e divisões não exatas (quando há um resto na divisão).
Por exemplo, se quisermos dividir 5 por 2, teremos uma divisão não exata, pois haverá um resto.
Não existe um número natural que multiplicado por 50 resulte em 25, então, qualquer valor que acrescentarmos ao quociente será menor do que 1. Portanto, para prosseguirmos, teremos uma divisão com vírgula, pois acrescentaremos uma vírgula ao quociente e um zero ao resto. Procuramos agora um número que multiplicado por 50 resulte em 250.
Esse número é o 5. Portanto, 225 : 50 = 4,5.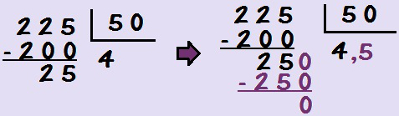 Para que não haja resto na divisão, nós acrescentamos a vírgula ao quociente para continuar uma divisão que seria inexata
Para que não haja resto na divisão, nós acrescentamos a vírgula ao quociente para continuar uma divisão que seria inexata
Vamos agora realizar a divisão de 201 por 4. Essa também é uma divisão não exata e deixará resto 1.
Quando estivermos próximos de finalizar a divisão e encontrarmos o resto, será necessário acrescentar uma vírgula ao quociente e um zero no fim do resto.
A partir daí, basta realizar a divisão normalmente até que não haja resto algum.
Nesse caso, há uma divisão com vírgula, pois a divisão de 201 por 4 resulta em 50,25.
Novamente, para que não haja resto na divisão, nós acrescentamos vírgula ao quociente para completar a divisão
Mas e quando o dividendo ou o divisor é um número decimal (com vírgula)?
Precisamos lembrar que um número decimal só divide ou é dividido por outro número decimal se houver a mesma quantidade de algarismos depois da vírgula.
Se um dos fatores da divisão é um número decimal, devemos escrever o outro na forma decimal também.
Por exemplo, o número 2 pode ser escrito como 2,0; 2,00; 2,000...
Vejamos como realizar a divisão de 3,4 por 2. O primeiro passo é observar que, como o 3,4 é um número decimal com um algarismo depois da vírgula, o 2 deve ter esse mesmo formato, por isso utilizamos o 2,0 no divisor.
Agora que ambos os fatores da divisão possuem a mesma quantidade de algarismos depois da vírgula, nós podemos desconsiderar as vírgulas e realizar a divisão de 34 por 20, obtendo como resultado 1,7.
Observe na imagem a seguir todo o processo para realizar essa divisão:
Precisamos escrever o divisor na forma decimal com um algarismo após a vírgula para então descartar as vírgulas e realizar a divisão
Imagine uma situação nova: no dividendo, há o número natural 30, e no divisor, um número racional 2,5. Lembre-se de que um número decimal só divide ou é dividido por outro número decimal se ambos possuem a mesma quantidade de algarismos após a vírgula.
Para realizar a divisão, vamos escrever o número 30 na forma 30,0. Agora que o dividendo e o divisor têm um número após a vírgula, podemos desconsiderar as vírgulas e realizar a divisão entre 300 e 25, obtendo como resultado o quociente 12, como podemos ver na figura a seguir.
Observe que uma divisão com vírgula pode resultar em um quociente sem vírgula!
Agora devemos escrever o dividendo na forma decimal com um algarismo após a vírgula para então realizar a divisão
E quando o dividendo e o divisor são decimais? Nesse caso, precisamos apenas igualar a quantidade de algarismos depois da vírgula em ambos os fatores, completando com zeros conforme for necessário. Por exemplo, ao dividir 31,775 por 15,5, precisamos acrescentar dois zeros ao divisor para que ambos tenham três algarismos após a vírgula. Feito isso, nós desconsideramos as vírgulas e realizamos a divisão de 31775 por 15500, obtendo como quociente o número 2,05, como podemos ver na exemplificação a seguir: Nesse caso, devemos escrever o dividendo e o divisor com a mesma quantidade de algarismos após a vírgula para depois desconsiderar as vírgulas.
Nesse caso, devemos escrever o dividendo e o divisor com a mesma quantidade de algarismos após a vírgula para depois desconsiderar as vírgulas.
Exemplo
3,6 : 0,12
Note que o primeiro número possui somente uma casa decimal. Já o segundo, possui duas. Assim, inicialmente igualamos as casas decimais, acrescentando um zero na parte decimal do primeiro número:
3,60 : 0,12
Resolução:
Agora que as casas decimais estão igualadas, basta retirar a vírgula e dividir:
360 : 12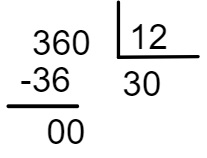
Números decimais e frações
Os números decimais podem ser representados também como fração. Para fazer sua representação, colocamos o número decimal no numerador, mas sem a vírgula, e contamos quantos algarismos esse número tinha em sua parte decimal. Se ele tiver 1 algarismo, o denominador é 10; se tiver 2, o denominador é 100; se 3, o denominador é 1000, e assim sucessivamente.
Exemplos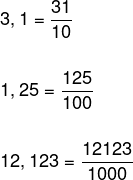
01) 3,280 + 2,100 + 0,023
Resolucao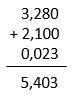
02) 5 + 0,5 + 24,365
Resolucao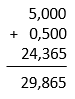
03) 0,04 + 7
Resolucao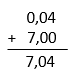
04) 12,5 – 4,825
Resolucao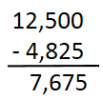
05) 4 – 2,351
Resolucao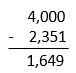
06) 8,4215 – 3
Resolucao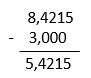
07) Mariana foi até a papelaria e comprou 2 canetas no valor unitário de R$ 1,50, 4 lápis no valor de R$ 0,65 cada e 1 caderno de R$ 15,75. Considerando que ela pagou a compra com uma nota de R$ 50,00, o valor que restou é igual a:
(A) R$ 35,00
(B) R$ 32,25
(C) R$ 28,65
(D) R$ 21,35
(E) R$ 18,65
Resolução
Queremos encontrar o valor gasto, que pode ser encontrado pela expressão numérica:
2 · 1,50 + 4 · 0,65 + 15,75
3,00 + 2,60 + 15,75
21,35
Sabendo que o gasto foi de 21,35, então o troco foi de
50,00 – 21,35 = R$ 28,65.
Alternativa C
08) Para a confraternização de um grupo de vôlei, cada um de seus membros ficou responsável por levar 600 gramas de carne. Braier foi até o açougue e comprou sua parte e de sua esposa. Sabendo que o kg da carne custava R$ 30,90, o valor pago por ele foi:
(A) R$ 18,54
(B) R$ 27,56
(C) R$ 32,90
(D) R$ 37,08
(E) R$ 42,20
Resolução:
Como Braier fez uma compra para duas pessoas, então ele comprou 1200 gramas de carne, ou seja, 1,2 kg.
Como cada kg custava 30,90, o valor gasto por ele foi de
1,2 · 30,90 = R$ 37,08.
Alternativa D
09) Mariana foi até a padaria e comprou um pedaço de torta de frango por R$ 6,50, um copo de suco por R$ 5,25 e, de sobremesa, dois brigadeiros por R$ 0,75 cada. O valor total pago por ela foi de:
(A) R$ 13,25
(B) R$ 12,50
(C) R$ 11,75
(D) R$ 10,00
(E) R$ 7,50
Resolucao
Realizando a soma dos numeros decimais:
6,50 + 5,25 + 2 ∙ 0,75
6,50 + 5,25 + 1,50
13,25
Alternativa A
10) Para fazer a decoração de Natal, seu Jerivaldo decidiu alugar um forro para a sua mesa. O comprimento e a largura do forro são de 2,20 metros e 1,10 metros, respectivamente. Podemos afirmar que a área da peça é de:
(A) 2,30 m²
(B) 2,42 m²
(C) 2,50 m²
(D)2,69 m²
(E) 2,85 m²
Resolucao
Para calcular a area nesse caso, basta multiplicar 2,20 por 1,10. Já que o forro é retangular, logo, se trata de um retangulo. Então, temos:
A = 2,20 ∙ 1,10 = 2,4200 m²
Sabemos que 2,4200 é equivalente a 2,42 m².
Alternativa B
11) Durante o ano, um dos itens com valor que sofreu aumentos consecutivos foi a carne bovina. Em um supermercado, no início de janeiro, pagava-se R$ 22,50 pelo quilo de determinada carne. Após os sucessivos aumentos, essa carne passou a custar R$ 39,90 em dezembro. A diferença paga por um cliente que comprou 2,5 kg desse produto em dezembro e em janeiro é igual a:
(A) R$ 99,75
(B) R$ 56,25
(C) R$ 43,50
(D) R$ 39,90
(E) R$ 30,75
Resolucao
Primeiramente, calcularemos o valor pago por 2,5 kg em janeiro e em dezembro, respectivamente:
2,5 ∙ 22,50 = 56,25
2,5 ∙ 39,90 = 99,75
Agora, calcularemos a diferenca entre os valores:
99,75 – 56,25 = 43,50
Alternativa C
12) Na figura a seguir, a medida dos lados está dada em metros: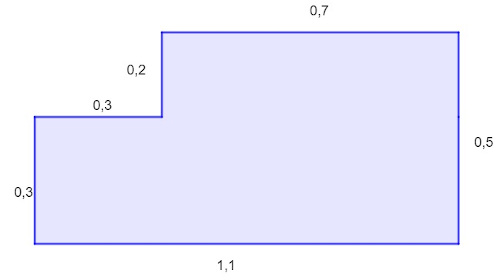 Podemos dizer que o perímetro dessa figura, em metros, é igual a:
Podemos dizer que o perímetro dessa figura, em metros, é igual a:
(A) 1,8
(B) 2,1
(C) 2,8
(D) 3,1
(E) 4,0
Resolucao
O perimetro é a soma de todos os lados:
P = 0,3 + 1,1 + 0,5 + 0,7 + 0,2 + 0,3
P = 3,1
Alternativa D
13) Ao abastecer seu veículo, um cliente pagou R$ 145,20. Sabendo que o litro de combustível naquele dia custava R$ 6,60, a quantidade de combustível colocada no veículo foi igual a:
(A) 11 litros
(B) 12 litros
(C) 15 litros
(D) 18 litros
(E) 22 litros
Resolucao
Para saber a quantidade de combustível necessária, basta realizar a divisao
145,2 : 6,6 = 22
Alternativa E
14) Para ladrilhar determinada região, foram utilizados 32 pisos de cerâmica com 25,8 cm² cada. Portanto, a área dessa região é igual a:
(A) 825,6 cm³
(B) 735,4 cm³
(C) 690,0 cm³
(D) 642,2 cm³
(E) 512,0 cm³
Resolucao
Para encontrar o valor da área, basta multiplicar 32 por 25,8:
32 ∙ 25,8 = 825,6 cm³
Alternativa A
15) O Índice de Massa Corporal (IMC) é calculado pela massa dividida pelo quadrado da altura. Uma pessoa que possui 1,80 metro e pesa 80 kg tem um IMC igual a, aproximadamente:
(A) 22,8
(B) 24,7
(C) 25,3
(D) 26,0
(E) 27,5
Resolucao
Calculando o IMC, obtemos: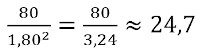
Alternativa B
16) Durante a copa do mundo, é comum a venda de figurinhas para álbuns nas bancas de revistas. Durante um mês, uma banca vendeu um total de 823 pacotes de figurinhas. Sabendo que cada pacote é vendido por R$ 2,50, qual foi o faturamento dessa loja com as vendas?
(A) R$ 1625,00
(B) R$ 1980,00
(C) R$ 2057,50
(D) R$ 2120,50
(E) R$ 2300,00
Resolucao
Para calcular o faturamento da loja, basta multiplicar:
823 ∙ 2,50 = 2057,50
Alternativa C
17) (Enem) Os hidrômetros são marcadores de consumo de água em residências e estabelecimentos comerciais. Existem vários modelos de mostradores de hidrômetros, sendo que alguns deles possuem uma combinação de um mostrador e dois relógios de ponteiro. O número formado pelos quatro primeiros algarismos do mostrador fornece o consumo em m³, e os dois últimos algarismos representam, respectivamente, as centenas e dezenas de litros de água consumidos. Um dos relógios de ponteiros indica a quantidade em litros e o outro em décimos de litros, conforme ilustrado na figura abaixo: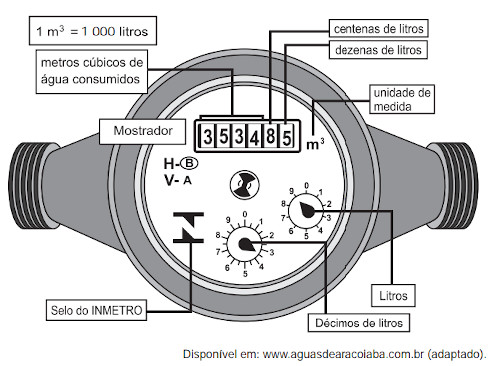 Considerando as informações indicadas na figura, o consumo total de água registrado nesse hidrômetro, em litros, é igual a
Considerando as informações indicadas na figura, o consumo total de água registrado nesse hidrômetro, em litros, é igual a
(A) 3 534,85.
(B) 3 544,20.
(C) 3 534 850,00.
(D) 3 534 859,35.
(E) 3 534 850,39.
Resolucao
No mostrador, foi marcado o total de 3534 m³. Para transformar isso em litros, basta multiplicar por 1000. Logo, há um total de 3 534 000 ℓ.
Além disso, há 8 centenas de litros, que equivalem a 800 ℓ, e 5 dezenas de litros, que equivalem a 50 ℓ.
Podemos analisar também que o marcador dos litros está em 9 e o décimo de litros está em 3,5. Assim, temos:
9 ℓ e 0,35 ℓ
Realizando a soma, o consumo do hidrômetro, em litros, é de:
3 534 000 + 800 + 50 + 9 + 0,35 = 3 534 859,35
Alternativa D
18) (Enem-segunda aplicação) Toda a esfera visível ao longo do ano, nos hemisférios celestes Norte e Sul, está dividida em 88 partes, incluindo, cada uma delas, um número variável de estrelas. A unidade de medida utilizada pelos astrônomos para calcular a área de uma constelação é o grau quadrado. Algumas constelações são imensas, como Erídano, o rio celeste, localizada no hemisfério celeste Sul e ocupa uma área de 1138 graus quadrados. Em contraponto, a constelação Norma, localizada no mesmo hemisfério, não passa de 165 graus quadrados.
Em um mapa do hemisfério celestial feito em uma escala de 1:1000, as constelações Erídano e Norma ocuparão, respectivamente, uma área, em graus quadrados, de
(A) 0,1138 e 0,0165.
(B) 0,1138 e 0,165.
(C) 1,138 e 0,165.
(D) 11 380 e 1 650.
(E) 1 138 000 e 165 000.
Resolucao
Para aplicar a escala 1:1000, realizaremos a divisão das medidas por 1000:
1138 : 1000 = 1,138
165 : 1000 = 0,165
Alternativa C
19) (Enem) A tabela compara o consumo mensal, em kWh, dos consumidores residenciais e dos de baixa renda, antes e depois da redução da tarifa de energia no estado de Pernambuco.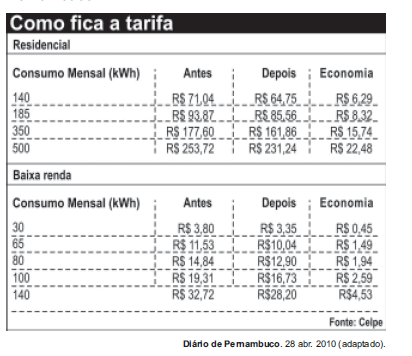 Considere dois consumidores: um que é de baixa renda e gastou 100 kWh e outro do tipo residencial que gastou 185 kWh.
Considere dois consumidores: um que é de baixa renda e gastou 100 kWh e outro do tipo residencial que gastou 185 kWh.
A diferença entre o gasto desses consumidores com 1kWh, depois da redução da tarifa de energia, mais aproximada, é de
(A) R$ 0,27.
(B) R$ 0,29.
(C) R$ 0,32.
(D) R$ 0,34.
(E) R$ 0,61.
Resolucao
Inicialmente, calcularemos quanto um consumidor residencial paga por 1kWh após a redução da tarifa.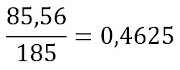
Agora, calcularemos o valor de 1kWh para um consumidor de baixa renda: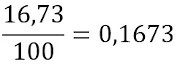
A diferença entre os gastos é dada por:
0,4625 – 0,1673 = 0,2952 ≈ 0,29.
Alternativa B
20) (Enem PPL) Um granjeiro detectou uma infecção bacteriológica em sua criação de 100 coelhos. A massa de cada coelho era de, aproximadamente, 4 kg. Um veterinário prescreveu a aplicação de um antibiótico, vendido em frascos contendo 16 mL, 25 mL, 100 mL, 400 mL ou 1 600 mL. A bula do antibiótico recomenda que, em aves e coelhos, seja administrada uma dose única de 0,25 mL para cada quilograma de massa do animal. Para que todos os coelhos recebessem a dosagem do antibiótico recomendada pela bula, de tal maneira que não sobrasse produto na embalagem, o criador deveria comprar um único frasco com a quantidade, em mililitros, igual a
(A) 16.
(B) 25.
(C) 100.
(D) 400.
(E) 1 600.
Resolucao
Como há 100 coelhos e cada um deles tem massa de aproximadamente 4 kg, deve-se comprar antibiótico para 4 × 100 = 400 kg.
Como para cada quilo é administrado 0,25 mL, faremos a multiplicacao de 400 × 0,25 = 100 mg.
Alternativa C
21) Qual é o resultado da expressão numérica abaixo?
41,32 + 56,4 – 81,932 + 5
(A) 102,72
(B) 20,8
(C) 20,7
(D) 20
(E) 20,788
Resolucao
Começaremos pelas somas. Colocando vírgula debaixo de vírgula e completando os espaços vazios possíveis com zero, teremos:
41,320
56,400
+ 5,000
102,720
Agora basta subtrair 81,932 desse resultado, seguindo o mesmo princípio de vírgula debaixo de vírgula:
102,720
– 81,932
20,788
Alternativa E
22) Qual é a área de um retângulo cuja largura mede 23,32 m e o comprimento mede 52,25 m?
(A) 1217,99 m2
(B) 1218,47 m2
(C) 1219,01 m2
(D) 1567,5 m2
(E) 1045,0 m2
Resolucao
A área do retângulo é o produto de sua base pela sua altura, o que também pode ser interpretado como produto da largura pelo comprimento. Observe:
52,25
x 23,32
10450
15675
15675
+ 10450
1218,4700
Alternativa B
23) Uma empresa utiliza um índice de massa corporal inventado por ela própria, no qual divide por dois a soma entre altura e peso dos funcionários. Qual é o índice de massa corporal de Rhuan, sabendo que sua altura é 1,78 m e seu peso é 72,3 kg?
(A) 74,08
(B) 31,15
(C) 37,04
(D) 37,4
(E) 37
Resolucao
Basta somar altura e peso e dividir o resultado por 2. Observe:
a) 1,78 + 72,30 = 74,08, pois:
72,30
+ 1,78
74,08
b) 74,08/2 = 37,04, pois:
74,08 | 2
74,08 | 2,00
7408 | 200
-600 37,04
1408
-1400
800
-800
0
Logo, o índice de massa corporal de Rhuan, conforme os métodos da empresa, é de 37,04.
Alternativa C
24) Em um feirão, Juarez aproveitou as promoções e comprou sete agendas, que custaram R$ 1,32; 4 canetas, que custaram R$ 0,26; e 45 lapiseiras a R$ 1,22. Qual é o troco de Juarez, sabendo que ele levou apenas uma nota de R$ 100,00?
(A) R$ 34,82
(B) R$ 65,18
(C) R$ 83,62
(D) R$ 49,80
(E) R$ 51,50
Resolucao
Em primeiro lugar, montaremos a expressão numérica que indicará o troco (T) de Juarez:
T = 100,00 – (7 · 1,32 + 4 · 0,26 + 45 · 1,22)
Resolveremos cada multiplicação separadamente e, depois, substituiremos na expressão acima:
1) 7 · 1,32:
1,32
x 7
9,24
2) 4 · 0,26:
0,26
x 4
1,04
3) 45 · 1,22:
1,22
x 45
610
+ 488
54,90
A expressão definida por T, que representa o troco, pode ser reescrita da seguinte maneira:
T = 100,00 – (9,24 + 1,04 + 54,90)
Para terminar o exercício, somamos os valores positivos e subtraímos de R$ 100,00. Observe:
54,90
9,24
+ 1,04
65,18
100,00
– 65,18
34,82
Alternativa A
25) Escreva o número decimal 8,466 em sua forma fracionária.
Resolução
O primeiro passo é “eliminar” a vírgula. Para isso, é necessário “andar” três casas decimais.
8,466
Devemos dividir o número 8466 por 1000:![]()
26) Um pacote de sabão com 4 barras custa R$ 2,88. Quanto custa cada barra de sabão?
Resolução
Sabemos que as 4 barras custam R$ 2,88, assim, para determinar o preço de cada uma delas, devemos dividir o preço total do pacote por 4.
2,88 ÷ 4
Para realizar a operação, é necessário igualar as casas decimais. Para isso, vamos multiplicar por 100 ambos os lados da divisão.
2,88 (x 100) ÷ 4 (x 100)
288 ÷ 400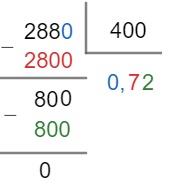
Portanto, cada sabão custa R$ 0,72.
27) Exemplos de adição com números na forma decimal
a) 3,280 + 2,100 + 0,023
Resolucao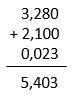
b) 5 + 0,5 + 24,365
Resolucao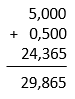
c) 0,04 + 7
Resolucao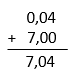
28) Exemplos de subtração com números na forma decimal
a) 12,5 – 4,825
Resolucao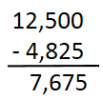
b) 4 – 2,351
Resolucao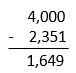
c) 8,4215 – 3
Resolucao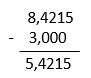
Como transformar esses números decimais em frações:
Decimais finitos: São aqueles que apresentam um número finito de casas decimais não nulas.
Observe que:
1) 7/10 = 0,7
2) 7/100 = 0,07
3) 7/1000 = 0, 007
4) 216/100 = 2,16
Dica: Todo número cuja representação decimal for finita pode ser escrito na forma de uma fração com denominador 10, 100, 1000, etc.
O numerador da fração é o número inteiro que se obtém abandonando a vírgula, e o denominador é formado pelo número 1 acrescido de tantos zeros quanto forem as casas após a vírgula do número fornecido.
O que são as Dízimas periódicas?
Dízimas Periódicas s=São numerais decimais em que há repetição periódica e infinita de um ou mais algarismos.
Observe as divisões:
1) 5/9 = 0,55555….
2) 32/99 = 0,32323232…
3) 121/999 = 0,121121121…
meros têm uma representação decimal infinita e periódica e são chamados de dízimas periódicas simples. A fração que os representa (Fração Geratriz) tem como denominador números 9.
Podemos estabelecer a seguinte regra para dízimas periódicas simples: o numerador da fração geratriz será o número do período e o denominador será 9 ou 99 ou 999, etc…, ou seja, será formado por tantos nove quanto forem os algarismos do período.
Exemplos:
1) 0,454545… = 45/99
2) 0,761576157615… = 7615/9999
3) 0,222222… = 2/9
E se o número for, por exemplo, 2,3222222…. ou 0, 43717171…?
Neste caso será chamado de dízima periódica composta e a sua transformação em fração pode ser feita da seguinte maneira:
Exemplos:
1) 2,3222222… = 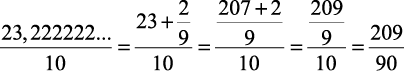
2) 0,43717171… = ![]()
Fração decimal é toda fração onde o denominador é 10 ou potência de 10 , 100, 100...
Nos números decimais , a vírgula separa a parte inteira da parte decimal onde o número de casas decimais é igual ao número de zeros do denominador 10, 100, 1000...
a) 5/10 = 0,5
b) 8/100 = 0,08
c) 527/1000 = 0,527
Continuacao ...





