PROPRIEDADES DA POTENCIACAO

Professor Diminoi

PROPRIEDADA DA POTENCIAÇÃO

A potenciação é uma operação matemática que representa a multiplicacao sucessiva de um número por ele mesmo. Ao multiplicar o 3 por ele mesmo 4 vezes, isso pode ser representado pela potência 3 elevada a 4: 3⁴.
Essa operação possui propriedades importantes que facilitam o cálculo das potências. Assim como a multiplicação possui a divisão como operação inversa, a potenciação possui a radiciação como operação inversa.

Cada elemento da potenciação recebe um nome específico: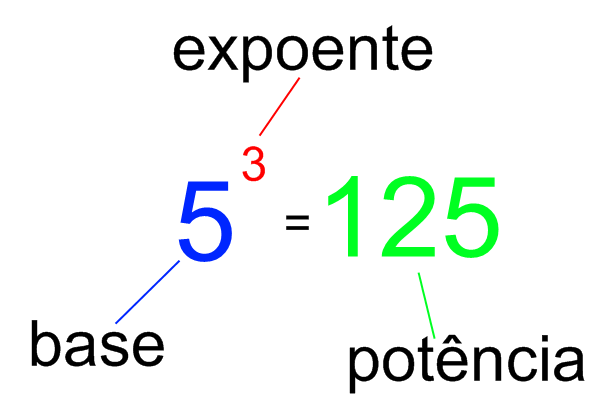

Como ler uma potência?
Saber ler uma potência é uma tarefa importante. A leitura é sempre feita começando pelo número que está na base elevado ao número que está no expoente, como nos exemplos a seguir:

Exemplos:
a) 4³ → Quatro elevado a três, ou quatro elevado à terceira potência, ou quatro elevado ao cubo.
b) 3⁴ → Três elevado a quatro, ou três elevado à quarta potência.
c) (-2)¹ → Menos dois elevado a um, ou menos dois elevado à primeira potência.
d) 8² → Oito elevado a dois, ou oito elevado à segunda potência, ou oito elevado ao quadrado.


Propriedades da potenciação
A potenciação corresponde à multiplicação de fatores iguais, que pode ser escrita de forma simplificada utilizando uma base e um expoente. A base é o fator que se repete e o expoente é o número de repetições.


Para resolver problemas com potências é necessário conhecer as suas propriedades. Veja a seguir as principais propriedades utilizadas em operações com potências.

1. Multiplicação de potências de mesma base
No produto de potências de mesma base devemos conservar a base e somar os expoentes.
a^m . aⁿ = a^{m + n}
Exemplo:
2² . 2³ = 2²⁺³ = 2⁵ = 32

2. Divisão de potências de mesma base
Na divisão de potências de mesma base conservamos a base e subtraímos os expoentes.
a^m : aⁿ = a^{m –} 
Exemplo:
2⁴ : 2² = 2^4-2 = 2² = 4

3. Potência de potência
Quando a base de uma potência também é uma potência devemos multiplicar os expoentes.
(a^m)ⁿ = a^m.n
Exemplo:
(3²)⁵ = 3^2.5 = 3¹⁰ = 59 049

4. Potência de produto
Quando a base de uma potência é um produto elevamos cada fator à potência.
(a . b)^m = a^m . b^m
Exemplo:
(2 . 3)² = 2² . 3² = 4 . 9 = 36

5. Potência de quociente
Quando a base de uma potência é uma divisão elevamos cada fator ao expoente.
Exemplo:
(2/3)² = 2²/3² = 4/9

6. Potência de quociente e expoente negativo
Quando a base de uma potência é uma divisão e o expoente é negativo inverte-se a base e o sinal do expoente.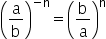
Exemplo:
(2/3)^-2 = (3/2)² = 3²/2² = 9/4


7. Potência de expoente negativo
Quando o sinal de uma potência for negativo devemos inverter a base para tornar o expoente positivo.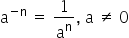
Exemplo:
(2)^-4 = (1/2)⁴ = 1/16


8. Potência com expoente racional
A radiciação é a operação inversa da potenciação. Portanto, podemos transformar um expoente fracionário em um radical.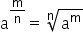
Exemplo:
5^1/2 = √5


9. Potência com expoente igual a 0
Quando uma potência apresenta expoente igual a 0, o resultado será 1.
a⁰ = 1
Exemplo:
4⁰ = 1


10. Potência com expoente igual a 1
Quando uma potência apresenta expoente igual a 1, o resultado será a própria base.
a¹ = a
Exemplo:
5¹ = 5

 
11. Potência de base negativa e expoente ímpar
Se uma potência tem base negativa e o expoente é um número ímpar, então, o resultado é um número negativo.
Exemplo:
(- 2)³ = (- 2) x (- 2) x (- 2) = - 8

12. Potência de base negativa e expoente par
Se uma potência tem base negativa e o expoente é um número par, então, o resultado é um número positivo.
Exemplo:
(- 3)² = (- 3) x (- 3) = + 9

 
VEJA OS EXEMPLOS A ABAIXO

a) 5³ = 5 . 5 . 5 = 125

b) 2⁴ = 2 . 2 . 2 . 2 = 16

c) 3² . 3⁴ = 3²⁺⁴ = 3⁶

d) 5³ . 5⁹ = 5³⁺⁹ = 5¹²

e) 3⁶ : 3⁴ = 3^6-4 = 3²

f) 5⁷ : 5³ = 5^7-4 = 5⁴

g) (3²)⁵ = 3⁵ = 3¹⁰

h) (5³)⁴ = 5⁴ = 5¹²

i) (4 . 5)² = 4² . 5²

j) (2. 4)³ = 2³ . 4³

k) (15 : 9)⁶ = 15⁶ : 9⁶

l) (8 : 5)³ = 8³ . 5³

m) 1¹⁰ = 1

n) 1³⁴²⁵⁶ = 1

o) 1231 = 123

p) 5290¹ = 5209

r) 600⁰ = 1

s) 2015⁰ = 1
 

QUESTÕES RESOLVIDAS
01) Simplifique a expressão abaixo.

2⁴ . 4³. 8¹⁰
      32⁶
Resolução:
Primeiramente, escreveremos todas as potências como potência de base 2.
Sabemos que 4 = 2², logo temos que 4³ = (2²)³. Utilizando a propriedade de potência, temos que:
(2²)³ = 2^2.3 = 2⁶
Sabemos que 8 = 2³, então:
8¹⁰ = (2³)¹⁰ = 2³⁰
Temos que 32 = 25:
32⁶ = (2⁵)⁶ = 2^5.6 = 2³⁰
Portanto
2⁴ . 4³ . 8¹⁰
     32⁶

2⁴ . 2⁶ . 2³⁰
      2³⁰

2⁴ . 4³ . 8¹⁰
     32⁶

2⁴⁺⁶⁺³⁰
    2³⁰

2⁴ . 4³ . 8¹⁰
      32⁶

 2⁴⁰
 2³⁰

2⁴ . 4³ . 8¹⁰
      32⁶

2^40-30

2⁴ . 4³ . 8¹⁰
      32⁶

2¹⁰

02) Analise as afirmativas a seguir e julgue cada uma como verdadeira ou falsa.
I) 2⁵ + 2⁸ = 2¹³
II) 2¹² : 8² = 2⁴
III) (2⁴)³ = 2¹²
Marque a alternativa correta:
(A) Somente I é falsa.
(B) Somente II é falsa.
(C) Somente III é falsa.
(D) Todas são verdadeiras.
Resolução:
Podemos perceber que a afirmativa I é falsa, pois somente na multiplicação de potência de mesma base é que podemos conservar as bases e somar os expoentes. Note que não temos uma multiplicação, mas sim uma adição. As demais afirmativas são verdadeiras, pois mostram, respectivamente, a propriedade da divisão de potência de mesma base e a propriedade da potência de potência.
Alternativa: A
 
03) Sabendo que o valor de 45 é 1024, qual o resultado de 46?
(A) 2988
(B) 4096
(C) 3184
(D) 4386
Resolução:
Observe que 45 e 46 possuem as mesmas bases. Portanto, a potência 46 pode ser reescrita como um produto de potências de mesma base.
46 = 45 . 41
Como sabemos o valor de 45 basta substituí-lo na expressão e multiplicar por 4, pois potência com expoente 1 tem como resultado a própria base.
46 = 45 . 41 = 1024 . 4 = 4096.
Alternativa: B

04) Com base nas propriedades da potenciação, qual das sentenças abaixo está correta?
(A) (x . y)² = x² . y²
(B) (x + y)² = x² + y²
(C) (x - y)² = x² – y²
(D) (x + y)0 = 0
Resolução:
(A) Neste caso temos a potência de um produto e, por isso, os fatores são elevados ao expoente.
(B) O correto seria (x + y)² = x² + ²xy + y².
(C) O correto seria (x - y)² = x² - 2xy + y².
(D) O resultado correto seria 1, pois toda potência elevada ao expoente zero tem como resultado 1.
Alternativa: A

05) Aplique as propriedades das potências para efetuar a simplificação da expressão (2⁵ . 2^-4) : 2³
Resolução:
Iniciamos a resolução da alternativa pelo que está dentro dos parênteses.
2⁵ . 2^-4 é a multiplicação de potências de bases iguais e, por isso, repetimos a base e somamos os expoentes.
2^{5 + (-4)} = 2¹
(2⁵ . 2^-4) : 2³ = 2¹ : 2³
Agora, a expressão se transformou em uma divisão de potências de mesma base. Por isso, vamos repetir a base e subtrair os expoentes.
2¹ : 2³ = 21^-3 = 2^-2
Como o resultado é uma potência de expoente negativo, devemos inverter a base e o sinal do expoente.
2^-2 = (1/2)²
Quando a potência tem como base um quociente podemos elevar cada termo ao expoente.
12/22 = 1/4
Portanto, (2⁵ . 2^-4) : 2³ = 1/4.

06) Simplificando a expressão (a³ · b^-7 · a2) : (a² · b^-4)², encontraremos:
(A) a/b
(B) ab
(C) b
(D) a²b
Resolução:
Usando as propriedades de multiplicação de potência de mesma base, potência de potência e divisão de potência de mesma base, temos que:
(a³ · b^-7 · a^²) : (a² · b^-4)²
(a³⁺² · b^-5 ) : (a^2.2 · b^-4.2)
(a⁵ · b^-7 ) : (a⁴ · b^-8)
a^5-4 · b^{-7 - (-8)}
a¹ · b^{-7 +8}
a¹ · b¹
a .b
Alternativa: B


2ª propriedade – Divisão de potências de mesma base
Na divisão de potências de mesma base, conservamos a base e subtrairmos o expoente do numerador pelo expoente do denominador.
aⁿ : a^m = a^n-m
Exemplo 1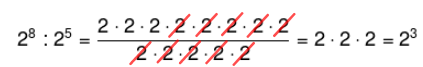
Logo, temos que:
2⁸ : 2⁵ = 2^8-5 = 2³


QUESTOES RESOLVIDAS
01) Simplificando a expressão (a³ . b^{-7 .} a²) : (a² . b^-4)², encontraremos:
(A) a/b
(B) ab
(C) b
(D) a²b
Resolução
Usando as propriedades de multiplicação de potência de mesma base, potência de potência e divisão de potência de mesma base, temos que:
(a³ · b^-7 · a²) : (a² · b^-4)²
(a³⁺² · b^-5 ) : (a^2.2 · b^-4.2)
(a⁵ · b^-7 ) : (a⁴ · b^-8)
a^5-4 · b^{-7 - (-8)}
a¹ · b^{-7 +8}
a¹ · b¹
a .b
Alternativa B

02) (IFG) O valor da expressão aritmética abaixo é equivalente a: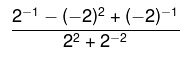
(A) 8/17
(B) -8/17
(C) 16/17
(D) -16/17
Resolução:
Resolvendo primeiro o numerador, temos que: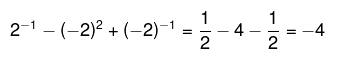
Agora vamos resolver o denominador:
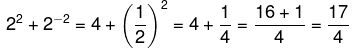Como temos uma divisão do numerador pelo denominador, vamos multiplicar pelo inverso da segunda fração: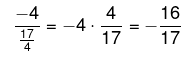

Alternativa D

03) Calcule o valor de x, sabendo que x³ = 8.
Resolucao
Para calcular o valor de x, é necessário realizar a operação inversa da potenciação, ou seja, a radiciação. Na realidade, estamos buscando qual é o número que, ao ser elevado ao cubo, tem como resultado o número 8.
Essa relação entre a radiciação e a potenciação torna fundamental dominar as regras de potenciação para avançar o aprendizado sobre a radiciação.

04) (PUC-RIO) O maior número abaixo é:
(A) 3³¹
(B) 8¹⁰
(C) 16⁸
(D) 81⁶
(E) 243⁴
Resolução
Realizar a comparação calculando cada um deles seria uma tarefa difícil, então vamos simplificar as alternativas,
a) 3³¹ →já está simplificada
b) 8 = 2³ → (2³)¹⁰ = 2³⁰
c) 16 = 2⁴→ (2⁴)⁸= 2³²
d) 81 = 3⁴→ (3⁴)⁶= 3²⁴
e) 243=3⁵→ (3⁵)⁴ = 3²⁰
Alternativa A

05) A simplificação da expressão [3¹⁰: (3⁵. 3)²]^- é igual a:
(A) 3^-4
(B) 3⁴
(C) 3⁰
(D)3²
(E) 3^-2
Resolução
[3¹⁰: (3⁵. 3)²]^-2
[3¹⁰: (3⁶)²]^-2
[3¹⁰: 3¹²]^-2
[3^-2]^-2
3⁴
Alternativa B

06) (TRF 3 região) Qual o resultado da expressão numérica abaixo?
(A) 120
(B) 1/5
(C) 55
(D) 25
(E) 620
Resolução
Vamos resolver a expressão aplicando as propriedades das potências:
Alternativa A

07) (PM PE) Carlos e Pedro são alunos muito aplicados em matemática. Certo dia, Carlos perguntou a Pedro se ele sabia resolver a seguinte questão: Determine o algarismo das unidades do número (8325474)^(642). Pedro resolveu o problema, chegando ao resultado correto. Qual foi o resultado a que Pedro chegou?
(A) 4
(B) 2
(C) 5
(D) 6
(E) 1
Resolucao
Se a e n são inteiros positivo aⁿ = a. a. a. a. . . a( n vezes)
Toda potência de um número inteiro e positivo, cujo algarismo das unidades é 4, tem como algarismo das unidades 6 ou 4.
Boserve
(14)¹ = 14
(14)² = 196
(14)³ = 2744
(14)⁴ = 38416
Nota-­se que existe um padrão no algarismo da unidade.
Quando o expoente é ímpar, o algarismo é 4.
Quando o expoente é par, o algarismo é 6.
Temos então que o algarismo da unidade de 8325474⁶⁴² é 6, pois o expoente é 642, que é um número par.
Alternativa D

08) Em um sítio há 12 árvores. Cada árvore possui 12 galhos e em cada galho tem 12 maçãs. Quantas maçãs existem no sítio?
(A) 144
(B) 1224
(C) 1564
(D) 1728
Resolucao
Temos uma potência onde o número 12 é a base e o número 3 é a quantidade de vezes que a base se repete.
Vamos tomar como exemplo uma das árvores. Em cada um dos 12 galhos de uma árvore encontram-se 12 maçãs, ou seja, 12 galhos vezes 12 maças: 12 x 12 = 144.
Só que no total temos 12 árvores, ou seja, 144 x 12 nos dá o número total de maçãs. Isso pode ser expresso na forma de potência.
12 x 12 x 12 = 123 = 1 728.
Portanto, o sítio apresenta 1 728 maçãs.
Alternativa D

09) Sabendo que o valor de 5⁷ é 78 125, qual o resultado de 5⁸?
(A) 156 250
(B) 390 625
(C) 234 375
(D) 312 500
Resolucao
Para resolver essa questão podemos transformar 58 em uma multiplicação de potências de bases iguais, pois ax . ay = ax+y
Como sabemos o valor de 57, transformamos o número 58 da seguinte forma:
58 = 57 . 5, pois 57 . 5 = 57+1 = 58
Sendo assim, para encontrar o resultado, precisamos apenas substituir o valor de 57 e multiplicar por 5.
57 . 5 = 78 125 . 5 = 390 625
Alternativa B

10) As potências (-2)⁴ e -2⁴ são iguais ou diferentes? E qual o resultado?
Resolucao
As potências são diferentes e apresentam como resultados 16 e -16, respectivamente.
Quando a base de uma potência é um número negativo e está elevada a um expoente par, o resultado será positivo. Entretanto, para sinalizar que a base é negativa seu valor deve estar entre parênteses.
(- 2)4 = (- 2) x (- 2) x (- 2) x (- 2) = +16
Quando não há parênteses separando a base, deve-se incluir o sinal de negativo no resultado.
- 24 = - 16
Portanto, os resultados são: (- 2)4 = 16 e - 24 = - 16.

11) O valor da expressão 20x³ + 2x²y⁵, para x = - 4 e y = 2 é:
(A) 256
(B) - 400
(C) 400
(D) – 256
Resolucao
Para resolver a expressão o primeiro passo é substituir as letras pelos valores, assim a expressão ficará:
20 . (- 4)3 + 2 . (- 4)2 . 25
Devemos ter cuidado com os sinais ao resolver a potenciação. Quando a base é negativa o resultado será positivo se o expoente for par e será negativo quando o expoente for ímpar. Assim, a expressão ficará:
20 . (- 64) + 2 . (+16) . 32
Agora que já resolvemos as potenciações, vamos resolver as demais operações, lembrando que primeiro resolvemos as multiplicações e depois a subtração.
- 1280 + 1024 = - 256
Alternativa D

12) (UFRGS) Um adulto humano saudável abriga cerca de 100 bilhões de bactérias, somente em seu trato digestivo. Esse número de bactérias pode ser escrito como
(A) 10⁹
(B) 10¹⁰
(C) 10¹¹
(D) 10¹²
Resolucao
Um bilhão é a mesma coisa que mil milhões, ou seja, 1000 x 1 000 000 = 1 000 000 000.
100 bilhões é igual a 100 x 1 000 000 000 = 100 000 000 000.
Números grandes como o dessa questão podem ser escritos em notação científica, cuja escrita segue o padrão N . 10n, onde N é um número menor que 10 e maior ou igual a 1. Já o expoente da base 10 é o número de casas decimais que a vírgula "andou" para obtermos o valor de N.
0,000 000 001
tabela linha com 1 vírgula 0 0 0 0 linha com blank seta para cima blank blank blank blank fim da tabela tabela linha com 0 0 0 0 0 0 linha com blank blank blank blank blank blank fim da tabela tabela linha com 0 linha com blank fim da tabela
Observe que para chegar até ao número 11 foi preciso "andar" 11 casas decimais. Portanto, temos a potência 1011 como resultado.
Alternativa C

13) (Enem) A Agência Espacial Norte Americana (NASA) informou que o asteroide YU 55 cruzou o espaço entre a Terra e a Lua no mês de novembro de 2011. A ilustração a seguir sugere que o asteroide percorreu sua trajetória no mesmo plano que contém a órbita descrita pela Lua em torno da Terra. Na figura, está indicada a proximidade do asteroide em relação à Terra, ou seja, a menor distância que ele passou da superfície terrestre.
Com base nessas informações, a menor distância que o asteroide YU 55 passou da superfície da Terra é igual a
(A) 3,25 .10² km
(B) 3,25 .10³ km
(C) 3,25 . 10⁴ km
(D) 3,25 . 10⁵ km
(E) 3,25 . 10⁶ km
Resolucao
Na figura, está indicada a a menor distância que ele passou da superfície terrestre, que é 325 mil km, ou seja, 325 000 km.
Esse número deve ser escrito em notação científica. Para isso, devemos "andar" com a vírgula até encontrar um número menor que 10 e maior ou igual a 1. O número de casas decimais que a vírgula "andou" corresponde ao expoente da base 10 na fórmula N . 10n.
3,25 000
tabela linha com 3 vírgula 2 5 0 0 linha com blank seta para cima blank blank blank blank fim da tabela tabela linha com 0 linha com blank fim da tabela
Chegamos ao número 3,25 e, para isso, a vírgula "andou" 5 casas decimais. Portanto, em notação científica, a proximidade do asteroide em relação à Terra é 3,25. 10⁵ km.
Alternativa D

14) (UPE) Na sequência de quadros a seguir, o valor da primeira célula de cada quadro é a soma dos valores das duas últimas células do quadro anterior.
Se o número da célula central do último quadro dessa sequência é 22013, quanto vale o produto dos números das duas outras células?
(A) 22013
(B) 22013 + 1
(C) 22013+1
(D) 24026 + 1
(E) 24026 – 1
Resolucao
Repare que temos três células. A questão nos diz que a célula central será 22013. Como podemos ver, a célula central tem sempre uma diferença de 1 para os outros números. Na primeira sequência, por exemplo, temos 2-1 | 2 | 2+1.
Então, na sequência de quadros pedida, teremos: 22013 + 1 | 22013 | 22013 – 1. Como o enunciado nos pede, temos que multiplicar esses dois quadros:
(22013 + 1) . (22013 + -1).
O que acontece aqui é essa expressão trata-se de um produto notável. Isso acontece quando temos a multiplicação de dois elementos em que um é uma soma e outra é uma subtração pelos mesmos números.
Quando isso ocorre, você pode aplicar a distributiva ou simplesmente tomar o atalho do produto da soma pela diferença, que é o quadrado do primeiro temos menos o quadrado do segundo termo:
(22013)² – (1)²
24026 – 1
Alternativa E

15) (MACK) A fração abaixo é igual a: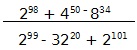
(A) 1
(B) – 11
        6
(C) 2
(D) – 5
        2
(E) 7
      4
Resolucao
Alternativa B

16) (FUVEST - SP) O valor de (0,2)³ + (0,16)² é:
(A) 0,0264
(B) 0,0336
(C) 0,1056
(D) 0,2568
(E) 0,6256
Resolucao
(0,2)³ + (0,16)² = (0,2)³ + (0,4)⁴ = 0,008 + 0,0256 =0,0336
Alternativa B

17) Encontre a solução da expressão numérica  [4² + ( 5 – 3)²] : ( 9 – 7)².
Resolucao
Encontre a solução da expressão numérica  [4² + ( 5 – 3)²] : ( 9 – 7)².

18) Reduza a uma potência [(-2²)²] =
Resolucao
[(-2²)²] = + 2^{2 . 2} = 2⁴

19) Reduza a uma potência 5² . 5⁵ . 5^-1 =
Resolucao
5² . 5⁵ . 5^-1 = 5^{( 2 + 5 -1 )} = 5⁶

20) Simplificando a expressão (a³ . b^{-7 .} a²) : (a² . b^-4)², encontraremos:
(A) a/b
(B) ab
(C) b
(D) a²b
Resolução
Usando as propriedades de multiplicação de potência de mesma base, potência de potência e divisão de potência de mesma base, temos que:
(a³ · b^-7 · a²) : (a² · b^-4)²
(a³⁺² · b^-5 ) : (a^2.2 · b^-4.2)
(a⁵ · b^-7 ) : (a⁴ · b^-8)
a^5-4 · b^{-7 - (-8)}
a¹ · b^{-7 +8}
a¹ · b¹
a .b
Alternativa B

21) (IFG) O valor da expressão aritmética abaixo é equivalente a: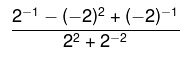
(A) 8/17
(B) -8/17
(C) 16/17
(D) -16/17
Resolução:
Resolvendo primeiro o numerador, temos que: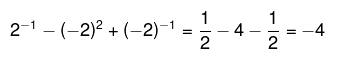
Agora vamos resolver o denominador:
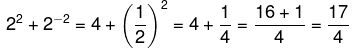Como temos uma divisão do numerador pelo denominador, vamos multiplicar pelo inverso da segunda fração:
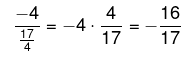Alternativa D

 

Continuacao ...