Professor Diminoi 001) (ENEM) O Brasil é um país com uma vantagem econômica clara no terreno dos recursos naturais, dispondo de uma das maiores áreas com vocação agrícola do mundo. Especialistas calculam que, dos 853 milhões de hectares do país, as cidades, as reservas indígenas e as áreas de preservação, incluindo florestas e mananciais, cubram por volta de 140 milhões de hectares. Aproximadamente 280 milhões se destinam à agropecuária, 200 milhões para pastagens e 80 milhões para a agricultura, somadas as lavouras anuais e as perenes, como o café e a fruticultura.
001) (ENEM) O Brasil é um país com uma vantagem econômica clara no terreno dos recursos naturais, dispondo de uma das maiores áreas com vocação agrícola do mundo. Especialistas calculam que, dos 853 milhões de hectares do país, as cidades, as reservas indígenas e as áreas de preservação, incluindo florestas e mananciais, cubram por volta de 140 milhões de hectares. Aproximadamente 280 milhões se destinam à agropecuária, 200 milhões para pastagens e 80 milhões para a agricultura, somadas as lavouras anuais e as perenes, como o café e a fruticultura.
De acordo com os dados apresentados, o percentual correspondente à área utilizada para agricultura em relação à área do território brasileiro é mais próximo:
(A) 32,8 %
(B) 28,6 %
(C) 10,7 %
(D) 8,0 %
(E) 9,4 %
Resolução:
Área do território nacional: 853mi Ha
Área agrícola útil: 80mi Ha
Percentual = Parte/Todo . (%)
P = 80/853 . 100
P = 9,38%
Resposta: E
002) (ENEM) Para aumentar as vendas no início do ano, uma loja de departamentos remarcou os preços de seus produtos 20% abaixo do preço original. Quando chegam ao caixa, os clientes que possuem o cartão fidelidade da loja têm direito a um desconto adicional de 10% sobre o valor total de suas compras.
Um cliente deseja comprar um produto que custava R$50,00 antes da remarcação de preços. Ele não possui o cartão fidelidade da loja.
Caso esse cliente possuísse o cartão fidelidade da loja, a economia adicional que obteria ao efetuar a compra, em reais, seria de
(A) 4,00
(B) 5,00
(C) 10,00
(D) 14,00
(E) 13,00
Resolução:
O primeiro desconto será de 20% sobre o produto que custa R$ 50,00.
20% de R$ 50
Percentual = Parte/Todo . (%)
20/100 = 0,2 . 50
10
R$ 10,00
Assim, o cliente terá um desconto de R$ 10,00. O cliente pagará, então R$ 40,00.
Se o cliente tivesse o cartão fidelidade, ainda receberia um desconto adicional de 10% sobre o valor de R$ 40,00 (após o desconto de 20%).
Resolução:
O desconto será 10% de 40
Percentual = Parte/Todo . (%)
10/100 = 0,1 . 40
4
R$ 4,00
O desconto seria de R$ 4,00. O cliente pagaria, então R$ 36,00. Mias a diferença entre os preços pagos com o cartão fidelidade e sem ele, ou seja, R$ 40,00 – R$ 36,00 = R$ 4,00.
Alternativa: A
003) (ENEM) Uma máquina copiadora que, trabalhando sem interrupção, fazia 90 fotocópias por minuto, foi substituída por uma nova com 50% mais veloz. Suponha que a nova máquina tenha de fazer o mesmo número de cópias que a antiga, em uma hora de trabalho ininterrupto, fazia. O tempo mínimo, em minutos, que essa nova máquina gastará para realizar o trabalho é igual a:
(A) 25
(B) 30
(C) 35
(D) 45
(E) 40
Resolução:
A nova máquina é 50% mais veloz, ela fará 90 + 50% de 90 cópias por minuto.
50% de 90 = 45, então ela fará 90 + 45 = 135 cópias por minuto.
A máquina antiga, em uma hora (60 minutos), fazia 90 . 60 = 5400 cópias.
Aplicando a Regra de três: 135 1
5400 t
135t = 5400
t = 5400/135
40
Alternativa: E
004) (ENEM) O Índice de Massa Corporal (IMC) é largamente utilizado há cerca de 200 anos, mas esse cálculo representa muito mais a corpulência que a adiposidade, uma vez que indivíduos musculosos e obesos podem apresentar o mesmo IMC. Uma nova pesquisa aponta o Índice de Adiposidade Corporal (IAC) como uma alternativa mais fidedigna para quantificar a gordura corporal, utilizando a medida do quadril e a altura. A figura mostra como calcular essas medidas, sabendo-se que, em mulheres, a adiposidade normal está entre 19% e 26%.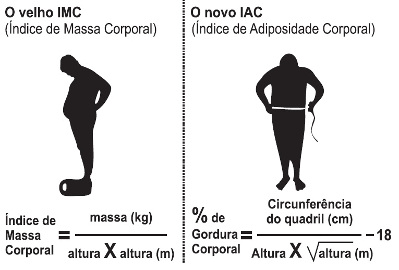 Uma jovem com IMC = 20 kg/m², 100 cm de circunferência dos quadris e 60 kg de massa corpórea resolveu averiguar seu IAC. Para se enquadrar aos níveis de normalidade de gordura corporal, a atitude adequada que essa jovem deve ter diante da nova medida é:
Uma jovem com IMC = 20 kg/m², 100 cm de circunferência dos quadris e 60 kg de massa corpórea resolveu averiguar seu IAC. Para se enquadrar aos níveis de normalidade de gordura corporal, a atitude adequada que essa jovem deve ter diante da nova medida é:
(Use √3 = 1,7 e √1,7 = 1,3)
(A) reduzir seu excesso de gordura em cerca de 27%.
(B) reduzir seu excesso de gordura em cerca de 1%.
(C) manter seus níveis atuais de gordura.
(D) aumentar seu nível de gordura em cerca de 1%.
(E) aumentar seu nível de gordura em cerca de 27%.
Resolução:
Para calcular o IAC da jovem, precisamos conhecer sua altura (h). Dessa forma, vamos utilizar a fórmula do cálculo do IMC:
IMC = massa
h . h
20 = 60
h²
h² = 60
20
h² = 3
h = √3
h = 1,7
Seja x a porcentagem de gordura corporal da jovem, vamos determiná-la através da fórmula do IAC:
x = circunferência do quadril – 18
h . √h
x = 100 – 18
1,7 . √1,7
x = 100 – 18
1,7 . 1,3
x = 100 – 18
2,21
x = 45,25 – 18
x = 27,25
O índice de adiposidade da jovem é de 27,25%, mas de acordo com o enunciado, o adequado deve estar entre 19% e 26%. Temos então que:
27,25% – 26% = 1,25%
Alternativa: B
005) (ENEM) Para aumentar as vendas no início do ano, uma loja de departamentos remarcou os preços de seus produtos 20% abaixo do preço original. Quando chegam ao caixa, os clientes que possuem o cartão fidelidade da loja têm direito a um desconto adicional de 10% sobre o valor total de suas compras.
Um cliente deseja comprar um produto que custava R$ 50,00 antes da remarcação de preços. Ele não possui o cartão fidelidade da loja.
Caso esse cliente possuísse o cartão fidelidade da loja, a economia adicional que obteria ao efetuar a compra, em reais, seria de
(A) 15,00
(B) 14,00
(C) 5,00
(D) 4,00
(E) 3,00.
Resolução:
Como o cliente não possui o cartão fidelidade da loja, o produto que ele comprará receberá apenas o desconto promocional de 20%. Para descobrir qual será o novo preço do produto que, originalmente, custava R$ 50
Usando regra de três temos:
100% = R$ 50,00
20% = x
100.x = 20 . 50
100 x = 1000
x = 1000
100
x = 10 reais
O produto recebeu um desconto de R$ 10. Se antes ele custava R$ 50, na promoção, custará R$ 40. Se o cliente possuísse o cartão fidelidade da loja, o preço promocional de R$ 40 receberia ainda um batimento de 10%. Vamos utilizar uma regra de três novamente para verificar o valor do novo desconto:
100% = R$ 40,00
10% = x
100.x = 10 . 40
100 x = 400
x = 400
100
x = 4 reais
Alternativa: D
006) (PM - ES - 2013 - Funcab) A Banda Junior da PMES atualmente atende cerca de 250 alunos da rede pública de ensino da Grande Vitória. Desde sua criação, já passaram pela Banda Júnior cerca de 1.000 alunos. O percentual de alunos, atualmente atendidos por esse projeto cultural da PMES, em relação ao total de alunos que já passaram por ele desde a sua criação corresponde a:
Resolução:
(A) 15%
(B) 20%
(C) 35%
(D) 25%
(E) 45%
Resolução:
Percentual = Parte/Todo . (%)
250/1000 = 0,25 . 100
25
Alternativa: D
007) (ENEM) Em mecânico de uma equipe de corrida necessita que as seguintes medidas realizadas em um carro sejam obtidas em metros:
a) distância a entre os eixos dianteiro e traseiro;
b) altura b entre o solo e o encosto do piloto.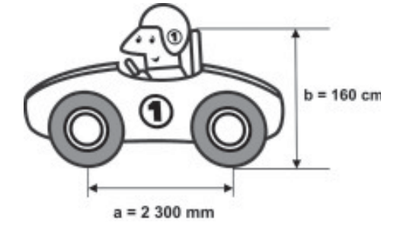 Ao optar pelas medidas a e b em metros, obtêm-se, respectivamente,
Ao optar pelas medidas a e b em metros, obtêm-se, respectivamente,
(A) 0,23 e 0,16.
(B) 23 e 16.
(C) 2,3 e 1,6.
(D) 230 e 160.
(E) 2 300 e 1 600.
Resolução:
Basta fazer a conversão de unidades.
2300mm = 2,3m
160cm = 1,6m
Alternativa: C
008) (ENEM) O medidor de energia elétrica de uma residência, conhecido por “relógio de luz”, é constituído de quatro pequenos relógios, cujos sentidos de rotação estão indicados conforme a figura:A medida é expressa em kWh. O número obtido na leitura é composto por 4 algarismos. Cada posição do número é formada pelo último algarismo ultrapassado pelo ponteiro.
O número obtido pela leitura em kWh, na imagem, é
(A) 2 624.
(B) 2 614.
(C) 2 715.
(D) 2 725.
(E) 4 162.
Resolução:
O “relógio de luz” funciona como um relógio comum independente do sentido de rotação. Depois basta fazer a composição das classes de algarismos, seguindo as instruções:
Milhar = 2
Centena = 6
Dezena = 1
Unidade = 4
Alternativa: B
009) (NEME) A bula de um antibiótico infantil, fabricado na forma de xarope, recomenda que sejam ministrados, diariamente, no máximo 500 mg desse medicamento para cada quilograma de massa do paciente. Um pediatra prescreveu a dosagem máxima desse antibiótico para ser ministrada diariamente a uma criança de 20 kg pelo período de 5 dias. Esse medicamento pode ser comprado em frascos de 10 mL, 50 mL, 100 mL, 250 mL e 500 mL. Os pais dessa criança decidiram comprar a quantidade exata de medicamento que precisará ser ministrada no tratamento, evitando a sobra de medicamento. Considere que 1 g desse medicamento ocupe um volume de 1 cm³.
A capacidade do frasco, em mililitro, que esses pais deverão comprar é
(A) 500.
(B) 250.
(C) 100.
(D) 50.
(E) 10.
Resolução:
A criança possui 20 kg e a dose diária máxima é de 0,5 gramas (500 mg) por quilo de massa do paciente.
20 . 0,5 = 10 gramas por dia
A questão informa que o pediatra prescreveu o remédio por 5 dias:
5 . 10 = 50 gramas
Sabendo-se que 1 g desse medicamento ocupa um volume de 1 cm³, então 50 gramas ocuparão um volume de 50 cm³.
Alternativa: D
010) (ENEM) Uma empresa tem diversos funcionários. Um deles é o gerente, que recebe R$ 1 000,00 por semana. Os outros funcionários são diaristas. Cada um deles trabalha 2 dias por semana, recebendo R$ 80,00 por dia trabalhado. Chamando de X a quantidade total de funcionários da empresa, a quantia Y, em reais, que esta empresa gasta semanalmente para pagar seus funcionários é expressa por
(A) Y = 80 X +920
(B) Y = 80 X + 1000
(C) Y = 80 X + 1080
(D) Y = 160 X + 1000
(E) Y = 160 X + 840
Resolução:
Como o número de funcionários total da empresa é X, para encontrar o de diaristas, basta tirar o gerente da conta. Assim, o número de diaristas é de X – 1.
Cada diarista recebe 2 . R$ 80,00 = R$ 160,00 por semana. Logo, o a quantia total Y que a fábrica paga semanalmente aos funcionários é de:
Y = (X – 1) . 160 + 1000
Y = 160 X + 840.
Alternativa E
011) (ENEM) Alguns objetos, durante a sua fabricação, necessitam passar por um processo de resfriamento. Para que isso ocorra, uma fábrica utiliza um tanque de resfriamento, como mostrado na figura. O que aconteceria com o nível da água se colocássemos no tanque um objeto cujo volume fosse de 2 400 cm³?
O que aconteceria com o nível da água se colocássemos no tanque um objeto cujo volume fosse de 2 400 cm³?
(A) O nível subiria 1 cm, fazendo a água ficar com 21 cm de altura.
(B) O nível subiria 20 cm, fazendo a água transbordar.
(C) O nível subiria 2 cm, fazendo a água ficar com 22 cm de altura.
(D) O nível subiria 8 cm, fazendo a água transbordar.
(E) O nível subiria 20 cm, fazendo a água transbordar.
Resolução:
O nível de água subirá 2 cm, pois, usando a fórmula de um prisma de base retangular, temos:
30 cm . 40 cm . x = 2 400 cm³
x = 2 cm
Alternativa: C
012) (ENEM) O diretor de uma escola convidou os 280 alunos de terceiro ano a participarem de uma brincadeira. Suponha que existem 5 objetos e 6 personagens numa casa de 9 cômodos; um dos personagens esconde um dos objetos em um dos cômodos da casa. O objetivo da brincadeira é adivinhar qual objeto foi escondido por qual personagem e em qual cômodo da casa o objeto foi escondido.
Todos os alunos decidiram participar. A cada vez um aluno é sorteado e dá a sua resposta. As respostas devem ser sempre distintas das anteriores, e um mesmo aluno não pode ser sorteado mais de uma vez. Se a resposta do aluno estiver correta, ele é declarado vencedor e a brincadeira é encerrada.
O diretor sabe que algum aluno acertará a resposta porque há
(A) 20 alunos a mais do que possíveis respostas distintas.
(B) 119 alunos a mais do que possíveis respostas distintas.
(C) 260 alunos a mais do que possíveis respostas distintas.
(D) 270 alunos a mais do que possíveis respostas distintas.
(E) 10 alunos a mais do que possíveis respostas distintas.
Resolução:
O número total de possibilidades de uma personagem esconder um dos 5 brinquedos em um dos 9 cômodos é 6 . 5 . 9 = 270.
Já que as respostas devem ser sempre diferentes, algum aluno acertou a resposta porque “há 10 alunos a mais do que possíveis respostas distintas”.
Alternativa: E
013) (ENEM) O acréscimo de tecnologias no sistema produtivo industrial tem por objetivo reduzir custos e aumentar a produtividade. No primeiro ano de funcionamento, uma indústria fabricou 8000 unidades de um determinado produto. No ano seguinte, investiu em tecnologia adquirindo novas máquinas e aumentou a produção em 50% Estima-se que esse aumento percentual se repita nos próximos anos, garantindo um crescimento anual de 50% Considere P a quantidade anual de produtos fabricados no ano t de funcionamento da indústria. Se a estimativa for alcançada, qual é a expressão que determina o número de unidades produzidas P em função de t para t ≥ 1 ?
(A) P(t) = 8000 . (1,5)t-1
(B) P(t) = 0,5t -1 + 8000
(C) P(t) = 50t -1 + 8000
(D) P(t) = 4000t -1 + 8000
(E) P(t) = 8000 . (0,5)t-1
Resolução:
Quando , teremos .
A partir daí, o número 8000 será multiplicado pelo fator de acréscimo .
Quando , teremos .
Quando , teremos .
E assim por diante.
Esta é a fórmula de Juros Compostos.
Alternativa: A
014) (NEMEM) Um produtor de café irrigado em Minas Gerais recebeu um relatório de consultoria estatística, constando, entre outras informações, o desvio padrão das produções de uma safra dos talhões de sua propriedade. Os talhões têm a mesma área de 30 000 m2 e o valor obtido para o desvio padrão foi de 90 kg/talhão. O produtor deve apresentar as informações sobre a produção e a variância dessas produções em sacas de 60 kg por hectare (10 000 m2).
A variância das produções dos talhões expressa em (sacas/hectare)2 é
(A) 20,25
(B) 0,25
(C) 0,71.
(D) 0,50
(E) 0,45.
Resolução:
A variância é igual ao quadrado do desvio padrão. Como a unidade pedida é em (sacas/ha)2, o desvio padrão deve ser encontrado em sacas/ha. Como cada saca tem 60kg, o desvio padrão é de Assim, a variância corresponde a 0,52 = 0,25(sacas/ha)2.
Alternativa: B
015) (ENEM) Os congestionamentos de trânsito constituem um problema que aflige, todos os dias, milhares de motoristas brasileiros. O gráfico ilustra a situação, representando, ao longo de um intervalo definido de tempo, a variação da velocidade de um veículo durante um congestionamento.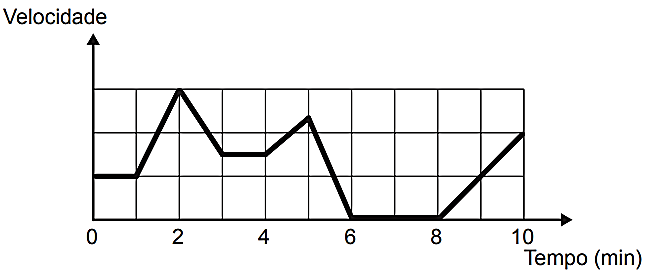 Quantos minutos o veículo permaneceu imóvel ao longo do intervalo de tempo total analisado?
Quantos minutos o veículo permaneceu imóvel ao longo do intervalo de tempo total analisado?
(A) 4
(B) 3
(C) 2
(D) 1
(E) 0
Resolução:
De 6 a 8 minutos a velocidade é nula. Logo o veículo está parado. Portanto, ele ficou 2 minutos parado.
Alternativa: C
016) (ENEM) Uma artesã confecciona dois diferentes tipos de vela ornamental a partir de moldes feitos com cartões de papel retangulares de 20 m x 10 cm (conforme ilustram as figuras abaixo). Unindo dois lados opostos do cartão, de duas maneiras, a artesã forma cilindros e, em seguida, os preenche completamente com parafina.
(A) o triplo.
(B) o dobro.
(C) igual.
(D) a metade.
(E) a terça parte.
Resolução:
Será preciso encontrar o volume de cada um dos cilindros, mas, para isso, é preciso encontrar primeiramente seus raios. Para tanto, basta notar que o comprimento da circunferência é igual ao comprimento do lado maior do retângulo no cilindro I e no cilindro II é igual ao lado menor desse mesmo retângulo. Usando a fórmula do comprimento da circunferência, encontraremos os raios:
CI = 2πrI
20 = 2πrI
20 = rI
2π
10 = rI
π
CII = 2πrII
10 = 2πrII
10 = rII
2π
5 = rII
π
O volume do primeiro cilindro é: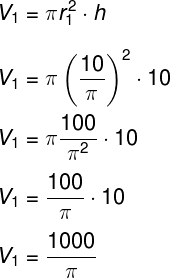
Já o volume do segundo cilindro é: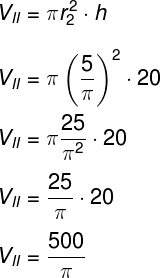
Portanto, o volume do cilindro 1 é o dobro do volume do cilindro 2.
Alternativa B
017) (ENEM) Um porta-lápis de madeira foi construído no formato cúbico, seguindo o modelo ilustrado a seguir. O cubo de dentro é vazio. A aresta do cubo maior mede 12 cm e a do cubo menor, que é interno, mede 8 cm.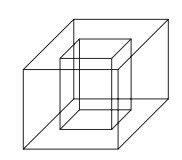 O volume de madeira utilizado na confecção desse objeto foi de
O volume de madeira utilizado na confecção desse objeto foi de
(A) 12 cm3
(B) 64 cm3
(C) 96 cm3
(D) 1216 cm3
(E) 728 cm3
Resolução:
O volume do cubo externo subtraído o volume do cubo interno é igual ao volume de madeira utilizado na confecção desse objeto, logo, tem-se que o volume de madeira utilizado na confecção foi de : 12³ -8³= 1216 cm³.
Alternativa: D
018) (ENEM) O proprietário de um parque aquático deseja construir uma piscina em suas dependências. A figura representa a vista superior dessa piscina, que é formada por três setores circulares idênticos, com ângulo central igual a 60°. O Raio R deve ser um número natural. O parque aquático já conta com uma piscina em formato retangular com dimensões 50m x 24m. O proprietário quer que a área ocupada pela nova piscina seja menor que a ocupada pela piscina já existente. Considere 3,0 como aproximação para π. O maior valor para R, em metros, deverá ser:
O parque aquático já conta com uma piscina em formato retangular com dimensões 50m x 24m. O proprietário quer que a área ocupada pela nova piscina seja menor que a ocupada pela piscina já existente. Considere 3,0 como aproximação para π. O maior valor para R, em metros, deverá ser:
(A) 16
(B) 28
(C) 29
(D) 31
(E) 49
Resolução:
Como a área da nova piscina deve ser menor do que a anterior, temos:
3 . (π.R² / 6) < 50 . 24
Como π = 3, temos:
3 . 3R² /6 < 1200
R² < 6 . 1200 / 9
R² < 800
R = 28
Já que 28² < 800 < 29².
Alternativa: B
019) (ENEM) Uma empresa de telefonia celular possui duas antenas que serão substituídas por uma nova, mais potente. As áreas de cobertura das antenas que serão substituídas são círculos de raio 2 km, cujas circunferências se tangenciam no ponto O, como mostra a figura. O ponto O indica a posição da nova antena, e sua região de cobertura será um círculo cuja circunferência tangenciará externamente as circunferências das áreas de cobertura menores. Com a instalação da nova antena, a medida da área de cobertura, em quilômetros quadrados, foi ampliada em
O ponto O indica a posição da nova antena, e sua região de cobertura será um círculo cuja circunferência tangenciará externamente as circunferências das áreas de cobertura menores. Com a instalação da nova antena, a medida da área de cobertura, em quilômetros quadrados, foi ampliada em
(A) 8 π
(B) 12 π
(C) 16 π
(D) 32 π
(E) 64 π
Resolução
A área de uma circunferência é dada pela fórmula πr².
A área ocupada pelas antenas antigas era de 8π, que temos que duas circunferência de raio 2, ou seja área = 2.2².π
Já a área coberta pela nova antena é de 16π, pois o seu raio, analisando a figura, vale 4. Assim, área = 4²π.
Ou seja, a área aumentou de 8π.
Alternativa: A
020) (ENEM) Para comemorar o aniversário de uma cidade, um artista projetou uma escultura transparente e oca, cujo formato foi inspirado em uma ampulheta. Ela é formada por três partes de mesma altura: duas são troncos de cone iguais e a outra é um cilindro. A figura é a vista frontal dessa escultura. No topo da escultura foi ligada uma torneira que verte água para dentro dela com vazão constante. O gráfico que expressa a altura (h) da água na escultura em função do tempo (t) decorrido é
No topo da escultura foi ligada uma torneira que verte água para dentro dela com vazão constante. O gráfico que expressa a altura (h) da água na escultura em função do tempo (t) decorrido é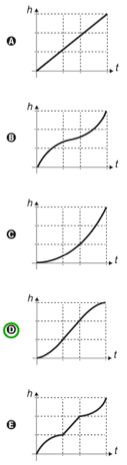
Resolução:
Particionando a figura, temos um cone, um cilindro e um cone, assim, temos que:
1 – no primeiro cone, a água sobe lentamente no início e mais rapidamente no final.
2- no cilindro, a água sobe linearmente, ou seja, não há variação de velocidade.
3 – no cone do final, temos que a água sobe rapidamente no início e mais lentamente no final.
Alternativa: D
021) (ENEM) Um senhor, pai de dois filhos, deseja comprar dois terrenos, com áreas de mesma medida, um para cada filho. Um dos terrenos visitados já está demarcado e, embora não tenha um formato convencional (como se observa na Figura B), agradou ao filho mais velho e, por isso, foi comprado. O filho mais novo possui um projeto arquitetônico de uma casa que quer construir, mas, para isso, precisa de um terreno na forma retangular (como mostrado na Figura A) cujo comprimento seja 7 m maior do que a largura. Para satisfazer o filho mais novo, esse senhor precisa encontrar um terreno retangular cujas medidas, em metro, do comprimento e da largura sejam iguais, respectivamente, a
Para satisfazer o filho mais novo, esse senhor precisa encontrar um terreno retangular cujas medidas, em metro, do comprimento e da largura sejam iguais, respectivamente, a
(A) 7,5 e 14,5
(B) 9,0 e 16,0
(C) 9,3 e 16,3
(D) 10,0 e 17,0
(E) 13,5 e 20,5
Resolução:
Primeiramente, dividimos a figura B em dois triângulos B1 e B2, um com altura de 21 m e base de 3 m e outro com altura e base medindo 15 m.
Assim, temos que área da figura A = área da figura B = B1 + B2
x(x + 7) = 15.15 / 2 + 21.3/2 = 144
Fatorando 144, temos que:
x(x + 7) = 9.16
x(x + 7) = 9(9 + 7)
Assim, as medidas do retângulo são 9 m e 16 m.
Alternativa: B
022) (ENEM) Um garçom precisa escolher uma bandeja de base retangular para servir quatro taças de espumante que precisam ser dispostas em uma única fileira, paralela ao lado maior da bandeja, e com suas bases totalmente apoiadas na bandeja. A base e a borda superior das taças são círculos de raio 4 cm e 5 cm, respectivamente. A bandeja a ser escolhida deverá ter uma área mínima, em centímetro quadrado, igual a
A bandeja a ser escolhida deverá ter uma área mínima, em centímetro quadrado, igual a
(A) 192.
(B) 300.
(C) 304.
(D) 320.
(E) 400.
Resolução:
Observe vista superior das taças organizadas sobre a bandeja.
Os diâmetro das bases das taças mede 8cm. São quatro taças. Mais 1cm de distância entre a borda da taça e a extremidade da base da mesma.
Nesse caso a área é dada por: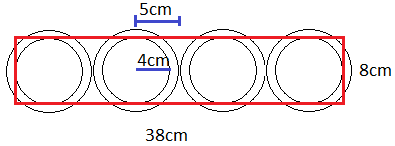
A = 8 . (8 . 4 + 6) = 304
Alternativa: C
023) (ENEM) Maria quer inovar em sua loja de embalagens e decidiu vender caixas com diferentes formatos. Nas imagens apresentadas estão as planificações dessas caixas. Quais serão os sólidos geométricos que Maria obterá a partir dessas planificações?
Quais serão os sólidos geométricos que Maria obterá a partir dessas planificações?
(A) Cilindro, prisma de base pentagonal e pirâmide.
(B) Cone, prisma de base pentagonal e pirâmide.
(C) Cone, tronco de pirâmide e pirâmide.
(D) Cilindro, tronco de pirâmide e prisma.
(E) Cilindro, prisma e tronco de cone.
Resolução:
Planificação de figuras espaciais. Cada figura espacial é formada por um conjunto específico ou variável (de acordo com sua característica) de figuras planas. Considerando as figuras espaciais retas, o cilindro é formado por 2 círculos e 1 retângulo, o cone por um círculo e um setor circular, com mesmo comprimento que o círculo. Já o prisma é formado por 2 bases (qualquer polígono) e “n” faces laterais retangulares, com “n” igual ao número de lados do polígono da base e a pirâmide por 1 base (qualquer polígono) e “k” faces laterais triangulares, com “k” igual ao número de lados do polígono da base. A base dos prismas e pirâmides os caracterizam. Assim, a primeira planificação representa um cilindro, a segunda um prisma de base pentagonal e a terceira uma pirâmide (de base triangular, também chamada de tetraedro).
Alternativa: A
024) (ENEM) O esquema I mostra a configuração de uma quadra de basquete. Os trapézios em cinza, chamados de garrafões, correspondem a áreas restritivas. Visando atender as orientações do Comitê Central da Federação Internacional de Basquete (Fiba) em 2010, que unificou as marcações das diferentes ligas, foi prevista uma modificação nos garrafões das quadras, que passariam a ser retângulos, como mostra o Esquema II.
Visando atender as orientações do Comitê Central da Federação Internacional de Basquete (Fiba) em 2010, que unificou as marcações das diferentes ligas, foi prevista uma modificação nos garrafões das quadras, que passariam a ser retângulos, como mostra o Esquema II. Após executadas as modificações previstas, houve uma alteração na área ocupada por cada garrafão, que corresponde a um(a)
Após executadas as modificações previstas, houve uma alteração na área ocupada por cada garrafão, que corresponde a um(a)
(A) aumento de 5 800 cm2.
(B) aumento de 75 400 cm2.
(C) aumento de 214 600 cm2.
(D) diminuição de 63 800 cm2.
(E) diminuição de 272 600 cm2.
Resolução:
Comecemos pela área do trapézio da figura I, que é dada por (600 + 360).580 / 2 = 278 400. Calculando a área da figura II temos 580 . 490 = 284 200 cm².
Assim, o aumento da área foi de 5 800 cm².
Alternativa: A
025) (ENEM) A siderúrgica “Metal Nobre” produz diversos objetos maciços utilizando o ferro. Um tipo especial de peça feita nessa companhia tem o formato de um paralelepípedo retangular, de acordo com  O produto das três dimensões indicadas na peça resultaria na medida da grandeza
O produto das três dimensões indicadas na peça resultaria na medida da grandeza
(A) massa
(B) volume
(C) superfície
(D) capacidade
(E) comprimento
Resolução:
O volume de um paralelepípedo é calculado através da multiplicação entre a área da base e a altura, em outras palavras, Volume de um paralelepípedo é exatamente o produto de suas três dimensões comprimento x largura x altura, como a questão especifica que o sólido é maciço, não existe a interpretação de “capacidade” no lugar de “volume”.
Alternativa: B
026) (ENEM) Dona Maria, diarista na casa da família Teixeira, precisa fazer café para servir as vinte pessoas que se encontram numa reunião na sala. Para fazer o café, Dona Maria dispõe de uma leiteira cilíndrica e copinhos plásticos, também cilíndricos.  Com o objetivo de não desperdiçar café, a diarista deseja colocar a quantidade mínima de água na leiteira para encher os vinte copinhos pela metade. Para que isso ocorra, Dona Maria deverá
Com o objetivo de não desperdiçar café, a diarista deseja colocar a quantidade mínima de água na leiteira para encher os vinte copinhos pela metade. Para que isso ocorra, Dona Maria deverá
(A) encher a leiteira até a metade, pois ela tem um volume 20 vezes maior que o volume do copo.
(B) encher a leiteira toda de água, pois ela tem um volume 20 vezes maior que o volume do copo.
(C) encher a leiteira toda de água, pois ela tem um volume 10 vezes maior que o volume do copo.
(D) encher duas leiteiras de água, pois ela tem um volume 10 vezes maior que o volume do copo.
(E) encher cinco leiteiras de água, pois ela tem um volume 10 vezes maior que o volume do copo.
Resolução:
O volume do copinho plástico, em centímetros cúbicos, é π.2².4 = 16π
O volume da leiteira, em centímetros cúbicos, é π.4².20 = 320π
(Volume da leiteira) ÷ (volume do copinho) = 320π/16π = 20
Assim, para encher os vinte copinhos plásticos pela metade, é suficiente encher a leiteira até a metade.
Alternativa: A
027) (ENEM) No gráfico abaixo, mostra-se como variou o valor do dólar, em relação ao real, entre o final de 2001 e o início de 2005. Por exemplo, em janeiro de 2002, um dólar valia cerca de R$ 2,40. Durante esse período, a época em que o real esteve mais desvalorizado em relação ao dólar foi no a) final de 2001.
Durante esse período, a época em que o real esteve mais desvalorizado em relação ao dólar foi no a) final de 2001.
(A) final de 2002.
(B) início de 2003.
(C) final de 2004.
(D) início de 2005.
(E) final de 2005
Resolução
O real é desvalorizado quando o preço do dólar é maior, ou seja, paga-se mais em reais para se comprar um dólar. Pelo gráfico, isto acontece no final de 2002.
Alternativa: A
029) (ENEM) O gás natural veicular (GNV) pode substituir a gasolina ou álcool nos veículos automotores. Nas grandes cidades, essa possibilidade tem sido explorada, principalmente, pelos táxis, que recuperam em um tempo relativamente curto o investimento feito com a conversão por meio da economia proporcionada pelo uso do gás natural. Atualmente, a conversão para gás natural do motor de um automóvel que utiliza a gasolina custa R$ 3.000,00. Um litro de gasolina permite percorrer cerca de 10 km e custa R$ 2,20, enquanto um metro cúbico de GNV permite percorrer cerca de 12 km e custa R$ 1,10. Desse modo, um taxista que percorra 6.000 km por mês recupera o investimento da conversão em aproximadamente:
(A) 2 meses.
(B) 4 meses.
(C) 6 meses.
(D) 8 meses.
(E) 10 meses.
Resolução
Primeiramente, vamos calcular o gasto do veículo quando utiliza gasolina e, em seguida, quando usa o GNV.
Gasto com gasolina: divide-se o preço do litro de gasolina (R$ 2,20) pela distância percorrida com esse litro (10 km) e depois multiplica-se pela distância percorrida no mês (6000 km).
G1 = (2,20/10). 6000 = R$ 1320,00
Gasto com GNV: divide-se o preço do metro cúbico de GNV (R$ 1,10) pela distância percorrida com esse metro cúbico (12 km) e depois multiplica-se pela distância percorrida no mês (6000 km).
G2 = (1,10/12).6000 = R$ 550,00
Agora vamos obter a diferença mensal de gastos dos dois combustíveis, que representará a economia (E):
E = R$ 1320,00 – R$ 550,00 = R$ 770,00
Como a conversão para gás natural do motor de um automóvel que utiliza gasolina custa R$3.000,00, basta dividir o valor por E para obtermos o tempo de retorno do investimento (t):
t = 3.000/770 = 3,89
Portanto, o tempo é de aproximadamente quatro meses.
Alternativa: C
030) (ENEM) As 23 ex-alunas de uma turma que completou o Ensino Médio há 10 anos se encontraram em uma reunião comemorativa. Várias delas haviam se casado e tido filhos. A distribuição das mulheres, de acordo com a quantidade de filhos, é mostrada no gráfico abaixo.Um prêmio foi sorteado entre todos os filhos dessas ex-alunas. A probabilidade de que a criança premiada tenha sido um(a) filho(a) único(a) é:
(A) 1/3
(B) 1/4
(C) 7/15
(D) 7/23
(E) 7/25
Resolução
Pelo gráfico dado, podemos obter a quantidade total de filhos:
8 mulheres não têm filho 8 x 0 = 0 filho
7 mulheres têm apenas 1 filho 7 x 1 = 7 filhos
6 mulheres têm 2 filhos 6 x 2 = 12 filhos
2 mulheres têm 3 filhos 2 x 3 = 6 filhos
Portanto, a quantidade de filhos é 0 + 7 + 12 + 6 = 25. Desse total, 7 são filhos únicos. Logo, a probabilidade de um filho único ser escolhido é de 7/25.
Alternativa: E
031) (ENEM) Um pátio de grandes dimensões vai ser revestido por pastilhas quadradas brancas e pretas, segundo o padrão representado ao lado, que vai ser repetido em toda a extensão do pátio.  As pastilhas de cor branca custam R$ 8,00 por metro quadrado e as de cor preta, R$ 10,00. O custo por metro quadrado do revestimento será de
As pastilhas de cor branca custam R$ 8,00 por metro quadrado e as de cor preta, R$ 10,00. O custo por metro quadrado do revestimento será de
(Aa) R$ 8,20.
(B) R$ 8,40.
(C) R$ 8,60.
(D) R$ 8,80.
(E) R$ 9,00.
Resolução
Através do desenho, podemos verificar que existem 20 pastilhas na horizontal e 10 na vertical.
Portanto, o número total de pastilhas é:
N = 20.10 = 200 pastilhas.
Como temos 10 pastilhas na horizontal e 4 são pretas, o número total de pastilhas pretas é:
Np = 10.4 = 40 pastilhas pretas.
Podemos então concluir, que 160 pastilhas são brancas, ou seja:
Nb = 200 – 40 = 160 pastilhas brancas.
As pastilhas de cor branca custam R$ 8,00 por metro quadrado e as de cor preta, R$ 10,00.
Assim sendo, supondo que cada pastilha corresponda a 1 m2, o custo total é dado por:
C = (160 x R$ 8,00) + (40 x R$ 10,00) = R$ 1.680,00
Como temos 200 pastilhas de 1 m2, o preço por metro quadrado: R$ 1.680,00 : 200 = R$ 8,40.
Alternativa: B
033) (ENEM) Os números de identificação utilizados no cotidiano (de contas bancárias, de CPF, de Carteira de Identidade etc) usualmente possuem um dígito de verificação, normalmente representado após o hífen, como em 17326-9. Esse dígito adicional tem a finalidade de evitar erros no preenchimento ou digitação de documentos. Um dos métodos usados para gerar esse dígito utiliza os seguintes passos:
— multiplica-se o último algarismo do número por 1, o penúltimo por 2, o antepenúltimo por 1, e assim por diante, sempre alternando multiplicações por 1 e por 2.
— soma-se 1 a cada um dos resultados dessas multiplicações que for maior do que ou igual a 10.
— somam-se os resultados obtidos .
— calcula-se o resto da divisão dessa soma por 10, obtendo-se assim o dígito verificador. O dígito de verificação fornecido pelo processo acima para o número 24685 é
(A) 1.
(B) 2.
(C) 4.
(D) 6.
(E) 8.
Resolução:
Para calcular o dígito de verificação de 24.685, vamos seguir os passos do método descrito pelo enunciado do problema:
5 . 1 = 5
8 . 2 = 16
6 . 1 = 6
4 . 2 = 8
2 . 1 = 2
Como temos um número maior que 10, no caso 16, devemos adicionar 1, obtendo 17. Soma-se os resultado obtidos:
5 + 17 + 6 + 8 + 2 = 38
Divide-se 38 por 10, obtendo 8 com resto. Este resto 8 é o dígito de verificação.
Alternativa: E
034) (ENEM) A escolaridade dos jogadores de futebol nos grandes centros é maior do que se imagina, como mostra a pesquisa acima, realizada com os jogadores profissionais dos quatro principais clubes de futebol do Rio de Janeiro. A escolaridade dos jogadores de futebol nos grandes centros é maior do que se imagina, como mostra a pesquisa acima, realizada com os jogadores profissionais dos quatro principais clubes de futebol do Rio de Janeiro. De acordo com esses dados, o percentual dos jogadores dos quatro clubes que concluíram o Ensino Médio é de aproximadamente:
A escolaridade dos jogadores de futebol nos grandes centros é maior do que se imagina, como mostra a pesquisa acima, realizada com os jogadores profissionais dos quatro principais clubes de futebol do Rio de Janeiro. De acordo com esses dados, o percentual dos jogadores dos quatro clubes que concluíram o Ensino Médio é de aproximadamente:
(A) 14%.
(B)48%.
(C) 54%.
(D) 60%.
(E) 68%.
Resolução
Olha é só somar todas que já terminaram o ensino médio temos 54 com médio completo e 14 com superior incompleto, logo temos 68 jogares com ensino médio completo
Total de 112 jogares
Divida os 68 jogadores por 112
% = 68/112
% = aproximadamente 0,60
0,60 . 110 = 60
Alternativa: C
035) (ENEM) O jornal de certa cidade publicou em uma página inteira a seguinte divulgação de seu caderno de classificados Para que a propaganda seja fidedigna à porcentagem da área que aparece na divulgação, a medida do lado do retângulo que representa os 4%, deve ser de aproximadamente
Para que a propaganda seja fidedigna à porcentagem da área que aparece na divulgação, a medida do lado do retângulo que representa os 4%, deve ser de aproximadamente
(A) 1 mm.
(B) 10 mm.
(C) 17 mm.
(D) 160 mm.
(E) 167 mm.
Resolução:
A partir do enunciado, temos:
x . 26 = 4% da área total, ou seja:
26x = 0,04 . 260 . 400
x = 4160/26
x = 160
Alternativa: D
036) (ENEM) No manejo sustentável de florestas, é preciso muitas vezes obter o volume da tora que pode ser obtida a partir de uma árvore. Para isso, existe um método prático, em que se mede a circunferência da árvore à altura do peito de um homem (1,30 m), conforme indicado na figura. A essa medida denomina-se "rodo" da árvore. O quadro a seguir indica a fórmula para se cubar, ou seja, obter o volume da tora em m3 a partir da medida do rodo e da altura da árvore
3 toras da espécie I, com 3 m de rodo, 12 m de comprimento e densidade 0,77 toneladas/m3;
2 toras da espécie II, com 4 m de rodo, 10 m de comprimento e densidade 0,78 toneladas/m3
Após realizar seus cálculos, o técnico solicitou que enviassem caminhões para transportar uma carga de, aproximadamente,
(A) 29,9 toneladas.
(B) 31,1 toneladas.
(C) 32,4 toneladas.
(D) 35,3 toneladas.
(E) 41,8 toneladas.
Resolução:
Volume de cada tora da espécie I: 3² . 12 . 0,06 = 6,48 m³
Volume de cada tora da espécie II: 4² . 10 . 0,06 = 9,60 m³
A massa das cinco toras será: 3 . 6,48 . 0,77 + 2 . 9,60 . 0,78 = 29,9448 toneladas
Aproximadamente 29,9 toneladas.
Alternativa: A
037) (ENEM) Para construir uma manilha de esgoto, um cilindro com 2 m de diâmetro e 4 m de altura (de espessura desprezível), foi envolvido homogeneamente por uma camada de concreto, contendo 20 cm de espessura.
Supondo que cada metro cúbico de concreto custe R$ 10,00 e tomando 3,1 como valor aproximado de π, então o preço dessa manilha é igual a
(A) R$ 230,40.
(B) R$ 124,00.
(C) R$ 104,16.
(D) R$ 54,56.
(E) R$ 49,60.
Resolução:
O volume de concreto é calculado a partir da diferença entre os volumes dos cilindros com raios diferentes: Vmaior com raio igual a 1,2m e Vmenor com raio igual a 1m e alturas iguais a 4 m
Volume do concreto: Vconc = Vmaior – Vmenor
Vconc = π (1,2² – 1²) 4 = 3,1 . 0,44 . 4 = 5,456 m³
Assim, o preço dessa manilha, em reais, é igual a:
5,456 . 10 = R$ 54,56
Alternativa: D
037) (ENEM) Embora o Índice de Massa Corporal (IMC) seja amplamente utilizado, existem ainda inúmeras restrições teóricas ao uso e às faixas de normalidade preconizadas. O Reciproco do Índice Ponderal (RIP), de acordo com o modelo alométrico, possui uma melhor fundamentação matemática, já que a massa é uma variável de dimensões cubicas e a altura, uma variável de dimensões lineares. As fórmulas que determinam esses índices são: Se uma menina, com 64 kg de massa, apresenta IMC igual a 25 kg/m2, então ela possui RIP igual a
Se uma menina, com 64 kg de massa, apresenta IMC igual a 25 kg/m2, então ela possui RIP igual a
(A) 0,4 cm/kg1/3.
(B) 2,5 cm/kg1/3.
(C) 8 cm/kg1/3.
(D) 20 cm/kg1/3.
(E) 40 cm/kg1/3.
Resolução:
Para descobrir a altura h da menina, fazemos:
25 = 64/h²
h² = 64/25
h = 1,6 m = 160 cm
Então:
RIP = 160/∛64 = 160/4 = 40
Alternativa: E
039) (ENEM) Um balão atmosférico, lançado em Bauru (343 quilômetros a Noroeste de São Paulo), na noite do último domingo, caiu nesta segunda-feira em Cuiabá Paulista, na região de Presidente Prudente, assustando agricultores da região. O artefato faz parte do programa Projeto Hibiscus, desenvolvido por Brasil, França, Argentina, Inglaterra e Itália, para a medição do comportamento da camada de ozônio, e sua descida se deu após o cumprimento do tempo previsto de medição. Na data do acontecido, duas pessoas avistaram o balão. Uma estava a 1,8 km da posição vertical do balão e o avistou sob um ângulo de 60º; a outra estava a 5,5 km da posição vertical do balão, alinhada com a primeira, e no mesmo sentido, conforme se vê na figura, e o avistou sob um ângulo de 30º.
Na data do acontecido, duas pessoas avistaram o balão. Uma estava a 1,8 km da posição vertical do balão e o avistou sob um ângulo de 60º; a outra estava a 5,5 km da posição vertical do balão, alinhada com a primeira, e no mesmo sentido, conforme se vê na figura, e o avistou sob um ângulo de 30º.
Qual a altura aproximada em que se encontrava o balão?
(A) 1,8 km
(B) 1,9 km
(C) 3,1 km
(D) 3,7 km
(E) 5,5 km
Resolução:
Comentário da questão
Para encontrar a altura h que se encontrava o balão, fazemos:
tg 60° = h/18
√3 = h/18
h = √3 . 18
h ≅ 3,11
Alternativa: C
040) (ENEM) Em canteiros de obras de construção civil é comum perceber trabalhadores realizando medidas de comprimento e de anguloso e fazendo demarcações por onde a obra deve começar ou se erguer. Em um desses canteiros foram feitas algumas marcas no chão plano. Foi possível perceber que, das seis estacas colocadas, três eram vértices de um triângulo retângulo e as outras três eram os pontos médios dos lados desse triângulo, foram indicadas por letras. A região demarcada pelas estacas A, B, M e N deveria ser calçada com concreto.
A região demarcada pelas estacas A, B, M e N deveria ser calçada com concreto.
Nessas condições, a área a ser calçada corresponde
(A) à mesma área do triângulo AMC.
(B) à mesma área do triângulo BNC.
(C) à metade da área formada pelo triângulo ABC.
(D) ao dobro da área do triângulo MNC.
(E) ao triplo da área do triângulo MNC.
Resolução:
Os triângulos BAC e MNC são semelhantes.
A razão k será:
k = AC/NC= 2
A razão entre suas áreas será:
k² = 2² = 4
Assim, a área S do triângulo MNC e a área
da região SR a ser calçada com concreto, tem-se:
(SR+S)/S = K²
(SR+S)/S = 4
SR = 3S
Alternativa: E
041) (ENEM) A ideia de usar rolos circulares para deslocar objetos pesados provavelmente surgiu com os antigos egípcios ao construírem as pirâmides. Representando por R o raio da base dos rolos cilíndricos, em metros, a expressão do deslocamento horizontal y do bloco de pedra em função de R, após o rolo ter dado uma volta completa sem deslizar, é
Representando por R o raio da base dos rolos cilíndricos, em metros, a expressão do deslocamento horizontal y do bloco de pedra em função de R, após o rolo ter dado uma volta completa sem deslizar, é
(A) y = R.
(B) y = 2R.
(C) y = πR.
(D) y = 2πR.
(E) y = 4πR.
Resolução:
O ponto mais alto do rolo cilíndrico, tem velocidade igual ao dobro da velocidade do centro desse mesmo rolo. Quando o tambor dá uma volta completa, o seu centro se desloca 2πR e o objeto que está em contato com o ponto mais alto vai deslocar-se o dobro, isto é, 4πR.
Alternativa: E
042) (ENEM) O gráfico mostra o número de favelas no município do Rio de Janeiro entre 1980 e 2004, considerando que a variação nesse número entre os anos considerados é linear. Se o padrão na variação do período 2004/2010 se mantiver nos próximos 6 anos, e sabendo que o número de favelas em 2010 é 968, então o número de favelas em 2016 será
Se o padrão na variação do período 2004/2010 se mantiver nos próximos 6 anos, e sabendo que o número de favelas em 2010 é 968, então o número de favelas em 2016 será
(A) menor que 1 150.
(B) 218 unidades maior que em 2004.
(C) maior que 1 150 e menor que 1 200.
(D) 177 unidades maior que em 2010.
(E) maior que 1 200.
Resolução:
Em 2004: 750 favelas – ano 2004
Em 2010: 968 favelas – ano 2010
Em 2016: y favelas – ano 2016
Como são lineares aplicaremos a equação do primeiro grau:
(2004,750); (2010,968) e (2016,y)
750 = a.2004 + b
968 = a.2006+b
Resolvendo o sistema por adição, temos:
968-750=2a
a = 218/6 = 109/3
750 = (109.2004)/3+b
b = – 72062
y(x) = (109x)/3 – 72062
y(2016) = (109.2016)/3 – 72062
y(2016) = 1186
Alternativa: C
043) (ENEM) O gráfico apresenta a quantidade de gols marcados pelos artilheiros das Copas do Mundo desde a Copa de 1930 até a de 2006. A partir dos dados apresentados, qual a mediana das quantidades de gols marcados pelos artilheiros das Copas do Mundo?
A partir dos dados apresentados, qual a mediana das quantidades de gols marcados pelos artilheiros das Copas do Mundo?
(A) 6 gols
(B) 6,5 gols
(C) 7 gols
(D) 7,3 gols
(E) 8,5 gols
Resolução:
Colocando em ordem crescente temos:
4; 5; 5; 6; 6; 6; 6; 6; 6; 7; 7; 8; 8; 9; 9; 10; 11; 13
Os elementos centrais são: 6 e 7
A mediana será: (6 + 7)/2 = 6,5 gols
Alternativa: B
044) (ENEM) Em um casamento, os donos da festa serviam champanhe aos seus convidados em taças com formato de um hemisfério (Figura 1), porém um acidente na cozinha culminou na quebra de grande parte desses recipientes. Para substituir as taças quebradas, utilizou-se um outro tipo com formato de cone (Figura 2). No entanto, os noivos solicitaram que o volume de champanhe nos dois tipos de taças fosse igual. Considere:
Considere: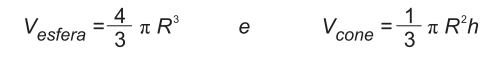 Sabendo que a taca com o formato de hemisfério é servida completamente cheia, a altura do volume de champanhe que deve ser colocado na outra taca, em centímetros, é de
Sabendo que a taca com o formato de hemisfério é servida completamente cheia, a altura do volume de champanhe que deve ser colocado na outra taca, em centímetros, é de
(A) 1,33
(B) 6,00
(C) 12,00
(D) 56,52
(E) 113,04
Resolução:
O volume da semiesfera (figura 1) é:
O volume do cone (figura 2) é:
Para que os volumes seja iguais a altura h será:
Alternativa: B
045) (ENEM) O Salto Triplo é uma modalidade do atletismo em que o atleta dá um salto em um só pé, uma passada e um salto, nessa ordem. Sendo que o salto com impulsão em um só pé será feito de modo que o atleta caia primeiro sobre o mesmo pé que deu a implosão; na passada ele cairá com o outro pé, do qual o salto é realizado.
Um atleta da modalidade Salto Triplo, depois de estudar seus movimentos, percebeu que, do segundo para o primeiro salto, o alcance diminuía em 1,2 m, e, do terceiro para o segundo salto, o alcance diminuía 1,5 m.
Querendo atingir a meta de 17,4 m nessa prova e considerando os seus estudos, a distância alcançada no primeiro salto teria de estar entre
(A) 4,0 m e 5,0 m.
(B) 5,0 m e 6,0 m.
(C) 6,0 m e 7,0 m.
(D) 7,0 m e 8,0 m.
(E) 8,0 m e 9,0 m.
Resolução:
Primeiro salto: s
Segundo salto: (s-1,2)
Terceiro salto: (s-2,7)
Logo para que o atleta alcance a meta de 17,4m no salto triplo, o valor de s será:
s + (s-1,2) + (s-2,7) = 17,4
3s = 17,4 + 1,2 +2,7
s = 21,3/3
s=7,1 m
Assim a distância alcançada no primeiro salto teria de estar entre 7,0 m e 8,0m
Alternativa: D
046) (ENEM) Marco e Paulo foram classificados em um concurso. Para classificação no concurso o candidato deveria obter média aritmética na pontuação igual ou superior a 14. Em caso de empate na média, o desempate seria em favor da pontuação mais regular. No quadro a seguir são apresentados os pontos obtidos nas provas de Matemática, Português e Conhecimentos Gerais, a média, a mediana e o desvio padrão dos dois candidatos.
Dados dos candidatos no concurso O candidato com pontuação mais regular, portanto mais bem classificado no concurso, é
O candidato com pontuação mais regular, portanto mais bem classificado no concurso, é
(A) Marco, pois a média e a mediana são iguais.
(B) Marco, pois obteve menor desvio padrão.
(C) Paulo, pois obteve a maior pontuação da tabela, 19 em Português.
(D) Paulo, pois obteve maior mediana.
(E) Paulo, pois obteve maior desvio padrão.
Resolução
As médias de Marco e Paulo são iguais, porém Marcos possui o menor desvio padrão, o que significa dizer que suas notas nas provas estão mais próximas da média do que as notas de Paulo.
Assim, as notas obtidas por Marco no concurso são mais regulares, logo Marco foi melhor classificado.
Alternativa: B
047) (ENEM) Um grupo de pacientes com Hepatite C foi submetido a um tratamento tradicional em que 40% desses pacientes foram completamente curados. Os pacientes que não obtiveram cura foram distribuídos em dois grupos de mesma quantidade e submetidos a dois tratamentos inovadores. No primeiro tratamento inovador, 35% dos pacientes foram curados e, no segundo, 45%.
Em relação aos pacientes submetidos inicialmente, os tratamentos inovadores proporcionaram cura de
(A) 16%
(B) 24%
(C) 32%
(D) 48%
(E) 64%
Resolução:
Pacientes que não foram curados com o tratamento tradicional: 100%-40% = 60%
Pacientes curados pelo primeiro tratamento: 1/2 . 60% .35% = 1/2 . 0,6 . 0,35 =0,105 = 10,5%.
Pacientes curados pelo segundo tratamento: 1/2 . 60% .45% = 1/2 . 0,6 .0,45 = 0,135 = 13,5%
Em relação ao total de pacientes submetidos inicialmente, os tratamentos inovadores proporcionaram cura de: 10,5% + 13,5% = 24%
Alternativa: B
048) (ENEM) Em 2006, a produção mundial de etanol foi de 40 bilhões de litros e a de biodiesel, de 6,5 bilhões. Neste mesmo ano, a produção brasileira de etanol correspondeu a 43% da produção mundial, ao passo que a produção dos Estados Unidos da América, usando milho, foi de 45%.
Considerando que, em 2009, a produção mundial de etanol seja a mesma de 2006 e que os Estados Unidos produzirão somente a metade de sua produção de 2006, para que o total produzido pelo Brasil e pelos Estados Unidos continue correspondendo a 88% da produção mundial, o Brasil deve aumentar sua produção em, aproximadamente,
(A) 22,5%.
(B) 50,0%.
(C) 52,3%.
(D) 65,5%.
(E) 77,5%.
Resolução:
Em 2009, a produção mundial de etanol será a mesma de 2006.
A produção do Brasil e Estados Unidos em 2006, foi de: 43% + 45% = 88%.
A produção dos Estados Unidos em 2009 será a metade da produção de 2006: 45%/2 = 22,5%.
Assim, a produção do Brasil será de: 88% – 22,5% = 65,5%.
0,43———————— 100%
0,65 ———————— x
x = (0,265 . 100)/0,43
x ≅ 1,523
Representando um aumento de (1,523 – 1) = 0,523 = 52,3%
Alternativa: C
049) (ENEM) João mora na cidade A e precisa visitar cinco clientes, localizados em cidades diferentes da sua. Cada trajeto possível pode ser representado por uma sequência de 7 letras. Por exemplo, o trajeto ABCDEFA, informa que ele sairá da cidade A, visitando as cidades B, C, D, E e F nesta ordem, voltando para a cidade A. Além disso, o número indicado entre as letras informa o custo do deslocamento entre as cidades. A figura mostra o custo de deslocamento entre cada uma das cidades. Como João quer economizar, ele precisa determinar qual o trajeto de menor custo para visitar os cinco clientes. somente parte das sequências, pois os trajetos ABCDEFA e AFEDCBA têm o mesmo custo. Ele gasta 1min30s para examinar uma sequência e descartar sua simétrica, conforme apresentado.
Como João quer economizar, ele precisa determinar qual o trajeto de menor custo para visitar os cinco clientes. somente parte das sequências, pois os trajetos ABCDEFA e AFEDCBA têm o mesmo custo. Ele gasta 1min30s para examinar uma sequência e descartar sua simétrica, conforme apresentado.
O tempo mínimo necessário para João verificar todas as sequências possíveis no problema é de
(A) 60 min.
(B) 90 min.
(C) 120 min.
(D) 180 min.
(E) 360 min.
Resolução:
Descartando as pontas, que devem ser os pontos A, as possibilidades de João efetuar as visitas são de:
P = 5!/2 = 160/2 = 60 possibilidades
Tempo gasto em cada sequência: 1 mim 30s = 90 segundos
90 seg ————– 1 sequência
x seg—————- 60 sequências
x =60 . 90
x = 5400 segundos = 90 minutos
Alternativa: B
050) (ENEM) O diretor de um colégio leu numa revista que os pés das mulheres estavam aumentando. Há alguns anos, a média do tamanho dos calçados das mulheres era de 35,5 e, hoje, é de 37,0. Embora não fosse uma informação científica, ele ficou curioso e fez uma pesquisa com as funcionárias do seu colégio, obtendo o quadro a seguir: Escolhendo uma funcionária ao acaso e sabendo que ela tem calçado maior que 36,0 a probabilidade de ela calçar 38,0 é
Escolhendo uma funcionária ao acaso e sabendo que ela tem calçado maior que 36,0 a probabilidade de ela calçar 38,0 é
(A) 1/3
(B) 1/5
(C) 2/5
(D( 5/7
(E) 5/14
Resolução:
Número de funcionárias com calçado maior que 36 é: 1 + 10 + 3 = 14 funcionárias
Número de funcionárias com calçado igual a 38: 10 funcionárias
Assim a probabilidade da funcionária calçar 38 será: P = 10/14 = 5/7
Alternativa: D
051) (ENEM) O quadro seguinte mostra o desempenho de um time de futebol no último campeonato. A coluna da esquerda mostra o número de gols marcados e a coluna da direita informa em quantos jogos o time marcou aquele número de gols. Se X, Y e Z são, respectivamente, a média, a mediana e a moda desta distribuição, então
Se X, Y e Z são, respectivamente, a média, a mediana e a moda desta distribuição, então
(A) X = Y < Z.
(B) Z < X = Y.
(C) Y < Z < X.
(D) Z < X < Y.
(E) Z < Y < X.
Resolução:
Média
Mediana
Colocando os dados em ordem crescente, temos:
A média aritmética entre os dois elementos centrais será: Y = 2
Moda
O valor de maior frequência será: Z =0
Assim: Z < Y <X
Alternativa: E
052) (ENEM) A disparidade de volume entre os planetas é tão grande que seria possível colocá-los uns dentro dos outros. O planeta Mercúrio é o menor de todos. Marte é o segundo menor: dentro dele cabem três Mercúrios. Terra é o único com vida: dentro dela cabem sete Martes. Netuno é o quarto maior: dentro dele cabem 58 Terras. Júpiter é o maior dos planetas: dentro dele cabem 23 Netunos.
Seguindo o raciocínio proposto, quantas Terras cabem dentro de Júpiter?
(A) 406
(B) 1334
(C) 4002
(D) 938
(D) 28014
Resolução:
Do enunciado temos que:
VMarte = 3.VMercúrio
VTerra = 7.VMarte
VTerra = 21.VMercúrio
VNetuno = 58.VTerra = 58.21.VMercúrio = 1218.VMercúrio
VJúpiter = 23.VNetuno = 23.1218.VMercúrio = 28014.VMercúrio
Assim: VJúpiter / VTerra = (28014.VMercúrio) / (21.VMercúrio) = 1334
VJúpiter = 1334 VTerra
Alternativa: B
053) (ENEM) Um dos grandes problemas da poluição dos mananciais (rios, córregos e outros) ocorre pelo hábito de jogar óleo utilizado em frituras nos encanamentos que estão interligados com o sistema de esgoto. Se isso ocorrer, cada 10 litros de óleo poderão contaminar 10 milhões (107) de litros de água potável.
Manual de etiqueta. Parte integrante das revistas Veja (ed. 2055), Claudia (ed. 555), National Geographic (ed. 93) e Nova Escola (ed. 208) (adaptado).
Suponha que todas as famílias de uma cidade descartem os óleos de frituras através dos encanamentos e consomem 1 000 litros de óleo em frituras por semana.
Qual seria, em litros, a quantidade de água potável contaminada por semana nessa cidade?
(A) 10-2
(B) 10³
(C) 104
(D) 106
(E) 109
Resolução:
10 litros de óleo contaminam 107 litros de água potável.
Regra de três simples
10 litros de óleo 107 litros de água potável.
1 000 litros de óleo x litros de água potável.
10x = 10³ . 107
x= 10³ . 107 . 10-1
x = 109 litros de água potável contaminada.
Alternativa: E
054) (ENEM) Ronaldo é um garoto que adora brincar com números. Numa dessas brincadeiras, empilhou caixas numeradas de acordo com a sequencia conforme mostrada no esquema a seguir. Ele percebeu que a soma dos números em cada linha tinha uma propriedade e que, por meio dessa propriedade, era possível prever a soma de qualquer linha posterior às já construídas.
Ele percebeu que a soma dos números em cada linha tinha uma propriedade e que, por meio dessa propriedade, era possível prever a soma de qualquer linha posterior às já construídas.
A partir dessa propriedade, qual será́ a soma da 9a linha da sequência de caixas empilhadas por Ronaldo?
(A) 9
(B) 45
(C) 64
(D) 81
(E) 285
Resolução:
A soma dos elementos da linha n será:
A soma da 9a. linha da sequência de caixas empilhadas por Ronaldo será:
S9 = 9² = 81
Alternativa: D
055) (ENEM) Para conseguir chegar a um número recorde de produção de ovos de Pascoa, as empresas brasileiras começam a se planejar para esse período com um ano de ovos de Pascoa produzidos no Brasil no período de 2005 a 2009. De acordo com o gráfico, o biênio que apresentou maior produção acumulada foi
De acordo com o gráfico, o biênio que apresentou maior produção acumulada foi
(A) 2004-2005
(B) 2005-2006
(C) 2006-2007
(D) 2007-2008
(E) 2008-2009
Resolução:
A partir do gráfico podemos estabelecer a produção de cada biênio. O biênio que apresentou maior produção acumulada foi 2008 – 2009.
Alternativa: E
056) (ENEM) Para realizar a viagem dos sonhos, uma pessoa precisava fazer um empréstimo no valor de R$ 5000,00. Para pagar as prestações, dispõe de, no máximo, R$ 400,00 mensais. Para esse valor de empréstimo, o valor da prestação (P) é calculado em função do número de prestações (n) segundo a fórmula Se necessário, utilize 0,005 como aproximação para log 1,013; 2,602 como aproximação para log 400; 2,525 como aproximação para log 335.
Se necessário, utilize 0,005 como aproximação para log 1,013; 2,602 como aproximação para log 400; 2,525 como aproximação para log 335.
De acordo com a fórmula dada, o menor número de parcelas cujos valores não comprometem o limite definido pela pessoa é
(A) 12
(B) 14
(C) 15
(D) 16
(E) 17
Resolução:
400 = ( 5 000.1,013^n.0,013) / (1,013^n-1)
400.(1,013^n – 1) = ( 5 000.1,013^n.0,013)
400.1,013^n – 400 = 65.1,013^n
400.1,013^n – 65.1,013^n = 400
335.1,013^n = 400
1,013^n = 400/335 , utilizando as informações do enunciado temos que:
(10^0,005)^n = 10^(2,602) / 10^(2,525)
(10^0,005)^n = 10^0,077
0,005 n = 0,077
n = 0,077/0,005
n = 15,4
n = 16
Alternativa: D
057) (ENEM) Raios de luz solar estão atingindo a superfície de um lago formando um ângulo X com a sua superfície, conforme indica a figura. Em determinadas condições, pode-se supor que a intensidade luminosa desses raios, na superfície do lago, seja dada aproximadamente por I(x) = k . sen(x) sendo k uma constante, e supondo-se que X está entre 0° e 90º. Quando x = 30º, a intensidade luminosa se reduz a qual percentual de seu valor máximo?
Em determinadas condições, pode-se supor que a intensidade luminosa desses raios, na superfície do lago, seja dada aproximadamente por I(x) = k . sen(x) sendo k uma constante, e supondo-se que X está entre 0° e 90º. Quando x = 30º, a intensidade luminosa se reduz a qual percentual de seu valor máximo?
(A) 33%
(B) 50%
(C) 57%
(D) 70%
(E)86%
Resolução:
O valor máximo será quando x = 90º, então i = k.1= k
Quando x = 30º, teremos i=k.(½)= k/2
Logo, a variação será de 50%
Alternativa: B
058) (ENEM) Em uma cantina, o sucesso de venda no verão são sucos preparados à base de polpa de frutas. Um dos sucos mais vendidos é o de morango com acerola, que é preparado com 2/3 de polpa de morango e 1/3 de polpa de acerola. Para o comerciante, as polpas são vendidas em embalagens de igual volume. Atualmente, a embalagem da polpa de morango custa R$ 18,00 e a de acerola, R$ 14,70. Porém, está prevista uma alta no preço da embalagem da polpa de acerola no próximo mês, passando a custar R$ 15,30.
Para não aumentar o preço do suco, o comerciante negociou com o fornecedor uma redução no preço da embalagem da polpa de morango.
A redução, em real, no preço da embalagem da polpa de morango deverá ser de
(A) 1,20.
(B) 0,90.
(C) 0,60.
(D) 0,40.
(E) 0,30
Resolução:
Usando dois terços do volume embalagem de polpa morango gastam – se 23 . 18 = 12 reais mais um terço do volume da embalagem da polpa de acerola, 1/3 . 14,70 = 4,90 totalizando um custo de 16,90.
Com o aumento de preço da polpa de acerola em 60 centavos, o custo total desta parte muda para:
1/3 . 15,30 = 5,10
Mantendo o preço total em 15,90,
o preço gasto com morango será de: 16,90 – 5,10 = 11,80. Porém, esse preço representa 1/3 . = 11,80 e por isso x = 17,70. Logo, a diminuição é de R$ 0,30.
Alternativa: E
059) (ENEM) Um casal realiza sua mudança de domicílio e necessita colocar numa caixa de papelão um objeto cúbico, de 80 cm de aresta, que não pode ser desmontado. Eles têm à disposição cinco caixas, com diferentes dimensões, conforme descrito:
Caixa 1: 86 cm x 86 cm x 86 cm
Caixa 2: 75 cm x 82 cm x 90 cm
Caixa 3: 85 cm x 82 cm x 90 cm
Caixa 4: 82 cm x 95 cm x 82 cm
Caixa 5: 80 cm x 95 cm x 85 cm
O casal precisa escolher uma caixa na qual o objeto caiba, de modo que sobre o menor espaço livre em seu interior.
A caixa escolhida pelo casal deve ser a de número
(A) 1.
(B) 2.
(C) 3.
(D) 4.
(E) 5.
Resolução:
A caixa que dar a menor diferença volumétrica em relação ao objeto cúbico citado é a de número 3.
Alternativa: C
060) (ENEM) Um brinquedo infantil caminhão-cegonha é formado por uma carreta e dez carrinhos nela transportados, conforme a figura. No setor de produção da empresa que fabrica esse brinquedo, é feita a pintura de todos os carrinhos para que o aspecto do brinquedo fique mais atraente. São utilizadas as cores amarelo, branco, laranja e verde, e cada carrinho é pintado apenas com uma cor. O caminhão-cegonha tem uma cor fixa. A empresa determinou que em todo caminhão-cegonha deve haver pelo menos um carrinho de cada uma das quatro cores disponíveis. Mudança de posição dos carrinhos no caminhão-cegonha não gera um novo modelo do brinquedo.
No setor de produção da empresa que fabrica esse brinquedo, é feita a pintura de todos os carrinhos para que o aspecto do brinquedo fique mais atraente. São utilizadas as cores amarelo, branco, laranja e verde, e cada carrinho é pintado apenas com uma cor. O caminhão-cegonha tem uma cor fixa. A empresa determinou que em todo caminhão-cegonha deve haver pelo menos um carrinho de cada uma das quatro cores disponíveis. Mudança de posição dos carrinhos no caminhão-cegonha não gera um novo modelo do brinquedo.
Com base nessas informações, quantos são os modelos distintos do brinquedo caminhão-cegonha que essa empresa poderá produzir?
(A) C6,4
(B) C9,3
(C) C10,4
(D) 64
(E) 46
Resolução:
Como todo caminhão cegonha deve ter pelo menos 1 carrinho de cada cor, é necessário colorir os 6 carrinhos restantes com as cores disponíveis. Isso pode ser feito de:
9!/(6! 3!) = C9,3
Alternativa: B
061) (ENEM) Uma empresa especializada em conservação de piscinas utiliza um produto para tratamento da água cujas especificações técnicas sugerem que seja adicionado 1,5 mL desse produto para cada 1 000 L de água da piscina. Essa empresa foi contratada para cuidar de uma piscina de base retangular, de profundidade constante igual a 1,7 m, com largura e comprimento iguais a 3 m e 5 m, respectivamente. O nível da lâmina d’água dessa piscina é mantido a 50 cm da borda da piscina.
A quantidade desse produto, em mililitro, que deve ser adicionada a essa piscina de modo a atender às suas especificações técnicas é
(A) 11,25.
(B) 27,00.
(C) 28,80.
(D) 32,25.
(E) 49,50.
Resolução:
De acordo com o enunciado temos que o volume de água na piscina é igual a:
V = 5.3.1,2 = 15.1,2 = 18 m³ = 18 000 l
Logo, a quantidade de produto será: (18 000.1,5) / 1 000 = 27 ml
Alternativa: B
062) (ENEM ) Um instituto de pesquisas eleitorais recebe uma encomenda na qual a margem de erro deverá ser de, no máximo, 2 pontos percentuais (0,02). O instituto tem 5 pesquisas recentes, P1 a P5, sobre o tema objeto da encomenda e irá usar a que tiver o erro menor que o pedido. Os dados sobre as pesquisas são os seguintes: em que σ é um parâmetro e N é o número de pessoas entrevistadas pela pesquisa.
O instituto tem 5 pesquisas recentes, P1 a P5, sobre o tema objeto da encomenda e irá usar a que tiver o erro menor que o pedido. Os dados sobre as pesquisas são os seguintes: em que σ é um parâmetro e N é o número de pessoas entrevistadas pela pesquisa.
Qual pesquisa deverá ser utilizada?
(A) P1.
(B) P2.
(C) P3.
(D) P4.
(E) P5.
Resolução:
a margem de erro: é calculada por :
p1 = 0,5/42 . 1,96 . 100 = 2,15%
p2 = 0,4/28 . 1,96 . 100 = 2,7%
p3 = 0,3/24 . 1,96 . 100= 2,45%
p4 = 0,2/21 . 1,96 . 100 = 1,76%
Alternativa: D
063) (ENEM) Em um teleférico turístico, bondinhos saem de estações ao nível do mar e do topo de uma montanha. A travessia dura 1,5 minuto e ambos os bondinhos se deslocam à mesma velocidade. Quarenta segundos após o bondinho A partir da estação ao nível do mar, ele cruza com o bondinho B, que havia saído do topo da montanha.
Quantos segundos após a partida do bondinho B partiu o bondinho A?
(A) 5.
(B) 10.
(C) 15.
(D) 20.
(E) 25.
Resolução:
Tt=90 segundos.
Ta = tb =40 segundos.
Como eles se encontraram e faltam 50 segundos para a encontrar B, então B partiu 10 segundos depois do bondinho A .
Alternativa: B
064) (ENEM) Num dia de tempestade, a alteração na profundidade de um rio, num determinado local, foi registrada durante um período de 4 horas. Os resultados estão indicados no gráfico de linhas. Nele, a profundidade h, registrada às 13 horas, não foi anotada e, a partir de h, cada unidade sobre o eixo vertical representa um metro. Foi informado que entre 15 horas e 16 horas, a profundidade do rio diminuiu em 10%.
Foi informado que entre 15 horas e 16 horas, a profundidade do rio diminuiu em 10%.
Às 16 horas, qual é a profundidade do rio, em metro, no local onde foram feitos os registros?
(A) 18.
(B) 20.
(C) 24.
(D) 36.
(E) 40.
Resolução:
Às 15h temos P =10k e ás 16h P = 9k (redução de 10%)
como k = 2m então ás 16h temos p =18
Alternativa: A
065) (ENEM) Uma rede hoteleira dispõe de cabanas simples na ilha de Gotland, na Suécia, conforme Figura 1. A estrutura de sustentação de cada uma dessas cabanas está representada na Figura 2. A ideia é permitir ao hóspede uma estada livre de tecnologia, mas conectada com a natureza A forma geométrica da superfície cujas arestas estão representadas na Figura 2 é
A forma geométrica da superfície cujas arestas estão representadas na Figura 2 é
(A) tetraedro.
(B) pirâmide retangular.
(C) tronco de pirâmide retangular.
(D) prisma quadrangular reto.
(E) prisma triangular reto.
Resolução:
Como a figura 2 possui faces opostas paralelas e iguais e base triangular, sua representação é dada por um prisma triangular reto.
Alternativa: E
066) (ENEM) A figura ilustra uma partida de Campo Minado, o jogo presente em praticamente todo computador pessoal. Quatro quadrados em um tabuleiro 16 x 16 foram abertos, e os números em suas faces indicam quantos dos seus 8 vizinhos contêm minas (a serem evitadas). O número 40 no canto inferior direito é o número total de minas no tabuleiro, cujas posições foram escolhidas ao acaso, de forma uniforme, antes de se abrir qualquer quadrado. Em sua próxima jogada, o jogador deve escolher dentre os quadrados marcados com as letras P, Q, R, S e T um para abrir, sendo que deve escolher aquele com a menor probabilidade de conter uma mina.
Em sua próxima jogada, o jogador deve escolher dentre os quadrados marcados com as letras P, Q, R, S e T um para abrir, sendo que deve escolher aquele com a menor probabilidade de conter uma mina.
O jogador deverá abrir o quadrado marcado com a letra
(A) P.
(B) Q.
(C) R.
(D) S.
(E) T.
Resolução:
[a probabilidade da bomba estar no ponto P] = 4/28 = 1/7 e [a probabilidade dele não estar] = 6/7
[a probabilidade da bomba estar no ponto Q] = 1/8 e [ a probabilidade de ele não estar ] = 7/8
[a probabilidade da bomba estar no ponto S] = 35/70 = 1/2 e [a probabilidade de ele não estar] = 35/70 = 1/2
[a probabilidade da bomba estar no ponto T] =2 1/56 = 3/8 e [a probabilidade de ele não estar] = 5/8
[a probabilidade da bomba estar no ponto R] = 30/220 = 3/22 e [a probabilidade de ele não estar] = 19/22
Como 7/8 > 19/22 > 6/7>5/8 >1/2.
Q > R > P > T > S Então o quadrado aberto será com a letra Q.
Alternativa: B
067) (ENEM) A imagem apresentada na figura é uma cópia em preto e branco da tela quadrada intitulada O peixe, de Marcos Pinto, que foi colocada em uma parede para exposição e fixada nos pontos A e B. Por um problema na fixação de um dos pontos, a tela se desprendeu, girando rente à parede. Após o giro, ela ficou posicionada como ilustrado na figura, formando um ângulo de 45° com a linha do horizonte.
Por um problema na fixação de um dos pontos, a tela se desprendeu, girando rente à parede. Após o giro, ela ficou posicionada como ilustrado na figura, formando um ângulo de 45° com a linha do horizonte.
Para recolocar a tela na sua posição original, deve-se girá-la, rente à parede, no menor ângulo possível inferior a 360°
A forma de recolocar a tela na posição original, obedecendo ao que foi estabelecido, é girando-a em um ângulo de
(A) 90° no sentido horário.
(B) 135° no sentido horário.
(C) 180° no sentido anti-horário.
(D) 270° no sentido anti-horário
(E) 315° no sentido horário.
Resolução:
Observando a figura, para retornar a posição original, girando-a no sentido horário o ângulo será de: 45º +90º = 145º.
Alternativa: B
068) (ENEM) A avaliação de rendimento de alunos de um curso universitário baseia-se na média ponderada das notas obtidas nas disciplinas pelos respectivos números de créditos, como mostra o quadro: Quanto melhor a avaliação de um aluno em determinado período letivo, maior sua prioridade na escolha de disciplinas para o período seguinte.
Quanto melhor a avaliação de um aluno em determinado período letivo, maior sua prioridade na escolha de disciplinas para o período seguinte.
Determinado aluno sabe que se obtiver avaliação “Bom” ou “Excelente” conseguirá matrícula nas disciplinas que deseja. Ele já realizou as provas de 4 das 5 disciplinas em que está matriculado, mas ainda não realizou a prova da disciplina I, conforme o quadro. Para que atinja seu objetivo, a nota mínima que ele deve conseguir na disciplina I é
Para que atinja seu objetivo, a nota mínima que ele deve conseguir na disciplina I é
(A) 7,00.
(B) 7,38.
(C) 7,50.
(D( 8,25.
(E) 9,00.
Resolução:
Calculando a média ponderada temos que:
M = (12.x + 4.8 + 8.6 + 8.5 + 10.7,5) / 42
M = (12x + 32 + 48 + 40 + 75) / 42
Para atingir o objetivo M = 7
7 = (12x + 195) /42
12x = 294 – 195
x = 99/12
x = 8,25
Alternativa: D
069) (ENEM) A água para o abastecimento de um prédio é armazenada em um sistema formado por dois reservatórios idênticos, em formato de bloco retangular, ligados entre si por um cano igual ao cano de entrada, conforme ilustra a figura. A água entra no sistema pelo cano de entrada no Reservatório 1 a uma vazão constante e, ao atingir o nível do cano de ligação, passa a abastecer o Reservatório 2. Suponha que, inicialmente, os dois reservatórios estejam vazios.
A água entra no sistema pelo cano de entrada no Reservatório 1 a uma vazão constante e, ao atingir o nível do cano de ligação, passa a abastecer o Reservatório 2. Suponha que, inicialmente, os dois reservatórios estejam vazios.
Qual dos gráficos melhor descreverá a altura h do nível da água no Reservatório 1, em função do volume V de água no sistema?
(A) 
(B) 
(C) 
(D) 
(E) 
Resolução:
Como o reservatório 1 é um prisma então seu crescimento até o nível do cano de ligação é uma função linear.
Durante a passagem pelo cano de ligação até o preenchimento do reservatório 2 temos uma função constante.
Após a passagem pelo cano de ligação, o reservatório 1 e o reservatório 2 crescem de forma linear com inclinação inferior a do primeiro instante.
Alternativa: D
070) (ENEM) manchete demonstra que o transporte de grandes cargas representa cada vez mais preocupação quando feito em vias urbanas. Caminhão entala em viaduto no Centro Um caminhão de grande porte entalou embaixo do viaduto no cruzamento das avenidas Borges de Medeiros e Loureiro da Silva no sentido Centro-Bairro, próximo à Ponte de Pedra, na capital. Esse veículo vinha de São Paulo para Porto Alegre e transportava três grandes tubos, conforme ilustrado na foto. Considere que o raio externo de cada cano da imagem seja 0,60 m e que eles estejam em cima de uma carroceria cuja parte superior está a 1,30 m do solo. O desenho representa a vista traseira do empilhamento dos canos.
Considere que o raio externo de cada cano da imagem seja 0,60 m e que eles estejam em cima de uma carroceria cuja parte superior está a 1,30 m do solo. O desenho representa a vista traseira do empilhamento dos canos. A margem de segurança recomendada para que um veículo passe sob um viaduto é que a altura total do veículo com a carga seja, no mínimo, 0,50 m menor do que a altura do vão do viaduto.
A margem de segurança recomendada para que um veículo passe sob um viaduto é que a altura total do veículo com a carga seja, no mínimo, 0,50 m menor do que a altura do vão do viaduto.
Considere 1,7 como aproximação para (3)1/2
Qual deveria ser a altura mínima do viaduto, em metro, para que esse caminhão pudesse passar com segurança sob seu vão?
(A) 2,82.
(B) 3,52.
(C) 3,70.
(D) 4,02.
(E) 4,20.
Resolução:
Altura mínima do viaduto H = r + r + h1 + h2 + h3
Onde: h1 = altura do triângulo equilátero formado pela ligação dos centros das circunferências
h2 = altura do solo até a carroceria.
h3 = distância do viaduto ao topo do veículo
H = 0,6 + 0,6 + 0,6 . 1,7 + 0,5 = 4,02
Alternativa: D
071) (ENEM) Um menino acaba de se mudar para um novo bairro e deseja ir à padaria. Pediu ajuda a um amigo que lhe forneceu um mapa com pontos numerados, que representam cinco locais de interesse, entre os quais está a padaria. Além disso, o amigo passou as seguintes instruções: a partir do ponto em que você se encontra, representado pela letra X, ande para oeste, vire à direita na primeira rua que encontrar, siga em frente e vire à esquerda na próxima rua. A padaria estará logo a seguir A padaria está representada pelo ponto numerado com
A padaria está representada pelo ponto numerado com
(A) 1.
(B) 2.
(C) 3.
(D) 4.
(E) 5.
Resolução:
Seguindo a oeste, virando à primeira rua à direita, seguindo em frente, virando à primeira rua à esquerda, encontramos a padaria situada no ponto 1.
Alternativa: A
072) (ENEM) Três alunos, X, Y e Z, estão matriculados em um curso de inglês. Para avaliar esses alunos, o professor optou por fazer cinco provas. Para que seja aprovado nesse curso, o aluno deverá ter a média aritmética das notas das cinco provas maior ou igual a 6. Na tabela, estão dispostas as notas que cada aluno tirou em cada prova. Com base nos dados da tabela e nas informações dadas, ficará(ão) reprovado(s)
Com base nos dados da tabela e nas informações dadas, ficará(ão) reprovado(s)
(A) apenas o aluno Y
(B) apenas o aluno Z
(C) apenas os alunos x e y
(D) apenas os alunos x e z
(E) os alunos x, y, z
Resolução:
Como a média para a reprovação é menor que 6 então: a média do aluno X=31/5=6,2
a média do aluno Y=30/5=6
a média do aluno Z = 29/5=5,8
Logo temos que o aluno Z foi reprovado.
Alternativa: B
073) (ENEM) Uma desenhista projetista deverá desenhar uma tampa de panela em forma circular. Para realizar esse desenho, ela dispõe, no momento, de apenas um compasso, cujo comprimento das hastes é de 10 cm, um transferidor e uma folha de papel com um plano cartesiano. Para esboçar o desenho dessa tampa, ela afastou as hastes do compasso de forma que o ângulo formado por elas fosse de 120o. A ponta seca está representada pelo ponto C, a ponta do grafite está representada pelo ponto B e a cabeça do compasso está representada pelo ponto A conforme a figura. Após concluir o desenho, ela o encaminha para o setor de produção. Ao receber o desenho com a indicação do raio da tampa, verificará em qual intervalo este se encontra e decidirá o tipo de material a ser utilizado na sua fabricação, de acordo com os dados.
Após concluir o desenho, ela o encaminha para o setor de produção. Ao receber o desenho com a indicação do raio da tampa, verificará em qual intervalo este se encontra e decidirá o tipo de material a ser utilizado na sua fabricação, de acordo com os dados. O tipo de material a ser utilizado pelo setor de produção será
O tipo de material a ser utilizado pelo setor de produção será
(A) I
(B) II
(C) III
(D) IV
(E) V
Resolução:
Utilizando lei dos cossenos no triângulo ABC:
BC² = 10² + 10² -2 . 10 . 10 . cos20º
BC = 10 . 1,7
BC = 17
Alternativa: D
074) (ENEM) Uma pessoa ganhou uma pulseira formada por pérolas esféricas, na qual faltava uma das pérolas. A figura indica a posição em que estaria faltando esta pérola. Ela levou a jóia a um joalheiro que verificou que a medida do diâmetro dessas pérolas era 4 milímetros. Em seu estoque, as pérolas do mesmo tipo e formato, disponíveis para reposição, tinham diâmetros iguais a: 4,025 mm; 4,100 mm; 3,970 mm; 4,080 mm e 3,099 mm.
Ela levou a jóia a um joalheiro que verificou que a medida do diâmetro dessas pérolas era 4 milímetros. Em seu estoque, as pérolas do mesmo tipo e formato, disponíveis para reposição, tinham diâmetros iguais a: 4,025 mm; 4,100 mm; 3,970 mm; 4,080 mm e 3,099 mm.
O joalheiro então colocou na pulseira a pérola cujo diâmetro era o mais próximo do diâmetro das pérolas originais.
A pérola colocada na pulseira pelo joalheiro tem diâmetro, em milímetro, igual a
(A) 3,099.
(B) 3,970.
(C) 4,025.
(D) 4,080.
(E) 4,100.
Resolução:
A pérola com o diâmetro mais próximo de 4mm será a de diâmetro 4,025 pois:
4,025 -4 = 0,025
4 -3,970 = 0,030
4 -3,099 = 0,901
4,080 -4 = 0,080
4,100 -4 = 0,1
Alternativa: C
075) (ENEM) Em uma de suas viagens, um turista comprou uma lembrança de um dos monumentos que visitou. Na base do objeto há informações dizendo que se trata de uma peça em escala 1: 400, e que seu volume é de 25 cm3.
O volume do monumento original, em metro cúbico, é de
(A) 100
(B) 400
(C) 1600
(D) 6250
(E) 10000
Resolução:
Como a escala é 1/400 e o volume 25cm³ então devemos utilizar (1/400)³. Por regra de três temos que o volume real é de 400³.25=1600000cm³ ou 1600m³
Alternativa: C
076) (ENEM) Uma bicicleta do tipo mountain bike tem uma coroa com 3 engrenagens e uma catraca com 6 engrenagens, que, combinadas entre si, determinam 18 marchas (número de engrenagens da coroa vezes o número de engrenagens da catraca). Os números de dentes das engrenagens das coroas e das catracas dessa bicicleta estão listados no quadro.
Os números de dentes das engrenagens das coroas e das catracas dessa bicicleta estão listados no quadro. Sabe-se que o número de voltas efetuadas pela roda traseira a cada pedalada é calculado dividindo-se a quantidade de dentes da coroa pela quantidade de dentes da catraca.
Sabe-se que o número de voltas efetuadas pela roda traseira a cada pedalada é calculado dividindo-se a quantidade de dentes da coroa pela quantidade de dentes da catraca.
Durante um passeio em uma bicicleta desse tipo, deseja-se fazer um percurso o mais devagar possível, escolhendo, para isso, uma das seguintes combinações de engrenagens (coroa x catraca): A combinação escolhida para realizar esse passeio da forma desejada é
A combinação escolhida para realizar esse passeio da forma desejada é
(A) I
(B) II
(C) III
(D) IV
(E) V
Resolução:
Devemos buscar a menor razão. Logo a IV que é 26/24=1,08 é o valor procurado
Alternativa: D
077) (ENEM) O comitê organizador da Copa do Mundo 2014 criou a logomarca da Copa, composta de uma figura plana e o slogan “Juntos num só ritmo”, com mãos que se unem formando a taça Fifa. Considere que o comitê organizador resolvesse utilizar todas as cores da bandeira nacional (verde, amarelo, azul e branco) para colorir a logomarca, de forma que regiões vizinhas tenham cores diferentes. De quantas maneiras diferentes o comitê organizador da Copa poderia pintar a logomarca com as cores citadas?
De quantas maneiras diferentes o comitê organizador da Copa poderia pintar a logomarca com as cores citadas?
(A) 15
(B) 30
(C) 108
(D) 360
(E) 972
Resolução:
Sejam A, B, C, D, E e F as 6 regiões da logomarca, como mostrado na figura.
O número de colorações possíveis, com no máximo 4 cores, é 4 . 3 . 3 . 3 . 3 . 3 = 972;
com exatamente 3 cores é :
C (4,3) x 3 . 2 . 2 . 2 . 2 . 2 = 384
com exatamente 2 cores:
C(4,2) x 2 . 1 . 1 . 1 . 1 . 1 = 12
e, com uma cor, é impossível.
Pelo Princípio da Inclusão-Exclusão, o número de maneiras de pintar usando todas as
cores é
972 − 384 + 12 = 600
Observação: no enunciado, caso o comitê resolvesse utilizar no máximo as quatro cores da bandeira nacional, a alternativa correta seria a E, 4 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 = 972.
Alternativa: E
078) (ENEM) Viveiros de lagostas são construídos, por cooperativas locais de pescadores, em formato de prismas reto-retangulares, fixados ao solo e com telas flexíveis de mesma altura, capazes de suportar a corrosão marinha. Para cada viveiro a ser construído, a cooperativa utiliza integralmente 100 metros lineares dessa tela, que é usada apenas nas laterais. Quais devem ser os valores de X e de Y, em metro, para que a área da base do viveiro seja máxima?
Quais devem ser os valores de X e de Y, em metro, para que a área da base do viveiro seja máxima?
(A) 1 e 49
(B) 1 e 99
(C) 10 e 10
(D) 25 E 25
(E) 50 E 50
Resolução:
O perímetro vale 100, ou seja, 2x + 2y = 100, logo x + y =5 0.
A área A = x.y.
Fazendo y = 50 -x temos que a A = x(50 -x) = -x² + 50x.
Calculando o x do vértice temos -50/-2 = 25.
Assim x = 25 e y = 25
Alternativa: D
079) (ENEM) O fisiologista inglês Archibald Vivian Hill propôs, em seus estudos, que a velocidade V de contração de um músculo ao ser submetido a um peso p é dada pela equação (p + a) (v +b) = K, com a, b e K constantes.
Um fisioterapeuta, com o intuito de maximizar o efeito benéfico dos exercícios que recomendaria a um de seus pacientes, quis estudar essa equação e a classificou desta forma:
TIPO DE CURVA
- Semirreta oblíqua
- Semirreta horizontal
- Ramo de parábola
- Arco de circunferência
- Ramo de hipérbole
O fisioterapeuta analisou a dependência entre v e p na equação de Hill e a classificou de acordo com sua representação geométrica no plano cartesiano, utilizando o par de coordenadas (p. V). Admita que K> 0.
O gráfico da equação que o fisioterapeuta utilizou para maximizar o efeito dos exercícios é do tipo
(A) Semirreta oblíqua.
(B) semirreta horizontal.
(C) ramo de parábola.
(D) arco de circunferência.
(E) ramo de hipérbole.
Resolução:
(p + a) . (v + b) = k
Onde a, b e k são constantes. Temos uma associação com as grandezas inversamente proporcionais y.x=k
Logo seu gráfico será dado por um ramo de hipérbole.
Alternativa: E
080) (ENEM) Em um parque há dois mirantes de alturas distintas que são acessados por elevador panorâmico. O topo do mirante 1 é acessado pelo elevador 1, enquanto que o topo do mirante 2 é acessado pelo elevador 2. Eles encontram-se a uma distância possível de ser percorrida a pé, e entre os mirantes há um teleférico que os liga que pode ou não ser utilizado pelo visitante. O acesso aos elevadores tem os seguintes custos:
O acesso aos elevadores tem os seguintes custos:
Subir pelo elevador 1: R$ 0,15;
Subir pelo elevador 2: R$ 1,80;
Descer pelo elevador 1: R$ 0,10;
Descer pelo elevador 2: R$ 2,30.
O custo da passagem do teleférico partindo do topo do mirante 1 para o topo do mirante 2 é de R$ 2,00, e do topo do mirante 2 para o topo do mirante 1 é de R$ 2,50.
Qual é o menor custo, em real, para uma pessoa visitar os topos dos dois mirantes e retornar ao solo?
(A) 2,25
(B) 3,90
(C) 4,35
(D) 4,40
(E) 4,45
Resolução:
O menor custo será dado por:
subir no elevador 1= 0,15
descer no elevador 1= 0,10
subir no elevador 2= 1,80
descer no elevador 2= 2,30
Cujo custo será de R$4,35.
Alternativa: C
081) (ENEM) A mensagem digitada no celular, enquanto você dirige, tira a sua atenção e, por isso, deve ser evitada. Pesquisas mostram que um motorista que dirige um carro a uma velocidade constante percorre “às cegas” (isto é, sem ter visão da pista) uma distância proporcional ao tempo gasto ao olhar para o celular durante a digitação da mensagem. Considere que isso de fato aconteça. Suponha que dois motoristas (X e Y) dirigem com a mesma velocidade constante e digitam a mesma mensagem em seus celulares. Suponha, ainda, que o tempo gasto pelo motorista X olhando para seu celular enquanto digita a mensagem corresponde a 25% do tempo gasto pelo motorista Y para executar a mesma tarefa.
A razão entre as distâncias percorridas às cegas por X e Y, nessa ordem, é igual a
(A) 5/4
(B) 1/4
(C) 4/3
(D) 4/1
(E) 3/4
Resolução:
D1/D2 = v . t1/v . t2 = v . 0,25t2/v . t2 = 0,25 = 1/4
Alternativa: B
082) (ENEM) O resultado de uma pesquisa eleitoral, sobre a preferência dos eleitores em relação a dois candidatos, foi representado por meio do Gráfico 1. Ao ser divulgado esse resultado em jornal, o Gráfico 1 foi cortado durante a diagramação, como mostra o Gráfico 2.
Ao ser divulgado esse resultado em jornal, o Gráfico 1 foi cortado durante a diagramação, como mostra o Gráfico 2. Apesar de os valores apresentados estarem corretos e a largura das colunas ser a mesma, muitos leitores criticaram o formato do Gráfico 2 impresso no jornal, alegando que houve prejuízo visual para o candidato B.
Apesar de os valores apresentados estarem corretos e a largura das colunas ser a mesma, muitos leitores criticaram o formato do Gráfico 2 impresso no jornal, alegando que houve prejuízo visual para o candidato B.
A diferença entre as razões da altura da coluna B pela coluna A nos gráficos 1 e 2 é
(A) 0.
(B) 1/2.
(C) 1/5.
(D) 2/15.
(E) 8/35.
Resolução:
No primeiro gráfico temos uma relação b/a de 30 para 70, considerando que a cada espaço vale 10, ou seja 3/7. No Segundo gráfico temos 1/5. logo 3/7-⅕ = 8/35
Alternativa: E
083) (ENEM) Um cientista, em seus estudos para modelar a pressão arterial de uma pessoa, utiliza uma função do tipo P(t) = A + Bcos(kt) em que A, B e K são constantes reais positivas e t representa a variável tempo, medida em segundo. Considere que um batimento cardíaco representa o intervalo de tempo entre duas sucessivas pressões máximas.
Ao analisar um caso específico, o cientista obteve os dados: A função P(t) obtida, por este cientista, ao analisar o caso específico foi
A função P(t) obtida, por este cientista, ao analisar o caso específico foi
(A) P(t) = 99 + 21cos(3πt)
(B) P(t) = 78 + 42cos(3πt)
(C) P(t) = 99 + 21cos(2πt)
(D) P(t) = 99 + 21cos(t)
(E) P(t) = 78 + 42cos(t)
Resolução:
Substituindo o cosseno de cada opção por 1 e -1, percebemos que as opções compatíveis com os valores de máximo e mínimos apresentados são letra a, c ou d. Como são 90 batimentos a cada 60 segundos temos, 2/3 de batimentos por segundo. Como o enunciado diz que o tempo entre dois valores máximos é o tempo de 1 batimento percebemos que o período deve ser igual a 2/3. Numa função trigonométrica p = 2 / |k|, por isso 2/3 = 2 / |k|, concluindo que c = 3.
Alternativa: A
084) (ENEM) Para decorar uma mesa de festa infantil, um chefe de cozinha usará um melão esférico com diâmetro medindo 10 cm, o qual servirá de suporte para espetar diversos doces. Ele irá retirar uma calota esférica do melão, conforme ilustra a figura, e, para garantir a estabilidade deste suporte, dificultando que o melão role sobre a mesa, o chefe fará o corte de modo que o raio r da seção circular de corte seja de pelo menos 3 cm. Por outro lado, o chefe desejará dispor da maior área possível da região em que serão afixados os doces. Para atingir todos os seus objetivos, o chefe deverá cortar a calota do melão numa altura h, em centímetro, igual a
Para atingir todos os seus objetivos, o chefe deverá cortar a calota do melão numa altura h, em centímetro, igual a
(A) 5 - √91/2
(B) 10 - √91
(C) 1
(D) 4
(E) 5
Resolução:
Observando o triângulo pitagórico OAB, temos AO = 4
logo: h + 4 = 5
h = 1
Alternativa: C
085) (ENEM) A Igreja de São Francisco de Assis, obra arquitetônica modernista de Oscar Niemeyer, localizada na Lagoa da Pampulha, em Belo Horizonte, possui abóbadas parabólicas. A seta na Figura 1 ilustra uma das abóbadas na entrada principal da capela. A Figura 2 fornece uma vista frontal desta abóbada, com medidas hipotéticas para simplificar os cálculos. Qual a medida da altura H, em metro, indicada na Figura 2?
Qual a medida da altura H, em metro, indicada na Figura 2?
(A) 16/3
(B) 31/5
(C) 25/4
(D) 25/3
(E) 75/2
Resolução:
Temos que a equação da parábola pode ser dada por:
Y = a(x + 5).(x - 5)
Y = a(x² - 25)
Substituindo o ponto (4,3) na equação temos que:
3 = a(16 - 25)
3 = a(-9)
logo a = -1/3
Então a equação y = -x²/3 + 25/3
Como yv = c temos que: yv = 25/3
Alternativa: D
086) (ENEM) Quanto tempo você fica conectado à internet? Para responder a essa pergunta foi criado um miniaplicativo de computador que roda na área de trabalho, para gerar automaticamente um gráfico de setores, mapeando o tempo que uma pessoa acessa cinco sites visitados. Em um computador, foi observado que houve um aumento significativo do tempo de acesso da sexta-feira para o sábado, nos cinco sites mais acessados. A seguir, temos os dados do miniaplicativo para esses dias. Analisando os gráficos do computador, a maior taxa de aumento no tempo de acesso, da sexta-feira para o sábado, foi no site
Analisando os gráficos do computador, a maior taxa de aumento no tempo de acesso, da sexta-feira para o sábado, foi no site
(A) X
(B) Y
(C) Z
(D) W
(E) U
Resolução:
Considere as taxas de aumento de cada um dos sites:
X: 9/12 = 0,75
Y:21/3 0= 0,7
Z:1/10 = 0,1
W:19/38 = 0,5
U:16/40 = 0,4
A maior taxa de aumento é a do site X.
Alternativa: A
087) (ENEM) Neste modelo de termômetro, os filetes na cor preta registram as temperaturas mínima e máxima do dia anterior e os filetes na cor cinza registram a temperatura ambiente atual, ou seja, no momento da leitura do termômetro.
Neste modelo de termômetro, os filetes na cor preta registram as temperaturas mínima e máxima do dia anterior e os filetes na cor cinza registram a temperatura ambiente atual, ou seja, no momento da leitura do termômetro.
Por isso ele tem duas colunas. Na da esquerda, os números estão em ordem crescente, de cima para baixo, de -30 °C até 50 °C. Na coluna da direita, os números estão ordenados de forma crescente, de baixo para cima, de -30 °C até 50 °C. A leitura é feita da seguinte maneira:
A leitura é feita da seguinte maneira:
a temperatura mínima é indicada pelo nível inferior do filete preto na coluna da esquerda;
a temperatura máxima é indicada pelo nível inferior do filete preto na coluna da direita;
a temperatura atual é indicada pelo nível superior dos filetes cinza nas duas colunas.
Qual é a temperatura máxima mais aproximada registrada nesse termômetro?
(A) 5 °C
(B) 7 °C
(C) 13 °C
(D) 15 °C
(E) 19 °C
Resolução:
Como a temperatura máxima é indicada pelo nível inferior do filete preto na coluna da direita, o valor mais próximo da máxima registrada é 19Cº.
Alternativa: E
088) (ENEM) Pivô central é um sistema de irrigação muito usado na agricultura, em que uma área circular é projetada para receber uma estrutura suspensa. No centro dessa área, há uma tubulação vertical que transmite água através de um cano horizontal longo, apoiado em torres de sustentação, as quais giram, sobre rodas, em torno do centro do pivô, também chamado de base, conforme mostram as figuras. Cada torre move-se com velocidade constante. Um pivô de três torres (T1, T2 e T3) será instalado em uma fazenda, sendo que as distâncias entre torres consecutivas bem como da base à torre T1 são iguais a 50 m. O fazendeiro pretende ajustar as velocidades das torres, de tal forma que o pivô efetue uma volta completa em 25 horas. Use 3 como aproximação para π.
Um pivô de três torres (T1, T2 e T3) será instalado em uma fazenda, sendo que as distâncias entre torres consecutivas bem como da base à torre T1 são iguais a 50 m. O fazendeiro pretende ajustar as velocidades das torres, de tal forma que o pivô efetue uma volta completa em 25 horas. Use 3 como aproximação para π.
Para atingir seu objetivo, as velocidades das torres T1, T2 e T3 devem ser, em metro por hora, de
(A) 12, 24 e 36.
(B) 6, 12 e 18.
(C) 2, 4 e 6.
(D) 300, 1200 e 2700.
(E) 600, 2400 e 5400.
Resolução:
Considerando a torre T1, temos
2πr = 2 . 3. 50 = 300 metros em 25 horas
Logo v = 300/25 = 12m/h
Alternativa: A
089) (ENEM) Dois reservatórios A e B são alimentados por bombas distintas por um período de 20 horas. A quantidade de água contida em cada reservatório nesse período pode ser visualizada na figura. O número de horas em que os dois reservatórios contêm a mesma quantidade de água é
O número de horas em que os dois reservatórios contêm a mesma quantidade de água é
(A) 1
(B) 2
(C) 4
(D) 5
(E) 6
Resolução:
Comparando os valores dos volumes dos reservatórios A e B mostrados nos eixos y, que estão em uma razão de 1/2,, apenas o valor de 30000 está com a mesma quantidade de água no mesmo instante de tempo entre 8 e 9.
Alternativa: A
090) (ENEM) Para uma temporada das corridas de Fórmula 1, a capacidade do tanque de combustível de cada carro passou a ser de 100 kg de gasolina. Uma equipe optou por utilizar uma gasolina com densidade de 750 gramas por litro, iniciando a corrida com o tanque cheio. Na primeira parada de reabastecimento, um carro dessa equipe apresentou um registro em seu computador de bordo acusando o consumo de quatro décimos da gasolina originalmente existente no tanque. Para minimizar o peso desse carro e garantir o término da corrida, a equipe de apoio reabasteceu o carro com a terça parte do que restou no tanque na chegada ao reabastecimento.
A quantidade de gasolina utilizada, em litro, no reabastecimento foi
(A) 20/0,075
(B) 20/0,75
(C) 20/7,5
(D) 20 x 0,075
(E) 20 x 0,75
Resolução:
A quantidade de gasolina é igual a: (1/3) . 0,6 . (100000/750) = 20 / 0,75
Alternativa: B
091) (ENEM) O gráfico apresenta a taxa de desemprego (em %) para o período de março de 2008 a abril de 2009, obtida com base nos dados observados nas regiões metropolitanas de Recife, Salvador, Belo Horizonte, Rio de Janeiro, São Paulo e Porto Alegre. A mediana dessa taxa de desemprego, no período de março de 2008 a abril de 2009, foi de
A mediana dessa taxa de desemprego, no período de março de 2008 a abril de 2009, foi de
(A) 8,1%
(B) 8,0%
(C) 7,9%
(D) 7,7%
(E) 7,6%
Resolução:
Observando que existem 14 taxas de desempregos, a mediana será dada pela média entre a 7ª e 8ª taxa, colocando em ordem crescente a mediana será: (7,9%+8,1%) / 2 = 8%
Alternativa: B
092) (ENEM) Numa avenida existem 10 semáforos. Por causa de uma pane no sistema, os semáforos ficaram sem controle durante uma hora, e fixaram suas luzes unicamente em verde ou vermelho. Os semáforos funcionam de forma independente; a probabilidade de acusar a cor verde é de 2/3 e a de acusar a cor vermelha é de 1/3. Uma pessoa percorreu a pé toda essa avenida durante o período da pane, observando a cor da luz de cada um desses semáforos.
Qual a probabilidade de que esta pessoa tenha observado exatamente um sinal na cor verde?
(A) ![]()
(B) 
(C) 
(D) 
(E) 
Resolução:
Considerando as probabilidades:
(probabilidade de ser verde) = 2/3
(probabilidade de ser vermelho) =1/3
como são 10 casos, para os casos favoráveis temos a probabilidade de extamente um sinal verde é : 2/3 .(1/3(sub)10(/sub)) . 10
porque percebemos que permutam as 10 posições logo 10 . 2/(3(sub)10(/sub))
Alternativa: A
093) (ENEM) A energia solar vai abastecer parte da demanda de energia do campus de uma universidade brasileira. A instalação de painéis solares na área dos estacionamentos e na cobertura do hospital pediátrico será aproveitada nas instalações universitárias e também ligada na rede da companhia elétrica distribuidora de energia.
O projeto inclui 100 m2 de painéis solares que ficarão instalados nos estacionamentos, produzindo energia elétrica e proporcionando sombra para os carros. Sobre o hospital pediátrico serão colocados aproximadamente 300 m2 de painéis, sendo 100 m2 para gerar energia elétrica utilizada no campus, e 200 m2 para geração de energia térmica, produzindo aquecimento de água utilizada nas caldeiras do hospital.
Suponha que cada metro quadrado de painel solar para energia elétrica gere uma economia de 1 kWh por dia e cada metro quadrado produzindo energia térmica permita economizar 0,7 kWh por dia para a universidade. Em uma segunda fase do projeto, será aumentada em 75% a área coberta pelos painéis solares que geram energia elétrica. Nessa fase também deverá ser ampliada a área de cobertura com painéis para geração de energia térmica.
Para se obter o dobro da quantidade de energia economizada diariamente, em relação à primeira fase, a área total dos painéis que geram energia térmica, em metro quadrado, deverá ter o valor mais próximo de
(A) 231.
(B) 431.
(C) 472.
(D) 523.
(E) 672.
Resolução:
No projeto inicial teremos as seguintes economias:
200 m² painéis solares à economia = 200 . 1 kWh = 200 kWh
200 m² energia térmica à economia = 200 . 0,7 kWh = 140 kWh
Totalizando, assim, uma economia de 200 + 140 = 340 kWh, no projeto inicial.
Na 2ª fase do projeto, temos que a economia da energia elétrica será aumentada em 75%, isto é,
Energia elétrica à 200 . 1,75 = 350 kWh
Para se obter o dobro da quantidade de energia economizada diariamente em relação ao projeto inicial, ou seja, 2 . 340 = 680 kWh, a energia térmica será então:
Energia térmica = 680 – 350 = 330 kWh
Pelo enunciado sabe-se que 1 m² equivale a 0,7 kWh, então 330 kWh, equivalerá a:
330/0,7 ≈ 472 m²
Alternativa: C
094) (ENEM) Uma empresa construirá sua página na internet e espera atrair um público de aproximadamente um milhão de clientes. Para acessar essa página, será necessária uma senha com formato a ser definido pela empresa. Existem cinco opções de formato oferecidas pelo programador, descritas no quadro, em que “L” e “D” representam, respectivamente, letra maiúscula e dígito. As letras do alfabeto, entre as 26 possíveis, bem como os dígitos, entre os 10 possíveis, podem se repetir em qualquer das opções.
As letras do alfabeto, entre as 26 possíveis, bem como os dígitos, entre os 10 possíveis, podem se repetir em qualquer das opções.
A empresa quer escolher uma opção de formato cujo número de senhas distintas possíveis seja superior ao número esperado de clientes, mas que esse número não seja superior ao dobro do número esperado de clientes.
A opção que mais se adequa às condições da empresa é
(A) I
(B) II
(C) III
(D) IV
(E) V
Resolução:
O número de senhas para cada modelo de senha é:
I – 26.10.10.10.10.10 = 26 . 10^5
II – 10.10.10.10.10.10 = 10^6
III – 26.26.10.10.10.10 = 26².10^4
IV – 10.10.10.10.10 = 10^5
V – 26.26.26.10.10 = 26³.10²
Calculando cada valor o que se enquadra nas restrições feitas é a opção V.
Alternativa: E
095) (ENEM) Como não são adeptos da prática de esportes, um grupo de amigos resolveu fazer um torneio de futebol utilizando videogame. Decidiram que cada jogador joga uma única vez com cada um dos outros jogadores. O campeão será aquele que conseguir o maior número de pontos. Observaram que o número de partidas jogadas depende do número de jogadores, como mostra o quadro: Se a quantidade de jogadores for 8, quantas partidas serão realizadas?
Se a quantidade de jogadores for 8, quantas partidas serão realizadas?
(A) 64
(B) 56
(C) 49
(D) 36
(E) 28
Resolução:
Para criar uma partida precisamos selecionar 2 jogadores entre 8 possíveis. Como a ordem de seleção dos jogadores não alteram a partida formada usaremos a combinação: C8,2 = 28.
Alternativa: E
096) (ENEM) Um morador de uma região metropolitana tem 50% de probabilidade de atrasar-se para o trabalho quando chove na região; caso não chova, sua probabilidade de atraso é de 25%. Para um determinado dia, o serviço de meteorologia estima em 30% a probabilidade da ocorrência de chuva nessa região.
Qual é a probabilidade de esse morador se atrasar para o serviço no dia para o qual foi dada a estimativa de chuva?
(A) 0,075
(B) 0,150
(C) 0,325
(D) 0,600
(E) 0,800
Resolução:
Chover a atrasar ou não chover e atrasar
30% . 50% + 70% . 25% = 32,5%
Alternativa: C
097) (ENEM) Às 17 h 15 min começa uma forte chuva, que cai com intensidade constante. Uma piscina em forma de um paralelepípedo retângulo, que se encontrava inicialmente vazia, começa a acumular a água da chuva e, às 18 horas, o nível da água em seu interior alcança 20 cm de altura. Nesse instante, é aberto o registro que libera o escoamento da água por um ralo localizado no fundo dessa piscina, cuja vazão é constante. Às 18 h 40 min a chuva cessa e, nesse exato instante, o nível da água na piscina baixou para 15 cm.
O instante em que a água dessa piscina terminar de escoar completamente está compreendido entre
(A) 19 h 30 min e 20 h 10 min.
(B) 19 h 20 min e 19 h 30 min.
(C) 19 h 10 min e 19 h 20 min.
(D) 19 h e 19 h 10 min.
(E) 18 h 40 min e 19 h.
Resolução:
Apenas chuva
20 cm / 45 min = 4 cm/ 9 min
Chuva – ralo
(4/9) – R = -5/40
Ralo = 4/9 + ⅛ = 41/72
(41/72).t = 15
t = 26
18h40 min + 26 min = 19 h 6 min
Alternativa: D
098) (ENEM) O colesterol total de uma pessoa é obtido pela soma da taxa do seu “colesterol bom” com a taxa do seu “colesterol ruim”. Os exames periódicos, realizados em um paciente adulto, apresentaram taxa normal de “colesterol bom”, porém, taxa do “colesterol ruim” (também chamado LDL) de 280 mg/dL. O quadro apresenta uma classificação de acordo com as taxas de LDL em adultos. O paciente, seguindo as recomendações médicas sobre estilo de vida e alimentação, realizou o exame logo após o primeiro mês, e a taxa de LDL reduziu 25%. No mês seguinte, realizou novo exame e constatou uma redução de mais 20% na taxa de LDL.
O paciente, seguindo as recomendações médicas sobre estilo de vida e alimentação, realizou o exame logo após o primeiro mês, e a taxa de LDL reduziu 25%. No mês seguinte, realizou novo exame e constatou uma redução de mais 20% na taxa de LDL.
De acordo com o resultado do segundo exame, a classificação da taxa de LDL do paciente é
(A) ótima.
(B) próxima de ótima.
(C) limite
(D alta.
(E) muito alta.
Resolução:
Pelo enunciado, vemos que a taxa inicial é igual a 280 mg/dL. Esta reduzirá, em um mês, 25%. Ou seja, a taxa foi para 280 . 0,75 = 210 mg/dL.
No segundo mês, ele reduziu em 20% sua taxa em relação ao mês anterior. Dessa forma, a taxa final dele, é de 210 . 0,8 = 168 mg/dL.
Consultando a tabela, sua taxa será considerada alta.
Alternativa: D
099) (ENEM) Uma empresa deseja iniciar uma campanha publicitária divulgando uma promoção para seus possíveis consumidores. Para esse tipo de campanha, os meios mais viáveis são a distribuição de panfletos na rua e anúncios na rádio local. Considera-se que a população alcançada pela distribuição de panfletos seja igual ã quantidade de panfletos distribuídos, enquanto que a alcançada por um anúncio na rádio seja igual à quantidade de ouvintes desse anúncio. O custo de cada anúncio na rádio é de R$ 120,00, e a estimativa é de que seja ouvido por 1 500 pessoas. Já a produção e a distribuição dos panfletos custam R$ 180,00 cada 1 000 unidades. Considerando que cada pessoa será alcançada por um único desses meios de divulgação, a empresa pretende investir em ambas as mídias.
Considere X e Y os valores (em real) gastos em anúncios na rádio e com panfletos, respectivamente.
O número de pessoas alcançadas pela campanha será dado pela expressão
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
Resolução:
Alternativa: A
100) (ENEM) A inclinação de uma rampa é calculada da seguinte maneira: para cada metro medido na horizontal, mede-se x centímetros na vertical. Diz-se, nesse caso, que a rampa tem inclinação de x%, como no exemplo da figura: A figura apresenta um projeto de uma rampa de acesso a uma garagem residencial cuja base, situada 2 metros abaixo do nível da rua, tem 8 metros de comprimento.
A figura apresenta um projeto de uma rampa de acesso a uma garagem residencial cuja base, situada 2 metros abaixo do nível da rua, tem 8 metros de comprimento. Depois de projetada a rampa, o responsável pela obra foi informado de que as normas técnicas do município onde ela está localizada exigem que a inclinação máxima de uma rampa de acesso a uma garagem residencial seja de 20%.
Depois de projetada a rampa, o responsável pela obra foi informado de que as normas técnicas do município onde ela está localizada exigem que a inclinação máxima de uma rampa de acesso a uma garagem residencial seja de 20%.
Se a rampa projetada tiver inclinação superior a 20%, o nível da garagem deverá ser alterado para diminuir o percentual de inclinação, mantendo o comprimento da base da rampa.
Para atender às normas técnicas do município, o nível da garagem deverá ser
(A) elevado em 40 cm.
(B) elevado em 50 cm.
(C) mantido no mesmo nível.
(D) rebaixado em 40 cm.
(E) rebaixado em 50 cm.
Resolução:
Alternativa: A
101) (ENEN) Para ganhar um prêmio, uma pessoa deverá retirar, sucessivamente e sem reposição, duas bolas pretas de uma mesma urna.
Inicialmente, as quantidades e cores das bolas são como descritas a seguir:
Urna A – Possui três bolas brancas, duas bolas pretas e uma bola verde;
Urna B – Possui seis bolas brancas, três bolas pretas e uma bola verde;
Urna C – Possui duas bolas pretas e duas bolas verdes;
Urna D – Possui três bolas brancas e três bolas pretas.
A pessoa deve escolher uma entre as cinco opções apresentadas:
Opção 1 – Retirar, aleatoriamente, duas bolas da urna A;
Opção 2 – Retirar, aleatoriamente, duas bolas da urna B;
Opção 3 – Passar, aleatoriamente, uma bola da urna C para a urna A; após isso, retirar, aleatoriamente, duas bolas da urna A;
Opção 4 – Passar, aleatoriamente, uma bola da urna D para a urna C; após isso, retirar, aleatoriamente, duas bolas da urna C;
Opção 5 – Passar, aleatoriamente, uma bola da urna C para a urna D; após isso, retirar, aleatoriamente, duas bolas da urna D.
Com o objetivo de obter a maior probabilidade possível de ganhar o prêmio, a pessoa deve escolher a opção
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
Resolução:
Alternativa: E
102) (ENEM) A Ecofont possui design baseado na velha fonte Vera Sans. Porém, ela tem um diferencial: pequenos buraquinhos circulares congruentes, e em todo o seu corpo, presentes em cada símbolo. Esses furos proporcionam um gasto de tinta menor na hora da impressão. Suponha que a palavra ECO esteja escrita nessa fonte, com tamanho 192, e que seja composta por letras formadas por quadrados de lados x com furos circulares de raio Para que a área a ser pintada seja reduzida a da área inicial, pretende-se reduzir o tamanho da fonte. Sabe-se que, ao alterar o tamanho da fonte, o tamanho da letra é alterado na mesma proporção.
Suponha que a palavra ECO esteja escrita nessa fonte, com tamanho 192, e que seja composta por letras formadas por quadrados de lados x com furos circulares de raio Para que a área a ser pintada seja reduzida a da área inicial, pretende-se reduzir o tamanho da fonte. Sabe-se que, ao alterar o tamanho da fonte, o tamanho da letra é alterado na mesma proporção.
Nessas condições, o tamanho adequado da fonte será
(A) 64.
(B) 48.
(C) 24.
(D) 21.
(E) 12.
Resolução:
Alternativa: B
103) (ENEM) Para criar um logotipo, um profissional da área de design gráfico deseja construí-lo utilizando o conjunto de pontos do plano na forma de um triângulo, exatamente como mostra a imagem. Para construir tal imagem utilizando uma ferramenta gráfica, será necessário escrever algebricamente o conjunto que representa os pontos desse gráfico.
Para construir tal imagem utilizando uma ferramenta gráfica, será necessário escrever algebricamente o conjunto que representa os pontos desse gráfico.
Esse conjunto é dado pelos pares ordenados ![]() Tais que
Tais que
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
Resolução:
Alternativa: B
104) (ENEM) A figura mostra uma praça circular que contém um chafariz em seu centro e, em seu entorno, um passeio. Os círculos que definem a praça e o chafariz são concêntricos. O passeio terá seu piso revestido com ladrilhos. Sem condições de calcular os raios, pois o chafariz está cheio, um engenheiro fez a seguinte medição: esticou uma trena tangente ao chafariz, medindo a distância entre dois pontos A e B, conforme a figura. Com isso, obteve a medida do segmento de reta AB: 16 m.
O passeio terá seu piso revestido com ladrilhos. Sem condições de calcular os raios, pois o chafariz está cheio, um engenheiro fez a seguinte medição: esticou uma trena tangente ao chafariz, medindo a distância entre dois pontos A e B, conforme a figura. Com isso, obteve a medida do segmento de reta AB: 16 m. Dispondo apenas dessa medida, o engenheiro calculou corretamente a medida da área do passeio, em metro quadrado.
Dispondo apenas dessa medida, o engenheiro calculou corretamente a medida da área do passeio, em metro quadrado.
A medida encontrada pelo engenheiro foi
(A) 4π.
(B) 8π.
(C) 48π.
(D) 64π.
(E) 192π.
Resolução: Alternativa: D
Alternativa: D
105) (ENEM) Um designer de jogos planeja um jogo que faz uso de um tabuleiro de dimensão n x n, com no qual cada jogador, na sua vez, coloca uma peça sobre uma das casas vazias do tabuleiro. Quando uma peça é posicionada, a região formada pelas casas que estão na mesma linha ou coluna dessa peça é chamada de zona de combate dessa peça. Na figura está ilustrada a zona de combate de uma peça colocada em uma das casas de um tabuleiro de dimensão 8 x 8. O tabuleiro deve ser dimensionado de forma que a probabilidade de se posicionar a segunda peça aleatoriamente, seguindo a regra do jogo, e esta ficar sobre a zona de combate da primeira, seja inferior a
O tabuleiro deve ser dimensionado de forma que a probabilidade de se posicionar a segunda peça aleatoriamente, seguindo a regra do jogo, e esta ficar sobre a zona de combate da primeira, seja inferior a
A dimensão mínima que o designer deve adotar para esse tabuleiro é
(A) 4 x 4.
(B) 6 x 6.
(C) 9 x 9.
(D) 10 x 10.
(E) 11 x 11.
Resolução:
Alternativa: D
106) (ENEM) O remo de assento deslizante é um esporte que faz uso de um barco e dois remos do mesmo tamanho. A figura mostra uma das posições de uma técnica chamada afastamento. Nessa posição, os dois remos se encontram no ponto A e suas outras extremidades estão indicadas pelos pontos B e C. Esses três pontos formam um triângulo ABC cujo ângulo tem medida de 170°.
Nessa posição, os dois remos se encontram no ponto A e suas outras extremidades estão indicadas pelos pontos B e C. Esses três pontos formam um triângulo ABC cujo ângulo tem medida de 170°.
O tipo de triângulo com vértices nos pontos A, B e C, no momento em que o remador está nessa posição, é
(A) retângulo escaleno.
(B) acutângulo escaleno.
(C) acutângulo isósceles.
(D) obtusângulo escaleno.
(E) obtusângulo isósceles.
Resolução:
Alternativa: E
107) (ENEM) Um rapaz estuda em uma escola que fica longe de sua casa, e por isso precisa utilizar o transporte público. Como é muito observador, todos os dias ele anota a hora exata (sem considerar os segundos) em que o ônibus passa pelo ponto de espera. Também notou que nunca consegue chegar ao ponto de ônibus antes de 6h 15 min da manhã. Analisando os dados coletados durante o mês de fevereiro, o qual teve 21 dias letivos, ele concluiu que 6 h 21 min foi o que mais se repetiu, e que a mediana do conjunto de dados é 6 h 22 min.
A probabilidade de que, em algum dos dias letivos de fevereiro, esse rapaz tenha apanhado o ônibus antes de 6 h 21 min da manhã é, no máximo,
(A) 4/21
(B) 5/21
(C) 6/21
(D) 7/21
(E) 8/21
Resolução:
Alternativa: D
108) 9ENEM) Um produtor de milho utiliza uma área de 160 hectares para as suas atividades agrícolas. Essa área é dividida em duas partes: uma de 40 hectares, com maior produtividade, e outra, de 120 hectares, com menor produtividade. A produtividade é dada pela razão entre a produção, em tonelada, e a área cultivada. Sabe-se que a área de 40 hectares tem produtividade igual a 2,5 vezes à da outra. Esse fazendeiro pretende aumentar sua produção total em 15%, aumentando o tamanho da sua propriedade. Para tanto, pretende comprar uma parte de uma fazenda vizinha, que possui a mesma produtividade da parte de 120 hectares de suas terras. Qual é a área mínima, em hectare, em que o produtor precisará comprar?
(A) 36
(B) 33
(C) 27
(D) 24
(E) 21
Resolução:
Alternativa: B
109) (ENEM) Minecraft é um jogo virtual que pode auxiliar no desenvolvimento de conhecimentos relacionados a espaço e forma. É possível criar casas, edifícios, monumentos e até naves espaciais, tudo em escala real, através do empilhamento de cubinhos.
Um jogador deseja construir um cubo com dimensões 4 x 4 x 4. Ele já empilhou alguns dos cubinhos necessários, conforme a figura. Os cubinhos que ainda faltam empilhar para finalizar a construção do cubo, juntos, formam uma peça única, capaz de completar a tarefa.
Os cubinhos que ainda faltam empilhar para finalizar a construção do cubo, juntos, formam uma peça única, capaz de completar a tarefa.
O formato da peça capaz de completar o cubo 4 x 4 x 4 é
(A) 
(B) 
(C) 
(D) 
(E) 
Resolução:
Alternativa: A
110) (ENEM) De acordo com um relatório recente da Agência Internacional de Energia (AIE), o mercado de veículos elétricos atingiu um novo marco em 2016, quando foram vendidos mais de 750 mil automóveis da categoria. Com isso, o total de carros elétricos vendidos no mundo alcançou a marca de 2 milhões de unidades desde que os primeiros modelos começaram a ser comercializados em 2011. No Brasil, a expansão das vendas também se verifica. A marca A, por exemplo, expandiu suas vendas no ano de 2016, superando em 360 unidades as vendas de 2015, conforme representado no gráfico. A média anual do número de carros vendidos pela marca A, nos anos representados no gráfico, foi de
A média anual do número de carros vendidos pela marca A, nos anos representados no gráfico, foi de
(A) 192.
(B) 240.
(C) 252.
(D) 320.
(E) 420.
Resolução:
Alternativa: D
111) (ENEM) Para apagar os focos A e B de um incêndio, que estavam a uma distância de 30m um do outro, os bombeiros de um quartel decidiram se posicionar de modo que a distância de um bombeiro ao foco A, de temperatura mais elevada, fosse sempre o dobro da distância desse bombeiro ao foco B, de temperatura menos elevada.
Nestas condições, a maior distância, em metro, que dois bombeiros poderiam ter entre eles é
(A) 30.
(B) 40.
(C) 45.
(D) 60.
(E) 68.
Resolução:

Alternativa: B
112) (ENEM) Torneios de tênis, em geral, são disputados em sistema de eliminatória simples. Nesse sistema, são disputadas partidas entre dois competidores, com a eliminação do perdedor e promoção do vencedor para a fase seguinte. Dessa forma, se na 1ª fase o torneio conta com 2n competidores, então na 2ª fase restarão n competidores, e assim sucessivamente até a partida final.
Em um torneio de tênis, disputado nesse sistema, participam 128 tenistas.
Para se definir o campeão desse torneio, o número de partidas necessárias é dado por
(A) 2 X 128
(B) 64 + 32 + 16 + 8 + 4 + 2
(C) 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1
(D) 128 + 64 + 32 + 16 + 8 + 4 + 2
(E) 64 + 32 + 16 + 8+ 4 + 2+ 1
Resolução:
Alternativa: E
113) (ENEM) O artigo 33 da lei brasileira sobre drogas prevê a pena de reclusão de 5 a 15 anos para qualquer pessoa que seja condenada por tráfico ilícito ou produção não autorizada de drogas. Entretanto, caso o condenado seja réu primário, com bons antecedentes criminais, essa pena pode sofrer uma redução de um sexto a dois terços.
Suponha que um réu primário, com bons antecedentes criminais, foi condenado pelo artigo 33 da lei brasileira sobre drogas.
Após o benefício da redução de pena, sua pena poderá variar de
(A) 1 ano e 8 meses a 12 anos e 6 meses.
(B) 1 ano e 8 meses a 5 anos.
(C) 3 anos e 4 meses a 10 anos.
(D) 4 anos e 2 meses a 5 anos.
(E) 4 anos e 2 meses a 12 anos e 6 meses.
Resolução:
Alternativa: A
114) (ENEM) Um edifício tem a numeração dos andares iniciando no térreo (T), e continuando com primeiro, segundo, terceiro, …, até o último andar. Uma criança entrou no elevador e, tocando no painel, seguiu uma sequência de andares, parando, abrindo e fechando a porta em diversos andares. A partir de onde entrou a criança, o elevador subiu sete andares, em seguida desceu dez, desceu mais treze, subiu nove, desceu quatro e parou no quinto andar, finalizando a sequência. Considere que, no trajeto seguido pela criança, o elevador parou uma vez no último andar do edifício.
De acordo com as informações dadas, o último andar do edifício é o
(A) 16º
(B) 22º
(C) 23º
(D) 25º
(E) 32º
Resolução:
Alternativa: C
115) (ENEM) O Salão do Automóvel de São Paulo é um evento no qual vários fabricantes expõem seus modelos mais recentes de veículos, mostrando, principalmente, suas inovações em design e tecnologia.
Uma montadora pretende participar desse evento com dois estandes, um na entrada e outro na região central do salão, expondo, em cada um deles, um carro compacto e uma caminhonete. Para compor os estandes, foram disponibilizados pela montadora quatro carros compactos, de modelos distintos, e seis caminhonetes de diferentes cores para serem escolhidos aqueles que serão expostos. A posição dos carros dentro de cada estande é irrelevante.
Uma expressão que fornece a quantidade de maneiras diferentes que os estandes podem ser compostos é
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
Resolução:
Alternativa: C
116) (ENEM) Os alunos da disciplina de estatística, em um curso universitário, realizam quatro avaliações por semestre com os pesos de 20%, 10%, 30% e 40%, respectivamente.
No final do semestre, precisam obter uma média nas quatro avaliações de, no mínimo, 60 pontos para serem aprovados. Um estudante dessa disciplina obteve os seguintes pontos nas três primeiras avaliações: 46, 60 e 50, respectivamente.
O mínimo de pontos que esse estudante precisa obter na quarta avaliação para ser aprovado é
(A) 29,8.
(B) 71,0.
(C) 74,5.
(D) 75,5.
(E) 84,0.
Resolução:
Alternativa: C
117) (ENEM) O gerente do setor de recursos humanos de uma empresa está organizando uma avaliação em que uma das etapas é um jogo de perguntas e respostas. Para essa etapa, ele classificou as perguntas, pelo nível de dificuldade, em fácil, médio e difícil, e escreveu cada pergunta em cartões para colocação em uma urna.
Contudo, após depositar vinte perguntas de diferentes níveis na urna, ele observou que 25% delas eram de nível fácil. Querendo que as perguntas de nível fácil sejam a maioria, o gerente decidiu acrescentar mais perguntas de nível fácil à urna, de modo que a probabilidade de o primeiro participante retirar, aleatoriamente, uma pergunta de nível fácil seja de 75%.
Com essas informações, a quantidade de perguntas de nível fácil que o gerente deve acrescentar à urna é igual a
(A) 10.
(B) 15.
(C) 35.
(D) 40.
(E) 45.
Resolução:
Alternativa: D
118) (ENEM) A raiva é uma doença viral e infecciosa, transmitida por mamíferos. A campanha nacional de vacinação antirrábica tem o objetivo de controlar a circulação do vírus da raiva canina e felina, prevenindo a raiva humana. O gráfico mostra a cobertura (porcentagem de vacinados) da campanha, em cães, nos anos de 2013, 2015 e 2017, no município de Belo Horizonte, em Minas Gerais. Os valores das coberturas dos anos de 2014 e 2016 não estão informados no gráfico e deseja-se estimá-los. Para tal, levou-se em consideração que a variação na cobertura de vacinação da campanha antirrábica, nos períodos de 2013 a 2015 e de 2015 a 2017, deu-se de forma linear. Qual teria sido a cobertura dessa campanha no ano de 2014?
Qual teria sido a cobertura dessa campanha no ano de 2014?
(A) 62,3%
(B) 63,0%
(C) 63,5%
(D) 64,0%
(E) 65,5%
Resolução:![]()
Alternativa: B
119) (ENEM) Uma empresa de comunicação tem a tarefa de elaborar um material publicitário de um estaleiro para divulgar um novo navio, equipado com um guindaste de 15m de altura e uma esteira de 90 m de comprimento. No desenho desse navio, a representação do guindaste deve ter sua altura entre 0,5 cm e 1 cm, enquanto a esteira deve apresentar comprimento superior a 4 cm. Todo o desenho deverá ser feito em uma escala 1 : X.
Os valores possíveis para X são, apenas,
(A) X > 1 500.
(B) X < 3 000.
(C) 1 500 < X < 2 250.
(D) 1 500 < X < 3 000.
(E) 2 250 < X < 3 000.
Resolução:
Alternativa: C
120) (ENEM) Em 2014 foi inaugurada a maior roda-gigante do mundo, a High Roller, situada em Las Vegas. A figura representa um esboço dessa roda-gigante, no qual o ponto A representa uma de suas cadeiras: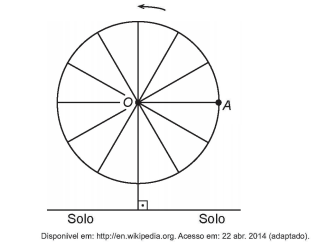 A partir da posição indicada, em que o segmento OA se encontra paralelo ao plano do solo, rotaciona-se a High Roller no sentido anti-horário, em torno do ponto O. Sejam t o ângulo determinado pelo segmento OA em relação à sua posição inicial, e f a função que descreve a altura do ponto A, em relação ao solo, em função de t. Após duas voltas completas, f tem o seguinte gráfico:
A partir da posição indicada, em que o segmento OA se encontra paralelo ao plano do solo, rotaciona-se a High Roller no sentido anti-horário, em torno do ponto O. Sejam t o ângulo determinado pelo segmento OA em relação à sua posição inicial, e f a função que descreve a altura do ponto A, em relação ao solo, em função de t. Após duas voltas completas, f tem o seguinte gráfico:
A expressão da função altura é dada por
(A) f(t) = 80sen(t) + 88
(B) f(t) = 80cos(t) + 8 8
(C) f(t) = 88cos(t) + 168
(D) f(t) = 168sen(t) + 88cos(t)
(E) f(t) = 88sen(t) + 168cos(t)
Resolução:
Alternativa: A
121) (ENEM) A rosa dos ventos é uma figura que representa oito sentidos, que dividem o círculo em partes iguais. Uma câmera de vigilância está fixada no teto de um shopping e sua lente pode ser direcionada remotamente, através de um controlador, para qualquer sentido. A lente da câmera está apontada inicialmente no sentido Oeste e o seu controlador efetua três mudanças consecutivas, a saber:
Uma câmera de vigilância está fixada no teto de um shopping e sua lente pode ser direcionada remotamente, através de um controlador, para qualquer sentido. A lente da câmera está apontada inicialmente no sentido Oeste e o seu controlador efetua três mudanças consecutivas, a saber:
1ª mudança: 135° no sentido anti-horário;
2ª mudança: 60° no sentido horário;
3ª mudança: 45° no sentido anti-horário.
Após a 3ª mudança, ele é orientado a reposicionar a câmera, com a menor amplitude possível, no sentido Noroeste (NO) devido a um movimento suspeito de um cliente.
Qual mudança de sentido o controlador deve efetuar para reposicionar a câmera?
(A) 75° no sentido horário.
(B) 105° no sentido anti-horário.
(C) 120° no sentido anti-horário.
(D) 135° no sentido anti-horário.
(E) 165° no sentido horário.
Resolução:
Alternativa: E
122) (ENEM) Na teoria das eleições, o Método de Borda sugere que, em vez de escolher um candidato, cada juiz deve criar um ranking de sua preferência para os concorrentes (isto é, criar uma lista com a ordem de classificação dos concorrentes). A este ranking é associada uma pontuação: um ponto para o último colocado no ranking, dois pontos para o penúltimo, três para o antepenúltimo, e assim sucessivamente. Ao final, soma-se a pontuação atribuída a cada concorrente por cada um dos juízes.
Em uma escola houve um concurso de poesia no qual cinco alunos concorreram a um prêmio, sendo julgados por 25 juízes. Para a escolha da poesia vencedora foi utilizado o Método de Borda. Nos quadros, estão apresentados os rankings dos juízes e a frequência de cada ranking. A poesia vencedora foi a de
A poesia vencedora foi a de
(A) Edu.
(B) Dani.
(C) Caio.
(D) Bia.
(E) Ana.
Resolução:![]()
Alternativa: E
123) (ENEM) Com o avanço em ciência da computação, estamos próximos do momento em que o número de transistores no processador de um computador pessoal será da mesma ordem de grandeza que o número de neurônios em um cérebro humano, que é da ordem de 100 bilhões.
Uma das grandezas determinantes para o desempenho de um processador é a densidade de transistores, que é o número de transistores por centímetro quadrado. Em 1986, uma empresa fabricava um processador contendo 100 000 transistores distribuídos em 0,25 cm² de área. Desde então, o número de transistores por centímetro quadrado que se pode colocar em um processador dobra a cada dois anos (Lei de Moore).
Considere 0,30 como aproximação para
Em que ano a empresa atingiu ou atingirá a densidade de 100 bilhões de transistores?
(A) 1999
(B) 2002
(C) 2022
(D) 2026
(E) 2146
Resolução:
Alternativa: C
124) (ENEM) Os guindastes são fundamentais em canteiros de obras, no manejo de materiais pesados como vigas de aço. A figura ilustra uma sequência de estágios em que um guindaste iça uma viga de aço que se encontra inicialmente no solo. Na figura, o ponto O representa a projeção ortogonal do cabo de aço sobre o plano do chão e este se mantém na vertical durante todo o movimento de içamento da viga, que se inicia no tempo t = 0 (estágio 1) e finaliza no (estágio 3). Uma das extremidades da viga é içada verticalmente a partir do ponto O, enquanto que a outra extremidade desliza sobre o solo em direção ao ponto O. Considere que o cabo de aço utilizado pelo guindaste para içar a viga fique sempre na posição vertical. Na figura, o ponto M representa o ponto médio do segmento que representa a
Na figura, o ponto O representa a projeção ortogonal do cabo de aço sobre o plano do chão e este se mantém na vertical durante todo o movimento de içamento da viga, que se inicia no tempo t = 0 (estágio 1) e finaliza no (estágio 3). Uma das extremidades da viga é içada verticalmente a partir do ponto O, enquanto que a outra extremidade desliza sobre o solo em direção ao ponto O. Considere que o cabo de aço utilizado pelo guindaste para içar a viga fique sempre na posição vertical. Na figura, o ponto M representa o ponto médio do segmento que representa a
O gráfico que descreve a distância do ponto M ao ponto O, em função do tempo, entre, é
(A) 
(B) 
(C) 
(D) 
(E) 
Resolução:
Alternativa: A
125) (ENEM) Uma loja vende automóveis em N parcelas iguais sem juros. No momento de contratar o financiamento, caso o cliente queira aumentar o prazo, acrescentando mais 5 parcelas, o valor de cada uma das parcelas diminui R$200,00, ou se ele quiser diminuir o prazo, com 4 parcelas a menos, o valor de cada uma das parcelas sobe R$ 232,00. Considere ainda que, nas três possibilidades de pagamento, o valor do automóvel é o mesmo, todas são sem juros e não ê dado desconto em nenhuma das situações.
Nessas condições, qual é a quantidade N de parcelas a serem pagas de acordo com a proposta inicial da loja?
(A) 20
(B) 24
(C) 29
(D) 40
(E) 58
Resolução:
Alternativa: B
126) (ENEM) O salto ornamental é um esporte em que cada competidor realiza seis saltos. A nota em cada salto é calculada pela soma das notas dos juízes, multiplicada pela nota de partida (o grau de dificuldade de cada salto). Fica em primeiro lugar o atleta que obtiver a maior soma das seis notas recebidas.
O atleta 10 irá realizar o último salto da final. Ele observa no Quadro 1, antes de executar o salto, o recorte do quadro parcial de notas com a sua classificação e a dos três primeiros lugares atê aquele momento. Ele precisa decidir com seu treinador qual salto deverá realizar. Os dados dos possíveis tipos de salto estão no Quadro 2.
Ele precisa decidir com seu treinador qual salto deverá realizar. Os dados dos possíveis tipos de salto estão no Quadro 2. O atleta optará pelo salto com a maior probabilidade de obter a nota estimada, de maneira que lhe permita alcançar o primeiro lugar.
O atleta optará pelo salto com a maior probabilidade de obter a nota estimada, de maneira que lhe permita alcançar o primeiro lugar.
Considerando essas condições, o salto que o atleta deverá escolher é o de tipo
(A) T1.
(B) T2.
(C) T3.
(D) T4.
(E) T5.
Resolução:
Alternativa: C
127) (ENEM) Devido ao não cumprimento das metas definidas para a campanha de vacinação contra a gripe comum e o vírus H1N1 em um ano, o Ministério da Saúde anunciou a prorrogação da campanha por mais uma semana. A tabela apresenta as quantidades de pessoas vacinadas dentre os cinco grupos de risco até a data de início da prorrogação da campanha Qual é a porcentagem do total de pessoas desses grupos de risco já vacinadas?
Qual é a porcentagem do total de pessoas desses grupos de risco já vacinadas?
(A) 12
(B) 18
(C) 30
(D) 40
(E) 50
Resolução:![]()
Alternativa: D
128) (ENEM) Durante uma festa de colégio, um grupo de alunos organizou uma rifa. Oitenta alunos faltaram à festa e não participaram da rifa. Entre os que compareceram, alguns compraram três bilhetes, 45 compraram 2 bilhetes, e muitos compraram apenas um. O total de alunos que comprou um único bilhete era 20% do número total de bilhetes vendidos, e o total de bilhetes vendidos excedeu em 33 o número total de alunos do colégio.
Quantos alunos compraram somente um bilhete?
(A) 34
(B) 42
(C) 47
(D) 48
(E) 79
Resolução:
Alternativa: D
128) (ENEM) Um quebra-cabeça consiste em recobrir um quadrado com triângulos retângulos isósceles, como ilustra a figura. Uma artesã confecciona um quebra-cabeça como o descrito, de tal modo que a menor das peças é um triângulo retângulo isósceles cujos catetos medem 2 cm.
Uma artesã confecciona um quebra-cabeça como o descrito, de tal modo que a menor das peças é um triângulo retângulo isósceles cujos catetos medem 2 cm.
Sendo:![]()
![]()
![]()
O quebra-cabeça, quando montado, resultará em um quadrado cuja medida do lado, em centímetro, é
(A) 14
(B) 12
(C) 7√2
(D) 6 + 4√2
(E) 6 + 2√2
Resolução:
Alternativa: A
129) (ENEM) Para decorar um cilindro circular reto será usada uma faixa retangular de papel transparente, na qual está desenhada em negrito uma diagonal que forma 30° com a borda inferior. O raio da base do cilindro mede 6/π cm, e ao enrolar a faixa obtém-se uma linha em formato de hélice, como na figura. O valor da medida da altura do cilindro, em centímetro, é
O valor da medida da altura do cilindro, em centímetro, é
(A) 36√3
(B) 24√3
(C) 4√3
(D) 36
(E) 72
Resolução:
Alternativa: B
130) (ENEM) Numa atividade de treinamento realizada no Exército de um determinado país, três equipes – Alpha, Beta e Gama – foram designadas a percorrer diferentes caminhos, todos com os mesmos pontos de partida e de chegada.
A equipe Alpha realizou seu percurso em 90 minutos com uma velocidade média de 6,0 km/h.
A equipe Beta também percorreu sua trajetória em 90 minutos, mas sua velocidade média foi de 5,0 km/h.
Com uma velocidade média de 6,5 km/h, a equipe Gama concluiu seu caminho em 60 minutos.
Com base nesses dados, foram comparadas as distâncias percorridas pelas três equipes.
A ordem das distâncias percorridas pelas equipes Alpha, Beta e Gama é
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
Resolução:
Alternativa: A
131) (ENEM) O cultivo de uma flor rara só é viável se do mês do plantio para o mês subsequente
o clima da região possuir as seguintes peculiaridades:
a variação do nível de chuvas (pluviosidade), nesses meses, não for superior a 50 mm;
a temperatura mínima, nesses meses, for superior a 15 °C;
ocorrer, nesse período, um leve aumento não superior a 5 °C na temperatura máxima.
Um floricultor, pretendendo investir no plantio dessa flor em sua região, fez uma consulta a um meteorologista que lhe apresentou o gráfico com as condições previstas para os 12 meses seguintes nessa região. Com base nas informações do gráfico, o floricultor verificou que poderia plantar essa flor rara.
Com base nas informações do gráfico, o floricultor verificou que poderia plantar essa flor rara.
O mês escolhido para o plantio foi
(A) janeiro
(B) fevereiro
(C) agosto
(D) novembro
(E)dezembro
Resolução:
Analisando gráfico, percebemos que em janeiro :
– Temperatura mínima > 15°
– Variação de Pluviosidade entre janeiro e fevereiro < 50 mm
– Aumento da temperatura máxima entre janeiro e fevereiro < 5°
Alternativa: A
132) (ENEM) Densidade absoluta (d) é a razão entre a massa de um corpo e o volume por ele ocupado. Um professor propôs à sua turma que os alunos analisassem a densidade de três corpos: dA, dB e dC. Os alunos verificaram que o corpo A possuía 1,5 vez a massa do corpo B e esse, por sua vez, tinha 3/4 da massa do corpo C. Observaram, ainda, que o volume do corpo A era o mesmo do corpo B e 20% maior do que o volume do corpo C.
Após a análise, os alunos ordenaram corretamente as densidades desses corpos da seguinte maneira
(A) dB < dA < dC
(B) dB = dA < dC
(C) dC < dB = dA
(D) dB < dC < dA
(A) dC < dB < dA
Resolução:
Ma = 1,5.Mb
Mb = 3/4Mc
Va = Vb
Va = 1,2.Vc
Vc = Vb/1,2
Da = 1,5.Mb/Vb = 1,5 . Db
Dc =(4/3.Mb)/(Vb/1,2) = 1,6 . Db
Db < Da < Dc
Alternativa: A
133) (ENEM) No tanque de um certo carro de passeio cabem até 50 L de combustível, e o rendimento médio deste carro na estrada é de 15 km/L de combustível. Ao sair para uma viagem de 600 km o motorista observou que o marcador de combustível estava exatamente sobre uma das marcas da escala divisória do medidor, conforme figura a seguir. Como o motorista conhece o percurso, sabe que existem, até a chegada a seu destino, cinco postos de abastecimento de combustível, localizados a 150 km, 187 km, 450 km, 500 km e 570 km do ponto de partida.
Como o motorista conhece o percurso, sabe que existem, até a chegada a seu destino, cinco postos de abastecimento de combustível, localizados a 150 km, 187 km, 450 km, 500 km e 570 km do ponto de partida.
Qual a máxima distância, em quilômetro, que poderá percorrer até ser necessário reabastecer o veículo, de modo a não ficar sem combustível na estrada?
(A) 570
(B) 500
(C) 450
(D) 187
(E) 150
Resolução:
O marcador de combustível indica que ainda restam (1/2 + 1)/2 = 3/4 do total do tanque, o que permitiria percorrer 3/4 ⋅ 50 ⋅ 15 = 562,5 km. Portanto, ele pode percorrer no máximo 500 km até o reabastecimento do veículo.
Alternativa: B
144) (ENEM) Sob a orientação de um mestre de obras, João e Pedro trabalharam na reforma de um edifício. João efetuou reparos na parte hidráulica nos andares 1, 3, 5, 7, e assim sucessivamente, de dois em dois andares. Pedro trabalhou na parte elétrica nos andares 1, 4, 7, 10, e assim sucessivamente, de três em três andares. Coincidentemente, terminaram seus trabalhos no último andar. Na conclusão da reforma, o mestre de obras informou, em seu relatório, o número de andares do edifício. Sabe-se que, ao longo da execução da obra, em exatamente 20 andares, foram realizados reparos nas partes hidráulica e elétrica por João e Pedro.
Qual é o número de andares desse edifício?
(A) 40
(B) 60
(C) 100
(D) 115
(E) 120
Resolução:
As interseções dos andares de João e Pedro formam a seguinte P.A. (1,7,13…A20). sendo A20 o vigésimo andar coincidentes, com razão 6 e primeiro termo 1. Usando o termo geral da P.A, An = A1 + (n – 1) ⋅ r, chegamos ao resultado que A20 =115 que corresponde ao número de andares.
Alternativa: D
145) (ENEM) Em uma cidade será construída uma galeria subterrânea que receberá uma rede de canos para o transporte de água de uma fonte (F) até o reservatório de um novo bairro (B).
Após avaliações, foram apresentados dois projetos para o trajeto de construção da galeria: um segmento de reta que atravessaria outros bairros ou uma semicircunferência que contornaria esses bairros, conforme ilustrado no sistema de coordenadas xOy da figura, em que a unidade de medida nos eixos é o quilômetro. Estudos de viabilidade técnica mostraram que, pelas características do solo, a construção de 1 m de galeria via segmento de reta demora 1,0 h, enquanto que 1 m de construção de galeria via semicircunferência demora 0,6 h. Há urgência em disponibilizar água para esse bairro.
Estudos de viabilidade técnica mostraram que, pelas características do solo, a construção de 1 m de galeria via segmento de reta demora 1,0 h, enquanto que 1 m de construção de galeria via semicircunferência demora 0,6 h. Há urgência em disponibilizar água para esse bairro.
Use 3 como aproximação para π e 1,4 como aproximação para √2.
O menor tempo possível, em hora, para conclusão da construção da galeria, para atender às necessidades de água do bairro, é de
(A) 1 260.
(B) 2 520.
(C) 2 800.
(D) 3 600.
(E) 4 000.
Resolução:
Os pontos F e B determinam a diagonal de um quadrado de lado 2, logo FB = 2 . √2 = 2 . 1,4 = 2,8 km , ou seja, 2800 m. Como o tempo é de 1 hora para cada 1 metro, conclui-se que o tempo gasto é de 2800 horas.
Os pontos F e O determinam a diagonal de um quadrado de lado 1, logo FO = 1 . √2 = 1,4 km, ou seja, 1400 m, que corresponde ao raio da semicircuferência. Assim, o comprimento dela é igual a 1/2 . 2 . 3 .1 400 = 4200 m. Como o tempo é de 0,6 hora para cada metro, conclui-se que o tempo gasto é de 2520 horas.
Alternativa: B
145) (ENEM) Um túnel deve ser lacrado com uma tampa de concreto. A seção transversal do túnel e a tampa de concreto têm contornos de um arco de parábola e mesmas dimensões. Para determinar o custo da obra, um engenheiro deve calcular a área sob o arco parabólico em questão. Usando o eixo horizontal no nível do chão e o eixo de simetria da parábola como eixo vertical, obteve a seguinte equação para a parábola: y = 9 – x2, sendo x e y medidos em metros.
Sabe-se que a área sob uma parábola como esta é igual a 2/3 da área do retângulo cujas dimensões são, respectivamente, iguais à base e à altura da entrada do túnel.
Qual é a área da parte frontal da tampa de concreto, em metro quadrado?
(A) 18
(B) 20
(C) 36
(D) 45
(E) 54
Resolução:
Área = 2/3 . (6 . 9) = 36 m²
Alternativa: C
146) (ENEM) Para cadastrar-se em um site, uma pessoa precisa escolher uma senha composta por quatro caracteres, sendo dois algarismos e duas letras (maiúsculas ou minúsculas). As letras e os algarismos podem estar em qualquer posição. Essa pessoa sabe que o alfabeto é composto por vinte e seis letras e que uma letra maiúscula difere da minúscula em uma senha.
O número total de senhas possíveis para o cadastramento nesse site é dado por
(A) 102 . 262
(B) 102 . 522
(C) 102 . 522 . 4!/2!
(D) 102 . 262 . 4!/2! . 2!
(E) 102 . 522 . 4!/2! . 2!
Resolução:
Total de senhas = 10 . 10 . 52 . 52 . 4! / 2!.2! = 10².52². 4! / 2!.2!
Alternativa: E
147) (ENEM) A distribuição de salários pagos em uma empresa pode ser analisada destacando-se a parcela do total da massa salarial que é paga aos 10% que recebem os maiores salários. Isso pode ser representado na forma de um gráfico formado por dois segmentos de reta, unidos em um ponto P, cuja abscissa tem valor igual a 90, como ilustrado na figura.
No eixo horizontal do gráfico tem-se o percentual de funcionários, ordenados de forma crescente pelos valores de seus salários, e no eixo vertical tem-se o percentual do total da massa salarial de todos os funcionários. O Índice de Gini, que mede o grau de concentração de renda de um determinado grupo, pode ser calculado pela razão A/(A + B) em que A e B são as medidas das áreas indicadas no gráfico.
O Índice de Gini, que mede o grau de concentração de renda de um determinado grupo, pode ser calculado pela razão A/(A + B) em que A e B são as medidas das áreas indicadas no gráfico.
A empresa tem como meta tornar seu Índice de Gini igual ao do país, que é 0,3. Para tanto, precisa ajustar os salários de modo a alterar o percentual que representa a parcela recebida pelos 10% dos funcionários de maior salário em relação ao total da massa salarial.
Para atingir a meta desejada, o percentual deve ser
(A) 40%
(B) 20%
(C) 60%
(D) 30%
(E) 70%
Resolução:
Seja Yp a ordenada do ponto P, de tal forma que :
B = 90 . Yp/2 + (Yp + 100) . 10/2 = 50 . Yp + 500.
Assim, teremos:
A = 100 . 100/2 – B = 4500 – 50Yp .
Desse modo, se a meta é 0,3, então:
A / (A+B) = 0,3 → A = 1500 → 4500 – 50Yp = 1500 → Yp = 60
Portanto, a resposta é (100 – 60)% = 40%
Alternativa: A
148) (ENEM) Ao iniciar suas atividades, um ascensorista registra tanto o número de pessoas que entram quanto o número de pessoas que saem do elevador em cada um dos andares do edifício onde ele trabalha. O quadro apresenta os registros do ascensorista durante a primeira subida do térreo, de onde partem ele e mais três pessoas, ao quinto andar do edifício. Com base no quadro, qual é a moda do número de pessoas no elevador durante a subida do térreo ao quinto andar?
Com base no quadro, qual é a moda do número de pessoas no elevador durante a subida do térreo ao quinto andar?
(A) 2
(B) 3
(C) 4
(D) 5
(E) 6
Resolução:
Térreo = 4
1° andar = 5
2° andar = 5
3° andar = 5
4° andar = 7
5° andar = 3
Moda é 5.
Alternativa: D
149) (ENEM) O censo demográfico é um levantamento estatístico que permite a coleta de várias informações. Atabela apresenta os dados obtidos pelo censo demográfico brasileiro nos anos de 1940 e 2000, referentes à concentração da população total, na capital e no interior, nas cinco grandes regiões. O valor mais próximo do percentual que descreve o aumento da população nas capitais da Região Nordeste é
O valor mais próximo do percentual que descreve o aumento da população nas capitais da Região Nordeste é
(A) 125%
(B) 231%
(C) 331%
(D) 700%
(E) 800%
Resolução:
Aumento da população: 10.162.346 / 1.270.729 = 7,99.
Aumento de 700%.
Alternativa: D
150) (ENEM) Um marceneiro está construindo um material didático que corresponde ao encaixe de peças de madeira com 10 cm de altura e formas geométricas variadas, num bloco de madeira em que cada peça se posicione na perfuração com seu formato correspondente, conforme ilustra a figura. O bloco de madeira já possui três perfurações prontas de bases distintas: uma quadrada (Q), de lado 4 cm, uma retangular (R), com base 3 cm e altura 4 cm, e uma em forma de um triângulo equilátero (T), de lado 6,8 cm. Falta realizar uma perfura- ção de base circular (C).
O marceneiro não quer que as outras peças caibam na perfuração circular e nem que a peça de base circular caiba nas demais perfurações e, para isso, escolherá o diâmetro do círculo que atenda a tais condições. Procurou em suas ferramentas uma serra copo (broca com formato circular) para perfurar a base em madeira, encontrando cinco exemplares, com diferentes medidas de diâmetros, como segue: (I) 3,8 cm; (II) 4,7 cm; (III) 5,6 cm; (IV) 7,2 cm e (V) 9,4 cm. Considere 1,4 e 1,7 como aproximações para √2 e √3 , respectivamente.
Considere 1,4 e 1,7 como aproximações para √2 e √3 , respectivamente.
Para que seja atingido o seu objetivo, qual dos exemplares de serra copo o marceneiro deverá escolher?
(A) I
(B) II
(C) III
(D) IV
(E) V
Resolução:
Quadrado: 4 < diâmetro < 5,6 Triângulo Equilátero: 4 < Diâmetro < 8 Retângulo: 4 < Diâmetro < 5. Logo, o único diâmetro possível é 4,7 cm.
Alternativa: B
151) (ENEM) Em um exame, foi feito o monitoramento dos níveis de duas substâncias presentes (A e B) na corrente sanguínea de uma pessoa, durante um período de 24 h, conforme o resultado apresentado na figura. Um nutricionista, no intuito de prescrever uma dieta para essa pessoa, analisou os níveis dessas substâncias, determinando que, para uma dieta semanal eficaz, deverá ser estabelecido um parâmetro cujo valor será dado pelo número de vezes em que os níveis de A e de B forem iguais, porém, maiores que o nível mínimo da substância A durante o período de duração da dieta. Considere que o padrão apresentado no resultado do exame, no período analisado, se repita para os dias subsequentes.
Considere que o padrão apresentado no resultado do exame, no período analisado, se repita para os dias subsequentes.
O valor do parâmetro estabelecido pelo nutricionista, para uma dieta semanal, será igual a
(A) 28
(B) 21
(C) 2
(D) 7
(E) 14
Resolução:
Como somente os pontos 1 e 3 apresentam níveis maiores que o nível mínimo da substância A, então o parâmetro diário estabelecido será 2.
Para uma dieta semanal, teremos o parâmetro igual a: 2 ⋅ 7 = 14.
Alternativa: E
152) (ENEM) Um paciente necessita de reidratação endovenosa feita por meio de cinco frascos de soro durante 24 h. Cada frasco tem um volume de 800 mL de soro. Nas primeiras quatro horas, deverá receber 40% do total a ser aplicado. Cada mililitro de soro corresponde a 12 gotas.
O número de gotas por minuto que o paciente deverá receber após as quatro primeiras horas será
(A) 16
(B) 20
(C) 24
(D) 34
(E) 40
Resolução:
Volume Total = 5 . 800 mL = 4000 mL
4 horas ——- 0,4 . 4000 mL = 1600 mL
Faltam 4000 – 1600 = 2400 mL
Como 1 mL = 12 gotas
2400 mL = y
y = 28.800 gotas
Então, o número de gotas/minuto restante será: 28800 / 20.60 = 24 gotas/min
Alternativa: C
153) (ENEM) É comum os artistas plásticos se apropriarem de entes matemáticos para produzirem, por exemplo, formas e imagens por meio de manipulações. Um artista plástico, em uma de suas obras, pretende retratar os diversos polígonos obtidos pelas intersecções de um plano com uma pirâmide regular de base quadrada.
Segundo a classificação dos polígonos, quais deles são possíveis de serem obtidos pelo artista plástico?
(A) Quadrados, apenas
(B) Triângulos e quadrados, apenas
(C) Triângulos, quadrados e trapézios, apenas
(D) Triângulos, quadrados, trapézios e quadriláteros irregulares, apenas.
(E) Triângulos, quadrados, trapézios, quadriláteros irregulares e pentágonos, apenas.
Resolução:
O número de polígonos formados depende do número de faces da pirâmide. Como podemos cortar suas faces em 3, 4 ou 5 pontos, podemos criar triângulos (3 pontos), quadrados, trapézio, quadriláteros irregulares (todos 4 pontos) e Pentágonos (5 pontos).
Alternativa: E
154) (ENEM) Um reservatório é abastecido com água por uma torneira e um ralo faz a drenagem da água desse reservatório. Os gráficos representam as vazões Q, em litro por minuto, do volume de água que entra no reservatório pela torneira e do volume que sai pelo ralo, em função do tempo t, em minuto. Em qual intervalo de tempo, em minuto, o reservatório tem uma vazão constante de enchimento?
Em qual intervalo de tempo, em minuto, o reservatório tem uma vazão constante de enchimento?
(A) De 0 a 10.
(B) De 5 a 10.
(C) De 5 a 15.
(D) De 15 a 25.
(E) De 0 a 25.
Resolução:
Sendo Q1(t) e Q2(t) as vazões, em litros por minuto, da torneira e do ralo, respectivamente, a vazão do reservatório é V(t) = Q1(t) – Q2(t).
Para que V(t) seja constante, devemos ter, de acordo com o gráfico, duas situações possíveis:
Q1(t) e Q2(t) são constantes, o que só ocorre no intervalo [5; 10]; ou
Q1(t) e Q2(t) são funções de primeiro grau com o mesmo coeficiente angular, o que não ocorre em algum intervalo.
Alternativa: B
155) (ENEM) O LIRAa, Levantamento Rápido do Índice de Infestação por Aedes aegypti, consiste num mapeamento da infestação do mosquito Aedes aegypti. O LIRAa é dado pelo percentual do número de imóveis com focos do mosquito, entre os escolhidos de uma região em avaliação.
O serviço de vigilância sanitária de um município, no mês de outubro do ano corrente, analisou o LIRAa de cinco bairros que apresentaram o maior índice de infestação no ano anterior. Os dados obtidos para cada bairro foram:
I. 14 imóveis com focos de mosquito em 400 imóveis no bairro;
II. 6 imóveis com focos de mosquito em 500 imóveis no bairro;
III. 13 imóveis com focos de mosquito em 520 imóveis no bairro;
IV. 9 imóveis com focos de mosquito em 360 imóveis no bairro;
V. 15 imóveis com focos de mosquito em 500 imóveis no bairro.
As ações de controle iniciarão pelo bairro
(A) I
(B) II
(C) III
(D) IV
(E) V
Resolução:
Bairro I -> 14/400 = 3,5%
Bairro II -> 6/500 = 1,2%
Bairro III -> 13/520 = 2,5%
Bairro IV -> 9/360 = 2,5%
Bairro V -> 15/500 = 3%
O bairro I apresentou o maior índice.
Alternativa: A
156) (ENEM) A figura representa o globo terrestre e nela estão marcados os pontos A, B e C. Os pontos A e B estão localizados sobre um mesmo paralelo, e os pontos B e C, sobre um mesmo meridiano. É traçado um caminho do ponto A até C, pela superfície do globo, passando por B, de forma que o trecho de A até B se dê sobre o paralelo que passa por A e B e, o trecho de B até C se dê sobre o meridiano que passa por B e C. Considere que o plano α é paralelo à linha do equador na figura. A projeção ortogonal, no plano α, do caminho traçado no globo pode ser representada por
A projeção ortogonal, no plano α, do caminho traçado no globo pode ser representada por
(A) 
(B) 
(C) 
(D) 
(E) 
Resolução:
O arco AB pertence a um plano paralelo a α, portanto sua projeção ortogonal em α também será um arco. Os pontos B e C não são simétricos em relação ao plano do equador e o arco BC pertence a um plano perpendicular a α, assim sua projeção ortogonal sobre α será um segmento de reta. Logo, a melhor representação é a da alternativa E.
Alternativa: E
157) (ENEM) Diante da hipótese do comprometimento da qualidade da água retirada do volume morto de alguns sistemas hídricos, os técnicos de um laboratório decidiram testar cinco tipos de filtros de água. Dentre esses, os quatro com melhor desempenho serão escolhidos para futura comercialização.
Nos testes, foram medidas as massas de agentes contaminantes, em miligrama, que não são capturados por cada filtro em diferentes períodos, em dia, como segue:
Filtro 1 (F1): 18 mg em 6 dias;
Filtro 2 (F2): 15 mg em 3 dias;
Filtro 3 (F3): 18 mg em 4 dias;
Filtro 4 (F4): 6 mg em 3 dias;
Filtro 5 (F5): 3 mg em 2 dias.
Ao final, descarta-se o filtro com a maior razão entre a medida da massa de contaminantes não capturados e o número de dias, o que corresponde ao de pior desempenho
O filtro descartado é o
(A) F1.
(B) F2.
(C) F3.
(D) F4.E) F5.
Resolução:
As razões entre as medidas das massas de agentes contaminantes não capturados e o número de dias, de cada filtro, estão descritas a seguir:
filtro 1 = 18/6 = 3.
filtro 2 = 15/3 = 5.
filtro 3 = 18/4 = 4,5.
filtro 4 = 6/3 = 2.
filtro 5 = 3/2 = 1,5.
A resposta é o filtro 2.
Alternativa: B
158) (ENEM) Em 2011, um terremoto de magnitude 9,0 na escala Richter causou um devastador tsunami no Japão, provocando um alerta na usina nuclear de Fukushima. Em 2013, outro terremoto, de magnitude 7,0 na mesma escala, sacudiu Sichuan (sudoeste da China), deixando centenas de mortos e milhares de feridos. A magnitude de um terremoto na escala Richter pode ser calculada por sendo E a energia, em kWh, liberada pelo terremoto e E0 uma constante real positiva. Considere que E1 e E2 representam as energias liberadas nos terremotos ocorridos no Japão e na China, respectivamente.
Considere que E1 e E2 representam as energias liberadas nos terremotos ocorridos no Japão e na China, respectivamente.
Qual a relação entre E1 e E2?
(A) E1 = E2 + 2
(B) E1 = 10².E2
(C) E1 = 10³.E2
(D) E1 = 109/7.E2
(E) E1 = 9/7.E2
Resolução:
Temos que:
9 = ⅔.(logE1/E0)
27/2 = (logE1/E0)
Além disso, 7 = ⅔.(logE2/E0)
21/2 = (logE2/E0)
Subtraindo (1) de (2) temos, 3 = (logE1/E2) então, E1/E2= 10³
Logo a relação é: E1 = 10³.E2
Alternativa: C
159) (ENEM) A Lei da Gravitação Universal, de Isaac Newton, estabelece a intensidade da força de atração entre duas massas. Ela é representada pela expressão: onde m1 e m2 correspondem às massas dos corpos, d à distância entre eles, G à constante universal da gravitação e F à força que um corpo exerce sobre o outro.
onde m1 e m2 correspondem às massas dos corpos, d à distância entre eles, G à constante universal da gravitação e F à força que um corpo exerce sobre o outro.
O esquema representa as trajetórias circulares de cinco satélites, de mesma massa, orbitando a Terra. Qual gráfico expressa as intensidades das forças que a Terra exerce sobre cada satélite em função do tempo?
Qual gráfico expressa as intensidades das forças que a Terra exerce sobre cada satélite em função do tempo?
(A) 
(B) 
(C) 
(D) 
(E) 
Resolução:
A distância d do satélite ao centro da Terra é constante e a força gravitacional terá intensidade constante e com valor inversamente proporcional ao quadrado da distância entre o planeta e o centro da Terra, assim:
dA > dB > dC > dD > dE e FA < FB < FC < FD < FE
Com isso o gráfico que melhor representa as intensidades das forças que a Terra exerce sobre cada satélite em função do tempo é:
Alternativa: B
160) (ENEN) Uma indústria tem um reservatório de água com capacidade para 900 m³. Quando há necessidade de limpeza do reservatório, toda a água precisa ser escoada. O escoamento da água é feito por seis ralos, e dura 6 horas quando o reservatório está cheio. Esta indústria construirá um novo reservatório, com capacidade de 500 m³, cujo escoamento da água deverá ser realizado em 4 horas, quando o reservatório estiver cheio. Os ralos utilizados no novo reservatório deverão ser idênticos aos do já existente.
A quantidade de ralos do novo reservatório deverá ser igual a
(A) 2
(B) 4
(C) 5
(D) 8
(E) 9
Resolução:
Cada ralo elimina: 900/6= 150 m³ de água em 6 horas
Cada ralo elimina por hora um total de: 150 m³/6 horas = 25 m³/hora
Em 4 horas cada ralo irá eliminar: 25 m³ . 4 horas = 100 m³
Como o novo reservatório tem 500 m³ de capacidade , o número de ralos necessários será:
500/100 = 5 ralos.
Alternativa: C
161) (ENEM) Uma fábrica de fórmicas produz placas quadradas de lados de medida igual a y centímetros. Essas placas são vendidas em caixas com N unidades e, na caixa, é especificada a área máxima S que pode ser coberta pelas N placas.
Devido a uma demanda do mercado por placas maiores, a fábrica triplicou a medida dos lados de suas placas e conseguiu reuni-las em uma nova caixa, de tal forma que a área coberta S não fosse alterada.
A quantidade X, de placas do novo modelo, em cada nova caixa será igual a:
(A) N/9
(B) N/6
(C) N/3
(D) 3N
(E) 9N
Resolução:
Antes: Depois
Área = y.y = y² Área = 3y . 3y = 9y²
1 placa —— y² 1 placa —— 9y²
N placas —- S X placas —- S
S = N.y² S = X. 9y²
N.y² = X. 9y²
X=N/9
Alternativa: A
162) (ENEM) Num parque aquático existe uma piscina infantil na forma de um cilindro circular reto, de 1 m de profundidade e volume igual a 12 m³, cuja base tem raio R e centro O. Deseja-se construir uma ilha de lazer seca no interior dessa piscina, também na forma de um cilindro circular reto, cuja base estará no fundo da piscina e com centro da base coincidindo com o centro do fundo da piscina, conforme a figura. O raio da ilha de lazer será r. Deseja-se que após a construção dessa ilha, o espaço destinado à água na piscina tenha um volume de, no mínimo, 4 m³.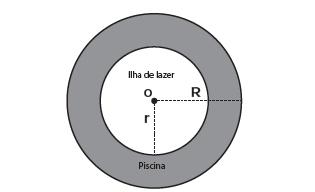 Considere 3 como valor aproximado para π
Considere 3 como valor aproximado para π
Para satisfazer as condições dadas, o raio máximo da ilha de lazer r, em metros, estará mais próximo de
(A) 1,6
(B) 1,7
(C) 2,0
(D) 3,0
(E) 3,8
Resolução:
Volume da piscina infantil: V1= 12 m ³
Volume da ilha de lazer seca: V2 = π. r².1 = 3.r².1 = 3 r²
Pelo enunciado teremos:
V1 – V2 ≥ 4
12 – 3r² ≥ 4
3r² ≤ 8
r ≤ 1,632
Alternativa: A
163) (ENEM) O contribuinte que vende mais de R$ 20 mil de ações em Bolsa de Valores em um mês deverá pagar Imposto de Renda. O pagamento para a Receita Federal consistirá em 15% do lucro obtido com a venda das ações.
Um contribuinte que vende por R$ 34 mil um lote de ações que custou R$ 26 mil terá de pagar de Imposto de Renda à Receita Federal o valor de:
(A) R$ 900,00.
(B) R$ 1 200,00.
(C) R$ 2 100,00.
(D) R$ 3 900,00.
(E) R$ 5 100,00.
Resolução:
O lucro do contribuinte será: L = 34 000 – 26 000 = 8 000 reais
O Imposto de Renda que esse contribuinte terá que pagar será: 15% . L =0,15 . 8 000= 1 200
Alternativa: B
164) (ENEM) Para se construir um contrapiso, é comum, na constituição do concreto, se utilizar cimento, areia e brita, na seguinte proporção: 1 parte de cimento, 4 partes de areia e 2 partes de brita. Para construir o contrapiso de uma garagem, uma construtora encomendou um caminhão betoneira com 14 m³ de concreto.
Qual é o volume de cimento, em m³, na carga de concreto trazido pela betoneira?
(A) 1,75
(B) 2,00
(C) 2,33
(D) 4,00
(E) 8,00
Resolução:
Sendo c, a, e b, as quantidades em metros cúbicos de cimento, cimento, areia e brita, então:
Alternativa: B
165) (ENEM) Cinco empresas de gêneros alimentícios encontram-se à venda. Um empresário, almejando ampliar os seus investimentos, deseja comprar uma dessas empresas. Para escolher qual delas irá comprar, analisa o lucro (em milhões de reais) de cada uma delas, em função de seus tempos (em anos) de existência, decidindo comprar a empresa que apresente o maior lucro médio anual.
O quadro apresenta o lucro (em milhões de reais) acumulado ao longo do tempo (em anos) de existência de cada empresa. O empresário decidiu comprar a empresa
O empresário decidiu comprar a empresa
(A) F
(B) G
(C) H
(D) M
(E) P
Resolução:
O lucro médio de cada empresa será:
F: 24 ÷ 3 = 8 milhões de reais
G: 24 ÷ 2 = 12 milhões de reais
H: 25 ÷ 2,5 = 10 milhões de reais
M: 15 ÷ 1,5 = 10 milhões de reais
P: 9 ÷ 1,5 = 6 milhões de reais
A empresa que apresenta o maior lucro anual é a empresa G.
Alternativa: B
166) (ENEM) Deseja-se postar cartas não comerciais, sendo duas de 100 g, três de 200 g e uma de 350 g. O gráfico mostra o custo para enviar uma carta não comercial pelos Correios: O valor total gasto, em reais, para postar essas cartas é de
O valor total gasto, em reais, para postar essas cartas é de
(A) 8,35
(B) 12,50
(C) 14,40
(D) 15,35
(E) 18,05
Resolução:
A partir do gráfico é possível observar que a postagem de uma carta de 100 g custa R$ 1,70, de uma carta de 200 g custa R$ 2,65 e de uma carta de 350 g custa R$ 4,00.
Então, a postagem de duas cartas de 100g, três de 200g e uma de 350g, será:
2 . 1,70 + 3 . 2,65 + 1 . 4 = 3,40 + 7,95 + 4 = 15,35.
Alternativa: D
167) (ENEM) Foi realizado um levantamento nos 200 hotéis de uma cidade, no qual foram anotados os valores, em reais, das diárias para um quarto padrão de casal e a quantidade de hotéis para cada valor da diária. Os valores das diárias foram: A = R$ 200,00; B = R$ 300,00; C = R$ 400,00 e D = R$ 600,00. No gráfico, as áreas representam as quantidades de hotéis pesquisados, em porcentagem, para cada valor da diária. O valor mediano da diária, em reais, para o quarto padrão de casal nessa cidade, é
O valor mediano da diária, em reais, para o quarto padrão de casal nessa cidade, é
(A) 300,00.
(B) 345,00.
(C) 350,00.
(D) 375,00.
(E) 400,00.
Resolução:
A partir do gráfico observamos que:
25% . 200 = 0,25 . 200 = 50 hotéis cobram a diária A (R$ 200,00);
25% . 200 = 0,25 . 200 = 50 hotéis cobram a diária B (R$ 300,00);
40% . 200 = 0,40 . 200 = 80 hotéis cobram a diária C (R$ 400,00)
e 10% . 200 = 0,25 . 200 = 20 hotéis cobram a diária D (R$ 600,00).
Colocando em ordem crescente esses valores, temos o valor mediano da diária, em reais, para o quarto padrão de casal nessa cidade, é
Alternativa: C
168) (ENEM) Para aumentar as vendas no início do ano, uma loja de departamentos remarcou os preços de seus produtos 20% abaixo do preço original. Quando chegam ao caixa, os clientes que possuem o cartão fidelidade da loja têm direito a um desconto adicional de 10% sobre o valor total de suas compras.
Um cliente deseja comprar um produto que custava R$ 50,00 antes da remarcação de preços. Ele não possui o cartão fidelidade da loja.
Caso esse cliente possuísse o cartão fidelidade da loja, a economia adicional que obteria ao efetuar a compra, em reais, seria de
(A) 15,00
(B) 14,00
(C) 10,00
(D) 5,00
(E) 4,00
Resolução:
Por não ter o cartão fidelidade, esse cliente pagará pelo produto: (100% – 20%) . 50 = 0,80 . 50 = 40 reais
Se tivesse o cartão fidelidade ele teria ainda um desconto adicional de 10%, ou seja, pagaria: (100% – 10%) . 40 = (1 – 0,1) . 40 = 36 reais.
A economia adicional desse cliente seria de: (40 – 36) = 4 reais.
Alternativa: E
169) (ENEM) Um programa de edição de imagens possibilita transformar figuras em outras mais complexas. Deseja-se construir uma nova figura a partir da original. A nova figura deve apresentar simetria em relação ao ponto O. A imagem que representa a nova figura é:
A imagem que representa a nova figura é:
(A) 
(B) 
(C) 
(D) 
(E) 
Resolução:
A nova figura deve apresentar simetria em relação ao ponto O, ou seja, a distância de todos os pontos de uma parte da figura ao ponto O devem ser a mesma dos pontos simétricos da outra figura em relação a esse mesmo ponto O. Traçando-se um eixo vertical (em vermelho) e um horizontal (em verde) passando pelo ponto O e pelos lados da figura, percebe-se que a original se encontra no segundo quadrante, sendo assim a figura simétrica deve estar no quarto.
Alternativa: E
170) (ENEM) Um artesão de joias tem à sua disposição pedras brasileiras de três cores: vermelhas, azuis e verdes. Ele pretende produzir joias constituídas por uma liga metálica, a partir de um molde no formato de um losango não quadrado com pedras nos seus vértices, de modo que dois vértices consecutivos tenham sempre pedras de cores diferentes.
A figura ilustra uma joia, produzida por esse artesão, cujos vértices A, B, C e D correspondem às posições ocupadas pelas pedras. Com base nas informações fornecidas, quantas joias diferentes, nesse formato, o artesão poderá obter?
Com base nas informações fornecidas, quantas joias diferentes, nesse formato, o artesão poderá obter?
(A) 6
(B) 12
(C) 18
(D) 24
(E) 36
Resolução:
Nessa questão, existem 3 casos diferentes que devem ser analisados:
1º caso: As pedras nos vértices A e C com a mesma cor e as pedras nos vértices B e D também com a mesma cor, porém de cor diferente das pedras A e C.
3 maneiras de escolher a cor de A e C 2 maneiras de escolher a cor de B e D
Quantidade de maneiras: 3 . 2 = 6 possíveis jóias diferentes
2º. caso: As pedras nos vértices A e C com a mesma cor e as pedras nos vértices B e D com cores diferentes entre sí e diferentes de A e C.
(3 . 2)/2= 3 possíveis jóias diferentes
3º. caso: As pedras nos vértices A e C com cores diferentes e as pedras nos vértices B e D com cores diferentes das cores de A e C.
(3 . 2)/2 = 3 possíveis jóias diferentes
No total é possível se obter: 6 + 3 + 3 = 12 jóias diferentes
Alternativa: B
171) (ENEM) Em setembro de 1987, Goiânia foi palco do maior acidente radioativo ocorrido no Brasil, quando uma amostra de césio-137, removida de um aparelho de radioterapia abandonado, foi manipulada inadvertidamente por parte da população. A meia-vida de um material radioativo é o tempo necessário para que a massa desse material se reduza à metade. A meia-vida do césio-137 é 30 anos e a quantidade restante de massa de um material radioativo, após t anos, é calculada pela expressão M(t) = A · (2,7)kt, onde A é a massa inicial e k é uma constante negativa.
Considere 0,3 como aproximação para log10 2.
Qual o tempo necessário, em anos, para que uma quantidade de massa do césio-137 se reduza a 10% da quantidade inicial?
(A) 27
(B) 36
(C) 50
(D) 54
(E) 100
Resolução:
A partir do enunciado, temos:
I) log 2 = 0,3 ⇔ 2 = 100,3
II) M (30) = A/2
A . (2,7)k.30 = A/2
(2,7)30k = 1/2
(2,7)30k = 2–1
(2,7)30k = (100,3)–1
(2,7)30k = 10–0,3
III) M (t) = 0,1. A
A . (2,7)kt= 0,1 . A
(2,7)kt = 0,1
Assim,
(2,7)30kt = (1/10)30
[(2,7)30k]t= 10-30
(10–0,3)t = 10–30
– 0,3 t = – 3,0
t = 100
Alternativa: E
172) (ENEM)
Considere o seguinte jogo de apostas:
Numa cartela com 60 números disponíveis, um apostador escolhe de 6 a 10 números. Dentre os números disponíveis, serão sorteados apenas 6. O apostador será premiado caso os 6 números sorteados estejam entre os números escolhidos por ele numa mesma cartela. O quadro apresenta o preço de cada cartela, de acordo com a quantidade de números escolhidos. Cinco apostadores, cada um com R$ 500,00 para apostar, fizeram as seguintes opções:
Cinco apostadores, cada um com R$ 500,00 para apostar, fizeram as seguintes opções:
Arthur: 250 cartelas com 6 números escolhidos;
Bruno: 41 cartelas com 7 números escolhidos e 4 cartelas com 6 números escolhidos;
Caio: 12 cartelas com 8 números escolhidos e 10 cartelas com 6 números escolhidos;
Douglas: 4 cartelas com 9 números escolhidos;
Eduardo: 2 cartelas com 10 números escolhidos.
Os dois apostadores com maiores probabilidades de serem premiados são
(A) Caio e Eduardo.
(B) Arthur e Eduardo.
(C) Bruno e Caio.
(D) Arthur e Bruno.
(E) Douglas e Eduardo.
Resolução:
De acordo com o enunciado, temos as seguintes possibilidades ganhar o prêmio:
Arthur: 250 . C6,6 = 250 . 1 = 250
Bruno: 41 . C7,6 + 4 . C6,6 = 41 . 7 + 4 . 1 = 287 + 4 = 291
Caio: 12 . C8,6 + 10 . C6,6 = 12 . 28 + 10 . 1 = 336 + 10 = 346
Douglas: 4 . C9,6 = 4 . 84 = 336
Eduardo: 2 . C10,6 = 2 . 210 = 420
Assim, os dois apostadores com maiores probabilidades de serem premiados são Eduardo com 420 possibilidades e Caio com 346 possibilidades.
Alternativa: A
173) (ENEM) Nos Estados Unidos a unidade de medida de volume mais utilizada em latas de refrigerante é a onça fluida (fl oz), que equivale a aproximadamente 2,95 centilitros (cL).
Sabe-se que o centilitro é a centésima parte do litro e que a lata de refrigerante usualmente comercializada no Brasil tem capacidade de 355 mL.
Assim, a medida do volume da lata de refrigerante de 355 mL, em onça fluida (fl oz), é mais próxima de
(A) 0,83
(B) 1,20
(C) 12,03
(D) 104,73
(E) 120,34
Resolução:
1 fl oz ≅ 2,95 cL = 2,95 . 10 = 29,5 mL
1 fl oz ____________ 29,5 mL
X ____________ 355 mL
X = 355/29,5
X ≅ 12,03 mL
Alternativa: C
174) (ENEM) Na aferição de um novo semáforo, os tempos são ajustados de modo que, em cada ciclo completo (verde-amarelo- vermelho), a luz amarela permaneça acesa por 5 segundos, e o tempo em que a luz verde permaneça acesa seja igual a 2/3 do tempo em que a luz vermelha fique acesa. A luz verde fica acesa, em cada ciclo, durante X segundos e cada ciclo dura Y segundos.
Qual é a expressão que representa a relação entre X e Y
(A) 5X − 3Y + 15 = 0
(B) 5X − 2Y + 10 = 0
(C) 3X − 3Y + 15 = 0
(D) 3X − 2Y + 15 = 0
€ 3X − 2Y + 10 = 0
Resolução:
Em cada ciclo Y:
Luz vermelha acesa : V segundos
Luz verde acesa: X segundos e 2/3 de V
Luz amarela acesa: 5 segundos
X = 2/3 . V ⇔ V = 3X/2
X + Y + V = Y ⇔ X + 5+ 3X/2 = Y ⇔ 5X – 2Y + 10 = 0
Alternativa: B
175) (ENEM) A temperatura T de um forno (em graus centígrados) é reduzida por um sistema a partir do instante de seu desligamento (t = 0) e varia de acordo com a expressão com t em minutos. Por motivos de segurança, a trava do forno só é liberada para abertura quando o forno atinge a temperatura de 39 ºC.
Qual o tempo mínimo de espera, em minutos, após se desligar o forno, para que a porta possa ser aberta?
(A) 19,0
(B) 19,8
(C) 20,0
(D) 38,0
(E) 39,0
Resolução:
O tempo mínimo de espera ocorre quando a temperatura chega à 39ºC, assim:
Alternativa: D
176) (ENEM) O ciclo de atividade magnética do Sol tem um período de 11 anos. O início do primeiro ciclo registrado se deu no começo de 1755 e se estendeu até o final de 1765. Desde então, todos os ciclos de atividade magnética do Sol têm sido registrados.
No ano de 2101, o Sol estará no ciclo de atividade magnética de número
(A) 32
(B) 34
(C) 33
(D) 35
(E) 31
Resolução:
Os anos de ínicio do ciclo forma uma progressão aritmética:
(1755, 1766, 1777, …)
a1 = 1755
r = 11
A questão quer saber em que ciclo de atividade magnética do sol, estará no ano de 2101, assim devemos calcular o n:
an = a1 + (n – 1) . r
2101 = 1755 + (n – 1) . 11
2101 = 1755 + 11n – 11
11n = 357
n = 32,45
Isso significa que o ano de 2101 está compreendido no 32º ciclo.
Alternativa: A
178) (ENEM) A figura apresenta dois mapas, em que o estado do Rio de Janeiro é visto em diferentes escalas. Há interesse em estimar o número de vezes que foi ampliada a área correspondente a esse estado no mapa do Brasil.
Há interesse em estimar o número de vezes que foi ampliada a área correspondente a esse estado no mapa do Brasil.
Esse número é
(A) menor que 10.
(B) maior que 10 e menor que 20.
(C) maior que 20 e menor que 30.
(D) maior que 30 e menor que 40.
(E) maior que 40.
Resolução:
A escala apresenta a relação entre duas medidas , a do desenho e a real. No mapa do brasil, 1 unidade do desenho equivale a 25 000 000 do real. Já no mapa do Rio de Janeiro, 1 unidade equivale a 4 000 000 do real.
Assim, temos:
Então, o número de vezes que foi ampliada a área é um um número maior que 30 e menor que 40.
Alternativa: D
179) (ENEM) Nos últimos anos, a televisão tem passado por uma verdadeira revolução, em termos de qualidade de imagem, som e interatividade com o telespectador. Essa transformação se deve à conversão do sinal analógico para o sinal digital. Entretanto, muitas cidades ainda não contam com essa nova tecnologia. Buscando levar esses benefícios a três cidades, uma emissora de televisão pretende construir uma nova torre de transmissão, que envie sinal às antenas A, B e C, já existentes nessas cidades. As localizações das antenas estão representadas no plano cartesiano: A torre deve estar situada em um local equidistante das três antenas.
A torre deve estar situada em um local equidistante das três antenas.
O local adequado para a construção dessa torre corresponde ao ponto de coordenadas
(A) (65 ; 35).
(B) (53 ; 30).
(C) (45 ; 35).
(D) (50 ; 20).
(E) (50 ; 30).
Resolução:
Considerando T ( xt, yt), o ponto onde será construído a nova torre equidistante aos pontos A (30,20), B (70,20) e C (60,50)
A coordenada xt, passa pela mediatriz do segmento de reta formado pelos pontos AB, assim:
xt = (30+70)/2 = 50.
A coordenada yt é equidistante aos pontos A e C:
O ponto onde a torre deve ser construída possui as coordenadas (50,30).
Alternativa: E
180) (ENEM) Uma cozinheira, especialista em fazer bolos, utiliza uma forma no formato representado na figura: Nela identifica-se a representação de duas figuras geométricas tridimensionais.
Nela identifica-se a representação de duas figuras geométricas tridimensionais.
Essas figuras são
(A) um tronco de cone e um cilindro.
(B) um cone e um cilindro.
(C) um tronco de pirâmide e um cilindro.
(D) dois troncos de cone.
(E) dois cilindros.
Resolução:
As duas figuras geométricas tridimensionais formadas são dois troncos de cone
Alternativa: D
181) (ENEM)
Uma falsa relação O cruzamento da quantidade de horas estudadas como desempenho no Programa Internacional de Avaliação de Estudantes (Pisa) mostra que mais tempo na escola não é garantia de nota acima da média.
O cruzamento da quantidade de horas estudadas como desempenho no Programa Internacional de Avaliação de Estudantes (Pisa) mostra que mais tempo na escola não é garantia de nota acima da média.
Dos países com notas abaixo da média nesse exame, aquele que apresenta maior quantidade de horas de estudo é
(A) Finlândia.
(B) Holanda.
(C) Israel.
(D) México.
(E) Rússia.
Resolução:
Observando o gráfico temos que os países com as notas abaixo da média são: Rússia, Portugal, Itália, Israel e México
E o que apresenta maior quantidade de horas de estudo é: Israel, com 8500 horas aproximadamente.
Alternativa: C
182) (ENEM) Um restaurante utiliza, para servir bebidas, bandejas com bases quadradas. Todos os copos desse restaurante têm o formato representado na figura: Considere que AC = 7/5 BD e que l é a medida de um dos lados da base da bandeja.
Considere que AC = 7/5 BD e que l é a medida de um dos lados da base da bandeja.
Qual deve ser o menor valor da razão lBD para que uma bandeja tenha capacidade de portar exatamente quatro copos de uma só vez?
(A) 2
(B) 14/5
(C) 4
(D) 24/5
(E) 28/5
Resolução:
Da figura e do enunciado podemos fazer:
Temos que: AC = 7/5 . BD e L é a medida do lado da bandeja, assim:
L = 2BD + 2AC
L = 2BD + 2.(7/5)BD
L = 2BD + (14/5)BD
L= (10/5)BD + (14/5)BD
L/BD = 24/5
Alternativa: D
183) (ENEM) Gangorra é um brinquedo que consiste de uma tábua longa e estreita equilibrada e fixada no seu ponto central (pivô). Nesse brinquedo, duas pessoas sentam-se nas extremidades e, alternadamente, impulsionam-se para cima, fazendo descer a extremidade oposta, realizando, assim, o movimento da gangorra. Considere a gangorra representada na figura, em que os pontos A e B são equidistantes do pivô:
Considere a gangorra representada na figura, em que os pontos A e B são equidistantes do pivô:
A projeção ortogonal da trajetória dos pontos A e B, sobre o plano do chão da gangorra, quando esta se encontra em movimento, é:
(A) 
(B) 
(C) 
(D) 
(E) 
Resolução:
A projeção ortogonal das trajetórias dos pontos A e B (movimento de subida e descida) no plano do chão são dois segmentos de reta na horizontal, assim a alternativa que melhor apresenta é a B.
Alternativa: B
184) (ENEM) A cidade de Guarulhos (SP) tem o 8º PIB municipal do Brasil, além do maior aeroporto da América do Sul. Em proporção, possui a economia que mais cresce em indústrias, conforme mostra o gráfico. Analisando os dados percentuais do gráfico, qual a diferença entre o maior e o menor centro em crescimento no polo das indústrias?
Analisando os dados percentuais do gráfico, qual a diferença entre o maior e o menor centro em crescimento no polo das indústrias?
(A) 75,28
(B) 64,09
(C) 56,95
(D) 45,76
(E) 30,07
Resolução:
A questão pede para que se calcule a diferença entre o maior e o menor percentual de crescimento no polo das indústrias que foram apresentados no gráfico, é possível observar que a o maior valor é da cidade de Guarulhos (60,52%) e o menor, da cidade de São Paulo (capital) com 3,57%.
A diferença será: 60,52% – 3,57% = 56,95%.
Alternativa: C
185) (ENEM) Em um certo teatro, as poltronas são divididas em setores. A figura apresenta a vista do setor 3 desse teatro, no qual as cadeiras escuras estão reservadas e as claras não foram vendidas. A razão que representa a quantidade de cadeiras reservadas do setor 3 em relação ao total de cadeiras desse mesmo setor é
A razão que representa a quantidade de cadeiras reservadas do setor 3 em relação ao total de cadeiras desse mesmo setor é
(A) 17/10
(B) 17/53
(C) 53/70
(D) 53/17
(E) 70/17
Resolução:
Quantidade de cadeiras no setor 3: 10. 7 = 70 cadeiras
Quantidade de cadeiras reservadas: 17 cadeiras
A razão entre quantidade de cadeiras reservadas do setor 3 em relação ao total de cadeiras é: 17/70
Alternativa: A
186) (ENEM) Uma loja acompanhou o número de compradores de dois produtos, A e B, durante os meses de janeiro, fevereiro e março de 2012. Com isso, obteve este gráfico: A loja sorteará um brinde entre os compradores do produto A e outro brinde entre os compradores do produto B.
A loja sorteará um brinde entre os compradores do produto A e outro brinde entre os compradores do produto B.
Qual a probabilidade de que os dois sorteados tenham feito suas compras em fevereiro de 2012?
(A) 1/20
(B) 3/242
(C) 5/22
(D) 6/25
(E) 7/15
Resolução:
Produto A
Número de compradores total = 10+30+60 = 100
Probabilidade de ser sorteado um comprador de fevereiro:
P1 =30100
Produto B
Número de compradores total = 20+20+80 = 120
Probabilidade de ser sorteado um comprador de fevereiro:
P2 =20/120
A probabilidade de que os dois sorteados tenham feito suas compras em fevereiro de 2012 é
P1 . P2 = (30/100) . (20/120) = 600/12000 = 1/20
Alternativa: A
187) (ENEM) Para o reflorestamento de uma área, deve-se cercar totalmente, com tela, os lados de um terreno, exceto o lado margeado pelo rio, conforme a figura. Cada rolo de tela que será comprado para confecção da cerca contém 48 metros de comprimento. A quantidade mínima de rolos que deve ser comprada para cercar esse terreno é
A quantidade mínima de rolos que deve ser comprada para cercar esse terreno é
(A) 6
(B) 7
(C) 8
(D) 11
(E) 12
Resolução:
Para que o terreno seja cercado (com exceção da margem do rio) é necessário: 81+190+81 = 352 m de cerca
Cada rolo tem 48 m então é necessário: 352÷48 ≅7,333..
Então é a quantidade mínima de rolos que deve ser comprada é 8.
Alternativa: C
188) (ENEM) Um dos grandes problemas enfrentados nas rodovias brasileiras é o excesso de carga transportada pelos caminhões. Dimensionado para o tráfego dentro dos limites legais de carga, o piso das estradas se deteriora com o peso excessivo dos caminhões. Além disso, o excesso de carga interfere na capacidade de frenagem e no funcionamento da suspensão do veículo, causas frequentes de acidentes.
Ciente dessa responsabilidade e com base na experiência adquirida com pesagens, um caminhoneiro sabe que seu caminhão pode carregar, no máximo, 1 500 telhas ou 1 200 tijolos.
Considerando esse caminhão carregado com 900 telhas, quantos tijolos, no máximo, podem ser acrescentados à carga de modo a não ultrapassar a carga máxima do caminhão?
(A) 300 tijolos
(B) 360 tijolos
(C) 400 tijolos
(D) 480 tijolos
(E) 600 tijolos
Resolução:
Considerando a, como o peso da telha e b, como peso do tijolo teremos:
O caminhão poderá receber o peso equivalente de: 1500 – 900 = 600 telhas
Então, podem ser carregados no caminhão 480 tijolos
Alternativa: D
189) (ENEM) As projeções para a produção de arroz no período de 2012 – 2021, em uma determinada região produtora, apontam para uma perspectiva de crescimento constante da produção anual. O quadro apresenta a quantidade de arroz, em toneladas, que será produzida nos primeiros anos desse período, de acordo com essa projeção. A quantidade total de arroz, em toneladas, que deverá ser produzida no período de 2012 a 2021 será de
A quantidade total de arroz, em toneladas, que deverá ser produzida no período de 2012 a 2021 será de
(A) 497,25.
(B) 500,85.
(C) 502,87.
(D) 558,75.
(E) 563,25.
Resolução:
Podemos observar que as projeções da produção para os anos de 2012 a 2015 formam uma progressão aritmética: (50,25; 51,50; 52,75; 54,00)
a1 = 50,25
r = 51,50 – 50,25 = 1,25
Assim, em 2021 teremos: a10 = 50,25 + (10-1) . 1,25 = 61,50
A quantidade total de arroz, em toneladas, que deverá ser produzida no período de 2012 a 2021 será de:
Alternativa: D
191) (ENEM) Durante uma aula de Matemática, o professor sugere aos alunos que seja fixado um sistema de coordenadas cartesianas (x, y) e representa na lousa a descrição de cinco conjuntos algébricos, I, II, III, IV e V, como se segue:
I — é a circunferência de equação x2 + y2 = 9;
II — é a parábola de equação y = − x2 − 1, com x variando de −1 a 1;
III — é o quadrado formado pelos vértices (−2, 1), (−1, 1), (−1, 2) e (−2, 2);
IV — é o quadrado formado pelos vértices (1, 1), (2, 1), (2, 2) e (1, 2);
V — é o ponto (0, 0).
A seguir, o professor representa corretamente os cinco conjuntos sobre uma mesma malha quadriculada, composta de quadrados com lados medindo uma unidade de comprimento, cada, obtendo uma figura.
Qual destas figuras foi desenhada pelo professor?
(A) 
(B) 
(C) 
(D) 
(E) 
Resolução:
Circunferência de equação x² + y² = 9, cujo o centro é o ponto (0,0) e o raio é 3.
Parábola de equação y= -x² – 1 , com -1≤x≤1
Quadrado de vértices (– 2; 1), (– 1; 1), (– 1; 2) e (– 2; 2), Quadrado de vértices (1; 1), (2; 1), (2; 2) e (1; 2) e ponto (0,0)
Alternativa: E
192) (ENEM) A parte interior de uma taça foi gerada pela rotação de uma parábola em torno de um eixo z, conforme mostra a figura. A função real que expressa a parábola, no plano cartesiano da figura, é dada pela lei onde C é a medida da altura do líquido contido na taça, em centímetros. Sabe-se que o ponto V, na figura, representa o vértice da parábola, localizado sobre o eixo x.
A função real que expressa a parábola, no plano cartesiano da figura, é dada pela lei onde C é a medida da altura do líquido contido na taça, em centímetros. Sabe-se que o ponto V, na figura, representa o vértice da parábola, localizado sobre o eixo x.
Nessas condições, a altura do líquido contido na taça, em centímetros, é
(A) 1
(B) 2
(C) 4
(D) 5
(E) 6
Resolução:
A função possui uma única raiz real (Ponto V), portanto ∆=0, assim:
b² – 4ac = 0
(-6)² – 4.(3/2) . C = 0
36 – 6C = 0
C = 6
Alternativa: E
193) (ENEM) O diretor de uma escola convidou os 280 alunos de terceiro ano a participarem de uma brincadeira. Suponha que existem 5 objetos e 6 personagens numa casa de 9 cômodos; um dos personagens esconde um dos objetos em um dos cômodos da casa. O objetivo da brincadeira é adivinhar qual objeto foi escondido por qual personagem e em qual cômodo da casa o objeto foi escondido.
Todos os alunos decidiram participar. A cada vez um aluno é sorteado e dá a sua resposta. As respostas devem ser sempre distintas das anteriores, e um mesmo aluno não pode ser sorteado mais de uma vez. Se a resposta do aluno estiver correta, ele é declarado vencedor e a brincadeira é encerrada.
O diretor sabe que algum aluno acertará a resposta porque há
(A) 10 alunos a mais do que possíveis respostas distintas.
(B) 20 alunos a mais do que possíveis respostas distintas.
(C) 119 alunos a mais do que possíveis respostas distintas.
(D) 260 alunos a mais do que possíveis respostas distintas.
(E) 270 alunos a mais do que possíveis respostas distintas.
Resolução:
O número total de possibilidades de uma personagem esconder um dos 5 brinquedos em um dos 9 cômodos é 6 . 5 . 9 = 270.
Já que as respostas devem ser sempre diferentes, algum aluno acertou a resposta porque “há 10 alunos a mais do que possíveis respostas distintas”.
Alternativa: A
194) (ENEM) Um biólogo mediu a altura de cinco árvores distintas e representou-as em uma mesma malha quadriculada, utilizando escalas diferentes, conforme indicações na figura a seguir. Qual é a árvore que apresenta a maior altura real?
Qual é a árvore que apresenta a maior altura real?
(A) I
(B) II
(C) III
(D) IV
(E) V
Resolução:
Sendo ℓ a medida do lado de cada quadrado, as alturas das árvores I, II, III, IV e V, são respectivamente: 900ℓ, 450ℓ, 900ℓ, 1350ℓ e 675ℓ.
Portanto, a árvore IV tem a maior altura real.
Alternativa: D
195) (ENEM) Em um jogo há duas urnas com 10 bolas de mesmo tamanho em cada urna. A tabela a seguir indica as quantidades de bolas de cada cor em cada urna. Uma jogada consiste em:
Uma jogada consiste em:
1º) o jogador apresenta um palpite sobre a cor da bola que será retirada por ele da urna 2;
2º) ele retira, aleatoriamente, uma bola da urna 1 e a coloca na urna 2, misturando-a com as que lá estão;
3º) em seguida ele retira, também aleatoriamente, uma bola da urna 2;
4º) se a cor da última bola retirada for a mesma do palpite inicial, ele ganha o jogo.
Qual cor deve ser escolhida pelo jogador para que ele tenha a maior probabilidade de ganhar?
(A) Azul.
(B) marela.
(C) Branca.
(D) Verde.
(E) Vermelha.
Resolução:
Após a transferência de uma bola da urna 1 para a urna 2, esta pode conter:
0 ou 1 bolas amarelas
1 ou 2 azuis
2 ou 3 brancas
3 ou 4 verdes
4 vermelhas
Um total de 11 bolas.
Sendo assim, a probabilidade de retirar uma vermelha será de 4/11, enquanto a probabilidade da verde será algum valor entre 3/11 e 4/11.
Assim, a probabilidade de ser retirada a bola vermelha é a maior.
Alternativa: E
196) (ENEM) Os hidrômetros são marcadores de consumo de água em residências e estabelecimentos comerciais. Existem vários modelos de mostradores de hidrômetros, sendo que alguns deles possuem uma combinação de um mostrador e dois relógios de ponteiro. O número formado pelos quatro primeiros algarismos do mostrador fornece o consumo em m3, e os dois últimos algarismos representam, respectivamente, as centenas e dezenas de litros de água consumidos. Um dos relógios de ponteiros indica a quantidade em litros, e o outro em décimos de litros, conforme ilustrados na figura a seguir. Considerando as informações indicadas na figura, o consumo total de água registrado nesse hidrômetro, em litros, é igual a
Considerando as informações indicadas na figura, o consumo total de água registrado nesse hidrômetro, em litros, é igual a
(A) 3 534,85.
(B) 3 544,20.
(C) 3 534 850,00.
(D)3 534 859,35.
(E)3 534 850,39.
Resolução:
No mostrador, temos: 3534 m³ = 3 534 000 ℓ, 8 centenas de litros = 800 ℓ e 5 dezenas de litros = 50 ℓ
Nos ponteiros, temos: 9 ℓ e 3,5 décimos de litro = 0,35 ℓ
Portanto, o consumo total de água indicado no hidrômetro, em litros, é:
3 534 000 + 800 + 50 + 9 + 0,35 = 3 534 859,35
Alternativa: D
197) (ENEM) O dono de uma farmácia resolveu colocar à vista do público o gráfico mostrado a seguir, que apresenta a evolução do total de vendas (em Reais) de certo medicamento ao longo do ano de 2011. De acordo com o gráfico, os meses em que ocorreram, respectivamente, a maior e a menor venda absolutas em 2011 foram
De acordo com o gráfico, os meses em que ocorreram, respectivamente, a maior e a menor venda absolutas em 2011 foram
(A) março e abril.
(B) março e agosto
(C) agosto e setembro
(D) junho e setembro
(E) junho e agosto
Resolução:
O eixo das ordenadas (eixo y) representa a venda, em reais, do medicamento e o eixo das abscissas (eixo x), os meses em que estas vendas foram efetuadas.
A linha vertical tracejada (no gráfico) é proporcional à quantidade vendida em cada mês, assim junho é o mês com maior venda, por apresentar maior ”y” e tamanho de sua linha. O mês de agosto apresenta menor “y” e tamanho de sua linha.
Alternativa: E
198) (ENEM) Jogar baralho é uma atividade que estimula o raciocínio. Um jogo tradicional é a Paciência, que utiliza 52 cartas. Inicialmente são formadas sete colunas com as cartas. A primeira coluna tem uma carta, a segunda tem duas cartas, a terceira tem três cartas, a quarta tem quatro cartas, e assim sucessivamente até a sétima coluna, a qual tem sete cartas, e o que sobra forma o monte, que são as cartas não utilizadas nas colunas.
A quantidade de cartas que forma o monte é
(A) 21
(B) 24
(C) 26
(D) 2
(E) 31
Resolução:
As cartas organizadas nas colunas formam uma PA de razão 1, (1,2,3,4,5,6,7). A soma desta PA pode ser calculada segundo a fórmula , sendo an o termo que ocupa a última posição e n o total de termos da PA.
Neste caso o monte é formado pelas cartas que sobraram 52 – 28 = 24.
Alternativa: B
199) (ENEM) O gráfico mostra a variação da extensão média de gelo marítimo, em milhões de quilômetros quadrados, comparando dados dos anos 1995, 1998, 2000, 2005 e 2007. Os dados correspondem aos meses de junho a setembro. O Ártico começa a recobrar o gelo quando termina o verão, em meados de setembro. O gelo do mar atua como o sistema de resfriamento da Terra, refletindo quase toda a luz solar de volta ao espaço. Águas de oceanos escuros, por sua vez, absorvem a luz solar e reforçam o aquecimento do Ártico, ocasionando derretimento crescente do gelo. Com base no gráfico e nas informações do texto, é possível inferir que houve maior aquecimento global em
Com base no gráfico e nas informações do texto, é possível inferir que houve maior aquecimento global em
(A) 1995.
(B) 1998.
(C) 2000.
(D)2005.
(E) 2007.
Resolução:
Quando o gelo marítimo tiver sua menor extensão, maior será o aquecimento, pois o gelo atua como sistema de resfriamento da Terra. De acordo com o gráfico, a menor extensão será em 2007.
Alternativa: E
200) (ENEM) Em exposições de artes plásticas, é usual que estátuas sejam expostas sobre plataformas giratórias. Uma medida de segurança é que a base da escultura esteja integralmente apoiada sobre a plataforma. Para que se providencie o equipamento adequado, no caso de uma base quadrada que será fixada sobre uma plataforma circular, o auxiliar técnico do evento deve estimar a medida R do raio adequado para a plataforma em termos da medida L do lado da base da estátua.
Qual relação entre R e L o auxiliar técnico deverá apresentar de modo que a exigência de segurança seja cumprida?
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
Resolução:
Para que a base quadrada seja fixada sobre a plataforma circular, o diâmetro do círculo deve ser maior ou igual à diagonal do quadrado de lado L. Logo, D ≥ L√2.
D = 2R ≥ L√2
R ≥ L√2/2
R ≥ L/√2
Alternativa: A
201) (ENEM) O globo da morte é uma atração muito usada em circos. Ele consiste em uma espécie de jaula em forma de uma superfície esférica feita de aço, onde motoqueiros andam com suas motos por dentro. A seguir, tem-se, na Figura 1, uma foto de um globo da morte e, na Figura 2, uma esfera que ilustra um globo da morte. Na Figura 2, o ponto A está no plano do chão onde está colocado o globo da morte e o segmento AB passa pelo centro da esfera e é perpendicular ao plano do chão. Suponha que há um foco de luz direcionado para o chão colocado no ponto B e que um motoqueiro faça um trajeto dentro da esfera, percorrendo uma circunferência que passa pelos pontos A e B.
Na Figura 2, o ponto A está no plano do chão onde está colocado o globo da morte e o segmento AB passa pelo centro da esfera e é perpendicular ao plano do chão. Suponha que há um foco de luz direcionado para o chão colocado no ponto B e que um motoqueiro faça um trajeto dentro da esfera, percorrendo uma circunferência que passa pelos pontos A e B.
A imagem do trajeto feito pelo motoqueiro no plano do chão é melhor representada por
(A) 
(B) 
(C) 
(D) 
(E) 
Resolução:
Se há um foco de luz direcionado para o chão colocado no ponto B, a imagem do trajeto feito pelo motoqueiro no plano do chão é mais bem representada por um segmento de reta ou, no limite, por uma reta. Entre as alternativas oferecidas, a única que satisfaz é a alternativa E.
Alternativa: E
202) (ENEM) Num projeto da parte elétrica de um edifício residencial a ser construído, consta que as tomadas deverão ser colocadas a 0,20 m acima do piso, enquanto os interruptores de luz deverão ser colocados a 1,47 m acima do piso. Um cadeirante, potencial comprador de um apartamento desse edifício, ao ver tais medidas, alerta para o fato de que elas não contemplarão suas necessidades. Os referenciais de alturas (em metros) para atividades que não exigem o uso de força são mostrados na figura seguinte. Uma proposta substitutiva, relativa às alturas de tomadas e interruptores, respectivamente, que atenderá àquele potencial comprador é
Uma proposta substitutiva, relativa às alturas de tomadas e interruptores, respectivamente, que atenderá àquele potencial comprador é
(A) 0,20 m e 1,45 m.
(B) 0,20 m e 1,40 m.
(C) 0,25 m e 1,35 m.
(D) 0,25 m e 1,30 m.
(E) 0,45 m e 1,20 m.
Resolução:
As tomadas devem ser colocadas a uma altura maior ou igual a 0,40 m.
Os interruptores devem ser colocados a uma altura menor ou igual a 1,35 m.
Alternativa: E
203) (ENEM) Uma pesquisa realizada por estudantes da Faculdade de Estatística mostra, em horas por dia, como os jovens entre 12 e 18 anos gastam seu tempo, tanto durante a semana (de segunda-feira a sexta-feira), como no fim de semana (sábado e domingo). A seguinte tabela ilustra os resultados da pesquisa. De acordo com esta pesquisa, quantas horas de seu tempo gasta um jovem entre 12 e 18 anos, na semana inteira (de segunda-feira a domingo), nas atividades escolares?
De acordo com esta pesquisa, quantas horas de seu tempo gasta um jovem entre 12 e 18 anos, na semana inteira (de segunda-feira a domingo), nas atividades escolares?
(A) 20
(B) 21
(C) 24
(D) 25
(E) 27
Resolução:
De acordo com a tabela, os estudantes passam 5 horas por dia estudando em cada um dos 5 dias da semana e 1 hora a cada dia no fim de semana. Assim estudam 5 . 5 + 1 . 2 = 27 horas por semana.
Alternativa: E
204) (ENEM) Certo vendedor tem seu salário mensal calculado da seguinte maneira: ele ganha um valor fixo de R$ 750,00, mais uma comissão de R$ 3,00 para cada produto vendido. Caso ele venda mais de 100 produtos, sua comissão passa a ser de R$ 9,00 para cada produto vendido, a partir do 101º produto vendido.
Com essas informações, o gráfico que melhor representa a relação entre salário e o número de produtos vendidos é
(A) 
(B) 
(C) 
(D) 
(E) 
Resolução:
O salário S em função de x, para:
1) 0 ≤ x ≤ 100, é S = 750 + 3 . x
2) x ≥ 101, é S = 1050 + 9 . (x – 100) = 9x + 150
Alternativa: E
205) (ENEM) Um maquinista de trem ganha R$ 100,00 por viagem e só pode viajar a cada 4 dias. Ele ganha somente se fizer a viagem e sabe que estará de férias de 1º a 10 de junho, quando não poderá viajar. Sua primeira viagem ocorreu no dia primeiro de janeiro. Considere que o ano tem 365 dias.
Se o maquinista quiser ganhar o máximo possível, quantas viagens precisará fazer?
(A) 37
(B) 51
(C) 88
(D) 89
(E) 91
Resolução:
Admitindo-se que cada viagem tenha duração de quatro dias e que o maquinista não pode retornar da viagem em período de férias, teremos:
1) de 1o de janeiro até 31 de maio, são 151 dias e neste período ele faz, no máximo, 37 viagens, pois 151 = 37 . 4 + 3
2) De 11 de junho até 31 de dezembro, são 204 dias e neste período ele faz, no máximo, 51 viagens, pois 204 = 51 . 4
3) No total, o número máximo de viagens é 37 + 51 = 88
Alternativa: C
206) (ENEM) Jorge quer instalar aquecedores no seu salão de beleza para melhorar o conforto dos seus clientes no inverno. Ele estuda a compra de unidades de dois tipos de aquecedores: modelo A, que consome 600 g/h (gramas por hora) de gás propano e cobre 35 m2 de área, ou modelo B, que consome 750 g/h de gás propano e cobre 45 m2 de área. O fabricante indica que o aquecedor deve ser instalado em um ambiente com área menor do que a da sua cobertura. Jorge vai instalar uma unidade por ambiente e quer gastar o mínimo possível com gás. A área do salão que deve ser climatizada encontra-se na planta seguinte (ambientes representados por três retângulos e um trapézio). Avaliando-se todas as informações, serão necessários
Avaliando-se todas as informações, serão necessários
(A) quatro unidades do tipo A e nenhuma unidade do tipo B.
(B) três unidades do tipo A e uma unidade do tipo B.
(C) duas unidades do tipo A e duas unidades do tipo B.
(D) uma unidade do tipo A e três unidades do tipo B.
(E) nenhuma unidade do tipo A e quatro unidades do tipo B.
Resolução:
Primeiro, devemos calcular a área de cada ambiente.
Aquele cuja área seja menor ou igual a 35 m², deve ser utilizado o aparelho do modelo A, pois cobrirá a área e será mais econômico na utilização do gás. Para os ambientes que tiverem área entre 35 e 45 m², o modelo B é o apropriado, apesar de gastar mais gás propano, é o que cobre a área.
Os ambientes I, II e III têm a forma retangular, suas áreas são calculadas pela fórmula A=b.h e o IV tem a forma de um trapézio, A= (B+b)⋅h/2 .
Assim:
AI = 8.5 = 40m²
AII= (14-8).5 = 6.5 = 30m²
AIII= 6.(9-5) = 6.4 = 24m²
AIV= (6+4)⋅72 = 10.72=35m²
Dessa maneira, o modelo A será utilizado nos ambientes II e III e o modelo B nos ambientes I e IV, obedecendo à indicação do fabricante de que “o aquecedor deve ser instalado em um ambiente com área menor do que a da sua cobertura”.
Alternativa: C
207) (ENEM) Para decorar a fachada de um edifício, um arquiteto projetou a colocação de vitrais compostos de quadrados de lado medindo 1 m, conforme a figura a seguir. Nesta figura, os pontos A, B, C e D são pontos médios dos lados do quadrado e os segmentos AP e QC medem 1/4 da medida do lado do quadrado. Para confeccionar um vitral, são usados dois tipos de materiais: um para a parte sombreada da figura, que custa R$ 30,00 o m², e outro para a parte mais clara (regiões ABPDA e BCDQB), que custa R$ 50,00 o m².
Nesta figura, os pontos A, B, C e D são pontos médios dos lados do quadrado e os segmentos AP e QC medem 1/4 da medida do lado do quadrado. Para confeccionar um vitral, são usados dois tipos de materiais: um para a parte sombreada da figura, que custa R$ 30,00 o m², e outro para a parte mais clara (regiões ABPDA e BCDQB), que custa R$ 50,00 o m².
De acordo com esses dados, qual é o custo dos materiais usados na fabricação de um vitral?
(A) R$ 22,50
(B) R$ 35,00
(C) R$ 40,00
(D) R$ 42,50
(E) R$ 45,00
Rsolução:
A área da região clara pode ser calculada através do quádruplo da área do triângulo APB, visto que os triângulos APB, APD, CQD e CQB são congruentes, possuindo mesmas áreas.
A área da região clara é igual à área da região sombreada e pode ser calculada através da diferença da área do quadrado pela área clara:
1-0,25 = 0,75m².
Calcula-se o preço do vitral através do produto da área de cada região pelo preço do m² correspondente.
Preço = 0,25.50 + 0,75 . 30 = 12,5 + 22,5 = 35 reais.
Alternativa: B
208) (ENEM) João decidiu contratar os serviços de uma empresa por telefone através do SAC (Serviço de Atendimento ao Consumidor). O atendente ditou para João o número de protocolo de atendimento da ligação e pediu que ele anotasse. Entretanto, João não entendeu um dos algarismos ditados pelo atendente e anotou o número 1 3 _ 9 8 2 0 7, sendo que o espaço vazio é o do algarismo que João não entendeu.
De acordo com essas informações, a posição ocupada pelo algarismo que falta no número de protocolo é a de
(A) centena.
(B) dezena de milhar.
(C) centena de milhar.
(D) milhão.
(E) centena de milhão.
Resolução:
A cada 3 algarismos forma-se uma classe. A cada classe, o algarismo mais a direita é o das unidades, o seguinte das dezenas e o mais a esquerda das centenas correspondente à classe. A primeira classe é a simples, a segunda do milhar, terceira do milhão e assim por diante. O algarismo que não foi entendido por João é o mais a esquerda da 2ª classe, portanto das centenas de milhar.
Alternativa: C
209) (ENEM) O gráfico fornece os valores das ações da empresa XPN, no período das 10 às 17 horas, num dia em que elas oscilaram acentuadamente em curtos intervalos de tempo. Neste dia, cinco investidores compraram e venderam o mesmo volume de ações, porém em horários diferentes, de acordo com a seguinte tabela.
Neste dia, cinco investidores compraram e venderam o mesmo volume de ações, porém em horários diferentes, de acordo com a seguinte tabela. Com relação ao capital adquirido na compra e venda das ações, qual investidor fez o melhor negócio?
Com relação ao capital adquirido na compra e venda das ações, qual investidor fez o melhor negócio?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
Resolução:
Calcula-se o ganho por ação de cada investidor através da diferença entre o valor da venda e o da compra. Os valores de compra e venda são retirados do gráfico de acordo com a hora em que foram efetuados. Aquele cujo valor for maior é o que fez o melhor negócio, uma vez que todos venderam a mesma quantidade de ações.
Investidor 1: 460 – 150 = 310
Investidor 2: 200 – 150 = 50
Investidor 3: 460 – 380 = 80
Investidor 4: 100 – 460 = -360 (prejuízo de R$ 360,00)
Investidor 5: 150 – 50 = 100
O maior valor é 310 reais, obtido pelo investidor 1.
Alternativa: A
210) (ENEM) A figura a seguir apresenta dois gráficos com informações sobre as reclamações diárias recebidas e resolvidas pelo Setor de Atendimento ao Cliente (SAC) de uma empresa, em uma dada semana. O gráfico de linha tracejada informa o número de reclamações recebidas no dia, o de linha contínua é o número de reclamações resolvidas no dia. As reclamações podem ser resolvidas no mesmo dia ou demorarem mais de um dia para serem resolvidas. O gerente de atendimento deseja identificar os dias da semana em que o nível de eficiência pode ser considerado muito bom, ou seja, os dias em que o número de reclamações resolvidas excede o número de reclamações recebidas.
O gerente de atendimento deseja identificar os dias da semana em que o nível de eficiência pode ser considerado muito bom, ou seja, os dias em que o número de reclamações resolvidas excede o número de reclamações recebidas.
O gerente de atendimento pôde concluir, baseado no conceito de eficiência utilizado na empresa e nas informações do gráfico, que o nível de eficiência foi muito bom na
(A) segunda e na terça-feira.
(B) terça e na quarta-feira.
(C) terça e na quinta-feira.
(D) quinta-feira, no sábado e no domingo.
(E) segunda, na quinta e na sexta-feira.
Resolução:
Verifica-se em cada vertical, aquelas que os pontos correspondentes da linha contínua (reclamações resolvidas) estão acima da linha tracejada (ligações recebidas).
Isso ocorre na terça e na quarta feira.
Alternativa: B
211) (ENEM) Uma mãe recorreu à bula para verificar a dosagem de um remédio que precisava dar a seu filho. Na bula, recomendava-se a seguinte dosagem: 5 gotas para cada 2 kg de massa corporal a cada 8 horas.
Se a mãe ministrou corretamente 30 gotas do remédio a seu filho a cada 8 horas, então a massa corporal dele é de
(A) 12 kg.
(B) 16 kg.
(C) 24 kg.
(D) 36 kg.
(E)75 kg.
Resolução:
A proporção recomendada da dosagem a cada 8 horas é de 5 gotas/2 kg de massa corporal (valor base) e a mãe ministrou corretamente 30 gotas a cada 8 horas.
Como a quantidade de gotas foi o sêxtuplo do valor base (5.6 = 30), seu filho tem o sêxtuplo de massa referente ao valor base (2 kg), 2.6 = 12 kg.
Alternativa: A
212) (ENEM) João propôs um desafio a Bruno, seu colega de classe: ele iria descrever um deslocamento pela pirâmide a seguir e Bruno deveria desenhar a projeção desse deslocamento no plano da base da pirâmide. O deslocamento descrito por João foi: mova-se pela pirâmide, sempre em linha reta, do ponto A ao ponto E, a seguir do ponto E ao ponto M, e depois de M a C.
O deslocamento descrito por João foi: mova-se pela pirâmide, sempre em linha reta, do ponto A ao ponto E, a seguir do ponto E ao ponto M, e depois de M a C.
O desenho que Bruno deve fazer é
(A) 
(B) 
(C) 
(D) 
(E) 
Resolução:
O único ponto mencionado que não pertence a base é o ponto E, logo deve ser projetado em relação à base. Sua projeção é feita a partir de uma reta perpendicular a base passando pelo ponto E, sendo o centro da base. A projeção do trajeto descrito por João vai do vértice A a projeção do ponto E, centro da figura, passando pelo ponto médio (M) do outro lado da base, seguindo até o vértice C, sempre em linha reta.
Alternativa: E
213) (ENEM) As curvas de oferta e de demanda de um produto representam, respectivamente, as quantidades que vendedores e consumidores estão dispostos a comercializar em função do preço do produto. Em alguns casos, essas curvas podem ser representadas por retas. Suponha que as quantidades de oferta e de demanda de um produto sejam, respectivamente, representadas pelas equações: em que QO é quantidade de oferta, QD é a quantidade de demanda e P é o preço do produto.
em que QO é quantidade de oferta, QD é a quantidade de demanda e P é o preço do produto.
A partir dessas equações, de oferta e de demanda, os economistas encontram o preço de equilíbrio de mercado, ou seja, quando QO e QD se igualam.
Para a situação descrita, qual o valor do preço de equilíbrio?
(A) 5
(B) 11
(C) 13
(D) 23
(E) 33
Resolução:
Sendo Q0 = – 20 + 4P e QD = 46 – 2P, o preço de equilí –
brio se obtém para Q0 = QD.
Logo:
– 20 + 4P = 46 – 2P ⇔ P = 11
Alternativa: B
214) (ENEM) Nos shopping centers costumam existir parques com vários brinquedos e jogos. Os usuários colocam créditos em um cartão, que são descontados por cada período de tempo de uso dos jogos. Dependendo da pontuação da criança no jogo, ela recebe um certo número de tíquetes para trocar por produtos nas lojas dos parques. Suponha que o período de uso de um brinquedo em certo shopping custa R$ 3,00 e que uma bicicleta custa 9 200 tíquetes.
Para uma criança que recebe 20 tíquetes por período de tempo que joga, o valor, em reais, gasto com créditos para obter a quantidade de tíquetes para trocar pela bicicleta é
(A) 153.
(B) 460.
(C) 1 218.
(D) 1 380.
(E) 3 066.
Resolução:
Primeiro, precisamos calcular o total de períodos (n) que precisam ser jogados para que a criança obtenha os 9 200 tíquetes.
Como ela ganha 20 por período jogado, e cada período jogado custa 3 reais, o total gasto é de 460 x 3 = 1380 reais.
Alternativa: D
215) (ENEM) Dentre outros objetos de pesquisa, a Alometria estuda a relação entre medidas de diferentes partes do corpo humano. Por exemplo, segundo a Alometria, a área A da superfície corporal de uma pessoa relaciona-se com a sua massa m pela fórmula A = k⋅m2/3, em que k é uma constante positiva.
Se no período que vai da infância até a maioridade de um indivíduo sua massa é multiplicada por 8, por quanto será multiplicada a área da superfície corporal?
(A) ∛16
(B) 4
(C) √24
(D) 8
(E) 64
Resolução:
Sendo A a área da superfície corporal de uma pessoa na infância e S a área da superfície corporal dessa mesma pessoa na maioridade, de acordo com o enunciado, tem-se:
A = k⋅m2/3 e S = k⋅(8m)2/3 = k⋅82/3m2/3
Assim:
S/A = (k⋅82/3m2/3)/(k⋅m2/3) = 82/3 = (2³)2/3 = 2² = 4.
Alternativa: B
216) (ENEM) Um aluno registrou as notas bimestrais de algumas de suas disciplinas numa tabela. Ele observou que as entradas numéricas da tabela formavam uma matriz 4×4, e que poderia calcular as médias anuais dessas disciplinas usando produto de matrizes. Todas as provas possuíam o mesmo peso, e a tabela que ele conseguiu é mostrada a seguir. Para obter essas médias, ele multiplicou a matriz obtida a partir da tabela por
Para obter essas médias, ele multiplicou a matriz obtida a partir da tabela por
(A) 
(B) 
(C) ![]()
(D) 
(E) 
Resolução:
Para calcular a média aritmética de quatro notas, devemos somar as quatro notas e dividi-la por 4. A matriz 4×4 obtida pelas notas deve ser multiplicada por uma matriz coluna 4×1, no qual cada um dos quatro elementos é igual 1/4.
Alternativa: E
217) (ENEM) Existem no mercado chuveiros elétricos de diferentes potências, que representam consumos e custos diversos. A potência (P) de um chuveiro elétrico é dada pelo produto entre sua resistência elétrica (R) e o quadrado da corrente elétrica (i) que por ele circula. O consumo de energia elétrica (E), por sua vez, é diretamente proporcional à potência do aparelho.
Considerando as características apresentadas, qual dos gráficos a seguir representa a relação entre a energia consumida (E) por um chuveiro elétrico e a corrente elétrica (i) que circula por ele?
(A) 
(B) 
(C) 
(D) 
(E) 
Resolução:
Como a energia (E) é diretamente proporcional à potência e a potência é diretamente proporcional ao quadrado da intensidade de corrente (i), a energia também é diretamente proporcional ao quadrado da intensidade de corrente.
Alternativa: D
218) (ENEM) Em 20 de fevereiro de 2011 ocorreu a grande erupção do vulcão Bulusan nas Filipinas. A sua localização geográfica no globo terrestre é dada pelo GPS (sigla em inglês para Sistema de Posicionamento Global) com longitude de 124° 3’ 0” a leste do Meridiano de Greenwich.
Dado: 1° equivale a 60’ e 1’ equivale a 60”.
A representação angular da localização do vulcão com relação a sua longitude na forma decimal é
(A) 124,02°.
(B) 124,05°.
(C) 124,20°.
(D) 124,30°.
(E) 124,50°.
Resolução:
Com os dados do enunciado, o cálculo é feito da seguinte maneira:
124° 3′ 0” = 124° + 3’/60 = 124° + 0,05° = 124,05°
Alternativa: B
219) (ENEM) A Agência Espacial Norte Americana (NASA) informou que o asteroide YU 55 cruzou o espaço entre a Terra e a Lua no mês de novembro de 2011. A ilustração a seguir sugere que o asteroide percorreu sua trajetória no mesmo plano que contém a órbita descrita pela Lua em torno da Terra. Na figura, está indicada a proximidade do asteroide em relação à Terra, ou seja, a menor distância que ele passou da superfície terrestre. Com base nessas informações, a menor distância que o asteroide YU 55 passou da superfície da Terra é igual a
Com base nessas informações, a menor distância que o asteroide YU 55 passou da superfície da Terra é igual a
(A) 3,25 × 102 km.
(B) 3,25 × 103 km.
(C) 3,25 × 104 km.
(D) 3,25 × 105 km.
(E) 3,25 × 106 km.
Resolução:
Colocando em notação científica a menos distância que o asteróide YU 55 passou pela superfície da Terra, teremos:
325 mil km = 325 000 km = 3,25 x 105 km
Alternativa: D
220) (ENEM) Há, em virtude da demanda crescente de economia de água, equipamentos e utensílios como, por exemplo, as bacias sanitárias ecológicas, que utilizam 6 litros de água por descarga em vez dos 15 litros utilizados por bacias sanitárias não ecológicas, conforme dados da Associação Brasileira de Normas Técnicas (ABNT).
Qual será a economia diária de água obtida por meio da substituição de uma bacia sanitária não ecológica, que gasta cerca de 60 litros por dia com a descarga, por uma bacia sanitária ecológica?
(A) 24 litros
(B) 36 litros
(C) 40 litros
(D) 42 litros
(E) 50 litros
Resolução:
Bacia não ecológica
15 litros gastos ——– 1 descarga
60 litros gastos ——- x descargas
X = 60/15 = 4 descargas
Bacia ecológica
6 litros gastos ——– 1 descarga
y litros gastos ——- 4 descargas
y = 6*4 = 24 litros gastos
Economia diária: 60 – 24 = 36 litros
Alternativa: B
221) (ENEM) A tabela a seguir mostra a evolução da receita bruta anual nos três últimos anos de cinco microempresas (ME) que se encontram à venda. Um investidor deseja comprar duas das empresas listadas na tabela. Para tal, ele calcula a média da receita bruta anual dos últimos três anos (de 2009 até 2011) e escolhe as duas empresas de maior média anual.
Um investidor deseja comprar duas das empresas listadas na tabela. Para tal, ele calcula a média da receita bruta anual dos últimos três anos (de 2009 até 2011) e escolhe as duas empresas de maior média anual.
As empresas que este investidor escolhe comprar são
(A) Balas W e Pizzaria Y.
(B) Chocolates X e Tecelagem Z.
(C) Pizzaria Y e Alfinetes V.
(D) Pizzaria Y e Chocolates X.
(E) Tecelagem Z e Alfinetes V.
Resolução:
As médias das três últimas receitas brutas das empresas fora:
Alfinetes V: (200 + 220 + 240)/3 = 220
Balas W = (200 + 230 + 200)/3 = 210
Chocolates X = (250 + 210 + 215)/3 = 225
Pizzaria Y = (230 +230 + 230)/3 = 230
Tecelagem Z = (160 + 210 + 245)/3 = 205
As duas empresas de maior média anual nas três últimas receitas brutas são Pizzaria Y e Chocolates X .
Alternativa: D
222) (ENEM) Um laboratório realiza exames em que é possível observar a taxa de glicose de uma pessoa. Os resultados são analisados de acordo com o quadro a seguir. Um paciente fez um exame de glicose nesse laboratório e comprovou que estava com hiperglicemia. Sua taxa de glicose era de 300 mg/dL. Seu médico prescreveu um tratamento em duas etapas. Na primeira etapa ele conseguiu reduzir sua taxa em 30% e na segunda etapa em 10%.
Um paciente fez um exame de glicose nesse laboratório e comprovou que estava com hiperglicemia. Sua taxa de glicose era de 300 mg/dL. Seu médico prescreveu um tratamento em duas etapas. Na primeira etapa ele conseguiu reduzir sua taxa em 30% e na segunda etapa em 10%.
Ao calcular sua taxa de glicose após as duas reduções, o paciente verificou que estava na categoria de
(A) hipoglicemia.
(B) normal.
(C) pré-diabetes.
(D) diabetes melito.
(E) hiperglicemia.
Resolução:
Na primeira etapa foi reduzido para:
300 mg/dL ———— 100%
x mg/dL ———— (100-30)%
x = (300 . 70) / 100
x = 210 mg/dL
Na segunda etapa foi reduzido para:
210 mg/dL ———— 100%
y mg/dL ———— (100-10)%
x = (210 . 90) / 100
x = 189 mg/dL
Assim, 189 mg/dL está entre 125 mg/dl e 250 ml/dL, se encaixando na categoria Diabetes Melito.
Alternativa: D
223) (ENEM) O designer português Miguel Neiva criou um sistema de símbolos que permite que pessoas daltônicas identifiquem cores. O sistema consiste na utilização de símbolos que identificam as cores primárias (azul, amarelo e vermelho). Além disso, a justaposição de dois desses símbolos permite identificar cores secundárias (como o verde, que é o amarelo combinado com o azul). O preto e o branco são identificados por pequenos quadrados: o que simboliza o preto é cheio, enquanto o que simboliza o branco é vazio. Os símbolos que representam preto e branco também podem estar associados aos símbolos que identificam cores, significando se estas são claras ou escuras.
De acordo com o texto, quantas cores podem ser representadas pelo sistema proposto?
(A) 14
(B) 18
(C) 20
(D) 21
(E) 23
Resolução:
Pra identificação das cores primárias são definidas 3 cores.
A partir da justaposição das 3 cores, 2 a 2, temos as seguintes possibilidades:
Assim, somadas, temos 6 possibilidades de cores primárias e secundárias que podem ser ainda associadas com quadrados que identificam se são claras ou escuras. Contabilizando, temos: 6 . 3 = 18 possibilidades
Ainda devemos contabilizar as cores: preto e branco (2 possibilidades)
No total temos: 18 + 2 = 20 possibilidades
Alternativa: C
224) (ENEM) José, Paulo e Antônio estão jogando dados não viciados, nos quais, em cada uma das seis faces, há um número de 1 a 6. Cada um deles jogará dois dados simultaneamente. José acredita que, após jogar seus dados, os números das faces voltadas para cima lhe darão uma soma igual a 7. Já Paulo acredita que sua soma será igual a 4 e Antônio acredita que sua soma será igual a 8.
Com essa escolha, quem tem a maior probabilidade de acertar sua respectiva soma é
(A) Antônio, já que sua soma é a maior de todas as escolhidas.
(B) José e Antônio, já que há 6 possibilidades tanto para a escolha de José quanto para a escolha de Antônio, e há apenas 4 possibilidades para a escolha de Paulo.
(C) José e Antônio, já que há 3 possibilidades tanto para a escolha de José quanto para a escolha de Antônio, e há apenas 2 possibilidades para a escolha de Paulo.
(D) José, já que há 6 possibilidades para formar sua soma, 5 possibilidades para formar a soma de Antônio e apenas 3 possibilidades para formar a soma de Paulo.
(E) Paulo, já que sua soma é a menor de todas.
Resolução:
Paulo:
Para somar 4 temos as seguintes 3 possibilidades: (1; 3), (2; 2) e (3; 1).
João:
Para somar 7 temos as seguintes 6 possibilidades: (1; 6), (2; 5), (3; 4), (4; 3), (5; 2) e (6; 1).
Antônio
Para somar 8 temos as seguintes 5 possibilidades: (2; 6), (3; 5), (4; 4), (5; 3) e (6; 2).
Quem tem a maior probabilidade de acertar sua respectiva soma é João, pois para a sua soma, tem-se 6 possibilidades.
Alternativa: D
225) (ENEM) O gráfico apresenta o comportamento de emprego formal surgido, segundo o CAGED, no período de janeiro de 2010 a outubro de 2010. Com base no gráfico, o valor da parte inteira da mediana dos empregos formais surgidos no período é
Com base no gráfico, o valor da parte inteira da mediana dos empregos formais surgidos no período é
(A) 212 952.
(B) 229 913.
(C) 240 621.
(D) 255 496.
(E) 298 041.
Resolução:
Em ordem crescente temos:
181.419, 181.796, 204.804, 209.425, 212.952, 246.875, 266.415, 298. 041, 299. 415 e 305.068.
Para o cálculo da mediana devemos pegar os valores centrais e realizar uma média aritmética entre eles, assim:
Termos centrais = 212.952 e 246.875
md = (212.952 + 246.875)/2 = 229.913,5
A parte inteira desse valor é 229.913.
Alternativa: B
226) (ENEM) A cerâmica possui a propriedade da contração, que consiste na evaporação da água existente em um conjunto ou bloco cerâmico submetido a uma determinada temperatura elevada: em seu lugar aparecendo “espaços vazios” que tendem a se aproximar. No lugar antes ocupado pela água vão ficando lacunas e, consequentemente, o conjunto tende a retrair-se. Considere que no processo de cozimento a cerâmica de argila sofra uma contração, em dimensões lineares, de 20%.
Levando em consideração o processo de cozimento e a contração sofrida, o volume V de uma travessa de argila, de forma cúbica de aresta a, diminui para um valor que é
(A) 20% menor que V, uma vez que o volume do cubo é diretamente proporcional ao comprimento de seu lado.
(B) 36% menor que V, porque a área da base diminui de a2 para ((1 − 0,2)a)².
(C) 48,8% menor que V, porque o volume diminui de a3 para (0,8a)³.
(D) 51,2% menor que V, porque cada lado diminui para 80% do comprimento original.
(E) 60% menor que V, porque cada lado diminui 20%.
Resolução:
No cubo de aresta a, seu volume será V = a3
Após o cozimento teremos:
a ——— 100%
x ——– (100-20)%
x= (80a)/100 = 0,8a (nova medida da aresta do cubo)
Assim seu novo volume será: V’ = (0,8a)3 = 0,512a3
a3 ———— 100%
0,512a3 ———— y%
y = (0,512a3 . 100)/a3 = 51,2%
Assim a diminuição representa: (100% – 51,2%) = 48,8 %, ou seja V’ é 48,8% menor que V.
Alternativa: C
Fim...






