Professor Diminoi
JUROS SIMPLES
Os juros simples são mais comuns em operações financeiras de curto prazo, onde a taxa de juros é aplicada apenas uma vez durante o período.
Juro simples é calculado tendo como base o valor inicial, conhecido como capital, a taxa de juro e o tempo.
J = C . i . t
Onde:
J = juro
C = capital
i = taxa
t = tempo
Observação: a taxa (i) por ser em porcentagem (%) o ideal e dividir o valor por 100 antes de aplicar na fórmula.
MONTANTE
O montante é outro conceito muito importante no estudo do juro simples. O montante o valor do capital somado ao juro.
M = C + J
Onde:
M = montante
C = capital
J = juros
QUESTÕES RESOLVIDAS
01) Qual o valor do montante produzido por um capital de R$ 1.200,00, aplicado no regime de juros simples a
uma taxa mensal de 2% durante 10 meses?
Resolução:
C = 1200
i = 2% = 2/100 = 0,02 ao mês (a.m.)
t = 10 meses
Juros:
J = C . i . t
J = 1200 . 0,02 . 10
J = 240
Montante:
M = C + j
M = 1200 + 240
M = 1440
Resposta: o montante produzido é de R$ 1.440,00.
02) Determine o valor do capital que, aplicado durante 14 meses a uma taxa de 6%, rendeu juros de R$ 2.688,00.
Resolução:
J = C . i . t
2688 = C . 0,06 . 14
2688 = C . 0,84
C = 2688 / 0,84
C = 3200
Resposta: o valor do capital é de R$ 3.200,00.
03) Qual o capital que, aplicado a juros simples de 1,5% ao mês, rende R$ 3.000,00 de juros em 45 dias?
Resolução:
J = 3000
i = 1,5% = 1,5/100 = 0,015
t = 45 dias = 45/30 = 1,5
J = C . i . t
3000 = C . 0,015 . 1,5
3000 = C . 0,0225
C = 3000 / 0,0225
C = 133.333,33
Resposta: o capital é de R$ 133.333,33.
04) Qual foi o capital que, aplicado à taxa de juros simples de 2% ao mês, rendeu R$ 90,00 em um trimestre?
Resolução:
J = C . i . t
90 = C . 0,02 . 3
90 = C . 0,06
C = 90 / 0,06
C = 1500
Resposta: o capital corresponde a R$ 1.500,00.
08) Uma pessoa aplicou o capital de R$ 1.200,00 a uma taxa de 2% ao mês durante 14 meses. Determine os
juros e o montante dessa aplicação.
Resolução:
C = R$ 1.200,00
t = 14 meses
i = 2% ao mês = 2/100 = 0,02
J = C . i . t
J = 1200 . 0,02 * 14
J = 336
Montante
M = C + J
M = 1200 + 336
M = 1536
Resposta: O valor dos juros da aplicação é de R$ 336,00 e o montante a ser resgatado é de R$ 1.536,00.
09) Determine a que taxa de juros simples um capital de 500 reais, aplicado durante 10 meses, produz 150 reais de juros.
Resolução:
Seja de 150 reais em 10 meses. Para isso, vamos substituir os dados na fórmula do juros simples:
J = C . i . t
150 = 500 . i . 10
150 = 5000 · i
Para deixar a taxa em sua forma percentual, devemos multiplicar o número encontrado por 100, assim:
0,03 ·100
3 %
Portanto, a taxa que deve ser imposta ao capital de 500 reais, durante 10 meses, para gerar um juros de 150 reais, é de 3% ao mês.
13) Um investidor aplica R$ 1.000,00 a juros simples de 3% ao mês. Determine o valor recebido após um ano:
Resolução:
P = 1.000,00
I = 3% ou 0,03
n = 1 ano = 12 meses
J = P . i . n
J = 1000 . 0,03. 12
J = 360
O juro obtido será de 360, somando-se ao capital, temos:
M = P + j
M = 1000 + 360
M = 1.360,00
Resolução: após um ano o investidor recebeu R$ 1.360,00.
14) (Termomecânica) Uma pessoa aplica R$ 5.400,00 à taxa de 12,5% ao ano, em regime de juros simples.
Para que esse capital seja duplicado, o tempo de aplicação deve ser de
(A) 6 meses.
(B) 8 meses.
(C) 7,5 anos.
(D) 8 anos.
(E) 8,5 anos.
Resolução:
J =
c = 5 400,00
i = 12,5
t = 1
J = c . i . t
j = 5 400 . 12,5 . 1/100
j = 675
675 . 8 = 5 400
Alternativa: D
15) Num balancete de uma empresa consta que certo capital foi aplicado a uma taxa de 30% ao ano durante 8 meses, rendendo juros simples no valor de R$ 192,00. O capital aplicado foi de:
(A) R$ 288,00.
(B) R$ 880,00.
(C) R$ 960,00.
(D) R$ 2.880,00.
Resolução:
Dados:
i = 30% ao ano;
t = 8 meses;
J = 192,00.
Note que o tempo e a taxa estão em unidades de medida diferentes. Vamos transformar a taxa de 30% ao ano para uma taxa mensal. Como o ano possui 12 meses, então 30% : 12 = 2,5%.
i = 2,5% a.m
Agora, substituindo na fórmula, temos que:
J = C · i · t
192 = C · 0,025 · 8
192 = 0,2 C
C = 192 / 0,2
C = 960
Alternativa: C
16) Ao completar seus 18 anos e adquirir sua independência financeira, João decidiu alugar um imóvel. Uma prática bastante comum para o aluguel de imóveis é o uso do devedor solidário ou então o pagamento de um cheque caução. Ambas as opções são para resguardar quem está alugando o imóvel. A primeira delas consiste em uma terceira pessoa se responsabilizar pelas dívidas caso o locatário não pague. A segunda é o pagamento, por parte do locatário, de um valor, que fica na conta do locador até o término do contrato. Ao final, esse valor é devolvido para o locatário.
Como não havia ninguém disposto a ser devedor solidário, João optou pela segunda opção, pegando dinheiro emprestado com o seu irmão, José. O empréstimo foi de R$ 3.000,00 e, para que José não ficasse em desvantagem, ele propôs para o seu irmão que o pagasse com juros simples de 1% a.m. Se, ao final de 1 ano, João pagar a sua dívida com o seu irmão, o valor pago por ele será de:
(A) R$ 3600,00.
(B) R$ 3360,00.
(C) R$ 3660,00.
(D) R$ 3930,00.](e) R$ 3036,00.
Resolução:
Dados:
C = 3.000,00;
i = 1% a.m. → 0,01;
t = 1 ano → 12 meses.
J = C · i · t
J = 3.000 · 0,01 · 12
J = 30 · 12
J = 360,00
O valor pago será o valor do empréstimo mais o juros:
3000,00 + 360,00 = 3360,00
Alternativa: B
17) Durante quanto tempo um capital deve ser mantido em investimento a juros simples com taxa de 2% a.m. para que ele gere um montante que seja o dobro do capital investido?
(A) 3 anos e 4 meses.
(B) 3 anos e 6 meses.
(C) 3 anos e 9 meses.
(D) 4 anos.
(E) 4 anos e 2 meses.
Resolução:
Se o montante será o dobro do capital, então M = 2C, logo o juro deve ser igual ao capital, ou seja, J = C.
J = C· i · t
C = C· 0,02 · t
Isolando o t, temos que:
C/C = 0,02t
1 = 0,02t
t= 1/0,02
t = 50 meses.
50 meses correspondem a 4 anos e 2 meses.
Alternativa: E
18) (Cespe) No regime de juros simples, determinado capital investido durante 2,5 meses produziu o montante de R$ 12.000,00. O mesmo capital, investido durante 5 meses, no mesmo regime de juros, produziu o montante de R$ 14.000,00. Nesse caso, é correto afirmar que esse capital é
(A) inferior a R$ 9.400,00.
(B) superior a R$ 9.400,00 e inferior a R$ 9.800,00.
(C) superior a R$ 9.800,00 e inferior a R$ 10.200,00.
(D) superior a R$ 10.200,00 e inferior a R$ 10.600,00.
(E) superior a R$ 10.600,00.
Resolução:
Sabemos que, em 2,5 meses, o montante é de R$ 12.000,00 e que, em 5 meses, esse montante é de R$ 14.000,00. Por outro lado, sabemos que a diferê3nça entre 2,5 e 5 é igual a 2,5 meses e que, nesse tempo a mais, a diferença entre montante gerado com 5 meses e o montante gerado com 2,5 meses é de 14.000 – 12.000 = 2.000. Isso significa que, em 2,5 meses, o juro gerado é de 2.000. Sendo assim, sabemos que o montante é a soma do capital com os juros e que o montante é 12.000, então temos que:
M = C + J
12.000 = C + 2.000
12.000 – 2.000 = C
C = 10.000
Alternativa: C
19) Um capital foi aplicado a juros simples com taxa de 5% ao mês, durante cinco meses. Se no fim desse período o juro produzido foi de R$ 152,25, qual foi o montante ao término da aplicação?
(A) R$ 761,25.
(B) R$590,75.
(C) R$609,00.
(D) R$706,12.
(E) R$ 692,30.
Resolução:
Dados:
t = 5 meses;
i = 5% a.m.;
J = 152,25.
Primeiro encontraremos o capital substituindo na fórmula os valores conhecidos:
J = C · i · t
152,25 = C · 0,05 · 5
152,25 = C · 0,25
152,25/0,25 = C
C = 609,00
Agora que sabemos o capital, somaremos os juros a esse valor:
609 + 152,25 = 761,25
Alternativa: A
20) (FGV) Um capital aplicado a juros simples produz o montante de R$ 7.200,00 em cinco meses e, em oito meses, esse montante passa a valer R$ 7.680,00.
Nessas condições, a taxa de juros aplicada a esse capital é de:
(A) 2,20% a.m.
(B) 2,25% a.m.
(C) 2,36% a.m.
(D) 2,44% a.m.
(E) 2,50% a.m.
Resolução:
Primeiro vamos calcular a diferença entre as duas situações. Faremos, então, a diferença entre o tempo: 8 – 5 = 3 meses. Em 3 meses, esse capital gerou juros de 7.680 – 7.200 = 480, ou seja, em 3 meses, os juros são R$ 480,00. Realizando a divisão 480 : 3 =160, sabemos que, em cada mês, o juro é de R$ 160,00.
Sabemos também que, em 5 meses, o juro é de 5 · 160 = 800 e que o montante é de 7.200,00, então o capital investido foi de 7.200 – 800 = 6.400. Agora, para encontrar a taxa de juros, faremos o seguinte:
J = C · i · t
800 = 6.400 · i ·5
800 = 32.000i
i = 800/32.000
i = 0,025 = 2,5% a.m.
Alternativa: E
21) Nos boletos de contas, além da data de vencimento, há também as informações sobre os juros a serem cobrados caso haja atraso no pagamento da conta. Uma determinada conta havia informações de que, no caso de atraso, seriam cobrados 2% de multa mais 1% a cada mês de atraso em cima do valor inicial da dívida.
Se em um determinado período uma conta nessas condições ficou atrasada durante 3 meses e o valor pago por ela foi de R$ 868,35, o valor da conta anterior aos juros e à multa é de:
(A) R$ 800,00.
(B) R$ 815,00.
(C) R$819,00.
(D) R$827,00.
(E) R$832,00.
Resolução:
Utilizaremos:
M = montante final pago
C = valor da conta
V = valor da multa
J = juros
M = C + J + V
Sabemos que V = 2% de C, então V = 0,02C.
Já os juros podem ser calculados com os dados t = 3 meses e i = 1% a.m.
J = C · i · t
J = C · 0,01 · 3
J = 0,03C
Então, temos que o montante pago M é:
M = C + J + V
Sabemos o valor pago, que foi de 868,35, temos que:
M = 868,35
868,35 = C + J + V
J = 0,03C e V = 0,02C
868,35 = C+ 0,03C + 0,02C
868,35 = 1,05C
C= 868,35 / 1,05
C = 827,00
Alternativa: D
22) Para completar a compra de um carro, Júlia pegou emprestado de sua amiga R$ 10.000,00 e pagou, ao final, R$ 12.250,00. Sabendo que a taxa de juros da operação empregada foi 2,5% a.m., quanto tempo Júlia levou para pagar sua amiga?
(A) 6 meses.
(B) 7 meses.
(C) 8 meses.
(D) 9 meses.
(E) 10 meses.
Resolução:
Dados:
i = 2,5% a.m
C = 10.000
M = 12.250
Primeiro vamos encontrar o juro gerado calculando a diferença entre o montante e o capital.
J = M – C
J = 12.250 – 10.000 = 2.250
Conhecendo o valor do juro, basta substituir os valores já conhecidos na fórmula:
J = C · i · t
2.250 = 10.000 · 0,025 · t
2.250 = 250t
t = 2.250 / 250
t = 9 meses
Alternativa: D
23) Qual deve ser o capital aplicado a uma taxa de juros simples de 10% a.a. para que, em 6 meses, renda R$ 217,50 de juro?
(A) R$ 4350,00.
(B) R$ 453,00.
(C) R$ 3.750,00.
(D) R$ 3.575,00.
(E) R$ 345,00.
Resolução:
Dados:
J = 217,50
i = 10% a.a.
t = 6 meses → 0,5 ano
Utilizando a fórmula:
J = C · i · t
217,50 = C · 0,1 · 0,5
217,50 = 0,05C
C = 217,50 / 0,05
C = 4.350,00
Alternativa: A
24) Alguns amigos se juntaram para fazer um investimento, e cada um realizou o investimento de R$ 2100,00. Esse dinheiro foi investido pelo organizador e, após 8 meses, todos os membros receberam de volta o seu dinheiro mais o valor do rendimento. Sabendo que cada um deles recebeu R$ 2604,00, qual foi a taxa de juros ao mês caso esse valor tenha sido investido em um regime de juros simples?
(A) 2% a.m.
(B) 3% a.m.
(C) 4% a.m.
(D) 5% a.m.
(E)6% a.m.
Resolução:
Dados:
M = 2.604
J = 2.100
t = 8 meses
Primeiro vamos calcular os juros:
J = M – C
J = 2604 – 2100 = 504
J = C · i · t
504 = 2100 · i · 8
504 = 16.800i
i = 504 / 16.800
i = 0,03 → 3 %
Alternativa: B
25) Uma mesa digitalizadora é vendida à vista no valor de R$ 600,00 ou a prazo por R$ 675,00. Caso o cliente opte pela segunda opção, ele precisa dar uma entrada de R$ 100,00 e pagar o restante após 1 mês. Nesse caso, a taxa de juros mensal que é cobrada pelo valor pago a prazo é de:
(A) 5%.
(B) 10%.
(C) 12%.
(D) 15%.
(E) 20%.
Resolução:
Para encontrar a taxa de juros, sabemos que o cliente precisa dar uma entrada de R$ 100,00 para o produto, restando uma dívida de 600 – 100 = R$ 500,00 em relação ao preço à vista; porém, com os juros, esse valor vai para 575, ou seja, 75 reais de juros em um mês. Então, temos que:
J = 75
t = 1 mês
C = 500
J = C · i · t
75 = 500· i · 1
75 = 500i
i = 75 / 500
i = 0,15
Alternativa: D
26) (IFMG) Chiquinho aplicou a quantia de R$ 500,00 a juros simples durante 6 meses. A taxa de aplicação foi de 5% ao mês. O montante obtido foi de:
(A) R$ 650,00.
(B) R$ 700,00.
(C) R$ 750,00.
(D) R$ 800,00.
Resolução:
Dados:
C = 500
t = 6 meses
i = 5% a.m
J = C · i · t
J = 500 · 0,05 · 6
J = 25 · 6
J = 150
Agora encontraremos o montante:
M = J + C
M = 150 + 500
M = 650
Alternativa: A
27) Um capital de R$ 600,00 foi investido em tesouro direto, com uma taxa de 12% a.a. para ser retirado após 5 anos. Qual será o juro ao final desse tempo?
Resolução:
Dados:
C = 600
i = 12% a.a.
t = 5 anos
Para calcular o juro, escreveremos a taxa de 12% como um número decimal, pois sabemos que 12% são equivalentes a 0,12.
J = C . i . t
J = 600 . 0,12 . 5
J = 72 ∙ 5
J = 360
O juro recebido após 5 anos será de R$ 360,00.
Caso queiramos calcular o montante, basta somar o juro com o capital:
M = 600 + 360 = 860
O montante será de R$ 860,00.
Observação: Vale ressaltar que os problemas envolvendo juro simples nem sempre pedem para calcular apenas o juro. Eles podem pedir o tempo, a taxa de juro ou até mesmo o capital.
28) Durante quanto tempo um capital de R$ 15.000,00 deve ficar em um investimento a juro simples com taxa de 12,5 % a.a. para que ele dobre o seu valor?
Resolução:
C = 15.0000
i = 12,5% a.a.
Para que o capital dobre de valor, é necessário que o montante seja de R$ 30.000,00. Para isso, o juro deve ser de 15.0000:
J = 15.000
J = C . i . t
15.000 = 15.000 . 0,125 . t
15.000 = 1.875 t
15.0001.875=t15.0001.875=t
t = 8
O período necessário é de 8 anos."
29) Renata acabou se esquecendo de pagar uma das contas de energia da sua residência. Como de costume, ela precisou pagar juros e multa pelo atraso de dois meses. Sabendo que o valor da conta era de R$ 160,00 antes do atraso e que a multa é de 1%, e os juros, de 3% ao mês, o valor pago a mais na conta devido ao atraso foi de:
(A) R$ 16,00.
(B) R$ 1,60.
(C) R$ 9,60.
(D) R$ 11,20.
(E) R$ 170,20.
Resolução:
Primeiro calcularemos o valor da multa, que é de 1% em relação ao valor.
Multa = 160 · 0,01 = 1,60
Calcularemos também os juros de 3% durante 2 meses.
J = C · i · t
J = 160 · 0,03 · 2
J = 4,8 · 2
J = 9,6
O valor pago a mais é a soma de 9,60 + 1,6 0 = 11,20.
Alternativa: D
30) Na aquisição de um novo imóvel, Rodrigo decidiu construir armários planejados. O valor dos armários planejados para toda a casa, mais o serviço do arquiteto, deu um total de R$ 65.000,00, para pagamento à vista. Caso Rodrigo decida parcelar, o valor pago terá juros simples de 1% a.m. Sabendo que ele pagou após 1 ano, o valor pago de juros foi de:
(A) R$ 7.800,00.
(B) R$ 6.600,00.
(C) R$ 8.200,00.
(D) R$ 5.900,00.
(E) R$ 9.000,00.
Resolução:
Primeiro calcularemos o juro gerado após 1 ano.
Sabendo que 1 ano possui 12 meses, temos:
C = 65.000,00
i = 1% a.m. → 0,01
t = 12 meses
Então:
J = C · i · t
J = 65.000 · 0,01 · 12
J = 7.800
Alternativa: A
31) Sílvio decidiu iniciar um novo negócio com a venda de anéis e brincos feitos de ouro. Para montar seu negócio, ele recorreu à sua amiga Lais, que lhe emprestou R$ 15.000,00. Esse empréstimo foi feito a juros simples, com uma taxa de 5% a.a. Suponha que ele consiga pagar a sua amiga após 6 meses, o valor da sua dívida será de:
(A) R$ 16.000,00.
(B) R$ 15.750,00.
(C) R$ 18.750,00.
(D) R$ 15.375,00.
(E) R$ 17.500,00.
Resolução:
Como a taxa está em ano e o tempo está em meses, sabemos que 6 meses é a metade de um ano, ou seja, 0,5 ano.
Nesse caso, temos que:
C = 15.000,00
i = 5% a.a.
t = 0,5 ano
J = C · i · t
J = 15.000 · 0,05 · 0,5
J = 375
Então, o valor pago é de 15.000 + 375 = 15.375,00.
Alternativa: D
32) Um capital foi investido a juros simples com uma taxa de 12% a.a. Durante quanto tempo esse capital deve ficar investido para que o montante seja o quádruplo do capital?
(A) 22 anos
(B) 20 anos
(C) 16 anos
(D) 17 anos
(E) 25 anos
Resolução:
Temos como dados que o montante é igual a 3 vezes o capital, ou seja, M = 3C, e que:
M = C + J
4C = C + J
4C – C = J
3C = J
Então, temos:
i = 12% a.a.
J = 3C
Substituindo na fórmula dos juros simples, temos que: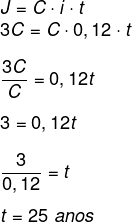
Alternativa: E
33) Um investidor aplicou um capital a juros simples com taxa de 3% ao mês, durante sete meses, gerando R$ 1.785,00 de juros. O valor do capital investido é igual a:
(A) R$ 9750,00.
(B) R$ 9200,00.
(C) R$ 9000,00.
(D) R$ 8750,00.
E( R$ 8500,00.
Resolução:
Dados:
i = 3% a.m.
t = 7
J = 1785,00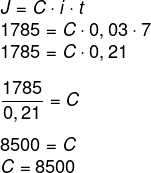
Alternativa: E
34) Em uma empresa de consórcio, quando um cliente é contemplado em um determinado momento, há uma correção a juros simples pelo tempo em que o cliente pagou o consórcio até o momento. Um cliente que comprou uma carta de R$ 16.000 foi contemplado após 1 ano e meio, recebendo um montante de R$ 16.288,00. A taxa de juros desse consórcio ao mês foi de:
(A) 0,1% a.m.
(B) 0,05% a.m.
(C) 0,01% a.m.
(D) 2% a.m.
(E) 0,2% a.m.
Resolução:
Dados:
M = 16.288,00
C = 16.000,00
Com esses dados, é possível encontrar o valor dos juros, pois:
J = M – C
J = 16.288,00 – 16.000,00
J = 288,00
Além dos juros, temos o tempo de 1 ano e meio. O exercício quer essa data em meses e sabemos que 1 ano e meio são 18 meses, logo: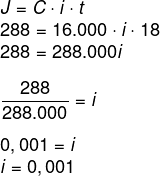
Para transformar em porcentagem, multiplicamos por 100, assim: i = 0,001 · 100 = 0,1%.
Alternativa: A
35) (Funcab – Adaptada) Adriana e Leonardo investiram R$ 20.000,00, sendo o 3/5 desse valor em uma aplicação que gerou lucro mensal de 4% ao mês durante dez meses. O restante foi investido em uma aplicação, que gerou um prejuízo mensal de 5% ao mês, durante o mesmo período. Ambas as aplicações foram feitas no sistema de juros simples.
Pode-se concluir que, no final desses dez meses, eles tiveram:
prejuízo de R$6.000,00
(B) lucro de R$3.200,00.
(C) lucro de R$5.000,00.
(D) prejuízo de R$ 800,00
(E) lucro de R$ 800,00.
Resolução:
Primeiro calcularemos o valor gerado na primeira aplicação. Para isso, vamos calcular o capital que foi investido em cada um dos investimentos.![]()
Então, no primeiro investimento, temos que:
C1 = 12.000
i1= 4% a.m.
t = 10
J = C · i · t
J = 12000 · 0,04 · 10
J = 12000 · 0,4
J = 4.8000
Agora calcularemos o segundo investimento, no qual ele teve prejuízo. O restante do valor é 20.000 – 12.000 = 8.000.
C2 = 8.000
Taxa = 5% a.m.
i2 = 5% a.m.
t = 10
J = C · i · t
J = 8.000 · 0,05 · 10
J = 8.000 · 0,5
J = 4.000
Sabendo que, no segundo caso, foi um prejuízo, então 4.800 – 4.000 = 800, logo ele obteve um lucro de R$ 800,00.
Alternativa: E
36) (Quadrix) Na cidade de Cuiabá, os planos de assistência médica locais emitem documentos para pagamento bancário, com as seguintes instruções: pagamento até a data do vencimento: x reais; pagamento após a data do vencimento: x reais + juros + multa. Uma pessoa tinha de pagar um boleto de R$ 452,00 até a data do vencimento. O atraso acarretaria uma multa de 10% e juros de R$ 0,40 ao dia. Ela pagou pelo boleto o valor de R$ 502,40.
Com base nesse caso hipotético, assinale a alternativa que apresenta o número de dias de atraso.
(A) 11
(B) 12
(C) 13
(D) 14
(E) 15
Resolução:
Analisando a situação, a diferença entre o valor da conta e o valor pago foi de 502,40 – 452,00 = 50,40, sendo esse valor composto por juros e multa.
A multa é 10% de 452,00, ou seja:
452 · 0,1 = 45,20
Então, calcularemos o valor dos juros subtraindo: 50,40 – 45,20 = 5,20.
Sabendo que, a cada dia de atraso, é cobrado R$ 0,40, então basta dividir 5,20 : 0,4 = 13 dias de atraso.
Alternativa: C
37) (Esaf) Um fogão é vendido por R$ 600,00 à vista ou com uma entrada de 22% e mais um pagamento de R$ 542,88, após 32 dias. Qual a taxa de juros mensal envolvida na operação?
(A) 5%
(B) 12%
(C) 15%
(D) 16%
(E) 20%
Resolução:
Sabemos que o valor pago é de 22% de 600 mais 542,88.
600 · 0,22 = 132,00
Então, o valor pago pelo fogão foi de 132 + 542,88 = 74,88 de juros.
Para calcular o juro, vamos encontrar o capital ao qual ele foi aplicado e o tempo.
Sabemos que foram dados R$ 132,00 de entrada e que o valor à vista era de 600,00, então:
600 – 132 = 468,00.
C = 468,00
J = 74,88
Note que ele quer a taxa de juros mensal, mas que o tempo foi dado em dias, então:
32 : 30 = 1,066.
t = 1,066
Agora calcularemos a taxa: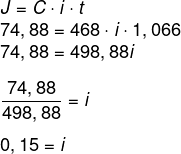
Como i = 15%, a taxa de juros é de 15%.
Alternativa: C
38) (PM SC – Cesiep) Mário comprou uma casa por $175.000,00. Para o pagamento foi dada uma entrada de $145.000,00 e o restante parcelado a juros simples com taxa de 12% ao ano durante 5 anos. Qual é o valor total dos juros?
(A) $36.000,00
(B) $18.000,00
(C) $16.000,00
(D) $24.000,00
Resolução:
Para calcular o capital, vamos subtrair o valor da casa pelo valor da entrada.
175.000 – 145.000 = 30.000
Então, temos que:
C = 30.000
t = 5 anos
i = 12% a.a.
Substituindo na fórmula:
J = C · i · t
J = 30.000 · 0,12 · 5
J = 30.000 · 0,60
J = 18.000
Alternativa: B
39) Julgue as afirmativas a seguir:
I → Montante é o valor do capital inicial adicionado dos juros.
II → Nos juros simples ao mês, o acréscimo mensal é sempre o mesmo.
III → Para calcular o montante, multiplicamos o capital pela taxa de juros pelo tempo.
Marque a alternativa correta:
A) Somente a afirmativa I é falsa.
(B) Somente a afirmativa II é falsa.
(C) Somente a afirmativa III é falsa.
(D) Todas as afirmativas são verdadeiras.
Resolução:
I → Verdadeira, pois, para calcular o montante, somamos o capital e os juros: M = C + J.
II → Verdadeiro, pois o juro simples sempre incide sobre o capital inicial.
III → Falsa, pois, quando multiplicamos o capital pela taxa de juros e pelo tempo, estamos calculando os juros.
Alternativa: C
40) Um capital foi aplicado a juros simples, com uma taxa de 5% a.a., gerando um saldo de R$ 9.750 após 6 anos. O valor do capital é de:
(A) R$ 7.500,00
(B) R$ 7. 950,00
(C R$ 8.000,00
(D) R$ 8.200,00
(E) R$ 8350,00
Resolução:
Sabemos que o juro é a diferença entre o montante e o capital:
M = C + J
J = M – C
Além disso, temos que:
i = 5% a.a.
M = 9750
t = 6 anos
Então: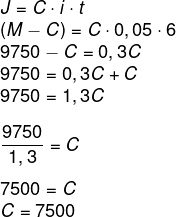
Alternativa: A





