Professor Diminoi

GEOMETRIA ANALITICA – CONICAS

Introdução
Chamamos de cônicas as curvas geradas ou encontradas na intersecção de um plano que atravessa um cone.

Estudaremos as seguintes cônicas:

Elipse: definida na interseção de um plano que atravessa a superfície de um cone;

Parábola: também definida na intersecção de um plano que penetra a superfície de um cone;

Hipérbole: definida na interseção de um plano que penetra num cone em paralelo ao seu eixo.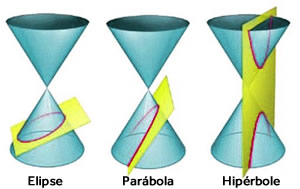

Elipse
Considerando, num plano a, dois pontos distintos, F₁ e F₂ e, sendo 2a um número real maior que a distância entre F₁ e F₂, chamamos de elipse o conjunto dos pontos do plano a tais que a soma das distâncias desses pontos a F₁ e F₂ seja sempre igual a 2a.

Exemplo
Sendo P, Q, R, S, F₁ e F₂ pontos de um mesmo plano e F₁F₂ < 2a, temos: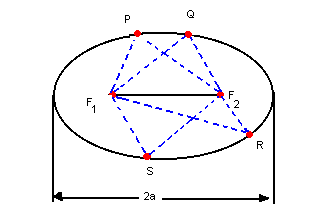

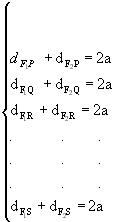
A figura obtida é uma elipse. Observações:
1ª) A Terra descreve uma trajetória elíptica em torno do sol, que é um dos focos dessa trajetória. A lua em torno da terra e os demais satélites em relação a seus respectivos planetas também apresentam esse comportamento.

2ª) O cometa de Halley segue uma órbita elíptica, tendo o Sol como um dos focos.

3ª) As elipses são chamadas cônicas porque ficam configuradas pelo corte feito em um cone circular reto por um plano oblíquo em relação à sua base.

Elementos
Observe a elipse a seguir. Nela, consideramos os seguintes elementos: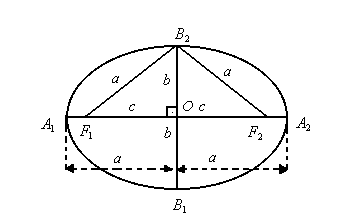
focos : os pontos F₁ e F₂ 
centro: o ponto O, que é o ponto médio de
- semi-eixo maior: a

- semi-eixo menor: b

- semidistância focal: c

- vértices: os pontos A₁, A₂, B₁, B₂

- eixo maior:
- eixo menor
- distância focal:

Relação fundamental
Na figura acima, aplicando o Teorema de Pitágoras ao triângulo OF₂B₂ , retângulo em O, podemos escrever a seguinte relação fundamental:
a² = b² + c²

Excentricidade
Chamamos de excentricidade o número real e tal que:
Pela definição de elipse, 2c < 2a, então c < a e, consequentemente, 0 < e < 1.

Observação: quando os focos são muito próximos, ou seja, c é muito pequeno, a elipse se aproxima de uma circunferência.

Equações da elipse
Vamos considerar os seguintes casos:
a) elipse com centro na origem e eixo maior horizontal
Sendo c a semidistância focal, os focos da elipse são F₁(-c, 0) e F₂(c, 0):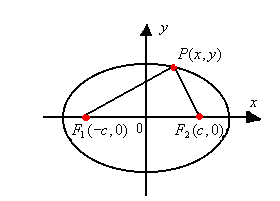
Aplicando a definição de elipse 
Obtemos a equação da elipse:

b) elipse com centro na origem e eixo maior vertical
Nessas condições, a equação da elipse é: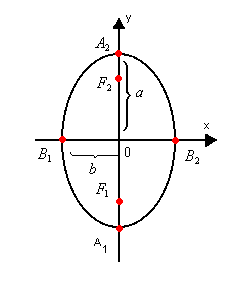

Hipérbole
Considerando, num plano a, dois pontos distintos, F₁ e F₂ e, sendo 2a um número real menor que a distância entre F₁ e F₂, chamamos de hipérbole o conjunto dos pontos do plano a tais que o módulo da diferença das distâncias desses pontos a F₁ e F₂ seja sempre igual a 2a.

Eexemplo
Sendo P, Q, R, S, F1 e F2 pontos de um mesmo plano e F₁F₂ = 2c, temos: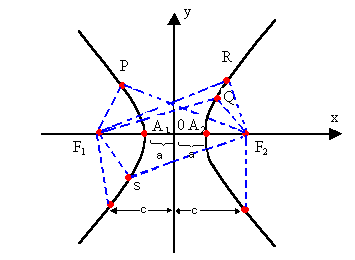


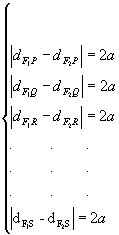
A figura obtida é uma hipérbole.
Observação: os dois ramos da hipérbole são determinados por um plano paralelo ao eixo de simetria de dois cones circulares retos e opostos pelo vértice: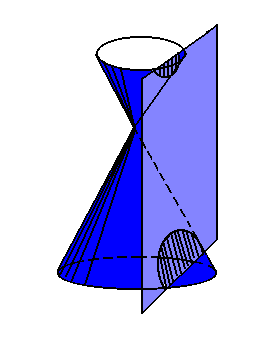

Elementos
Observe a hipérbole representada a seguir. Nela, temos os seguintes elementos: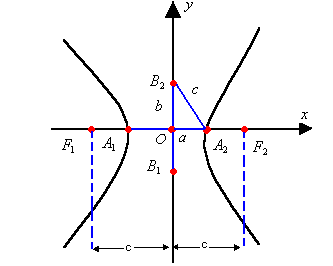
- focos: os pontos F₁ e F₂
- vértices: os pontos A₁ e A₂
- centro da hipérbole: o ponto O, que é o ponto médio de
- semi-eixo real: a
- semi-eixo imaginário: b
- semidistância focal: c
- distância focal:
- eixo real: 
- eixo imaginário:

Excentricidade
Chamamos de excentricidade o número real e tal que:
Como c > a, temos e > 1.

Equações da hipérbole
Vamos considerar os seguintes casos:
a) hipérbole com centro na origem e focos no eixo Ox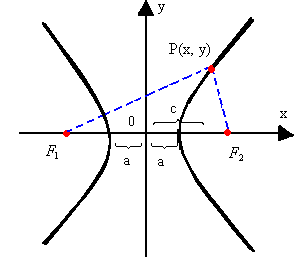
F₁ (-c, 0)
F₂ (c, 0)

Aplicando a definição de hipérbole:
Obtemos a equação da hipérbole:

b) hipérbole com centro na origem e focos no eixo Oy
Nessas condições, a equação da hipérbole é:

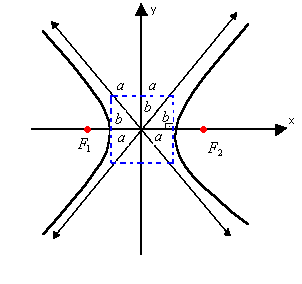
Hipérbole equilátera
Uma hipérbole é chamada equilátera quando as medidas dos semi-eixos real e imaginário são iguais: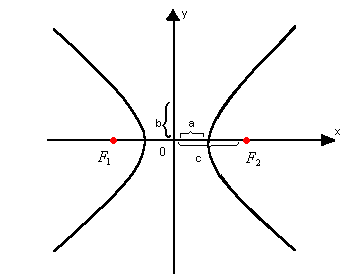
a = b

Assíntotas da hipérbole
Assíntotas são retas que contêm as diagonais do retângulo de lados 2a e 2b.
Quando o eixo real é horizontal, o coeficiente angular dessas retas é
Quando é vertical, o coeficiente é

Equação
Vamos considerar os seguintes casos:
a) eixo real horizontal e C(0, 0)
As assíntotas passam pela origem e têm coeficiente angular
Logo, suas equações são da forma:

b) eixo vertical e C(0, 0)
As assíntotas passam pela origem e têm coeficiente angular
Logo, suas equações são da forma:

Parábola
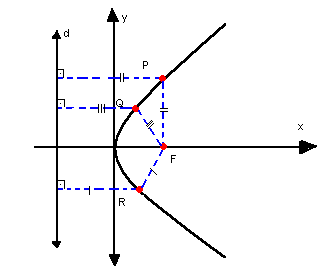
Dados uma reta d e um ponto F (F não pertence a d) , de um plano a, chamamos de parábola o conjunto de pontos do plano a equidistantes de F e d.

Exemplo
Sendo F, P, Q e R pontos de um plano a e d uma reta desse mesmo plano, de modo que nenhum ponto pertença a d, temos: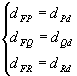


Observações:
1ª) A parábola é obtida seccionando-se obliquamente um cone circular reto: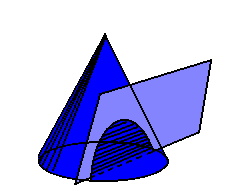
2ª) Os telescópios refletores mais simples têm espelhos com secções planas parabólicas.
3ª) As trajetórias de alguns cometas são parábolas, sendo que o Sol ocupa o foco.
4ª) A superfície de um líquido contido em um cilindro que gira em torno de seu eixo com velocidade constante é parabólica.

Elementos
Observe a parábola representada a seguir. Nela, temos os seguintes elementos: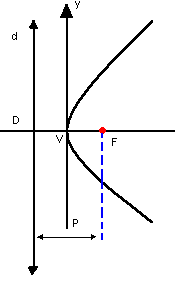
- foco: o ponto F
- diretriz: a reta d
- vértice: o ponto V
- parâmetro: p

Então, temos que:
o vértice V e o foco F ficam numa mesma reta, o eixo de simetria e.

Assim, sempre temos
DF = p
V é o ponto médio de 

Equações da parábola
Vamos considerar os seguintes casos:
a) parábola com vértice na origem, concavidade para a direita e eixo de simetria horizontal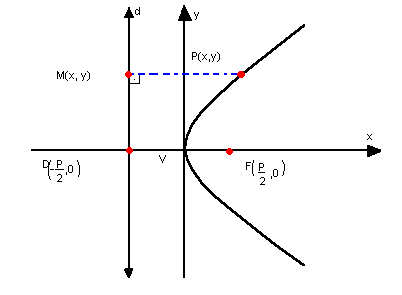
Como a reta d tem equação
E na parábola temos:
P(x, y);
d_PF = d_Pd ( definição);
Obtemos, então, a equação da parábola:
y² = px

b) parábola com vértice na origem, concavidade para a esquerda e eixo de simetria horizontal
Nessas condições, a equação da parábola é: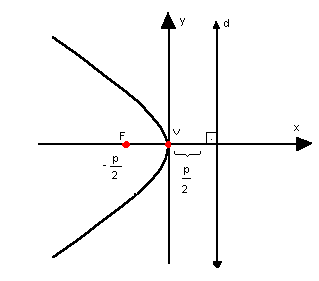
y² = 2px

c) parábola com vértice na origem, concavidade para cima e eixo de simetria vertical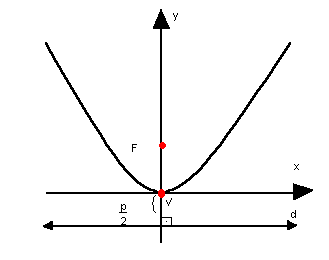
x² = 2py

d) parábola com vértice na origem, concavidade para baixo e eixo de simetria vertical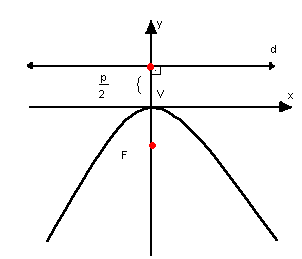
x² = - 2py


Continua ...