MOVIMENTO UNIFORME - (MU)

Professor Diminoi

 CINEMÁTICA

É a parte da Mecânica que estuda os movimentos sem que haja preocupação com suas causas e efeitos. Alguns conceitos de Cinemática são muito importantes para a correta compreensão de fenômenos físicos e pleno entendimento da forma de se construir o raciocínio necessário para a resolução de problemas.

Observação: cinemática  estuda o movimento dos corpos sem se preocupar com a causa  deste movimento.

O movimento esta presente em toda a natureza: nos movimentos de translação e de rotação dos astros, nas massa de ar, nas marés, na migração de aves, entre inúmeros outros exemplos. A maioria das atividades humanas também está relacionada as movimento. Movimentos como o do leão fugindo dos búfalos bem como os movimentos dos búfalos afugentando o leão representado na figura abaixo.

Neste link  estudarmos CINEMÁTICA que é a parte da física que descreve os movimentos sem se preocupar com suas causas e consequências.

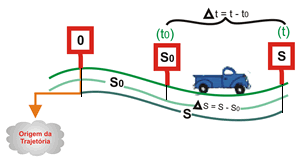
TRAJETÓRIA/TRAJÉTO

É o caminho descrito pelo móvel (nem sempre o trajeto para se ir de um ponto A  um ponto B e igual a distância em linha reta entre A a B). 

Observação: A Trajetória é uma linha imaginária que representa as sucessivas posições de o corpo ocupa ao longo do tempo.

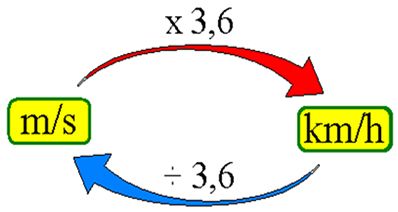
No Sistema Internacional a velocidade e em metros por segundo (m/s) e o tempo em segundo (s).

Observação: para transformar m/s em km/h basta multiplicar o valor por 3,6 e para transformar k/h em m/s basta dividir o valor por 3,6.

PONTO MATERIAL

É um corpo cujas dimensões pode  ser desprezada na resolução do problema (quando estudamos a velocidade da luz do Sol até chegar a Terra.

POSIÇÃO DE UM CORPO

É onde o corpo se encontra no momento em questão.

REFERENCIAL

É qualquer corpo que adotamos para comparar com outro. Na figura abaixo tomamos como referencial o homem sentado no morrinho ao lado da rodovia.

CORPO EM MOVIMENTO OU REPOUSO

Para saber se um corpo esta em movimento ou em repouso é necessário adotarmos um referencial (observe o item anterior). Se a posição entre o ônibus e o homem estiver variando no decorrer do tempo, o ônibus esta em movimento em relação ao homem, assim, como o homem está em movimento em relação ao ônibus e aos passageiro. 

Também podemos dizer: o ônibus está em movimento em relação ao homem e em repouso em relação aos passageiros.

Observe a ilustração: na ilustração temos o 1 carro, 1 home, 1 passarinho e 2 árvores. Pergunta-se, quem esta em movimento? Quem está em repouso? Justifique sua resposta.

ESPAÇO PERCORRIDO

É a distância percorrida pelo móvel ou seja, a posição final (S) menos a posição inicia (S_o).

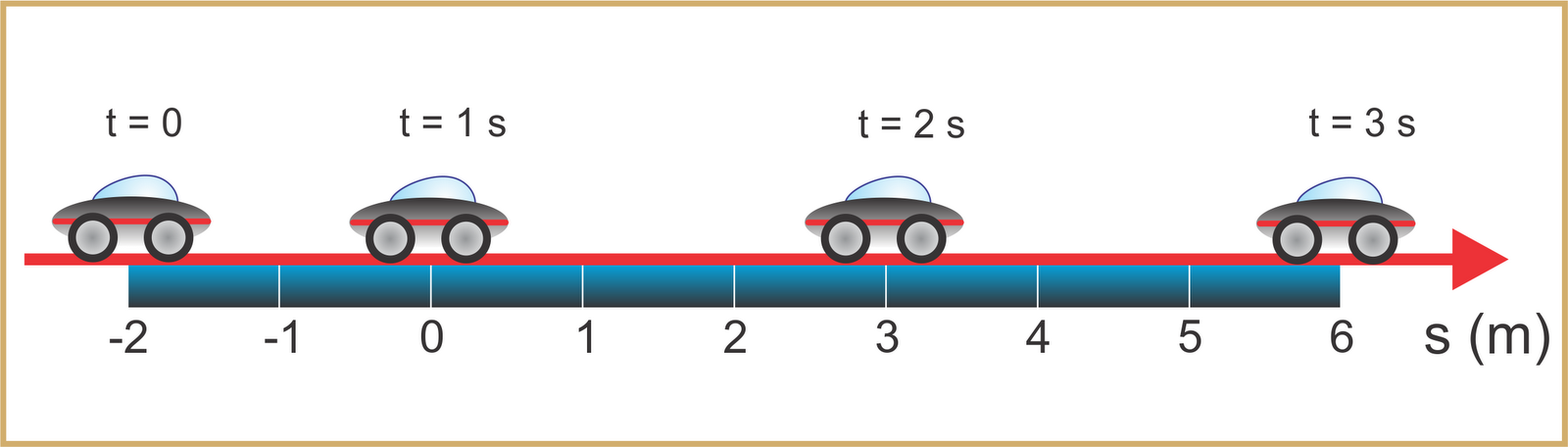
MOVIMENTO UNIFORME (MU)

O movimento uniforme ocorre quando um móvel se desloca em linha reta e com velocidade constante. No movimento uniforme, o móvel percorre espaços iguais em intervalos de tempo iguais.

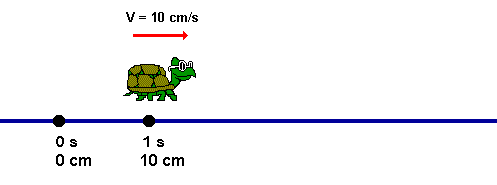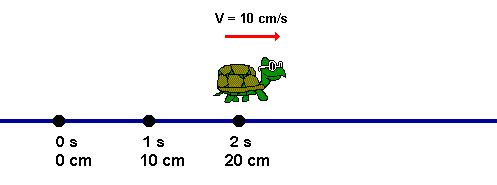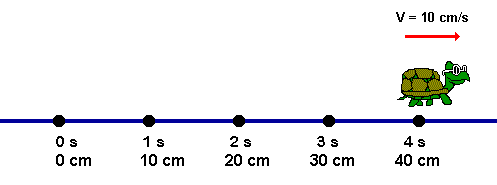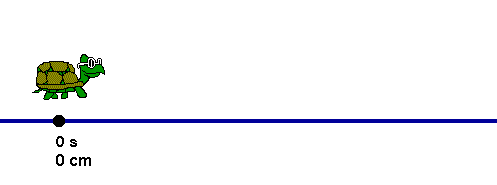
Um corpo está em movimento uniforme quando sua velocidade é constante, isso é não vaia no decorrer do tempo.  Isto é, Percorre distâncias iguais em intervalos de temos iguais.

MOVIMENTO RETILÍNEO UNIFORME (MRU)

É a mesma coisa que o MU, exceto pelo fato de que, obrigatóriamente, o trajeto percorrido pelo corpo deve ser uma linha reta.

Gráficos do Movimento Uniforme (MU)

VELOCIDADE MÉDIA

A velocidade média de um móvel pode ser interpretada como o valor da velocidade constante que um segundo móvel deveria manter para fazer o mesmo percurso no mesmo tempo que o móvel em estudo. Para calcular a velocidade média divide-se a distância percorrida pelo temo gasto.

Observação: no Sistema Internacional S.I a velocidade é em (m/s), o tempo em (s) e a distância em(m).

Vm = ΔS/Δt

Vm = velocidade média (m/s)

ΔS = distância percorrida (m)

Δt = tempo (s)

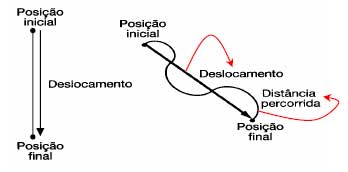
Sabemos que o conceito de deslocamento é a medida da distância entre duas posições ocupadas pelo corpo em movimento, sobre uma trajetória. Essa medida costuma ser obtida entre duas referências como, por exemplo, entre marcos quilométricos de uma estrada.

Observação:

- Transformar km/h em m/s (divide o valor por 3,6)

- Transformar m/s em km/h (multiplica o valor por 3,6)

A velocidade escalar instantânea

Representa a velocidade de um móvel num determinado instante de seu movimento.

S = S_o+ v. t

S = posição final (m)

S_o = posição inicial (m)

v = velocidade (m/s)

t = tempo (s)

Gráfico da Velocidade em Função do Tempo (velocidade mádia).

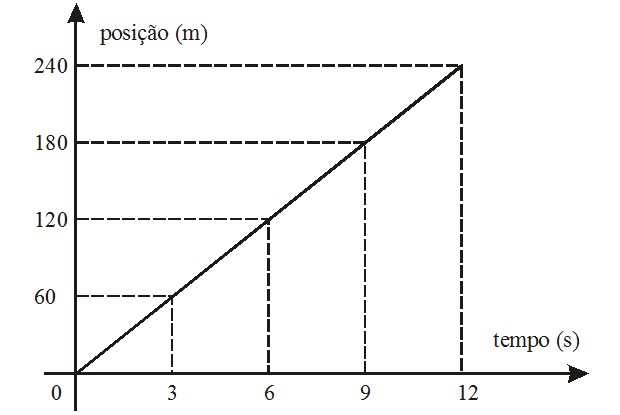
Movimento Progressivo ou Movimento a Favor da Trajetória

Um móvel está em movimento progressivo quando seu deslocamento tem sentido a favor da trajetória, isto é, se afasta da origem das posição. Nesse caso a velocidade é positiva.

Movimento Retrógrado ou Movimento Contrário a Trajetória

Um móvel está em movimento retrógrado quando seu deslocamento tem sentido contrário a trajetória, isto é, se aproxima da origem das posição. Nesse caso a velocidade é negativa.

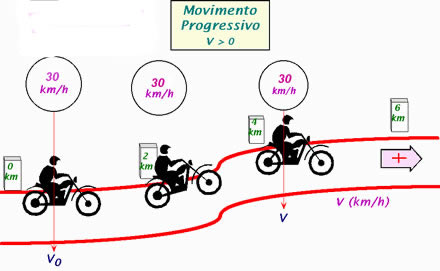
Gráfio do Movimento Progressivo e Movimento Retrógrado

Observação: 

• Quando a velocidade é crescente (positiva),  dizemos que o movimento é progressivo.
• Quando a velocidade é decrescente (negativa) dizemos que o movimento é retardado.

Gráficos do Movimento Uniforme (MU)

Função horária das posições.

Imaginemos que um ponto material esteja deslocando-se ao longo de uma trajetória retilínea com velocidade constante. Para estabelecer a função da posição do móvel (ponto material) em MRU, em relação ao tempo, é necessário, inicialmente, estabelecer adequadamente o sistema de referência.

Vejamos a figura abaixo.

Nesse sistema de referência estão fixadas a origem 0 e a posição inicial s₀, medida no instante t₀ = 0, a partir dessa origem. Estão representados também o valor algébrico da velocidade v e a posição s do ponto material no instante t. Com base na definição de velocidade escalar média, escrevemos:

Adotando t₀ = 0, podemos escrever:

A equação acima é a função horária das posições em um Movimento Uniforme. Onde:

- s é o espaço final ocupado pelo móvel

- s­₀ é o espaço inicial ocupado pelo móvel

- t é o tempo

- v é a velocidade do móvel

MOVIMENTO UNIFORME - (MR)

01) Um veículo trafega em uma rodovia com velocidade média de 80 km/h. Sabendo que a viagem teve uma duração de 1 hora e 30 minutos (1,5 h), qual foi a distância percorrida pelo veículo?

(A) 80 km

(B) 10 km

(C) 120 km

(D) 160 km

(E) 100 km

Resolução:

Vamos resolver esse exercício utilizando a fórmula da velocidade média, confira:

Por meio do cálculo realizado, foi possível encontrarmos a distância percorrida, nesse caso, de 120 km.

Alternativa: C

02) Uma locomotiva afasta-se de um observador enquanto sua velocidade aumenta a cada segundo. O movimento descrito por essa locomotiva pode ser classificado como:

(A) progressivo e retardado.

(B) regressivo e retardado.

(C) progressivo e retilíneo.

(D) regressivo e acelerado.

(E) progressivo e acelerado.

Resolução:

Pelo fato de a locomotiva afastar-se do observador, o seu movimento é progressivo, além disso, como a sua velocidade aumenta, dizemos que o seu movimento é também acelerado.

Alternativa: E

03) Um macaco que pula de galho em galho em um zoológico, demora 6 segundos para atravessar sua jaula, que mede 12 metros. Qual a velocidade média dele?

Resolução:

S = 12m

t = 6s

v = ?

04) Um carro viaja de uma cidade A a uma cidade B, distantes 200km. Seu percurso demora 4 horas, pois decorrida uma hora de viagem, o pneu dianteiro esquerdo furou e precisou ser trocado, levando 1 hora e 20 minutos do tempo total gasto. Qual foi a velocidade média que o carro desenvolveu durante a viagem?

Resolução:

S = 200km

t = 4h

v = ?

Mesmo o carro tendo ficado parado algum tempo durante a viagem, para o cálculo da velocidade média não levamos isso em consideração.

05) No exercício anterior, qual foi a velocidade nos intervalos antes e depois de o pneu furar? Sabendo que o incidente ocorreu quando faltavam 115 km para chegar à cidade B.

Resolução:

Antes da parada:

S = 200 -115 = 85km

t = 1hora

v = ?

Depois da parada:

S = 115km

t = 4h-1h -1h20min = 1h40min = 1,66h (utilizando-se regra de três simples)

v = ?

06) Um bola de basebol é lançada com velocidade igual a 108m/s, e leva 0,6 segundo para chegar ao rebatedor. Supondo que a bola se desloque com velocidade constante. Qual a distância entre o arremessador e o rebatedor?

Resolução:

Se isolarmos S:

07) Durante uma corrida de 100 metros rasos, um competidor se desloca com velocidade média de 5m/s. Quanto tempo ele demora para completar o percurso?

Resolução:

Se isolarmos t:

08) Um carro desloca-se em uma trajetória retilínea descrita pela função S = 20 + 5t (no SI).

Determine:

(a) a posição inicial;

(b) a velocidade;

(c) a posição no instante 4s;

(d) o espaço percorrido após 8s;

(e) o instante em que o carro passa pela posição 80m;

(f) o instante em que o carro passa pela posição 20m.

Comparando com a função padrão: 

S_final = S_inicial + v . Δt

(a) Posição inicial = 20m

(b) Velocidade = 5m/s

(c)

S = 20 + 5t

S = 20 + 5.4

S = 40m

(d)

S = 20 + 5 . 8

S = 60m

ΔS = S - S_o

ΔS = 60 – 20 = 40m

(e)

80 = 20 + 5t

80 - 20 = 5t

60 = 5t

12s = t

(f) 

20 = 20 + 5t

20 – 20 = 5t

T = 0

09) O gráfico a seguir mostra as posições em função do tempo de dois ônibus. Um parte de uma cidade A em direção a uma cidade B, e o outro da cidade B para a cidade A. As distâncias são medidas a partir da cidade A. A que distância os ônibus vão se encontrar?

Resolução:

Para que seja possível fazer este cálculo, precisamos saber a velocidade de algum dos dois ônibus, e depois, calcular a distância percorrida até o momento em que acontece o encontro dos dois, onde as trajetórias se cruzam.

Calculando a velocidade ônibus que sai da cidade A em direção a cidade B (linha azul)

Sabendo a velocidade, é possível calcular a posição do encontro, quando t = 3h.

S = S_o + v . t

S = 0 + 90 . 3

S = 270m

10) Um carro, se desloca a uma velocidade de 20m/s em um primeiro momento, logo após passa a se deslocar com velocidade igual a 40m/s, assim como mostra o gráfico abaixo. Qual foi a distância percorrida pelo carro?

Resolução:

Tendo o gráfico da v x t, o deslocamento é igual à área sob a reta da velocidade.

S = Área A + Área B

S = 20 5 + 40 (15 - 5)

S = 100 + 400

S = 500m

11) Dois trens partem simultaneamente de um mesmo local e percorrem a mesma trajetória retilínea com velocidades, respectivamente, iguais a 300km/h e 250km/h. Há comunicação entre os dois trens se a distância entre eles não ultrapassar 10km. Depois de quanto tempo após a saída os trens perderão a comunicação via rádio?

Resolução:

Para este cálculo estabelece-se a velocidade relativa entre os trens, assim pode-se calcular o movimento como se o trem mais rápido estivesse se movendo com velocidade igual a 50km/h (300km/h-250km/h) e o outro parado.

Assim:

v = 50km/h

S = 10km

t = ?

12) Um veículo move-se com velocidade constante de 36 km/h. Ao seu lado, um outro veículo trafega com velocidade constante de 54 km/h. Assinale a alternativa que indica qual será a distância, em km, entre esses veículos após um intervalo de tempo de 5 minutos.

(A) 5,0 km

(B) 2,0 km

(C) 1,5 km

(D) 3,0 km

(E) 18 km

Resolução:

A resolução desse exercício requer que calculemos o espaço percorrido pelos dois veículos, para que, em seguida, descubramos qual foi a diferença de espaço percorrido por eles. No entanto, nesse exercício, existem algumas unidades de medida de velocidade e tempo que requerem atenção. Por isso, transformamos as velocidades, dadas em km/h em m/s, dividindo-as pelo fator 3,6. Em seguida, é necessário multiplicar o tempo de 60 minutos por 60, a fim de utilizarmos o tempo informado em segundos.

Alternativa: C

13) Uma pessoa sobe por uma escada rolante de 8 m de base por 6 m de altura com uma velocidade constante de 0,5 m/s. Determine o intervalo de tempo necessário para que ela consiga chegar ao topo dessa escada.

(A) 15 s

(B) 20 s

(C) 10 s

(D) 40 s

(E) 12 s

Resolução:

Para calcularmos o tempo necessário de subida, precisamos usar a fórmula da velocidade média. No entanto, o deslocamento sofrido enquanto a pessoa sobe a escada ocorre na direção da hipotenusa de um triângulo cujos catetos são 8 m e 6m e, por isso, precisamos calculá-lo por meio do teorema de Pitágoras, confira a resolução:

Alternativa: B

14) Deseja-se fazer uma viagem de 90 km de distância com velocidade média de 60 km/h. Um veículo percorre os primeiros 30 km desse trajeto em um intervalo de tempo de 30 minutos (0,5 h). Assinale a alternativa que mostra o tempo restante para o motorista terminar o percurso, a fim de que ele mantenha a velocidade média desejada.

(A) 3,0 h

(B) 2,0 h

(C) 0,5 h

(D) 1,0 h

(E) 0,25 h

Resolução:

Como dito no enunciado do exercício, deseja-se que a velocidade média de todo o percurso seja de 60 km/h. Para tanto, vamos determinar qual é o tempo que essa viagem deve acontecer:

Como o motorista gasta 30 minutos nos primeiros 30 km do trajeto e o tempo total de viagem não pode exceder 1,5 h, então, o tempo que lhe resta para percorrer os 60 km seguintes é de 1 h.

Alternativa: D

15) Um trem necessita completar uma viagem de 400 km em um tempo máximo de 4h, movendo-se a 80 km/h. Após 30 minutos de viagem, o trem quebra e fica parado por 30 minutos. Determine a velocidade média que o trem precisará desenvolver no restante do trajeto para chegar a tempo em seu destino.

(A)) 100 km/h

(B) 120 km/h

(C) 160 km/h

(D) 90 km/h

(E) 70 km/h

Resolução;

Para resolver esse exercício, precisamos descobrir quanto o trem andou antes de ter quebrado. De acordo com o exercício, o trem movia-se a 80 km/h e, após 30 minutos, quebrou. Fazendo o cálculo, descobrimos que esse trem andou uma distância de 40 km. Como o conserto do trem demorou mais 30 minutos, restam apenas 3h do tempo total de viagem, para que o trem não se atrase, e uma distância de 360 km. 

Alternativa: B

16) Um observador percebe que um veículo, inicialmente a uma distância de 30 m, afasta-se com velocidade constante de 90 km/h. Em relação a esse movimento, responda:

a) Qual é a classificação do movimento desse veículo? Explique.

Resolução:

Como o veículo afasta-se de seu observador, o seu movimento é progressivo. Além disso, como sua velocidade é constante, trata-se de um movimento uniforme e progressivo.

b) Determine a função horária da posição desse veículo em unidades do SI.

Resolução:

Para determinarmos a função horária do movimento, precisamos ler o exercício e identificar algumas grandezas, como posição inicial e velocidade. Ao fazê-lo, é possível perceber que a trajetória do veículo foi iniciada na posição 30 m, logo, S₀ = 30 m. Já a sua velocidade, de 90 km/h, precisa ser expressa no SI. Para isso, basta dividi-la pelo fator 3,6, portanto, v = 25 m/s.

c) Em qual instante de tempo esse veículo estará na posição 80 m?

Resolução:

Podemos calcular o instante em que o veículo passará pela posição S = 80 m substituindo esse número na fórmula encontrada acima.

17) Uma ave migratória consegue voar enormes distâncias. Suponha que ela consiga voar com velocidade constante de 10 m/s durante o período de uma semana. Qual terá sido a distância, em quilômetros, percorrida pela ave durante esse período?

(A) 2056 km

(B) 6048 km

(C) 7512 km

(D) 8600 km

Resolução:

Podemos resolver o exercício utilizando a equação da velocidade média, entretanto é necessário que as unidades sejam adequadas. Para tanto, podemos simplesmente converter a velocidade, que está em metros por segundo, para quilômetros por hora, multiplicando-a pelo fator 3,6. Além disso, também é necessário transformar o período de uma semana em horas (1 semana = 7 dias, 1 dia = 24 h, portanto 1 semana equivale a 168 h). Em seguida, basta fazermos o cálculo a seguir:

Alternativa:  B

18) Um navio cargueiro completamente carregado tem uma massa de 1,5. 10⁵ kg. Sabendo que esse navio percorre uma distância de 4000 km em 30 dias com velocidade constante, calcule o valor da força resultante sobre o navio durante o percurso.

(A) 400.000 N

(B) 150.000 N

(C) 0 N

(D) 3000 N

(E) 1.200.000 N

Resolução:

O exercício pede que calculemos o valor da força resultante sobre o navio, e não o módulo da força responsável por propeli-lo. Sendo assim, uma vez que o navio desloca-se nesse trajeto com velocidade constante, a força resultante sobre ele deve ser igual a 0,

Alternativa:  C

19) No instante de tempo t₀, um corpo encontra-se na posição 3 m com relação a um sistema de referência, movendo-se com uma velocidade de 10 m/s. A alternativa que representa corretamente a função horária da posição desse móvel é:

(A) S = 3 + 10t

(B) S =10 + 3t

(C) S = 3t + 5t²

(D) S = 10t + 3t²

Resolução:

 função horária da posição do movimento uniforme é escrita na forma S = S₀ + v.t, sendo S₀ a posição inicial, v a velocidade e t o instante de tempo.

Alternativa:  A

20) Com relação a um corpo que descreve um movimento retilíneo e uniforme, assinale a alternativa correta.

(A) Um corpo em MU percorre espaços cada vez maiores a cada intervalo de tempo posterior.

(B) Um corpo em MU percorre distâncias iguais em intervalos de tempos iguais.

(C) Um corpo em MU move-se com aceleração constante.

(D) Um corpo em MU permanece em uma posição constante em todos os instantes de tempo.

Resolução:

Quando um corpo descreve um movimento uniforme, dizemos que ele percorre espaços iguais para intervalos de tempos iguais.

Alternativa:  B

21) Sobre dois móveis A e B cujas funções horárias são S_A = 15 + 20t e S_B = 20 – 5t, são feitas as seguintes afirmações:

I – O móvel A descreve um movimento acelerado.

II – O móvel B descreve um movimento retrógrado.

III – A velocidade de A é 10 m/s.

IV – Nos instantes iniciais, A e B se aproximam a cada segundo.

São verdadeiras:

(A) I e IV.

(B) II e III.

(C) II e IV.

(D) III e IV.

Resolução:

Vamos analisar as afirmações:

I – FALSA. O móvel A se desloca com velocidade constante em um movimento progressivo e não acelerado.

II – VERDADEIRA.

III – FALSA. A velocidade do móvel A é de 10 m/s, e não 20 m/s.

IV – VERDADEIRA. Uma vez que o A move-se para frente e B move-se para esquerda, nos primeiros instantes, eles se deslocam um em direção ao outro, portanto a afirmativa é verdadeira até que eles se encontrem.

Alternativa:  C

22) Dois carros, A e B, movem-se em uma pista retilínea com velocidades constantes de 20 m/s e 30 m/s, respectivamente. Sabendo que o carro A encontra-se 100 m à frente do carro B, analise as afirmativas a seguir:

I – A cada instante de tempo, o carro A se afasta do carro B.

II – A velocidade relativa entre os carros é de 10 m/s.

III –Em 10 s o carro B terá alcançado o carro A.

Está(ão) correta(s):

(A) I.

(B) II.

(C) III.

(D) II e III.

Resolução:

Vamos analisar o que dizem as afirmativas:

I – FALSA. De acordo com a situação descrita, o carro A, de menor velocidade, é “perseguido” pelo carro B, de maior velocidade, por isso eles se aproximam com o passar do tempo,

II – VERDADEIRA. A cada segundo, um dos veículos move-se 30 m enquanto o outro, 20 m, dessa maneira, a velocidade relativa entre eles é de 10 m/s.

III – VERDADEIRA. Como a velocidade relativa entre os dois carros é de 10 m/s e a distância inicial entre eles era de 100 m, em 10 s os dois carros se encontrarão.

Alternativa:  D

23) Dois móveis, A e B, movem-se de acordo com as funções horárias S_A = 5 + 3t e S_B = 15 + 2t, em unidades do Sistema Internacional. O instante em que esses móveis se encontram é:

(A) 10 s.

(B) 20 s.

(C) 5 s.

(D) 15 s.

Resolução:

Para resolver essa questão, basta igualar as posições SA e SB. Confira o cálculo:

Alternativa:  A

24) Em um dia normal, um veículo gasta 5 minutos para atravessar uma ponte, movendo-se a uma velocidade de 20 m/s. Com base nos dados apresentados, calcule a extensão dessa ponte, em km.

(A) 10 km

(A) 100 km

(C) 6 km

(D) 10 km

Resolução:

Vamos resolver o exercício usando a fórmula da velocidade no MU, porém, antes disso, é necessário converter o tempo, que está em minutos, para segundos. Para tanto, multiplicamos os minutos por 60:

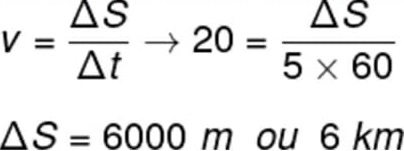
Alternativa:  C

25) (UFTPR) Um navio de pesquisa equipado com SONAR está mapeando o fundo do oceano. Em determinado local, a onda ultrassonora é emitida e os detectores recebem o eco 0,6 s depois.

Sabendo que o som se propaga na água do mar com velocidade aproximada de 1500 m/s, assinale qual é a profundidade, em metros, do local considerado.

(A) 450 m

(B) 380 m

(C) 620 m

(D) 280 m

(E) 682 m

Resolução:

Para resolver esse exercício, utilizamos a fórmula da velocidade no movimento uniforme. Além disso, consideramos o tempo de 0,3 s, uma vez que o tempo informado considera a ida e a volta da onda sonora.

26) (Famema) De dentro do ônibus, que ainda fazia manobras para estacionar no ponto de parada, o rapaz, atrasado para o encontro com a namorada, a vê indo embora pela calçada. Quando finalmente o ônibus para e o rapaz desce, a distância que o separa da namorada é de 180 m.

Sabendo que a namorada do rapaz se movimenta com velocidade constante de 0,5 m/s e que o rapaz pode correr com velocidade constante de 5 m/s, o tempo mínimo para que ele consiga alcançá-la é de:

(A) 10 s.

(B) 45 s.

(C) 25 s.

(D) 50 s.

(E) 40 s.

Resolução:

Para resolver o exercício, precisamos escrever as funções horárias do rapaz e de sua namorada. Para tanto, consideramos a posição do rapaz como zero e a posição de sua namorada como 180. Em seguida, igualamos suas posições:

Alternativa:  E

27) Na pista de testes de uma montadora de automóveis, foram feitas medições do comprimento da pista e do tempo gasto por um certo veículo para percorrê-la. Os valores obtidos foram, respectivamente, 1030 m e 25,0 s. Levando-se em conta a precisão das medidas efetuadas, é correto afirmar que a velocidade média desenvolvida pelo citado veículo foi, em m/s, de:

(A) 4,10.

(B) 41.

(C) 41,2.

(D) 41,20.

(E) 41,200.

Resolução:

Basta dividirmos a distância pelo tempo citado no enunciado, observe:

Alternativa:  C

28) (Unitau) Um automóvel percorre uma estrada com função horária S = - 40 + 80t, sendo que S é dado em km e t está em horas. O automóvel passa pelo km zero após:

(A) 1,0 h.

(B) 1,5 h.

(C) 0,5 h.

(D) 2,0 h.

(E) 2,5 h.

Resolução:

Para resolver o exercício, basta que, no lugar de S, coloquemos 0. Com isso, o cálculo a ser feito é bastante simples:

Alternativa:  C

29) O gráfico a seguir representa a função horária do espaço de um móvel em trajetória retilínea e em movimento uniforme.

Com base nele, determine a velocidade e a função horária do espaço deste móvel.

Resolução:

v = Δs/Δt

v = (250 – 50)/(10 - 0)

v = 200/10

v = 20m/s – velocidade

x = xo+ v.t

x = 50 + 20.t

30) (FMTM MG) Partículas ejetadas de núcleos são observadas no laboratório pela impressão que deixam nas chapas fotográficas de seus detectores. Uma partícula, movendo-se à velocidade de 0,995 c, produz um rastro de 1,25 mm. O tempo correspondente ao rastro deixado é, em segundos, aproximadamente igual a:

Dado: c = 3 × 10⁵ km/s = 3 x 10⁸ m/s

(A) 5 × 10^-11.

(B) 2 × 10^-11.

(C) 6 × 10^-12.

(D) 4 × 10^-12.

(E) 3 × 10^-12.

Resolução:

Como a velocidade (v) da partícula é de 0,995c, temos que v = 0,995 x 3 . 10⁸ = 2,99 x 10⁸ m/s. Podemos considerar a velocidade da partícula constante. Logo,

v = d/t

2,99 x 10⁸ = 1,25 x 10^-3 / t.

Logo t = 1,25 x 10^-3 / 2,99 x 10⁸

t = 0,4 x 10^-11s = 4 x 10^-12s

Alternativa: D