Professor Diminoi
POLINOMIOS
Definição
Chamamos de função polinomial ou, simplesmente, polinômio a função definida por:
P(x) = anxn + an-1xn-1 + an-2 xn-2 + … +a2x2 + a1x + a0
Em que:
anxn , an-1xn-1, an-2 xn-2, ..., a2x2 , a1x , a0
Com n são os termos do polinômio (note que todos os expoentes devem ser números naturais);
São números reais chamados coeficientes;
an, an -1, an-2, ..., a2, a1 e a0
a0 é o termo independente de x;
x é a variável.
Grau de um polinômio
O grau de um polinômio é o expoente máximo que ele possui.
Se (a for diferente de 0)
Então o expoente máximo n é dito grau do polinômio e indicamos gr(P) = n.
Exemplos
P(x) = 5 ou P(x) = 5xº é um polinômio constante, ou seja, gr(P) = 0.
P(x) = 3x + 5 é um polinômio do 1º grau, isto é, gr(P) = 1.
P(x) = 4x³ + 7x² é um polinômio do 3º grau, ou seja, gr(P) = 3
Obs.: Se P(x) = 0, não se define o grau do polinômio.
Valor numérico
O valor numérico de um polinômio P(x), para x = a, é o número que se obtém substituindo x por a e efetuando todas as operações indicadas pela relação que define o polinômio.
Exemplo
Considere o polinômio
P(x) = x2 – 2x - 3
P(x) = 22 – 2 . 2 – 3 = 3
P(1) = 12 – 2 . 1 = P(1) = - 4
Raiz de um polinômio
Se P(a) = 0, o número a é chamado de raiz ou zero de P(x).
Exemplo
Considere o polinômio P(x) = x2 – 4x - 12
Resolucao
P(x) = 62 – 4 . 6 – 12 = P(6) = 0
P(-2) = (-2)2 – 4(-2) – 12 = P(-2) = 0
6 e - 2 são raízes de P(x)
Exemplo
Sabendo-se que – 3 é raiz de P(x) = x³ + 4x² - ax + 1, calcule o valor de a.
Resolução
Como -3 é raiz de P(x) temos que:
P(-3) = 0
(-3)3 + 4(-3)2 –a.(-3) + 1 = 0
- 27 + 36 + 36a + 1 = 0
3a = -10
a = -10:3
Exemplo
Seja P(x) um polinômio do 2º grau. Sabendo-se que 2 é raiz de P(x), P(-1) = 12 e P(0) = 6, calcule P(3).
Resolução
Sabemos que um polinômio do 2º grau é da forma P(x) = ax² + bx + c. Podemos encontrar os valores de a, b e c através dos dados fornecidos pelo enunciado:
Como 2 é raiz de P(x):
P(2) = 0
a.22 + b.2 + c = 0
4a + 2b = - c (I)
Como P(-1) = 12:
P(-1) = 12
a.(-1)2 + b(-1) + c = 12
a – b 12 – c (II)
Como P(0) = 6:
P(0) = 6
a.02 + b . 0 + c = 6
c = 6
Substituindo o valor de c em (I) e (II), temos um sistema de equações: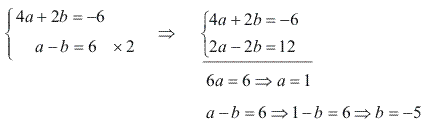
Assim:
P(x) = ax2 + bx + c
P(3) = x2 – 5x + 6
Calculando o valor de P(3):
P(x) = x2 – 5x + 6
P(3) = -32 – 5 .5 + 3 + 6
P(3) = 9 – 15 + 6
P(3) = 0
Polinômios idênticos
Dizemos que dois polinômios A(x) e B(x) são idênticos e indica-se A(x) = B(x)
Uando assumem valores numéricos iguais para qualquer valor comum atribuído à variável x.
A condição necessária para que dois polinômios sejam iguais ou idênticos é que os coeficientes dos termos correspondentes sejam iguais.
Exemplo
Os polinômios abaixo são idênticos?
A(x) = x2 – 1 e B(x + 1)(x – 1)
Resolução
Efetuando a multiplicação em B(x), temos:
B(x) = (x + 1)(x – 1)
B = x2 - 1
Note que os coeficientes dos termos correspondentes de A(x) e B(x) são iguais. Portanto são identicos.
A(x) = B(x)
Exemplo
Calcule a, b e c, sabendo-se que
x2 - 2x + 1 = a(x2 + x + 1) + (bx + c)(x +1)
Resolução
Vamos chamar o primeiro membro de A(x) e o segundo membro de B(x):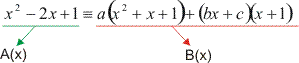
Efetuando as multiplicações e somando os termos semelhantes de B(x) temos:
B(x) = a(x2 + x + 1) + (bx + c)(x + 1)
B(x) = ax2 + ax + a + bx2 + bx + cx + c
B(x) = (a + b)2 + (a + b + c) . x + (a + c)
Assim:
A(x) = B(x)
1x2 – 2x + 1 =
(a + b)x2 + (a + b + c) . x + (a + c)
Igualando os coeficientes correspondentes, temos o seguinte sistema: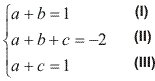
Substituindo (I) em (II):
a + b + c = - 2
a – 3 = 1
a = 4
Substituindo o valor de c em (III):
a + c = 1
a – 3 = 1
a = 4
Substituindo o valor de a em (I):
a + b = 1
4 + b = 1
b = - 3
Portanto, a = 4, b = -3 e c = -3.
Obsersvacao Um polinômio é dito identicamente nulo se tem todos os seus coeficientes nulos.
Operações com polinômios
A adição, a subtração e a multiplicação de polinômios seguem os procedimentos de Álgebra estudados no Ensino Fundamental.
Quando temos somas ou subtrações basta reduzirmos termos semelhantes, ou seja, operar separadamente potências de mesmo grau.
Nas multiplicações, basta aplicarmos a propriedade distributiva e em seguida reduzirmos os termos semelhantes.
Adição de polinômios
Exemplo
(3x3 – x2 + 5x – 6) + (-4x2 + 3x + 5) = 3x3 – 5x2 + 8x - 1
Subtração de polinômios
Exemplo
(7x4 – 2x2 + 4x - 4) – (x2 – 3x + 2) = 7x4 + 7x2 + 7x - 6
Multiplicação de polinômios
Exemplo
(3x2 – 4)(- 2x +5) = - 6x3 + 15x2 + 8x - 20
- Se A(x) e B(x) são polinômios, temos que:
- Se A(x) e B(x) possuem graus diferentes, o grau de A(x) + B(x) ou A(x) – B(x) é igual ao maior entre os graus de A(x) e B(x).
- Se A(x) e B(x) são de mesmo grau, o grau de A(x) + B(x) ou de A(x) – B(x) pode ser menor ou igual ao grau dos polinômios A(x) e B(x) ou, ainda, o polinômio resultante pode ser nulo.
- O grau de A(x).B(x) é a soma dos graus de A(x) e B(x).
Divisão de polinômios
Vamos pensar em uma divisão de números naturais. Dividir 7 por 5 significa obter o quociente 1 e o resto 2. Podemos escrever: ![]() Agora vamos pensar na divisão do polinômio A(x) pelo polinômio não-nulo B(x), que gera o quociente Q(x) e o resto R(x).
Agora vamos pensar na divisão do polinômio A(x) pelo polinômio não-nulo B(x), que gera o quociente Q(x) e o resto R(x).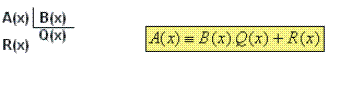 Nessa divisão:
Nessa divisão:
A(x) é o dividendo;
B(x) é o divisor;
Q(x) é o quociente;
R(x) é o resto da divisão.
O grau de R(x) deve ser menor que o grau de B(x) ou R(x) = 0.
Quando A(x) é divisível por B(x), dizemos que a divisão é exata, isto é, R(x) = 0
Exemplo
Determine o quociente de A(x) = x4 + x3 – 7x2 + 9x – 1 por B(x) = x2 + 3x - 2
Resolução
Dividimos o termo de maior grau do dividendo pelo termo de maior grau do divisor. O resultado será um termo do quociente:![]()
Multiplicamos x² por B(x) e subtraímos o produto de A(x), obtendo o primeiro resto parcial: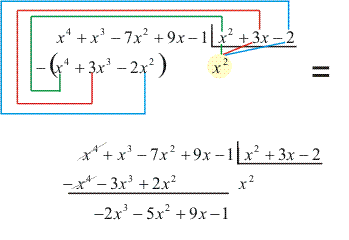
Dividimos o termo de maior grau do primeiro resto parcial pelo termo de maior grau do divisor, e obteremos como o resultado um termo do quociente:![]()
Multiplicamos -2x por B(x) e subtraímos o produto do primeiro resto parcial, obtendo o segundo resto parcial: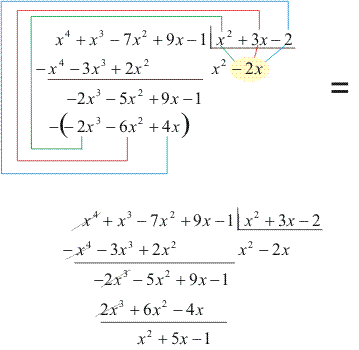
Dividimos o termo de maior grau do segundo resto parcial pelo termo de maior grau do divisor, e obteremos como o resultado um termo do quociente:![]()
Multiplicamos 1 por B(x) e subtraímos o produto do segundo resto parcial: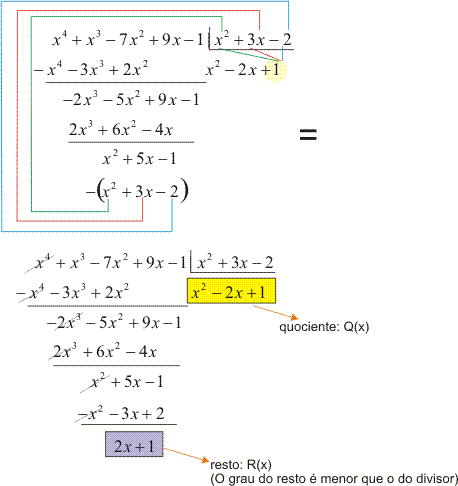
Como o grau do resto é menor que o grau do divisor, a divisão está encerrada.
Verificamos que: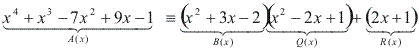
Exemplo
Determine o quociente de
A(x) = x3 + 4x2 + x – 6 por B(x) = x + 2
Resolução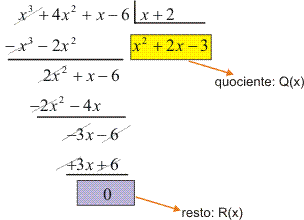
Verificamos facilmente que:![]()
Nesses dois exemplos, utilizamos o método da chave para efetuar a divisão de polinômios.
Pelos exemplos verificamos que:
grau do quociente = grau do dividendo – grau do divisor
Teorema do resto
Vamos calcular o resto da divisão de P(x) = 4x2 – 2x + 3 por B(x) = 2x - 1
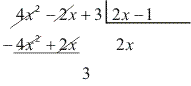
R(x) = 3
A raiz do divisor é![]()
Note que: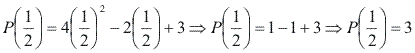
Ou seja, quando B(x) é um polinômio de grau 1, o resto é igual ao valor numérico de P(x) quando x assume o valor da raiz de B(x).![]()
Note que o grau do resto é 0, pois é menor que o grau do divisor, que é 1. Assim, o resto é uma constante r.
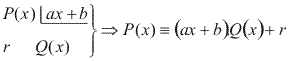
Efetuando![]()
Temos:
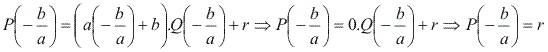
Assim, podemos enunciar o seguinte teorema:
Teorema do resto
O resto da divisão de um polinômio P(x) pelo binômio ax + b é igual ao valor numérico desse polinômio para![]() Ou seja,
Ou seja,![]() Exemplo
Exemplo
Calcule o resto da divisão de P(x) = x² + 5x - 1 por B(x) = x + 1:
Resolução
Achamos a raiz do divisor:
x + 1= 0
x = - 1
Pelo teorema do resto, sabemos que o resto é igual a P(-1):
P(-1) = (-1)² + 5.(-1) -1
P(- 1) = - 5 = r
Portanto, o resto da divisão de x² + 5x - 1 por x + 1 é - 5.
Note que P(x) é divisível por ax + b quando r = 0, ou seja, quando![]() Daí vem o enunciado do seguinte teorema:
Daí vem o enunciado do seguinte teorema:
Teorema de D’Alembert
Um polinômio P(x) é divisível pelo binômio 1 se e somente se![]() O caso mais importante da divisão de um polinômio P(x) é aquele em que o divisor é da forma (x - ).
O caso mais importante da divisão de um polinômio P(x) é aquele em que o divisor é da forma (x - ).
Note que é a raiz do divisor. Então o resto da divisão de P(x) por (x – ) é:
r = P( )
Assim:
P(x) é divisível por (x – ) quando r = 0, ou seja, quando P( ) = 0.
Exemplo
Determine o valor de p, para que o polinômio
P(x) = 2x3 + 5x2 – px + 2
Seja divisível por x – 2:
Resolução
Para que P(x) seja divisível por x – 2 devemos ter P(2) = 0, pois 2 é a raiz do divisor:
P(x) = 0
2 . 23 + 5 . 22 – p.2 + 2 = 0
2 . 8 = 5 . 4 – 2p + 2 = 0
16 + 20 – 2p + 2 = 0
2p – 28
P = 19
Assim, para que
P(x) = 2x3 + 5x2 – px + 2
Seja divisível por x – 2 devemos ter p = 19.
Divisão de um polinômio por (x – a)(x – b)
Vamos supor que um polinômio P(x) é divisível por (x – a) e por (x –b), sendo a b . Será que P(x) é divisível pelo produto (x – a)(x – b)?
O divisor (x – a)(x – b) tem grau 2, logo o resto terá, no máximo, grau 1.
Então, podemos escrever:![]() Como P(x) é divisível por (x – a), então P(a) = 0:
Como P(x) é divisível por (x – a), então P(a) = 0:
P(a) = 0
(a – a)(a – b) . Q(a) + m . a + n = 0
0(a – b) . Q(a) + m . a + n = 0
m . a + n = 0
Como P(x) é divisível por (x –b), então P(b) = 0:
P(x) = 0
(a – b)(b – b).Q(b) + m.b + n = 0
(a – b).0.Q(b) + m . b + n = 0
m . b + n = 0
Temos o seguinte sistema de equações: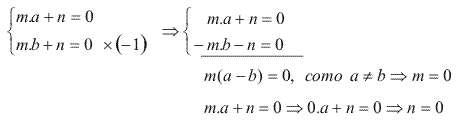
R(x) = mx + n
R(x) = 0x + 0
R(x) = 0
Portanto, podemos concluir que P(x) é divisível por (x – a)(x – b).
Temos, deste modo, o seguinte teorema:
Se P(x) é divisível por (x – a) e por (x – b) com a b, então P(x) é divisível por (x – a)(x – b).
Generalizando o teorema, se P(x) é divisível por (x – a1) (x – a2), ..., (x – na) com a1, a2, ... . an
distintos, então P(x) é divisível por (x – a1)(x –a2), ..., (x –na).
Exemplo
O polinômio
P(x) = x3 – 6x2 + 11x - 6
E divisível por (x - 1)(x - 2)?
Resolução
Se P(x) for divisível por (x - 1) e por (x - 2), então P(x) será divisível por (x - 1)(x - 2).
P(x) é divisível por (x -1), isto é, P(1) = 0?
P(1) = 13 – 6 . 12 + 11 . 1 – 6 = 1 - 6 + 11 – 6 = 0
Sim.
P(x) é divisível por (x - 2), isto é, P(2) = 0?
P(2) = 23 – 6 . 22 + 11 . 2 – 6 = 8 – 24 + 22 – 6 = 0
Sim.
Como P(x) é divisível por (x -1) e por (x - 2) então P(x) é divisível por (x - 1)(x - 2).
Exemplo
Um polinômio P(x), dividido por x – 1, dá resto 4; dividido por x +1, dá resto 2. Qual o resto da divisão de P(x) por (x – 1)(x + 1)?
Resolução
Como o divisor (x – 1)(x + 1) tem grau 2, o grau do resto será no máximo 1.
Podemos escrever: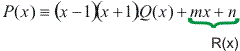 P(x) dividido por x – 1 dá resto 4. Assim, P(1) = 4:
P(x) dividido por x – 1 dá resto 4. Assim, P(1) = 4:
P(1) = 4
(1 - 1)(1 + 1)Q(1) + m . 1 + n = 4
m + n = 4
P(x) dividido por x + 1 dá resto2. Assim, P(-1) = 2:
P(-1) = 2
(-1 - 1)(-1 + 1)Q(-1) + m . (-1) + n = 2
m + n = 2
Temos o seguinte sistema de equações: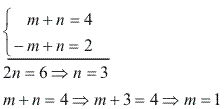
R(x)= mx + n
R(x) = x + 3
Portanto, o resto da divisão de P(x) por (x – 1)(x + 1) é x + 3.
Dispositivo prático de Briot-Ruffini
Para efetuarmos a divisão de um polinômio P(x) por um binômio da forma (x – ), podemos utilizar o dispositivo prático de Briot-Ruffini.
Vamos efetuar a divisão de
P(x) = 3x5 – 2x4 + 3x2 + 1
Por x - 2 através desse dispositivo. Acompanhe o roteiro para a resolução:
1º) Colocamos a raiz do divisor e os coeficientes do dividendo (ordenadamente do termo de maior grau para o termo de menor grau, completando com zero os termos que não aparecem) no dispositivo: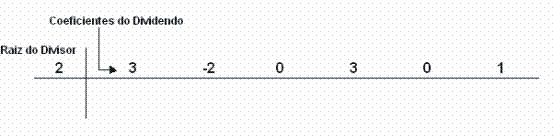 2º) Abaixamos o primeiro coeficiente do dividendo:
2º) Abaixamos o primeiro coeficiente do dividendo: 3º) Multiplicamos a raiz do divisor pelo coeficiente repetido e somamos o produto com o segundo coeficiente do dividendo, colocando o resultado abaixo deste:
3º) Multiplicamos a raiz do divisor pelo coeficiente repetido e somamos o produto com o segundo coeficiente do dividendo, colocando o resultado abaixo deste:
 4º) Multiplicamos a raiz do divisor pelo número colocado abaixo do 2º coeficiente e somamos o produto com o 3º coeficiente, colocando o resultado abaixo deste, e assim sucessivamente:
4º) Multiplicamos a raiz do divisor pelo número colocado abaixo do 2º coeficiente e somamos o produto com o 3º coeficiente, colocando o resultado abaixo deste, e assim sucessivamente: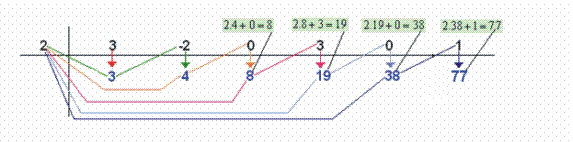 5º) Fazemos um traço entre o último e o penúltimo números obtidos. O último número é igual ao resto da divisão e os números que ficam à esquerda deste são os coeficientes do quociente:
5º) Fazemos um traço entre o último e o penúltimo números obtidos. O último número é igual ao resto da divisão e os números que ficam à esquerda deste são os coeficientes do quociente: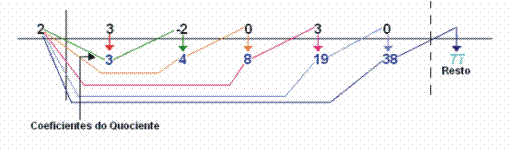 Portanto
Portanto![]()
Exemplo
Obtenha o quociente e o resto da divisão de x³ - 3x² + 5x - 1 por 2x - 1:
Resolução
Temos:
P(x) = (2x – 1)Q(x) + r
Para aplicarmos o dispositivo de Briot-Ruffini, o coeficiente de x no divisor deve ser 1. Nesse caso, utilizamos o seguinte artifício:
![]()
Fazemos
![]()
![]()
Aplicando o dispositivo de Briot-Ruffini: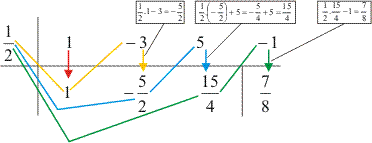
![]()
Como
Q(x) = 2Q(x)![]()
Portanto![]()
e![]()
Divisões sucessivas
Vamos supor que P(x) é divisível por (x – a) e o quociente dessa divisão é divisível por (x – b).
Será que P(x) é divisível por (x – a)(x – b)?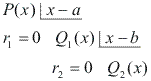 Note que:
Note que:![]() Então:
Então:
P(x) = (x – a(x – b).Q2(x)
Portanto, P(x) é divisível por (x - a)(x - b).
Exemplo
Verifique se
P(x) = x3 – 6x2 + 11x - 6
E divisível por (x - 1)(x - 2):
Resolução
Dividindo P(x) por (x – 1):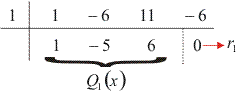
Como r1 = 0, P(x) é divisível por (x – 1).
Dividindo Q1(x) por (x – 2):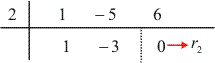
Como r2 = 0 e Q1(x)
E divisível por (x – 2).
Assim, P(x) é divisível por (x – 1) e o quociente dessa divisão é divisível por (x – 2); logo P(x) é divisível pelo produto (x – 1)(x – 2).
Exemplo
Verifique se P(x) = x6 – 2x5 – x2 + 2x
E divisível por
(x2 – 1)(x – 2)
E obtenha o quociente final:
Resolução
Note que
(x2 – 1)(x – 2) = (x – 1)(x + 1)(x – 2)
Vamos fazer, num só dispositivo, as divisões de P(x) por (x - 1), do quociente obtido nessa divisão por (x + 1) e do novo quociente por (x – 2) (as divisões sucessivas não precisam ser feitas obrigatoriamente nessa ordem):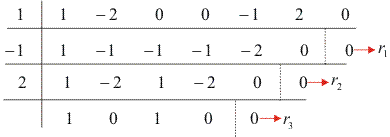
Podemos concluir então que P(x) é divisível por (x2 – 1)(x - 2) e que Q(x) = x3 + x.
Equações polinomiais
Equação polinomial é toda equação redutível à forma P(x) = 0, em que P(x) é um polinômio de grau maior ou igual
Exemplos
a) x5 – x4 + x2 + 2 = 0
b) ix2 + 5x – 4 = 0
c) x3 – 4x + 5x + 1 = 0
As raízes de uma equação polinomial são as raízes do polinômio P(x). O conjunto de todas as raízes de uma equação é o conjunto solução dessa equação.
Observe os seguintes polinômios e as suas raízes. Podemos escrevê-los nas seguintes formas fatoradas:
Polinomios Formas Fatoradas
P(x) = 5x - 15, de raiz 3. P(x) = 5(x – 3)
P(x) = x2 – 5x + 6, de raízes 2 e 3. P(x) = (x – 2)(x – 3)
P(x) = 2x4 – 20x3 + 70x2 – 100x + 48, de raízes 1, 2, 3 e 4. P(x) = 2(x – 1)(x– 2)(x - 3)(x – 4)
De maneira geral, todo polinômio
P(x) = anxn + na-1xn-1 + an-2 xn-2 + ... + a2x2 + a1x + a0
pode ser escrito na seguinte forma fatorada:
P(x) = an(x – r1)(x – r2) ...(x – rn)
Em que r1, r2, ... rn são raízes de P(x).
Daí vem o seguinte teorema:
Toda equação polinomial P(x) = 0, de grau n, , tem exatamente n raízes reais ou complexas.
Exemplo
Qual é a forma fatorada de 3x3 – 15x2 – 3x + 15 = 0 , cujas raízes são 1, -1 e 5?
Resolução
Como trata-se de uma equação do 3º grau com as 3 raízes distintas, temos:
3(x - 1)(x + 1)(x - 5) = 0
Exemplo
Qual é a forma fatorada de x3 – 5x2 – 34x + 80 = 0 , sabendo que uma de suas raízes é 2?
Resolução
Se 2 é raiz de P(x) , podemos obter o quociente Q(x) dividindo P(x) por (x – 2):
![]()
Fazendo Q(x) = 0, determinamos as outras raízes da equação:![]()
A forma fatorada de x3 – 5x2 – 34x + 80 = 0 é (x – 8)(x – 2)(x + 5).
Multiplicidade de uma raiz
As raízes de uma equação algébrica podem ser todas distintas ou não. O número de vezes que uma mesma raiz aparece inidica a sua multiplicidade.
Exemplo
Na equação (x – 3)2 . (x + 2)3 . (x – 1) = 0, notamos que:
Exemplo
Qual a multiplicidade da raiz 2 do polinômio
P(x) = x4 – 5x3 + 6x2 + 4x - 8?
Resolução
Vejamos quantas divisões sucessivas por (x – 2) cujo resto é nulo são possíveis: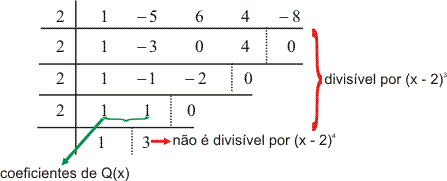
Portanto, P(x) = (x – 2)³.Q(x). Logo, 2 é uma raiz tripla ou de multiplicidade 3.
Raízes nulas, complexas e racionais
Raízes nulas
Toda equação algébrica cujo termo independente é zero admite o número zero como raiz, cuja multiplicidade é igual ao menor expoente da incógnita.
Essas raízes são denominadas raízes nulas.
Exemplos
Raízes complexas
Vamos resolver a equação algébrica x² -2x + 2 = 0: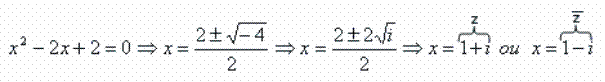 É possível demonstrar que, se um número complexo cuja parte imaginária não é nula é raiz de uma equação com coeficientes reais, seu conjugado também é raiz dessa equação.
É possível demonstrar que, se um número complexo cuja parte imaginária não é nula é raiz de uma equação com coeficientes reais, seu conjugado também é raiz dessa equação.
Consequências
- O número de raízes complexas de uma equação algébrica de coeficientes reais é necessariamente par;
- Se uma equação algébrica de coeficientes reais for de grau ímpar, ela admitirá pelo menos uma raiz real.
Raízes racionais
Dada uma equação algébrica de coeficientes inteiros Anxn + na-1 xn-1 + na-2 xn-2 + ,... + a2x2 + a1x + a0 = 0 com (a diferente 0) e (a0 diferente 0).
Se existirem raízes racionais, elas serão da forma p/q, com p e q primos entre si, em que p é um divisor de e q é divisor de .
Por exemplo, na equação 2x4 – 5x3 – 4x2 + 15x – 6 = 0 temos:
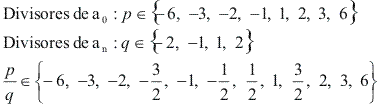
Observações:
Nem todo número obtido é raiz da equação. Após a listagem dos candidatos a raízes racionais temos de fazer a verificação.
- Essa pesquisa de raízes racionais só pode ser feita em equações de coeficientes inteiros.
- Se = 1, os candidatos a raízes são os divisores de .
- Se a soma dos coeficientes da equação for igual a zero, o número 1 será raiz da equação.
Exemplo
Resolva a equação x4 + x3 – 7x2 – x + 6 = 0.
Resolução
Como o coeficiente do termo de maior grau é 1, os candidatos a raízes racionais são os divisores do termo independente:
{-6, -3, -2, -1, 1, 2, 3, 6}
Vamos fazer a verificação de alguns desses valores:
P(-6) = 840 (- 6 não é raiz ) P(6) = 1260 (6 não é raiz )
P(1) = 0 → 1 é raiz P(-1) = 0 → -1 é raiz
Como temos uma equação do 4º grau e conhecemos duas de suas raízes, aplicando o dispositivo de Briot-Ruffini obtemos uma equação do 2º grau: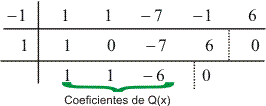 Portanto, a equação pode ser escrita como (x - 1)(x + 1).Q(x) = 0, com Q(x) = x² + x – 6. As soluções da equação são -1, 1 e as raízes de Q(x):
Portanto, a equação pode ser escrita como (x - 1)(x + 1).Q(x) = 0, com Q(x) = x² + x – 6. As soluções da equação são -1, 1 e as raízes de Q(x):![]() Por conseguinte, o conjunto solução da equação é: S = {-3, -1, 1, 2}
Por conseguinte, o conjunto solução da equação é: S = {-3, -1, 1, 2}
Exemplo
Resolva a equação x5 + 2x4 – 2x3 + 2x2 – 3x = 0
Resolução
Colocando x em evidência, temos:
x(x4 + 2x3 – 2x2 – 3) = 0
Desse modo, uma raiz é 0 e as outras são soluções da equação x4 + 2x3 – 2x2 + 2x – 3 = 0
Note que em x4 + 2x3 – 2x2 + 2x – 3 = 0 todos os coeficientes são inteiros. Como o coeficiente do termo de maior grau é 1, os candidatos a raízes racionais são os divisores do termo independente:
{-3, -1, 1, 3}
Fazendo a verificação:
P(-3) = 0 → -3 é raiz P(3) = 120
P(-1) = - 8 P(1) = 0 → 1 é raiz
Podemos escrever a equação x5 + 2x4 – 2x3 + 2x2 – 3x = 0 da seguinte forma:
x(x + 3)(x – 1)Q(x) = 0
Já sabemos que o quociente de x5 + 2x4 – 2x3 + 2x2 – 3x por x é x4 + 2x3 – 2x2 + 2x - 3
Agora vamos dividir x4 + 2x3 – 2x2 + 2x - 3 por (x + 3) e esse quociente por (x – 1) para obtermos Q(x): Q(x) = x² + 1
Q(x) = x² + 1![]() Portanto, o conjunto solução da equação x5 + 2x4 – 2x3 + 2x2 – 3x = 0 e S = {-3, 0, 1, -i, i}
Portanto, o conjunto solução da equação x5 + 2x4 – 2x3 + 2x2 – 3x = 0 e S = {-3, 0, 1, -i, i}
Relações de Girard
Albert Girard, matemático belga nascido no ano de 1595, em seus estudos estabeleceu fórmulas matemáticas que relacionam os coeficientes e as raízes de uma equação algébrica.
Considere o polinômio do 2º grau:
P(x) = ax² + bx + c, com a 0,
cujas raízes são r1 e r2. Note que: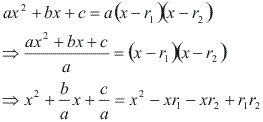
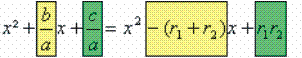 Igualando os coeficientes:
Igualando os coeficientes:![]()
![]()
![]()
Considere o polinômio do 3º grau P(x) = ax³ + bx² + cx + d, com a 0, cujas raízes são r1, r2 e r3. Note que: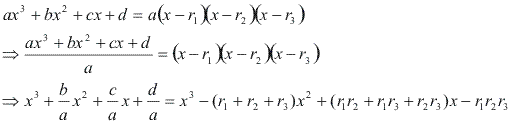
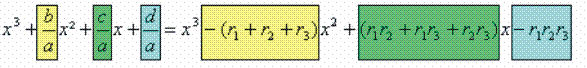
Igualando os coeficientes:![]()
![]()
![]()
Fazendo um raciocínio análogo aos anteriores, encontramos as relações para uma equação algébrica de um grau qualquer n: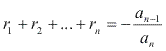
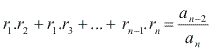
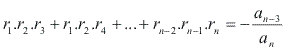
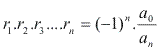
Exemplo
Resolva a equação x3 – 10x2 + 31x – 30 = 0, sabendo que uma raiz é igual à soma das outras duas r1 + r2 = r3 :
Resolução
Relação de Girard: ![]()
![]() Vamos dividir x³ - 10x² + 31x - 30 por (x – 5) para encontrar as outras raízes:
Vamos dividir x³ - 10x² + 31x - 30 por (x – 5) para encontrar as outras raízes:
Q(x) = x² - 5x + 6![]()
Portanto, o conjunto solução da equação x3 – 10x2 +31x – 30 = 0 é S = {2, 3, 5}
Continua ...





