FATORACAO

Professor Diminoi

Polinômios & Fatoração Algébrica
A fatoração surge como um recurso da Matemática para facilitar os cálculos algébricos; através dela conseguimos resolver situações mais complexas. Na fatoração por fator comum em evidência, utilizamos a idéia de fazer grupos de polinômios, ao fatorar escrevemos a expressão na forma de produto de expressões mais simples.

Polinômios & Fatoração Algébrica
Os produtos notáveis são polinômios que possuem uma forma geral para realizar a sua resolução. Eles são utilizados para simplificar problemas envolvendo multiplicação de polinômios. Conhecer a forma de resolução de cada um dos cinco produtos notáveis facilita na resolução de situações-problemas que envolvem polinômios, que são bastante comuns na geometria analítica e outras áreas da Matemática.

Fatoração de expressão algébrica - Expressões algébricas são expressões que apresentam números e variáveis, e fazer a fatoração de expressão algébrica significa escrever a expressão como uma multiplicação de dois ou mais termos.

Fatoração por Fator comum - O fator comum é a fatoração por meio do termo em comum ou colocação de termos em evidência. Para fatorar uma expressão algébrica utilizando esse caso de fatoração, todos os monômios da expressão algébrica devem ter pelo menos algum termo em comum.
A fatoração é feita colocando o termo comum em evidência:

Exemplos

a – ab = a(1 – b)

EXERCÍCIOS RESOLVIDOS
Fatoração colocando o Fator Comum em Evidência

01) 8x³ - 2x² + 6x (fator comum: 2x)
2x (4x² - x + 3)

02) a⁶ – 4a² (fator comum: a²)
a² (a⁴ – 4)

03) 4x³ + 2x² + 6x (notamos que o monômio 2x é comum a todos os termos)
2x (2x² + x + 3)

04) 6x³y³ – 9x²y + 15xy² (fator comum: 3xy)
3xy (2x²y² – 3x + 5y)

05) 8b⁴ – 16b² – 24b (fator comum: 8b)
8b (b³ – 2b – 3)

06) 8x² – 32x – 24 (fator comum: 8)
8 (x² – 4x – 3)

07) 3x² – 9xy + 6x + 21x³ (fator comum: 3x)
3x (x – 3y + 2 + 7x²)

08) 2x² - 200 = 0
Resolução:
2x² = 200
x² = 200/2
x² = 100
√x² = √100
x’ = 10
x’’ = – 10

09) (3x – 2) (x – 5) = 0
Resolução:
3x – 2 = 0
3x = 2
x’ = 2/3
x – 5 = 0
x’’ = 5

Propriedades dos Produtos Notáveis
Quadrado da soma de dois termos - O quadrado da soma dos dois termos é representado pela expressão
(a + b)² = a² + 2ab + b²

Quadrado da diferença de dois termos - O quadrado da diferença dos dois termos é representado pela expressão
(a – b)² = a² - 2ab + b²

Produto da soma pela diferença de dois termos - O produto da soma pela diferença dois termos é representado pela expressão
a² - b² = (a + b) . (a – b)

Cubo da soma de dois termos - O cubo da soma de dois termos é representado pela expressão
(a + b)³ = a³ + 3a²b + 3ab² + b³

Cubo da diferença de dois termos - O cubo da diferença de dois termos é representado pela expressão
(a – b)³ = a³ - 3a²b + 3ab² - b³

Métodos para fatorar expressões algébricas
Agora veremos os principais métodos de fatoração, nos mais utilizados faremos uma breve justificativa geométrica.

Fatoração por evidência
Considere o retângulo:
Observe que a área do retangulo azul mais a área do retângulo verde resultam no retângulo maior. Vamos analisar cada uma dessas áreas:
A_AZUL = b · x
A_VERDE = b · y
A_MAIOR = b · (x + y)
Assim, temos que:
A_MAIOR = A_AZUL + A_VERDE
b (x + y) = bx + by
AQUIIIII

Exemplos
a)Para fatorar a expressão: 12x + 24y.
Resolução:
Nota-se que 12 é o fator em evidência, uma vez que ele aparece em ambas as parcelas, assim, para determinar os números que vão no interior dos parênteses, basta dividir cada parcela pelo fator em evidência.
12x : 12 = x
24y : 12 = 2y
12x + 24y = 12 · (x + 2y)

b) Para fatorar a expressão21ab² – 70a²b.
Resolução:
Do mesmo modo, inicialmente, determina-se o fator em evidência, isto é, o fator que se repete nas parcelas. Veja que da parte numérica temos o 7 como fator comum, uma vez que ele é o único que divide ambos os números. Agora, em relação à parte literal, veja que se repete somente o fator ab, logo, o fator em evidência é: 7ab.
21ab² – 70a²b = 7ab (3b – 10^a)

Fatoração por agrupamento
A fatoração por agrupamento é decorrente da fatoração por evidência, a única diferença é que, em vez de termos um monômio como fator comum ou fator em evidência, teremos um polinômio, veja o exemplo:
Considere a expressão (a + b) · xy + (a + b) · wz²
Resolução:
Observe que o fator comum é o binômio (a + b), logo, a forma fatorada da expressão anterior é:
(a + b) · (xy + wz²)

Diferença entre dois quadrados
Considere dois números a e b, quando temos a diferenca do quadrado desses números, isto é, a² – b², então podemos escrevê-los como sendo o produto da soma pela diferença, ou seja:
a² – b² = (a + b) · (a – b)

Exemplos
a)Para fatorar a expressão x²– y².
Resolução:
Podemos utilizar a diferença entre dois quadrados, logo:
x² – y² = (x + y) · (x – y)

b) Para fatorar 020²– 2.019².
Resolução:
Podemos utilizar a diferença entre dois quadrados, logo:
2.020² – 2.019² 
(2.020 + 2.019) · (2.020 – 2.019)
2.020² – 2.019² = 4.039 · 1
2.020² – 2.019² = 4.039

Trinômio do quadrado perfeito
Considere o quadrado seguinte de lado (a + b) e observe as áreas dos quadrados e retângulos formados em seu interior.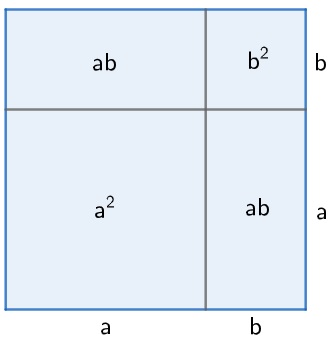
Veja que a área do quadrado maior é dada por (a + b)², mas, por outro lado, a área do quadrado maior pode ser obtida pela soma dos quadrados e retângulos do seu interior, assim:
(a + b)² = a² + ab + ab + b²
(a + b)² = a² + 2ab + b²
(a + b)² = a² + 2ab + b²
De maneira análoga, temos que:
(a – b)² = a² – 2ab + b²

Exemplo:
Considere a expressão x² + 12x + 36.
Resolução:
Para fatorar uma expressão desse tipo, basta identificar o coeficiente da variável x e o coeficiente independente, e comparar com a fórmula dada, veja:
x² + 12x + 36
a² + 2ab + b²
Fazendo as comparações, veja que x = a, 2b = 12 e b² = 36; das igualdades, temos que b = 6, assim a expressão fatorada é:
x² + 12x + 36 = (x + 6)²

Trinômio do segundo grau
Considere o trinômio ax² + bx + c. A sua forma fatorada pode ser encontrada utilizando suas raízes, ou seja, os valores de x que zeram tal expressão. Para determinar os valores que zeram tal expressão, basta resolver a equação ax² + bx + c = 0 utilizando o método que achar conveniente. Aqui ressaltamos o método mais conhecido: metodo de Bascara.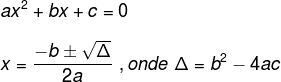

A forma fatorada do trinômio ax² + bx + c é:
ax² + bx + c = a · (x – x₁) · (x – x₂)

Exemplo:
Considere a expressão x² + x – 20.
O primeiro passo é determinar as raízes da equação x² + x – 20 = 0.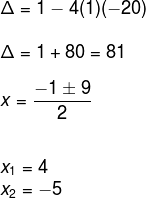

Assim a forma fatorada da expressão x² + x – 20 é:
(x – 4) · (x + 5)

Cubo da diferença entre dois números
O cubo da diferença entre dois números a e b é dado por:
(a – b)³ = (a – b) · (a – b)²
(a – b)³ = (a – b) · (a² – 2ab + b²)

Cubo da soma de dois números
De maneira análoga, temos que (a + b)³ = (a + b) · (a + b)² , logo:
(a + b)³ = (a + b) · (a² + 2ab + b²)

A fatoração é um instrumento que facilita a resolução das expressões algébricas.

EXERCÍCIOS RESOLVIDOS
09) (Cefet-MG) Sendo o número n = 684² – 683², a soma dos algarismos de n é:
(A) 14
(B) 15
(C) 16
(D) 17
(E) 18
Resolução:
Para determinar a soma dos algarismos de n, inicialmente fatorarmos a expressão, uma vez que calcular os quadrados e, em seguida, realizar a subtração geram trabalho desnecessário. Fatorando a expressão utilizando a diferença entre dois quadrados, temos:
n = 684² – 683²
n = (684 + 683) · (684 – 683)
n = 1.367 · 1
n = 1.367
Portanto, a soma dos algarismos de n é dada por 1 + 3 + 6 + 7 = 17
Alternativa: D

10) (Insper-SP-modificada) Determine o valor da expressão:
Resolução:
Com a intenção de facilitar a notação, vamos nomear a = 2.009 e b = 2. Lembre-se de que 2² = 4, assim temos que: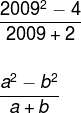

Veja que, no numerador da fração, temos a diferença entre dois quadrados, logo, podemos escrever a² – b² = (a + b) (a – b).
Assim:

a – b = 2009 – 2 = 2007.

11) (Termomecânica) Simplificando a expressão ³√√a⁸.b¹², obtém-se
(A) a² . b⁴ . √a
(B) a⁴ . b⁶ . ³√a
(C) a . b² . ³√a
(D) a . b² . ⁶√a
Resolução
³√√a⁸. b^12
3√a⁴. b^6
3√a² . a . b⁶.√a
a .b².³√.
Alternativa: C

12) Simplifique a expressão algébrica: x³ + 4y + 7x² + 3x³
Resolução:
Simplificando adição e subtração em expressões algébricas, realizando as operações nos coeficientes e mantendo a parte literal.
x³ + 4y + 7x² + 3x³
(1 + 3)x³ + 4y + 7x²
4x³ + 7x² + 4y

13) Simplifique a expressão: 3x² – 7x² + 4x³ – 5x²
Resolução:
Para simplificamos uma subtração subtraindo os coeficientes e mantendo as variáveis, fazemos a mesma coisa que na adição.
3x² – 7x² + 4x³ – 5x²
(3 – 7 – 5)x² + 4x³
-9x² + 4x³
4x³ – 9x²

14) Simplifique a seguinte expressão: 4x³ + x³ – 2x² + 5x² – 4y + 8y
Resolução:
Para simplificar realizando as operações sobre os coeficientes e mantendo as variáveis.
4x³ + x³ – 2x² + 5x² – 4y + 8y
(4 + 1)x³ + (- 2 + 5)x² + (- 4 + 8)y
5x³ + 3x² + 4y

15) Analisando as alternativas a seguir, marque aquela que contém de forma correta a solução do produto notável (x – 5)²
(A) x² + 25
(B) x² – 25
(C) x² – 10x + 25
(D) x² + 10x – 25
(E) x² + 10
Resolução:
Note que estamos calculando o quadrado de uma diferença. Nesse produto notável, temos como resposta:
(x – 5)² = x² – 2 · 5 · x + 5²
(x – 5)² = x² – 10x + 25
Alternativa: C

16) Durante as aulas de matemática, o professor Raul decidiu revisar com os estudantes os produtos notáveis. Então, ele escreveu no quadro as seguintes expressões:
I → (x – 2) (x + 2)
II → (x + 3)²
III → (x – 2)³
Os produtos notáveis listados pelo professor são conhecidos, respectivamente, como:
(A) Quadrado da diferença, quadrado da soma e cubo da diferença.
(B) Produto da soma pela diferença, quadrado da soma e cubo da diferença.
(C) Trinômio quadrado perfeito, cubo da soma, cubo da diferença.
(D) Quadrado da soma, produto da soma pela diferença e cubo da diferença.
(E) Produto da soma pela diferença, quadrado do cubo, cubo da diferença.
Resolução:
I → produto da soma da diferença
II → quadrado da soma
III → cubo da diferença
Alternativa: B

17) Realizando a simplificação da expressão algébrica a seguir, encontraremos:
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
Resolução:
Podemos observar que, no numerador, temos um produto da soma pela diferença, então, temos que: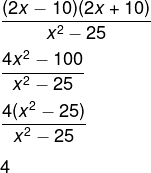

Alternativa: D

18) Simplificando a expressão (x + 5)² – x (x + 10), encontraremos:
(A) 25
(B) 30
(C) 50
(D) 75
(E) 100
Resolução:
Calculando, temos que:
(x + 5)² – x(x + 10)
x² + 10x + 25 – x² – 10x
25
Alternativa: A

19) Resolvendo os produtos notáveis da expressão (2x – 5) (2x + 5) – (2x – 5)² e simplificando, encontraremos como resultado o polinômio:
(A) 20x
(B) 20x – 50
(C) 8x³ + 2x²
(D) 50
(E) 2x – 25
Resolução:
Resolvendo os produtos notáveis, temos que:
(2x – 5) (2x + 5) – (2x – 5)²
4x² – 25 – (4x² – 20x + 25)
4x² – 25 – 4x² + 20x – 25
20x – 50
Alternativa: B

20) Durante os estudos de cálculo 1, um matemático se deparou com a seguinte expressão: (g + a) (g – a), vendo-se diante de um produto notável conhecido como o produto da soma pela diferença. A solução desse produto notável é sempre igual ao:
(A) quadrado do primeiro termo, mais duas vezes o primeiro, vezes o segundo termo, mais o quadrado do segundo termo.
(B) quadrado do primeiro termo, menos duas vezes o primeiro, vezes o segundo termo, mais o quadrado do segundo termo.
(C) quadrado do primeiro termo menos o segundo termo.
(D) quadrado do primeiro termo mais o quadrado do segundo termo.
(E) quadrado do primeiro termo menos o quadrado do segundo termo.
Resolução:
Temos um caso de produto da soma pela diferença, que tem como resposta o quadrado do primeiro termo menos o quadrado do segundo termo.
Alternativa: D

21) Ao desenvolver o produto (2x + 4)², encontramos como solução o polinômio:
(A) 4x² + 16x + 16
(B) 4x + 16
(C) 4x² + 16
(D) 2x² + 8x + 8
(E) 4x + 8
Resolução:
Calculando o produto notável conhecido como quadrado da soma, temos como resultado:
(2x + 4)² = 4x² + 16x + 16
Alternativa: A

22) Das alternativas a seguir, marque aquela que contém um produto notável:
(A) x² + 25
(B) (x² – 3)
(C) (a – 3)²
(D) (x + 2) (x – 4)
(E) (x – 1) (x – 2) (x + 3)
Resolução:
Note que, na alternativa C, temos o cubo da diferença, que é um produto notável; as demais não são produtos notáveis.
Alternativa: C

23) Sobre os produtos notáveis, julgue as afirmativas a seguir:
I → A multiplicação de dois polinômios é sempre um produto notável.
II → O produto (a + b)³ é um produto notável.
III → O produto da soma pela diferença é sempre igual à soma do quadrado do primeiro e segundo termos.
Marque a alternativa correta:
(A) Somente a afirmativa I é falsa.
(B) Somente a afirmativa II é falsa.
(C) Somente a afirmativa III é falsa.
(D) Todas as afirmativas são falsas.
(E) Todas as afirmativas são verdadeiras.
Resolução:
I → A multiplicação de dois polinômios é sempre um produto notável. (falsa)
Nem sempre uma multiplicação é um produto notável.
II → O produto (a + b)³ é um produto notável. (verdadeiro)
Verdadeira, pois trata-se do cubo da soma.
III → O produto da soma pela diferença é sempre igual à soma do quadrado do primeiro e segundo termos. (verdadeira)
Sempre que encontramos um produto da soma pela diferença, ele será igual ao quadrado do primeiro termo menos o quadrado do segundo termo.
Alternativa: A

24)  (UFRGS) Se x + y = 13 e x · y = 1, então, x² + y² é:
(A) 166
(B) 167
(C) 168
(D) 169
(E) 170
Resolução:
Calculando o quadrado da soma, temos que:
(x + y)² = x² + 2xy + y²
Sabemos que x + y = 13 e que xy = 1:
(13)² = x² + 2 · 1 + y²
169 = x² + 2 + y²
169 – 2 = x² + y²
167 = x² + y²
Alternativa: B

25) A diferença entre (1522² – 1520²) é igual a:
(A) 2000
(B) 2340
(C) 5040
(D) 6084
(E) 7320
Resolução:
Transformando essa operação em um produto da soma pela diferença, temos que:
(1522 + 1520) (1522 – 1520)
34420 · 2
6084
Alternativa: D

26)  (IMNEC) A diferença entre o quadrado da soma e o quadrado da diferença entre dois números reais é igual:
(A) à diferença dos quadrados dos dois números.
(B) à soma dos quadrados dos dois números.
(C) à diferença dos dois números.
(D) ao dobro do produto dos números.
(E) ao quádruplo do produto dos números.
Resolução:
Seja a e b dois números, sabemos que:
(a + b)² =a² + 2ab + b²
Por outro lado, o quadrado da diferença é dado por:
(a – b)² = a² – 2ab + b²
Então, queremos a diferença do quadrado da soma e o quadrado da diferença:
a² + 2ab + b² – (a² – 2ab + b²)
a² + 2ab + b² – a² + 2ab – b²
4ab
Alternativa: E

27) A área do retângulo a seguir pode ser representada pelo polinômio:
(A) x – 2.
(B) x² – 4.
(C) x² + 2.
(D) x + 4.
(E) x³ – 8.
Resolução
A área de um retângulo é a multiplicação da sua base pela altura, então:
A = (x + 2 ) ( x – 2)
Note que esse é um produto notável: produto da soma pela diferença.
A = (x + 2 ) ( x – 2) = x² – 4
Alternativa: B

28) Simplificando a expressão (x + 3 )² – (x + 3) ( x – 3 ) - 6x, encontraremos:
(A) 0.
(B) x³ – 18.
(C) 2x².
(D) x² + 9.
(E) 18.
Resolução
Nesse caso, temos dois produtos notáveis e resolveremos cada um deles.
(x+3)² = x² + 6x + 9
(x + 3) ( x – 3) = x² – 9
Então, temos que:
x² + 6x + 9 – (x² – 9) -6x
x² + 6x + 9 – x² + 9 – 6x
x² – x² 6x – 6x + 9 + 9
18
Alternativa: E

29) (Cefet-MG) Sendo o número n = 684² – 683², a soma dos algarismos de n é:
(A) 14
(B) 15
(C) 16
(D) 17
(E) 18
Resolução
Para determinar a soma dos algarismos de n, inicialmente fatorarmos a expressão, uma vez que calcular os quadrados e, em seguida, realizar a subtração geram trabalho desnecessário. Fatorando a expressão utilizando a diferença entre dois quadrados, temos:
n = 684² – 683²
n = (684 + 683) · (684 – 683)
n = 1.367 · 1
n = 1.367
Portanto, a soma dos algarismos de n é dada por 1 + 3 + 6 + 7 = 17
Alternativa: D

30) (Cefet-MG) Sendo o número n = 684² – 683², a soma dos algarismos de n é:
(A) 14
(B) 15
(C) 16
(D) 17
(E) 18
Resolução
Alternativa d. Para determinar a soma dos algarismos de n, inicialmente fatorarmos a expressão, uma vez que calcular os quadrados e, em seguida, realizar a subtração geram trabalho desnecessário. Fatorando a expressão utilizando a diferença entre dois quadrados, temos:
n = 684² – 683²
n = (684 + 683) · (684 – 683)
n = 1.367 · 1
n = 1.367
Portanto, a soma dos algarismos de n é dada por 1 + 3 + 6 + 7 = 17

31) (Insper-SP modificada) Determine o valor da expressão: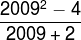
Resolução
Com a intenção de facilitar a notação, vamos nomear a = 2.009 e b = 2. Lembre-se de que 2² = 4, assim temos que: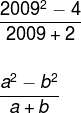

Veja que, no numerador da fração, temos a diferença entre dois quadrados, logo, podemos escrever a² – b² = (a + b) (a – b). Logo:

a – b = 2009 – 2 = 2007.

32) Qual é a forma fatorada do produto entre os polinômios x² + 14x + 49 e x² – 14x + 49?
(A) (x + 7)²·(x – 7)²
(B) (x² + 14x + 49)·(x² – 14x + 49)
(C) (x + 7)·(x – 7)²
(D) (x + 7)²·x – 7²
(E) x + 7²·(x – 7)²
Resolucao:
Como estamos buscando a forma fatorada do produto, não é necessário multiplicar os polinômios, basta fatorá-los e escrever o produto entre as formas fatoradas. Observe:
A forma fatorada de x² + 14x + 49, seguindo o método do trinomio quadrado perfeito, é:
x² + 14x + 49 = (x + 7)²
Já a forma fatorada de x² – 14x + 49, seguindo o mesmo método, é:
x² – 14x + 49 = (x – 7)²
Portanto, o produto entre as formas fatoradas é:
(x + 7)²·(x – 7)²
Alternativa: A

33) Qual é a forma simplificada da expressão algébrica abaixo?
(x² + 14x + 49)·( x² – 49)
x² – 14x + 49
(A) (x + 7)·(x + 7)
          x – 7
(B) x + 7
    x – 7
(C) (x + 7)³
     x – 7
(D) (x + 7)²
      x – 7
(E) (x² + 14x + 49)
          x – 7
Resolucao:
Observe que existem três polinômios que podem ser fatorados nessa expressão algébrica. Para fatorá-los, utilizaremos os casos de trinomio do quadrda perfeitoi e difwerenca de dois quadrados. Observe:
(x² + 14x + 49)·( x² – 49)
x² – 14x + 49
(x + 7)²·(x – 7)·(x + 7)
(x – 7)²
(x + 7)·(x + 7)·(x – 7)·(x + 7)
(x – 7)·(x – 7)
Agora basta “cortar” os termos idênticos no numerador e denominador. Nessa questão, existe apenas um termo idêntico, a saber (x – 7). O resultado final será:
(x + 7)·(x + 7)·(x + 7)
x – 7
Esse resultado pode ser reescrito da seguinte maneira:
(x + 7)³
x – 7
Alternatica: C

34) A razão entre as formas fatoradas dos polinômios ax + 2a + 5x + 10 e a² + 10a + 25 é:
(A) (a + 5)(x – 2)
    (a + 5)(a + 5)
(B) a + 5
(C) a – 5
(D) x – 2
   a + 5
(E) x + 2
   a + 5
Resolucao:
No numerador, utilizaremos o método de fatoração por agrupamento, que faz uso da fatoração por fator comum em evidencia repetidas vezes. Já no denominador, utilizaremos o método de fatoração do trinômio quadrado perfeito. Escrevendo a razão proposta, obteremos:
ax + 2a + 5x + 10
a² + 10a + 25
a(x + 2) + 5(x + 2)
(a + 5)(a + 5)
(a + 5)(x + 2)
(a + 5)(a + 5)
Agora vamos dividir os termos idênticos presentes na expressão algébrica acima:
x + 2
a + 5
Alternativa: E

35) A forma simplificada da razão entre os polinômios x³ – 8y³ e x² – 4xy + 4y² é:
(A) (x + 4y)²
     x – 4y
(B) (x² + 2xy + 4y²)
          x – 2y  
(C) (x + y)²
     x – y
(D) (2x + 2)²
      x – y
(E) (x + y)²
     2x – y
Resolucao:
Para resolver essa questão, devemos escrever a razão entre os polinômios:
      x³ – 8y³     
x² – 4xy + 4y²
Agora utilize o método de fatoração da diferenca entre dois cubos no numerador e do trinômio quadrado perfeito no denominador.
(x – 2y)(x² + 2xy + 4y²)
   (x – 2y)²
Escrevendo o denominador em forma de produto teremos:
(x – 2y)(x² + 2xy + 4y²)
(x – 2y)(x – 2y)
Agora basta “cortar” os fatores idênticos que aparecem tanto no numerador quanto no denominador:
(x² + 2xy + 4y²)
x – 2y  
Alternativa: B
 

 Continuacao...