Professor Diminoi
CONJUNTOS NUMÉRICOS
Os conjuntos numéricos reúnem diversos conjuntos cujos elementos são números. Eles são formados pelos números naturais, inteiros, racionais, irracionais e reais. O ramo da matemática que estuda os conjuntos numéricos é a Teoria dos conjuntos.
A teoria dos conjuntos é estudada na álgebra, que é uma área da Matemática. Um conjunto é um agrupamento de elementos que possuem uma determinada característica em comum, como o conjunto de vogais, conjunto de números, conjunto de pessoas, entre outros.
Memorize a nomenclatura
 Observe a seguir as características de cada um deles tais como conceito, símbolo e subconjuntos.
Observe a seguir as características de cada um deles tais como conceito, símbolo e subconjuntos.
Conjunto dos Números Naturais (N)
O conjunto dos números naturais é representado por N. Ele reúne os números que usamos para contar (incluindo o zero) e é infinito.
Subconjuntos dos Números Naturais
N* = {1, 2, 3, 4, 5..., n, ...} ou N* = N – {0}: conjuntos dos números naturais não-nulos, ou seja, sem o zero.
Np = {0, 2, 4, 6, 8..., 2n, ...}, em que n ∈ N: conjunto dos números naturais pares.
Ni = {1, 3, 5, 7, 9..., 2n+1, ...}, em que n ∈ N: conjunto dos números naturais ímpares.
P = {2, 3, 5, 7, 11, 13, ...}: conjunto dos números naturais primos.
Conjunto dos números naturais (IN)
IN={0, 1, 2, 3, 4, 5,...}
Um subconjunto importante de IN é o conjunto IN*:
IN*={1, 2, 3, 4, 5,...} à o zero foi excluído do conjunto IN.
Podemos considerar o conjunto dos números naturais ordenados sobre uma reta, como mostra o gráfico abaixo:
Conjunto dos números inteiros (Z)
Z = {..., -3, -2, -1, 0, 1, 2, 3,...}
O conjunto IN é subconjunto de Z.
Temos também outros subconjuntos de Z:
Z* = Z-{0}
Z+ = conjunto dos inteiros não negativos = {0,1,2,3,4,5,...}
Z_ = conjunto dos inteiros não positivos = {0,-1,-2,-3,-4,-5,...}
Observe que Z += IN.
Podemos considerar os números inteiros ordenados sobre uma reta, conforme mostra o gráfico abaixo:
Conjunto dos números racionais (Q)
Os números racionais são todos aqueles que podem ser colocados na forma de fração (com o numerador e denominador Î Z). Ou seja, o conjunto dos números racionais é a união do conjunto dos números inteiros com as frações positivas e negativas.
O conjunto dos números racionais engloba todos os algarismos na forma de a/b, com b ≠ 0, isto é, os números fracionários e as dízimas periódicas (números decimais).
O conjunto é representado pela letra Q maiúscula.
Observe alguns exemplos de números racionais:
a) 3/5 ou 0,6
b) 4/9 ou 0,4444...
c) 2/11 ou 0,18181818...
d) 1/3 ou 0,33333...
e) –36/10 ou –3,6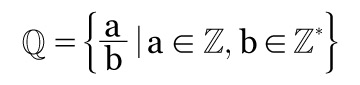 Observações importantes sobre os números racionais.
Observações importantes sobre os números racionais.
1º – Todo número inteiro é um número racional.
0 = 0/1 – 6 = – 6/1 2250 = 2250/1 – 500 = –500/1
2º – Todo número decimal exato é um número racional.
7,6 = 76/10 0,5 = 1/2 – 12,8 = 128/10 6,32 = 632/100
3º – Toda dízima periódica é um número racional.
0,444444... = 4/9 0,33333... = 1/3 0,6777777.... = 61/90 –0,344444... = –31/90
Todo número inteiro é um número racional, portanto, o conjunto dos números inteiros (Z) é um subconjunto do conjunto dos números racionais (Q).
Observe a demonstração através da utilização de diagramas:
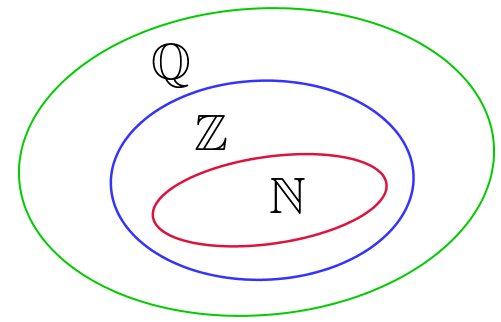
Dentro do conjunto dos números existem os seguintes subconjuntos:
Q* = conjunto dos números racionais com ausência do zero.
Q+ = engloba somente os números racionais positivos.
Q– = engloba somente os números racionais negativos.
Q*+ = engloba somente os números racionais positivos com ausência do zero.
Q*– = engloba somente os números racionais negativos com ausência do zero.
Conjunto dos números irracionais
Os números irracionais são decimais infinitas não periódicas, ou seja, os números que não podem ser escrito na forma de fração (divisão de dois inteiros). Como exemplo de números irracionais, temos a raiz quadrada de 2 e a raiz quadrada de 3:
Um número irracional bastante conhecido é o número p = 3,1415926535...
Conjunto dos números reais (IR)
Dados os conjuntos dos números racionais (Q) e dos irracionais, definimos o conjunto dos números reais como:
IR = Q È {irracionais} = {x|x é racional ou x é irracional}
O diagrama abaixo mostra a relação entre os conjuntos numéricos Portanto, os números naturais, inteiros, racionais e irracionais são todos números reais. Como subconjuntos importantes de IR temos:
Portanto, os números naturais, inteiros, racionais e irracionais são todos números reais. Como subconjuntos importantes de IR temos:
IR* = IR-{0}
IR+ = conjunto dos números reais não negativos
IR_ = conjunto dos números reais não positivo
Observação: entre dois números inteiros existem infinitos números reais.
Exemplos:
Entre os números 1 e 2 existem infinitos números reais:
1,01 ; 1,001 ; 1,0001 ; 1,1 ; 1,2 ; 1,5 ; 1,99 ; 1,999 ; 1,9999 ...
Entre os números 5 e 6 existem infinitos números reais:
5,01 ; 5,02 ; 5,05 ; 5,1 ; 5,2 ; 5,5 ; 5,99 ; 5,999 ; 5,9999 ...
Intervalos Numéricos
Há ainda um subconjunto relacionado com os números reais que são chamados de intervalos. Sejam a e b números reais e a < b, temos os seguintes intervalos reais:
Intervalo aberto de extremos
]a,b[ = {x ∈ R│a < x < b} Intervalo fechado de extremos
Intervalo fechado de extremos
[a,b] = {x ∈ R│a ≤ x ≤ b}![]() Intervalo aberto à direta (ou fechado à esquerda) de extremos
Intervalo aberto à direta (ou fechado à esquerda) de extremos
[a,b[ = {x ∈ R│a ≤ x < b}![]() Intervalo aberto à esquerda (ou fechado à direita) de extremos
Intervalo aberto à esquerda (ou fechado à direita) de extremos
]a,b] = {x ∈ R│a < x ≤ b}
QUESTÕES RESOLVIDAS
01) (UFBA) 35 estudantes estrangeiros vieram ao Brasil. 16 visitaram Manaus; 16, S. Paulo e 11, Salvador. Desses estudantes, 5 visitaram Manaus e Salvador e, desses 5, 3 visitaram também São Paulo. O número de estudantes que visitaram Manaus ou São Paulo foi:
(A) 29.
(B) 24.
(C) 11.
(D) 8.
(E) 5.
Resolução
Analisando as quantidades dadas, queremos saber quantos visitaram Manaus ou São Paulo. Para isso, sabemos que 16 visitaram Manaus e 16 visitaram São Paulo, somando 32; porém, estamos contando duas vezes os estudantes que visitaram as duas cidades ao mesmo tempo, que nesse caso é igual a 3.
Fazendo 32 – 3, encontramos o total de estudantes que visitaram uma cidade ou a outra, 32 – 3 = 29.
Alternativa A
02) (UFSE) Os senhores A, B e C concorriam à liderança de certo partido político. Para escolher o líder, cada eleitor votou apenas em dois candidatos de sua preferência. Houve 100 votos para A e B, 80 votos para B e C e 20 votos para A e C. Em consequência:
(A) venceu A, com 120 votos.
(B) venceu A, com 140 votos.
(C) A e B empataram em primeiro lugar.
(D) venceu B, com 140 votos.
(E) venceu B, com 180 votos.
Resolução
Analisando o total de votos, temos que:
A = 100 + 20 = 120 votos
B = 100 + 90 = 180 votos
C = 80 + 20 = 100 votos
Logo, o vencedor é o candidato B, com 180 votos.
Alternativa E
03) (Enem) Um fabricante de cosméticos decide produzir três diferentes catálogos de seus produtos, visando a públicos distintos. Como alguns produtos estarão presentes em mais de um catálogo e ocupam uma página inteira, ele resolve fazer uma contagem para diminuir os gastos com originais de impressão. Os catálogos C1, C2 e C3 terão, respectivamente, 50, 45 e 40 páginas. Comparando os projetos de cada catálogo, ele verifica que C1 e C2 terão 10 páginas em comum; C1 e C3 terão 6 páginas em comum; C2 e C3 terão 5 páginas em comum, das quais 4 também estarão em C1. Efetuando os cálculos correspondentes, o fabricante conclui que, para a montagem dos três catálogos, necessitará de um total de originais de impressão igual a:
(A) 135.
(B) 126.
(C) 118.
(D) 114.
(E) 110.
Resolução
Temos que:
C1 → 50 páginas
C2 → 45 páginas
C3 → 40 páginas
Além disso, há as intersecções, ou seja, páginas em comum:
C1 e C2 → 10 páginas
C1 e C3 → 6 páginas
C2 e C3 → 5 páginas
C1, C2 e C3 → 4 páginas.
Para realizar a contagem, temos:
4 páginas que pertencem a C1, C2 e C3;
5 – 4 = 1 → 1 página que pertence somente a C2 e C3;
6 – 4 = 2 → 2 páginas que pertencem somente a C1 e C3;
10 – 4 = 6 → 6 páginas que pertencem somente a C1 e C2.
→ C1 → 50 – 4 – 2 – 6 = 38 → 38 páginas que pertencem somente a C1.
→ C2 → 45 – 4 – 1 – 6 = 34 → 34 páginas que pertencem somente a C2.
→ C3 → 40 – 4 – 1– 2 = 33 → 33 páginas que pertencem somente a C3.
Realizando a soma, temos que:
33 + 34 + 38 + 6 + 2 + 1 + 4 = 118
Alternativa C
04) Dado o conjunto A = {1,2,5, 10, 15, 28}, o número de subconjuntos possíveis para esse conjunto é:
(A) 2.
(B) 8.
(C) 16.
(D) 32.
(E) 64.
Resolução
Para calcular o número de subconjuntos que um conjunto possui, basta calcular 2n, em que n é o número de elementos do conjunto. Nesse caso, o conjunto possui 5 elementos, então temos que:
25 = 32.
Alternativa D
05) Dado o conjunto U = números naturais de 0 até 20. Sabendo que B = números múltiplos de 3, podemos afirmar que o conjunto Bc (complementar de B) é igual ao conjunto:
(A) {3,6,9,12,15,18}
(B) {1,2,4,5,7,8,10,11,13,14,16,17,19,20}
(C) {0,2,4,6,12,15}
(D) {1,2,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20}
(E) {3}
Resolução
O conjunto complementar são todos os elementos que estão em U e não estão em B. Primeiro vamos listar os elementos de U e de B.
U = { 0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20}
B ={0,3,6,9,12,15,18}
Então, o complementar de B em relação a U é igual ao conjunto:
Bc = {1,2,4,5,7,8,10,11,13,14,16,17,19,20}
Alternativa B
06) Sobre os conjuntos numéricos, marque a alternativa incorreta.
(A) Todo número natural é também um número racional.
(B) Um número racional não pode ser irracional.
(C) Todo número negativo é um número inteiro.
(D) O conjunto dos números reais é formado pela união dos números racionais e irracionais.
(E) As dízimas periódicas são consideradas números racionais, portanto são também números reais.
Resolução
Estamos procurando a alternativa incorreta.
a) Correta, pois o conjunto dos números naturais está contido no conjunto dos números racionais.
b) Correta, um número racional não pode ser irracional, pois a intersecção entre esses conjuntos é vazia.
c) Incorreta, pois, por mais que o conjunto dos números inteiros seja o acréscimo dos números negativos, vale ressaltar que números decimais negativos não são inteiros, como – 2,5, ou até mesmo números irracionais, como o - π.
d) Correta, pois essa é a definição dos números reais.
e) Correta, pois as dízimas periódicas podem ser representadas por frações, logo são racionais, e todo número racional é também um número real.
Alternativa C
07) Em uma escola, 300 alunos foram entrevistados sobre as práticas esportivas. Os estudantes foram questionados sobre a prática de exercícios fora da escola. Com esse questionário, foi possível dividir os estudantes em grupos:
110 alunos afirmaram que fazem musculação fora da escola;
140 alunos afirmaram que jogam futebol fora da escola; e
80 estudantes afirmaram que praticam outros tipos de atividade física, como corrida e natação.
Sabendo que 40 alunos praticam futebol e musculação, 33 praticam futebol e outra atividade física, 24 praticam musculação e outra atividade física e que 8 estudantes praticam os três, o número de estudantes sedentários, ou seja, que não praticam nenhuma das três modalidades, é:
(A) 35.
(B) 42.
(C) 59.
(D) 74.
(E) 95.
Resolução
Sabemos que há um total de 300 alunos e temos os seguintes dados:
Musculação → 110 alunos;
Futebol → 140 alunos;
Outros → 80 alunos;
Porém, há intersecções, ou seja, alunos que pertencem a dois conjuntos ao mesmo tempo.
Musculação e futebol → 40 alunos
Futebol e outros → 33 alunos
Musculação e outros → 24 alunos
Musculação, futebol e outros → 8 alunos
Agora vamos subtrair 8 dos alunos que praticam musculação e futebol, futebol e outros, musculação e outros.
40 – 8 = 32 alunos praticam somente musculação e futebol.
33 – 8 = 25 alunos praticam somente futebol e outros.
24 – 8 = 16 alunos praticam somente musculação e outra atividade física.
Agora vamos calcular a quantidade de estudantes que praticam só uma modalidade, subtraindo do total as intersecções.
Musculação → 110 – 32 – 16 – 8 = 54
Futebol → 140 – 25 – 32 – 8 = 75
Outros → 80 – 25 – 16 – 8 = 31
Realizando a soma, temos que:
54 + 75 + 31 + 25 + 8 + 32 + 16 + 31 = 241
Como há um total de 300 alunos, então temos que:
300 – 241 = 59
Logo, 59 alunos não praticam nenhuma das modalidades.
Alternativa C
08) Seja A = {2,5}, B = {2,5,6} e C = {6,10}, determine os elementos da operação (A U B) ∩ (B (U C).
(A) {2,5,6}
(B) {2,5}
(C) {6,10}
(D) {2,5,6,10}
(E) {2,10}
Resolução
Primeiro vamos calcular as uniões:
A U B = {2,5,6}
B U C = {2,5,6,10}
Então:
(A U B) ∩ (B U C) = {2,5,6}
Alternativa A
09) Sobre os conjuntos numéricos, julgue as afirmativas a seguir.
I – A diferença entre o conjunto dos números reais e o conjunto dos números racionais é igual ao conjunto dos números irracionais.
II – Zero pertence ao conjunto dos números irracionais.
III – O resultado de | -7,5 | é um número natural.
Marque a alternativa correta.
(A) Somente a afirmativa I é verdadeira.
(B) Somente a afirmativa II é verdadeira.
(C) Somente a afirmativa III é verdadeira.
(D) Somente as afirmativas I e III são verdadeiras.
(E) Todas as afirmativas são verdadeiras.
Resolução
I → verdadeira, pois, se tirarmos os números racionais do conjunto dos números reais, restará somente o conjunto dos números irracionais.
II → falsa, 0 é um número racional, portanto não é irracional.
III → |-7,5| = 7,5, que é um número racional.
Alternativa A
10) A quantidade de subconjuntos do conjunto (A – B) U C, em que A = {2,4,6,8,10,12,14} B = {3,6,8,12} e C = {0,4,7}, é:
(A) 22
(B) 23
(C) 24
(D) 25
(E) 26
Resolução
Primeiro vamos listar os termos de A – B:
A – B = {2,4,10,14}
Agora faremos (A – B) U C = {2,4,7,9,10,14}.
Como esse conjunto possui 6 elementos, então o número de subconjuntos possíveis é 26.
Alternativa E
11) (IFPE) Em uma cooperativa de agricultores do município de Vitória de Santo Antão, foi realizada uma consulta em relação ao cultivo de cana-de-açúcar e do algodão. Constatou-se que 125 associados cultivavam a cana-de-açúcar, 85 cultivavam o algodão e 45 cultivavam ambos. Sabendo que todos os cooperativados cultivavam pelo menos uma dessas duas culturas. Qual é o número de agricultores da cooperativa?
(A) 210
(B) 255
(C) 165
(D) 125
(E) 45
Resolução
Para calcular o total, faremos:
n(A) + n(B) = n(A) + n(B) – n(A∩B)
n(A) + n(B) = 125 + 85 – 45 = 165
Alternativa C
00) Sobre os conjuntos numéricos, podemos afirmar que:
I – a soma de dois números racionais é sempre um número racional.
II – a divisão de dois números naturais é sempre um número natural.
III – a diferença entre dois números inteiros é sempre um número inteiro.
IV – o produto entre dois números reais é sempre igual a um número real.
Julgando as afirmativas, temos que:
(A) somente a afirmativa I é falsa.
(B) somente a afirmativa II é falsa.
(C) somente a afirmativa III é falsa.
(D) somente a afirmativa IV é falsa
(E) todas as afirmativas são verdadeiras.
Resolução
a) Verdadeira, pois, dados dois números racionais, a soma também será um número racional.
b) Falsa, pois a divisão de dois naturais pode gerar um número racional, por exemplo 7: 2 = 3,5.
c) Verdadeira, pois a diferença de dois inteiros sempre será um número inteiro.
d) Verdadeira, pois a multiplicação de dois números reais será um número real.
Alternativa B
12) (Enem) Após o Fórum Nacional Contra a Pirataria (FNCP) incluir a linha de autopeças em campanha veiculada contra a falsificação, as agências fiscalizadoras divulgaram que os cinco principais produtos de autopeças falsificados são: rolamento, pastilha de freio, caixa de direção, catalisador e amortecedor.
Após uma grande apreensão, as peças falsas foram cadastradas utilizando-se a codificação: 1: rolamento, 2: pastilha de freio, 3: caixa de direção, 4: catalisador e 5: amortecedor.
Ao final obteve-se a sequência: 5, 4, 3, 2, 1, 2, 3, 4, 5, 4, 3, 2, 1, 2, 3, 4, 5, 4, 3, 2, 1, 2, 3, 4, que apresenta um padrão de formação que consiste na repetição de um bloco de números. Essa sequência descreve a ordem em que os produtos apreendidos foram cadastrados. O 2015º item cadastrado foi um(a)
(A) rolamento.
(B) catalisador.
(C) amortecedor.
(D) pastilha de freio
(E) caixa de direção.
Resolução
Matemática se baseia muito em padrões. Por isso, precisamos identificar o padrão que nos foi dado. Então, vamos observar novamente a sequência apresentada:
5, 4, 3, 2, 1, 2, 3, 4, 5, 4, 3, 2, 1, 2, 3, 4, 5, 4, 3, 2, 1, 2, 3, 4
Note que é possível reconhecer o padrão logo de cara (números em negrito), pois após esse intervalo, o padrão volta a se repetir. Repare que a repetição acontece a cada oito números.
Para descobrirmos a posição 2015º, vamos simplesmente pegar esses elementos e dividir em grupos de oito em oito: 2015 / 8. Observe que essa divisão não é exata. Ao fazermos as contas, teremos 251 grupos de oito completos e uma sobra de sete elementos.
Então, basta irmos à nossa sequência (que acaba em 4) e adicionarmos mais sete elementos. Isso vai fazer com que a posição número 2015 seja representada pelo número 3, que se refere à caixa de direção.
Alternativa E
13) (Unicamp) A representação decimal de certo número inteiro positivo tem dois algarismos. Se o triplo da soma desses algarismos é igual ao próprio número, então o produto dos algarismos é igual a
(A) 10.
(B) 12.
(C) 14.
(D) 16.
Resolução:
Perceba que o enunciado nos diz que o número tem dois algarismos. Vamos pensar em um exemplo qualquer: 13. O que você tem que saber, aqui, é escrever esse mesmo número no formato decimal. Se pensarmos no 13, ele é formado pelo 3 como algarismo das unidades e o 1 como algarismo das dezenas. A chave está aqui: 13 pode ser escrito como 10 + 3.
Com isso em mente, para resolver a questão, em vez de pensarmos em 13, vamos pensar em um número do tipo ab, em que o a é dezena e o b é unidade. Seguindo o que vemos, vamos escrever de outra forma:
N = 10a + b
Para deixar mais claro: se pensarmos no número 29, baseado nessa fórmula acima, sua forma decimal seria: 10 . 2 + 9. Entendeu?
Agora, voltamos ao enunciado, que diz que o triplo da soma desses algarismos é igual ao próprio número. Vamos colocar isso de forma matemática:
3 . (a + b) = 10a + b
3a + 3b = 10a + b
2b = 7a
a = 2b / 7
Agora a chave é saber quem será o nosso b. Repare que a e b são números inteiros, isto é, eles não podem ser quebrados (decimais). Se estamos fazendo a divisão por 7, temos que pensar em um número que faça a conta funcionar e dar um resultado exato.
Nesse caso, temos duas possibilidades: ou b = 0 ou b = 7. Afinal, b é o algarismo das unidades, ou seja, deve ser de 0 a 9. Agora, veja que b não pode ser igual a 0, pois isso zeraria toda a conta, e o enunciado nos informou que o número não é nulo.
Então, sabemos que b = 7:
a = 2b / 7
a = 14 / 7
a = 2
Portanto:
N = 27
a . b = 14
Alternativa C
14) (Enem) Em um aeroporto, os passageiros devem submeter suas bagagens a uma das cinco máquinas de raio-X disponíveis ao adentrarem a sala de embarque. Num dado instante, o tempo gasto por essas máquinas para escanear a bagagem de cada passageiro e o número de pessoas presentes em cada fila estão apresentados em um painel, como mostrado na figura. Um passageiro, ao chegar à sala de embarque desse aeroporto no instante indicado, visando esperar o menor tempo possível, deverá se dirigir à máquina
Um passageiro, ao chegar à sala de embarque desse aeroporto no instante indicado, visando esperar o menor tempo possível, deverá se dirigir à máquina
(A) 1.
(B) 2.
(C) 3.
(D) 4.
(E) 5.
Resolução
O tempo de espera nas maquinas 1, 2, 3, 4 e 5 são, respectivamente, iguais a
35 . 5 = 175s
25 . 6 = 150s
22 . 7 = 154s
40 . 4 = 160s
20 . 8 = 160s
Portanto o passageiro deverá se dirigir à máquina 2
Alternativa B
15) (IFPE) Pedro, um aluno do curso de Almoxarife do IFPE – Cabo, em seu estágio, se deparou com a seguinte situação: no almoxarifado, encontravam-se 20 caixas de lápis, cada caixa com 30 lápis. Ele precisava mandar 1/10 dessas caixas para o laboratório de matemática. Ao abrir as caixas que chegaram ao laboratório, o professor de matemática colocou 5/6 dos lápis sobre as mesas, guardando o restante dos lápis no armário.
Nessas condições, podemos afirmar que o professor guardou, no armário do laboratório, um total de
(A) 10 lápis.
(B) 20 lápis.
(C) 30 lápis.
(D) 40 lápis.
(E) 50 lápis.
Resolução:
1/10 . 20 = 2 caixa (60 lápis)
5/6 . 60 = 50 (lápis sobre a mesa)
60 -50 = 10 (lápis guardados no armário)
Alternativa A
16) (Enem) O artigo 33 da lei brasileira sobre drogas prevê a pena de reclusão de 5 a 15 anos para qualquer pessoa que seja condenada por tráfico ilícito ou produção não autorizada de drogas. Entretanto, caso o condenado seja réu primário, com bons antecedentes criminais, essa pena pode sofrer uma redução de um sexto a dois terços.
Suponha que um réu primário, com bons antecedentes criminais, foi condenado pelo artigo 33 da lei brasileira sobre drogas.
Após o benefício da redução de pena, sua pena poderá variar de
(A) 1 ano e 8 meses a 12 anos e 6 meses.
(B) 1 ano e 8 meses a 5 anos.
(C) 3 anos e 4 meses a 10 anos.
(D) 4 anos e 2 meses a 5 anos.
(E) 4 anos e 2 meses a 12 anos e 6 meses.
Resolução
A menor pena possível seria a de 5 anos. Com o benefício da redução, o tempo de reclusão 1/3 . 5 = 1mínimo passaria a ser de ano e 8 meses.
Por outro lado, a maior pena possível seria a de 15 anos. Assim, no pior caso da redução, ele
teria que cumprir 5/6 . 15 = 12 anos e 6 meses.
Alternativa A
17) (IFAL) De acordo com os conjuntos numéricos, analise as afirmativas abaixo:
I. Todo número natural é inteiro.
II. A soma de dois números irracionais é sempre irracional.
III. Todo número real é complexo.
IV. Todo número racional é inteiro.
São verdadeiras as afirmativas
(A) I e II.
(B) I e III.
(C) I e IV.
(D) II e III.
Resolução
[I] Verdadeira. O conjunto dos números naturais compreendem os números inteiros e positivos.
[II] Falsa. A soma de dois números irracionais pode ser irracional ou racional.
[III] Verdadeira. O conjunto dos números reais é subconjunto do conjunto dos números complexos, portanto todo número real é complexo.
[IV] Falsa. O conjunto dos números racionais é formado por números inteiros, decimais ou fracionários, positivos ou negativos.
Alternativa B
18) Qual das afirmações abaixo está correta com relação às representações por Diagrama de Venn dos conjuntos dos números naturais, pares e ímpares?
a) Existem elementos na interseção dos números pares com os números ímpares, isto é, existem números que são pares e ímpares ao mesmo tempo.
b) O conjunto dos números pares contém o conjunto dos números ímpares.
c) O conjunto dos números ímpares contém o conjunto dos números pares.
d) O conjunto dos números naturais contém apenas o conjunto dos números pares
e) O conjunto dos números naturais contém os conjuntos dos números pares e dos números ímpares, que, por sua vez, não possuem nenhum elemento em comum.
Resolução
a) Falsa. O conjunto dos números pares e o conjunto dos números ímpares não possuem nenhum elemento em comum. Ou um número é par, ou um número é impar, não é possível que seja os dois ao mesmo tempo.
b) Falsa. O conjunto dos números ímpares não contém o conjunto dos números pares, pois, nesse caso, haveria elementos pares e ímpares ao mesmo tempo.
c) Falsa. O conjunto dos números pares também não contém o conjunto dos números ímpares pelo mesmo motivo da alternativa anterior.
d) Falsa! O conjunto dos números naturais é composto por todos os inteiros maiores que zero. Logo, 1, que é um número ímpar, pertence ao conjunto dos naturais. Portanto, ele não contém apenas números pares.
e) Verdadeira.
Continua ...





