Professor Diminoi

DÍZIMAS PERIÓDICAS
A dízima periódica é um número que possui sua parte decimal infinita e periódica, isto é, em sua parte decimal, há um número que se repete infinitamente. Considerada um numero racional, ela pode ser representada como uma fracao, que é chamada de fração geratriz. Também pode ser simples ou composta.

Representação da dízima periódica
Além da forma de fração, conhecida como fração geratriz, a dízima periódica pode ser representada como um número decimal de duas maneiras. Podemos inserir, ao final do número, reticências ( … ) ou podemos colocar um traço acima do seu período (parte que se repete na dízima), logo uma mesma dízima pode ser representada de dois jeitos.

Exemplos: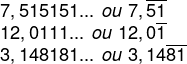


Dízima periódica simples
Uma dízima periódica simples possui uma parte inteira (que vem antes da vírgula) e o período, que vem depois da vírgula.

Exemplos
1,333…
1→ parte inteira
3 → período

0,76767676…
0 → parte inteira
76 → período

Dízima periódica composta
Uma dízima periódica composta possui parte inteira (que vem antes da vírgula), parte não periódica e período, que vem depois da vírgula. O que diferencia uma dízima periódica simples de uma composta é que, na simples, só há o período depois da vírgula; na composta, existe uma parte que não se repete depois da vírgula.

Exemplos:
1,5888…
1 → parte inteira
5 → parte não periódica
8→ período

32,01656565…
32 → parte inteira
01 → parte não periódica
65 → período

Exemplos de dízimas periódicas

Fração geratriz
Encontrar a fração que gera a dízima nem sempre é uma tarefa fácil. Precisamos dividir em dois casos: quando a dízima é simples e quando ela é composta. Para encontrar a fração geratriz, utilizamos uma equação.

Fração geratriz de uma dízima periódica simples

Exemplo
Vamos encontrar a fracao geratirz da dízima 1,353535…
Seja x = 1,353535…, como essa dízima possui 2 números no seu período (35), vamos multiplicar x por 100. Então,
100x = 135,3535…

Agora realizando a subtração,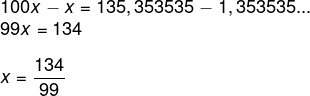


Existe um método prático para encontrarmos a fração geratriz de uma dízima periódica simples que evita a construção de equações. Vamos encontrar novamente a fração geratriz da dízima 1,353535…, porém pelo método prático.
1º passo: identificar período e parte inteira.
Parte inteira → 1
Período → 35

2º passo: encontrar o numerador.
O numerador é o número formado pela parte inteira e o período (no exemplo, é 135) menos a parte inteira, ou seja:
135 – 1 = 134
3º passo: encontrar o denominador.

Para isso, vamos avaliar quantos números têm no período da dízima, e, para cada número, acrescentaremos o número 9 no denominador. Como nesse caso há dois números, o denominador é 99. Logo, a fração geratriz é:


QUESTOES RESOLVIDAS
01) Apresente o resultado da expressão na forma fracionária:
0,66666... + 0,25252525... – 0,77777...
Resolucao
Há duas opções de resolução para esse exercício: a primeira é encontrar a fração geratriz de cada dízima periódica e resolver a expressão utilizando as frações. A segunda opção é encontrar a fração geratriz do resultado da expressão. Para realizarmos menos cálculos, optaremos pela segunda opção, mas vale lembrar que chegaríamos ao mesmo resultado se optássemos pela primeira sugestão. Vamos então realizar a soma inicial através do algoritmo da adição, lembrando que é necessário colocar “vírgula embaixo de vírgula”:
0,66666666...
+0,25252525...
0,91919191...
Desse resultado, vamos subtrair 0,7777777...
0,91919191...
– 0,777777777...
0,14141414...
Vamos agora encontrar a fração geratriz de 0,14141414...
x = 0,14141414...
Multiplicando ambos os lados da equação por 100, temos:
100.x = 14,141414...
Vamos então subtrair dessa equação sua antecedente: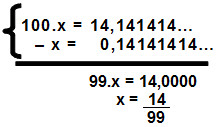

Portanto, a equação tem como resultado a fração 14/99.

02) (PUC – RJ) A soma 1,3333... + 0,1666666... é igual a:
(A) ¹/₂
(B) ⁵/₂
(C) ⁴/₃
(D) ⁵/₃
(E) ³/₂
Resolucao
Vamos encontrar a fração geratriz dos dois números decimais do exercício. Para o número 1,3333..., temos:
x = 1,3333...
Multiplicando ambos os lados da equação por 10:
10x = 13,3333...
Vamos agora subtrair a equação anterior da última, da seguinte forma: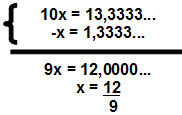

Simplificando o numerador e o denominador por 3:
x = 4
      3
Vamos fazer o mesmo processo para 0,166666...
x = 0,16666...
Multiplicando ambos os lados da equação por 10, e novamente por 10:
10x = 1,6666...
100x = 16,6666...
Subtraindo a última equação da equação anterior, o resultado será o seguinte sistema: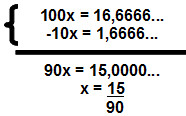

Simplificando a fração final por 15:
x = 1
      6
Agora, em vez de realizarmos a soma de números decimais, faremos a soma das frações geratrizes:
1,3333... + 0,16666... = 4 + 1 = 2.4 +1.1 = 9 = 3
                                 3    6          6         6   2
Alternativa E

04 (TJ CE – ESAF) Qual a fração que dá origem à dízima 2,54646… em representação decimal?
(A) 2.521 / 990
(B) 2.546 / 999
(C) 2.546 / 990
(D) 2.546 / 900
(E) e) 2.521 / 999
Resolução
Note que temos uma sequência infinita de “46” a partir da segunda casa decimal.
2,54646… = 2,5 + 0,04646…
2,54646… = 2,5 + 0,4646…/10
2,54646… = 2,5 + (46/99)/10
2,54646… = 25/10 + 46/990
2,54646… = (2475 + 46)990
2,54646… = 2521/990
Alternativa A

05) (SUSEP – ESAF) Indique qual o número racional geratriz da dízima periódica 7,233…
(A) 723/99
(B) 723/90
(C) 716/99
(D) 716/90
(E) 651/90
Resolução
Veja que o algarismo 3 é repetido infinitamente a partir da segunda casa decimal
7,233… = 7,2 + 0,033…
7,233… = 72/10 + 0,33…/10
7,233… = 36/5 + (1/3)/10
7,233… = 36/5 + 1/30
7,233… = (216 + 1)/30
7,233… = 217/30
7,233… = 651/90
Alternativa E

06) (PM SC – CESIEP) Leia as afirmações a seguir:
I. Os números Naturais são aqueles inteiros não positivos mais o zero.
II. Os números Irracionais são aqueles que representam dízimas periódicas.
III. Os números Reais representam a soma dos números Racionais com os Irracionais.
Assinale a alternativa correta:
(A) Somente a assertiva II está correta.
(B) Somente a assertiva III está correta.
(C) Somente a assertiva I está correta.
(D) Somente as assertivas II e III estão corretas.
Resolução
I. Falsa – Os números Naturais são os inteiros positivos mais o zero.
II. Falsa – Os números representados por dízimas periódicas pertencem ao conjunto dos números Racionais.
III. Correto – Os Reais é a união dos irracionais com os racionais.
Alternativa B

07) (TRT 15 – FCC) Renato dividiu dois números inteiros positivos em sua calculadora e obteve como resultado a dízima periódica 0,454545… . Se a divisão tivesse sido feita na outra ordem, ou seja, o maior dos dois números dividido pelo menor deles, o resultado obtido por Renato na calculadora teria sido
(A) 0,22.
(B) 0,222…
(C) 2,22.
(D) 2,222…
(E) 2,2.
Resolução
O “45” está sendo repetido infinitamente.
0,454545… = 45/99
0,454545… = 5/11
Descobrimos os números que geram a dízima periódica. Basta agora inverter a ordem e dividir novamente.
11/5 = 2,2
Alternativa E

08) (UFAC – MS Concursos) Sejam x e y dois números reais. Sendo x = 2,333… e y = 0,1212…, dízimas periódicas. A soma das frações geratrizes de x e y é:
(A) 7/3.
(B) 4/33.
(C) 27/11.
(D) 27/33.
(E) 27/3.
Resolução
Calculando a fração geratriz de x:
2,333… = 2 + 0,333…
2,333… = 2 + 1/3
2,333… = (6 + 1)/3
2,333… = 7/3
Calculando a fração geratriz de y:
0,1212… = 12/99
0,1212… = 4/33
Somando as frações geratrizes:
7/3 + 4/33
(77 + 4)/33
81/33
27/11
Alternativa C

09) (Pref. Teresina – NUCEPE) Sendo p/q a fração irredutível equivalente a 0,0222… / 0,001818… Qual o valor de p – q?
(A) 92.
(B) 99.
(C) 100.
(D) 101.
(E) 110.
Resolução
O número 0,222… é uma dízima periódica que equivale a fração 2/9, ou seja, o numerador 0,0222… equivale a fração 2/90, por ser 10 vezes menor.
O número 0,1818… também é uma dízima periódica, e equivale a fração 18/99, ou seja, o denominador 0,001818… equivale a fração 18/9900.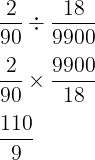

Calculando p – q:
110 – 9 = 101
Alternativa D

10) Dos números a seguir, assinale aquele que corresponde a uma dízima periódica composta.
(A) 3,14159284…
(B) 2,21111
(C) 0,3333….
(D) 1,21111….
Resolução
Analisando as alternativas, temos que:
a) É uma dízima não periódica. Perceba que, por mais que seja infinita, não há como prever os próximos números.
b) Não é uma dízima.
c) É uma dízima periódica simples.
d) Verdadeira, pois é uma dízima periódica composta.
Alternativa D
 

Continua...