Professor Diminoi
ANÁLISE COMBINATÓRIA
A análise combinatória é um campo de estudo da matemática associado com as regras de contagem. No início do século XVIII, o estudo sobre jogos envolvendo dados e cartas fez com que as teorias de contagem tivessem grande desenvolvimento.
O trabalho da análise combinatória possibilita a realização de contagens cada vez mais precisas. O princípio fundamental da contagem (PFC), o fatorial e os tipos de agrupamento são exemplos de conceitos estudados na análise combinatória, que, além de propiciar maior precisão, auxilia no desenvolvimento de outras áreas da matemática, como a probabilidade e o binômio de Newton.
Para que serve a análise combinatória?
A analise combinatória está associada com o processo de contagem, ou seja, o estudo dessa área da matemática possibilita-nos desenvolver ferramentas que nos auxiliam na realização de contagens de maneira mais eficiente. Vamos analisar um problema típico de contagem, veja:
Exemplo:
01) Considere três cidades A, B e C interligadas pelas rodovias R1, R2, R3, R4 e R5. Determine de quantas maneiras podemos ir da cidade A para cidade C passando pela cidade B.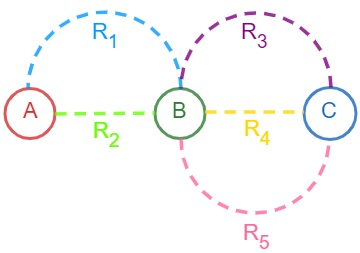
Para que serve a análise combinatória?
Observe que precisamos sair da cidade A e ir para cidade B, e somente depois podemos seguir viagem para cidade C, assim vamos analisar todas as possibilidades de realizarmos o evento seguindo as rodovias.
1ª maneira: R1 → R3
2ª maneira: R1 → R4
3ª maneira: R1 → R5
4ª maneira: R2 → R3
5ª maneira: R2 → R4
6ª maneira: R2 → R5
Portanto, temos seis maneiras diferentes de ir da cidade A para cidade C passando pela cidade B. No entanto, observe que o problema proposto é relativamente simples e que a análise realizada foi pouco trabalhosa. Assim, a partir de agora, vamos estudar ferramentas mais sofisticadas que possibilitam resolver problemas com bem menos trabalho.
Princípio fundamental da contagem (PFC)
Considere um evento E que possa ser realizado em n etapas independentes e consecutivas. Agora, considere que o número de possibilidades de realizar-se a primeira etapa seja igual a P1, imagine também que o número de possibilidades de realizar-se a segunda etapa seja de P2, e assim sucessivamente, até que cheguemos à última etapa, que possui Pn possibilidades de ser realizada.
O princípio fundamental da contagem (PFC) afirma que o total de possibilidades de realizar-se o evento E é dado por:
P1 ·P2 · … · Pn
Dessa forma, o total é dado pelo produto das possibilidades de cada uma das etapas que constituem o evento E. Observe que, para determinar-se o total de possibilidades de realização do evento E, é necessário conhecer-se o total de possibilidades de cada uma das etapas.
Exemplo:
02) Vamos refazer o exemplo 1 utilizando-nos do princípio fundamental da contagem.
Considere a imagem do exemplo 1.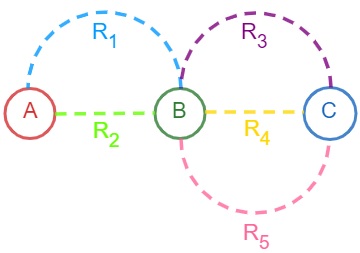
Para que serve a análise combinatória?
Observe que o evento pode ser realizado em duas etapas, a primeira consiste em ir da cidade A para cidade B, e a segunda, em ir da cidade B para cidade C. Para realizarmos a primeira etapa, temos duas possibilidades (estradas R1 e R2), e, para realizarmos a segunda etapa, temos três possibilidades (R3, R4 e R5).
1ª etapa → duas possibilidades
2ª etapa → três possibilidades
Pelo princípio fundamental da contagem, devemos multiplicar o total de possibilidades de cada etapa.
2 · 3 = 6
Portanto, para ir da cidade A para cidade C passando pela cidade B, temos o total de seis possibilidades.
Exemplo:
03) De quantas maneiras podem ser distribuídas as três medalhas olímpicas numa prova de mountain bike com cinco competidores?
Organizar a distribuição das medalhas é um evento que pode ser realizado em três etapas. A primeira etapa consiste em analisar-se o total de possibilidades de quem ficará com a medalha de ouro, ou seja, cinco possibilidades.
A segunda etapa consiste em analisar-se as possibilidades de quem ficará com a medalha de prata, ou seja, quatro, uma vez que o primeiro colocado não entra nessa escolha. A terceira etapa consiste em analisar-se o total de possibilidades de quem ficará com a medalha de bronze, ou seja, três, uma vez que os dois primeiros já foram escolhidos.
1ª etapa → cinco possibilidades
2ª etapa → quatro possibilidades
3ª etapa → três possibilidades
Então, pelo princípio fundamental da contagem, temos:
5 · 4 · 3 = 60 possibilidades
Fatorial
O fatorial é uma forma de decompor-se um número natural. Para calcular-se o fatorial de um número, basta multiplicá-lo por todos os seus antecessores até o número 1. O fatorial é representado pelo sinal de exclamação — “!”.
Veja alguns exemplos de como se calcular o fatorial de alguns números.
a)2! (lê-se: dois fatorial)
Para o cálculo, basta multiplicarmos o número que acompanha o fatorial por todos seus antecessores até o número 1, assim:
a) 2! = 2 ·1 = 2
b) 4! = 4 · 3 · 2 ·1 = 24
c) 5! = 5 · 4 · 3 · 2 · 1 = 120
d) 1! = 1
Formalmente podemos escrever o fatorial da seguinte maneira:
Considere um número natural n > 2. O fatorial de n é indicado por n! e é dado pela multiplicação de n por todos seus antecessores inteiros positivos.
n! = n (n – 1) · (n – 2) · (n – 3) · … · 1
Observe os fatoriais a seguir:
4! e 5!
Agora realize o desenvolvimento de ambos:
5! = 5 · 4 · 3 · 2 · 1
4! = 4 · 3 · 2 ·1
Observe que no desenvolvimento do 5! aparece o desenvolvimento do 4!. Portanto, podemos escrever o 5! desta forma:
5! = 5 · 4 · 3 · 2 · 1
5! = 5 · 4!
Exemplo:
04) Calcule o fatorial a seguir: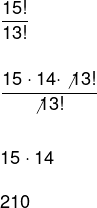
Observe que o 15! foi desenvolvido até o 13!. Observe também que, no numerador da fração, os elementos estão sendo multiplicados, logo, podemos “cortar” o 13!, resultando somente em 15 · 14.
Observação: 0! = 1
Tipos de agrupamento
Alguns problemas de contagem são mais complexos e resolvidos com maior facilidade mediante novas ferramentas. Essas ferramentas são chamadas de agrupamento, pois elas agrupam elementos de diferentes maneiras, facilitando o processo de contagem. São esses agrupamentos: arranjo simples, permutação, e combinação simples.
Arranjo simples
Considere um conjunto com n elementos distintos. Vamos chamar de arranjo de n os elementos tomados p a p, qualquer sequência ordenada por p, e os elementos distintos escolhidos entre os n elementos.
Dessa forma, a quantidade de subconjuntos formados por p elementos será o arranjo de n elementos tomados p a p. A fórmula que nos permite realizar o cálculo do número de arranjos é dada por:
![]()
Exemplo:
05) Calcule o valor de A4,2 + A5,2.
Para calcularmos o valor da expressão, vamos determinar cada um dos arranjos e, em seguida, somar esses valores. Para determinarmos o valor de cada arranjo, devemos substituir os valores na fórmula.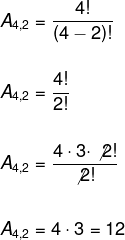
Observe que n = 4 e p = 2, ambos foram substituídos na fórmula. Agora, devemos calcular o valor do arranjo de cinco elementos tomados dois a dois.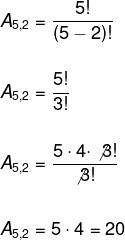
Assim, temos que:
A4,2 + A5,2
12 + 20
32
Exemplo:
06) Quantos números naturais de quatro algarismos distintos podem ser formados usando-se os algarismos 2, 3, 4, 5, 6, 7, 8 e 9?
Nesse problema podemos utilizar o arranjo simples, uma vez que 2435 ≠ 4235. Veremos que, em alguns casos, a ordem dos elementos não os diferencia, e, dessa forma, não podemos utilizar o arranjo.
Como queremos determinar o total de números que podem ser formados, observe que o total de elementos é igual a oito, e queremos agrupá-los de quatro em quatro, portanto: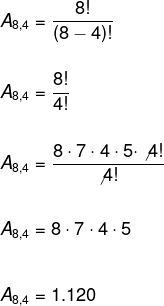
Permutação simples
Considere um conjunto com n elementos. Vamos chamar de permutação simples de n elementos todo arranjo de n elementos tomados n a n. Assim temos que: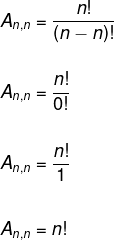
Para que não haja confusão entre os conceitos, vamos denotar a permutação simples de n elementos por Pn. Portanto, temos que:
Pn = n!
Exemplo:
07) Calcule P7 e P3.
Para calcularmos essas permutações, devemos substituir os valores na fórmula.
Veja:
P7 = 7 · 6 · 5· 4 · 3 · 2 · 1
P7 = 5040
P3 = 3 · 2 · 1
P3 = 6
Exemplo:
08) Determine quantos anagramas podem haver na palavra Brasil.
Entendemos como anagrama todas as possíveis transposições das letras da palavra, por exemplo, “Lisarb” é um anagrama da palavra Brasil. Para determinarmos a quantidade de anagramas, devemos calcular a permutação das letras da palavra, assim temos que:
P6 = 6!
P6 = 6 · 5 · 4 · 3 · 2 · 1
P6 = 720
Portanto, a palavra Brasil possui 720 anagramas.
Combinação simples
Considere um conjunto A com n elementos distintos. Vamos chamar de combinação dos n elementos tomados p a p qualquer subconjunto de A formado por p elementos.
A fórmula para o calculo da combinação é dada por:![]()
Exemplo:
09) Calcule a combinação de 10 elementos tomados de quatro a quatro.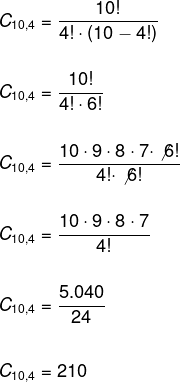
Exemplo:
10) Quantos quadriláteros distintos podemos formar com vértices nos pontos A, B, C, D, E e F?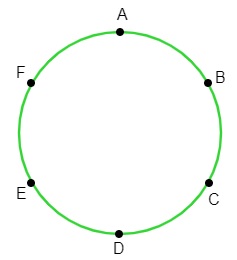 Veja que o quadrilátero ABCD é igual ao quadrilátero CDBA nesse contexto, logo, devemos utilizar a combinação e não arranjos. Temos o total de seis pontos e queremos combiná-los de quatro em quatro, assim:
Veja que o quadrilátero ABCD é igual ao quadrilátero CDBA nesse contexto, logo, devemos utilizar a combinação e não arranjos. Temos o total de seis pontos e queremos combiná-los de quatro em quatro, assim: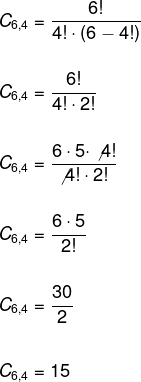
Portanto, podemos formar 15 quadriláteros distintos.
Análise combinatória e probabilidade
O estudo da probabilidade está intimamente relacionado com o estudo da análise combinatória. Em alguns problemas da probabilidade, é necessário determinar-se o espaço amostral, que consiste em um conjunto formado por todos os possíveis resultados de um determinado evento.
Em alguns casos, o espaço amostral E é escrito de maneira bem direta, como no lançamento de uma moeda honesta, em que os possíveis resultados são cara ou coroa e são denotados da seguinte maneira:
E = {cara, coroa}
Agora imagine a seguinte situação: um dado é lançado três vezes consecutivas e estamos interessados em determinar o espaço amostral desse experimento. Veja que anotar todas as possibilidades já não é uma tarefa tão simples, precisamos utilizar o princípio fundamental da contagem (PFC). O evento pode ser realizado em três etapas, em cada uma delas temos seis possibilidades, uma vez que um dado possui seis faces, assim:
1ª etapa → seis possibilidades
2ª etapa → seis possibilidades
3ª etapa → seis possibilidades
Pelo PFC, temos que o total de possibilidades é de:
6 · 6 · 6 = 216
Assim podemos dizer que o espaço amostral desse evento é 216.
Para o estudo da probabilidade é necessário ter-se um conhecimento básico de análise combinatória, pois, sem determinarmos o espaço amostral de um experimento, é impossível resolvermos a grande maioria dos exercícios de probabilidade.
Exemplo:
11) Determine a quantidade de anagramas da palavra castelo. Em seguida, determine a quantidade de anagramas que começam com a letra c.
Resolução
Para determinarmos a quantidade de anagramas, devemos calcular a permutação da quantidade de letras, assim:
P7 = 7!
P7 = 7 · 6 · 5 · 4 · 3 · 2 · 1
P7 = 5040
A palavra possui 5040 anagramas. Agora, para determinarmos a quantidade de anagramas que começam com a letra c, devemos fixar a letra e calcular o anagrama das demais, veja:
C __ __ __ __ __ __
Ao fixarmos a letra c, note que sobraram seis campos para calcularmos a permutação, assim:
P6 = 6!
P6 = 6 · 5 · 4 · 3 · 2 · 1
P6 = 720
Portanto, temos 720 anagramas da palavra castelo.
Exemplo:
12) Em uma sala de aula, tem-se cinco homens e sete mulheres. Quantos grupos de três homens e quatro mulheres podem ser formados?
Resolução
Primeiramente, veja que a ordem na qual escolhemos as pessoas não importa, por exemplo o grupo formado por João, Marcos e José é o mesmo grupo formado por Marcos, João e José, portanto, devemos utilizar a combinação para o cálculo.
Vamos calcular separadamente a quantidade de grupos que podem ser formados por homens e mulheres, e, em seguida, vamos multiplicar esses resultados, pois cada grupo de homens pode misturar-se com cada grupo de mulheres.
Homens
Total → 5
Quantidade no grupo → 3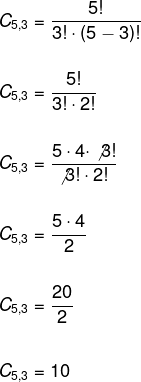
Mulheres
Total → 7
Quantidade no grupo → 4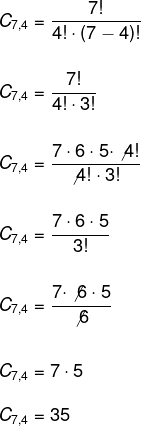
Portanto, o total de grupos que podem ser formados por três homens e quatro mulheres é de:
C5,3 · C7,4
10 · 35
350
Fatorial
Calcular o fatorial de um número só faz sentido quando estamos trabalhando com números naturais. Essa operação é bastante comum na análise combinatória, facilitando o cálculo de arranjos, permutações, combinações e demais problemas envolvendo contagem. O fatorial é representado pelo símbolo “!”. Definimos como n! (n fatorial) a multiplicação de n por todos os seus antecessores até chegar em 1.
n! = n · (n – 1)· (n – 2) · … · 3 · 2 · 1.
O que é fatorial?
O fatorial é uma operação muito importante para o estudo e desenvolvimento da análise combinatória. Na matemática o número seguido do símbolo de exclamação (!) é conhecido como fatorial, por exemplo, x! (x fatorial).
Conhecemos como fatorial de um número natural a multiplicação desse número por seus antecessores com exceção do zero, ou seja:
n! = n · (n-1) · (n-2) … 3 · 2 · 1
Vale ressaltar que, para que essa operação faça sentido, n é um número natural, ou seja, não calculamos fatorial de um número negativo, ou mesmo de um número decimal, ou de frações.
O fatorial de um número natural n é a multiplicação de n pelos seus antecessores.

Cálculo do fatorial
Para encontrar o fatorial de um número, basta calcular o produto. Note também que o fatorial é uma operação que, ao aumentar o valor de n, o resultado também aumentará muito.
Exemplos:
4! = 4 · 3 · 2 · 1 = 24
5! = 5 · 4 · 3 · 2 · 1= 120
6! = 6 · 5 · 4 · 3 · 2 · 1 = 720
7! = 7· 6 · 5 · 4 · 3 · 2 · 1 = 5040
Por definição, temos:
0! = 1
1! = 1
Operações com fatorial
Para resolver operações com fatorial, é importante tomar cuidado para não cometer alguns erros. Quando vamos somar, subtrair ou multiplicar dois fatoriais, é necessário calcular cada um deles separadamente. Somente a divisão possui formas específicas para a realização de simplificações.
Não cometa o erro de realizar a operação e conservar o fatorial, seja para adição e subtração, seja para multiplicação.
2! + 3! ≠ 5!
4! · 2! ≠ 12!
7! – 5! ≠ 2!
Na hora de resolver qualquer uma dessas operações, devemos calcular cada um dos fatoriais.
Exemplos:
a) 2! + 3! = (2 · 1) + (3 · 2 · 1) = 2 + 6 = 8
b) 4! · 2! = (4 · 3 · 2 · 1) · (2 · 1) = 24 · 2 = 48.
c) 7! - 5! = (7 · 6· 5· 4 · 3 · 2 · 1) - (5· 4 · 3 · 2 · 1) = 5040 – 120 = 4920.
Simplificação de fatorial
As divisões são bastante recorrentes. Em fórmulas de combinação, arranjo e permutação com repetição, sempre vamos recorrer à simplificação para resolver problemas envolvendo fatorial. Para isso, vamos seguir alguns passos.
Exemplo 1
![]()
1º passo: identificar o maior dos fatoriais — nesse caso, é 8!. Agora, analisando o denominador, que é 5!, vamos escrever a multiplicação de 8 pelos seus antecessores até chegar a 5!.
O fatorial de um número n, ou seja, n!, pode ser reescrito como a multiplicação de n até k!. Assim,
n! = n·(n -1 ) · ( n- 2 ) · … · k!, logo vamos reescrever 8! como a multiplicação de 8 até 5!.
8! = 8 · 7 · 6 · 5!
Então vamos reescrever a razão como:![]()
2° passo: após reescrever a razão, é possível simplificar o numerador com o denominador, já que 5! está tanto no numerador quanto no denominador. Após a simplificação, basta realizar a multiplicação.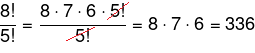
Exemplo 2![]()
Análise combinatória e fatorial
Ao realizar o estudo mais aprofundado em análise combinatória, o fatorial de um número sempre aparecerá. Os principais agrupamentos da análise combinatória, que são a permutação, a combinação e o arranjo, usam o fatorial de um número em suas fórmulas.
Permutação
A permutação é a reordenação de todos os elementos de um conjunto. Para calcular uma permutação, nós recorremos ao fatorial, pois a permutação de n elementos é calculada por:
Pn = n!
Exemplo:
Quantos anagramas podemos construir com o nome HEITOR?
Esse é um problema típico de permutação. Como há 6 letras no nome, para calcular a quantidade de anagramas possíveis, basta calcular P6.
P6 = 6! = 6 · 5 · 4 · 3 · 2 · 1 = 720
Arranjos
Calcular arranjos também exige o domínio do fatorial de um número. Arranjo, assim como a permutação, é a formação de um reordenamento. A diferença é que, no arranjo, estamos reordenando parte do conjunto, ou seja, queremos saber quantos reordenamentos possíveis podemos formar escolhendo uma quantidade k de um conjunto com n elementos.![]()
Exemplo:
Em uma empresa, há 6 candidatos à gestão da instituição, e dois serão selecionados para os cargos de diretor e vice-diretor. Sabendo que eles serão eleitos por votação, qual é a quantidade de resultados possíveis?
Nesse caso, calcularemos o arranjo de 6 tomados de 2 em 2, já que há 6 candidatos para duas vagas.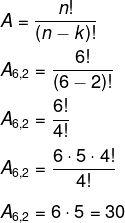
Combinação
Na combinação, assim como as demais, é necessário o domínio do fatorial de um número. Definimos como combinação os subconjuntos de um conjunto. A diferença é que, na combinação, não se tem um reordenamento, pois a ordem não é importante. Logo, estamos calculando quantos subconjuntos com k elementos podemos formar em um conjunto de n elementos.
![]()
Exemplo:
Uma comissão de 3 alunos será escolhida para representar a turma. Sabendo-se que há 5 candidatos, quantas comissões podem ser formadas?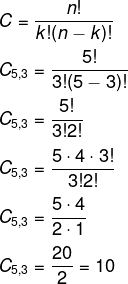
13) Sobre o fatorial de um número, julgue as afirmativas a seguir.
I) 0! + 1! = 2
II) 5! - 3! = 2!
III) 2! · 4! = 8
(A) Somente I é verdadeira.
(B) Somente II é verdadeira.
(C) Somente III é verdadeira.
(D) Somente I e II são verdadeiras.
(E) Somente II e II são verdadeiras.
Resolução
I) Verdadeira.
0! = 1
1! = 1
0! + 1! = 1+1 = 2
II) Falsa.
5! = 5 · 4 · 3 · 2 · 1= 120
3! = 3 · 2 · 1 = 6
5! – 3! = 120 – 6 = 114
III) Falsa.
2! = 2 · 1
4! = 4 · 3 · 2 · 1= 24
Alternativa: A
14) (UFF) O produto 20 · 18 · 16 ·14 … · 6 · 4 · 2 é equivalente a?
(A) 20! : 2
(B) 2 · 10!
(C) 20! : 210
(D) 210 · 10!
(E) 20! : 10!
Resolução
Analisando o produto de todos os números pares de 2 até 20, sabemos que:
20 = 2 · 10
18 = 2 · 9
16 = 2 · 8
14 = 2 · 7
12 = 2 · 6
10 = 2 · 5
8 = 2 · 4
6 = 2 · 3
4 = 2 · 2
2 = 2 · 1
Logo, podemos reescrever como 210 · 10 · 9 · … ·2 · 1 = 210 · 10!
Alternativa D.
Permutação simples
Podemos considerar a permutação simples como um caso particular de arranjo, onde os elementos formarão agrupamentos que se diferenciarão somente pela ordem. As permutações simples dos elementos P, Q e R são: PQR, PRQ, QPR, QRP, RPQ, RQP.
Para determinarmos o número de agrupamentos de uma permutação simples utilizamos a seguinte expressão P =
n!.
n! = n .(n-1) . (n-2) . (n-3)*....*3 . 2 . 1
Por exemplo
4! = 4 . 3 . 2 . 1 = 24
Exemplo:
Quantos anagramas podemos formar com a palavra GATO?
Resolução:
Podemos variar as letras de lugar e formar vários anagramas, formulando um caso de permutação simples.
P = 4! = 24.jpg)
Exemplo:
De quantas maneiras distintas podemos organizar as modelos Ana, Carla, Maria, Paula e Silvia para a produção de um álbum de fotografias promocionais
Resolução:
Note que o princípio a ser utilizado na organização das modelos será o da permutação simples, pois formaremos agrupamentos que se diferenciarão somente pela ordem dos elementos.
P = n!
P = 5!
P = 5 . 3 . 2 . 1
P = 120
Portanto, o número de posições possíveis é 120.
Exemplo:
De quantas maneiras distintas podemos colocar em fila indiana seis homens e seis mulheres:
a) em qualquer ordem
Resolução:
Podemos organizar as 12 pessoas de forma distinta, portanto utilizamos
12! = 12 . 11 . 10 . 9 . 8 . 7 . 6 . 5 . 4 . 3 . 2 . 1 = 479.001.600 possibilidades
b) iniciando com homem e terminando com mulher
Resolução:
Ao iniciarmos o agrupamento com homem e terminarmos com mulher teremos:
Seis homens aleatoriamente na primeira posição.
Seis mulheres aleatoriamente na última posição..jpg)
P = (6 . 6) . 10!
P = 36 . 10!
P = 130.636.800 possibilidades
O que é uma combinação simples?
Se um conjunto A tem n elementos, a combinação simples de p elementos escolhidos entre esses n elementos dados (p ≤ n) é qualquer subconjunto de A com p elementos.
Indica-se:
Cn,p ou Cpn
Exemplo:
Suponha que os estudantes Andreia, Bernardo, Caio, Daniel e Érica disputam duas vagas no conselho da escola. Quantas comissões de 2 estudantes podemos formar escolhendo entre os 5 estudantes?
Responder a essa pergunta é o mesmo que calcular quantos subconjuntos de dois elementos podem ser formados com os 5 elementos do conjunto: {A, B, C, D e E}. Cada um desses subconjuntos é uma combinação simples de 2 elementos escolhidos entre os cinco elementos dados.
Observem as possíveis combinações no diagrama de árvore abaixo: São ao todo comissões com 2 estudantes. Podemos notar que, dado um conjunto de 5 elementos, o número de subconjuntos com 2 elementos é metade (½) do total dos agrupamentos de 2 elementos formados com os 5 algarismos disponíveis. Isto se deve ao fato de, por exemplo, os agrupamentos {A,B} ; {B, A} serem iguais, enquanto {A, B} e {C, B} são diferentes.
São ao todo comissões com 2 estudantes. Podemos notar que, dado um conjunto de 5 elementos, o número de subconjuntos com 2 elementos é metade (½) do total dos agrupamentos de 2 elementos formados com os 5 algarismos disponíveis. Isto se deve ao fato de, por exemplo, os agrupamentos {A,B} ; {B, A} serem iguais, enquanto {A, B} e {C, B} são diferentes.
Quando, pelo princípio multiplicativo, indicamos 5 . 4 = 20, estamos considerando a ordem dos elementos. Como na formação de subconjuntos a ordem dos elementos não importa, devemos dividir o resultado anterior por 2 = 2 . 1 = 2!, isto é, devemos dividir pela permutação de 2, que é o número de elementos em cada subconjunto.
Generalizando, podemos dizes que o princípio multiplicativo leva em conta a ordem dos elementos do grupo formado. Se essa ordem não importar, devemos excluir as repetições dividindo o resultado, obtido com o princípio multiplicativo, pelo número de permutações dos componentes do grupo.
Cálculo do número de Combinações simples
Cpn = Cn,p = n!(n−p)! ⋅ p!
Exercícios resolvidos
01) Uma empresa é formada por 6 sócios brasileiros e 4 japoneses. De quantos modos podemos formar uma diretoria de 5 sócios, sendo 3 brasileiros e é 2 japoneses?
Resolução: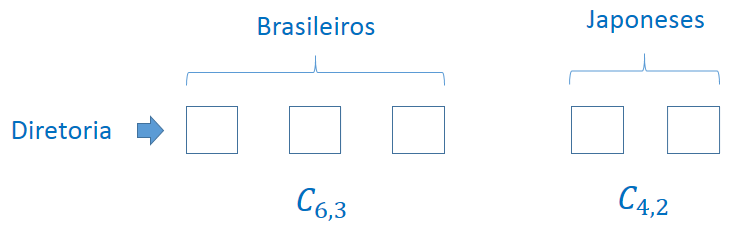
Resposta: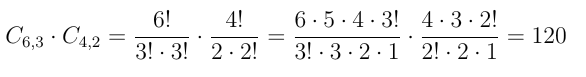
2º) Sobre uma circunferência tomam-se 7 pontos distintos. Calcule o número de polígonos convexos que se pode obter com vértices nos pontos dados.

Logo, o total de polígonos é: 35 + 35 + 21 + 7 + 1 = 99
3º) Considere, num plano, 10 pontos distintos entre si. Suponha que 4 desses pontos pertençam a uma mesma reta e que 2 quaisquer dos demais não estejam alinhados com nenhum dos pontos restantes. Calcule o número de retas determinadas por esses 10 pontos.
Resolução:
Admitindo-se que o alinhamento de 3 pontos do total de 10 só seja possível entre os 4 pontos da reta dada, temos:![]()
Logo, o resultado final é: 45 – 6 + 1 = 40
4º) Um baralho tem 52 cartas. De quantos modos diferentes podemos distribuí-las entre 4 jogadores de modo que cada um receba 13 cartas?
Resolução:
Questões de Vestibulares
01) (PUC) O número total de maneiras de escolher 5 dos números 1, 2, 3, ..., 52 sem repetição é:
(A) entre 1 e 2 milhões.
(B) entre 2 e 3 milhões.
() entre 3 e 4 milhões.
(D) menos de 1 milhão
(E) mais de 10 milhões.
Alternativa: B
02) (UDESC) Doze equipes participarão de um torneio internacional de vôlei; os participantes foram divididos em dois grupos de seis equipes cada. A fase classificatória deste torneio prevê a realização de dois turnos. No primeiro turno, cada equipe jogará contra os adversários do seu próprio grupo e, no segundo, as equipes enfrentarão os times do outro grupo. Ao término da fase de classificação, os dois primeiros colocados de cada grupo avançarão para a fase final, que será disputada em turno único, num só grupo, com cada classificado jogando contra todos os outros times. O time que obtiver a primeira colocação na fase final será declarado campeão do torneio. De acordo com este regulamento, o total de jogos realizados durante o torneio é igual a:
(A) 102
(B) 35
(C) 723
(D) 72
Alternativa: D
03) (ADVISE) Uma farmácia dispõe de sete vagas de estacionamento para clientes em atendimento, representadas pelas letras de A a G, conforme figura abaixo.
Se pelo menos duas dessas vagas sempre estão ocupadas, o número de maneiras que esse estacionamento poderá ser ocupado é:
(A) 128
(B) 67
() 34
(D) 21
(E) 120
Alternativa: E
04) (FUVEST) João tem R$ 150,00 para comprar canetas em 3 lojas. Na loja A, as canetas são vendidas em dúzias, cada dúzia custa R$ 40,00 e há apenas 2 dúzias em estoque. Na loja B, as canetas são vendidas em pares, cada par custa R$ 7,60 e há 10 pares em estoque. Na loja C, as canetas são vendidas avulsas, cada caneta custa R$ 3,20 e há 25 canetas em estoque. O maior número de canetas que João pode comprar nas lojas A, B e C utilizando no máximo R$ 150,00 é igual a:
(A) 46
(B) 45
(C) 44
(D) 43
(E) 42
Alternativa: B
05) Sabe-se que, em um grupo de 10 pessoas, o livro A foi lido por 5 pessoas e o livro B foi lido por 4 pessoas. Podemos afirmar corretamente que, nesse grupo:
(A) pelo menos uma pessoa leu os dois livros.
(B) nenhuma pessoa leu os dois livros.
(C) pelo menos uma pessoa não leu nenhum dos dois livros.
(D) todas as pessoas leram pelo menos um dos dois livros.
Alternativa: C
06) O número mínimo de pessoas que deve haver em um grupo para que possamos garantir que nele há pelo menos três pessoas nascidas no mesmo dia da semana é igual a:
(A) 21
(B) 20
(C) 15
(D) 14
Alternativa: C
Continua...





