MECÂNICA

ONLINE

MECÂNICA

Professor Diminoi

MECÂNICA

A Mecânica é uma área da Física comumentemente subdividida em Mecânica Clássica, Mecânica Relativística e Mecânica Quântica.

A Mecânica é a área da Física que explica grande parte dos fenômenos que ocorrem em nosso cotidiano.

A Mecânica é uma das grandes áreas da Física.

Ela estuda o movimento e o repouso dos corpos a partir da aplicação ou não de forças sobre eles e é subdividida em:

- Mecânica Clássica

- Mecânica Relativística

- Mecânica Quântica.

Através do seu estudo, é possível calcularmos a velocidade dos corpos, o alcance máximo em um lançamento, a aceleração da gravidade e muitas outras coisas.

Resumo sobre Mecânica

A Mecânica é uma importante área da Física (ciência que explica os fenômenos da natureza por meio da Matemática).

Ela explica uma grande parte dos fenômenos que ocorrem no cotidiano.

As áreas de estudo da Mecânica são a Mecânica Clássica, a Mecânica Relativística e a Mecânica Quântica.

A Mecânica contribuiu na investigação dos efeitos e causas do movimento e repouso dos corpos, além do desenvolvimento e verificação dos estudos a respeito do Universo.

Na Mecânica, o conteúdo mais cobrado no Enem são as partes de Hidrostática, Cinemática e Dinâmica, estudadas na área de

Mecânica Clássica.

A Mecânica está presente em várias situações cotidianas. Ela pode ser observada, por exemplo, em qualquer tipo de colisão e quando andamos.

O que a Mecânica estuda?

A Mecânica estuda o movimento, repouso e equilíbrio dos corpos sofrendo ou não a ação de forças. Por isso, ela é uma área da Física bastante extensa, conseguindo descrever quase todos os eventos que ocorrem no cotidiano.

Historicamente, a Mecânica teve seu estudo iniciado com as leis de movimento de Sir Isaac Newton, publicadas em seu livro Princípios Matemáticos da Filosofia Natural, contudo ela existe desde o nascimento do Universo.

Diversos profissionais lidam diariamente com a Mecânica, como pilotos de avião, físicos, metereologistas, geólogos, engenheiros, arquitetos etc.

Áreas da Mecânica

A Mecânica é dividida em três grandes áreas: a Mecânica Clássica, a Mecânica Relativística e a Mecânica Quântica. Entenda um pouco sobre cada uma delas a seguir.

Mecânica Clássica

A Mecânica Classica estuda o movimento dos corpos na Terra ou imersos nos fluidos abaixo da velocidade da luz, além das causas desses movimentos. Ela é dividida em Cinemática, Dinâmica, Estática, Hidrostática e Hidrodinâmica:

Cinemática: na Cinemática são investigados os movimentos dos corpos desconsiderando as razões que o ocasionaram. Nessa parte, estudamos movimento uniforme, movimento uniformemente variado, lançamento horizontal, lançamento oblíquo, movimento circular uniforme e movimento circular uniformemente variado.

Dinâmica: na Dinâmica são investigadas as causas do movimento dos corpos. Nessa parte, estudamos as leis de Newton, energia, trabalho, impulso, momento linear, colisões e gravitação universal.

Estática: na Estática são investigadas as condições necessárias para que os corpos estejam em equilíbrio. Nessa parte, estudamos centro de massa, equilíbrio, alavanca, torque e momento angular.

Hidrostática: na Hidrostática são investigados os fluidos em condições de equilíbrio estático. Nessa parte, estudamos massa específica, pressão, princípio de Stevin, teorema de Pascal e teorema de Arquimedes.

Hidrodinâmica: na Hidrodinâmica são investigados os fluidos em movimento quando sujeitos a forças externas não nulas. Nessa parte, estudamos vazão, equação da continuidade e princípio de Bernoulli.

Mecânica Relativística

A Mecânica Relativística estuda o movimento dos corpos a velocidades próximas à velocidade da luz e a relação entre tempo e espaço. Ela é dividida em relatividade restrita e em relatividade geral, que são teorias desenvolvidas por Albert Einstein.

Mecânica Quântica

A Mecânica Quântica estuda os fenômenos que acontecem nas escalas subatômicas e atômicas. As suas divisões ainda estão em andamento.

Importância da Mecânica

A Mecânica é uma área da Física de extrema importância em diversos aspectos. Os conhecimentos obtidos a partir dela permitiram sabermos modos, causas e consequências dos movimentos e repouso dos corpos, possibilitando que nós os recriássemos quando desejado, como o desenvolvimento do navio, avião e automóveis.

Além disso, a Mecânica propociou a ampliação e comprovação do conhecimento sobre os planetas, a partir da descoberta da lei da gravitação universal de Newton e das leis de Kepler.

Com a Mecânica, é possível prever o comportamento dos corpos nos planetas, como a força peso e a aceleração da gravidade que atuam sobre eles.

Mecânica no Enem

No Enem, sempre cai alguma questão relacionada à Mecânica Clássica, e as áreas de Hidrostática, Cinemática e Dinâmica são as mais abordadas.

Em relação à Mecânica Relativística, é raro cair questões relacionadas a ela no Enem, já que a sua inserção nos conteúdos programáticos do ensino médio ainda é recente.

E a Mecânica Quântica só é estudada no ensino superior, portanto não é cobrada no Enem.

Exemplos da Mecânica

- A Mecânica explica diversos fenômenos que observamos em nosso cotidiano, como:

- A queda dos corpos ocasionada pela gravidade.

- A aceleração de um corpo pela aplicação de uma força.

- Os acidentes automobilísticos, em que o carro sai da curvatura devido à perda do atrito ou à alta velocidade.

- Ao abrirmos a maçaneta ou brincarmos na gangorra, utilizamos o princípio de alavanca estudado na Mecânica.

- Órbitas dos planetas e satélites.

- Máquinas simples, como roldanas, planos inclinados, talhas, balanças e outras.

- O ato de andar, já que aplicamos uma força no chão e recebemos a força que o chão faz sobre nós, caso contrário afundaríamos.

- A porta automática dos shoppings, que funciona a partir da Mecânica Relativística.

QUESTÕES RESOLVIDAS

01) Das grandezas citadas nas opções a seguir, assinale aquela que estudamos na Mecânica.

(A) reflexão da luz.

(B) força eletromotriz.

(D) campo elétrico.

(E) força.

Resolução:

A grandeza força é um conteúdo estudado na Mecânica, através das leis de Newton.

Alternativa: E

02) (PUC) A respeito do conceito de inércia, pode-se dizer que:

(A) inércia é uma força que mantém os objetos em repouso ou em movimento com velocidade constante.

(B) inércia é uma força que leva todos os objetos ao repouso.

(D) objetos que se movem rapidamente têm mais inércia que os que se movem lentamente.

Resolução:

A primeira lei de Newton fala que a inércia é a força que mantém os objetos em repouso ou em movimento com velocidade constante.

Alternativa: A

03) (Fatec) Na teoria da relatividade restrita de Einstein, dois conceitos estudados referem-se ao fato de que, ao considerar um objeto propagando-se à velocidade da luz, podemos verificar

(A) a dilatação do tempo e a dilatação do comprimento.

(B) a contração do tempo e a dilatação do comprimento.

(D) a dilatação do tempo sem contração do comprimento.

(E) a contração do tempo sem contração do comprimento.

Resolução:

Na teoria da relatividade restrita de Einstein, quando um objeto está propagando-se à velocidade da luz, ele observa a dilatação do tempo e a contração do comprimento.

Alternativa: C

04) (Uerj) A figura abaixo ilustra uma ferramenta utilizada para apertar ou desapertar determinadas peças metálicas.

Para apertar uma peça, aplicando a menor intensidade de força possível, essa ferramenta deve ser segurada de acordo com o esquema indicado em:

(A)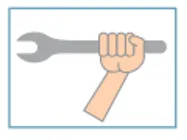

(B)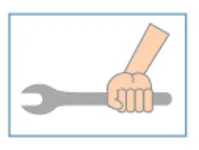

(C)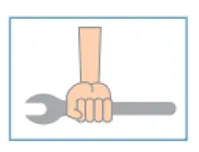

(D)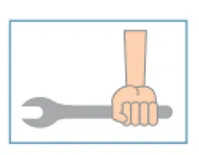

Resolução:

Para apertar a peça com a menor intensidade de força possível, precisamos aplicar a força na extremidade e na vertical, já que quanto mais próximo a mão estiver do orifício direito, mais força é feita.

Alternativa: D

05) Qual das forças abaixo é responsável pela deformação e elongação dos corpos?

(A) força elétrica.

(B) força normal.

(D) força peso.

(E) força de atrito.

Resolução:

A força responsável pela deformação e elongação dos corpos é a força elástica, calculada através da lei de Hooke.

Alternativa: D

06) A partir dos seus conhecimentos a respeito das leis de Kepler, qual das alternativas não corresponde a uma delas?

(A) lei das órbitas elípticas

(B) lei das áreas

(D) lei da ação e reação

Resolução:

A lei de ação e reação não é uma das leis de Kepler, mas uma das leis de Newton. Ela diz respeito ao princípio de ação e reação das forças sobre os corpos.

Alternativa: D

Professor Diminoi

QUESTÕES RESOLVIDAS – SEDUC-SP/2025

MRU - MRUV - (MRUC-Interpretação de gráfico) - MCU – HIDROSDATICA - GRAVITAÇÃO UNIVERSAL – ENERGIA E TRABALHO – QUANTIDADE DE MOVIMENTO – IMPULSO - ELETRODINÂMICA

MRU

01) (Livro do aluno-SEDUC-SP/2025 - UEM 2023 – Adaptada) (UEM 2023 – Adaptada) Três partículas (A, B e C) percorrem o mesmo caminho linear em velocidades instantâneas constantes, vA = 6 m/s, vB = 4 m/s e vC = 5 m/s.

Suponha que no tempo t = 0 s, os seus respectivos pontos de partida sejam sA = −120 m, sB = −80 m e sC = −100 m. Considerando sA(t), sB(t) e sC(t) as posições das partículas A, B e C, respectivamente, em metros, em função do tempo t, em segundo, dê a soma das alternativas corretas.

01) As partículas encontrar-se-ão no marco zero espacial em t = 20 s.

Resolução:

Com base nas informações fornecidas pelo enunciado, vamos, primeiro, determinar as equações horárias das posições das 3 partículas:

sA(t) = –120 + 6t

sB(t) = –80 + 4t

sC(t) = –100 + 5t

Para verificar se as partículas se encontrarão no marco zero no instante t = 20 s basta substituir esse valor em cada equação horária das posições, desenvolvê-la e verificar se a posição das três partículas, no instante desejado, é 0 m:

sA(t) = –120 + 6t

sA(20) = –120 + 6 · 20

sA(20) = –120 + 120 = 0

sB(t) = –80 + 4t

sB(20) = –80 + 4 · 20

sB(20) = –80 + 80 = 0

sC(t) = –100 + 5t

sC(20) = –100 + 5 · 20

sC(20) = –100 + 100 = 0

Portanto a afirmativa 01 é verdadeira.

02) Em t = 35 s, as partículas A, B e C estarão nas posições 90 m, 60 m e 75 m, respectivamente.

Resolução:

De forma análoga ao raciocínio da afirmativa anterior, para descobrir a posição que cada partícula ocupará no instante t = 35 s basta substituir esse valor na equação horária de cada uma, desenvolver a equação e verificar se a posição encontrada coincide com a posição proposta pelo enunciado. Para tanto:

sA(t) = –120 + 6t

sA(35) = –120 + 6 · 35

sA(35) = –120 + 210 = 90 m

sB(t) = –80 + 4t

sB(35) = –80 + 4 · 35

sB(35) = –80 + 140 = 60 m

sC(t) = –100 + 5t

sC(35) = –100 + 5 · 35

sC(35) = –100 + 175 = 75 m

Portanto a afirmativa 02 é verdadeira.

04) O movimento de cada partícula é um movimento uniforme.

Resolução:

Por definição, a velocidade, em um movimento uniforme, não varia. Em outras palavras, em um movimento uniforme a velocidade é constante. Como o enunciado afirma que as velocidades instantâneas das três partículas são constantes, a afirmativa 04 é verdadeira.

08) As três partículas encontrar-se-ão na posição s = 120 m.

Resolução:

Como as partículas A, B e C possuem velocidades constantes e diferentes (6m/s, 4 m/s e 5 m/s, respectivamente), e já foi demonstrado que elas se encontraram no marco zero (em t = 20 s), é fisicamente impossível que voltem a se encontrar em qualquer outra posição, incluindo s = 120 m. Portanto a afirmativa 08 é falsa. 01 + 02 + 04 = 07.

02) (Livro do aluno-SEDUC-SP/2025 - ENEM PPL 2013) Antes das lombadas eletrônicas, eram pintadas faixas nas ruas para controle da velocidade dos automóveis. A velocidade era estimada com o uso de binóculos e cronômetros. O policial utilizava a relação entre a distância percorrida e o tempo gasto, para determinar a velocidade de um veículo. Cronometrava-se o tempo que um veículo levava para percorrer a distância entre duas faixas fixas, cuja distância era conhecida. A lombada eletrônica é um sistema muito preciso, porque a tecnologia elimina erros do operador. A distância entre os sensores é de 2 metros, e o tempo é medido por um circuito eletrônico.

O tempo mínimo, em segundos, que o motorista deve gastar para passar pela lombada eletrônica, cujo limite é de 40 km/h, sem receber uma multa, é de:

(A) 0,05

(B) 11,1

(D) 22,2

(E) 0,50

Resolução:

Podemos calcular o tempo em um MRU pela equação da velocidade média:

Porém, para determinar o tempo em segundos é preciso transformar a velocidade para m/s. Portanto

Substituindo na equação os valores conhecidos, obtém-se:

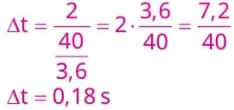
Alternativa: C

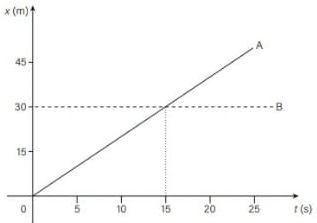
03) (Livro do aluno-SEDUC-SP/2025 - UFPR 2022 – Adaptada) A figura a seguir apresenta o comportamento gráfico da posição x em função do tempo t para os objetos A (linha cheia) e B (linha tracejada), que se movem ao longo de duas pistas retas, paralelas e de origens coincidentes.

De acordo com os dados apresentados no enunciado e no gráfico, considere as seguintes afirmativas:

I O objeto A tem uma velocidade constante, de módulo v = 2 m/s.

II Os objetos se encontram no instante t = 15 s.

III O objeto B está parado.

IV O objeto A inicia o movimento em x₀ = 0 m.

Assinale a alternativa correta.

(A) Somente a afirmativa II é verdadeira.

(B) Somente as afirmativas I e III são verdadeiras.

(D) Somente as afirmativas I, III e IV são verdadeiras.

(E)As afirmativas I, II, III e IV são verdadeiras.

Resolução:

I Verdadeira. Pode-se concluir que o movimento do objeto A é retilíneo, pois o enunciado diz que as pistas são retas e uniformes, já que sua representação no gráfico posição versus tempo é uma reta ascendente. Podemos verificar a velocidade desse objeto pelo cálculo:

II Verdadeira. Os objetos se encontram no instante em que ocupam a mesma posição (30 m), portanto 15 s.

III Verdadeira. Analisando o gráfico pode-se concluir que a posição do objeto B não se altera ao longo do tempo, o que caracteriza velocidade nula.

IV Verdadeira. De acordo com o gráfico, a posição inicial do objeto A é a origem das posições, portanto x₀ = 0 m.

Alternativa: E

04) (Livro do aluno-SEDUC-SP/2025 - UFJF 2023) Segundo o livro dos recordes, a maior estrada em linha reta do mundo fica na Arábia Saudita. São 240 km sem curvas nem declives consideráveis, no meio do deserto. O gráfico abaixo mostra a contagem da quilometragem no painel de um carro que se desloca nesta estrada, em função do tempo.

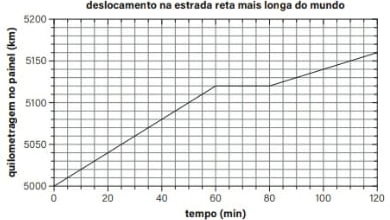
Assinale a alternativa correta.

(A) A velocidade do carro possui maior módulo nos últimos 40 min do trajeto.

(B) A velocidade do carro é constante somente no trecho percorrido entre 60 e 80 min.

(D) A velocidade do carro nos últimos 10 min de viagem é aproximadamente 33,3 m/s.

(E) A velocidade média do carro nos primeiros 80 min de viagem é 25 m/s.

Resolução:

Pela análise do gráfico podemos concluir que nos três trechos a velocidade é constante, pois a representação dos três, no gráfico quilometragem versus tempo (S × t), é feita por retas. Precisamos, portanto, determinar a velocidade em cada trecho.

Nos primeiros 60 min (1h):

Pelos cálculos podemos concluir que a alternativa A é falsa, pois a velocidade nos primeiros 60 min de viagem é maior do

que nos últimos 40 min.

A alternativa B é falsa, pois nos trechos percorridos entre 0 e 60 min e entre 80 e 120 min as velocidades também são constantes, mas diferentes de zero.

A alternativa C é falsa, pois a velocidade média do trajeto todo (120 min = 2h) é

Alternativa: E

05) (Livro do aluno-SEDUC-SP/2025 - UDESC 2023) Considere que dois veículos estão em movimento uniforme sobre uma rodovia. Admita que o primeiro veículo partiu da origem, e o segundo partiu da posição 300 km. Considerando que a velocidade do primeiro é 90 km/h e a do segundo é –110 km/h, determine quais os tempos cuja distância entre eles será de 100 km:

(A) 30 e 120 minutos.

(B) 90 e 120 minutos.

(D) 60 e 180 minutos.

(E) 60 e 120 minutos.

Resolução:

Analisando as posições iniciais e os sinais das velocidades, podemos concluir que os veículos se movem um em direção ao outro, portanto a distância entre eles será de 100 km em um instante antes que os veículos se cruzem e em outro instante depois do cruzamento.

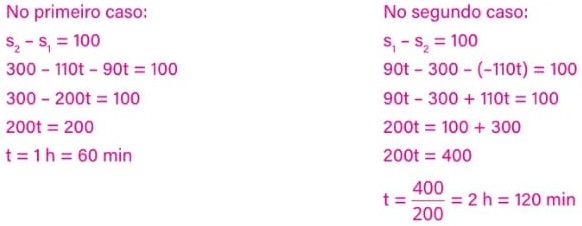
Alternativa: E

06) (Livro do aluno-SEDUC-SP/2025 - ENEM 2024) Um aeroporto disponibiliza o serviço de transporte gratuito entre seus dois terminais utilizando os ônibus A e B, que partem simultaneamente, de hora em hora, de terminais diferentes. A distância entre os terminais é de 9000 metros, e o percurso total dos ônibus, de um terminal ao outro, é monitorado por um sistema de cinco câmeras que cobrem diferentes partes do trecho, conforme o esquema.

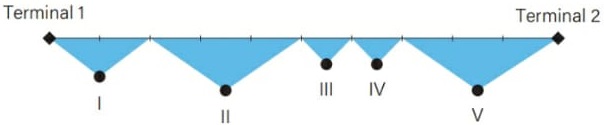
O alcance de cada uma das cinco câmeras é:

I. 1/5 do percurso;

II. 3/10 do percurso;

III. 1/10 do percurso;

IV. 1/10 do percurso;

V. 3/10 do percurso.

Qual câmera registra o momento em que os ônibus A e B se encontram?

(A) I

(B) II

(D) IV

(E) v

Resolução:

Inicialmente vamos determinar a equação horária das posições de cada ônibus. Para facilitar, vamos considerar que a posição inicial do ônibus A é o ponto 0 m e a posição inicial do ônibus B é 9000 m. As equações horárias serão, então

sA = 250t e sB = 9000 – 150t

O encontro entre os ônibus ocorrerá no instante em que a posição deles for a mesma, ou seja, quando sA = sB.

Para determinar o instante deste encontro, basta desenvolver essa igualdade:

sA = sB

250t = 9000 – 150t

400t = 9000

t = 9000

400

t = 22,5 min

Portanto, o ponto da trajetória em que esse encontro ocorrerá será:

sA = sB = 250t = 250 · 22,5 = 5625 m

Sabendo o ponto de encontro entre os ônibus, basta descobrir qual câmera cobre o trecho em que este ponto se encontra.

A câmera I cobre 1/5 do percurso de 9000 m (1800 m), ou seja, do ponto 0 m ao ponto 1800 m;

A câmera II cobre 3/10 do percurso (2700 m), ou seja, do ponto 1800 m ao ponto 4500 m.

A câmera III cobre 1/10 do percurso (900 m), ou seja, do ponto 4500 m ao ponto 5400 m.

A câmera IV cobre 1/10 do percurso também (900 m), ou seja, do ponto 5400 m ao ponto 6300 m.

Portanto, o ponto de encontro (5625 m) é na área de cobertura da câmera IV.

Alternativa: D

07) (Livro do aluno-SEDUC-SP/2025 - ENEM) O petróleo é uma matéria-prima muito valiosa e métodos geofísicos são úteis na sua prospecção. É possível identificar a composição de matérias estratificadas medindo-se a velocidade de propagação do som (onda mecânica) através deles. Considere que uma cama de 450m de um líquido se encontra presa no subsolo entre duas camadas rochosas, conforme o esquema. Um pulso acústico (que gera vibração mecânica) é emitido a partir da superfície do solo, onde são posteriormente recebidas duas vibrações refletidas (ecos).

A primeira corresponde à reflexão do pulso na interfase superior do líquido com a camada rochosa. A segunda vibração deve-se à reflexão do luso na interfase inferior. O tempo entre a emissão do pulso e a chagada do primeiro eco é de 0,5 s. O segundo eco chega 1,1 s após a emissão do pulso.

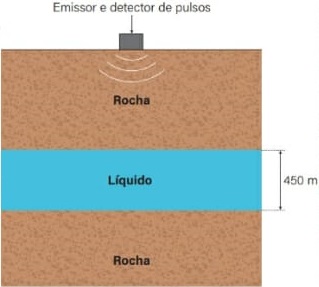
A velocidade da cama líquida em metros por segundo é:

(A) 270

(B) 540

(D) 1500

(E) 1800

Resolução:

A situação descrita no enunciado pode ser representada pela ilustração a seguir:

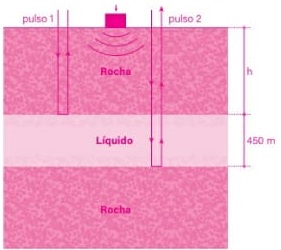
Pela ilustração, pode-se afirmar que o pulso 1, que reflete na interface superior, percorre uma distância h do emissor até

a interface, e uma distância h da interface até o emissor; ou seja, seu deslocamento, d1, é d1 = 2h.

Já o deslocamento do pulso 2 corresponde a 2h mais 900 (450+ 450). Ou seja, d2 = 2h + 900.

As equações horárias das posições dos dois pulsos podem ser escritas da seguinte forma:

d₁ = v · t₁
2h = v · t₁
d₂ = v · t₂
2h + 900 = v · t₂

A partir dessas equações, podemos propor a seguinte afirmação:

d2 – d1 = v · t₂ – v · t₁

Como d₁ = 2h e d₂ = 2h + 900, podemos reescrever essa igualdade da seguinte forma:

Alternativa: D

MRUV

09) (Livro do aluno-SEDUC-SP/2025 - ENEM PPL 2020) Os acidentes de trânsito são causados geralmente por excesso de velocidade. Em zonas urbanas no Brasil, o limite de velocidade normalmente adotado é de 60 km ^h−1. Uma alternativa para diminuir o número de acidentes seria reduzir esse limite de velocidade. Considere uma pista seca em bom estado, onde um carro é capaz de frear com uma desaceleração constante de 5 m s⁻² e que o limite de velocidade reduza de 60 km h⁻¹ para 50 km ^h−1.

Nessas condições, a distância necessária para a frenagem desde a velocidade limite até a parada completa do veículo será reduzida em um valor mais próximo de

(A) 1 m

(B) 9 m

(D) 19 m

(E) 38 m

Resolução:

Para resolver essa questão, precisaremos calcular duas situações:

Distância percorrida até a parada completa, quando a velocidade inicial é v₀ = 60 km/h ≅ 17 m/s;

Distância percorrida até a parada completa, quando a velocidade inicial é v₀ = 50 km/h ≅ 14 m/s;

Como não é informado o tempo de duração desse movimento, precisamos calcular a distância percorrida usando a equação de Torricelli.

A aceleração e a velocidade final são as mesmas para os dois casos,

Assim, temos:

v₀= 60 km/h ≅ 17 m/s:

v₀ = 50 km/h ≅ 14 m/s:

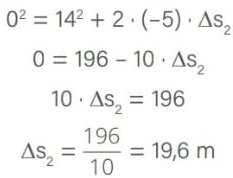
Logo, a redução na distância necessária até a frenagem completa é ∆s₁ – ∆s₂ = 28,9 – 19,6 = 9,3 m

Alternativa: B

10) (Livro do aluno-SEDUC-SP/2025 - UNICAMP 2024) Uma das etapas mais difíceis de um voo espacial tripulado é a reentrada na atmosfera terrestre. Ao reencontrar as camadas mais altas da atmosfera, a nave sofre forte desaceleração e sua temperatura externa atinge milhares de graus Celsius. Caso a reentrada não ocorra dentro das condições apropriadas, há risco de graves danos à nave, inclusive de explosão, e até mesmo risco de ela ser lançada de volta ao espaço.

Logo ao reentrar na atmosfera terrestre, uma cápsula espacial passa a descrever, durante certo tempo, um movimento retilíneo uniformemente variado em que ela é freada com aceleração a = –5,0 m/s². Se no início dessa etapa (t = 0) do movimento a velocidade da cápsula é v₀ = 7000 m/s, qual é a distância percorrida até o tempo t = 200 s?

(A) 1300 km

(B) 1400 km

(D) 4900 km

Resolução:

Para resolver essa questão, e evitar operar números muito grandes, vamos utilizar os valores de velocidade inicial e tempo em notação científica: v₀ = 7000 = 7 · 10³ m/s e t = 200 = 2 · 10² s.

Com os valores informados pelo enunciado, podemos calcular a distância desejada utilizando a equação horária das posições do MRUV:

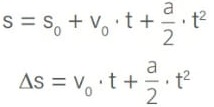
Substituindo os valores informados, tem-se:

Alternativa: A

11) (Livro do aluno-SEDUC-SP/2025 - UNIFESP 2005) A velocidade em função do tempo de um ponto material em movimento retilíneo uniformemente variado, expressa em unidades do SI, é v = 50 – 10t.

Pode-se afirmar que, no instante t = 5,0 s, esse ponto material tem:

(A) velocidade e aceleração nulas.

(B) velocidade nula e daí em diante não se movimenta mais.

(D) velocidade nula e a sua aceleração muda de sentido.

(E) aceleração nula e a sua velocidade muda de sentido.

Resolução:

Em um movimento retilíneo uniformemente variado a aceleração é sempre constante. Na equação horária das velocidades, a aceleração é a constante que multiplica a variável “tempo” (v = v₀ + at).

Portanto, de acordo com a equação v = 50 – 10t, podemos concluir que a aceleração do ponto material é a = –10 m/s².

Para determinarmos a velocidade de um móvel, que descreve um movimento retilíneo uniformemente variado, em um instante t, basta substituirmos o t da sua equação horária das velocidades pelo instante desejado e resolver a equação.

Para t = 5,0 s, obtemos então:

v = 50 – 10t

v = 50 – 10 · 5

v = 50 – 50

v = 0 m/s

Alternativa: C

12) (Livro do aluno-SEDUC-SP/2025 - UFPR 2024) Um objeto de massa m constante inicia um movimento no instante t = 0 s a partir do repouso quando está na posição x(0) = 5 m. O movimento é retilíneo e uniformemente variado (MRUV). No instante t = 2 s, sua velocidade vale v(2) = 16 m/s, e no instante t = 5 s, sua velocidade vale v(5) = 40 m/s.

Determine o valor da posição do objeto no instante t = 3 s.

Resolução:

Podemos determinar a posição de um objeto que se desloca em um movimento retilíneo uniformemente variado usando a equação horária das posições para o MRUV:

Como o movimento inicia a partir do repouso, então, a velocidade inicial é v₀ = 0 m/s.

A posição inicial (s0), de acordo com o enunciado, é s₀ = x(0) = 5 m.

Logo, para definir a posição final do objeto através da equação horária das posições para o MRUV é necessário calcular a aceleração desse objeto. A aceleração de um objeto que descreve um MRUV pode ser calculada por:

Sabe-se que v(2) 16 m/s e v(5) 40 m/s. Logo:

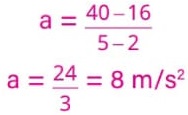
São conhecidos, então, as constantes:

v₀ = 0 m/s;

s₀ = 5 m;

a = 8 m/s².

Substituindo esses valores na equação horária das posições e considerando t = 3 s, obteremos:

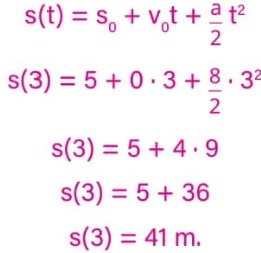
13) (Livro do aluno-SEDUC-SP/2025 - ENEM PPL 2013) O trem de passageiros da Estrada de Ferro Vitória-Minas (EFVM), que circula diariamente entre a cidade de Cariacica, na Grande Vitória, e a capital mineira Belo Horizonte, está utilizando uma nova tecnologia de frenagem eletrônica. Com a tecnologia anterior, era preciso iniciar a frenagem cerca de 400 metros antes da estação. Atualmente, essa distância caiu para 250 metros, o que proporciona redução no tempo de viagem.

Considerando uma velocidade de 72 km/h, qual o módulo da diferença entre as acelerações de frenagem depois e antes da adoção dessa tecnologia?

(A) 0,08 m/s²

(B)0,30 m/s²

(D) 1,60 m/s²

(E) 3,90 m/s²

Resolução:

Partiremos do pressuposto que a desaceleração é constante nos dois casos. Utilizaremos a velocidade inicial v0

em unidades do SI: v₀ = 72 km/h = 20 m/s.

Desaceleração da tecnologia anterior:

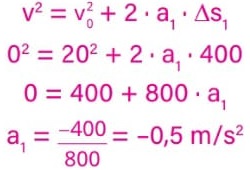
Desaceleração da tecnologia atual:

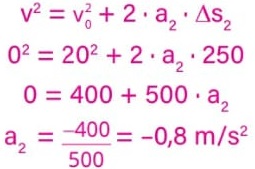
Logo, o módulo da diferença entre a desaceleração (acelerações de frenagem) depois e antes da nova tecnologia é:

Alternativa: B

14) (Livro do aluno-SEDUC-SP/2025 - UFRGS 2023) Um móvel desloca-se em linha reta com aceleração constante. Sua velocidade no instante t0 = 0 é não nula. Entre t₀= 0 e t₁= 5 segundos, o móvel percorre 100metros. Entre t₁ = 5 segundos e t₂ = 8 segundos, o móvel percorre 100 metros adicionais.

Qual das alternativas abaixo representa corretamente, com algarismos até a primeira casa decimal, o módulo da aceleração desse móvel?

(A) 2,1 m/s²

(B) 3,3 m/s²

(D) 9,7 m/s₂

(E) 7,6 m/s²

Resolução:

A partir das informações apresentadas no enunciado, vamos determinar a equação horária dos espaços para a primeira parte desse movimento (de t₀ a t₁) e a equação horária dos espaços para todo o movimento descrito (de t₀ a t₂).

De t₀ a t₁:

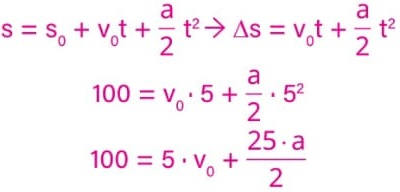
Multiplicando os dois lados da igualdade por 2, obtemos:

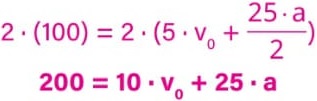
De t₀ a t₂:

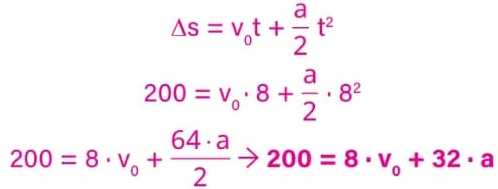
Obtemos duas equações com duas incógnitas. Podemos descobrir o valor dessas incógnitas fazendo um sistema de equações.

Para isso, vamos simplificar ambas:

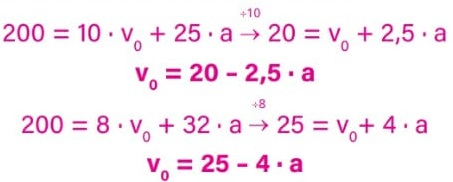
Como a velocidade inicial v₀ é a mesma para as duas equações, podemos igualá-las e encontrar o valor da aceleração:

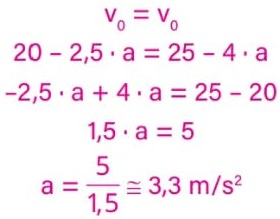
Alternativa: B

15) (Livro do aluno-SEDUC-SP/2025 - ENEM 2017) Um motorista que atende a uma chamada de celular é levado à desatenção, aumentando a possibilidade de acidentes ocorrerem em razão do aumento de seu tempo de reação. Considere dois motoristas, o primeiro atento e o segundo utilizando o celular enquanto dirige. Eles aceleram seus carros, a partir do repouso, inicialmente a 1,00 m/s². Em resposta a uma emergência, freiam com uma desaceleração igual a 5,00 m/s². O motorista atento aciona o freio à velocidade de 14,0 m/s, enquanto o desatento, em situação análoga, leva 1,00 segundo a mais para iniciar a frenagem.

Que distância o motorista desatento percorre a mais do que o motorista atento, até a parada total dos carros?

(A) 2,90 m

(B) 14,0 m

(D) 15,0 m

(E) 17,4 m

Resolução:

Vamos analisar primeiro o movimento descrito pelo motorista atento. Na primeira parte do seu movimento, o carro tem aceleração constante a = 1 m/s², indo do repouso (v₀ = 0 m/s) até a velocidade v = 14 m/s. Para isso, leva um tempo:

Nesse tempo, o motorista atento percorre a distância:

A partir daí, o motorista atento freia o automóvel, aplicando uma desaceleração constante a = –5 m/s² até parar o veículo. Nesse movimento é percorrida a distância:

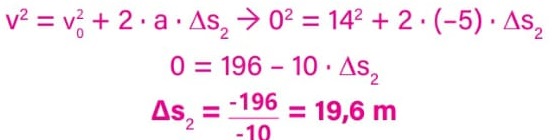
Logo, a distância total percorrida pelo motorista atento é ∆s₁ + ∆s₂= 98 + 19,6 = 117,6 m.

O motorista que utiliza o celular mantém a aceleração a = 1 m/s² por 1 s a mais, ou seja, 15 s, no total. Portanto, no início da frenagem, sua velocidade será:

Logo, seu veículo percorrerá, no período de aceleração, a distância:

Ao atingir a velocidade v = 15 m/s, esse motorista inicia a frenagem, também com a = –5 m/s², até parar, percorrendo nesse processo a distância:

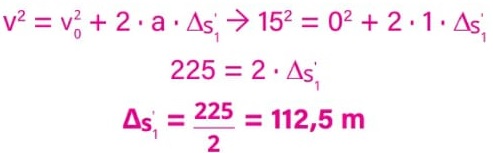
Logo, a distância total percorrida pelo motorista que usa o celular é:

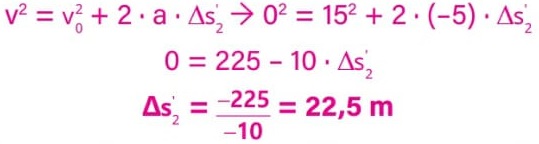
∆s'₁+ ∆s₂' = 112,5 + 22,5 = 135 m.

A distância que o motorista desatento percorre a mais é, então:

∆s = 135 – 117,6.

∆s = 17,4 m.

Alternativa: E

MRUV – INTERPRETAÇÃO DE GRÁFICOS

16) (Livro do aluno-SEDUC-SP/2025 - UERJ 2023) Ao longo de uma estrada retilínea, um automóvel trafega durante certo intervalo de tempo, variando sua velocidade V linearmente em função do tempo t, como representado no gráfico.

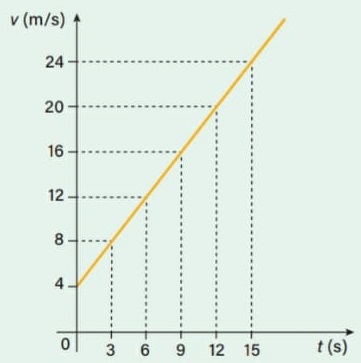
No intervalo de tempo compreendido entre t = 0 e t = 15 s, a velocidade média do automóvel, em m/s, é igual a:

(A) 7

(B) 11

(D) 18

Resolução:

Do MRU, sabemos que a velocidade média de um movimento pode ser calculada por:

Como é pedida a velocidade média no intervalo de tempo compreendido entre t = 0 e t = 15 s, logo, Δt = 15 s.

Como o gráfico apresentado é um gráfico v × t, a área sob ele é numericamente igual a Δs. A área abaixo do gráfico forma um trapézio cuja base menor bm = 4, base maior b_M = 24 e altura h = 15. Logo, a área abaixo do gráfico será:

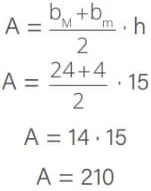
Δs = 210 m, logo a velocidade média desse percurso será:

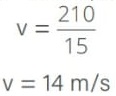
Alternativa: C

17) (Livro do aluno-SEDUC-SP/2025 - UCPEL 2021) Um professor de física usa um carrinho de brinquedo, movido por um motor elétrico, para fazer experimentos com uma turma de estudantes. O carrinho é acelerado, a partir do repouso, e o seu movimento retilíneo é analisado pelos estudantes. Em um desses experimentos, a posição do carrinho é registrada em diversos instantes e, usando os dados numéricos, os estudantes traçam o gráfico abaixo, obtendo um arco de parábola.

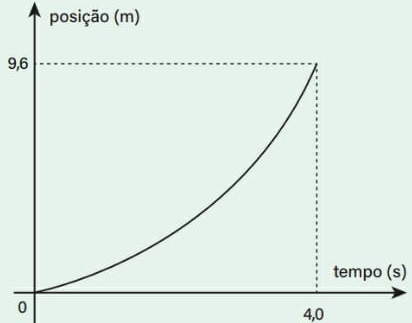
Com base no gráfico, os estudantes concluem, corretamente, que:

(A) o movimento é uniformemente acelerado com aceleração de módulo igual a1,2 m/s².

(B) o movimento é uniformemente acelerado com aceleração de módulo igual a 2,4 m/s².

(D) o movimento é uniforme com velocidade de módulo igual a 1,2 m/s.

(E) o movimento é uniformemente retardado com aceleração de módulo igual a 1,2 m/s².

Resolução:

O gráfico de um movimento uniforme é uma reta. Como o gráfico obtido é um arco de parábola, já podemos descartar as alternativas C e D. Como o movimento representado pelo gráfico é um MRUV, a aceleração é constante por todo o movimento e podemos determiná-la usando as informações do gráfico, do enunciado e da equação horária das posições do MRUV:

De acordo com o gráfico e com o enunciado, s = 9,6 m, s₀ = 0, v0 = 0 e t = 4 s. Substituindo esses valores na equação, obtemos:

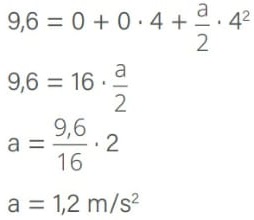
Como o movimento acontece no sentido positivo do eixo das posições e a aceleração também é positiva, esse movimento é acelerado.

Alternativa: A

18) (Livro do aluno-SEDUC-SP/2025 - UFRR 2023) O gráfico a seguir representa o movimento de uma partícula, onde S é a posição e t o tempo. Sobre esse movimento, é CORRETO afirmar que:

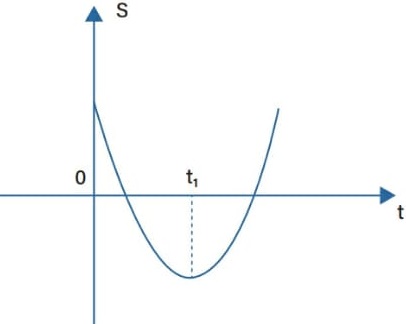
(A) de t = 0 até t = t₁ o movimento da partícula é acelerado.

(B) de t = 0 até t = t₁ a aceleração é negativa.

(D) a trajetória da partícula é curvilínea.

(E) em t = t₁ a aceleração é zero.

Resolução:

Alternativa A: o ponto t₁corresponde ao vértice da parábola e representa o ponto em que a velocidade é zero, e a partir dele o sentido da velocidade é invertido.

Para que a velocidade seja zero nesse ponto, de t = 0 s até t₁ o seu módulo diminui. Logo, velocidade e aceleração, neste intervalo, possuem sentidos opostos, o que caracteriza um movimento retardado. Portanto, a alternativa A é falsa.

Alternativa B: um gráfico s × t cuja parábola tem a concavidade para cima representa um MRUV cuja aceleração é positiva. Portanto, a alternativa B é falsa.

Alternativa C: de acordo com a análise da alternativa A, para que a velocidade seja zero no ponto t₁, de t = 0 s até t₁o seu módulo diminui. Logo, velocidade e aceleração, neste intervalo, têm sentidos opostos, o que caracteriza um movimento retardado. Portanto, a alternativa C é verdadeira.

Alternativa D: o gráfico s × t ser uma parábola não caracteriza um movimento curvilíneo.

Portanto, a alternativa D é falsa.

Alternativa E: o gráfico s × t ser uma parábola representa um movimento de aceleração constante e diferente de zero.

Portanto, a alternativa E é falsa.

Alternativa: C

19) (Livro do aluno-SEDUC-SP/2025 - UERJ 2014) O gráfico representa a variação da velocidade dos carros A e B que se deslocam em uma estrada.

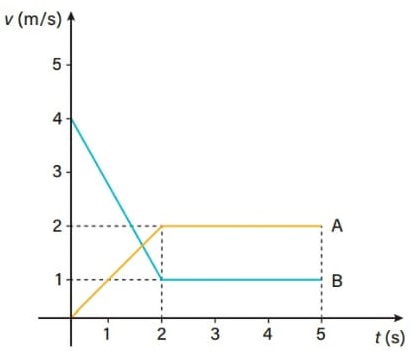
Determine as distâncias percorridas pelos carros A e B durante os primeiros cinco segundos do percurso. Calcule, também, a aceleração do carro A nos dois primeiros segundos.

Resolução:

Em um gráfico v × t, a distância percorrida é numericamente igual à área abaixo do gráfico. Logo, ΔsA é numericamente igual à área de um trapézio de base maior bM = 5, base menor bm = 3 e altura h = 2. Portanto:

Porém, a área abaixo do gráfico do móvel B não possui a forma de um polígono regular. Para calcular essa área, vamos dividi-la em duas partes: um trapézio de base maior bM = 4, base menor bm = 1 e altura h = 2; e um retângulo de base b = 3 e altura h = 1.

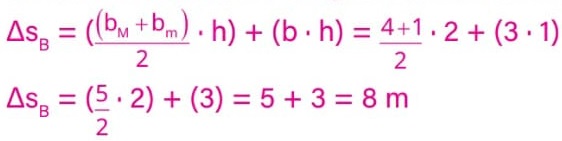
Nos primeiros dois segundos (Δt = 2 s), a velocidade do móvel A aumenta de v₀= 0 m/s a v = 2 m/s. Logo, sua aceleração nesse período foi de:

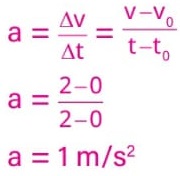
20) (Livro do aluno-SEDUC-SP/2025 - UFRGS 2024) Um móvel percorre uma trajetória retilínea sobre uma superfície horizontal, durante 1 minuto. O móvel parte do repouso e é submetido à aceleração, cuja componente a, na direção do movimento, varia com o tempo t, conforme mostra a figura abaixo.

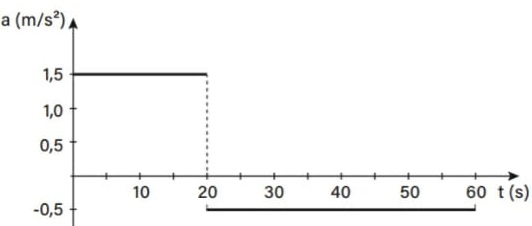
Qual dos gráficos abaixo melhor representa a componente v, da velocidade do móvel, na mesma direção, no intervalo de tempo de 0 a 60 s?

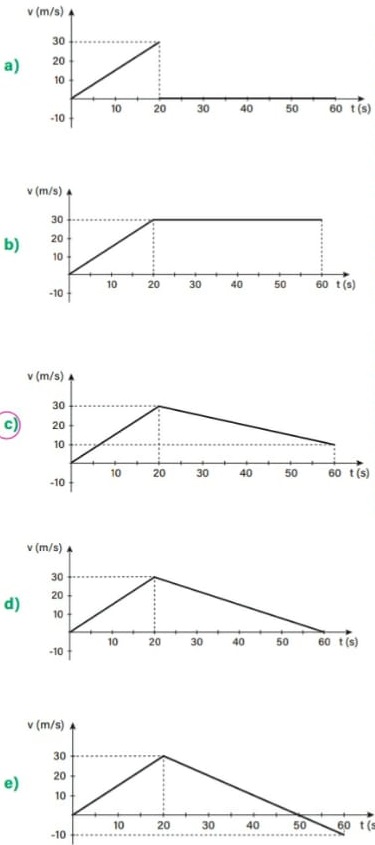
Resolução:

O gráfico a × t nos mostra que, do instante t = 0 s ao instante t = 20 s, o móvel descreve um MRUV cuja aceleração é a = 1,5 m/s². Como a aceleração é positiva, a representação desse movimento em um gráfico v × t é uma reta ascendente.

Do instante t = 20 s ao instante t = 60 s, o móvel descreve um MRUV cuja aceleração é a = –0,5 m/s². Neste caso, a aceleração é negativa, logo, a representação desse movimento em um gráfico v × t é uma reta descendente.

Com essas duas análises, já é possível afirmar que as alternativas A e B são falsas.

Como a representação do intervalo entre t = 0 s e t = 20 s é igual nas alternativas a, b e c, basta determinar a velocidade no móvel no instante t = 60 s para encontrarmos a resposta certa.

A segunda parte do movimento do móvel inicia em t₀ = 20 s. Nesse instante v₀ = 30 m/s e a = –0,5 m/s². Logo, a velocidade no instante t = 60 s será:

v = v0 + a · Δt

v = 30 + (–0,5) · (60 – 20)

v = 30 + (–0,5) · (40)

v = 30 – 20

v = 10 m/s

Portanto, a alternativa que apresenta a representação correta deste movimento em um gráfico v × t é

Alternativa: C

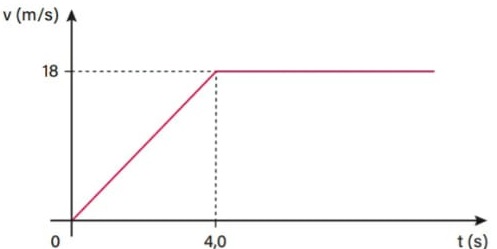
21) (Livro do aluno-SEDUC-SP/2025 - FMJ 2023) O ser humano é capaz de correr a uma velocidade de até 64,4 km/h [aproximadamente 18 m/s], superando a velocidade atingida pelo atleta jamaicano Usain Bolt, recordista mundial dos 100 m rasos – segundo estudo realizado nos Estados Unidos. O número foi estabelecido depois que cientistas calcularam a mais alta velocidade pela qual os músculos do corpo humano podem se mover biologicamente.

(www.bbc.com. Adaptado.)

Suponha que um atleta na prova dos 100 m, partindo do repouso e com aceleração constante, atingisse essa velocidade máxima e a mantivesse constante até o final dessa prova, como mostrado no gráfico.

Esse atleta percorreria os 100 m em um intervalo de tempo de, aproximadamente:

(A) 6,42 s

(B) 9,24 s

(D) 7,56 s

(E) 6,98 s

Resolução:

A área abaixo do gráfico v × t é numericamente igual ao deslocamento durante o movimento.

Como é pedido o tempo necessário para que o atleta percorra 100 m, ou seja, para Δs = 100 m, logo, a área do gráfico (que tem a forma de um trapézio) mostrado é A_trap = 100.

Precisamos, então, determinar o valor de t para que a área desse trapézio seja Atrap = 100. Para facilitar, vamos dividir o trapézio em dois: um triângulo e um retângulo. Logo, A_trap = A_tri + Aret = 100.

Portanto:

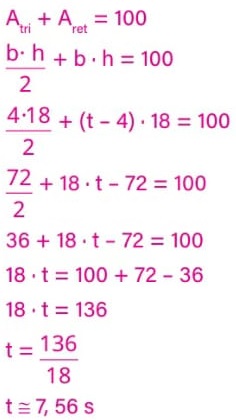
Alternativa: D

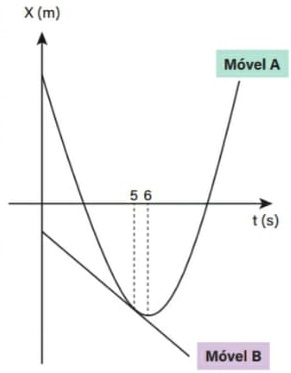
22) (Livro do aluno-SEDUC-SP/2025 - ACAFE 2023) Dois móveis A e B descrevem trajetórias retilíneas e seus movimentos estão representados no gráfico, posição (X), em função do tempo de movimento (t) a seguir. O móvel A inicia seu movimento com velocidade de módulo 12 m/s. Sabendo que os móveis se encontram no instante t = 5 s e que a distância inicial entre eles é de 15 m, o módulo da velocidade do móvel B é:

(A) 10 m/s

(B) 6 m/s

(D) 2 m/s

Resolução:

O enunciado diz que os móveis se encontram no instante t = 5 s. Isso significa que nesse instante os dois móveis ocupam a mesma posição, ou seja, sA(5) = sB(5).

Com base no gráfico e no enunciado, podemos afirmar que o móvel A descreve um MRUV, pois sua trajetória é retilínea e o gráfico é uma parábola, portanto sua posição em um instante t pode ser definida por

Da mesma forma, podemos afirmar que o móvel B descreve um MRU, pois sua trajetória é retilínea e o gráfico é uma reta não paralela ao eixo t, portanto sua posição em um instante t pode ser definida por sB(t) = sB0 + v · t.

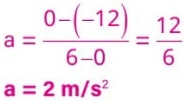
Substituindo os valores encontrados na equação que definimos, obteremos:

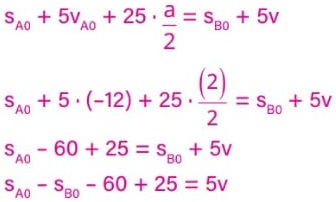
Como sA(5) = sB(5), podemos escrever:

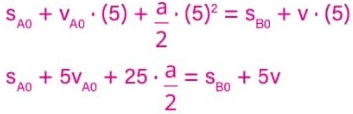
sA(5) = sB(5)

Para determinarmos a velocidade do móvel B v, na equação

Precisamos determinar o valor das outras incógnitas.

O enunciado diz que o módulo da velocidade inicial de A é |vA0| = 12 m/s. Mas, como no intervalo t = 0 s até t = 6 s o movimento é retrógrado, então vA0 = –12 m/s.

Como no instante t = 0 a velocidade é vA0 = –12 m/s e em t = 6 s (vértice da parábola) a velocidade é v = 0, a aceleração do móvel A é:

Apesar de não sabermos as posições iniciais dos móveis, o enunciado diz que, no início dos movimentos, a distância entre eles era de 15 m.

Ou seja, sA0 – sB0 = 15 m.

Logo:

15 – 60 + 25 = 5v – 20 = 5v

v = – 4 m/s

|v| = 4 m/s

Alternativa: C

23) (Livro do aluno-SEDUC-SP/2025 - UNESP 2020) O gráfico representa a velocidade escalar de um nadador em função do tempo, durante um ciclo completo de braçadas em uma prova disputada no estilo nado de peito, em uma piscina.

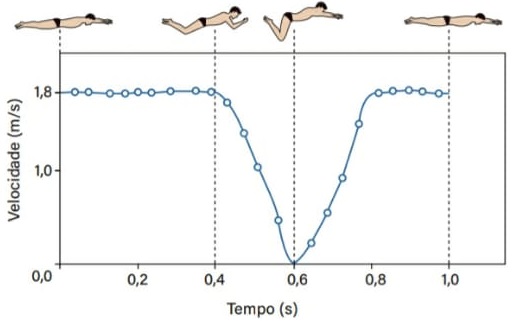
Considerando que, em um trecho de comprimento 36 m, o nadador repetiu esse ciclo de braçadas e manteve o ritmo de seu nado constante, o número de braçadas completas dadas por ele foi em torno de:

(A) 20

(B) 35

(D) 30

(E) 25

Resolução:

Sabendo que a trajetória a ser percorrida pelo nadador é 36 m, basta determinarmos a distância percorrida pelo atleta em um ciclo completo de braçadas que poderemos calcular a quantidade de braçadas necessária para percorrer a trajetória inteira.

Como a área abaixo do gráfico v × t é numericamente igual ao deslocamento, para o movimento desse nadador podemos aproximar as linhas do gráfico para retas. Fazendo isso, obtemos:

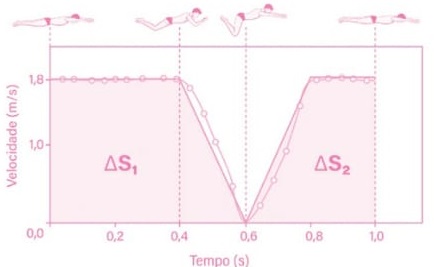
Portanto, o deslocamento (Δs) do nadador em um ciclo completo de braçada será:

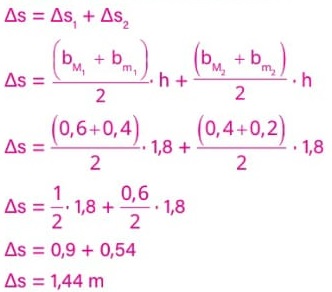
Se a cada ciclo de braçada o nadador percorre 1,44 m e a trajetória possui 36 m, o número n de braçadas necessário para percorrer todo o trajeto é:

Alternativa: E

MCU

24) (Livro do aluno-SEDUC-SP/2025 - ESPCEX 2019) Duas polias, A e B, ligadas por uma correia inextensível têm raios RA = 60 cm e RB = 20 cm, conforme o desenho abaixo. Admitindo que não haja escorregamento da correia e sabendo que a frequência da polia A é fA = 30 rpm, então a frequência da polia B é:

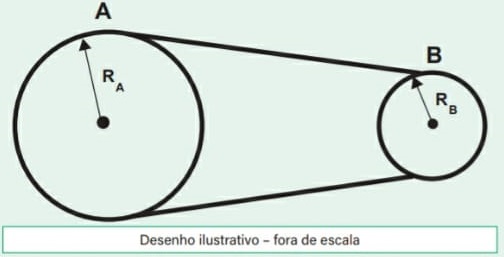
(A) 10 rpm

(B) 20 rpm

(D) 90 rpm

(E) 120 rpm

Resolução:

Como as duas polias estão ligadas por uma correia, as velocidades escalares delas são iguais:

vA = vB

Como v = ω · R e ω = 2π · f, temos:

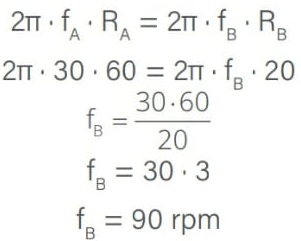
Alternativa: D

25) (Livro do aluno-SEDUC-SP/2025 - UNESP 2016) Um pequeno motor a pilha é utilizado para movimentar um carrinho de brinquedo. Um sistema de engrenagens transforma a velocidade de rotação desse motor na velocidade de rotação adequada às rodas do carrinho. Esse sistema é formado por quatro engrenagens, A, B, C e D, sendo que A está presa ao eixo do motor, B e C estão presas a um segundo eixo e D a um terceiro eixo, no qual também estão presas duas das quatro rodas do carrinho.

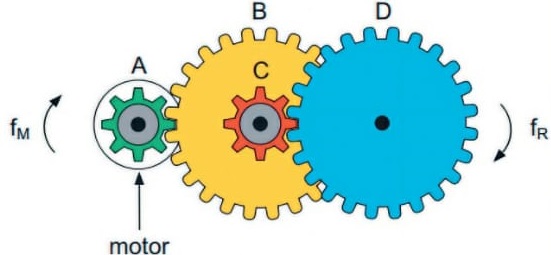
Nessas condições, quando o motor girar com frequência fM, as duas rodas do carrinho girarão com frequência fR. Sabendo que as engrenagens A e C possuem 8 dentes, que as engrenagens B e D possuem 24 dentes, que não há escorregamento entre elas e que fM = 13,5 Hz, é correto afirmar que fR, em Hz, é igual a:

(A) 1,5

(B) 3,0

(D) 1,0

(E) 2,5

Resolução:

O raio de uma engrenagem é proporcional ao número de dentes que contém. Como A e C têm o mesmo número de dentes e B e D também, devido à proporção entre raio (R) e número de dentes (n), podemos estabelecer as seguintes relações:

Como A e B estão acopladas tangencialmente, suas velocidades escalares são iguais. Sabendo que fA = fM, temos:

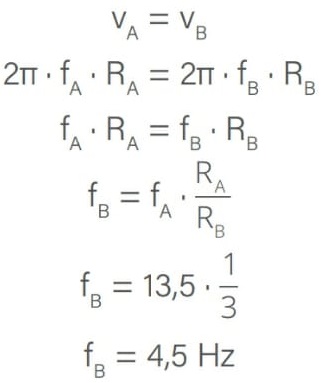
As engrenagens B e C, por outro lado, estão acopladas coaxialmente, ou seja, estão ligadas por um eixo. Neste caso:

ωB = ωC

Como ω = 2π · f, temos:

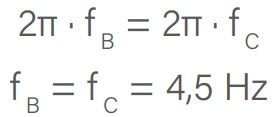
Agora as engrenagens C e D também estão acopladas tangencialmente, portanto vale a relação:

vC = vD

Substituindo as velocidades, obtemos:

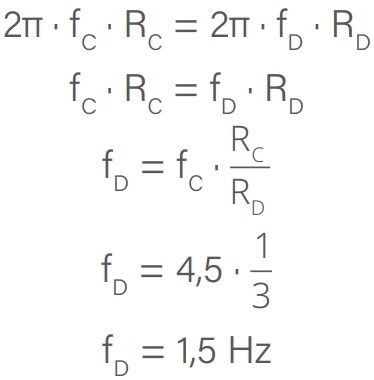
Alternativa: A

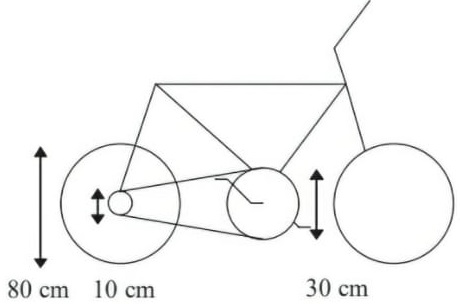
26) (Livro do aluno-SEDUC-SP/2025 - ENEM 1998 – Adaptada) Quando se dá uma pedalada na bicicleta abaixo (isto é, quando a coroa acionada pelos pedais dá uma volta completa), qual é a distância aproximada percorrida pela bicicleta, sabendo-se que o comprimento de um círculo de raio R é igual a 2πR, onde π ≈ 3?

(A) 1,2 m

(B) 2,4 m

(D) 14,4 m

(E) 48,0 m

Resolução:

Como as duas coroas da bicicleta estão ligadas por uma corrente, suas velocidades escalares são iguais (vM = vm). Substituindo as velocidades, obtemos:

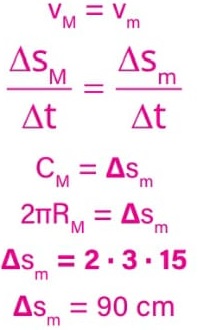
Como o comprimento da coroa menor é Cm = 2πRm = 2 · 3 · 5 = 30 cm, para cada volta da coroa maior (cada pedalada) a coroa menor gira um número n de vezes, que é igual a:

Logo, com uma pedalada a coroa menor gira três vezes. Como a coroa menor está acoplada à roda da bicicleta coaxialmente, ou seja, através de um eixo, cada vez que a coroa menor completa uma volta, a roda também o fará.

Portanto, com uma pedalada, a roda também gira três vezes.

Então, a distância percorrida pela bicicleta (∆sB) será igual a três vezes o seu comprimento, ou seja:

Alternativa: C

27) (Livro do aluno-SEDUC-SP/2025 - UECE 2022) Em um torno mecânico de bancada, duas polias são conectadas por meio de uma correia. Uma das polias tem 10 cm de raio e realiza 80 voltas por segundo. O número de voltas que a segunda polia dará por minuto, caso tenha 20 cm de raio, é:

(A) 1200

(B) 7200

(D) 3600

Resolução:

Como as polias são conectadas por uma correia, chamando uma polia de A e a outra de B, podemos afirmar que:

vA = vB

Mas como v = ω · R e ω = 2π · f, então:

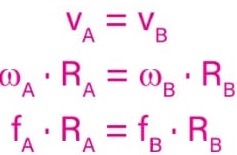
De acordo com o enunciado, uma das polias (A) possui raio RA = 10 cm e f_A = 80 voltas por segundo, ou seja,

f_A = 80 Hz. Se considerarmos que a outra polia possua raio RB = 20 cm, então sua frequência será:

Porém, o enunciado pede que definamos a frequência da segunda polia em voltas por minuto, ou seja, em rpm.

Para converter um valor de frequência que está em Hertz para rpm, basta multiplicá-lo por 60.

Logo:

Alternativa: C

28) (Livro do aluno-SEDUC-SP/2025 - ENEM 2013) Para serrar ossos e carnes congeladas, um açougueiro utiliza uma serra de fita que possui três polias e um motor. O equipamento pode ser montado de duas formas diferentes, P e Q. Por questão de segurança, é necessário que a serra possua menor velocidade linear.

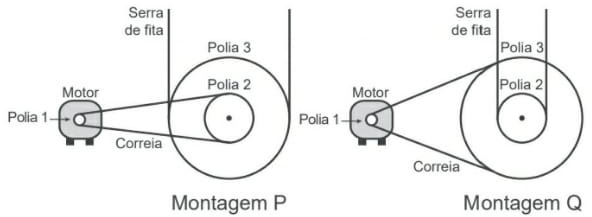
Por qual montagem o açougueiro deve optar e qual a justificativa desta opção?

(A) Q, pois as polias 1 e 3 giram com velocidades lineares iguais em pontos periféricos e a que tiver maior raio terá menor frequência.

(B) Q, pois as polias 1 e 3 giram com frequências iguais e a que tiver maior raio terá menor velocidade linear em um ponto periférico.

(C) P, pois as polias 2 e 3 giram com frequências diferentes e a que tiver maior raio terá menor velocidade linear em um ponto periférico.

(D) P, pois as polias 1 e 2 giram com diferentes velocidades lineares em pontos periféricos e a que tiver menor raio terá maior frequência.

(E) Q, pois as polias 2 e 3 giram com diferentes velocidades lineares em pontos periféricos e a que tiver maior raio terá menor frequência.

Resolução:

Alternativa A é verdadeira. Como as polias 1 e 3 são acopladas por correia, as velocidades lineares das suas extremidades são iguais.

Mas nesse tipo de acoplamento, por correia, as frequências de cada polia e os respectivos raios estão relacionados pela equação:

fA · RA = fB · RB

Por esse motivo, no acoplamento de polias por correia, quanto maior o raio da polia, menor sua frequência.

A alternativa B é falsa, pois, como vimos, no acoplamento de polias por correia, raio e frequência são grandezas inversamente proporcionais. Nessas condições, as frequências só seriam iguais se os raios fossem iguais.

Alternativa C é falsa, pois as polias 2 e 3 estão acopladas pelo mesmo eixo de transmissão.

Nesse tipo de acoplamento as frequências das polias acopladas, ou das engrenagens, são iguais.

Alternativa D é falsa, pois se as polias 1 e 2 foram acopladas por correia, as velocidades lineares dos seus pontos periféricos serão iguais.

Alternativa E é falsa, pois apesar da primeira afirmação (“pois as polias 2 e 3 giram com diferentes velocidades lineares em pontos periféricos”) ser verdadeira, a segunda é falsa. Quando duas polias são acopladas pelo mesmo eixo de transmissão, as suas frequências são iguais.

Alternativa: A

29) (Livro do aluno-SEDUC-SP/2025 - ENEM 2016) A invenção e o acoplamento entre engrenagens revolucionaram a ciência na época e propiciaram a invenção de várias tecnologias, como os relógios. Ao construir um pequeno cronômetro, um relojoeiro usa o sistema de engrenagens mostrado. De acordo com a figura, um motor é ligado ao eixo e movimenta as engrenagens fazendo o ponteiro girar.

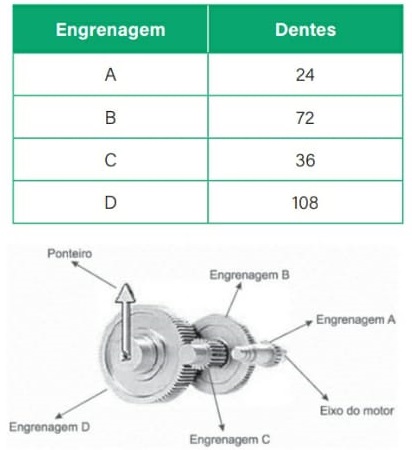
A frequência do motor é de 18 RPM, e o número de dentes das engrenagens está apresentado no quadro.

A frequência de giro do ponteiro, em RPM, é

(A) 1

(B) 2

(D) 81

(E) 162

Resolução:

A engrenagem A está acoplada ao eixo do motor, por isso, sua frequência é a mesma do motor:

f_A = fM = 18 rpm

Já o acoplamento entre a engrenagem A e a B é de contato. Nesse tipo de acoplamento, vale a relação:

fA · RA = · fB · RB

Como o raio (R) de uma engrenagem é proporcional ao número (n) de dentes que ela contém, podemos reescrever a relação acima da seguinte forma:

f_A· n_A = · f_B · n_B

Como nA = 24, nB = 72 e fA = 18 rpm, então:

Agora as engrenagens B e C estão acopladas pelo mesmo eixo, logo:

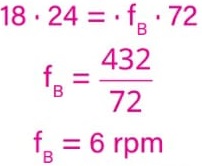
f _C = f_B = 6 rpm

Novamente, o acoplamento entre as engrenagens C e D é por contato, logo, é válida a relação:

F C · n_C= · f_D · n_D

Como n_C= 36, n_D = 108 e f_C = 6 rpm, então:

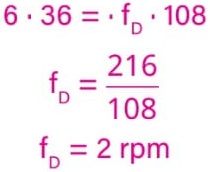
Como o ponteiro está acoplado à engrenagem D, sua frequência é fD = 2 rpm.

Alternativa: B

30) (Livro do aluno-SEDUC-SP/2025 - UNESP 2025) A figura 1 mostra um secador de saladas por centrifugação, que funciona com base no acoplamento de duas engrenagens que, quando em rotação, fazem girar um cesto em que estão acomodadas as folhas de salada a serem secas.

A figura 2 mostra o esquema do mecanismo desse utensílio. A engrenagem A gira quando uma pessoa aciona a manivela M. A engrenagem B, que é articulada com a engrenagem A, está ligada à roda R que é fixa no cesto que acomoda as folhas de salada. A engrenagem B e a roda R giram solidárias, presas a um mesmo eixo de rotação.

Sabendo que o raio da engrenagem A tem o triplo do comprimento do raio da engrenagem B, se a manivela M girar com uma frequência de 2,4 Hz, o cesto girará com uma frequência de:

(A) 7,2 Hz

(B) 3,6 Hz

(D) 6,0 Hz

(E) 10,8 Hz

Resolução:

O cesto e a engrenagem B estão acoplados ao mesmo eixo. Logo, suas frequências durante o movimento são iguais:

fC = fB

Como as engrenagens A e B estão acopladas por contato, as velocidades lineares dos seus pontos mais extremos são iguais, logo:

vA = vB

Novamente, como v = ω · R e ω = 2π · f, então:

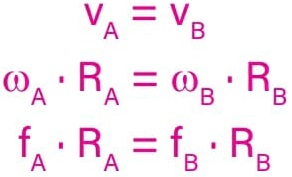
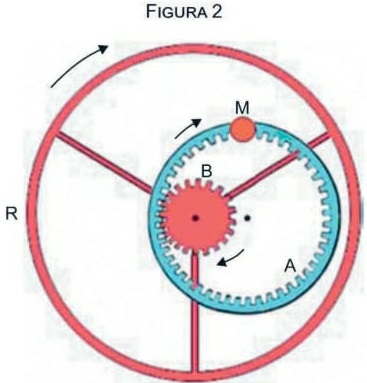
Mas, de acordo com o enunciado, o raio da engrenagem A é o triplo do raio da engrenagem B, ou seja, RA = 3 · RB

Por isso, a relação fA · RA = fB · RB assumirá a seguinte forma:

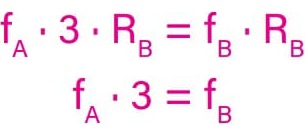
Como o enunciado pede para considerarmos a manivela girando com frequência fM = 2,4 Hz, e sabendo que a engrenagem A gira junto com a manivela, ou seja, fM = fA = 2,4 Hz, então:

Alternativa: A

31) (Livro do aluno-SEDUC-SP/2025 - FICSAE 2024) O mecanismo mostrado na figura foi adaptado para afiar facas. Ele é constituído de engrenagens de tamanhos diferentes e de uma fita abrasiva. O motor que faz a engrenagem 1 girar tem frequência de 75 rpm e os pinos com os quais a fita abrasiva faz contato têm raios de curvatura iguais, medindo 5 cm cada um. Nesse procedimento, a faca é mantida em contato com a fita abrasiva e em repouso em relação ao solo.

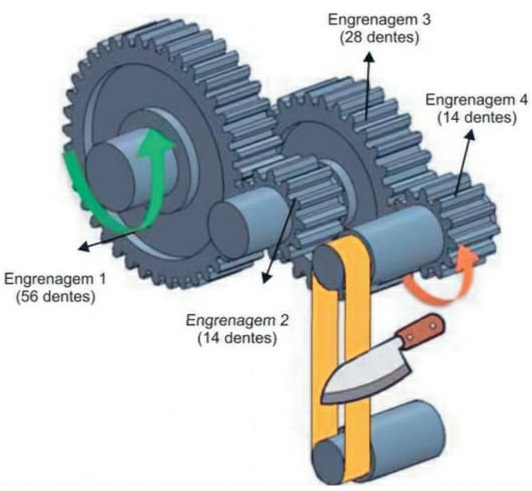
Sabendo que o número de dentes na periferia de uma engrenagem é diretamente proporcional ao raio dessa engrenagem, que não há escorregamento entre a fita abrasiva e os pinos com os quais ela faz contato e adotando π = 3, a velocidade escalar com que a fita passa pela faca que está sendo afiada é de:

(A) 2 m/s

(B) 2,5 m/s

(D) 3,0 m/s

(E) 1,5 m/s

Resolução:

Como não há escorregamento entre a fita e os pinos, podemos considerar esse arranjo como um acoplamento de polias por correia. Por isso, a velocidade linear da fita é a mesma dos pontos periféricos dos pinos:

v_fita = v_pino

Como a velocidade linear de um corpo descrevendo um MCU é v = 2π · R · f, π = 3 e o raio do pino é R_pino = 5 cm = 5 · 10^–2m, basta descobrir a frequência de rotação dos pinos para calcularmos sua velocidade linear.

Como a engrenagem 1 está acoplada ao mesmo eixo do motor, e o motor tem frequência fM = 75 rpm, a frequência da engrenagem 1 também é f1 = 75 rpm.

Analisando a transmissão entre as engrenagens 1 e 2 notamos que elas estão acopladas por contato. Portanto é válida a relação:

f1 · R1 = f2 · R2

Mas como o número de dentes (n) na periferia de uma engrenagem é diretamente proporcional ao raio dessa engrenagem, é válida também a seguinte relação:

f 1 · n1 = f2 · n2

De acordo com o enunciado, f1 = 75 rpm, n1 = 56 dentes e n2 = 14. Substituindo na relação anterior, obtemos:

75 · 56 = f2 · 14
f 2 = 300 rpm

Já as engrenagens 2 e 3 estão acopladas pelo mesmo eixo de transmissão, portanto:

f2 = f3 = 300 rpm

As engrenagens 3 e 4 também estão acopladas por contato.

Sendo f3 = 300 rpm, n3 = 28 dentes e n4 = 14 dentes, a frequência f4 será:

f3 · n3 = f4 · n4
300 · 28 = f4 · 14

f4 = 600 rpm

Como a engrenagem 4 e o pino estão conectados ao mesmo eixo de transmissão, então:

fpino = f4 = 600 rpm

Antes de calcularmos a velocidade do pino, porém, precisamos converter a frequência do pino para Hz (rotações por segundo), pois as velocidades das alternativas estão em m/s:

fpino = 10 Hz

Como a velocidade da fita é a mesma do pino, e v_pino= 2π · f_pino, substituindo na equação os valores calculados, obtemos:

v_pino = 2 · 3 · 5 · 10^–2 · 10
v_pino = 300 · 10^–2 m/s
v_pino = 3 m/s

Alternativa: D

HIDROSTÁTICA

32) (Livro do aluno-SEDUC-SP/2025 - PUCRS 2023) A figura a seguir mostra dois recipientes A e B que contêm álcool (µ = 0,8 g/cm³) e glicerina (µ = 1,2 g/cm³), respectivamente.

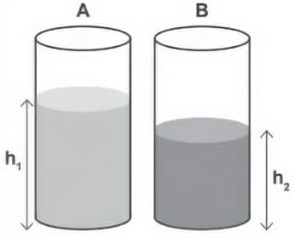
Para que a pressão exercida no fundo dos recipientes seja a mesma, a razão h1/h2 deve ser igual a:

(A) 0,6

(B) 0,8

(D) 2,0

Resolução:

Sejam pA e pB as pressões exercidas no fundo de cada recipiente, partiremos de uma situação em que:

pA = pB

Como, de acordo com o teorema de Stevin (para um ponto na superfície livre do líquido), p = patm + μ · g · h, temos:

patm + μA · g · h1 = patm + μB · g · h2

Cancelando os termos em comum aos dois lados (patm e g), obtemos:

μA · h1 = μB · h2

Como µA = 0,8 g/cm³e glicerina µB = 1,2 g/cm³:

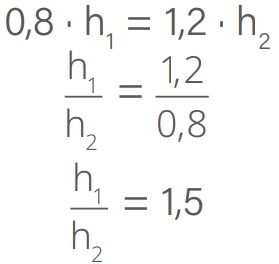
Alternativa: C

33) (Livro do aluno-SEDUC-SP/2025 - FUVEST 2024 – Adaptada) No manual de instalação de um filtro de torneira, consta a seguinte mensagem:

Instruções para obter vazão de água recomendada: para filtração adequada, acima de 100 kPa, utilize o redutor de vazão que acompanha o produto, encaixando-o no filtro. Dica: caso não saiba qual a pressão no ponto de uso do filtro, meça o tempo para encher com água um copo de 240 mL.

Se o tempo for menor que 6 segundos, recomenda-se encaixar o redutor de vazão na base do filtro.

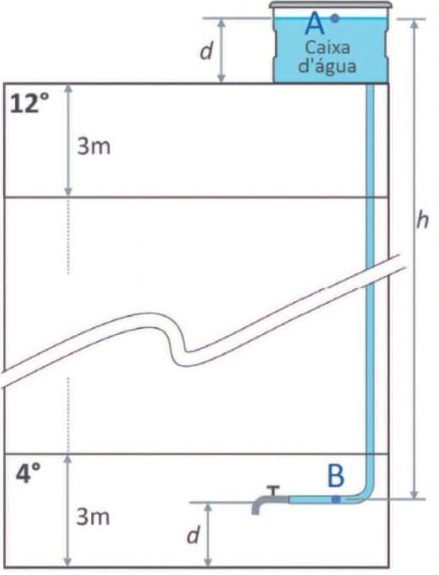
a) Calcule a força sobre um tampão de vedação colocado na ponta de um cano de 40 mm de diâmetro se a pressão da água no interior do cano neste local é de 100 kPa.

b) Considere que uma torneira esteja instalada no 4º andar de um prédio de 12 andares (ponto B) e esteja conectada a uma caixa d’água localizada na laje desse prédio (ponto A), conforme a figura. Calcule a distância vertical h e a diferença de pressão entre os pontos B e A.

Note e adote:

A altura padrão de cada andar de um prédio é de 3 metros.

Considere a água como um fluido ideal com densidade de 1000 kg/m³.

Aceleração da gravidade (g) = 10 m/s²

1 Pa = 1 N/m²

Considere π ≈ 3

Resolução de (a)

Por definição, a pressão em uma área qualquer é:

p = F
      A

F = p · A

A pressão, como trazida pelo enunciado, é p = 100 kPa e a área é a seção transversal do cano por onde passa a água, ou seja, a área de um círculo de diâmetro D = 40 mm.

Sendo a área do círculo

A força sobre um tampão, nessas condições, será:

F = p · π · r²

F = 100 · 10³ · 3 · (20 · 10^–3)²

F = 3 · 10⁵ · 400 · 10^–6

F = 1200 · 10^–1

F = 120 N

Portanto, a força sobre um tampão, nessas condições, será 120 N.

Resolução

Como os pontos A e B estão à mesma distância (d) do piso dos seus respectivos andares, a altura (h) entre eles é igual à altura de nove andares. Como cada andar tem 3 m de altura, então:

h = 3 · 9 = 27 m

De acordo com o teorema de Stevin, a diferença de pressão entre dois pontos é:

ΔpAB = μ · h · g

O enunciado pede para considerarmos a água como um fluido ideal e de densidade μ = 1000 kg/m³ e a gravidade no local igual a g = 10 m/s².

Sabendo que h = 27 m, então:

ΔpAB = 1000 · 27 · 10

ΔpAB = 270 000

ΔpAB = 2,7 · 10⁵ Pa

Portanto, a diferença de pressão entre os pontos A e B é 2,7 · 10⁵ Pa.

34) (Livro do aluno-SEDUC-SP/2025 - UERJ 2025) Um dos animais de maior massa já identificado no planeta Terra é a baleia azul. Admita que uma baleia dessa espécie tenha massa de 90 toneladas e volume de 86,5 m³. A densidade dessa baleia, em g/cm³, é aproximadamente de:

(A) 1,36

(B) 1,04

(D) 0,88

Resolução:

A densidade de um corpo é calculada pela razão entre a sua massa (m) e o volume (V) que ocupa:

d = m
      V

De acordo com o enunciado, a massa da baleia é m = 90 toneladas e seu volume é V = 86,5 m³.

Para calcular a densidade da baleia em g/cm³, precisamos, primeiro, converter as unidades:

m = 90 toneladas = 90 · 10³ kg = 90 · 10⁶g e V = 86,5 m³= 86,5 · (102)3 cm³ = 86,5 · 10⁶ cm³

Substituindo esses valores na equação da densidade, obtemos:

Alternativa: B

35) (Livro do aluno-SEDUC-SP/2025 - UERJ 2024) A aferição da pressão intraocular é feita com um aparelho chamado tonômetro de aplanação, mediante aplicação de uma força de baixa intensidade sobre a superfície da córnea do paciente. O diagnóstico é estabelecido por meio da correspondência entre a escala de quilopascais (kPa), própria do aparelho, e a escala de milímetros de mercúrio (mmHg). Observe na tabela os valores de pressão em escala de mmHg e seus respectivos diagnósticos.

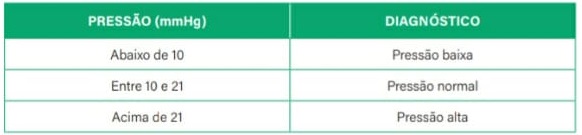
Considere um paciente com pressão intraocular de 25 kPa e córnea com área de 7,0 mm². Admita, ainda, que 1,0 kPa ≅ 0,8 mmHg e 1,0 mm² = 10^{− 6} m². Calcule, em Newtons, a força aplicada sobre a córnea desse paciente durante o uso do tonômetro. Em seguida, com base na tabela, indique o diagnóstico do paciente, justificando sua resposta.

Resolução:

Como, F = A, então
                  P

F = p · A

Sendo a pressão intraocular do paciente p = 25 kPa = 25 · 10³ Pa e a área da sua córnea A = 7,0 mm² = 7,0 · 10^–6 m², então a força aplicada sobre a córnea é:

F = 25 · 10³ · 7,0 · 10^–6

F = 175 · 10^–3

F = 0,175 N

Para indicar o diagnóstico do paciente, com base nas informações da tabela, é necessário converter

o valor de pressão intraocular para mmHg. Sendo 1,0 kPa ≅ 0,8 mmHg, então:

p = 25 kPa = 25 · 0,8 mmHg

p = 20 mmHg

Portanto, de acordo com a tabela, o paciente (de pressão intraocular igual a 20 mmHg) tem pressão normal.

36) (Livro do aluno-SEDUC-SP/2025 - UEA – SIS1 2022) Um dispositivo foi projetado para medir a velocidade do ar, baseando-se na diferença de pressão dentro de um tubo. Em determinada ocasião, conforme o ar em movimento entra pelo orifício direito do tubo, o êmbolo é empurrado para baixo fazendo com que o fluido no lado esquerdo do tubo suba 4 cm, como mostra a figura.

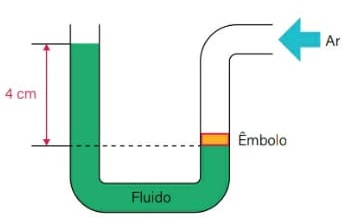
Sabendo que a densidade desse fluido é de 900 kg/m³, que a aceleração da gravidade é 10 m/s² e que o peso do êmbolo é desprezível, a diferença de pressão entre o nível do fluido na parte esquerda do tubo e o fluido sob o êmbolo, após ser empurrado para baixo, é de:

(A) 90 Pa

(B) 180 Pa

(D) 360 Pa

(E) 540 Pa

Resolução:

A pressão sobre dois pontos submersos em um fluido e alinhados horizontalmente é igual. Então, podemos dizer que a pressão no fluido sob o êmbolo (ponto A) é igual à pressão no ponto B:

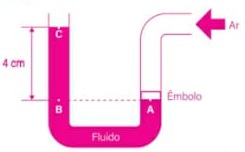
(ponto A) é igual à diferença de pressão entre os pontos B e C. Pelo teorema de Stevin, podemos calcular a diferença de pressão entre os pontos B e C (ΔpBC) por: ΔpBC = μ · h · g

De acordo com o enunciado, a densidade do fluido é μ = 900 kg/m³, a gravidade no local é g = 10 m/s² e, pela ilustração, a altura entre os pontos B e C é h = 4 cm = 0,04 m.

Substituindo os valores na equação do teorema de Stevin, obtemos:

ΔpBC = 900 · 0,04 · 10

ΔpBC = 360 Pa

Alternativa: D

37) (Livro do aluno-SEDUC-SP/2025 - UFRGS 2019) Em um tubo transparente em forma de U contendo água, verteu-se, em uma de suas extremidades, uma dada quantidade de um líquido não miscível em água. Considere a densidade da água igual a 1 g/cm³.

A figura abaixo mostra a forma como ficaram distribuídos a água e o líquido (em cinza) após o equilíbrio.

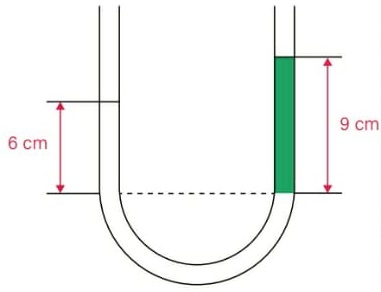
Qual é, aproximadamente, o valor da densidade do líquido, em g/cm³?

(A) 1,5

(B) 1,0

(D) 0,7

(E) 0,5

Resolução:

Quando dois líquidos imiscíveis são colocados em um recipiente em formato de U, criando um padrão como a imagem do enunciado, dois pontos alinhados horizontalmente e imersos no mesmo líquido experimentam a mesma pressão. Consideraremos, então, os seguintes pontos:

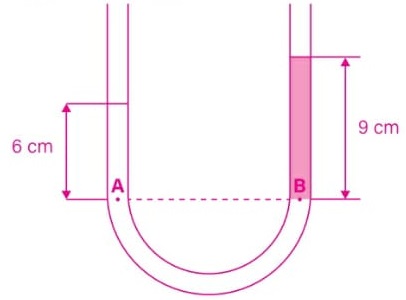
Como os pontos A e B estão alinhados e imersos na água, podemos afirmar que:

pA = pB

Como, neste caso, p = p_atm + μ · h · g, podemos reescrever a igualdade da seguinte forma:

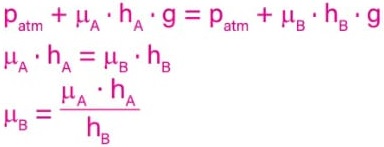
De acordo com o enunciado, a densidade da água é μA = 1 g/cm³, hA = 6 cm e hB = 9 cm. Substituindo esses valores na expressão anterior, obtemos:

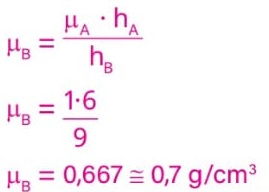
Alternativa: D

38) (Livro do aluno-SEDUC-SP/2025 - PUC-RIO 2023) A pressão atmosférica na superfície de um lago é igual a 1,0 · 10⁵ Pa. Um mergulhador experimental mergulha nesse lago até uma profundidade tal, que a pressão total sentida por ele é o triplo da pressão atmosférica externa.

Qual é a profundidade, em metros, em que se encontra o mergulhador?

Dados:

g = 10 m/s²

Densidade da água = 1,0 g/cm³

(A) 20

(B) 15

(D) 5

(E) 0

Resolução:

Para resolver essa questão, podemos aplicar a expressão do teorema de Stevin, pois ele relaciona justamente as pressões em dois pontos distintos de um fluido e a distância entre esses pontos (altura):

p – p1 = μ · h · g
p = p1 + μ · h · g

De acordo com o enunciado, a densidade do líquido (água) é μ = 1,0 g/cm³ = 1,0 · 10³ kg/m³, a gravidade no local é g = 10 m/s², a pressão atmosférica é p_atm = 1,0 · 10⁵ Pa e a pressão na profundidade em que o mergulhador se encontra deve ser p = 3 · p_atm.

Substituindo essas informações na expressão do teorema de Stevin, obtemos:

Portanto, o mergulhador encontra-se a uma profundidade de 20 m.

Alternativa: A

39) (Livro do aluno-SEDUC-SP/2025 - PUC-RIO 2022 – Adaptada) A figura mostra um macaco hidráulico, contendo óleo, e constituído de dois êmbolos de áreas A₁ = 1,2 . 10¹ mm²e A₂ = 1,2 . 104 mm2. Sobreo êmbolo de área A₂, é colocado, em repouso, um bloco de massa 6,0 . 10² kg.

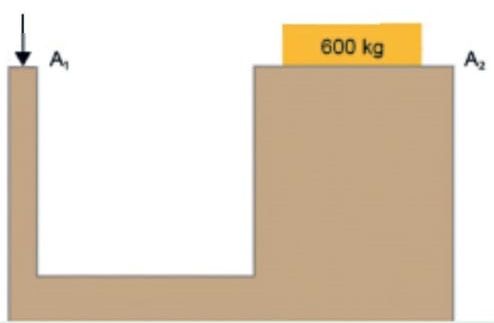
Determine o valor, em newtons, da força aplicada no êmbolo de área A₁ para que essa estrutura permaneça em equilíbrio.

Considere g = 10 m/s²

(A) 6,0

(B) 10

(D) 5,0

Resolução

De acordo com o teorema de Pascal, aplicado à prensa hidráulica:

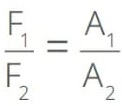
A força F₂ corresponde ao peso do bloco sobre o êmbolo A. Portanto:

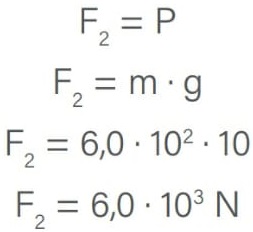
Como A₁ = 1,2 . 10¹ mm² e A₂= 1,2 . 10⁴ mm², então:

Portanto, a força F₁ aplicada sobre o êmbolo de área A₁ deve ter módulo de 6,0 N para que a estrutura permaneça em equilíbrio.

Alternativa: A

40) (Livro do aluno-SEDUC-SP/2025 - FUVEST 2024) Uma empresa júnior de alunos de engenharia projetou um termômetro mecânico para medir a temperatura do óleo utilizado em máquinas e equipamentos, com base na variação da densidade do óleo com a temperatura.

Com essa finalidade, emprega-se um objeto de massa M igual a 18 g e volume de 20 cm3, que permanece imerso em um óleo e está preso, por um fio, ao fundo da superfície, conforme mostra a figura.

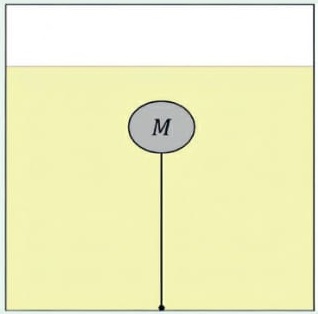
A temperatura é medida por meio da variação na tensão do fio, que muda devido à variação da densidade do óleo com a temperatura. O gráfico a seguir mostra a dependência da densidade do óleo com a temperatura.

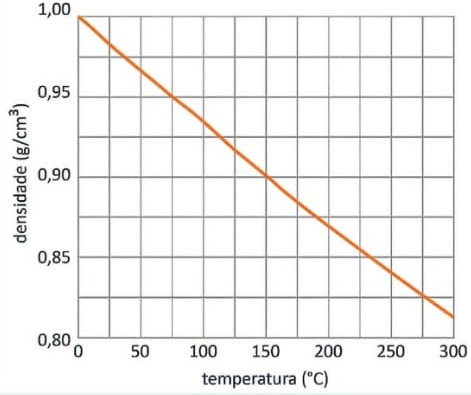
Nessa configuração, a temperatura na qual a tensão na corda se anula é igual a:

Note e adote: despreze a massa do fio.

(A) 0 ºC

(B) 75 °C

(D) 150 °C

(E) 275 °C

Resolução:

A tração no fio que prende o objeto será nula quando as forças peso e empuxo, atuantes no objeto, se anularem completamente.

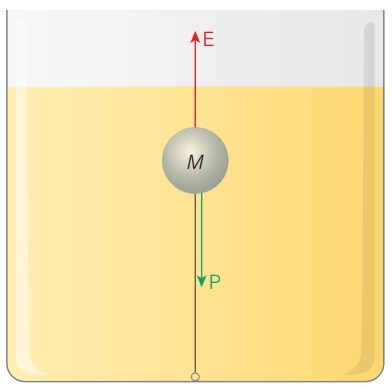
Nessa situação:

E = P

Desmembrando as duas forças, obtemos:

df · g · V = mob · g 
df · V = mob

Como o objeto está totalmente submerso no óleo, o volume do fluido deslocado e o volume do objeto são iguais (V = Vob), logo: df = dob.

Ou seja, a tração no fio será nula quando a densidade do óleo atingir o mesmo valor da densidade do objeto. Esse valor de densidade é:

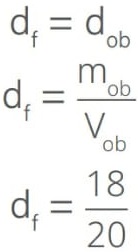
Alternativa: D

41) (Livro do aluno-SEDUC-SP/2025 - UERJ 2024) Em um sistema hidráulico de freios automotivos, ao pisar no pedal de freio, uma força de intensidade FA é aplicada sobre a área do pistão do cilindro mestre e uma força hidráulica de intensidade FH é aplicada sobre a área do pistão do cilindro de roda, conforme ilustra a imagem.

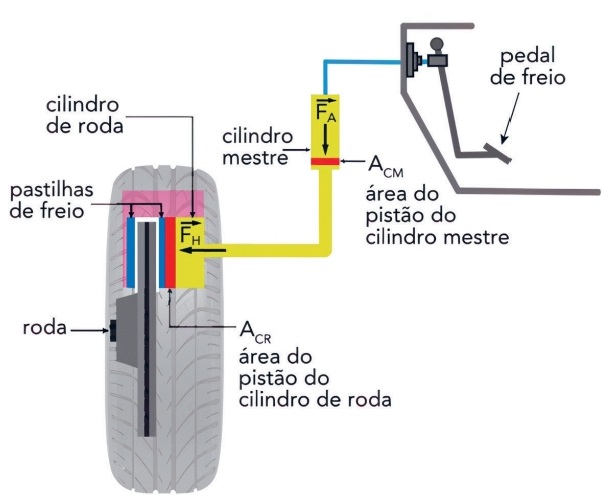
Considere os seguintes valores para esse sistema:

- intensidade da força FA = 200 N;

- área do pistão do cilindro mestre ACM = 2 cm²;

- área do pistão do cilindro de roda ACR = 12 cm².

Admitindo que o sistema se encontra em equilíbrio, calcule, em newtons, a intensidade de FH.

Resolução:

De acordo com o teorema de Pascal, aplicado ao elevador hidráulico:

Sendo F1 = FA = 200 N, A₁ = ACM = 2 cm², F2 = FH e A₂ = ACR = 12 cm², temos:

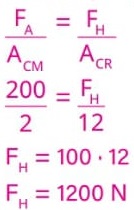
42) (Livro do aluno-SEDUC-SP/2025 - UFRGS 2024) O peso de uma pedra no ar, medido com um dinamômetro, é 50 N. Quando a pedra está totalmente mergulhada em água, o dinamômetro indica 30 N. Considerando o módulo da aceleração da gravidade igual a 10 m/s² e a massa específica da água igual a 10³ kg/m³, o volume e a massa específica da pedra valem, respectivamente:

(A) 5 dm³ e 1,0 · 10³ kg/m³.

(B) 3 dm³ e 1,5 · 10³kg/m³.

(D) 2 dm³ e 2,0 · 10³ kg/m³.

(E) 2 dm³ e 2,5 · 10³ kg/m³.

Resolução:

Podemos calcular o volume da pedra por meio do princípio de Arquimedes:

E = μf · g · V

Mas, para isso, é preciso determinar o empuxo que atua sobre o objeto.

A ilustração mostra as forças que atuam sobre a pedra na situação apresentada.

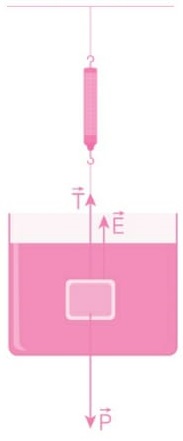
Como, na situação ilustrada, o objeto se encontra em equilíbrio, o somatório das forças que atuam sobre ela tem que ser zero, ou seja:

T + E – P = 0

De acordo com o enunciado, o peso da pedra foi aferido usando-se o dinamômetro em um instante anterior, obtendo-se o peso P = 50 N. O valor que o dinamômetro indica (30 N) corresponde à força de tração no fio que liga a pedraao dispositivo, portanto, T = 30 N.

Substituindo-se esses valores na relação anterior, obtemos:

30 + E – 50 = 0

E = 50 – 30

E = 20 N

Sendo o empuxo sobre a pedra E = 20 N, a massa específica da água μ = 10³kg/m³ e a gravidade no local g = 10 m/s², o volume da pedra será:

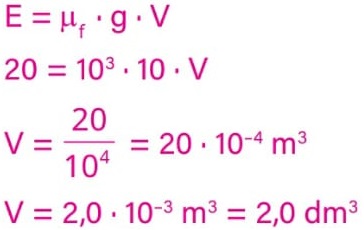
Como a massa específica (μ) de uma substância é definida por

μ = m
       V

Precisamos, primeiro, determinar sua massa.

Como o peso da pedra é

P = 50 N e P = m · g, sua massa será:

50 = m · 10

m = 5 kg

Logo, a massa específica da pedra é:

Alternativa: E

43) (Livro do aluno-SEDUC-SP/2025 - ACAFE 2023) Uma substância química que atua impedindo a contração dos músculos. Muito utilizado para o tratamento de diversas doenças, tornou-se o principal recurso estético para a redução de rugas e linhas de expressão. A substância foi descoberta ainda no século XIX, mas seu uso só se popularizou nos consultórios médicos a partir de 1977, quando o botox foi utilizado pela primeira vez para testes no tratamento de estrabismo.

De lá para cá, passou a ser usado para reduzir os sintomas de alterações como bruxismo, doenças neurológicas, ortopédicas e oftalmológicas. Desde 2002, a Food and DrugAdministration (FDA) – órgão regulador de medicamentos dos Estados Unidos – aprovou a utilização do botox para fins estéticos. Segundo o Censo de 2022 da Sociedade Brasileira de Cirurgia Plástica, a aplicação de toxina botulínica aparece como procedimento não cirúrgico mais realizado no Brasil, chegando a 95% dos tratamentos.

Apesar de um importante aliado para a saúde e beleza, é fundamental que o procedimento seja realizado por profissionais qualificados e habilitados. Tudo isso porque se a aplicação for realizada de forma indevida, podem ocorrer efeitos colaterais, como paralisação de um grupo muscular.

O método do microagulhamento contempla mínimas perfurações na pele com pequenas agulhas, visando estimular a fabricação de colágeno e fibras naturais, o que deixa a textura mais harmônica.

Considere uma seringa contendo toxina botulínica para aplicação por microagulhamento com áreas de secção transversal conforme a figura.

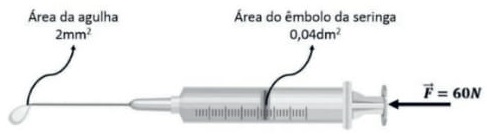
Se o profissional aplicar uma força de 60N no êmbolo da seringa, a força aplicada na saída da agulha vale ____________ e o acréscimo de pressão do fluido ___________________.

(A) 0,3N – será totalmente transmitido a todos os pontos das partículas da toxina.

(B) 0,03N – será maior na agulha da seringa devido a redução da área de contato.

(D) 0,03N – será crescente no sentido êmbolo-agulha.

Resolução:

De acordo com o teorema de Pascal, podemos afirmar que:

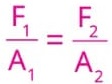
Note que as áreas do êmbolo e da agulha estão em unidades diferentes. Como as áreas vão se dividir no decorrer do cálculo

Não é necessário convertê-las para unidades do SI (m₂), mas é preciso que estejam com a mesma unidade de medida. Converteremos então a unidade de A₁:

A₁ = 0,04 dm² = 0,04 · 10⁴ mm² = 400 mm² e A₂ = 2 mm².

Vamos considerar que a força exercida no êmbolo da seringa seja F1, então F = F1 = 60 N. Substituindo-se esses valores na expressão do teorema de Pascal, obtemos:

Como, de acordo com o teorema de Pascal, qualquer acréscimo de pressão sobre um ponto de um líquido em repouso é totalmente transmitido para todos os pontos nele contidos.

Alternativa: A

44) (Livro do aluno-SEDUC-SP/2025 - FAMERP 2023) Após ver uma maçã flutuando na água, um garoto ficou curioso para saber a densidade dessa maçã. Não dispondo de uma balança, colocou 400 mL de água em um recipiente graduado, pôs a maçã na água e verificou que o volume indicado passou a ser 520 mL. Em seguida, afundou totalmente a maçã na água do recipiente e o volume indicado foi 550 mL. A partir desses dados, e sabendo que a densidade da água é 1,0 g/mL, o garoto calculou a densidade da maçã obtendo o valor de:

(A) 0,70 g/mL

(B) 0,75 g/mL

(D) 0,90 g/mL

(E) 0,80 g/mL

Resolução:

Quando a maçã está flutuando, a resultante das forças que atuam sobre ela é zero. Isso quer dizer que as duas forças que atuam sobre a maçã, peso (P) e empuxo (E), estão se anulando. Portanto: P = E

Como o peso de um objeto é P = mob · g e o empuxo sobre um objeto é E = μf · g · Vfd, então:

mob · g = μf · g · Vfdmob = μf · Vfd

Mas, partindo da densidade de um corpo, sua massa pode ser calculada por:

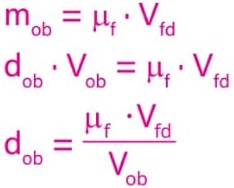
Logo:

O volume de um objeto submerso em um fluido corresponde ao volume do fluido que se desloca devido a sua presença.

Então, se o volume de água sem a maçã era de 400 mL e, após afundar totalmente a maçã, passou a ser 550 mL, então o volume da maçã é Vob = 550 – 400 = 150 mL.

Já o volume de fluido deslocado (Vfd) corresponde ao aumento na indicação de volume do fluido quando a maçã está flutuando. Nesse caso, Vf d = 520 – 400 = 120 mL.

Sabendo que μf = 1,0 g/mL, e substituindo esses valores na relação acima, obtemos:

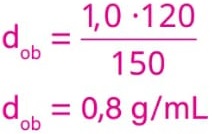
Alternativa: E

45) (Livro do aluno-SEDUC-SP/2025 - UERJ 2013) Observe, na figura a seguir, a representação de uma prensa hidráulica, na qual as forças F1 e F2 atuam, respectivamente, sobre os êmbolos dos cilindros I e II. Admita que os cilindros estejam totalmente preenchidos por um líquido.

O volume do cilindro II é igual a quatro vezes o volume do cilindro I, cuja altura é o triplo da altura do cilindro II.

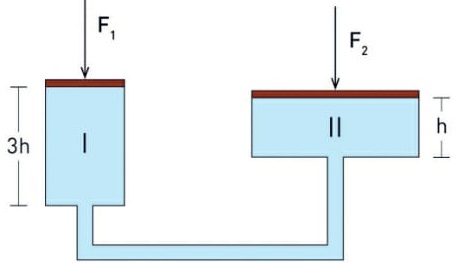
A razão F2/F1 entre as intensidades das forças, quando o sistema está em equilíbrio, corresponde a:

(A) 12

(B) 6

(D) 2

Resolução:

Para resolvemos essa questão, precisamos recordar que o volume de um cilindro é determinado pelo produto entre a área da base pela altura. Assim, podemos dizer que:

Pistão I: V₁ = A₁ · 3h;

Pistão II: V₂ = A₂ · h

Como, de acordo com o enunciado, V₂ = 4 · V₁

Então, V2 = A2 · h = 4. A₁· 3h

A₂ = 12 · A₁ Agora que encontramos uma expressão que relaciona as áreas dos dois pistões, faremos:

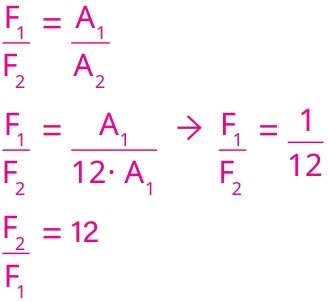
Alternativa: A

46) (Livro do aluno-SEDUC-SP/2025 - EFOMM 2023) Considere uma embarcação com massa total de 10250 kg, flutuando em água salgada, com densidade de 1025 kg/m³, e que esteja com seu volume submerso máximo permitido. Se essa embarcação passar por um trecho de água doce com densidade de 1000 kg/m³, sofrerá um aumento do volume submerso. Qual quantidade de massa deve ser rejeitada do navio, para que o volume submerso da embarcação retorne ao valor inicial?

(A) 40 kg

(B) 100 kg

(D) 750 kg

(E) 1000 kg

Resolução:

Se um objeto flutua sobre um líquido, é porque as duas forças que atuam sobre ele, peso e empuxo, se equilibram, ou seja, têm a mesma intensidade, a mesma direção e sentidos opostos. Podemos representar essa afirmação matematicamente por: E = P.

Como o enunciado estabeleceu a condição de que o volume submerso da embarcação precisa ser constante, podemos desmembrar a relação acima e isolar o volume submerso (Vs) para determinar uma forma

de calculá-lo.

Como

E = μf · g · Vs e P = m · g:

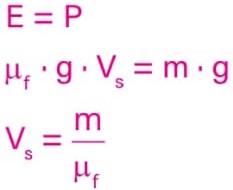
Isso significa que o volume submerso da embarcação corresponde à razão entre a sua massa e a densidade do fluido sobre o qual ele se encontra.

Na situação proposta, o volume da embarcação submerso em água salgada (Vsal) tem que ser o mesmo em água doce (Vdoce).

Então, sendo m1 e μsal a massa inicial da embarcação e a massa específica da água salgada, e m² e μdoce a massa final da embarcação e a massa específica da água doce:

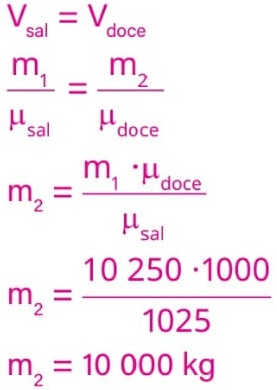
Ou seja, para que o volume submerso em água doce seja o mesmo submerso em água salgada, a massa da embarcação deve ser m₂ = 10 000 kg.

Portanto a massa rejeitada para atingir tal objetivo é:

m = m₁ – m₂ =10 250 – 10 000 = 250 kg.

Alternativa: C

GRAVITAÇÃO UNIVERSAL

47) (Livro do aluno-SEDUC-SP/2025 - UEM 2020 – Adaptada) Analise as afirmações abaixo e indique se são verdadeiras ou falsas:

(A) Os planetas do nosso Sistema Solar descrevem órbitas elípticas nas quais o Sol está em um dos focos da elipse.

(B) Os períodos de revolução dos planetas ao redor do Sol são diretamente proporcionais aos raios médios das suas órbitas.

(C) Durante o movimento de translação dos planetas, as áreas “varridas” pelo vetor que liga o planeta ao Sol são iguais em intervalos de tempos iguais.

(D) As forças de atração entre dois corpos quaisquer são inversamente proporcionais ao produto das suas massas e à distância entre seus centros.

(E) As forças de atração gravitacional entre dois corpos quaisquer são exemplos do par ação-reação de que trata a Terceira Lei de Newton.

Resolução:

a) Verdadeira. Está de acordo com a primeira lei de Kepler.

b) Falsa. De acordo com a terceira lei de Kepler, o quadrado dos períodos de revolução dos planetas ao redor do Sol é diretamente proporcional ao cubo dos raios médios das suas órbitas.

c) Verdadeira. Está de acordo com a segunda lei de Kepler.

d) Falsa. De acordo com a lei da gravitação de Newton, as forças de atração entre dois corpos quaisquer são diretamente proporcionais ao produto das massas dos corpos e inversamente proporcionais ao quadrado da distância entre eles

e) Verdadeira. As forças de atração gravitacional entre dois corpos quaisquer formam um par ação-reação. Por isso, possuem mesma intensidade, mesma direção e sentidos opostos.

Alternativa: A, C e E.

48) (Livro do aluno-SEDUC-SP/2025 - PUC-CAMPINAS 2023) Em 1609, Kepler publicou sua obra Astronomia nova... de motibus stellae Martis (Nova astronomia... Sobre o movimento da estrela Marte), na qual, a partir das medidas precisas que possuía dos movimentos de Marte, enunciou duas leis do movimento planetário que hoje levam seu nome. A primeira afirma que as órbitas dos planetas são elípticas e a segunda que o raio vetor que une o Sol a um determinado planeta varre áreas iguais em iguais intervalos de tempo. Embora Kepler tenha enunciado suas leis para os planetas, elas são válidas também para os corpos menores do Sistema Solar, que na época de Kepler não eram conhecidos.

Considere um asteroide que descreve a órbita representada na figura, na qual o ponto S representa o foco e o ponto U representa o centro da elipse.

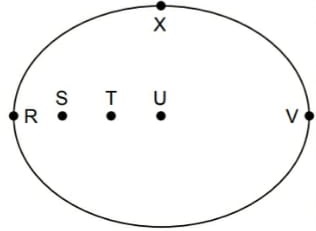
De acordo com as leis de Kepler, o Sol está localizado no ponto I _______________ e _________ o asteroide apresenta maior velocidade escalar em relação ao Sol quando passa pelo ponto ___________ II _________ .

As lacunas I e II da frase acima são preenchidas, correta e respectivamente, por:

(A) S – R

(B) S – V

(C)T – X

(D) U – R

(E) U – X

Resolução:

De acordo com a primeira lei de Kepler, as órbitas dos corpos celestes em torno do Sol são elipses, e a estrela ocupa um dos focos dessa elipse. Como, dos pontos apresentados na imagem, S é o único que representa um foco da elipse, então esse é o ponto que o Sol deve ocupar.

Já em relação à segunda lei de Kepler, o segmento que liga o Sol ao asteroide varre áreas iguais em tempos iguais. Por consequência, a velocidade escalar do asteroide é maior quando está próximo do Sol e menor quando está mais afastado. Ou seja, a velocidade escalar do asteroide no ponto R é maior do que as velocidades escalares em X e em V.

Alternativa: A

49) (Livro do aluno-SEDUC-SP/2025 - UNICAMP 2023) O planeta anão Ceres foi descoberto em 1801 por Giuseppe Piazzi. Resultados científicos recentes indicam que Ceres teria sido formado nas zonas mais afastadas do Sistema Solar e, posteriormente, lançado para a região onde se encontra atualmente, entre as órbitas de Marte e Júpiter. A tabela a seguir apresenta o período de translação T, a distância média ao Sol R, bem como T², R³ e a razão T₂/R³ para alguns planetas do Sistema Solar.

De acordo com a 3ª lei de Kepler, a razão T²/R³ é constante. A partir dos dados da tabela, pode-se concluir que o período orbital de Ceres, T_Ceres, é aproximadamente igual a:

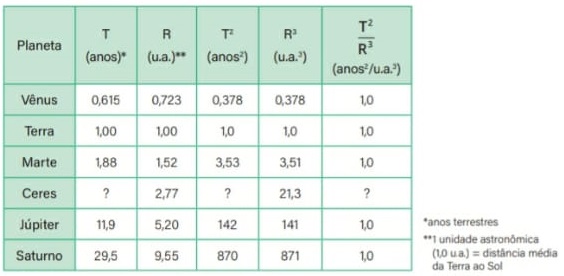
(A) 1,00 ano.

(B) 2,77 anos.

(D) 21,3 anos.

Resolução:

De acordo com a terceira lei de Kepler, o quociente entre o quadrado do período de revolução (T²) dos corpos celestes em torno do Sol e o cubo do raio médio de suas órbitas

É uma constante:

Ou seja, se calcularmos essa razão usando os valores fornecidos na tabela para um planeta qualquer, o resultado tem que ser o mesmo se calcularmos a mesma razão usando os valores de qualquer um dos outros planetas:

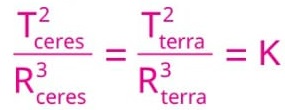
Alternativa: C

50) (Livro do aluno-SEDUC-SP/2025 - ENEM 2022) Um buraco negro é um corpo celeste que possui uma grande quantidade de matéria concentrada em uma pequena região do espaço, de modo que sua força gravitacional é tão grande que qualquer partícula fica aprisionada em sua superfície, inclusive a luz. O raio dessa região caracteriza uma superfície-limite, chamada de horizonte de eventos, da qual nada consegue escapar. Considere que o Sol foi instantaneamente substituído por um buraco negro com a mesma massa solar, de modo que o seu horizonte de eventos seja de, aproximadamente, 3,0 km.

SCHWARZSCHILD, K. On the gravitational field of a mass point according to Einstein’s theory.

Disponível em: arxiv.org. Acesso em: 26 maio 2022 (adaptado).

Após a substituição descrita, o que aconteceria aos planetas do Sistema Solar?

(A) Eles se moveriam em órbitas espirais, aproximando-se sucessivamente do buraco negro.

(B) Eles oscilariam aleatoriamente em torno de suas órbitas elípticas originais.

(D) Eles passariam a rotacionar mais rapidamente.

(E) Eles manteriam suas órbitas inalteradas.

Resolução:

De acordo com a lei da gravitação universal de Newton, a força gravitacional entre cada planeta do Sistema Solar e o Sol é:

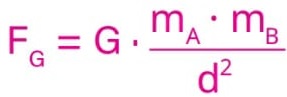
Nesta equação, G é uma constante (constante gravitacional), portanto seu valor não se altera com a troca do Sol por um buraco negro. A massa mA de cada planeta também é constante.

A massa mB do buraco negro é a mesma do Sol e ele ocupa a mesma posição que a nossa estrela, ou seja, a distância d, entre o centro do buraco negro e o centro dos planetas, teria os mesmos valores das distâncias em relação ao centro do Sol.

Podemos concluir, então, que as intensidades das forças gravitacionais entre os planetas e o buraco negro seriam iguais às intensidades das forças gravitacionais entre os planetas e o Sol. Logo, os planetas manteriam suas órbitas inalteradas.

Alternativa: E

51) (Livro do aluno-SEDUC-SP/2025 - FCMSCSP 2024) Em sua obra Harmonices Mundi Libri V (A harmonia dos mundos em 5 volumes, 1616), Kepler apresentou sua “terceira lei”, na qual estabelece que o tempo de revolução de um planeta ao redor do Sol é proporcional a R^2/3, em que R é o raio médio da órbita do planeta. Sabendo que o raio médio da órbita de Netuno em torno do Sol é, aproximadamente, trinta vezes o raio médio da órbita da Terra, o intervalo de tempo em que o planeta Netuno completa uma volta ao redor do Sol é, aproximadamente:

(A) 160 anos terrestres.

(B) 10 anos terrestres.

(D) 90 anos terrestres.

(E) 270 anos terrestres.

Resolução:

De acordo com o enunciado, se o raio médio da órbita da Terra é R_terra, o raio médio da órbita de Netuno é R_netuno = 30 · R_terra. Além disso, o tempo de revolução da Terra em torno do Sol é Tterra = 1 ano. Substituindo essas informações na equação, obtemos:

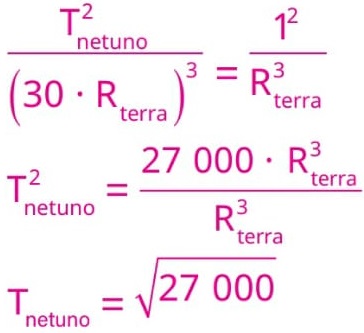
T_netuno ≅ 164,3 anos

Portanto, Netuno demora aproximadamente 164 anos terrestres para completar uma volta em torno do Sol.

Alternativa:

TRABALHO E ENERGIA

52) (Livro do aluno-SEDUC-SP/2025 - PUC-Rio 2023) Um objeto de peso 40 N se move no espaço fazendo uma trajetória curva sob a ação apenas de duas forças: seu próprio peso e uma força conservativa F de módulo constante. Em sua trajetória, as alturas verticais inicial e final são, respectivamente, 1,0 m e 3,0 m. Sabendo que as velocidades inicial e final têm o mesmo módulo, calcule, em joules, o trabalho total realizado pela força F sobre a partícula ao longo dessa trajetória.

Dado: g = 10 m/s²

(A) 1,0

(B) 2,0

(D) 40,0

(E) 80,0

Resolução:

Como tanto a força peso quanto a força F são conservativas, nenhuma delas depende da trajetória, apenas na distância vertical entre os pontos inicial e final (altura).

O trabalho da força peso, nesta situação, é:

τP= – F · d

τP= – P · h

τP= – 40 · 2

τP= – 80 J

Esse trabalho é negativo porque, pela descrição do enunciado, o movimento tem sentido para cima. Como a força peso é vertical para baixo, ela atua contra o movimento, retirando energia do sistema, por isso representamos com sinal de menos.

Se as velocidades inicial e final têm módulos iguais, significa que, apesar de a força peso retirar energia desse sistema, a força F compensa esse trabalho resistente, realizando trabalho motor de mesma intensidade.

Portanto, o trabalho da força F é:

τF= |τP| = 80 J

Alternativa:

53) (Livro do aluno-SEDUC-SP/2025 - UERJ 2020) Uma criança em um velocípede é puxada por seu pai por uma distância horizontal de 20 m, sob a ação da força resultante constante FR, orientada conforme o esquema. Desprezando as forças dissipativas, calcule, em joules, o trabalho realizado por FR quando o conjunto velocípede e criança percorre a distância de 20 m.

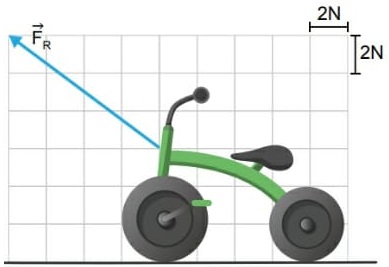
Resolução:

Analisando a imagem que representa a situação, podemos perceber que a força F_R não tem a mesma direção do movimento. Como apenas a componente da força que tem a mesma direção do deslocamento é capaz de realizar trabalho, precisamos determinar o módulo da componente F_X da força resultante. Como a situação está representada em uma malha quadriculada, podemos determinar o módulo de FX como mostra a imagem:

Sendo F_X = 8 N, d = 20 m e sabendo que o trabalho de uma força é calculado por τ = F · d, neste caso, temos:

τ = F_X · d

τ = 8 · 20

τ = 160 J

Portanto, o trabalho realizado por FR quando o conjunto velocípede e criança percorre a distância de 20 m é 160 J.

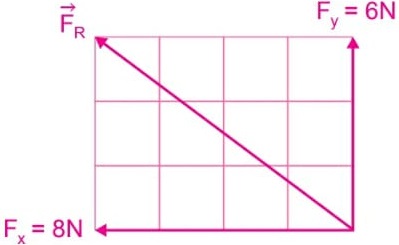
54) (Livro do aluno-SEDUC-SP/2025 - ENEM PPL 2016) Para reciclar um motor de potência elétrica igual a 200 W, um estudante construiu um elevador e verificou que ele foi capaz de erguer uma massa de80 kg a uma altura de 3 metros durante 1 minuto. Considere a aceleração da gravidade 10,0 m/s². Qual a eficiência aproximada do sistema para realizar tal tarefa?

(A) 10%

(B) 20%

(D) 50%

(E) 100%

Resolução:

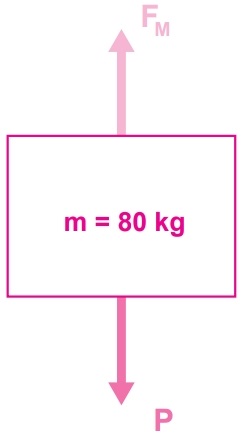
Para erguer a massa m = 80 kg, o motor precisa exercer sobre ela uma força (F_M) cujo trabalho supere o trabalho realizado pela força peso (P), que “puxa” a massa para baixo.

Ou seja, o trabalho da força aplicada pelo motor (τ_M) para erguer amassa é:

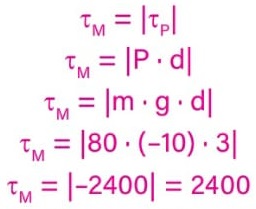
Como o motor levou 1 minuto para erguer a massa (Δt = 60 s), a potência útil desenvolvida por esse motor é:

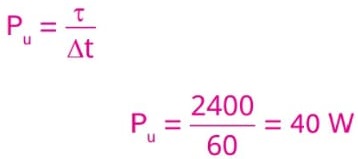
Sabendo que a eficiência de um motor é a razão entre a potência útil e a potência total fornecida, a eficiência desse motor é:

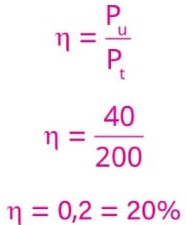
Portanto, a eficiência aproximada do sistema para realizar tal tarefa é 20%.

Alternativa: B

55) (Livro do aluno-SEDUC-SP/2025 - UFMS 2022) O Wall Ball é um daqueles exercícios que se ama ou se odeia, pensando que é difícil encontrar um meio-termo para esse exercício. A situação mostrada a seguir apresenta o exercício em três estágios:

Se considerarmos apenas o trabalho mínimo para lançar a bola (m = 20 kg) verticalmente para cima, da primeira posição agachada para a posição em que a bola atinge o alvo, o valor encontrado será:

(Considere: a aceleração da gravidade igual a 10 m/s2, resistência do ar desprezível.)

(A) 800 J

(B) 560 J

(D) 240 J

(E) 200 J

Resolução:

Na situação descrita, o trabalho mínimo necessário para que a bola se desloque da posição em que

a mulher está agachada até o alvo (h = 2,80 m) é numericamente igual à energia potencial gravitacional que a bola terá armazenada na altura do alvo. Sabendo que a energia potencial gravitacional armazenada é calculada por:

E_pg = m · g · h

E que a massa da bola é m = 20 kg, g = 10 m/s² e a altura entre a primeira posição e o alvo é h = 2,80 m, a energia potencial armazenada pelo sistema bola-Terra, ao atingir o alvo, é:

Epg = 20 · 10 · 2,80

Epg = 560 J

Como essa energia será transferida ao sistema bola-Terra pela força exercida pela atleta, o trabalho mínimo realizado pela força que a atleta exerce é τ = 560 J.

Alternativa: B

56) (Livro do aluno-SEDUC-SP/2025 - UNESP 2023) O gráfico representa a frequência média de oscilação (f) das pernas de um animal em função do comprimento de suas pernas (L), quando ele caminha de forma natural. Esse mesmo gráfico pode ser utilizado para uma pessoa caminhando nas mesmas condições.

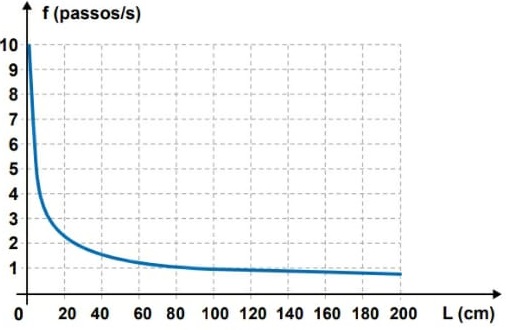
Considere uma pessoa adulta de 80 kg, cujas pernas medem 1 m, caminhando em um parque sobre uma superfície plana e horizontal, com velocidade escalar constante.

Se, em determinado trecho dessa caminhada, para cada passo dado, essa pessoa deslocar-se 90 cm, sua energia cinética será de:

(A) 40,0 J

(B) 32,4 J

(D) 36,0 J

(E) 16,2 J

Resolução:

A energia cinética de um corpo em movimento é determinada por:

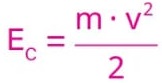
Analisando o gráfico, podemos perceber que, para animais/humanos cujas pernas medem 1 metro (100 cm), a frequência dos passos é de 1 passo por segundo.

O enunciado diz que cada passo corresponde a um deslocamento Δs = 90 cm = 0,9 m. Então, uma pessoa se deslocando nessas condições tem velocidade v igual a:

Como, de acordo com o enunciado, a massa da pessoa é m = 80 kg, a energia cinética dessa pessoa, nas condições descritas, será:

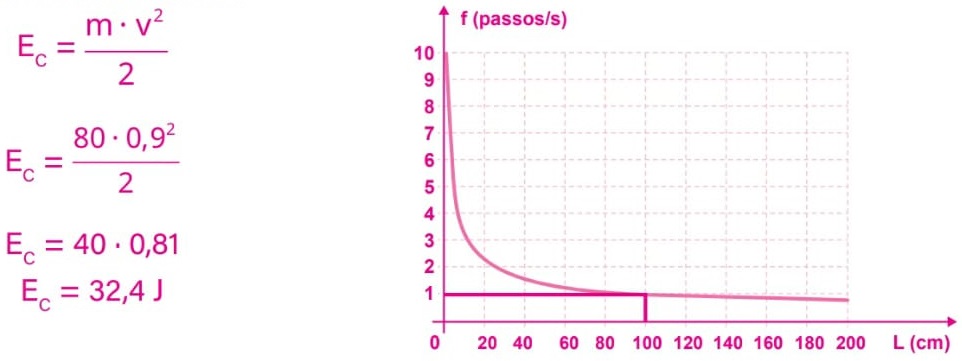
Alternativa: B

57) (Livro do aluno-SEDUC-SP/2025 - UERR 2023 – Adaptada) A figura a seguir apresenta um corpo de 10 kg sobre um plano inclinado. Há atrito entre o corpo e o plano, caracterizado pela constante de atrito dinâmico µ = 0,2. No local em questão, o valor da aceleração da gravidade é igual a 10 m/s²

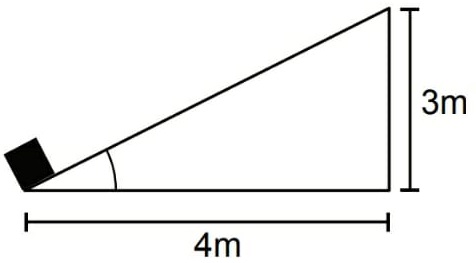
Nessa situação hipotética, o trabalho mínimo realizado por uma força para erguer o corpo até o topo do plano inclinado será:

(A) inferior a 400 J.

(B) superior a 400 J e inferior a 450 J.

(D) superior a 500 J e inferior a 550 J.

(E) superior a 550 J.

Resolução:

Para que uma força consiga levantar o corpo até o topo do plano inclinado, ela deve realizar um trabalho mínimo igual à soma do trabalho realizado pela força peso e pela força de atrito (em módulo).

Matematicamente, temos:

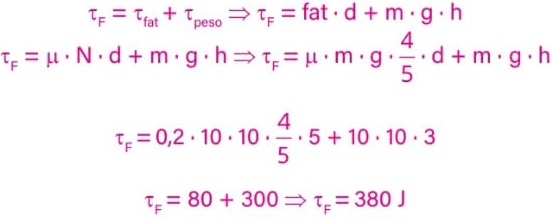
Alternativa: A

58) (Livro do aluno-SEDUC-SP/2025 - FAMERP 2024) Uma bola de basquetebol de massa 600 g é abandonada de uma altura de 1,90 m em relação ao solo. A bola colide com o solo e retorna a uma altura de 1,50 m. Desprezando a resistência com o ar e adotando o valor de 10 m/s²

Para a aceleração da gravidade, a energia mecânica dissipada durante a colisão dessa bola com o solo possui valor de

(A) 3,6 J

(B) 1,2 J

(D) 7,8 J

(E) 9,0 J

Resolução:

De acordo com o enunciado, a bola é “abandonada de uma altura de 1,90 m em relação ao solo”. Por esse motivo, a velocidade inicial da bola é zero.

Ou seja, no momento do abandono, a energia mecânica da bola (EMi) é:

EMi = Epg + Ec

EMi = Epg + 0

EMi = Epg

Como a energia potencial gravitacional é calculada por Epg = m · g · h, e, de acordo com o enunciado, a massa da bola é m = 600 g = 0,6 kg, g = 10 m/s² e a altura é h = 1,90 m, a energia mecânica da bola no momento do abandono é:

EMi = m · g · h

EMi = 0,6 · 10 · 1,90

EMi = 11,4 J

Após colidir com o solo, a bola retorna a altura de 1,50 m. No instante que atinge essa altura máxima, novamente sua velocidade é zero, logo, a energia cinética nesse instante também é zero. Portanto, no instante em que a bola atinge a altura h = 1,50 m, a energia mecânica da bola será:

EMf = m · g · h

EM_f = 0,6 · 10 · 1,50

EM_f= 9 J

A energia mecânica dissipada será, portanto, a diferença entre os valores da energia nesses dois instantes. Logo:

EM_dissipada = EMi – EMf

EM_dissipada = 11,4 – 9

EM_dissipada = 2,4 J

Alternativa: C

59) (Livro do aluno-SEDUC-SP/2025 - FUVEST 2024) Uma das modalidades de skate é o bowl, disputado em um espaço em formato aproximado de bacia.

Supondo um bowl com profundidade de 2,45 m, qual a máxima velocidade que um skatista, partindo do repouso no ponto mais alto da bacia, poderia alcançar no ponto mais baixo?

Note e adote:

Aceleração da gravidade: g = 10 m/s².

(A) 3 m/s

(B) 5 m/s

(D) 9 m/s e) 11 m/s

Resolução:

A máxima velocidade será alcançada pelo skatista se não houver dissipação de energia. Nesse caso será válida a relação:

EMi = EMf

Epgi + Eci = Epgf + Ecf

Como o skatista parte do repouso, sua velocidade no ponto mais alto é v = 0, logo, sua energia cinética neste ponto é ECi = 0.

No ponto mais baixo, a altura entre o skatista e o plano de referência é h = 0, logo, neste caso, a energia potencial gravitacional neste ponto é Epgf = 0

Com base nessas informações, a relação estabelecida anteriormente ficará:

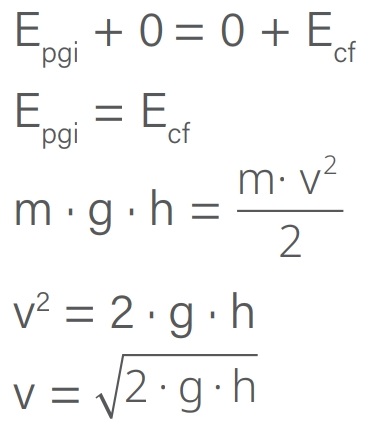
Como, de acordo com o enunciado, g = 10 m/s² e h = 2,45 m:

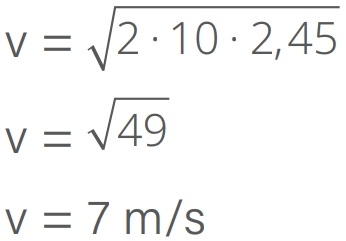
Alternativa: C

60) (Livro do aluno-SEDUC-SP/2025 - ENEM 2018) Um projetista deseja construir um brinquedo que lance um pequeno cubo ao longo de um trilho horizontal, e o dispositivo precisa oferecer a opção de mudar a velocidade de lançamento. Para isso, ele utiliza uma mola e um trilho onde o atrito pode ser desprezado, conforme a figura.

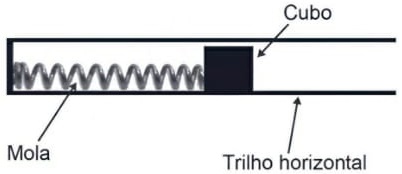
Para que a velocidade de lançamento do cubo seja aumentada quatro vezes, o projetista deve

(A) manter a mesma mola e aumentar duas vezes a sua deformação.

(B) manter a mesma mola e aumentar quatro vezes a sua deformação.

(D) trocar a mola por outra de constante elástica duas vezes maior e manter a deformação.

(E) trocar a mola por outra de constante elástica quatro vezes maior e manter a deformação.

Resolução:

Podemos determinar a velocidade que o cubo adquire após o lançamento por meio da conservação da energia mecânica.

Como o atrito pode ser desprezado, esse sistema é conservativo, por isso é válida a igualdade:

EM_f = EM_i

No início da situação, o cubo deforma a mola até um valor de deformação x. Nesse momento, a velocidade do cubo é v = 0, logo, a energia mecânica inicial é EM_i = Epel.

Ao final do lançamento, a mola volta para o seu comprimento natural e o cubo perde contato com a mola. Nesse momento, toda energia potencial elástica armazenada pelo sistema foi transformado em cinética, logo EM_f = Ec.

Portanto:

EM_f= EM_iEc = Epel

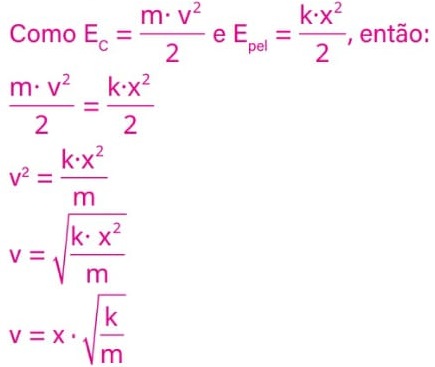
Logo, a velocidade de lançamento do cubo é

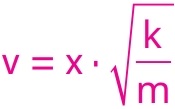
Analisando a equação da velocidade de lançamento, podemos perceber que para obter uma velocidade de lançamento quatro vezes maior, basta aumentar a deformação da mola em quatro vezes também, sem alterar a mola (constante elástica k) e a massa do cubo (m)

Alternativa: B

61) (Livro do aluno-SEDUC-SP/2025 - ENEM PPL 2012) Um automóvel, em movimento uniforme, anda por uma estrada plana, quando começa a descer uma ladeira, na qual o motorista faz com que o carro se mantenha sempre com velocidade escalar constante. Durante a descida, o que ocorre com as energias potencial, cinética e mecânica do carro?

(A) A energia mecânica mantém-se constante, já que a velocidade escalar não varia e, portanto, a energia cinética é constante.

(B) A energia cinética aumenta, pois a energia potencial gravitacional diminui e quando uma se reduz, a outra cresce.

(D) A energia mecânica diminui, pois a energia cinética se mantém constante, mas a energia potencial gravitacional diminui.

(E) A energia cinética mantém-se constante, já que não há trabalho realizado sobre o carro.

Resolução:

Para resolver essa questão, vamos analisar o comportamento de cada uma das formas de energia envolvidas na situação:

Durante a descida, o motorista mantém o carro com velocidade escalar constante. Como a velocidade não se altera, a energia cinética do veículo é constante durante o trajeto.

Como o trajeto descrito é uma descida, a altura entre o ponto mais alto (início da descida) e o ponto mais baixo (fim da descida) diminui ao longo do trajeto. Como a energia potencial gravitacional é uma função altura entre os pontos de referência, com a diminuição da altura a energia potencial gravitacional associada ao movimento também diminui.

Como a energia mecânica corresponde à soma das energias cinética e potencial e, nesse caso, a energia cinética se mantém constante, enquanto a energia potencial gravitacional diminui, então a energia mecânica diminui durante esse trajeto.

Alternativa: B

62) (Livro do aluno-SEDUC-SP/2025 - ENEM 2017) Bolas de borracha, ao caírem no chão, quicam várias vezes antes que parte da sua energia mecânica seja dissipada. Ao projetar uma bola de futsal, essa dissipação deve ser observada para que a variação na altura máxima atingida após um número de quiques seja adequada às práticas do jogo. Nessa modalidade é importante que ocorra grande variação para um ou dois quiques. Uma bola de massa igual a 0,40 kg é solta verticalmente de uma altura inicial de 1,0 m e perde, a cada choque com o solo, 80% de sua energia mecânica. Considere desprezível a resistência do ar e adote g = 10 m/s².

O valor da energia mecânica final, em joule, após a bola quicar duas vezes no solo, será igual a

(A) 0,16

(B) 0,80

(E) 3,20

Resolução:

No momento que a bola é solta, a velocidade inicial é zero, logo, a energia cinética inicial é zero.

Portanto a energia mecânica inicial é:

EM₁ = Epg

EM₁ = m · g · h

Sendo a massa da bola m = 0,40 kg, a altura inicial h = 1 metro e g = 10 m/s²

EM₁ = 0,40 · 10 · 1

EM₁ = 4,0 J

Após cada quique, a bola perde 80% da sua energia mecânica. Logo, a energia mecânica após o

primeiro quique (EM₂) será:

EM₂ = 20% · EM₁ = 0,2 · EM₁

EM₂ = 0,2 · 4,0

EM₂ = 0,8 J

Após o segundo quique, a bola perde mais 80% da sua energia mecânica. Logo:

EM₃ = 0,2 · EM₂

EM₃= 0,2 · 0,8

EM₃ = 0,16 J

Portanto, o valor da energia mecânica final após a bola quicar duas vezes no solo será igual a 0,16 J.

Alternativa: A

63) (Livro do aluno-SEDUC-SP/2025 - ENEM 2022 - Adaptada) Um pai faz um balanço utilizando dois segmentos paralelos e iguais da mesma corda para fixar uma tábua a uma barra horizontal. Por segurança, opta por um tipo de corda cuja tensão de ruptura seja 25% superior à

tensão máxima calculada nas seguintes condições:

- O ângulo máximo atingido pelo balanço em relação à vertical é igual a 90°;

- Os filhos utilizarão o balanço até que tenham uma massa de 24 kg.

Além disso, ele aproxima o movimento do balanço para o movimento circular, considera que a aceleração da gravidade é igual a 10 m/s² e despreza forças dissipativas.

Qual é a tensão de ruptura da corda escolhida?

(A) 120 N

(B) 300 N

(D) 450 N

(E) 900 N

Resolução:

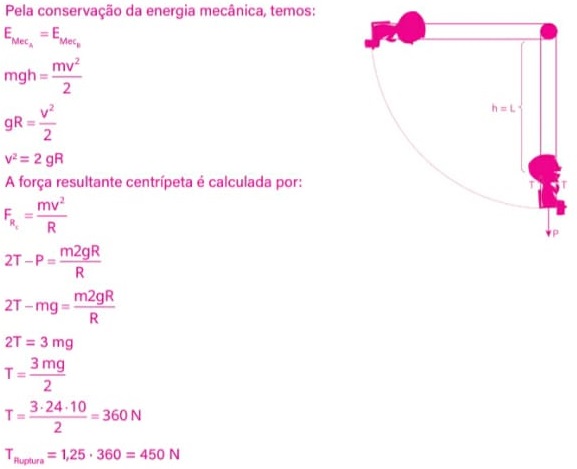
Alternativa: D

64) (Livro do aluno-SEDUC-SP/2025 - UERJ 2024) leia o texto a seguir.

Fonte de luz síncrotron Sirius

Sirius, a nova fonte de radiação síncrotron brasileira, funciona como um grande microscópio que − ao revelar a estrutura atômica, molecular e eletrônica dos mais diversos materiais − permite pesquisas com aplicações em praticamente todas as áreas do conhecimento. Para produzir a radiação síncrotron, feixes de elétrons são acelerados em várias etapas até alcançarem o anel principal do acelerador Sirius, um tubo fechado onde se produz vácuo. Nesse espaço confinado, os elétrons se movimentam em trajetória circular com rapidez próxima à da luz.

Considere que, antes de entrar no anel principal do Sirius, um feixe de elétrons percorre um acelerador linear adquirindo energia adicional. Nesse percurso, os elétrons passam de 150,0 MeV para 3,0 GeV de energia cinética. Admitindo 1,0 eV = 1,6 · 10⁻¹⁹ J, calcule, em joules, o trabalho realizado pela força resultante sobre os elétrons, em seu percurso no acelerador linear.

Resolução:

De acordo com o teorema da energia cinética, o trabalho da força resultante é igual à variação da energia cinética:

τ = ΔEc

τ = Ecf – Eci

De acordo com o enunciado, a energia cinética inicial dos elétrons é Eci = 150,0 MeV = 150,0 · 10⁶ eV e a energia cinética final dos elétrons é Ecf = 3,0 GeV = 3,0 · 10⁹ eV. Logo, o trabalho da força resultante sobre os elétrons será:

τ = 3,0 · 10⁹– 150,0 · 10⁶

τ = 3,0 · 10⁹ – 0,150 · 10⁹

τ = 2,85 · 10⁹ eV

Como 1 eV = 1,6 · 10^–19 J, então 2,85 · 10⁹ eV é:

τ = 2,85 · 10⁹ · 1,6 · 10^–19

τ = 4,56 · 10^–10 J

Portanto, o trabalho realizado pela força resultante sobre os elétrons, em seu percurso no acelerador linear foi de: 4,56 · 10–10 J.

65) (Livro do aluno-SEDUC-SP/2025 - ENEM 2021) Analisando a ficha técnica de um automóvel popular, verificam-se características em relação ao seu desempenho. Considerando o mesmo automóvel em duas versões, uma delas funcionando a álcool e outra, a gasolina, tem-se os dados apresentados no quadro, em relação ao desempenho de cada motor.

Considerando desprezível a resistência do ar, qual versão apresenta a maior potência?

(A) Como a versão a gasolina consegue a maior aceleração, esta é a que desenvolve a maior potência.

(B) Como a versão a gasolina atinge o maior valor de energia cinética, esta é a que desenvolve a maior potência.

(C) Como a versão a álcool apresenta a maior taxa de variação de energia cinética, esta é a que desenvolve a maior potência.

(D) Como ambas as versões apresentam a mesma variação de velocidade no cálculo da aceleração, a potência desenvolvida é a mesma.

(E) Como a versão a gasolina fica com o motor trabalhando por mais tempo para atingir os 100 km/h, esta é a que desenvolve a maior potência.

Resolução:

Para analisar a potência de cada versão desse carro, vamos partir da equação de cálculo da potência mecânica:

De acordo com o teorema da energia cinética, o trabalho é igual à variação da energia cinética (W = ΔEc ). Logo:

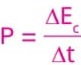
Como, em ambos os casos, a velocidade inicial é zero, a energia cinética inicial também é zero. Então, a potência, para os dois modelos, será:

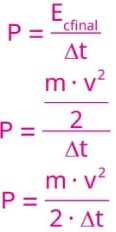
Calculando a potência de cada modelo, obtemos:

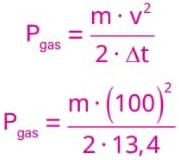
Como a massa m é a mesma para os dois modelos, podemos definir qual a maior potência fazendo a razão entre elas:

Como a razão é

O resultou em um número maior que 1, então a potência do motor a álcool é maior do que a potência do motor a gasolina.

Alternativa: C

66) (Livro do aluno-SEDUC-SP/2025) Supondo que a massa desse corredor seja igual a 90 kg, o trabalho total realizado nas 13 primeiras passadas é mais próximo de:

(A) 5,4 · 10² J

(B) 6,5 · 10³ J

(D) 1,3 · 10⁴ J

(E) 3,2 · 10⁴J

Resolução:

O trabalho realizado durante um movimento pode ser determinado pelo teorema da energia cinética:

τ = ΔEc

Como o corredor parte do repouso, sua energia cinética inicial é zero. Logo:

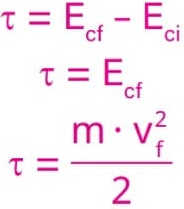
De acordo com o enunciado, a massa do corredor é m = 90 kg e a velocidade que ele atinge, após as 13 passadas, é vf = 12 m/s.

Substituindo esses valores na equação acima, obtemos:

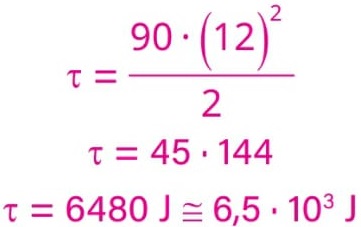
Portanto, o trabalho total realizado nas 13 primeiras passadas é mais próximo de 6,5 · 10³ J.

Alternativa: B

67) (Livro do aluno-SEDUC-SP/2025 - UNESP 2021) Em uma pista de patinação no gelo, um rapaz e uma garota estão inicialmente em repouso, quando ele começa a empurrá-la, fazendo com que ela percorra cinco metros em linha reta. O gráfico indica a intensidade da resultante das forças aplicadas sobre a garota, em função da distância percorrida por ela.

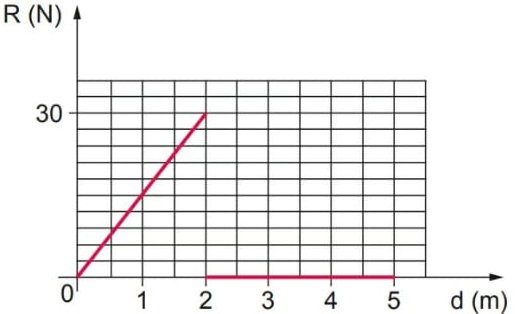
Sabendo que a massa da garota é 60 kg, sua velocidade escalar, após ela ter percorrido 3,5 m, será:

(A) 0,4 m/s

(B) 0,6 m/s

(D) 1,2 m/s

(E) 1,0 m/s

Resolução:

O trabalho realizado por uma força pode ser determinado pela área do gráfico F × d. A área abaixo do gráfico da resultante das forças sobre a garota em função da distância percorrida corresponde à área de um triângulo de base 2 (m) e altura 30 (N).

Logo, o trabalho da resultante das forças sobre a garota é:

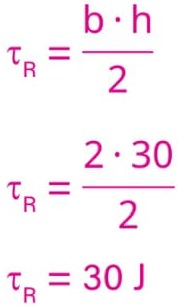
Como, de acordo com o teorema da energia cinética, τR = ΔEc, e Eci = 0, pois a garota está inicialmente em repouso, então:

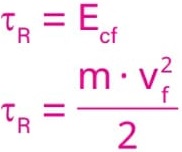
Sendo a massa da garota, de acordo com o enunciado, m = 60 kg, eWR = 30 J, então:

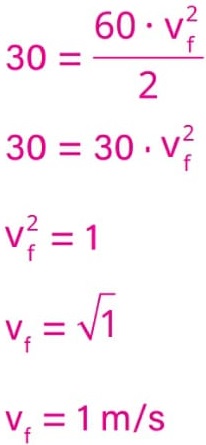
Portanto, a velocidade escalar da garota, após ela ter percorrido 3,5 m, será 1 m/s.

Alternativa: E

QUANTIDADE DE MOVIMENTO E IMPULSO

68) (Livro do aluno-SEDUC-SP/2025 - UERJ 2022) As chamadas estrelas cadentes nada mais são que meteoros. Esses pedaços de rocha são atraídos pelo campo gravitacional da Terra e incandescem no atrito com a atmosfera. Admita que um meteoro, ao penetrar na atmosfera terrestre, tenha, em determinado instante, massa de 10 kg e velocidade de 252 000 km/h. Nessas condições, a quantidade de movimento do meteoro, em kg · m/s, é igual a:

(A) 560 000

(B) 680 000

(D) 820 000

Resolução:

O módulo da quantidade de movimento de um objeto pode ser calculado por:

Q = m · v

Na situação descrita, o objeto é um meteoro de massa m = 10 kg que atravessa a atmosfera com velocidade v = 252 000 km/h. Como pede-se a quantidade de movimento em kg · m/s, é preciso converter a velocidade para m/s:

v = 252 000 km/h ÷ 3,6

v = 70 000 m/s

Logo, a quantidade de movimento do meteoro na situação descrita é:

Q = m · v

Q = 10 · 70 000

Q = 700 000 kg · m/s

Alternativa: C

69) (Livro do aluno-SEDUC-SP/2025 - ENEM PPL 2022) Esteiras e escadas rolantes são dispositivos que deslocam, a velocidade constante, os objetos neles colocados, por meio de sistemas de controle com sensores. Quando a massa total do dispositivo varia, seja pelo acréscimo ou pela retirada de objetos, a ação de forças impulsivas mantém a velocidade constante. Como exemplo, considere que a massa total diminua de 1200 kg para 1000 kg em um intervalo de tempo de 0,10 s, e que, então, seja aplicada uma força impulsiva constante de 250 N para manter constante a velocidade.

No exemplo mencionado, o valor da velocidade constante do dispositivo rolante é, em m/s:

(A) 0,011

(B) 0,021

(D) 0,125

(E) 0,500

Resolução:

Para manter a velocidade constante, uma força impulsiva é aplicada ao dispositivo por 0,10 s. Porém, como a massa diminuiu, a força impulsiva de 250 N é contra o movimento, pois ela é aplicada para evitar que a velocidade do dispositivo aumente.

Logo, o impulso dessa força é:

I = –F · Δt

I = –250 · 0,1

I = –25 N · s

De acordo com o teorema do impulso:

I = ΔQ

I = m · v – m₀· v₀

Mas, neste caso, a velocidade é constante (v₀ = v) e a massa varia. Então:

I = m · v – m₀ · v

I = v · (m – m₀)

Sendo assim, conforme o enunciado, m₀ = 1200 kg e m = 1000 kg, a velocidade v do dispositivo é:

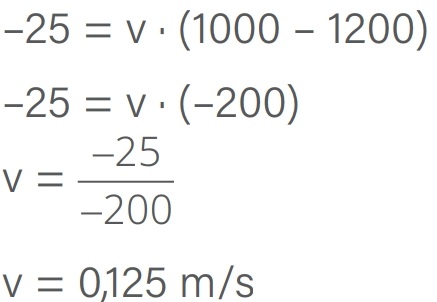
Alternativa: D

70) (Livro do aluno-SEDUC-SP/2025 - UERJ 2025) A cada batimento, o coração humano bombeia cerca de 85 g de sangue. Admita que a velocidade de saída do sangue bombeado pelo coração seja de 0,4 m/s. A quantidade de movimento do sangue, em kg · m/s, produzida pelo coração em um batimento, corresponde aproximadamente a:

(A) 0,064

(B) 0,048

(D) 0,018

Resolução:

Podemos calcular o módulo da quantidade de movimento do sangue pela expressão:

Q = m · v.

Como é pedido que a unidade da quantidade de movimento seja kg · m/s, é preciso converter a unidade de massa do sangue, pois foi fornecida em gramas: m = 85 g = 85 · 10^–3 kg

Sabendo que a velocidade de saída do sangue é v = 0,4 m/s, então:

Q = m · v

Q = 0,4 · 85 · 10^–3

Q = 34 · 10^–3

Q = 0,034 kg · m/s

Portanto, a quantidade de movimento do sangue, produzida pelo coração em um batimento, corresponde aproximadamente a 0,034 kg · m/s.

Alternativa: C

71) (Livro do aluno-SEDUC-SP/2025 - UNIFESP 2022) Nas duas extremidades da pista de pouso e decolagem de alguns aeroportos há áreas de escape, cujo objetivo é reter os aviões caso eles não consigam parar até o final da pista. A superfície dessas áreas de escape é composta por um material que se deforma devido ao peso da aeronave, de modo a dificultar o seu deslocamento. A figura mostra um avião que adentrou em uma dessas áreas de escape.

Considere que esse avião chegou à área de escape com velocidade de 54 km/h, percorrendo uma trajetória retilínea, com aceleração média de 5,0 m/s² em sentido contrário ao da velocidade, e que parou após um intervalo de tempo igual a 3,0 s.

a) Converta a velocidade inicial do avião para m/s e determine a distância, em metros, que ele percorreu na área de escape.

Resolução:

Para transformar a velocidade inicial do avião para m/s, basta dividir o valor em km/h por 3,6:

V0 = 54 km/h ÷ 3,6

V0 = 15 m/s

Se o sentido da aceleração é contrário ao da velocidade, então a = – 5 m/s². Além disso, o avião para (v = 0) após um intervalo de tempo Δt = 3 s. A partir desses valores, podemos determinar a distância percorrida pelo avião nesse processo utilizando a equação horária dos espaços:

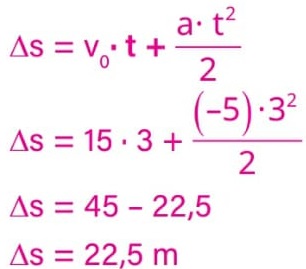
b) Suponha que a massa desse avião seja 2,4 · 10⁴ kg e que apenas as forças de resistência atuem sobre ele durante a frenagem. Calcule, em newtons, a intensidade média da resultante das forças de resistência que atuaram sobre o avião durante a sua frenagem na área de escape. Determine a intensidade média do impulso, em N · s, aplicado por essa resultante sobre o avião.

Resolução:

De acordo com o princípio fundamental da mecânica (2ª lei de Newton), o módulo da resultante das forças que atuam sobre um corpo pode ser calculada por:

FR = m · |a|

Sendo a massa desse avião m = 2,4 · 10⁴e a aceleração a = – 5 m/s², o módulo da resultante das forças resistivas é:

FR = 2,4 · 10⁴ · |–5|

FR = 12 · 10⁴

FR = 1,2 · 105 N

Como as forças de resistência atuam sobre o avião por todo o movimento, então o tempo de atuação dessas forças é Δt = 3 s. Logo, a intensidade média do impulso aplicado pela resultante das forças sobre o avião é:

I = FR · Δt

I = 1,2 · 10⁵ · 3

I = 3,6 · 10⁵ N · s

72) (Livro do aluno-SEDUC-SP/2025 - EEAR 2021) No gráfico da figura a seguir tem-se a intensidade da força (F), em newtons, em função do tempo (t), em segundos. Neste gráfico, a força, que é a resultante das forças exercidas sobre o corpo de massa m, tem direção constante.

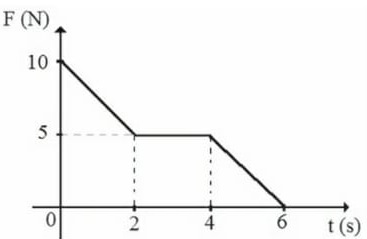
Sabendo que no instante t = 0 o corpo está em repouso, determine o valor do impulso da força, em N · s, sobre o corpo, somente, no intervalo de 0 a 4 segundos.

(A) 5

(B) 15

(D) 30

Resolução:

Como a intensidade da resultante das forças que atuam sobre o corpo é variável, porém com direção constante, teremos de calcular o impulso da resultante pela área do gráfico.

O impulso de uma força é numericamente igual à área do gráfico F × t. Como o enunciado pede o impulso referente ao intervalo de 0 a 4 segundos, precisamos determinar a área mostrada abaixo.

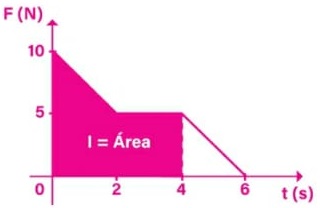
Podemos notar que a área do gráfico é composta por um retângulo de base b = 4 e altura

h = 5, e um triângulo de base b = 2 e altura

h = 5. Logo, o impulso da força F será:

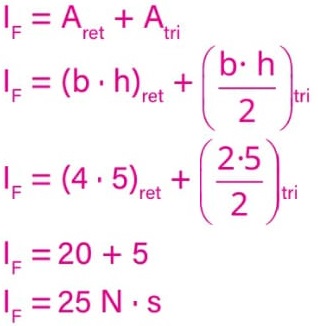
Portanto, o valor do impulso da força F sobre o corpo no intervalo de 0 a 4 segundos é 25 N · s.

Alternativa: C

73) (Livro do aluno-SEDUC-SP/2025 - EPCAR/AFA 2024) Uma partícula de massa 2 kg desloca-se em uma trajetória horizontal, sem atrito, com velocidade escalar de 10 m/s, quando uma força F, de intensidade constante na direção do deslocamento, passa a agir sobre ela durante

um intervalo de tempo Δt. Dado que o impulso dessa força é igual a –28 N ∙ s, a velocidade escalar da partícula no instante em que cessa a ação da força F, em m/s, é:

(A) 3

(B) 0

(D) – 4

Resolução:

De acordo com o teorema do impulso, o impulso de uma força sobre um corpo é igual à variação da quantidade de movimento:

I = ΔQ

I = Qf – Qi

I = m · vf – m · vi

De acordo com o enunciado, a massa da partícula é m = 2 kg, a velocidade inicial é v = 10 m/s e o impulso da força F é I = –28 N · s. Substituindo esses valores na equação acima, obtemos:

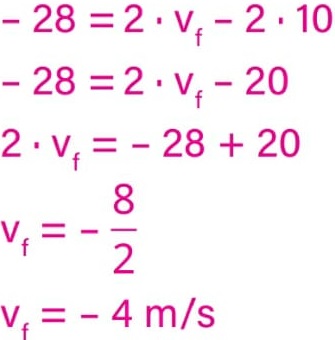
Portanto, a velocidade escalar da partícula no instante em que cessa a ação da força F é – 4 m/s.

Alternativa: D

74) (Livro do aluno-SEDUC-SP/2025 0 UTFPR 2024) Popularmente, o estilingue é conhecido como: “Arco atirador com elásticos presos pelas extremidades que, sendo ativado por um gatilho, arremessa pedrinhas, bolas de argila; atiradeira, badoque, bodoque.”

Considere um corpo de argila com massa de 60 g lançado de um estilingue colidindo horizontalmente com um bloco de tijolo liso de massa 240 g. Sabendo que, no momento da colisão, o corpo de argila apresentava uma velocidade horizontal de 5,0 m/s e o bloco de tijolo estava em repouso sobre uma superfície sem atrito, determine a velocidade do conjunto de corpos argila-tijolo imediatamente após a colisão, sabendo que o bloco de argila aderiu ao bloco de tijolo. Despreze a resistência do ar.

(A) 2 m/s

(B) 0,5 m/s

(D) 1 m/s

(E) 2,5 m/s

Resolução:

Como o enunciado pede para que desprezemos a resistência do ar, vamos considerar que as velocidades se mantêm e o sistema formado pelo corpo de argila e o tijolo é isolado. Por isso, é válida a igualdade:

Q_inicial = Q_final

mA · v_iA + mT · vi T = mA · v_f A+ mT · v_f T

De acordo com o enunciado, as massas do corpo de argila e do tijolo são, respectivamente, mA = 60 g e mT = 240 g. A velocidade inicial do corpo de argila é v_i A = 5 m/s e do tijolo, por estar em repouso, v_i T = 0.

Além disso, o corpo de argila aderiu ao tijolo com a colisão, portanto vf A = vf B = v.

Logo:

60 · 5 + 240 · 0 = 60 · v + 240 · v

300 = 300 · v

v = 1 m/s

Assim, a velocidade do conjunto de corpos argila-tijolo imediatamente após a colisão é 1 m/s.

Alternativa: D

75) (Livro do aluno-SEDUC-SP/2025- UEPG 2023 – Adaptada) Um corpo A, de MA = 3 kg, tem uma velocidade VA = 4 m/s, ao longo de uma superfície horizontal sem atrito, no sentido positivo do eixo x. Um corpo B, de massa MB = 2 kg, encontra-se inicialmente em repouso

em relação ao corpo A. Considerando que a colisão entre os dois corpos é perfeitamente elástica e frontal, e que a velocidade do corpo A após a colisão é de 0,8 m/s, dê a soma das alternativas corretas.

(01) Após a colisão, o corpo A move-se no sentido negativo do eixo x.

(02) A energia cinética do corpo A após a colisão é de 0,96 J.

(04) O módulo da velocidade do corpo B após a colisão é de 4,8 m/s.

(08) O impulso fornecido ao corpo B devido à colisão é de 9,6 kg · m/s.

Resolução:

01) Falsa. O próprio enunciado informa que a velocidade do corpo A após a colisão é positiva, portanto, no sentido positivo do eixo x: “a velocidade do corpo A após a colisão é de 0,8 m/s”.

02) Verdadeira. Sendo a massa do corpo A MA = 3 kg e sua velocidade vA = 0,8 m/s, sua energia cinética, após a colisão, será:

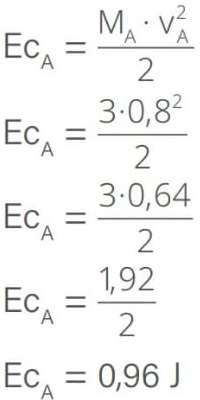
04) Verdadeira. O enunciado diz que a superfície sobre a qual ocorrem os movimentos é horizontal e sem atrito, por isso, vamos considerar que o sistema formado pelos dois corpos é isolado. Por esse motivo, podemos afirmar que:

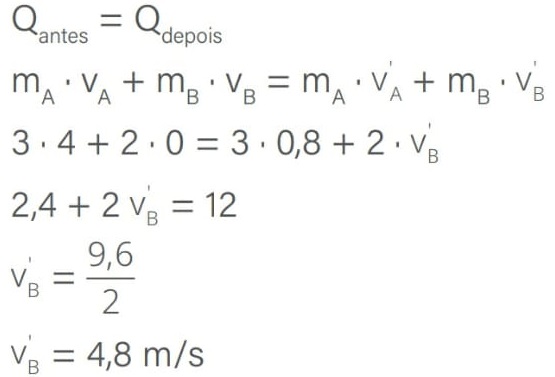
08) Verdadeira. De acordo com o teorema do impulso:

Portanto: 02 + 04 + 08 = 14

Alternativa:

76) (Livro do aluno-SEDUC-SP/2025 - FCMSCSP 2023) Um caminhão de massa 4000 kg, que se deslocava com velocidade de 15 m/s, colidiu com um automóvel de massa 1000 kg que se deslocava à sua frente, na mesma direção e sentido, com velocidade de 10 m/s.

a) Calcule a intensidade da velocidade relativa, em m/s, entre os dois veículos e a energia cinética, em joules, do automóvel antes da colisão.

Resolução:

Quando dois móveis se deslocam com mesma direção e mesmo sentido, a velocidade relativa entre eles é determinada pela diferença entre os módulos da velocidade de cada um. Sendo vC a velocidade do caminhão e vA a velocidade do automóvel, a velocidade relativa entre os dois veículos é:

Sendo a massa do automóvel mA = 1000 kg, sua energia cinética, antes da colisão, é:

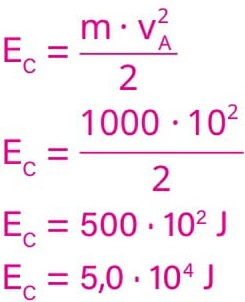
b) Sabendo que, após a colisão, os veículos permaneceram unidos e que não houve mudança na direção de suas velocidades, calcule a intensidade do impulso, em N ⋅ s, aplicado pelo caminhão sobre o automóvel nessa colisão.

Resolução:

De acordo com o teorema do impulso, a intensidade do impulso de uma força pode ser determinada por:

I = ΔQ

Nesse caso, o impulso que o caminhão aplica sobre o automóvel é igual à variação da quantidade de movimento do automóvel. Mas, para determinar esse impulso, é preciso saber a velocidade do automóvel após a colisão.

Como o enunciado não menciona a presença de forças externas, vamos considerar que o sistema é isolado.

Logo:

v = 14 m/s

Portanto, o impulso aplicado pelo caminhão sobre o automóvel foi:

77) (Livro do aluno-SEDUC-SP/2025 - PUC Rio 2023) Em uma superfície plana sem atrito, um bloco A de massa 2,0 kg, com velocidade de 3,0 m/s, colide com o bloco B, idêntico ao A, inicialmente em repouso. O bloco B sai, após a colisão, com velocidade 2,0 m/s, na mesma direção e sentido que o bloco A possuía originalmente. Qual é a razão entre a energia cinética final e a inicial do bloco A?

(A) 1/16

(B) 1/9

(D) 1/4

(E) 1/2

Resolução:

Para determinar a energia cinética do bloco A, é preciso determinar sua velocidade após a colisão.

Sendo o sistema formado pelos dois blocos um sistema isolado, a quantidade de movimento se conserva. Logo:

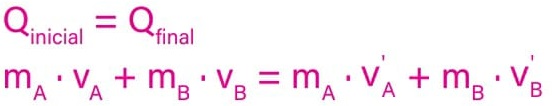
Como as massas dos blocos são iguais, podemos representá-las pela mesma incógnita e colocá-la em evidência:

Sabendo a intensidade da velocidade do corpo A após a colisão (vA), a razão entre a energia cinética final (após a colisão) e a energia cinética inicial (antes da colisão) será:

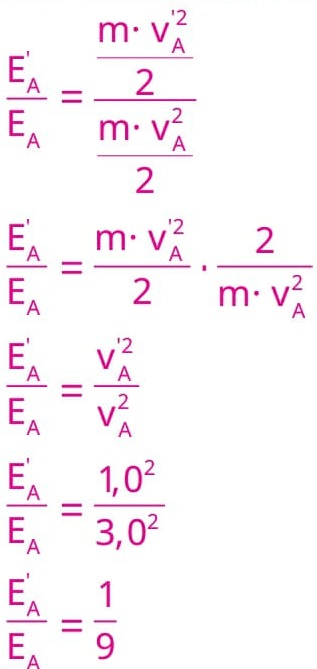
Alternativa: B

78) (Livro do aluno-SEDUC-SP/2025 - UEPG 2023 – Adaptada) Dois blocos, bloco A e bloco B, cujas massas são, respectivamente, 2 kg e 3 kg, deslizam sobre uma superfície horizontal, sem atrito. Os dois blocos se movem na mesma direção no sentido positivo do eixo x. O bloco A se move com uma velocidade de 6 m/s e o bloco B, com uma velocidade de 4 m/s, ambas em relação à superfície horizontal. Considerando que, para t = 0 s, o bloco A se encontra na origem e o bloco B na posição x = 10 m, que a colisão entre os dois blocos é perfeitamente inelástica e desprezando a resistência do ar, dê a soma das alternativas corretas.

(01) Nessa situação, o coeficiente de restituição é 1.

(02) Após a colisão, a velocidade dos dois blocos é de 5 m/s.

(04) A energia cinética total do sistema constituído pelos dois blocos é conservada.

(08) A colisão entre os dois blocos ocorre em t = 5 s.

(16) A velocidade do bloco A em relação ao bloco B é de 2 m/s.

Resolução:

01) Falsa. Após uma colisão perfeitamente inelástica, os objetos se mantêm unidos. Por isso, a velocidade de afastamento é V_afastamento= 0 e, portanto, o coeficiente de restituição é:

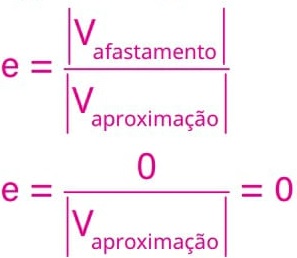
02) Falsa. Considerando que o sistema formado pelos dois blocos é isolado, é válido o princípio de conservação da quantidade de movimento. Logo:

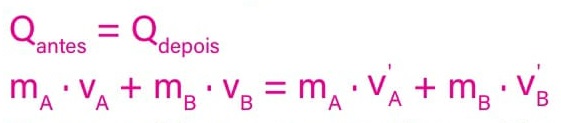
Como os blocos se mantêm unidos após a colisão, vA ' =vB ’ = v.

Logo:04) Falsa. Pois, em uma colisão perfeitamente inelástica, não há conservação da energia cinética.

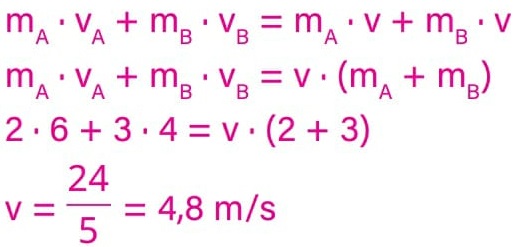
08) Verdadeira. O enunciado diz que em t = 0 o bloco A se encontra na origem do eixo x, ou seja, x = 0, e o bloco B se encontra na posição x = 10 m. Como os dois blocos se movem com mesma direção e mesmo sentido, a velocidade relativa entre eles é:

Como os dois blocos descrevem movimentos retilíneos e uniformes, ou seja, não possuem aceleração, e só nos interessa o movimento até a colisão, podemos considerar, para calcular o instante do encontro, que o bloco B está parado na posição x = 10 m e que o bloco A se desloca em direção ao B com velocidade v = 2 m/s.

Dessa forma, o tempo necessário para o bloco A ir do ponto x = 0 a x = 10 m será:

16) Verdadeira. Como já foi calculado no item anterior, a velocidade relativa de aproximação entre os blocos é vrel = 2 m/s.

Portanto: 08 + 16 = 24.

79) (Livro do aluno-SEDUC-SP/2025 - UFJF PISM1 2021) Um corpo de 1,0 kg desliza sem atrito sobre uma superfície horizontal a uma velocidade constante de magnitude igual a 60 cm/s. Ao se chocar frontalmente com outro corpo que estava parado no caminho, ele para. Se considerarmos que o choque foi totalmente elástico, a massa do corpo que estava parado e o módulo da velocidade que ele adquire logo depois da colisão são, respectivamente:

(A) 0,7 kg e 72 cm/s

(B) 2,0 kg e 30 cm/s

(D) 2,0 kg e 42 cm/s

(E) 1,0 kg e 60 cm/s

Resolução:

Considerando que o sistema formado pelos dois corpos é isolado, e de acordo com o princípio da conservação da quantidade de movimento, temos:

De acordo com o enunciado, o corpo A tem massa mA = 1 kg e velocidade, antes da colisão, vi A = 60 cm/s = 0,6 m/s. Após a colisão, a velocidade de A é vf A = 0.

Logo:

1 · 0,6 + mB · 0 = 1 · 0 + mB ·vf

BmB · vf B = 0,6 (equação I)

Como o choque foi totalmente elástico, ou perfeitamente elástico, a energia cinética do sistema se conversa.

Logo:

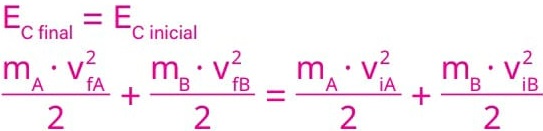
Como a velocidade inicial do outro corpo (B) é zero e a velocidade final do primeiro corpo (A) também é zero:

Dividindo a equação II pela equação I, obtemos:

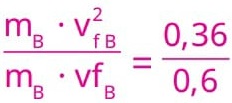
Substituindo esse valor na equação I, concluímos que a massa de B é:

Alternativa: E

ELETRODINÂMICA

(CIRCUITOS ELÉTRICOS)

80) (Livro do aluno-SEDUC-SP/2025 - UNICAMP 2024) Em um estudo do comportamento elétrico de neurônios, aplica-se uma diferença de potencial elétrico (ddp, da ordem de 10^–3V) e mede-se a corrente elétrica (da ordem de 10^–12 A) que passa pelo sistema. A partir dos resultados desse experimento, representados no gráfico da figura a seguir, conclui-se que a resistência elétrica do sistema é igual a:

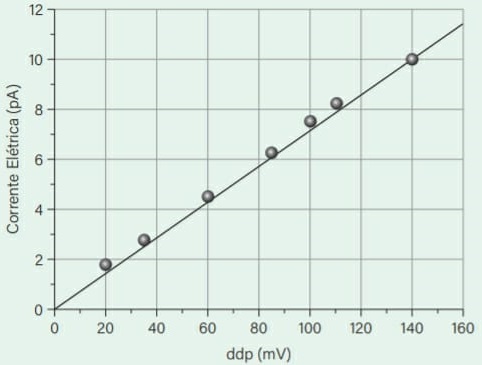
(A) 14 Ω

(B) 70 mΩ

(D) 14 GΩ

Resolução:

Analisando o gráfico, podemos notar que existe um ponto que fornece um valor exato de ddp e o valor exato da corrente elétrica correspondente:

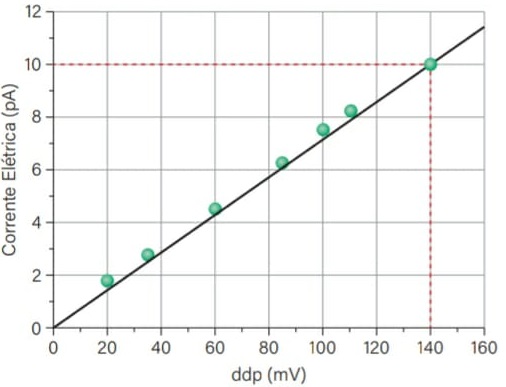
Com base no ponto destacado no gráfico, para a ddp V = 140 mV = 140 · 10^–3 V, passa pelo sistema uma corrente elétrica i = 10 pA = 10 · 10^–12 A.

Substituindo esses valores na equação da primeira lei de Ohm, concluímos que a resistência elétrica do sistema é igual a:

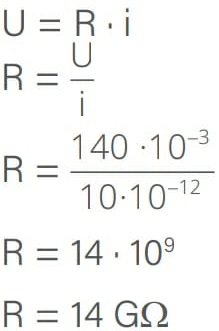
Alternativa: D

81) (Livro do aluno-SEDUC-SP/2025 - ENEM PPL 2022) Em virtude do frio intenso, um casal adquire uma torneira elétrica para instalar na cozinha. Um eletricista é contratado para fazer um novo circuito elétrico para a cozinha, cuja corrente será de 30 A, com a finalidade de alimentar os terminais da torneira elétrica. Ele utilizou um par de fios de cobre, de área da seção reta igual a 4 mm² e de 28 m de comprimento total, desde o quadro de distribuição (onde ficam os disjuntores) até a cozinha. A tensão medida na saída do quadro de distribuição é 220 V. Considere que a resistividade do fio de cobre é de 1,7 · 10^–8 Ω · m.

Considerando a resistência da fiação, a tensão aplicada aos terminais da torneira é mais próxima de:

(A) 211 V

(B) 213 V

(D) 219 V

(E) 220 V

Resolução:

Podemos determinar a resistência elétrica da fiação aplicando a segunda lei de Ohm:

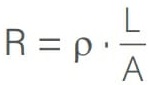
De acordo com o enunciado, a resistividade do fio de cobre é ρ = 1,7 · 10^–8 Ω · m, a área de seção reta do fio é A = 4 mm² = 4 · 10^–6 m, e o comprimento é L = 28 m. Substituindo esses valores na equação acima, obtemos:

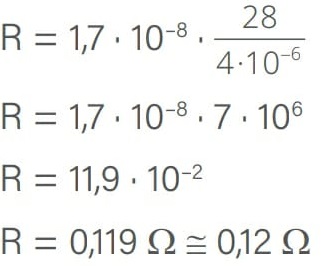
Como a torneira é um tipo de aquecedor elétrico, ela também atua como um resistor. Logo, como o fio não é ideal e tem certa resistência elétrica, podemos considerar que o fio e a torneira formam uma associação de resistores em série, portanto a tensão total (U = 220) é:

Sendo a resistência elétrica do fio R = 0,12 Ω e a corrente elétrica que atravessa o circuito i = 30 A, a tensão consumida pela resistência do fio é:

Logo, a tensão aplicada aos terminais da torneira é mais próxima de:

Alternativa:

82) (Livro do aluno-SEDUC-SP/2025 - UEA – SIS3 2022) Um medidor de tensão, V, e um medidor de corrente, A, ambos ideais, foram associados a um resistor, como é mostrado na figura.

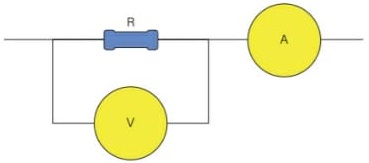
Ligando-se os extremos da montagem apresentada a um gerador, as leituras desses medidores possibilitaram a construção dos gráficos que se seguem.

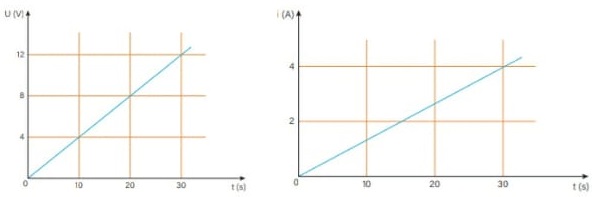
De acordo com as informações presentes nos gráficos, conclui-se que a resistência desse resistor é de:

(A) 1 Ω

(B) 3 Ω

(D) 16 Ω

(E) 24 Ω

Resolução:

Analisando os gráficos fornecidos, podemos determinar os valores de ddp e corrente elétrica em algum instante específico.

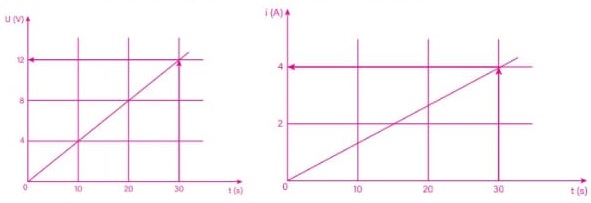
De acordo com os gráficos, no instante t = 30 s a ddp nos terminais do resistor é U = 12 V e a corrente elétrica que o atravessa é i = 4 A.

Aplicando a equação da resistência elétrica, concluímos que a resistência elétrica desse resistor é de:

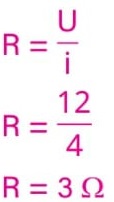
Alternativa: B

83) (Livro do aluno-SEDUC-SP/2025 - ENEM 2021) Cientistas da Universidade de New South Wales, na Austrália, demonstraram em 2012 que a lei de Ohm é válida mesmo para fios finíssimos, cuja área da seção reta compreende alguns poucos átomos. A tabela apresenta as áreas e comprimentos de alguns dos fios construídos (respectivamente com as mesmas unidades de medida). Considere que a resistividade mantém-se constante para todas as geometrias (uma aproximação confirmada pelo estudo)

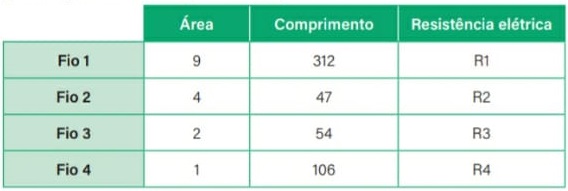
As resistências elétricas dos fios, em ordem crescente, são:

(A) R1 < R2 < R3 < R4.

(B) R2 < R1 < R3 < R4.

(D) R4 < R1 < R3 < R2.

(E) R4 < R3 < R2 < R1.

Resolução:

Como a resistividade ρ tem o mesmo valor para os 4 fios, então, com base nos resultados obtidos, as resistências elétricas dos fios, em ordem crescente, são R2 < R3 < R1 < R4.

Alternativa: C

84) (Livro do aluno-SEDUC-SP/2025 - ENEM 2020) Um estudante tem uma fonte de tensão com corrente contínua que opera em tensão fixa de 12 V. Como precisa alimentar equipamentos que operam em tensões menores, ele emprega quatro resistores de 100 Ω para construir um divisor de tensão. Obtém-se este divisor associando-se os resistores, como exibido na figura. Os aparelhos podem ser ligados entre os pontos A, B, C, D e E, dependendo da tensão especificada.

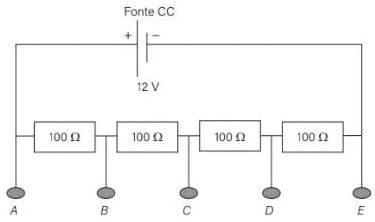
Ele tem um equipamento que opera em 9,0 V com uma resistência interna de 10 kΩ.

Entre quais pontos do divisor de tensão esse equipamento deve ser ligado para funcionar corretamente e qual será o valor da intensidade da corrente nele estabelecida?

(A) Entre A e C; 30 mA.

(B) Entre B e E; 30 mA.

(D) Entre B e E; 0,9 mA.

(E) Entre A e E; 0,9 mA.

Resolução:

Analisando a ilustração, podemos notar que os quatro resistores estão associados em série. Como têm valores iguais de resistência elétrica, as tensões elétricas entre terminais consecutivos são iguais também.

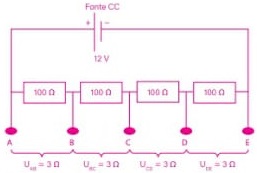
Como o equipamento do estudante opera em 9 V, ele precisa ser conectado aos pontos A e D ou B e E. Aplicando os valores de tensão e resistência elétricas à equação

Obtemos um valor de corrente elétrica igual a:

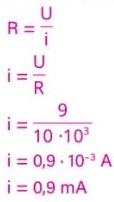
Alternativa: D

85) (Livro do aluno-SEDUC-SP/2025 - FUVEST 2023) Termistores são termômetros baseados na variação da resistência elétrica com a temperatura e são utilizados em diversos equipamentos, como termômetros digitais domésticos, automóveis, refrigeradores e fornos. A curva de calibração de um termistor é mostrada na figura:

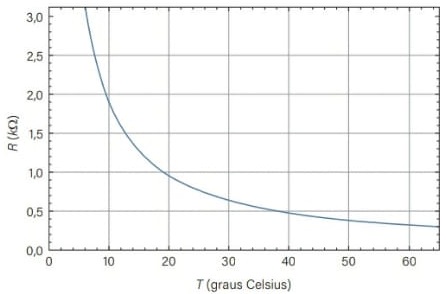
Considere que o termistor se rompa quando percorrido por uma corrente maior do que 10 mA. Supondo que o termistor seja conectado a uma bateria de 5 V, assinale a alternativa que contém uma faixa de temperaturas em que o dispositivo sempre funcionará adequadamente.

Note e adote: a relação entre a resistência R de um dispositivo, a corrente I que o percorre e a diferença de potencial elétrico V entre seus terminais é V = RI.

(A) 10 °C < T < 35 °C

(B) 20 °C < T < 45 °C

(D) 40 °C < T < 65 °C

(E) 50 °C < T < 75 °C

Resolução:

Analisando a equação fornecida pelo enunciado, se:

V = R · I

Então:

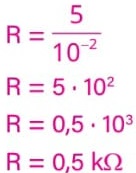
Como, com base na equação, corrente elétrica e resistência elétrica são inversamente proporcionais, associado ao valor máximo de corrente elétrica está um valor mínimo de resistência elétrica igual a:

Ou seja, para uma resistência R = 0,5 kΩ, uma corrente elétrica A = 10 mA atravessa o sistema, portanto, para o termistor funcionar adequadamente, a resistência elétrica precisa ser R > 0,5 kΩ.

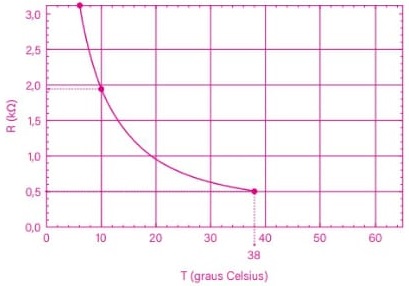
Analisando o gráfico, a temperatura correspondente à resistência elétrica:

R = 0,5 kΩ é T = 38 °C

A única alternativa que apresenta um intervalo abaixo de 38 °C é A: 10 °C < T < 35 °C.

Alternativa: A

86) (Livro do aluno-SEDUC-SP/2025 - UFPR 2025) Um aquecedor elétrico dissipa uma potência média P = 4,4 kW quando está ligado e sujeito a uma tensão ΔV = 220 V. Com base nesses dados, assinale a alternativa que apresenta corretamente o valor da intensidade da corrente elétrica i que circula pelo aquecedor quando ele está operando na condição descrita.

(A) i = 20 A

(B) i = 10 A

(D) i = √20 A

(E) i = 0,050 A

Resolução:

A potência elétrica de um aparelho elétrico pode ser definida, matematicamente, por:

P = i · U

Logo, a corrente elétrica que atravessa o aparelho pode ser calculada por:

É dito que o aquecedor elétrico dissipa uma potência média P = 4,4 kW, que em unidades do SI é P = 4,4 · 103 W. Também é dito que o aparelho está sujeito a uma tensão elétrica ΔV = 220 V. Logo, a corrente elétrica i que circula pelo aquecedor quando ele está operando na condição descrita é:

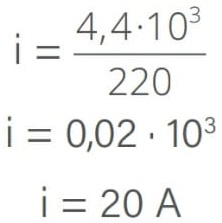
Alternativa: A

87) (Livro do aluno-SEDUC-SP/2025 - UFJF-PISM 3 2023) Para proteger um sistema elétrico de sobrecargas na rede, foi inserido um fusível na entrada de alimentação. Sabendo que a tensão de operação do sistema é de 110 V e fazendo um circuito equivalente, determina-se que a resistência total é de 55 ohms. Calcule a corrente máxima que o fusível deve suportar e a potência elétrica máxima que o equipamento dissipa.

(A) 1 A e 110 W

(B) 1,5 A e 165 W

(D) 1 A e 165 W

(E) 2 A e 165 W

Resolução:

Sabendo que a tensão de operação do sistema é U = 110 V e que a resistência elétrica total é R = 55 Ω, a corrente elétrica máxima que o fusível deve suportar é:

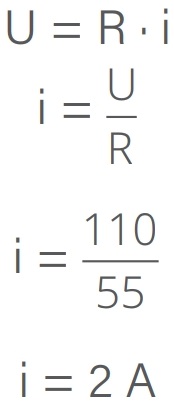
Partindo dos valores conhecidos, a potência elétrica máxima que o equipamento dissipa é:

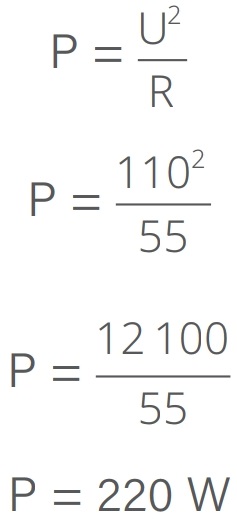
Alternativa: C

88) (Livro do aluno-SEDUC-SP/2025 - UEA-SIS 1 2024) Uma pessoa deixou seu computador ligado ininterruptamente durante 30 dias. Sabendo que a potência média desse computador é de 300 W, a quantidade de energia utilizada por ele nesse período, em kWh, foi de:

(A) 162

(B) 174

(D) 204

(E) 216

Resolução:

A potência elétrica é definida como a razão entre a quantidade de energia (ΔE) convertida por um componente elétrico e o intervalo de tempo correspondente (Δt):

Logo, a quantidade de energia convertida, ou, como o enunciado disse, “energia utilizada”, pode ser calculada por:

ΔE = P · Δt

Como o enunciado pede que a energia seja determinada em kW · h, é conveniente converter a potência e o tempo antes do cálculo.

Dessa forma:

Logo, a quantidade de energia consumida pelo computador neste período foi:

ΔE = 0,3 · 720

ΔE = 216 kW · h

Alternativa: E

89) (Livro do aluno-SEDUC-SP/2025 - UNESP 2025) Uma situação comum em residências antigas é a incompatibilidade entre os cabos elétricos instalados e a demanda atual de energia elétrica. Nessas residências, dispositivos de proteção podem interromper o circuito quando vários eletrodomésticos são ligados simultaneamente. A figura mostra a planta da cozinha e da lavanderia de uma residência antiga, em que a instalação elétrica é protegida por um disjuntor de 30 A.

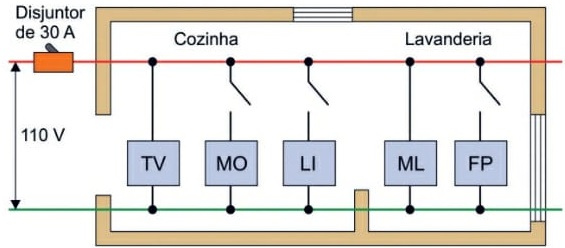
Nesses locais, já estão em funcionamento uma televisão (TV) e uma máquina de lavar roupas (ML).

Também constam dessa instalação um forno de micro-ondas (MO), um liquidificador (LI) e um ferro de passar (FP). As potências desses eletrodomésticos estão indicadas na tabela.

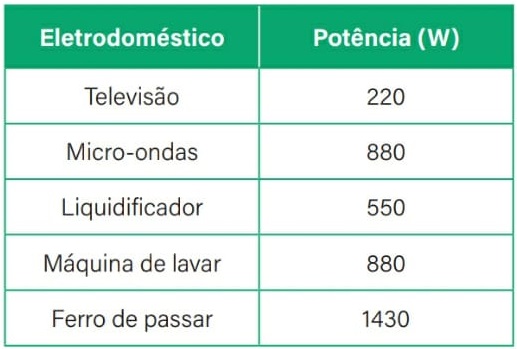
O disjuntor interromperá a corrente elétrica se, simultaneamente com a televisão e com a máquina de lavar:

(A) for ligado o forno de micro-ondas.

(B) forem ligados o forno de micro-ondas e o liquidificador.

(D) for ligado o ferro de passar.

(E) forem ligados o liquidificador e o ferro de passar.

Resolução:

Como a instalação elétrica é protegida por um disjuntor de 30 A, esse dispositivo interromperá a passagem de corrente elétrica caso sua intensidade supere esse valor. Logo, sendo i = 30 A a corrente máxima suportada pelo circuito e V = 110 V a tensão elétrica da rede, a potência máxima que o disjuntor suporta sem interromper a passagem de corrente elétrica é:

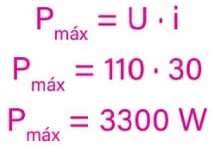
Analisando a tabela, podemos perceber que a televisão e a máquina de lavar juntas desenvolvem uma potência elétrica

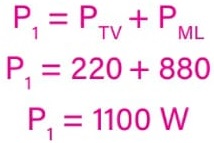
Logo, sendo P2 um valor de potência que o disjuntor ainda suporta, temos

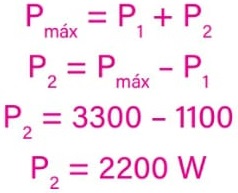
Ou seja, o disjuntor interromperá a passagem de corrente elétrica pelo circuito se a soma das potências dos equipamentos (fora a TV e a máquina de lavar) superar 2200 W.

Entre as opções fornecidas, o forno de micro-ondas e o ferro de passar juntos desenvolvem potência elétrica igual a:

P = 880 + 1430

P = 2310 W

Como P > P2, o disjuntor interromperá a corrente elétrica se, simultaneamente com a televisão e com a máquina de lavar, forem ligados o forno de micro-ondas e o ferro de passar.

Alternativa: C

90) (Livro do aluno-SEDUC-SP/2025 - UERJ 2025) Para determinar a potência dissipada por um equipamento industrial, verificou-se a relação entre a corrente elétrica i, em ampères, e a tensão U, em volts, aferidas no circuito. O valor da tensão x, correspondente à corrente de 5 A, não foi registrada, conforme indica o gráfico.

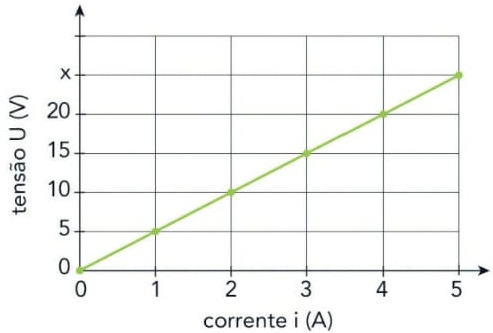
Nesse circuito, quando i = 5 A, a potência instantânea dissipada pelo equipamento, em watts, é igual a:

(A) 125

(B) 150

(D) 200

Resolução:

Como o gráfico é uma reta, podemos concluir que a resistência elétrica desse equipamento não varia com a tensão, pois a

razão U/I é constante. Logo, a resistência elétrica desse equipamento é:

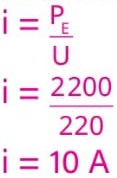
Como o valor da resistência elétrica é o mesmo para qualquer valor de tensão, a potência dissipada pelo equipamento

quando i = 5 A é:

Alternativa: A

91) (Livro do aluno-SEDUC-SP/2025 - ENEM PPL 2023) Lâmpadas incandescentes são constituídas de um filamento de tungstênio dentro de um bulbo de vidro com um gás a baixa pressão. Essas lâmpadas podem apresentar diferentes potências quando submetidas à mesma tensão elétrica. Um estudante precisa selecionar uma lâmpada que forneça o maior brilho, para isso deverá selecionar aquela que possui o filamento mais:

(A) curto, pois terá a menor resistência.

(B) comprido, pois terá a maior resistência.

(D) curto, pois terá a menor corrente elétrica.

(E) comprido, pois terá a menor resistividade

Resolução:

O filamento das lâmpadas incandescentes atua como um resistor. Logo, podemos determinar a potência elétrica de uma lâmpada dessas pela equação:

Podemos notar, então, que a potência elétrica de uma lâmpada incandescente é inversamente proporcional à resistência elétrica do filamento.

Já a resistência elétrica de um condutor, de acordo com a segunda lei de Ohm, é determinada por:

Ou seja, a resistência elétrica do filamento é diretamente proporcional ao seu comprimento.

Portanto para selecionar a lâmpada que fornece o maior brilho, ou seja, a lâmpada de maior potência, é necessário selecionar aquela que possui o filamento mais curto, pois terá a menor resistência.

Alternativa: A

92) (Livro do aluno-SEDUC-SP/2025 - UNESP 2020) O Programa Brasileiro de Etiquetagem (PBE) tem o objetivo de orientar o consumidor quanto ao consumo e à eficiência energética dos principais eletrodomésticos nacionais. A figura 1 ilustra a etiqueta de um chuveiro elétrico, apresentando a tensão nominal de funcionamento e as potências nominal e econômica (potência máxima e mínima do chuveiro). Em um banheiro, foram instalados esse chuveiro (C) e duas lâmpadas idênticas (L), de valores nominais (110 V – 60 W) cada, conforme a figura 2.

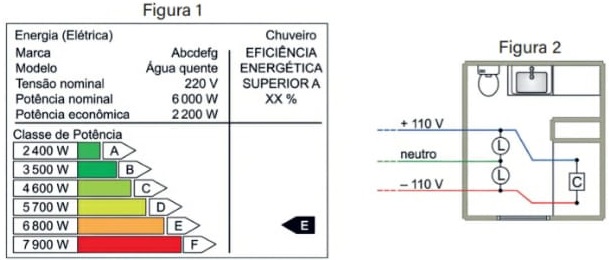
a) Calcule a intensidade da corrente elétrica, em ampères, que atravessa o chuveiro e determine a resistência elétrica, em Ω, desse chuveiro quando ele opera com sua potência econômica.

b) Considere que as duas lâmpadas desse banheiro fiquem acesas simultaneamente por 30 minutos e que, nesse intervalo de tempo, o chuveiro permaneça ligado por 20 minutos, operando com sua potência nominal. Admitindo que 1 kWh de energia elétrica custe R$ 0,50, calcule o gasto, em reais, gerado nos 30 minutos desse banho, devido ao funcionamento do chuveiro e das lâmpadas.

Resolução:

De acordo com o enunciado, a tensão nominal à qual o chuveiro está submetido é U = 220 V e sua potência econômica é PE = 2200 W.

Como: P = U · i então a intensidade da corrente elétrica que atravessa o chuveiro quando ele opera com potência

econômica é:

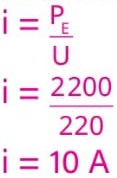
Logo, a resistência elétrica do chuveiro para as condições descritas é:

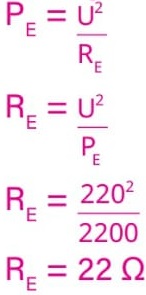
Como o custo pelo consumo da energia elétrica é R$ 0,50 para cada kW · h, é conveniente determinar a energia elétrica consumida na situação descrita nessa unidade. Calculando a energia consumida pelas lâmpadas, obtemos:

Calculando a energia consumida pelo chuveiro, obtemos:

Logo, o consumo total de energia pelos aparelhos, nos intervalos descritos, foi:

Como cada kW · h custa R$ 0,50, o gasto (G) gerado nos 30 minutos desse banho, devido ao funcionamento do chuveiro e das lâmpadas, foi:

topo