Professor Diminoi
PLANIFICAÇÃO DE SÓLIDOS GEOMÉTRICOA
A planificação de um sólido geométrico é a figura geométrica plana formada pela superfície desse sólido. Ou seja é a apresentação de todas as formas que constituem sua superfície em um plano, ou seja, em duas dimensões. Essas planificações são usadas de várias maneiras, como para calcular a área da superfície de um sólido.
Planificação de um dado
Conhecemos como planificação de um sólido geométrico a representação de todas as suas faces em forma bidimensional, permitindo visualizar o todo do sólido. Utilizamos a planificação também como molde para a criação desses sólidos.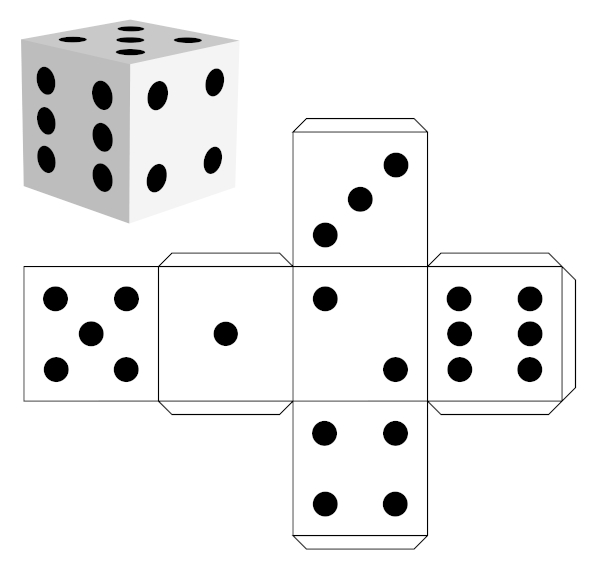 Planificação do Cubo
Planificação do Cubo
O cubo é uma das formas bastante comuns no nosso dia a dia. O dado, por exemplo, possui formato de um cubo, assim como o cubo mágico e caixas. O cubo é composto por 12 arestas, 6 faces quadradas e 8 vértices.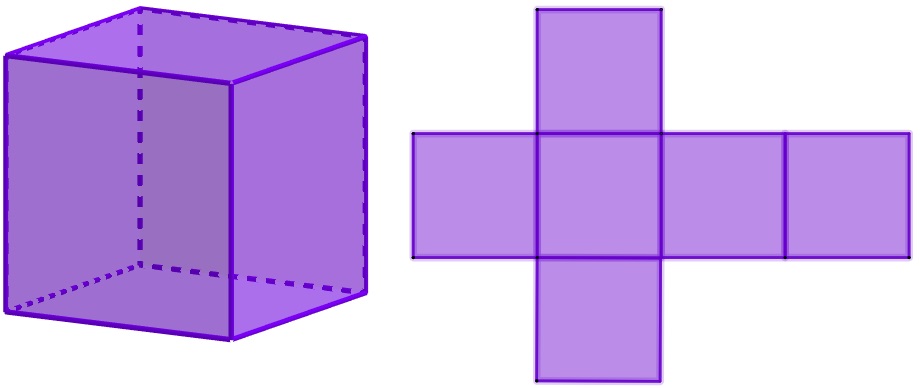

Planificação do Paralelepípedos
O paralelepípedo pode ser identificado em caixas de sapato, tijolos, entre outros. Ele possui 6 faces (formadas por quadriláteros no formato de paralelogramos), 12 arestas e 8 vértices.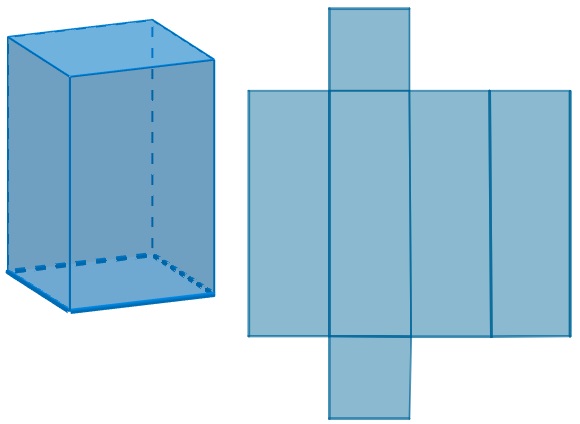

Planificação de Prismas
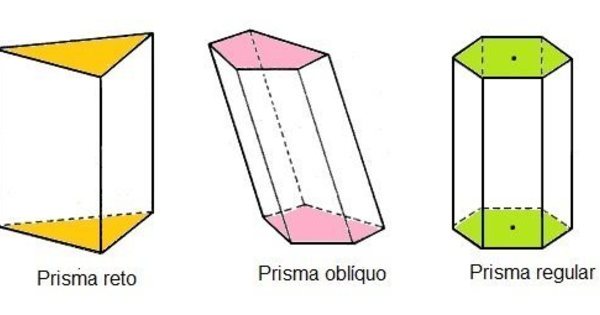
De forma geral, o prisma é um polígono que possui duas bases iguais, ligadas pelas faces laterais. Essas bases podem ter vários formatos, como triângulos, quadrados, pentágonos, hexágonos, entre outros. O número de faces, arestas e vértices depende da base. Ele também é muito comum no nosso dia a dia, já que existem caixas que possuem formatos diferentes em suas bases.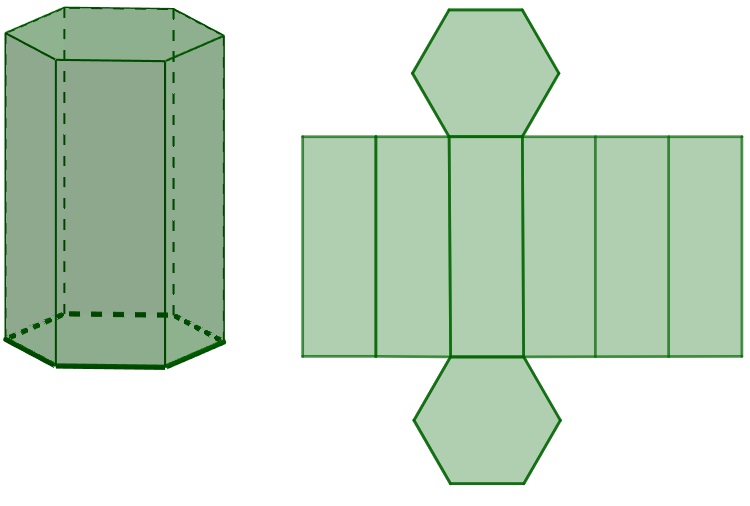


Planificação de pirâmides
As pirâmides também podem possuir bases diferentes, que podem ser triangulares, quadradas, pentagonais, entre outras. A planificação também depende da base da pirâmide, assim como o número de faces, vértices e arestas. As pirâmides do Egito, por exemplo, possuem base quadrada.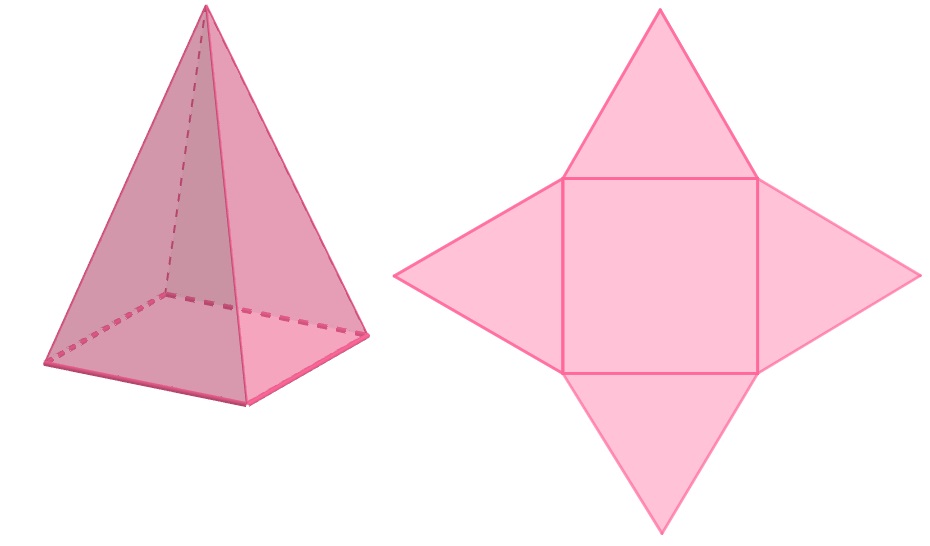

Planificação de Cilindros
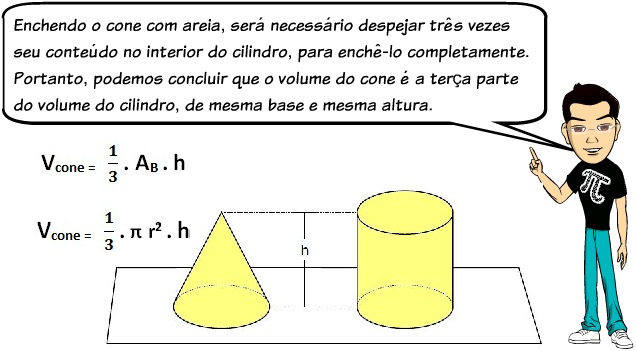
O cilindro é um corpo redondo e é igualmente comum no nosso dia a dia. Essa é a forma geométrica de latas de refrigerante, canos, entre outros objetos. O cilindro possui duas bases no formato de círculo, e sua face lateral tem o formato de um retângulo. Em sólidos arredondados, não faz sentido falarmos de números de faces e arestas, já que elas são arredondadas.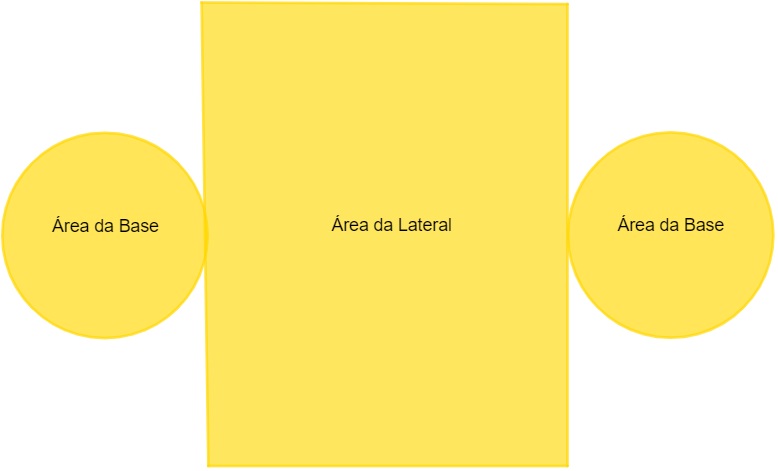 O cilindro é um sólido formado por duas bases circulares congruentes e por uma superfície curva, como mostra a figura anterior. Essa figura pode ser compreendida como um retângulo ou um paralelogramo que foi “enrolado”.
O cilindro é um sólido formado por duas bases circulares congruentes e por uma superfície curva, como mostra a figura anterior. Essa figura pode ser compreendida como um retângulo ou um paralelogramo que foi “enrolado”.
Planificação de Cones
O cone possui uma base circular, e sua área lateral possui formato de um arco. Objetos como casquinha de sorvete, chapéu de aniversário, entre outros, possuem formato de um cone.
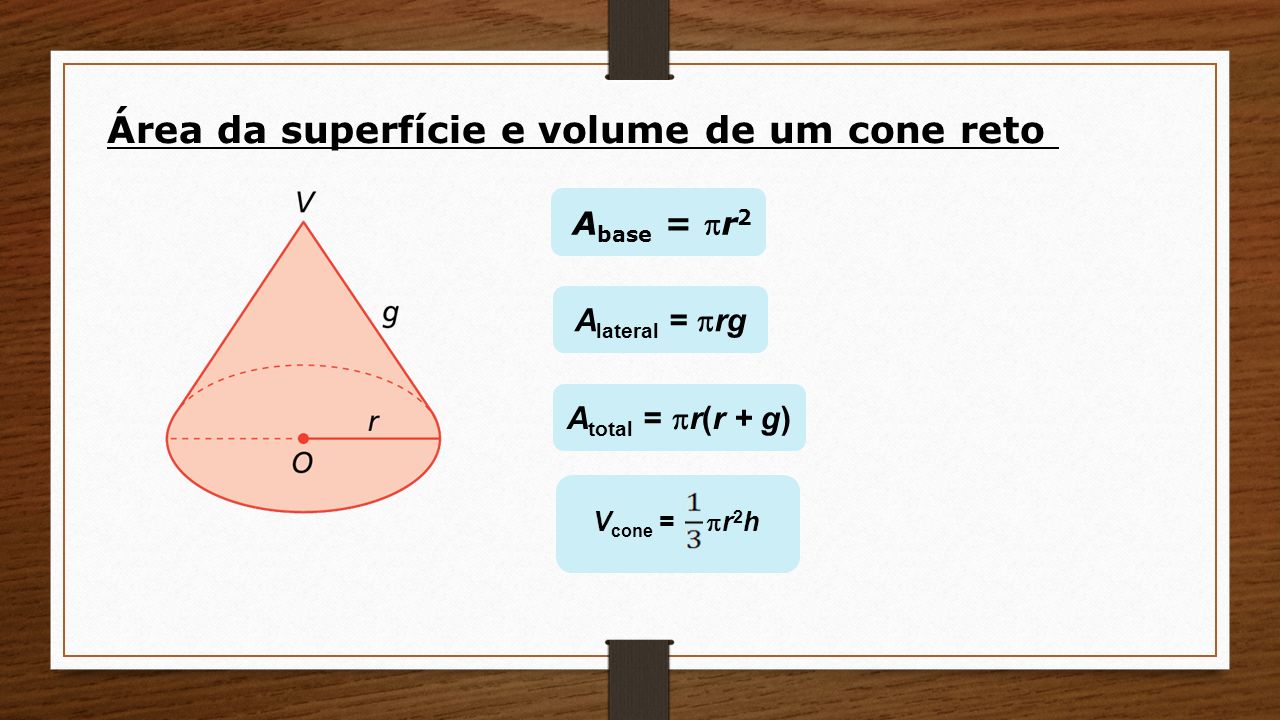
Conhecendo a planificação de um cone, calcular a área total é somar a área lateral com a área da base.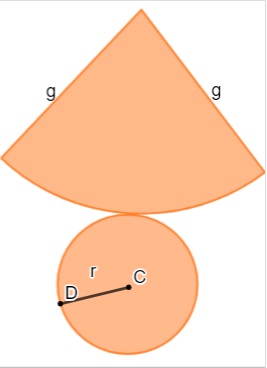 Como a base do cone é um círculo, a área da base é calculada a partir da fórmula:
Como a base do cone é um círculo, a área da base é calculada a partir da fórmula:
Ab = πr²
Para calcular a área lateral, precisamos conhecer ou encontrar o valor da geratriz g do cone. Ela pode ser calculada pelo Teorema de Pitágoras:
g² = r²+ h²
Já a área lateral que é um setor circular é calculada por:
Al = π . r . g
Então, a área total do cone é a soma de Ab + Al:
AT = r(πr + g)
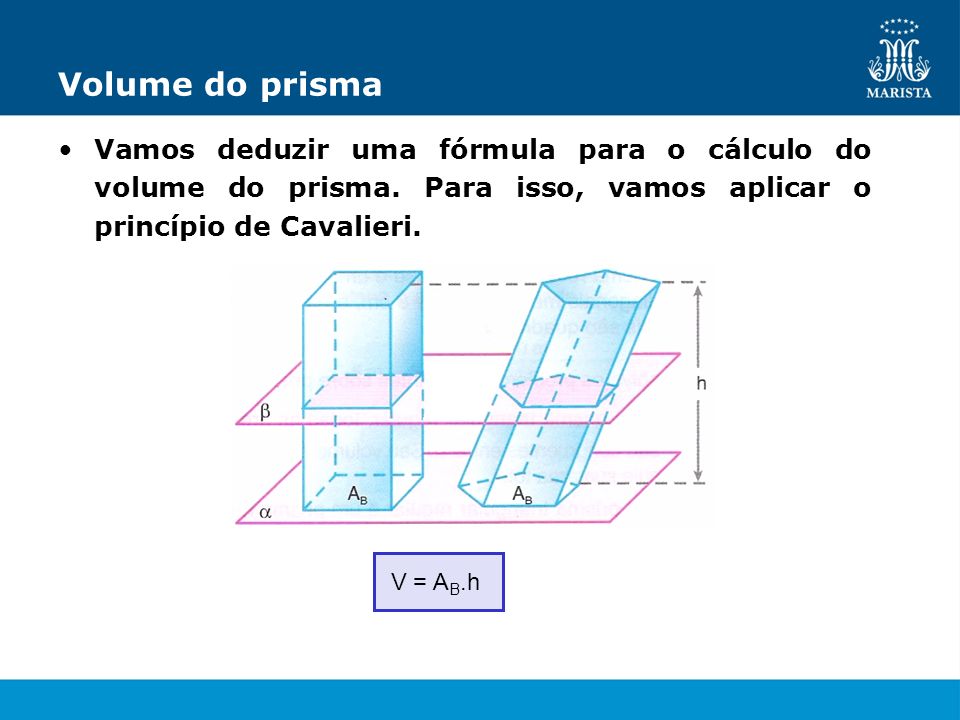
Prisma de base pentagonal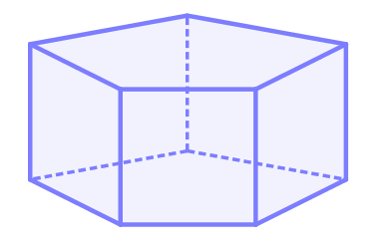 O prisma é um sólido geométrico formado por duas bases poligonais congruentes e por faces laterais que são paralelogramos.
O prisma é um sólido geométrico formado por duas bases poligonais congruentes e por faces laterais que são paralelogramos.
O número de paralelogramo presentes na planificação do prisma é igual ao número de lados de uma de suas bases. Além disso, na planificação, aparecerão dois polígonos congruentes, que são as bases. A figura a seguir mostra a planificação de um prisma de base pentagonal: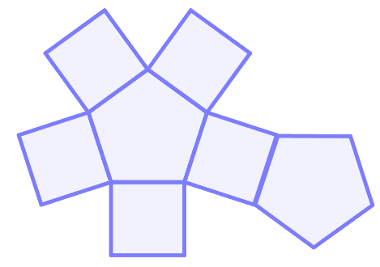
Como o número de paralelogramos é igual ao número de lados da base do prisma, um prisma de base octogonal possui oito paralelogramos em sua planificação. Esses paralelogramos não necessariamente são congruentes, apenas nos casos em que o prisma é reto.
Nos prismas, a quantidade de faces laterais também é igual ao número de lados de uma de suas bases. Sendo assim, sua planificação sempre apresenta dois polígonos congruentes e alguns paralelogramos, que só serão todos iguais se as bases do prisma forem regulares.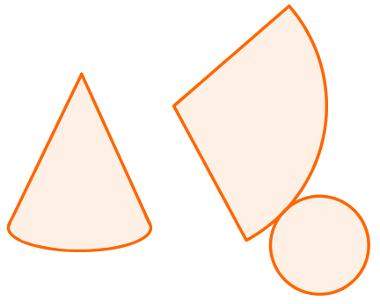 A área dos cones pode ser encontrada pela seguinte expressão:
A área dos cones pode ser encontrada pela seguinte expressão:
A = πr(g + r)
Na fórmula, r é o raio do cone e g é a geratriz. Mais detalhes sobre essa fórmula podem ser encontrados.
Como calcular a área de um Cone
A área do cone é calculada somando-se a área da base com a área lateral. Para calcular a área da base é o mesmo que calcular a área de uma circunferência. Para calcular a área lateral precisamos planificar a lateral cônica sobre um plano.
Panificação do Cone
A planificação do cone nada mais é do que abrir a lateral do cone de forma que ela fique sobre um plano e não mais no espaço.
Ao abrirmos a lateral do cone, obtemos uma figura com um raio g e uma parte curva com comprimento l.
Onde:
l = 2 . π . r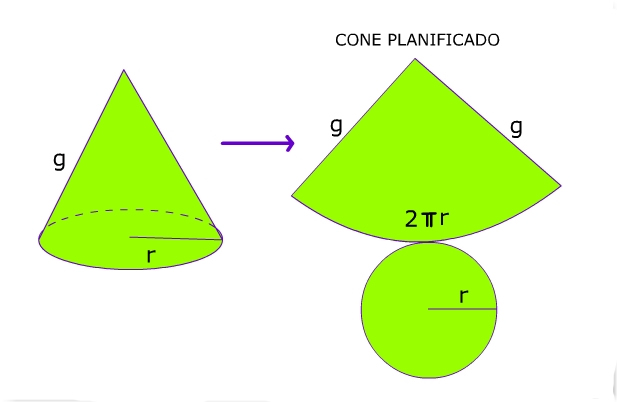
Elementos da panificação do Cone
Quando abrimos a lateral do cone e colocamos num plano, obtemos uma figura com uma parte circular com os seguintes elementos:
Raio: o raio g da figura em questão é a geratriz do cone;
Comprimento do arco: o setor circular da figura possui comprimento igual 2πr, que é igual ao perímetro da base do cone, ou seja, o perímetro de uma circunferência.
Fórmula da área do Cone
Agora que já temos conhecimento suficiente, podemos apresentar a fórmula para calcular a área.
Para calcular a área do cone como um todo precisamos aprender a calcular a área da base e da lateral do cone.
Área da base
A área da base do cone é calculada da mesma forma que a área de uma circunferência. Então, a área da base é calculada pela seguinte fórmula:
Ab = π . r²
Onde:
Π = número pi (3,14);
R = raio da circunferência da base.
Área lateral
A área lateral do cone equivale a medida da superfície cônica. Para calcular a área lateral usamos a seguinte fórmula:
Al = π . r . g
Onde:
Π = número pi (3,14);
R = raio da base;
G = medida da geratriz que forma a lateral cônica.
Área total
A área total é calculada somando-se a área da base com a área lateral. Então, para calcular a área total usamos a seguinte fórmula:
At = π . r . (g + r)
Onde:
Π = número pi (3,14);
R = raio da base;
G = medida da geratriz.
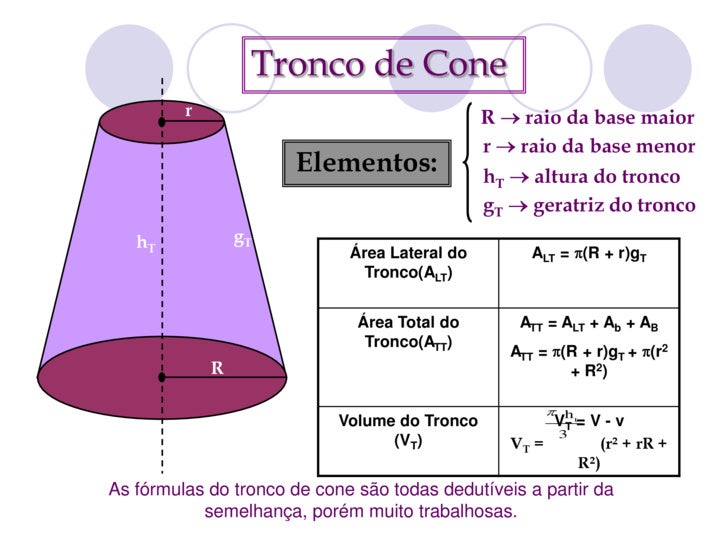
Área do troco do Cone
Se cortarmos uma parte do cone, obtemos um cone contendo duas bases: uma parte contém o vértice do cone, chamada de base menor e a outra contém a base do cone, chamada de base maior.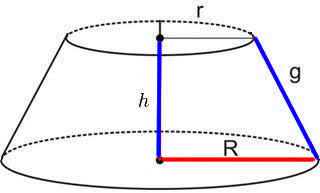
Corpos redondos
O cilindro o cone e a esfera são corpos redondos.
Os corpos redondos, também chamados de sólidos de revolução, são objetos de estudo da geometria espacial. Eles são sólidos geométricos que possuem superfícies arredondadas e estão bastante presentes no nosso dia a dia, em objetos como uma bola de futsal, um chapéu de aniversário, uma lata de refrigerante etc.
Os sólidos geométricos considerados corpos redondos são a esfera, o cilindro e o cone. Cada um deles possui fórmulas específicas para o cálculo de sua área total e volume.
Chamamos de corpos redondos os sólidos geométricos que possuem suas superfícies curvas. Eles também são conhecidos como sólidos de revolução, por serem construídos a partir da rotação de uma figura plana.
Os corpos redondos são bastante presentes no nosso dia a dia, é possível percebê-los numa lata de refrigerante, que possui o formato cilíndrico; numa bola de futebol, que possui formato esférico; e também num chapéu de festa infantil ou nos cones utilizados pelo departamento de trânsito possuem formatos de cone.
Esfera
Diferente dos sólidos anteriores, a esfera não possui uma base circular. Ela é construída a partir da rotação de uma semicircunferência. A esfera é um corpo redondo construído a partir da rotação de um círculo. Para calcular o volume da esfera é necessário conhecer somente o raio:
A esfera é um corpo redondo construído a partir da rotação de um círculo. Para calcular o volume da esfera é necessário conhecer somente o raio:![]() Já a área total da esfera pode ser calculada por:
Já a área total da esfera pode ser calculada por:
AT = 4πr²
Planificação de Sólidos Geométricos - Resolvidos
01) (Prova Brasil) Fabiana trabalha numa fábrica de caixas. Observe as caixas que Fabiana fabricou. As caixas mais vendidas para colocar bombons têm a forma de cubos e paralelepípedos. Quais são elas?
As caixas mais vendidas para colocar bombons têm a forma de cubos e paralelepípedos. Quais são elas?
(A) Tipo I e II
(B) Tipo I e III
(C) Tipo II e III
(D) Tipo II e IV
Alternativa: A
02) (Prova Brasil) Observe o bumbo que Beto gosta de tocar. Ele tem a forma de um cilindro.
(A) 
(B) 
(C ) 
(D) 
Alternativa: D
03) (Prova Brasil) Mariana colou diferentes figuras numa página de seu caderno de Matemática, como mostra o desenho abaixo. Essas figuras têm em comum
Essas figuras têm em comum
(A) o mesmo tamanho.
(B) o mesmo número de lados.
(C) a forma de quadrado.
(D) a forma de retângulo.
Alternativa: B
04) (Prova Brasil) Chegando a uma cidade, Fabiano visitou a igreja local. De lá, ele se dirigiu à pracinha, visitando em seguida o museu e o teatro, retornando finalmente para a igreja. Ao fazer o mapa do seu percurso, Fabiano descobriu que formava um quadrilátero com dois lados paralelos e quatro ângulos diferentes. O quadrilátero que representa o percurso de Fabiano é um
O quadrilátero que representa o percurso de Fabiano é um
(A) quadrado.
(B) losango.
(C) trapézio.
(D) retângulo.
Alternativa: C
05) (Prova Brasil) O desenho abaixo representa um sólido. Uma possível planificação desse sólido é
Uma possível planificação desse sólido é

(B) 
(C) 
(D) 
Alternativa: B
06) Das alternativas a seguir sobre os poliedros, assinale aquela que for correta:
(A) Um poliedro é um sólido geométrico limitado por qualquer tipo de superfície.
(B) Os elementos dos poliedros são os mesmos elementos dos polígonos, uma vez que ambos possuem vértices.
(C) Prismas são poliedros que possuem duas bases poligonais e todas as faces laterais com formato de paralelogramo.
(D) Prismas e pirâmides são os únicos exemplos de poliedros existentes.
(E) As esferas são poliedros.
Resolução:
A) Incorreta!
Um poliedro é um sólido geométrico limitado por polígonos, ou seja, por figura planas. Os poliedros não podem ser limitados por curvas.
B) Incorreta!
Os poliedros e polígonos possuem em comum os vértices e os segmentos de reta. Entretanto, nos polígonos, esses segmentos são chamados de lados e, nos poliedros, de arestas. Além disso, os polígonos não possuem faces, que são elementos dos poliedros.
C) Correta!
D) Incorreta!
Existe uma terceira classe de poliedros, que são aqueles que não são prismas nem pirâmides. Um exemplo deles são os troncos de pirâmides.
E) Incorreta!
As esferas não são poliedros porque não são limitadas por polígonos.
Alternativa: C
07) Observe o sólido geométrico a seguir e assinale a alternativa correta: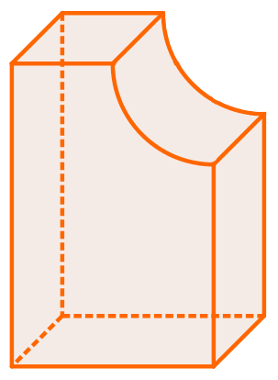 (A) É um prisma, pois possui duas bases e faces laterais planas.
(A) É um prisma, pois possui duas bases e faces laterais planas.
(B) É uma pirâmide, pois afunila em sua parte superior.
(C) É um cilindro, pois possui uma parte arredondada.
(D) É um corpo redondo, pois possui uma parte arredondada.
(E) Nenhuma das alternativas anteriores está correta.
Resolução:
O sólido em questão não é prisma nem pirâmide, pois possui uma parte arredondada, o que não é encontrado nos sólidos. Também não é cilindro, uma vez que as “bases” de um cilindro são círculos. Além disso, não é um corpo redondo, pois esse tipo de sólido possui a característica de rolar se colocado em uma superfície plana levemente inclinada. O sólido em questão não rola, independentemente do modo como for colocado.
Assim, nenhuma das alternativas está correta.
Alternativa: E
08) (ENEM) João propôs um desafio a Bruno, seu colega de classe: ele iria descrever um deslocamento pela pirâmide a seguir e Bruno deveria desenhar a projeção desse deslocamento no plano da base da pirâmide..jpg) O deslocamento descrito por João foi: mova-se pela pirâmide, sempre em linha reta, do ponto A ao ponto E, a seguir, do ponto E ao ponto M e, depois, de M a C.
O deslocamento descrito por João foi: mova-se pela pirâmide, sempre em linha reta, do ponto A ao ponto E, a seguir, do ponto E ao ponto M e, depois, de M a C.
O desenho que Bruno deve fazer é: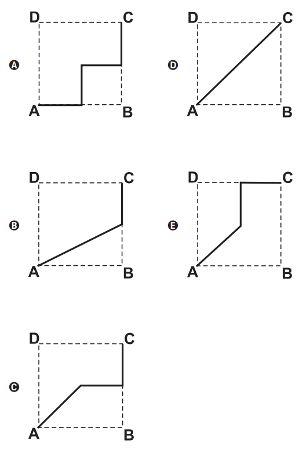
Resolução:
A vista superior dessa pirâmide é a seguinte: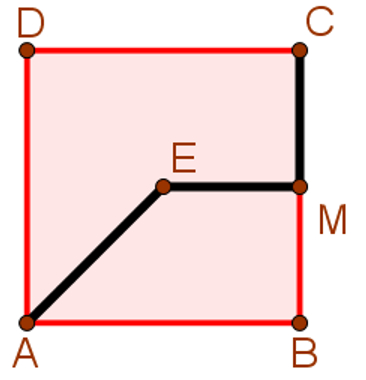
Observe que as ligações propostas por João já foram feitas sobre a vista superior dessa pirâmide. A alternativa que mais se assemelha a essa resposta é a letra C.
Alternativa: C
09) A planificação de um sólido geométrico é uma figura geométrica bidimensional formada pela superfície de objetos tridimensionais. Assim, a planificação de uma pirâmide de base pentagonal será formada por:
(A) Dois pentágonos e cinco retângulos congruentes.
(B) Dois pentágonos e cinco retângulos.
(C) Um pentágono e cinco triângulos congruentes.
(D) Um pentágono e cinco triângulos.
(E) Um pentágono e cinco triângulos equiláteros.
Resolução:
A) Incorreta, pois o sólido geométrico formado por dois pentágonos e cinco retângulos congruentes é o prisma de base pentagonal.
B) Incorreto, uma vez que o sólido geométrico formado por dois pentágonos e cinco retângulos quaisquer também é um prisma.
C) Incorreta. Embora uma pirâmide de base pentagonal seja formada por um pentágono e cinco triângulos, não há garantia de que eles sejam congruentes neste exercício.
D) Correta. Como o exercício não se refere ao formato da pirâmide, devemos assumir que os triângulos, os quais serão suas faces, possuem formas diversas.
E) Incorreta. Neste exercício, não foi informado se os triângulos são equiláteros.
Alternativa: D
10) A planificação de um sólido geométrico é uma figura geométrica plana obtida a partir da superfície do sólido em questão. Assinale, das alternativas a seguir, aquela que contém as figuras bidimensionais obtidas da planificação do cone reto.
(A) Um triângulo e uma circunferência.
(B) Um triângulo e um círculo.
(C) Um setor circular e uma circunferência.
(D) Um setor circular e um círculo.
(E) Um setor circular e um triângulo.
Resolução:
A planificação do cone terá como resultado as seguintes figuras: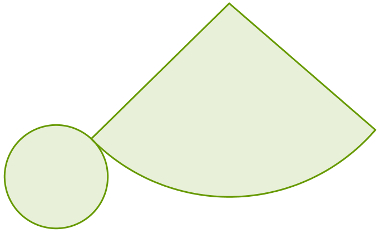
Observando essa planificação, podemos notar que as figuras obtidas são um setor circular e um círculo.
Alternativa: D
11) Qual das imagens abaixo é a melhor planificação do prisma oblíquo?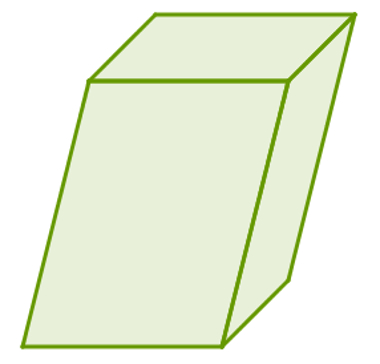
.jpg)
Resolução:
Observe que o prisma é oblíquo, mas nem todas as suas faces laterais são paralelogramos quaisquer. A face lateral direita é um retângulo, e a face frontal é um paralelogramo. A única alternativa que intercala paralelogramos e retângulos é a letra A.
Alternativa: A
12) (ENEM) Uma empresa que embala seus produtos em caixas de papelão, na forma de hexaedro regular, deseja que seu logotipo o seja impresso nas faces opostas pintadas de cinza, conforme a figura: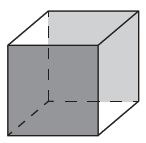 A gráfica que fará as impressões dos logotipos apresentou as seguintes sugestões planificadas:
A gráfica que fará as impressões dos logotipos apresentou as seguintes sugestões planificadas: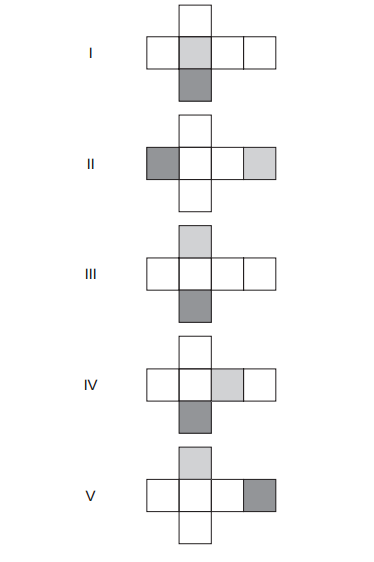
Que opção sugerida pela gráfica atende ao desejo da empresa?
(A) I
(B) II
(C) III
(D) IV
(E) V
Resolução
Alternativa C. Analisando as planificações, a alternativa que possui duas faces opostas pintadas é a III, que, ao construir o cubo, respeita as características solicitadas pela empresa. Quanto às demais, ao formarem a caixa, as faces pintadas ficariam uma ao lado da outra, contrariando o pedido da empresa.
Alternativa: C
18) Sabe-se que o raio da Terra equivale a 6371 km. Com essa informação, calcule a área superficial do planeta Terra.
Resolução:
Como a Terra é uma esfera, então podemos utilizar a fórmula da esfera para calcular a área superficial de um objeto esférico:
A = 4πr² = 4 . 3,14159 . 6.371² = 510.064.041,1 km²
Portanto, a área superficial da Terra é de aproximadamente: 510.064.041,1 km²
Observação: Entendimento para a resolução da questão 19.
Cilindros em sua planificação, temos dois círculos e um retângulo. 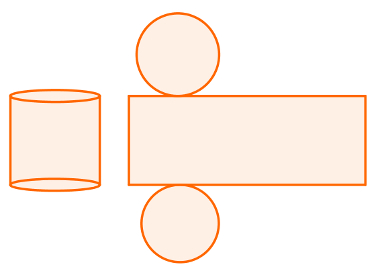 A área do cilindro é determinada pela soma das áreas das duas bases e da superfície lateral. Sabendo que essas figuras são dois círculos congruentes e um retângulo, podemos realizar a seguinte soma:
A área do cilindro é determinada pela soma das áreas das duas bases e da superfície lateral. Sabendo que essas figuras são dois círculos congruentes e um retângulo, podemos realizar a seguinte soma:
A = 2AC + AR
A = 2πr2 + bh
Nessa fórmula, r é o raio do cilindro, h é a sua altura e b é a base do retângulo obtido na planificação. Essa base é exatamente o comprimento do círculo: 2πr.
A = 2πr2 + 2πrh
A = 2πr(r + h)
19) Um cilindro possui base circular cujo raio é 2 cm e a altura é 10 cm. Calcule sua área.
Resolução:
substituindo na fórmula acima os valores dados e considerando π = 3,14, teremos:
A = 2πr(r + h)
A = 2·3,14·2·(2 + 10)
A = 12,56·12
A = 150,72 cm2
20) (UDESC) Uma bola esférica é composta por 24 faixas iguais, como indica a figura.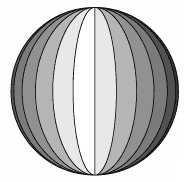 Sabendo-se que o volume da bola é de 2304 π cm³ então a área da superfície de cada faixa é de:
Sabendo-se que o volume da bola é de 2304 π cm³ então a área da superfície de cada faixa é de:
(A)20π cm²
(B)24π cm²
(C)28π cm²
(D)27π cm²
(E)25π cm²
Resolução
1º Passo: Encontrar o raio da esfera.
Conhecendo o volume, vamos calcular o raio da esfera.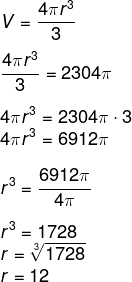
2º passo: calcular a área total, sabendo que o raio mede 12 cm.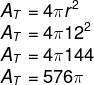
3º passo: calcular a área de uma faixa.
576π : 24 = 24π cm²
Alternativa B
21) Qual é a razão entre o volume de um cone e o volume de um cilindro que possuem a mesma altura?
(A) 1/3
(B) 2/3
(C) 3/1
(D) 3/2
(E) 1/6
Resolução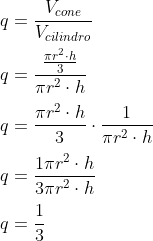
Alternativa A
22) Calcule a área lateral, a área da base e a área total de um cone circular reto com as seguintes medidas:
Altura: 5 cm
Raio: 2 cm
Resolução:
Área lateral:
Para calcular a área lateral precisamos encontrar a medida da geratriz. Para isso, vamos aplicar o teorema de Pitágoras:
g² = r² + h²
g² = 2² + 5²
g² = 4 + 25
g² = 29 ⇒
g = √29 ⇒
g = 5,4 cm
Com a medida da geratriz em mãos podemos calcular a área da lateral, para isso vamos aplicar a fórmula:
Al = π . r . g
Al = π . 2 . 5,4 ⇒ Al = 10,8π cm²
Área da base:
Na área da base aplicamos a seguinte fórmula:
Ab = π . r²
Ab = π . 2²
Ab = 4π cm²
Área total:
A área total é a soma das área lateral e da base:
At = Ab + Al
At = (4 + 10,8)π
At = 14,8π cm²
Poderíamos aplicar a fórmula, mas estaríamos fazendo trabalho repetido. Veja:
At = π . r .(g + r)
At = π . 2 . (5,4 + 2)
At = π . 2 . 7,4
At = 14,8π cm²
23) Qual é a área de um cone cuja geratriz mede 10 cm e o raio mede 5 cm?
Resolução:
Substitua esses dados na fórmula acima e considere π = 3,14.
A = πr(g + r)
A = 3,14·5(10 + 5)
A = 15,7·15
A = 235,50 cm2
24) Qual é a área de um cone cuja geratriz mede 10 cm e o raio mede 5 cm?
Resolução:
Substitua esses dados na fórmula acima e considere π = 3,14.
A = πr(g + r)
A = 3,14·5(10 + 5)
A = 15,7·15
A = 235,50 cm2
25) Qual a área da planificação de um cone reto cuja geratriz mede 100 cm e cujo raio mede 25 cm?
(A) 9812,5 cm2
(B) 10812,5 cm2
(C) 11812,5 cm2
(D) 12812,5 cm2
(E) 13812,5 cm2
Resolução:
Para resolver o exercício, basta substituir os dados na fórmula da área do cone:
A = πr(g + r)
A = 3,14·25·(100 + 25)
A = 78,5·(125)
A = 9812,5 cm2
Alternativa: A
26) (Prova Brasil - 9 Ano) Observe a caixa representada abaixo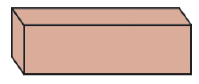 Uma planificação dessa caixa é:
Uma planificação dessa caixa é:
Alternativa: C
27) (Prova Brasil - 9 Ano) A forma geométrica espacial que pode ser associada à planificação abaixo é: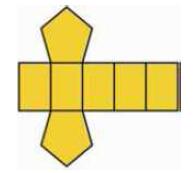 (A) um cilindro
(A) um cilindro
(B) uma pirâmide de base pentagonal
(C) um prisma de base pentagonal
(D)um paralelepípedo
Alternativa: C
28) (Prova Brasil - 9 Ano) As figuras 1, 2 e 3 correspondem, respectivamente, às planificações dos sólidos: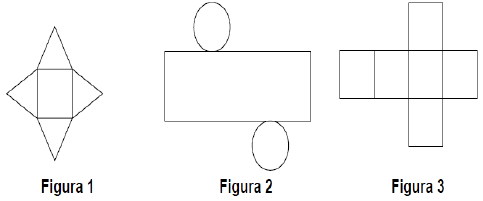 (A) Cubo, cone, pirâmide
(A) Cubo, cone, pirâmide
(B) Pirâmide, cilindro, cubo
(C) Cubo, cilindro, pirâmide
(D) Pirâmide, cone, cubo
Alternativa: B
29) (Prova Brasil - 9 Ano) Observe abaixo o modelo de um cubo. Ele tem 11 planificações diferentes, isto é, existem 11 diferentes moldes possíveis para se montar um cubo, por meio de dobradura.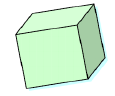 Identifique dentre as alternativas abaixo, uma dessas planificações:
Identifique dentre as alternativas abaixo, uma dessas planificações:
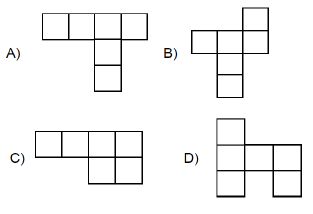
Alternativa: B
30) (Prova Brasil - 9 Ano) Observe as circunferências abaixo: Agora assinale a alternativa correta.
Agora assinale a alternativa correta.
(A) O valor de pi (π ) na circunferência I é maior que na circunferência II e III
(B) O valor de pi (π ) na circunferência III é maior que nas circunferências I e II
(C) O valor de pi (π ) na circunferência III é igual à soma dos valores de pi (π ) das circunferências I e II
(D) O valor de pi (π ) é o mesmo em todas as circunferências
Alternativa: D
31) (Prova Brasil - 9 Ano) Determinar área e perímetro de uma figura utilizando composição e decomposição de figuras. A figura a seguir é formada por um quadrado, cujo lado mede 6 cm, e um retângulo, cujos lados medem 10 cm e 4 cm.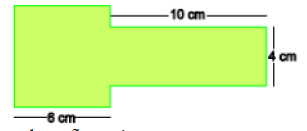 A medida do perímetro dessa figura é:
A medida do perímetro dessa figura é:
(A) 56 cm
(B) 44 cm
(C) 40 cm
(D) 12 cm
Alternativa: B
32) (Prova Brasil - 9 Ano) A figura abaixo representa o salão de festa de um clube formado por quatro lados iguais a 6 m. Para reformar esse espaço, o orçamento do trabalho de um pedreiro depende do valor do perímetro e da área do salão.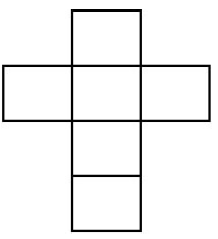 Assinale a alternativa que mostra corretamente e nessa ordem, as medidas do perímetro e da área em metros quadrados.
Assinale a alternativa que mostra corretamente e nessa ordem, as medidas do perímetro e da área em metros quadrados.
(A)36 e 180
(B)72 e 180
(C)48 e 30
(D)72 e 36
Alternativa: A
33) (Prova Brasil - 9 Ano) O copo de água da figura abaixo é dividido em três partes iguais por linhas pontilhadas. A fração do copo com água é:
A fração do copo com água é:
(A) 1/2
(B) 2/3
(C) 1/3
(D) 1/4
Alternativa: B
34) (Prova Brasil - 9 Ano) Uma loja vende botijões térmicos para bebidas em dois tamanhos.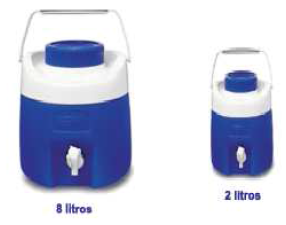 O botijão com capacidade para 8 litros é vendido por R$ 56,00. Se o preço dos botijões for proporcional à capacidade, o preço do botijão de 2
O botijão com capacidade para 8 litros é vendido por R$ 56,00. Se o preço dos botijões for proporcional à capacidade, o preço do botijão de 2
litros é:
(A) R$ 50,00
(B) R$ 28,00
(C) R$ 20,00
(D) R$14,00
Alternativa: D
35) (Prova Brasil - 9 Ano) Uma pessoa, para manter-se saudável, precisa fazer caminhadas, dando dois passos a cada metro percorrido. Mantendo-se nesse ritmo, quantos metros ela percorre após 500 passos dados?
Resposta: 250m
Continua...