Professor Diminoi
GRANDEZAS DIRETAMENTE E INVERSAMENTE PROPORCIONAIS
Grandezas
Grandeza em matemática é tudo aquilo que pode ser medido, contado ou observado.
As grandezas podem ser escalares ou vetoriais, e podem ser comparadas entre si, classificando-as como diretamente proporcionais ou inversamente proporcionais.
Grandezas escalares
Massa,
Temperatura
Distância
Área
Volume
Tempo.
Grandezas vetoriais para serem compreendidas necessitam de:
Módulo
Direção
Sentido
Grandezas diretamente proporcionais
Quando duas grandezas variam na mesma taxa, ou proporção
Exemplos:
a) Consumo de combustível e quilômetros percorridos por um veículo.
b) Quantidade de tijolos e área de uma parede.
c) Desconto dado em um produto e o valor final pago.
d) Número de torneiras de mesma vazão e tempo para encher uma piscina.
Exemplo com valores numéricos:
Se um carro percorre 100 km a uma velocidade de 50 km/h, qual seria a distância percorrida por ele se estivesse a 75 km/h?
Resolução:
50 — 100
75 — x
Nesse caso, a relação está montada de maneira diretamente proporcional, já que a distância aumentará quando aumentarmos a velocidade do veículo. A resolução da equação é feita de maneira simples, cruzando as variáveis.
50x = 100 . 75
x = 7500 ÷ 50
x = 150 km
Grandezas inversamente proporcionais
Quando uma grandeza aumente na outra diminui ou vice-versa.
Exemplo com valores numéricos:
Um veículo a 50 km/h gasta 2 horas para chegar ao seu destino. Se ele aumentar a velocidade para 75 km/h, em quantas horas completará o mesmo percurso?
Resolução:
50 — 2
75 — x
Invertendo uma das frações, temos:
50 — x
75 — 2
Assim, a resolução do cálculo é:
75x = 50 . 2
x = 100 ÷ 75
x = 1,33 h
Gráficos
Graficamente a variação diretamente proporcional de uma grandeza em relação à outra forma uma reta que passa pela origem, pois temos y = k.x, sendo k uma constante.
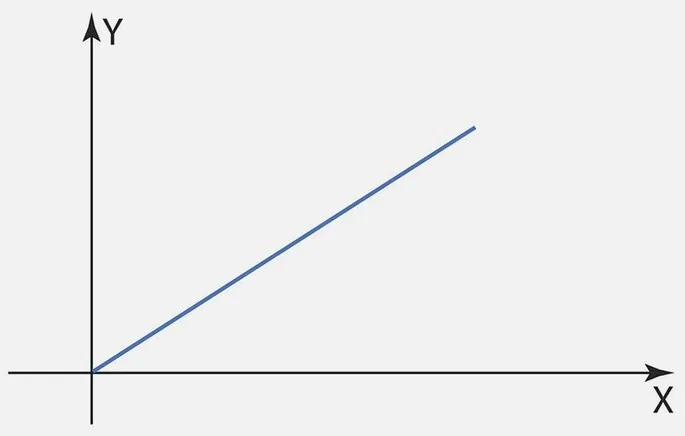
Graficamente a variação inversamente proporcional de uma grandeza em relação à outra forma uma hipérbole, pois temos y = k/x, sendo k uma constante.
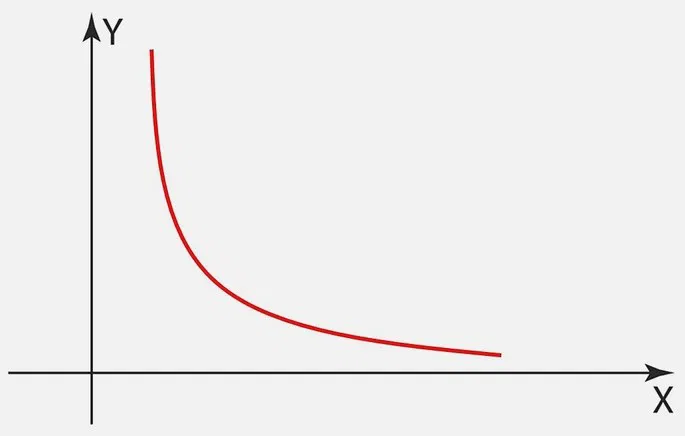
Exemplos de grandeza: distância, peso, velocidade, velocidade, distância e tempo etc.
QUESTÕES RESOLVIDAS
02) Em uma fábrica, há 5 máquinas que produzem 4920 peças diárias. Em um determinado dia, 2 máquinas ficaram paradas para manutenção. Sabendo que não há diferença na quantidade de peças produzidas entre as máquinas, o número de peças produzidas nesse dia foi de?
Resolução:
Sabendo que 5 máquinas produzem 4920 peças, queremos encontrar quantas peças serão produzidas pelas 3 máquinas restantes durante a manutenção. Como as grandezas são proporcionais, a razão entre 5 e 4920 tem que ser igual à razão entre 3 e x:![]() Multiplicando cruzado, temos que:
Multiplicando cruzado, temos que:
5x = 4920 . 3
5x = 14.760
x = 14.760 : 5
x = 2.952
Isso significa que 3 máquinas produzem um total de 2.952 peças.
03) Em um açougue, um cliente pede R$ 18,00 de um determinado tipo de carne. Sabendo que 1 kg dessa carne custa R$ 25,00, então a quantidade de carne que esse cliente vai levar é de?
Resolução:
Então, podemos montar a proporção, na qual x é o peso de R$ 18,00 desse determinado tipo de carne:![]() Multiplicando cruzado, temos que:
Multiplicando cruzado, temos que:
25x = 18 . 1
25x = 18
x = 18 : 25
x = 0,72
Isso significa que, com R$ 18 reais, o cliente comprará 0,72 kg, que é igual a 720 gramas de carne."
04) (Enem) Há um novo impulso para produzir combustível a partir de gordura animal. Em abril, a High Plains Bioenergy inaugurou uma biorrefinaria próxima a uma fábrica de processamento de carne suína em Guymon, Oklahoma. A refinaria converte a gordura do porco, juntamente com o óleo vegetal, em biodiesel. A expectativa da fábrica é transformar 14 milhões de quilogramas de banha em 112 milhões de litros de biodiesel.
Considere que haja uma proporção direta entre a massa de banha transformada e o volume de biodiesel produzido.
Para produzir 48 milhões de litros de biodiesel, a massa de banha necessária, em quilogramas, será de, aproximadamente:
(A) 6 milhões.
(B) 33 milhões.
(C) 78 milhões.
(D) 146 milhões.
(E) 384 milhões.
Resolução
Note que 14 milhões de quilogramas de banha são convertidos em 112 milhões de litros de biodiesel. Seja x a quantidade de banha necessária para produzir 48 milhões de litros de biodiesel, temos que:![]() Multiplicando cruzado, temos que:
Multiplicando cruzado, temos que:
112x = 14 · 48
112x = 672
x=672 : 112
x = 6 milhões
Alternativa: A
05) Em uma empresa distribuidora de mala direta, João, Marcelo e Pedro são responsáveis por ensacar e etiquetar revistas. Certa vez, receberam um lote de 6120 revistas e, ao terminarem a tarefa, perceberam que o lote de revistas havia sido dividido em partes diretamente proporcionais ao respectivo tempo de trabalho de cada um deles na empresa.
Sabendo que João trabalha há 9 meses na empresa, Marcelo há 12 meses e Pedro há 15 meses, o número de revistas que João ensacou e etiquetou foi:
(A) 1 360.
(B) 1 530.
(C) 1 890.
(D) 2 040.
(E) 2 550.
Resolução
Primeiro realizaremos a soma dos temos: 9 + 12 + 15 = 36. Sabemos que 6120 revistas foram divididas proporcionalmente a 36 meses e que João trabalhou 12 meses. Logo, a razão entre 36 e 6120 é igual à razão entre 12 e a quantidade x de revistas que João ensacou e etiquetou:![]() Multiplicando cruzado, temos que:
Multiplicando cruzado, temos que:
36x = 12 · 6120
36x = 73440
x = 73440 : 36
x = 2040
Alternativa: D
06) Uma gráfica, em 5 horas, quantos livros serão impressos?
2 horas imprimem 40 livros
5 horas imprimem x livros
Resolução:
Mais horas de trabalho = mais livros impressos (grandezas diretas)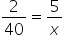 Usando a propriedade fundamental das proporções, temos:
Usando a propriedade fundamental das proporções, temos: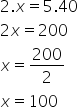 Como havíamos visto na tabela, em 5 h, 100 livros são impressos.
Como havíamos visto na tabela, em 5 h, 100 livros são impressos.
GRANDEZAS INVERSAMENTE PROPORCIONAIS
Quando uma aumenta a outra diminui.
QUESTÕES RESOLVIDAS
07) Um veículo, a 120 km/h, gasta 2 horas em determinado percurso. Qual seria sua velocidade se o tempo gasto nesse percurso fosse de 6 horas?
Resolução:
Aumentando o tempo gasto na viagem, a velocidade diminui, portanto, essas grandezas são inversamente proporcionais.
120 = 2
x 6
Antes de aplicar a propriedade fundamental das proporções, é necessário inverter uma das razões.
120 = 6
x 2
6x = 2·120
6x = 240
x = 240
6
x = 40 km/h
09) Um automóvel está a uma velocidade de 50 km/h e gasta duas horas para chegar a seu destino. Esse mesmo automóvel gastaria quantas horas se estivesse a 75 km/h?
Resolução:
Montando a proporção, teremos:
50 = 2
75 x
Antes de aplicar a propriedade fundamental das proporções, é necessário inverter uma das razões.
50 = x
75 2
75x = 50·2
75x = 100
x = 100
75
x = 1,33
Isso significa que o tempo gasto será de uma hora e 20 minutos. (1,33 h está na base decimal, por isso precisa ser convertido para horas, o que também pode ser feito por regra de três).
10) Um automóvel gasta 2 horas para realizar um determinado percurso. Sabendo que outro automóvel fez o mesmo percurso a uma velocidade média de 60 km/h e levou 3 horas, qual foi a velocidade do primeiro automóvel?
(A) 50 km/h
(B) 65 km/h
(C) 70 km/h
(D) 80 km/h
(E) 90 km/h
Resolução:
x = 2
60 3
Antes de aplicar a propriedade fundamental das proporções, é necessário inverter uma das razões.
x = 3
60 2
60 . 3 = 2x
180 = 2x
x = 180 : 2
x = 90 km/h
QUESTOES RESOLVIDAS DIRETA E INVERSAMENTE PROPORCIONAIS
11) Em uma determinada prova, um candidato que acertou 12 questões recebeu um total de 39 pontos. Sabendo que o valor das questões é sempre o mesmo, um candidato que obteve 52 pontos acertou um total de:
(A) 15 questões
(B) 16 questões
(C) 17 questões
(D) 18 questões
(E) 20 questões
Resolucao
Sabemos que a pontuação é diretamente proporcional à quantidade de pontos, então, temos que: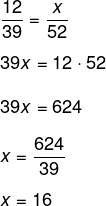
Alternativa B
02) Os ângulos de um triângulo são proporcionais aos números 4, 5 e 6, então, a medida do seu menor ângulo é de:
(A) 12º
(B) 36º
(C) 48º
(D) 60º
(E) 72º
Resolucao
Sabemos que a soma dos angulos internos de um triangulo é sempre igual a 180º, e que 4 + 5 + 6 =15, então, 15 está para 180º, assim como 4 está para o menor ângulo: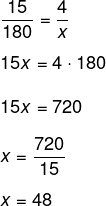
Alternativa C
03) Uma herança de R$ 3.000.000 será dividida de forma diretamente proporcional entre as idades dos três herdeiros. Sabendo que eles possuem 24, 28 e 44 anos, o herdeiro de maior idade receberá um total de:
(A) R$ 950.000
(B) R$ 975.000
(C) R$ 1.225.000
(D) R$ 1.375.000
(E) R$ 1.625.000
Resolucao
Ao realizar a soma das idades, temos que 24 + 28 + 44 = 96, então, 96 está para 3.000.000, assim como 44 está para x, em que x é a herança recebida pelo herdeiro de maior idade: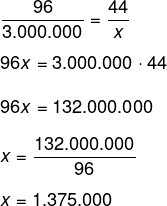
Alternativa D
04) Um automóvel percorreu 272 km e consumiu um total de 32 litros de etanol. Supondo que esse consumo se mantenha o mesmo, e que o tanque do carro tem capacidade máxima de 50 litros, então, a quantidade de quilômetros que esse automóvel percorre quando está de tanque cheio é igual a:
(A) 280 km
(B) 298 km
(C) 350 km
(D) 375 km
(E) 425 km
Resolucao
Sabemos que o consumo e a distância são grandezas diretamente proporcionais. Seja x a quantidade de quilômetros que o veículo faz com 50 litros, então, temos que: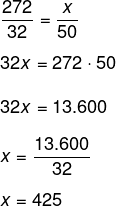
Alternativa E
05) Das situações a seguir, marque aquela que contém uma relação entre duas grandezas diretamente proporcionais:
(A) Velocidade de um automóvel e o tempo que ele demora para fazer determinado percurso.
(B) Tempo de funcionamento de um aparelho eletrônico e a energia consumida.
(C) Quantidade de funcionários para executar um serviço e o número de acidentes de trabalho ocorridos.
(D) Número de eleitores e a quantidade de votos obtidos por um determinado candidato.
Resolucao
O tempo de funcionamento de um aparelho é diretamente proporcional à energia consumida, pois quanto maior o tempo de funcionamento, maior será o consumo, e sabemos que esse aumento será de forma proporcional.
Alternativa B
06) (Enem) Nos shopping centers, costumam existir parques com vários brinquedos e jogos. Os usuários colocam créditos em um cartão, que são descontados por período de uso dos jogos.
Dependendo da pontuação da criança no jogo, ela recebe certo número de tíquetes para trocar por produtos nas lojas dos parques.
Suponha que o período de uso de um brinquedo em certo shopping custa R$ 3 e que uma bicicleta custa 9200 tíquetes.
Para uma criança que recebe 20 tíquetes por tempo de jogo, o valor, em reais, gasto com créditos para obter a quantidade de tíquetes para trocar pela bicicleta é
(A) 153.
(B) 460.
(C) 1218.
(D) 1380.
(E) 3066.
Resolucao
Montando a proporção, temos que: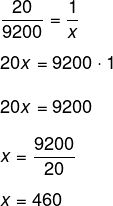
Agora basta multiplicar por R$ 3:
460 · 3 = 1380
Alternativa D
07) Para a produção de 15 litros de etanol, são necessários 187,5 kg de cana-de-açúcar. Com um total de 250 kg de cana-de-açúcar, é possível produzir um total de:
(A) 18 L
(B) 20 L
(C) 22 L
(D) 25 L
(E) 30 L
Resolucao
Seja x a quantidade de litros produzidos por 280 kg, montando a proporcao, temos que: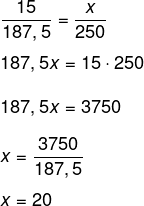
Alternativa B
08) (OMNI) Grandeza é tudo aquilo que pode ser medido ou calculado, porém quando analisamos duas grandezas proporcionais, elas podem ser diretamente proporcionais ou inversamente proporcionais. Sabendo disso, analise as alternativas abaixo e marque a opção CORRETA.
(A) Distância e tempo são grandezas inversamente proporcionais, pois quanto maior a distância que precisa ser percorrida, menos tempo será gasto no percurso.
(B) Velocidade e quantidade de alimento comprado por uma família são grandezas diretamente proporcionais.
(C) Em um churrasco, a quantidade de carne e a quantidade de pessoas são grandezas diretamente proporcionais.
(D) Velocidade e tempo são grandezas diretamente proporcionais, pois quanto maior a velocidade, menor o tempo gasto em um percurso.
Resolucao
Sabemos que quanto maior a quantidade de pessoas, maior deve ser a quantidade de carne, e esse aumento é de forma proporcional.
Alternativa C
09) Na bula de um remédio para crianças, a dosagem recebida é diretamente proporcional ao peso da criança. Sabendo que são recomendadas 3 gotas do medicamento a cada 2 kg, então, a dosagem oferecida para uma criança que tem 18 kg é de:
(A) 22 gotas
(B) 24 gotas
(C) 27 gotas
(D) 30 gotas
(E) 54 gotas
Resolucao
Sabemos que são gastas 3 gotas para cada 2 kg, então, de forma proporcional, se a criança tem 18 kg, basta dividir seu peso por 2, e multiplicar por 3, ou seja, 18 : 2 = 9 e 9 · 3 = 27 gotas.
Alternativa C
10) Em uma fábrica de luvas, uma certa máquina, funcionando 5 horas por dia, consegue fabricar um total de 14.000 luvas. Devido a um pedido de emergência de produção para atender a demanda da pandemia, a fábrica realizou uma produção de 33.600 luvas. O tempo de funcionamento dessa máquina para realizar essa produção é de:
(A) 8 horas
(B) 9 horas
(C) 10 horas
(D) 11 horas
(E) 12 horas
Resolucao
De forma proporcional, sabemos que 5 está para 14.000, assim como x está para 33.600.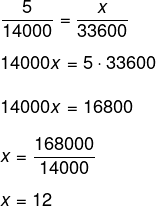
Alternativa E
11) (UDF) Uma máquina varredeira limpa uma área de 5100 m² em 3 horas de trabalho. Nas mesmas condições, em quanto tempo limpará uma área de 11.900 m²?
(A) 4 horas
(B) 5 horas
(C) 7 horas
(D) 9 horas
Resolucao
Montando a proporção, temos que: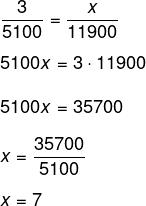
Alternativa C
12) Os ângulos de um quadrilátero são diretamente proporcionais aos números 2, 3, 4 e 7. Então, a medida do menor ângulo desse quadrilátero é igual a:
(A) 45º
(B) 75º
(C) 90º
(D) 180º
(E) 35º
Resolucao
Sabemos que a soma dos ângulos internos de um quadrilatero é sempre igual a 360º. Realizando a soma dos números 2 + 3 + 4 + 7 = 16, então sabemos que 16 está para 360º assim como 2 está para o menor ângulo, representado por x. Montando a proporção, temos que: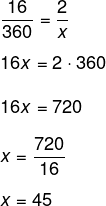
Alternativa A
13) (Vunesp) Para uma prova, 150 candidatos deveriam ser acomodados nas salas A, B, C e D de um colégio, com capacidade para receber 60, 50, 40 e 30 candidatos, respectivamente. A organização decidiu preencher inicialmente todos os lugares da sala menor, e os candidatos restantes foram repartidos entre as demais salas de forma diretamente proporcional à capacidade de cada uma. O número de lugares não ocupados na sala de maior capacidade foi igual a:
(A) 8
(B) 10
(C) 12
(D) 14
(E) 16
Resolucao
Sabendo que a sala menor será toda preenchida, 150 – 30 = 120 candidatos restantes. Os 120 candidatos restantes serão divididos de forma proporciaonal, então, sabemos que: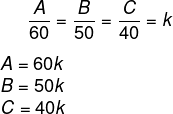
Sabemos que:
A + B + C = 120
Substituindo os valores encontrados, temos que:
60k + 50k + 40k = 120
150k = 120
k = 120/150
k = 0,8
Dessa forma, a ocupação de cada uma das salas será:
60k → 60 · 0,8 = 48
Como há uma capacidade de 60 lugares, 60 – 48 = 12 lugares não ocupados.
Alternativa C
14) (Enem) Nos shopping centers, costumam existir parques com vários brinquedos e jogos. Os usuários colocam créditos em um cartão, que são descontados por período de uso dos jogos.
Dependendo da pontuação da criança no jogo, ela recebe certo número de tíquetes para trocar por produtos nas lojas dos parques.
Suponha que o período de uso de um brinquedo em certo shopping custa R$ 3 e que uma bicicleta custa 9200 tíquetes.
Para uma criança que recebe 20 tíquetes por tempo de jogo, o valor, em reais, gasto com créditos para obter a quantidade de tíquetes para trocar pela bicicleta é
(A) 153.
(B) 460.
(C) 1218.
(D) 1380.
(E) 3066.
Resolucao
Sabendo que a criança precisa de 9200 tíquetes, e que ela ganha 20 por período, ao realizar a divisao, encontraremos quantos períodos ela jogará.
9200 : 20 = 460
Para cada período, gasta-se R$ 3. Sendo assim, 460 · 3 = 1380.
Alternativa D
15) (Enem)
Fontes alternativas
Há um novo impulso para produzir combustível a partir de gordura animal. Em abril, a High Plains Bioenergy inaugurou uma biorrefinaria próxima a uma fábrica de processamento de carne suína em Guymon, Oklahoma. A refinaria converte a gordura do porco, juntamente com o óleo vegetal, em biodiesel. A expectativa da fábrica é transformar 14 milhões de quilogramas de banha em 112 milhões de litros de biodiesel.
Revista Scientific American. Brasil, ago. 2009 (adaptado).
Considere que haja uma proporção direta entre a massa de banha transformada e o volume de biodiesel produzido.
Para produzir 48 milhões de litros de biodiesel, a massa de banha necessária, em quilogramas, será de, aproximadamente,
(A) 6 milhões.
(B) 33 milhões.
(C) 78 milhões.
(D) 146 milhões.
(E) 384 milhões.
Resolucao
Sabendo que 14 milhões de quilogramas de banha são convertidos em 112 milhões de litros de biodiesel, ao dividir 112 milhões por 14, vamos encontrar quantos litros de biodiesel podem ser produzidos com 1 milhão de quilogramas de banha.
112 : 14 = 8, ou seja, 1 milhão de kg de banha é convertido em 8 milhões de litros de biodiesel. Agora, para saber quantos kg de banha são necessários para produzir 48 milhões de litros de biodiesel, basta dividir 48 por 8.
48 : 8 = 6 milhões
Alternativa A
16) (Enem) A suspeita de que haveria uma relação causal entre tabagismo e câncer de pulmão foi levantada pela primeira vez a partir de observações clínicas. Para testar essa possível associação, foram conduzidos inúmeros estudos epidemiológicos.
Dentre esses, houve o estudo do número de casos de câncer em relação ao número de cigarros consumidos por dia, cujos resultados são mostrados no gráfico a seguir.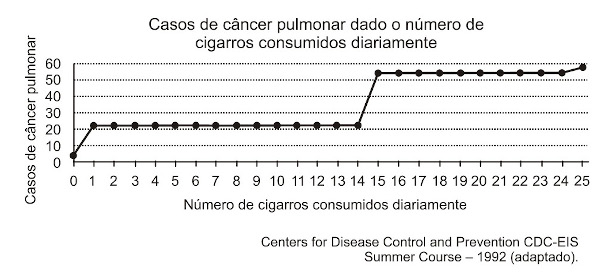 De acordo com as informações do gráfico,
De acordo com as informações do gráfico,
(A) o consumo diário de cigarros e o número de casos de câncer de pulmão são grandezas inversamente proporcionais.
(B) o consumo diário de cigarros e o número de casos de câncer de pulmão são grandezas que não se relacionam.
(C) o consumo diário de cigarros e o número de casos de câncer de pulmão são grandezas diretamente proporcionais.
(D) uma pessoa não fumante certamente nunca será diagnosticada com câncer de pulmão.
(E) o consumo diário de cigarros e o número de casos de câncer de pulmão são grandezas que estão relacionadas, mas sem proporcionalidade.
Resolucao
Sabe-se que existe sim relação entre o tabagismo e os casos de câncer de pulmão, porém, analisando o gráfico, é possível perceber que o crescimento não é proporcional, note que, em alguns intervalos, os casos de câncer são constantes.
Alternativa E
17) Os ângulos de um triângulo são diretamente proporcionais aos números 3, 7 e 15, então, podemos afirmar que o menor ângulo mede:
(A) 108º
(B) 50,4º
(C) 21,6º
(D) 42º
(E) 50,4º
Resolucao
Sabemos que a soma dos ângulos internos de um triângulo é sempre 180º.
Seja x, y, e z os ângulos do triângulo, como eles são proporcionais a 3,7 e 15, então, temos que: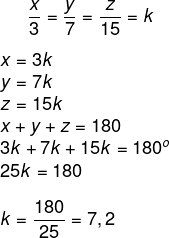
x = 3 · 7,2 = 21,6º
y = 7 · 7,2 = 50,4º
z = 15 · 7,2 = 108º
Alternativa C
18) Os lados de um retângulo são proporcionais a 2 e 3. Sabendo que a sua área é de 216 m², as dimensões dos retângulos são, respectivamente:
(A) 12 e 18
(B) 4 e 54
(C) 8 e 27
(D) 10 e 26
(E) 13,5 e 16
Resolucao
Sabendo que os lados são proporcionais a 2 e 3, então, seja x e y os lados do retangulo, existe k, tal que:![]()
Assim, temos que:
x = 2k
y = 3k
Sabendo que a área é 216 m², então, temos que:
A = 2k · 3k = 6k²
6k² = 216
k² = 216/6
k² = 36
k = √36
k = 6
Alternativa A
19) Uma herança de R$ 1.500.000 foi dividida entre os filhos de forma diretamente proporcional à idade de cada um deles. Sabendo que há três filhos, com 14, 16 e 20 anos de idade, podemos afirmar que o filho do meio receberá:
(A) R$ 600.000
(B) R$ 420.000
(C) R$ 480.000
(D) R$ 500.000
(E) R$ 450.000
Resolucao
Sejam A, B e C os filhos de 14, 16 e 20 anos, respectivamente:![]()
x = 14k
y = 16k
z = 20k
Então, temos que:
14k + 16k + 20k = 1.500.000
50k = 1.5000.000
k = 1.500.000/50
k = 30.000
y = 16 · 30.000 = 480.000
Alternativa C
20) Os ângulos de um quadrilátero são proporcionais a 3, 6, 12, 15. Assim, podemos afirmar que o valor do maior ângulo é:
(A) 150º
(B) 120º
(C) 60º
(D) 30º
(E) 135º
Resolucao
A soma dos angulos internos de um quadrilátero é igual a 360º. Sejam x, y, z e w os ângulos do quadrilateros, temos que: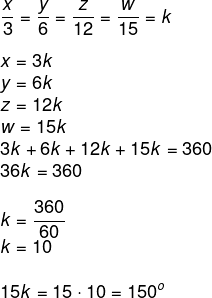
Alternativa A
21) A idade de três irmãos é diretamente proporcional a 4, 6 e 10 anos. Sabendo que a soma da idade dos três é igual a 70, podemos afirmar que o mais novo possui:
(A) 10 anos
(B) 12 anos
(C) 14 anos
(D) 16 anos
(E) 18 anos
Resolucao
Como as idades são proporcionais, e sejam A, B e C as idades de cada um desses irmãos, então, temos que:![]()
Assim, temos que:
A = 4k
B = 6k
C = 10k
Sabendo que a soma é igual a 70, então:
4k + 6k + 10 k = 70
20k = 70
k = 70/20
k = 3,5
Como queremos a idade do mais novo:
A = 4 · 3,5 = 14 anos
Alternativa C
22) Um automóvel faz 35 km com 5 litros de etanol. Realizando uma viagem de uma cidade para outra, com base nesse consumo, qual deve ser a quantidade de etanol necessária para percorrer 196 km?
(A) 28 litros
(B) 25 litros
(C) 20 litros
(D) 30 litros
(E) 18 litros
Resolucao
Sabendo que existe proporção entre a distância percorrida e o consumo de combustível, ao dividir 35 por 5, encontraremos o consumo 35 : 5 = 7 km/l. Sabendo que a viagem é de 196 km, 196 : 7 = 28 litros.
Alternativa A
23) Das relações entre as grandezas a seguir, identifique aquela que não é diretamente proporcional.
(A) Quantidade de funcionários e produtividade
(B) Distância percorrida e consumo do veículo
(C) Velocidade do automóvel e tempo para completar o percurso
(D) Valor pago pela verdura e peso
Resolucao
Quanto maior a velocidade, menor será o tempo gasto no percurso.
Alternativa C
24) Um triângulo retângulo possui os lados diretamente proporcionais a 3, 4 e 5. Sabendo que sua hipotenusa é igual a 31 cm, o valor do perímetro desse triângulo é:
(A) 28,4 cm
(B) 42,6 cm
(C) 65 cm
(D) 74,4 cm
(E) 82,8 cm
Resolucao
Sejam a e b os catetos do triangulo, vamos montar a proporção: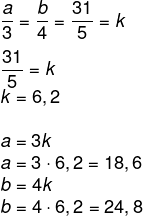
P = a + b + 31
P = 18,6 + 24,8 + 31 = 74,4
Alternativa D
Grandezas Inversamente Proporcionais
Duas grandezas que são inversamente proporcionais ainda variam uma em consequência da outra e na mesma proporção, entretanto, o aumento da medida relativa à primeira faz com que a medida relativa à segunda diminua. Se diminuirmos a medida relativa à primeira grandeza, isso fará com que a medida relativa à segunda aumente. É por isso que essa proporcionalidade é chamada de inversa.
Exemplo 1:
Em uma fábrica de sapatos que possui 25 funcionários, é produzida uma determinada quantidade de sapatos em 10 horas. Se o número de funcionários for 50, essa mesma quantidade de sapatos será produzida em 5 horas.
É evidente que o dobro de funcionários fará o trabalho na metade do tempo. Isso acontece porque as grandezas horas trabalhadas e quantidade de funcionários são inversamente proporcionais.
Regra de três
A regra de três é a ferramenta usada para descobrir uma das medidas de uma proporção. Ela também é válida para quando essa proporção é obtida por meio de grandezas.
Quando as grandezas forem diretamente proporcionais, monte a proporção entre as medidas observadas e utilize a propriedade fundamental das proporções para encontrar a medida procurada.
Exemplo 2:
Um automóvel a 50 km/h percorre 100 km. Se esse automóvel estivesse a 75 km/h, teria percorrido quantos quilômetros no mesmo período de tempo?
Resolucao
50 = 75
100 x
50x = 75·100
50x = 7500
x = 7500
50
x = 150 km.
Além disso, quando as grandezas forem inversamente proporcionais, será necessário inverter uma das frações da proporção formada por elas antes de aplicar a propriedade fundamental das proporções.
Exemplo 3:
Um automóvel está a uma velocidade de 50 km/h e gasta duas horas para chegar a seu destino. Esse mesmo automóvel gastaria quantas horas se estivesse a 75 km/h?
Resolucao
Montando a proporção, teremos:
50 = 2
75 x
Aumentando a velocidade, o tempo gasto no percurso deve diminuir, portanto, as grandezas são inversamente proporcionais. Invertendo uma das frações, teremos:
50 = x
75 2
Aplicando a propriedade fundamental das proporções, teremos:
75x = 50·2
75x = 100
x = 100
75
x = 1,33
Isso significa que o tempo gasto será de uma hora e 20 minutos. (1,33 h está na base decimal, por isso precisa ser convertido para horas, o que também pode ser feito por regra de três).
Exemplo 4:
Um automóvel desloca-se a 60 km/h e demora 3 horas para chegar a seu destino. Se esse mesmo automóvel estivesse a 90 km/h, quanto tempo levaria para completar esse mesmo percurso?
Resolucao
A proporção construída a partir dessa situação é:
60 = 3
90 x
Essas grandezas são inversamente proporcionais, pois, aumentando a velocidade, gastaremos menos tempo em um mesmo percurso. Portanto, inverteremos uma das equações:
90 = 3
60 x
Agora, basta aplicar a propriedade fundamental das proporções e resolver a equação resultante:
90x = 3 . 60
80x = 180
x = 180
90
x = 2
Serão gastas duas horas a 90 km/h.
QUESTOES RESOLVIDAS
01) Das situações abaixo, marque aquela que descreve duas grandezas inversamente proporcionais:
(A) Quantidade de pessoas em um churrasco e a quantidade de carne necessária.
(B) Número de habitantes em uma cidade e a taxa de mortalidade.
(C) Velocidade de um automóvel e a distância percorrida em um mesmo intervalo de tempo.
(D) Comprimento da altura e a área de um polígono.
(E) Vazão de um ralo e o tempo necessário para esvaziar um reservatório.
Resolucao
Quanto maior a vazão da água para esvaziar o reservatório, menor será o tempo necessário para tanto, ou seja, essas grandezas são inversamente proporcionais.
Alternativa E
02) (IF-SP) Para fazer uma viagem, levamos em consideração duas grandezas: velocidade do meio de transporte e tempo de viagem. Essas duas grandezas são
(A) completamente proporcionais.
(B) desproporcionais.
(C) diretamente proporcionais.
(D) subitamente proporcionais.
(E) inversamente proporcionais.
Resolucao
A relação entre velocidade e tempo nessa situação é inversamente proporcional, pois se eu aumento a velocidade, o tempo que eu levo para chegar até o destino será menor.
Alternativa E
03) Em uma empresa, os três melhores funcionários serão premiados e dividirão um valor de R$ 38.200 de forma inversamente proporcional ao número de vendas perdidas durante o ano.
Sabendo que o funcionário que ficou em primeiro lugar perdeu 28 vendas, o segundo, 32, e o terceiro, 36, o valor recebido pelo funcionário que perdeu menos vendas é igual a:
(A) R$ 8600
(B) R$ 9000
(C) R$ 10.500
(D) R$ 11.200
(E) R$ 14.400
Resolucao
Sejam a, b, c a quantidade recebida por funcionário, sabemos que a + b + c = 38.200. Montando as proporções, temos que: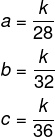
Substituindo na soma, temos que: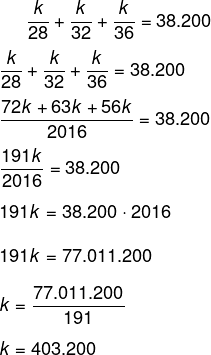
Agora que encontramos o valor de k, queremos o valor recebido pelo funcionário que perdeu menos vendas, para isso, basta dividir k por 28.![]()
Alternativa E
04) Um triângulo possui ângulos internos proporcionais aos números 1, 3 e 6, então, o valor do seu maior ângulo é:
(A) 30°
(B) 60°
(C) 90°
(D) 120°
(E) 150°
Resolucao
Sejam a, b e c os ângulos internos dotriangulo, e sabendo que a soma deles é sempre igual a 180º, então, temos que a + b + c = 180º. Como eles são inversamente proporcionais a 1, 3 e 6, escreveremos a proporcoa:![]()
Substituindo os valores de a, b e c, temos que: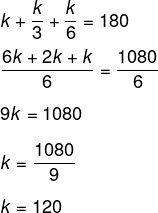
Agora que sabemos o valor de k, o maior ângulo é a = k, então, a = 120º.
Alternativa D
05) Marque a alternativa que melhor define quando duas grandezas são inversamente proporcionais:
(A) Duas grandezas, A e B, são inversamente proporcionais quando existe uma relação entre elas, em uma determinada situação, que faz com que na medida em que a grandeza A aumenta o seu valor, a grandeza B também aumente, na mesma proporção. Um exemplo disso é a quantidade de partidas vencidas e a pontuação de um time no campeonato.
(B) Duas grandezas são inversamente proporcionais quando elas não possuem nenhuma relação, ou seja, se uma das grandezas aumentar o seu valor, a outra pode aumentá-lo ou diminui-lo.
(C) Duas grandezas são inversamente proporcionais quando na medida em que o valor de uma delas aumenta, o valor da outra diminui na mesma proporção. Um exemplo disso é a relação entre a velocidade e o tempo gasto em um percurso fixo.
(D) Duas grandezas nunca serão inversamente proporcionais, pois existem grandezas diretamente proporcionais e grandezas que não se relacionam e são improporcionais.
Resolucao
A alternativa que define corretamente as grandezas inversamente proporcionais .
Alternativa C
06) Durante a pandemia de covid-19, os cientistas buscaram sempre relacionar grandezas para compreender melhor o fenômeno. Os estatísticos perceberam que existe uma relação entre as grandezas: número de vacinados e quantidade de casos graves. Como era de se esperar, com metade da população vacinada, o número de casos graves da doença caiu também pela metade. Sabendo da eficácia da vacina, podemos afirmar que as grandezas citadas se relacionam de forma
(A) inversamente proporcional.
(B) diretamente proporcional.
(C) desproporcional.
(D) subitamente proporcional.
(E) essas grandezas se relacionam, mas não há proporção entre elas.
Resolucao
Note que se o número de vacinados dobrou e a quantidade de casos graves caiu pela metade, existe então proporção entre as grandezas e de forma inversa.
Alternativa A
07) (Enem) Para contratar três máquinas que farão o reparo de vias rurais de um município, a prefeitura elaborou um edital que, entre outras cláusulas, previa:
- cada empresa interessada só pode cadastrar uma única máquina para concorrer ao edital;
- o total de recursos destinados para contratar o conjunto das três máquinas é de R$ 31 000;
- o valor a ser pago a cada empresa será inversamente proporcional à idade de uso da máquina cadastrada pela empresa para o presente edital.
As três empresas vencedoras do edital cadastraram máquinas com 2, 3 e 5 anos de idade de uso.
Quanto receberá a empresa que cadastrou a máquina com maior idade de uso?
(A) R$ 3100
(B) R$ 6000
(C) R$ 6200
(D) R$ 15.000
(E) R$ 15.500
Resolucao
Cada empresa receberá de forma inversamente proporcional ao tempo de uso da máquina, então, sejam x, y, z o recebimento de cada empresa, temos que:![]()
Sabemos que a soma x + y + z = 31.000, logo, temos que: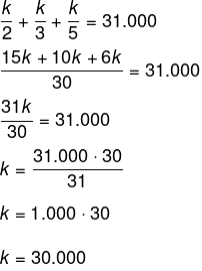
Conhecendo o valor de k, 5 anos são a maior idade de uso da máquina por uma empresa, então, basta calcular k dividido por 5.![]()
Alternativa B
08) Um automóvel gasta 2 horas para realizar um determinado percurso. Sabendo que outro automóvel fez o mesmo percurso a uma velocidade média de 60 km/h e levou 3 horas, qual foi a velocidade do primeiro automóvel?
(A) 50 km/h
(B) 65 km/h
(C) 70 km/h
(D) 80 km/h
(E) 90 km/h
Resolucao
Sabemos que essas grandezas se relacionam de forma inversamente proporcional, pois à medida que a velocidade aumentar, o tempo diminuirá. Então, temos que:
Velocidade Tempo
60 km/h 3 horas
x 2 horas
Como as grandezas são inversamente proporcionais, temos que:
60 · 3 = 2x
180 = 2x
x = 180 : 2
x = 90 km/h
Alternativa E
09) Sabemos que a densidade de uma substância é calculada pela razão entre a massa e o volume. Se determinada substância possui 2 cm³ de volume, com densidade de 100 g/cm³, tendo a mesma massa, qual deve ser o volume de uma outra substância para que a sua densidade seja de 80 g/cm³?
(A) 2,2 cm³
(B) 2,5 cm³
(C) 2,8 cm³
(D) 3,0 cm³
(E) 3,4 cm³
Resolucao
Analisando as grandezas, sabemos que o volume é inversamente proporcional à densidade. Montando a tabela, é possível calcular o valor de x.
Densidade Volume
80 g/cm³ x cm³
100 g/cm³ 2 cm³
Então, multiplicando reto, temos que:
80x = 100 · 2
80x = 200
x = 200 : 80
x = 2,5 cm³
Alternativa B
10) Um ângulo raso foi dividido em três partes inversamente proporcionais aos números 1, 3 e 6. Nessas condições, o menor ângulo mede:
(A) 20º
(B) 45º
(C) 60º
(D) 90º
(E) 120º
Resolucao
Sejam a, b e c os angulos internos desse tringulo, então, temos que: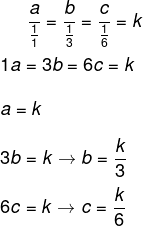
Sabemos que a soma dos ângulos internos de um triângulo é sempre igual a 180º, então, temos que: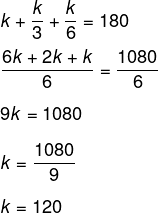
Por fim, o menor ângulo é o ângulo c, que é k : 6.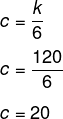
Alternativa A
11) (Objetiva 2015) Em determinado dia de trabalho, três auxiliares administrativos arquivaram 1324 processos ao todo. Sabendo-se que a quantidade de processos que cada auxiliar arquivou é inversamente proporcional às suas idades, que são 28, 30 e 54 anos, respectivamente, assinalar a alternativa CORRETA:
(A) O auxiliar administrativo com 28 anos arquivou 542 processos.
(B) O auxiliar administrativo com 30 anos arquivou 504 processos.
(C) O auxiliar administrativo com 54 anos arquivou 282 processos.
(D) O auxiliar administrativo com 28 anos arquivou 544 processos.
Resolucao
Sejam x, y e z a produção dos funcionários de 28, 30 e 54 anos respectivamente, então, temos que: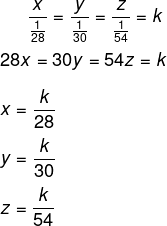
Realizando a soma x + y + z = 1324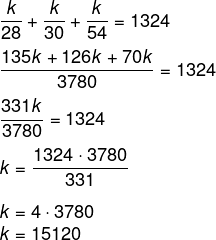
Conhecendo o valor de k, agora calcularemos a produção de cada um dos funcionários: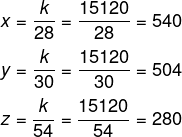
Podemos afirmar que o funcionário que possui 30 anos arquivou 504 processos.
Alternativa B
12) Para a realização de uma obra, foram contratados 6 operários que levaram 18 dias para executar a metade desse trabalho. Se forem contratados mais 3 funcionários, qual será o tempo total gasto na obra?
(A) 12 dias
(B) 24 dias
(C) 28 dias
(D) 30 dias
(E) 36 dias
Resolucao
Sabemos que 6 operários levaram 18 dias para fazer a metade da obra, agora há 9 operários, então, podemos montar a tabela a seguir:
Operários Tempo
6 18
9 x
Multiplicando reto, temos que:
9x = 18 · 6
9x = 108
x = 108 : 8
x = 12
Sabemos que eles levarão 12 dias para finalizar a obra, logo, o tempo total gasto será: 18 + 12 = 30 dias.
Alternativa D
13) Uma herança de R$ 2.950.000 foi dividida aos três herdeiros de forma inversamente proporcional aos números 2, 5 e 7. Sendo assim, o herdeiro que recebeu a maior parte herdou um total de:
(A) R$ 1.950.000
(B) R$ 2.100.000
(C) R$ 1.800.000
(D) R$ 1.750.000
(E) R$ 900.000
Resolucao
Sejam x, y e z os valores recebidos por cada um dos herdeiros, então, temos que: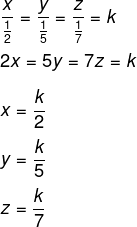
Sabemos que a soma x + y + z = 2.950.000.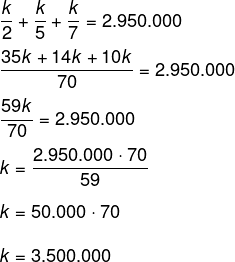
Agora queremos encontrar o valor recebido pelo herdeiro que teve a maior parte, então, temos que: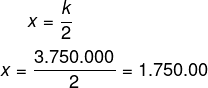
Alternativa D
14) (Enem) Para contratar três máquinas que farão o reparo de vias rurais de um município, a prefeitura elaborou um edital que, entre outras cláusulas, previa:
Cada empresa interessada só pode cadastrar uma única máquina para concorrer ao edital;
O total de recursos destinados para contratar o conjunto das três máquinas é de R$ 31 000;
O valor a ser pago a cada empresa será inversamente proporcional à idade de uso da máquina cadastrada pela empresa para o presente edital.
As três empresas vencedoras do edital cadastraram máquinas com 2, 3 e 5 anos de idade de uso.
Quanto receberá a empresa que cadastrou a máquina com maior idade de uso?
(A) R$ 3100
(B) R$ 6000
(C) R$ 6200
(D) R$ 15.000
(E) R$ 15.500
Resolucao
Cada empresa receberá de forma inversamente proporcional ao tempo de uso da máquina, então, sejam x, y, z o recebimento de cada empresa, temos que:![]()
Sabemos que a soma x + y + z = 31.000, logo, temos que: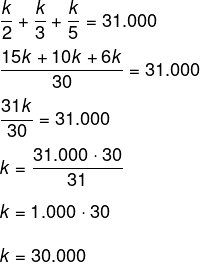
Conhecendo o valor de k, a empresa que tem maior idade é a de 5 anos, então, basta calcular k divido por 5.![]()
Alternativa B
15) Em uma fábrica, há três máquinas e a produção é inversamente proporcional ao tempo de uso das máquinas em meses. Sabendo que as três possuem, respectivamente, 28, 32 e 36 meses de uso, e que, em um determinado tempo, as máquinas produziram, ao todo, 3820 peças, a quantidade de peças produzidas pela máquina mais nova é igual a:
(A) 860
(B) 900
(C) 1050
(D) 1120
(E) 1440
Resolucao
Sejam x, y e z a produção de cada uma das máquinas, temos que: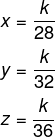
A soma de x + y + z = 3820, então, temos que: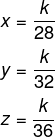
A máquina mais nova tem 28 meses de uso, então, basta realizar a divisão de k por 28.![]()
Alternativa E
16) Analisando as alternativas abaixo, marque aquela em que as grandezas se relacionam de forma inversamente proporcional.
(A) A distância percorrida por um veículo e o tempo de percurso em uma velocidade constante.
(B) A idade da pessoa e o seu salário mensal.
(C) A vazão da água de uma mangueira e o tempo que ela leva para preencher um reservatório.
(D) A quantidade de concreto produzido e a quantidade de cimento necessária.
(E) O número de acertos em uma prova e a nota obtida pelo candidato.
Resolucao
Sabemos que, quanto maior a vazão da água, menor o tempo que a mangueira levará para encher o reservatório.
Alternativa C
17) As sequências de números (a, -2, 1) e (2, b, 4) são inversamente proporcionais, então, o valor da soma a + b é igual a:
(A) -1
(B) 0
(C) 1
(D) 2
(E) 4
Resolucao
Sabendo que as grandezas são inversamente proporcionais, temos que: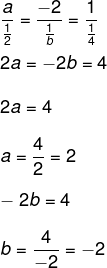
Assim, a soma a + b = 2 + (-2) = 0
Alternativa B
18) (Enem) A resistência mecânica S de uma viga de madeira, em forma de um paralelepípedo retângulo, é diretamente proporcional à sua largura (b) e ao quadrado de sua altura (d) e inversamente proporcional ao quadrado da distância entre os suportes da viga, que coincide com o seu comprimento (x), conforme ilustra a figura. A constante de proporcionalidade k é chamada de resistência da viga.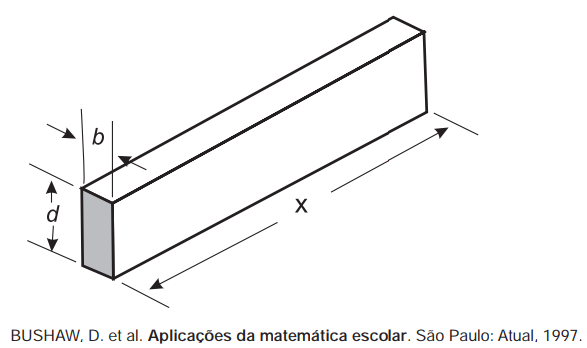 A expressão que traduz a resistência S dessa viga de madeira é:
A expressão que traduz a resistência S dessa viga de madeira é:
(A) S = k.b.d2
x2
(A) S = k.b.d
x2
(C) S = k.b.d2x
(D) S = k.b2.d
x2
(E) S = k.b.2d
2x
Resolucao
Multiplicamos a constante k pelos valores diretamente proporcionais e dividimos k pelos valores inversamente proporcionais, então, temos que b e d² são proporcionais a k, e x² é inversamente proporcional.![]()
Alternativa A
19) (IFSP) Para fazer uma viagem, levamos em consideração duas grandezas: velocidade do meio de transporte e tempo de viagem. Essas duas grandezas são:
(A) completamente proporcionais.
(B) desproporcionais.
(C) diretamente proporcionais.
(D) subitamente proporcionais.
(E) inversamente proporcionais.
Resolucao
5Sabemos que à medida que a velocidade aumentar, o tempo diminuirá, o que faz com que essas grandezas sejam inversamente proporcionais.
Alternativa E
20) Para alimentar o seu cão, uma pessoa gasta 10 kg de ração a cada 15 dias. Qual a quantidade total de ração consumida por semana, considerando que por dia é sempre colocada a mesma quantidade de ração?
Resolução:
Devemos sempre começar identificando as grandezas e as suas relações. É muito importante identificar corretamente se as grandezas são diretamente ou inversamente proporcionais.
Neste exercício as grandezas quantidade total de ração consumida e o número de dias são diretamente proporcionais, pois quanto mais dias maior será a quantidade total gasta.
Para melhor visualizar a relação entre as grandezas, podemos usar setas. O sentido da seta aponta para o maior valor de cada grandeza.
As grandezas cujos pares de setas apontam para o mesmo sentido, são diretamente proporcionais e as que apontam em sentidos contrários, são inversamente proporcionais.
Vamos então resolver o exercício proposto, conforme o esquema abaixo: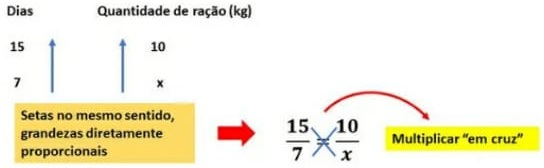 Resolvendo a equação, temos:
Resolvendo a equação, temos: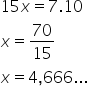 Assim, a quantidade de ração consumida por semana é de aproximadamente 4,7 kg.
Assim, a quantidade de ração consumida por semana é de aproximadamente 4,7 kg.
21) Uma torneira enche um tanque em 6 h. Quanto tempo o mesmo tanque levará para encher, se forem utilizadas 4 torneiras com a mesma vazão da torneira anterior?
Resolução:
Neste problema, as grandezas envolvidas serão número de torneiras e tempo. Contudo, é importante observar que quanto maior o número de torneiras, menor será o tempo para encher o tanque.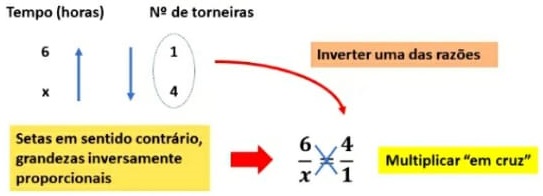 Portanto, as grandezas são inversamente proporcionais. Neste caso, ao escrever a proporção, devemos inverter uma das razões, conforme mostramos no esquema abaixo:
Portanto, as grandezas são inversamente proporcionais. Neste caso, ao escrever a proporção, devemos inverter uma das razões, conforme mostramos no esquema abaixo:
Resolvendo a equação: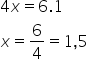 Assim, o tanque ficará totalmente cheio em 1,5 h.
Assim, o tanque ficará totalmente cheio em 1,5 h.
22) Em uma empresa, 50 funcionários, produzem 200 peças, trabalhando 5 horas por dia. Se o número de funcionários cair pela metade e o número de horas de trabalho por dia passar para 8 horas, quantas peças serão produzidas?
Resolução:
As grandezas indicadas no problema são: número de funcionários, número de peças e horas trabalhadas por dia. Portanto, temos uma regra de três composta (mais de duas grandezas).
Neste tipo de cálculo, é importante analisar separadamente o que acontece com a incógnita (x), quando mudamos o valor das outras duas grandezas.
Fazendo isso, percebemos que o número de peças será menor se reduzirmos o número de funcionários, portanto, essas grandezas são diretamente proporcionais.
O número de peças aumenta se aumentarmos o número de horas de trabalho por dia. Portanto, também são diretamente proporcionais.
No esquema abaixo, indicamos esse fato através das setas, que apontam para o sentido crescente dos valores.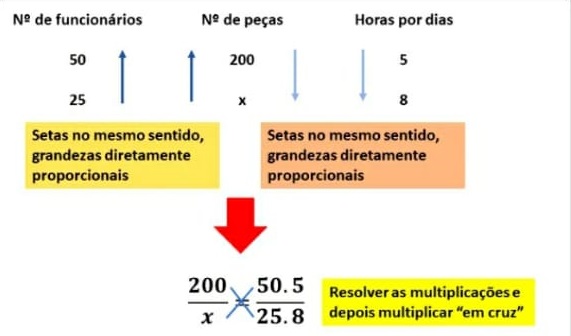 Resolvendo a regra de três, temos:
Resolvendo a regra de três, temos: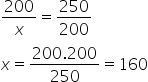 Assim, serão produzidas 160 peças.
Assim, serão produzidas 160 peças.
Alternativa: B
23) (Epcar - 2016) Duas máquinas A e B de modelos diferentes, mantendo cada qual sua velocidade de produção constante, produzem juntas n peças iguais, gastando simultaneamente 2 horas e 40 minutos. A máquina A funcionando sozinha, mantendo sua velocidade constante, produziria, em 2 horas de funcionamento, n/2 dessas peças.
É correto afirmar que a máquina B, mantendo sua velocidade de produção constante, produziria também n/2 dessas peças em
(A) 40 minutos.
(B) 120 minutos.
(C) 160 minutos.
(D) 240 minutos.
Resolução:
Como o tempo total de produção é 2h e 40 min, e já sabemos que a máquina A produz sozinha em 2 horas n/2 peças, então vamos descobrir quanto só ela produz nos 40 min restantes. Para isso, vamos utilizar a regra de três.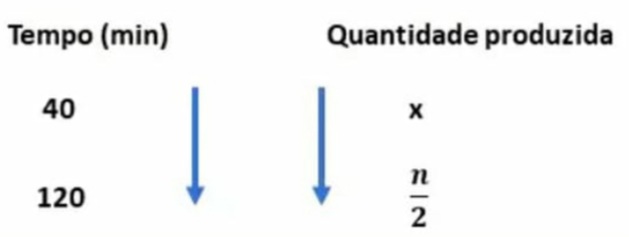 Resolvendo a regra de três:
Resolvendo a regra de três: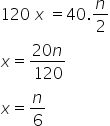 Essa é ahttps://img.comunidades.net/pro/professordiminoi/m19aqqw2s1.png quantidade de peças produzidas em 40 min pela máquina A, portanto em 2 h e 40 min ela sozinha produz:
Essa é ahttps://img.comunidades.net/pro/professordiminoi/m19aqqw2s1.png quantidade de peças produzidas em 40 min pela máquina A, portanto em 2 h e 40 min ela sozinha produz: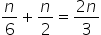 Podemos então, calcular a quantidade produzida pela máquina B em 2h e 40 min, subtraindo da quantidade produzida pelas duas máquinas (n) da quantidade produzida pela máquina A:
Podemos então, calcular a quantidade produzida pela máquina B em 2h e 40 min, subtraindo da quantidade produzida pelas duas máquinas (n) da quantidade produzida pela máquina A: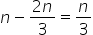 Agora, é possível calcular quanto tempo a máquina B levaria para produzir n/2 peças. Para isso, vamos fazer novamente uma regra de três:
Agora, é possível calcular quanto tempo a máquina B levaria para produzir n/2 peças. Para isso, vamos fazer novamente uma regra de três: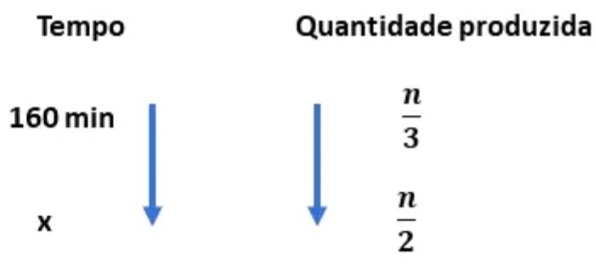 Resolvendo a regra de três, temos:
Resolvendo a regra de três, temos: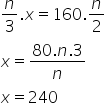 Assim, a máquina B produzirá n/2 peças em 240 min.
Assim, a máquina B produzirá n/2 peças em 240 min.
Alternativa: B
24) (Cefet - MG - 2015) Em uma empresa, 10 funcionários produzem 150 peças em 30 dias úteis. O número de funcionários que a empresa vai precisar para produzir 200 peças, em 20 dias úteis, é igual a
(A) 18
(B) 20
(C) 22
(D) 24
Resolução:
Esse problema envolve regra de três composta, pois temos três grandezas: número de funcionários, número de peças e número de dias.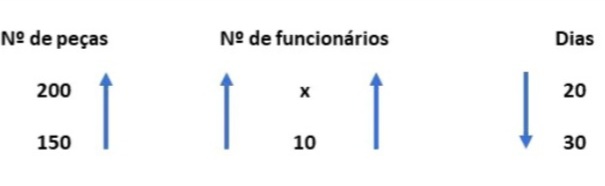 Observando as setas, identificamos que o número de peças e o número de funcionários são grandezas diretamente proporcionais. Já dias e número de funcionários são inversamente proporcionais.
Observando as setas, identificamos que o número de peças e o número de funcionários são grandezas diretamente proporcionais. Já dias e número de funcionários são inversamente proporcionais.
Assim, para resolver a regra de três, temos que inverter o número de dias.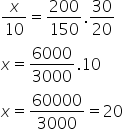 Logo, serão necessários 20 funcionários.
Logo, serão necessários 20 funcionários.
Alternativa: B
25) (ENEM) Uma indústria tem um reservatório de água com capacidade para 900 m3. Quando há necessidade de limpeza do reservatório, toda a água precisa ser escoada. O escoamento da água é feito por seis ralos, e dura 6 horas quando o reservatório está cheio. Esta indústria construirá um novo reservatório, com capacidade de 500 m3, cujo escoamento da água deverá ser realizado em 4 horas, quando o reservatório estiver cheio. Os ralos utilizados no novo reservatório deverão ser idênticos aos do já existente.
A quantidade de ralos do novo reservatório deverá ser igual a
(A) 2
(B) 4
(C) 5
(D) 8
(E) 9
Resolução:
Essa questão é de regra de três composta, sendo as grandezas envolvidas a capacidade do reservatório, o número de ralos e o número de dias.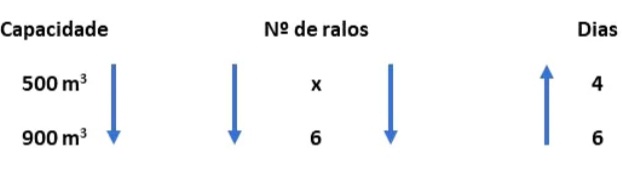 Pelas posição das setas, observamos que a capacidade e o número de ralos são diretamente proporcionais. Já o número de dias e o número de ralos são inversamente proporcionais, vamos inverter então o número de dias:
Pelas posição das setas, observamos que a capacidade e o número de ralos são diretamente proporcionais. Já o número de dias e o número de ralos são inversamente proporcionais, vamos inverter então o número de dias: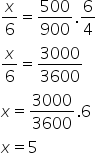 Assim, serão necessários 5 ralos.
Assim, serão necessários 5 ralos.
Alternativa: C
26) (UERJ - 2014) Observe no gráfico o número de médicos ativos registrados no Conselho Federal de Medicina (CFM) e o número de médicos atuantes no Sistema Único de Saúde (SUS), para cada mil habitantes, nas cinco regiões do Brasil.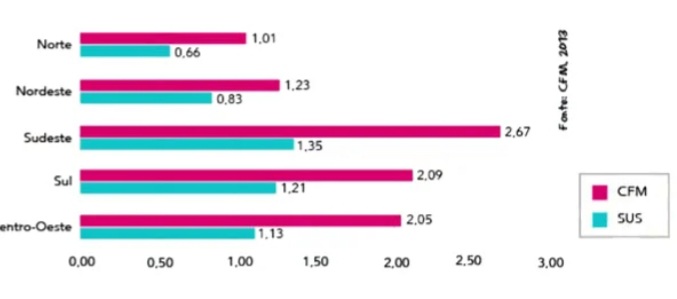
O SUS oferece 1,0 médico para cada grupo de x habitantes.
Na região Norte, o valor de x é aproximadamente igual a:
(A) 660
(B) 1000
(C) 1334
(D) 1515
Resolução:
Para resolver a questão, iremos considerar as grandezas número de médicos do SUS e número de habitantes da região Norte. Portanto, devemos retirar essa informação no gráfico apresentado.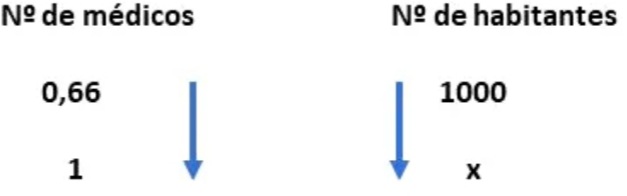 Fazendo a regra de três com os valores indicados, temos:
Fazendo a regra de três com os valores indicados, temos: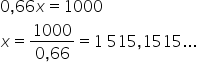 Resolvendo a regra de três, temos:
Resolvendo a regra de três, temos:
Logo, o SUS disponibiliza aproximadamente, 1 médico para cada 1515 habitantes na região Norte.
Alternativa: D
27) (ENEM) Às 17 h 15 min começa uma forte chuva, que cai com intensidade constante. Uma piscina em forma de um paralelepípedo retângulo, que se encontrava inicialmente vazia, começa a acumular a água da chuva e, às 18 horas, o nível da água em seu interior alcança 20 cm de altura. Nesse instante, é aberto o registro que libera o escoamento da água por um ralo localizado no fundo dessa piscina, cuja vazão é constante. Às 18 h 40 min a chuva cessa e, nesse exato instante, o nível da água na piscina baixou para 15 cm.
O instante em que a água dessa piscina terminar de escoar completamente está compreendido entre
(A) 19 h 30 min e 20 h 10 min
(B) 19 h 20 min e 19 h 30 min
(C) 19 h 10 min e 19 h 20 min
(D) 19 h e 19 h 10 min
(E) 18 h 40 min e 19 h
Resolução:
As informações nos indicam que em 45 min de chuva, a altura de água da piscina passou para 20 cm. Depois desse tempo, foi aberto o registro do ralo, entretanto continuou chovendo durante 40 min.
Vamos então, calcular a altura de água que foi adicionada na piscina neste intervalo de tempo, através da seguinte regra de três: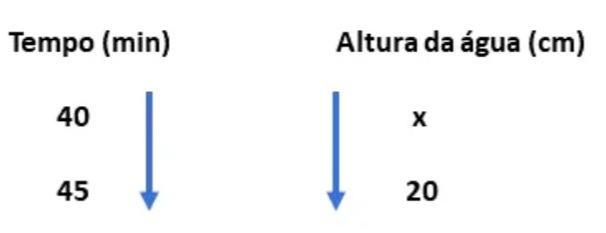 Calculando essahttps://img.comunidades.net/pro/professordiminoi/m33aqqw2s1.png regra de três, temos:
Calculando essahttps://img.comunidades.net/pro/professordiminoi/m33aqqw2s1.png regra de três, temos: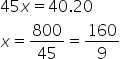 Agora, vamos calcular a quantidade de água que escoou, já que o ralo foi aberto. Essa quantidade será igual a soma de água que foi adicionada, menos a quantidade que ainda existe na piscina, ou seja:
Agora, vamos calcular a quantidade de água que escoou, já que o ralo foi aberto. Essa quantidade será igual a soma de água que foi adicionada, menos a quantidade que ainda existe na piscina, ou seja: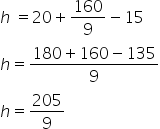 Portanto, escoou 205/9 cm de água desde que o ralo foi aberto (40 min). Agora, vamos calcular quanto tempo será necessário para escoar a quantidade que ficou na piscina, após ter parado de chover.
Portanto, escoou 205/9 cm de água desde que o ralo foi aberto (40 min). Agora, vamos calcular quanto tempo será necessário para escoar a quantidade que ficou na piscina, após ter parado de chover.
Para isso, vamos usar mais uma regra de três: Calculando, temos:
Calculando, temos: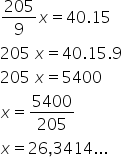 Assim, a piscina ficará vazia em aproximadamente 26 min. Somando esse valor ao instante que se encerra a chuva, ela irá se esvaziar aproximadamente às 19 h 6 min.
Assim, a piscina ficará vazia em aproximadamente 26 min. Somando esse valor ao instante que se encerra a chuva, ela irá se esvaziar aproximadamente às 19 h 6 min.
Alternativa: D
Continua....






