PROBLEMAS MATEMÁRICOS

Professor Diminoi

PROBLEMAS MATEMÁTICOS
Os problemas matemáticos são resolvidos utilizando inúmeros recursos matemáticos, destacando, entre todos, os princípios algébricos, os quais são divididos de acordo com o nível de dificuldade e abordagem dos conteúdos. Nas séries iniciais os cálculos envolvem adições e subtrações; posteriormente, multiplicações e divisões.
Na 2ª fase do Ensino Fundamental os problemas são resolvidos com a utilização dos fundamentos algébricos, isto é, criamos equações matemáticas com valores desconhecidos (letras). Observe algumas situações que podem ser descritas com utilização da álgebra.

O dobro de um número adicionado com 4 → 2x + 4.
A soma de dois números consecutivos → x + (x + 1)
O quadrado de um número mais 10 → x² + 10
O triplo de um número adicionado ao dobro do número → 3x + 2x
A metade da soma de um número com 15 → (x + 15)/2
A quarta parte de um número → x/4

01) (Prova Brasil) Fazendo-se as operações indicadas em 0,74 + 0,5 – 1,5 obtém-se
(A) – 0,64.
(B) – 0,26.
(C) 0,26.
(D) 0,64.
Alternativa: B

02) (Prova Brasil) Numa sacola estão 3 kg de batata, 750 g de feijão, 400 g de queijo, 250 g de azeitona e 500 g de arroz. Qual é o peso total dos alimentos?
(A) 1,9 kg
(D) 3,85 kg
(C) 4,75 kg
(D) 4,9 kg
Alternaviva: D

03) Para uma excursão a um museu, um colégio alugou 4 ônibus. Em cada ônibus foram colocados 35 alunos . Além dos alunos 10 professores acompanham esses alunos na excursão. Quantas pessoas ao todo participaram dessa excursão ?
(A) 100
(B) 150
(C) 160
(D) 170
Resolução:
4 . 35 = 140
Participaram dessa excursão 150 pessoas
Alternativa: B

04) O triplo de um número natural somado a 4 é igual ao quadrado de 5. Calcule-o:
(A) 7
(B) 9
(C) 11
(D) 13
Resolução:
3x + 4 = 5²
3x = 25 – 4
3x = 21
x = 21/3
x = 7
Alternativa: 7

05) O dobro de um número adicionado ao seu triplo corresponde a 20. Qual é o número?
(A) 1
(B) 2
(C) 3
(D) 4
Resolução
2x + 3x = 20
5x = 20
x = 20/5
x = 4
Alternataiva: D

06) Se ao dobro de um número natural adicionarmos 135, vamos obter 503. Qual o número procurado?
(A) 90
(B) 362
(C) 184
(D) 538
Resolução:
2x + 135 = 505
2x = 503 – 135
2x = 362
x = 362/2
x = 184
Alternativa: C
 
07) A soma de um número com seu quíntuplo é igual ao dobro desse mesmo número somado com 40. Que número é esse?
(A) 6
(B) 7
(C) 8
(D) 9
(E) 10
Resolução:
x + 5x – 2x = 40
6x – 2x = 40
4x = 40
x = 40
      4
x = 10
Alternativa: E

09) Em uma caixa existem 12 ovos.
Quantos ovos existem em 24 caixas?
(A) 36 avos
(B) 234 ovos
(C) 500 ovos
(D) 288 avos
Resolução:
São 12 ovos  em cada caixa. Portanto são 12 . 24 = 288
Alternativa: D

10) Uma sala teatral será construída em uma escola para as apresentações de final de ano. A sala possuirá 15 filas de poltronas e cada fila contará com 32 poltronas. Quantas pessoas poderão ser convidadas para a festa de final de ano, no intuito de que todas permaneçam sentadas?
Quantas pessoas poderão ser convidadas para a festa de final de ano, no intuito de que todas permaneçam sentadas?
(A) 36 pessoas
(B) 234 pessoas
(C) 500 pessoas
(D) 480 pessoas
Resolução:
São 32 poltronas em cada fila. Portanto são 32 . 15 = 480
Alternativa: D

11) Na escola de Laís existem 22 salas de aula e em cada uma existem 25 cadeiras. Quantas cadeiras existem na escola de Laís?
(A) 36 cadeiras
(B) 234 cadeiras
(C) 500 cadeiras
(D) 480 cadeiras
Resolução:
São 22 salas com 25 cadeiras cada sala. Portanto 22 . 25 = 550
Alternativa: D

12) Carlos comprou uma televisão no valor de R$ 950,00, dividida em 10 prestações iguais. Ao pagar a 4º prestação, recebeu de presente de seu avô, o restante do dinheiro para a quitação do aparelho. Quanto Carlos recebeu?
Resolução:
O valor do aparelho é igual a R$ 950,00.
Carlos resolveu dividir o televisor em 10 prestações iguais, então devemos realizar uma operação de divisão: 950: 10 = 95 reais.
Carlos efetuou o pagamento de 4 prestações, dessa forma, ainda faltam 6. São as prestações restantes que o avô de Carlos resolveu pagar. Portanto, 95 . 6 = 570 reais.
Resposta: Carlos recebeu R$ 570,00 de seu avô.

13) João tinha uma quantia, gastou 35% e ainda ficou com R$ 97,50. Qual o valor que João tinha inicialmente?
Quando trabalhamos com porcentagem, sempre precisamos nos lembrar de que o valor corresponde a 100%. Dos 100%, João gastou 35%, então: 100% – 35% = 65%.
Resolução:
Os 65% restante, correspondem a R$ 97,50. Dessa forma, temos que:

Resposta: João tinha o valor inicial de R$ 150,00.

14) O preço de uma geladeira, à vista, é R$ 1 200,00. No pagamento em três prestações ocorre um acréscimo de 10% de juros. Qual será o valor da prestação no pagamento parcelado?
Resolução:
Veja que no pagamento parcelado, o preço da televisão aumenta de acordo com o juro de 10%. Vamos calcular 10% do valor à vista da geladeira:

A geladeira sofrerá um aumento de R$ 120,00 R$ 1.200,00 + R$ 120,00 = R$ 1320,00
O preço final para o financiamento é de R$ 1 320,00, que será dividido em três prestações:
1 320 : 3 = 440 reais.
Resposta: Na compra da geladeira a prazo, o valor de cada prestação será de R$440,00.

15) O dobro de um número adicionado ao seu triplo, é igual ao próprio número adicionado a 168. Qual é o número?
Resolução:
Como você não conhece o número, deverá representá-lo por “x”.
Dobro de x = 2 . x = 2x
Triplo de x = 3 . x = 3x
2x + 3x = x + 168
2x + 3x – x = 168
4x = 168
x = 168/4
x = 42
Resposta: O número procurado é o 42

16) A soma de três números pares consecutivos é igual a 96. Determine-os.
Resolução:
1º número: x
2º número: x + 2
3º número: x + 4
( x )+(x + 2) + (x + 4) = 96
x + x + 2 + x + 4 = 96
3x = 96 – 4 – 2
3x = 96 – 6
3x = 90
x = 90/3
x = 30
1º número: x → 30
2º número: x + 2 → 30 + 2 = 32
3º número: x + 4 → 30 + 4 = 34
Resposta: Os números procurados são 30, 32 e 34.

17) O triplo de um número natural somado a 4 é igual ao quadrado de 5. Calcule-o:
(A) 7
(B) 9
(C) 11
(D) 13
Resolução:
3x + 4 = 5²
3x = 25 – 4
3x = 21
x = 21/3
x = 7
Alternativa: 7

18) A idade de um pai é o quádruplo da idade de seu filho. Daqui a cinco anos, a idade do pai será o triplo da idade do filho. Qual é a idade atual de cada um?
Resolução:
Atualmente
Filho: x
Pai: 4x
Futuramente
Filho: x + 5
Pai: 4x + 5
4x + 5 = 3 . (x + 5)
4x + 5 = 3x + 15
4x – 3x = 15 – 5
x = 10
Pai: 4x → 4 . 10 = 40
Resposta: O filho tem 10 anos e o pai tem 40.

19) O dobro de um número adicionado ao seu triplo corresponde a 20. Qual é o número?
(A) 1
(B) 2
(C) 3
(D) 4
Resolução
2x + 3x = 20
5x = 20
x = 20/5
x = 4
Alternataiva: D

20) Em uma chácara existem galinhas e coelhos totalizando 35 animais, os quais somam juntos 100 pés. Determine o número de galinhas e coelhos existentes nessa chácara.
Resolução:
Galinhas: g
Coelhos: c
g + c = 35
Cada galinha possui 2 pés e cada coelho 4, então:
2g + 4c = 100
Sistema de equações
Isolando c na 1ª equação:
g + c = 35
c = 35 – g
Substituindo c na 2ª equação:
2g + 4c = 100
2g + 4  . (35 – g) = 100
2g + 140 – 4g = 100
2g – 4g = 100 – 140
– 2g = – 40
g = 40/2
g = 20
Calculando c
c = 35 – g
c = 35 – 20
c = 15

21) A soma de três números inteiros consecutivos é igual a 72. Determine o valor dos números.
Resolução:
1º número: x
2º  número: x + 1
3º número: x + 1 + 1
x + (x + 1) + (x + 1 + 1) = 72
x + x + 1 + x + 2 = 72
3x = 72 – 1 – 2
3x = 69
x = 69/3
x = 23
Os números procurados são:
1º número: 23
2º número: 24
3º número: 25

22) A adição de cinco números pares positivos e consecutivos corresponde a 240. Calcule o valor desses números.
Resolução:
1º número par: 2x
2º número par consecutivo: 2x + 2
3º número par consecutivo: 2x + 2 + 2
4º número par consecutivo: 2x + 2 + 2 + 2
5º número par consecutivo: 2x + 2 + 2 + 2 + 2
2x + 2x + 2 + 2x + 2 + 2 + 2x + 2 + 2 + 2 + 2x + 2 + 2 + 2 + 2 = 240
10x + 20 = 240
10x = 240 – 20
10x = 220
x = 220/10
x = 22
1º: 2x → 2 . 22 = 44
2º: 2x + 2  → 2 . 22 . 2 = 46
3º: 2x + 2 + 2 → 2 * 22 + 2 + 2 = 48
4º: 2x + 2 + 2 + 2 → 2 * 22 + 2 + 2 + 2 = 50
5º: 2x + 2 + 2 + 2 + 2 → 2 * 22 + 2 + 2 + 2 + 2 = 52
Os números são 44, 46, 48, 50 e 52.

23) Em uma eleição para a escolha do representante do grêmio estudantil de uma escola, votaram 943 alunos. Carlos teve 7 votos a mais que Paulo, e André teve 5 votos a mais que Carlos. Quantos votos teve o aluno vencedor?
Resolução:
Carlos: (x + 7) votos
Paulo: x votos
André: (x + 7) + 5 votos
(x + 7) + x + (x + 7) + 5 = 943
x + 7 + x + x + 7 + 5 = 943
3x + 19 = 943
3x = 943 – 19
3x = 924
x = 924/3
x = 308
Carlos: (x + 7) → 308 + 7 = 315 votos
Paulo: x → 308 votos
André: (x + 7) + 5 → 308 + 7 + 5 = 320 votos.
O aluno vencedor foi André, com 320 votos.

24) (Unifor–CE) José ganhou um prêmio no valor de R$ 5.000,00 e dividiu-o entre seus três filhos da seguinte forma: Pedro recebeu R$300,00 a menos que João, que, por sua vez, recebeu R$ 100,00 a mais que Antônio. Determine a quantia recebida por Pedro.  
Resolução:
Antônio: x
João: x + 100
Pedro: (x + 100) – 300 → x + 100 – 300 → x – 200
x + (x + 100) + (x – 200) = 5000
x + x + 100 + x – 200 = 5000
3x – 100 = 5000
3x = 5000 + 100
3x = 5100
x = 5100/3
x = 1700
Pedro: x – 200 → 1700 – 200 → 1500
Pedro recebeu a quantia de R$1.500,00.

25) As idades de Carlos e Bruno, se somadas, correspondem o total de 45 anos. Há 6 anos, a idade de Carlos era o dobro da idade de Bruno. Calcule o valor da idade de Bruno. 
Resolução:
C + B = 45 → B = 45 – C
Há 6 anos, as idades eram: C – 6  e  B – 6, e o problema diz que a idade de Carlos era o dobro da idade de Bruno, então:
C – 6 = 2 . (B – 6)
C – 6 = 2B – 12
C – 6 = 2 . (45 – C) – 12
C – 6 = 90 – 2C – 12
C + 2C = 90 – 12 + 6
3C = 84
C = 84/3
C = 28
C + B = 45
B = 45 – C
B = 45 – 28
B = 17
Resposta: A idade de Bruno corresponde a 17 anos.

26) (UFMG) A soma entre dois números é 125. Um deles é igual a 2/3 do outro. A diferença entre o maior e o menor, nesta ordem, é:
(A) 25 
(B) 42 
(C) 45 
(D) 60 
(E) 75
Resolução:
As equações são as seguintes:
x + y = 125
x = 2/3y
x + y = 125
2/3y + y = 125
2y + 3y = 375
5y = 375
y = 375/5
y = 75
x = 2/3y
x = 2/3 * 75
x = 50
Diferença entre x e y: 75 – 50 = 25
Alternativa: A

27) (VUNESP-99) Um clube promoveu um show de música popular brasileira ao qual compareceram 200 pessoas entre sócios e não sócios. No total, o valor arrecadado foi de R$ 1 400,00 e todas as pessoas pagaram ingresso. Sabendo-se que o preço do ingresso foi de R$ 10,00 e que cada sócio pagou metade desse valor, o número de sócios presentes foi:
(A) 80 
(B) 100 
(C) 120 
(D) 140 
(E) 160
Resolução:
Sócios: x (pagaram a metade = 5 reais)
Não sócios: y (pagaram inteira = 10 reais)
Equações:
x + y = 200 → x = 200 – y
5x + 10y = 1400
5x + 10y = 1400
5 .(200 – y) + 10y = 1400
1000 – 5y + 10y = 1400
5y = 1400 – 1000
5y = 400
y = 400/5
y = 80
x = 200 – y
x = 200 – 80
x = 120
O número de sócios que compareceram ao show é igual a 120.
Alternativa: C  

28) (ANGLO) Pedro pediu que seu primo Carlos pensasse em um número e, a seguir, fizesse as seguintes operações:
1 – Adicionasse 40 ao número pensado.
2 – Multiplicasse por 5 o resultado obtido.
3 – Dividisse por 2 o novo resultado.
Ao término dessas operações, Carlos encontrou 120 como resultado. O número que  Carlos pensou era :
(A) negativo
(B) zero           
(C) positivo maior que 8
(D) par   
(E) ímpar
Resolução:
Equação referente ao problema proposto:
O número pensado por Carlos é igual a 8.
Alternativa: D

29) (VUNESP-04) Maria tem em sua bolsa R$15,60 em moedas de R$ 0,10 e de R$ 0,25. Dado que o número de moedas de 25 centavos é o dobro do número de moedas de 10 centavos, o total de moedas na bolsa é:
(A) 68.
(B) 75.
(C) 78.
(D) 81.
(E) 84.
Resolução
Seja x o número de moedas de R$ 0,10 e y o número de moedas de R$ 0,25. Portanto, se multiplicarmos 0,10 por x e adicionarmos ao produto de 0,25 por y, teremos o total de R$ 15,60, como a equação aponta:
0,10.x + 0,25.y = 15,60 (*)
A segunda informação no texto nos garante que y = 2.x. Resolvendo pelo método da substituição, substituiremos o valor encontrado para y em (*). Sendo assim:
0,10.x + 0,25.(2.x) = 15,60
0.10.x + 0,5 x = 15,60
0,6. x = 15,6
x = 26
Retornando à equação y = 2.x, vamos substituir o valor encontrado para x:
y = 2.x
y = 2.26
y = 52
Portanto, Maria tem 26 moedas de R$ 0,10 e 52 moedas de R$ 0,25. No total, Maria tem 78 moedas.
Alternativa: C

30) (UNIFESP-04) Numa determinada livraria, a soma dos preços de aquisição de dois lápis e um estojo é R$10,00. O preço do estojo é R$5,00 mais barato que o preço de três lápis. A soma dos preços de aquisição de um estojo e de um lápis é:
(A) R$3,00.
(B) R$6,00.
(C) R$12,00.
(D) R$4,00.
(E) R$7,00.
Resolução:
Seja l o preço de um lápis e e o preço de um estojo. Sabemos que se somarmos o preço de dois lápis com o de um estojo, teremos:
l + e = 10
Se o preço do estojo é R$5,00 mais barato que o preço de três lápis, podemos dizer que o valor de três lápis equivale ao preço de um estojo mais R$ 5,00, isto é:
l = e + 5
e = 3.l – 5
Utilizaremos novamente o método da substituição. Se e = 3.l – 5, substituiremos esse valor em 2.l + e = 10. Haverá, assim, a formação da seguinte equação:
2.l + 3.l – 5 = 10
5.l = 10 + 5
l = 15
     5
l = 3
Portanto, o preço do lápis é R$ 3,00. Mas se o preço do estojo é dado por e = 3.l – 5, temos:
e = 3 . 3 – 5
e = 9 – 5
e = 4
O preço do estojo é R$ 4,00. Dessa forma, a aquisição de um estojo e de um lápis custará R$ 7,00. Alternativa: E

31) Em uma praça há 18 crianças andando de bicicleta ou de skate. No total, há 50 rodas girando pela praça. Quantas crianças andam de bicicleta e quantas andam de skate?
Resolução:
Nós não conhecemos o número de bicicletas e de skates que circulam pela praça, mas nós sabemos que a soma das bicicletas e dos skates é a mesma do total de crianças. Portanto, se chamarmos por b as bicicletas e por s os skates, teremos:
s + b = 18
Se há 50 rodas girando pela praça, podemos dizer que a soma das rodas das bicicletas e dos skates é 50. Vale lembrar que cada skate tem 4 rodas e cada bicicleta tem 2 rodas. Teremos uma nova equação em função das rodas:
4.s + 2.b = 18
Podemos formar o seguinte sistema de equações: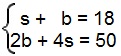
​
Agora, multiplicamos a primeira equação por menos 2, somando-a com a segunda:
– 2b – 2s = – 36
2b + 4s = 50
2s = 14
s = 14
      2
s = 7
Então, nesse parque, há 7 skates. Resta-nos encontrar a quantidade de bicicletas. Para isso, utilizaremos a equação s + b = 18, na qual substituiremos o valor de skates encontrado:
s + b = 18
7 + b = 18
b = 18 – 7
b = 11
Portanto, nessa praça há 7 crianças andando de skate e 11 crianças andando de bicicleta.

32) A soma de dois números é 37. A diferença entre eles é 9. Quais são esses números?
Resolução:
Vamos identificar os números que procuramos como x e y. Vamos supor ainda que x > y. Temos então que x + y = 37 e x – y = 9.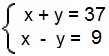
​
Utilizaremos o método da adição, somando as duas equações:
x + y = 37
x – y = 9
2x = 46
x = 46
      2
x = 23
Substituindo esse valor em alguma das equações, teremos:
x + y = 37
y = 37 – x
y = 37 – 23
y = 14
Portanto, os números procurados são 23 e 14.

33) Mariana comprou 3 canetas e uma lapiseira, gastando ao todo 60 reais. A lapiseira custou 24 reais. Quanto custou cada caneta, se elas tem o mesmo preço?
Resolução:
60 - 24 = 36
36 : 3 = 12
Resposta: cada caneta custou 12 reais

23) Para uma excursão a um museu, um colégio alugou 4 ônibus. Em cada ônibus foram colocados 35 alunos . Além dos alunos 10 professores acompanham esses alunos na excursão. Quantas pessoas ao todo participaram dessa excursão ?
(A) 100
(B) 150
(C) 160
(D) 170
Resolução:
4 . 35 = 140
Participaram dessa excursão 150 pessoas
Alternativa: B

34) Se ao dobro de um número natural adicionarmos 135, vamos obter 503. Qual o número procurado?
(A) 90
(B) 362
(C) 184
(D) 538
Resolução:
2x + 135 = 505
2x = 503 – 135
2x = 362
x = 362/2
X = 184
Alternativa: C

35) (UFSM-RS adaptada) Sabe-se que o preço a ser pago por uma corrida de táxi inclui uma parcela fixa, que é denominada bandeirada, e uma parcela variável, que é função da distância percorrida. Se o preço da bandeirada é R$4,60 e o quilômetro rodado é R$0,96, qual a distância percorrida por um passageiro que pagou R$19,00?
(A) 15 km
(B) 16 km
(C) 17 km
(D) 18 km
(E) 19 km
Resolução:
O problema proposto é um exemplo de função, em que o custo da viagem (variável dependente) depende da quantidade de quilômetros rodados (variável independente). Quando uma dessas variáveis é dada, o problema reduz-se a resolver uma equação para descobrir a outra.
Assim, o primeiro passo é construir uma função que represente a situação acima. Sendo x a quantidade de quilômetros rodados e C o custo da viagem, essa função será:
C = 0,96x + 4,60
Observe que o problema afirma que a viagem custou R$ 19,00. Substituindo esse valor, teremos:
19 = 0,96x + 4,60
Agora, basta resolver essa equação para encontrar x, que é a distância percorrida pelo passageiro. Coloque no primeiro membro os termos que possuem incógnita e, no segundo, aqueles que não possuem, lembrando-se de mudar o sinal do termo que muda de lado.
– 0,96x = 4,6 – 19
Realize os cálculos necessários:
– 0,96x = – 14,4
Nessa condição, multiplique a equação por – 1.
– 0,96x = – 14,4 (– 1)
0,96x = 14,4
Agora divida toda a equação por 0,96 (ou passe 0,96 para o outro lado dividindo).
x = 14,4
      0,96
x = 15
A distância percorrida pelo passageiro foi de 15 quilômetros. 
Alternativa: A

36) A soma de três números inteiros consecutivos é 60. Qual é o produto entre esses três números?
(A) 19, 20 e 21
(B) 19
(C) 7980
(D) 6859
(E) 44
Resolução:
Números inteiros são aqueles que não são decimais, isto é, que não precisam de vírgula para serem escritos. Já consecutivo é um número que vem imediatamente após o anterior na ordem de contagem. Por isso, a diferença entre números consecutivos sempre é 1.
Dessa forma, tomando x como o primeiro dos números consecutivos do problema, podemos afirmar que o segundo é x + 1 e o terceiro é (x + 1) + 1 ou x + 2. A soma desses três números é igual a 60, assim, podemos escrever:
x + (x + 1) + (x + 2) = 60
Por meio dessa equação, é possível descobrir o valor do primeiro número da sequência, depois adicionar 1 para descobrir o segundo e, por fim, adicionar 2 para descobrir o terceiro. Para tanto, elimine os parênteses. Como são números positivos, não é necessário fazer jogo de sinais. Observe:
x + (x + 1) + (x + 2) = 60
x + x + 1 + x + 2 = 60
No primeiro membro devem permanecer apenas os números acompanhados de incógnitas e, no segundo, todos os números que não possuem incógnita. Para trocar um número de lado, troque seu sinal:
x + x + 1 + x + 2 = 60
x + x + x = 60 – 1 – 2
Realize as operações que forem possíveis.
3x = 57
Agora divida toda a equação por 3:
x = 57
      3
x = 19
Assim, o menor número é 19, o segundo é 19 + 1 = 20 e o terceiro é 19 + 2 = 21. Observe que a soma entre eles realmente é igual a 60.
19 + 20 + 21 = 60
Como o exercício pede o produto entre esses números, é necessário resolver ainda a seguinte expressão:
19·20·21 = 7980
Alternativa: C

37) Um terreno retangular possui o comprimento cinco vezes maior que a largura. Sabendo que o perímetro desse terreno é igual a 180 metros, a largura e o comprimento medem, respectivamente:
(A) 30 m e 150 m
(B) 75 m e 15 m
(C) 15 m e 75 m
(D) 150 m e 30 m
(E) 90 m e 90 m
Resolução:
Seja x a largura desse retângulo, então, 5x é o seu comprimento. Sabendo que os retângulos possuem lados opostos iguais e que o perímetro de um retângulo é dado pela soma dos comprimentos de todos os seus lados, podemos escrever a seguinte equação:
x + 5x + x + 5x = 180
Como todos os termos já estão no lado adequado, faremos as operações que são possíveis:
12x = 180
Agora basta dividir a equação por 12:
x = 180
      12
x = 15
A largura do terreno é 15 metros. Sabendo que o comprimento é cinco vezes maior, podemos calculá-lo:
5x = 5·15 = 75 metros
Alternativa: C

38) A soma de um número com seu quíntuplo é igual ao dobro desse mesmo número somado com 40. Que número é esse?
(A) 6
(B) 7
(C) 8
(D) 9
(E) 10
Resolução:
x + 5x – 2x = 40
6x – 2x = 40
4x = 40
x = 40
      4
x = 10
Alternativa: E

Soma dos números consecutivos 1, 2, 3
A sequência 1, 2 e 3 e regularidades numéricas
a) a soma dos termos
1 + 2 + 3 = 6
b) O produto de cada parcela pela soma
1 . 6 = 6
2 . 6 = 12
3 . 6 = 18
c) A soma dos produtos
6 + 12 + 18 = 36
36 é um quadrado perfeito e a sua raiz quadrada é 6.
6 é a soma da sequência: 1, 2 e 3.
Soma dos números consecutivos 2, 3, 4
A sequência 2, 3 e 4 e regularidades numéricas
a) a soma dos termos
2 + 3 + 4 = 9
b) O produto de cada parcela pela soma
2 . 9 = 18
3 . 9 = 27
4 . 9 = 36
c) A soma dos produtos
18 + 27 + 36 = 81
81 é um quadrado perfeito e a sua raiz quadrada é 9.
9 é a soma da sequência: 2, 3 e 4.
Soma dos números consecutivos 4, 5, 6
A sequência 4, 5 e 6 e regularidades numéricas
a) a soma dos termos
4 + 5 + 6 = 15
b) O produto de cada parcela pela soma
4 . 15 = 60
5 . 15 = 75
6 . 15 = 90
c) A soma dos produtos
60 + 75 + 90 = 225
225 é um quadrado perfeito e a sua raiz quadrada é 15.
15 é a soma da sequência: 4, 5 e 6.

Soma dos números consecutivos 5, 6, 7
A sequência 5, 6 e 7 e regularidades numéricas
a) a soma dos termos
5 + 6 + 7 = 18
b) O produto de cada parcela pela soma
5 . 18 = 90
6 . 18 = 108
7 . 18 = 126
c) A soma dos produtos
90 + 108 + 126 = 324
324 é um quadrado perfeito e a sua raiz quadrada é 18.
18 é a soma da sequência: 5, 6 e 7.

Soma dos números consecutivos 6, 7, 8
A sequência 6, 7 e 8 e regularidades numéricas
a) a soma dos termos
6 + 7 + 8 = 21
b) O produto de cada parcela pela soma
6 . 21 = 126
7 . 21 = 147
8 . 21 = 168
c) A soma dos produtos
126 + 147 + 168 = 441
441 é um quadrado perfeito e a sua raiz quadrada é 21.
21 é a soma da sequência: 6, 7 e 8.

Soma dos números consecutivos 7, 8 , 9
A sequência 7, 8 e 9 regularidades numéricas
a) a soma dos termos
7 + 8 + 9 = 24
b) O produto de cada parcela pela soma
7 . 24 = 168
8 . 24 = 192
9 . 24 = 216
c) A soma dos produtos
168 + 192 + 216 = 576
576 é um quadrado perfeito e a sua raiz quadrada é 24.
24 é a soma da sequência: 7, 8 e 9.

39) Como queremos o produto de três números naturais consecutivos, sendo que um desses números é o 13, então temos três possibilidades:
O 13 é o menor número
O 13 é o maior número
O 13 está entre os outros dois números.

Se o 13 for o menor número, então os três números consecutivos serão: 13, 14, 15. Logo, a multiplicação é: 2730.
Se o 13 for o maior número, então os três números consecutivos serão: 11, 12, 13. Logo, a multiplicação é: 1716.
Se o 13 estiver entre os outros dois números, então os três números consecutivos serão: 12, 13, 14. Logo, a multiplicação  de
13 . 14 . 15 = 2184

40) Se o menor deles é 19, e são três números consecutivos, os outros dois são 20 e 21. 
Pra saber o produto deles é fácil, só multiplicar:
Com isso, 19 . 20 . 21 = 7980

41) A soma de três números consecutivos é igual a 249. Qual a soma dos algarismos do primeiro número?
x + x + 1 + x + 2 = 249
3x = 249 -1 -2
3x = 246
x = 246/3
x = 82 (1º)
x = 8+2
x = 10

42) Dado o sistema abaixo, encontre o conjunto solução.
Resolução:
Isolando x na 1ª equação
x + y = 7
x = 7 – y
Isolando x na 2ª equação
x – 2y = – 5
x = – 5 + 2y
Realizando a comparação
x = x
7 – y = – 5 + 2y
– y – 2y = –5 –7
– 3y = – 12 *(–1)
3y = 12
y = 12/3
y = 4
Para calcularmos o valor de x utilizamos qualquer uma das equações substituindo y por 4.
x = – 5 +2y
x = – 5 + 2 * 4
x = – 5 + 8
x = 3
Solução do sistema: (3; 4)

43 Dado o sistema abaixo, encontre o conjunto solução.
Isolando x na 1ª equação
x + 2y = 40
x = 40 – 2y
Isolando y na 2ª equação
x – 3y = – 35
x = – 35 + 3y
Realizando a comparação
x = x
–35 + 3y = 40 – 2y
3y + 2y = 40 + 35
5y = 75
y = 15
Calculamos o valor de x substituindo y = 15 em qualquer das equações.
x = – 35 + 3y
x = – 35 + 3 . 15
x = –35 + 45
x = 10

Solução do sistema: (10; 15)

44) Dado o sistema abaixo, encontre o conjunto solução.
Isolar y na 1ª equação
2x + y = 4
y = 4 – 2x
Isolar y na 2ª equação
3x + y = – 3
y = – 3 – 3x
Realizando a comparação
y = y
4 – 2x = – 3 – 3x
–2x + 3x = –3 – 4
x = –7
Calculando y através de x = – 7
y = – 3 – 3x
y = –3 – 3 * (–7)
y = –3 + 21
y = 18
Solução do sistema: (–7; 18)

 

Continua...