MONÔMIOS & EXPRESSÕES ALGÉBRICAS

Professor Diminoi

MONÔMIOS & EXPRESSÕES ALGÉBRICAS

Partes de um monômio
Um monômio é dividido em duas partes, um número, que é o coeficiente do monômio e uma variável ou o produto de variáveis (letras), inclusive suas potências, caso existam.

Exemplos:
a) 2x → 2 é o coeficiente desse monômio e x é sua parte literal
b) 3xy²→ 3 é o coeficiente desse monômio e xy² é sua parte literal
c) wz → 1 é o coeficiente desse monômio e wz é sua parte literal

Grau de um monômio
Para um monômio com coeficientes não nulos, temos que seu grau se dará através da soma entre os expoentes da parte literal.

Exemplos:
a) 1/2x²y³z⁴→ esse é um monômio do 9º grau (2 + 3 + 4 = 9)
b) bcd → esse é um monômio do 3º grau (1 + 1 + 1+ = 3).
c) 25 → esse é um monômio de grau zero (ausência da parte literal);
d) Entre os monômios 2x², 1/3x³e 0,5x⁵o de maior grau é 0,5x⁵, pois 5 > 2 > 1/3.

Observação: Pode-se também atribuir o grau de um monômio em relação a uma de suas incógnitas. Para isso é necessário fazer menção a incógnita considerada.

Exemplos:
a) ab²→ esse é um monômio do 2º grau em relação a variável b.
b) wz³→ esse é um monômio do 1º grau em relação a variável w
c) 4 → esse é um monômio de grau zero pela ausência de variável (eis)

Semelhança entre monômios
Dois ou mais monômios são semelhantes quando suas partes literais são iguais.
a) 3xy e 2/5xy são iguais, pois possuem a mesma parte literal xy;
b) 0,5a³b²e 10a³b²são iguais, pois possuem a mesma parte literal a³b²;
c) - 4vwz, 2,3vwz e 1/3vwz são iguais, pois possuem a mesma parte literal vwz.

Adicionando e/ou subtraindo monômios
Na adição de monômios com a mesma parte literal, adicionaremos os coeficientes entre si e manteremos a parte literal.
a) 2mn + 14mn + 5mn = 21mn(2 + 14 + 5 = 21)
b) 2,5 x²y + 1,5x²y – 0,5x²y = 3,5x²y(2,5 + 1,5 – 0,5 = 3,5)
c) 3/2cd³– 1/2cd³+ 5/2cd³ = 7/2cd³ (3/2 – 1/2 + 5/2 = 7/2)

Um refrigerante custa x reais. Márcio comprou 3 refrigerantes, Aline comprou 2, Poliana comprou 4 e Arthur comprou 1. Qual é o monômio que representa quanto essas pessoas gastaram? → 3 + 2 + 4 + 1 = 10, portanto 10x 

Multiplicação de monômios
Antes de prosseguirmos nesse tópico, devemos relembrar uma propriedade muito importante da potenciação.
a^m . aⁿ = a^m+n

Na multiplicação de monômios, multiplicamos entre si os coeficientes, assim como, a parte literal.
a) 6x²y . 2x⁴. 3y → 6.2.3 = 36 e x².x⁴.y.y = x⁶y², ou seja, 36x⁶y²
b) 4abc⁴. 4ab²c → 4.4 = 16e a.b.b².c⁴.c = a²b³c⁵, ou seja, 16a²b³c⁵
c) 1/2wz . 2/3z → 1/2.2/3 = 2/6ou 1/3e z.z = wz², ou seja, 1/3wz²

Divisão de monômios
Convém relembrarmos mais uma propriedade importante da potenciação.
a^m : aⁿ = a^{m – n}

Na divisão de monômios, dividimos entre si os coeficientes, bem como, a parte literal.
a) 12x⁴y : 3x²y → 12:3 = 4, x⁴:x²= x²e y:y = 1, ou seja, 4x²
b) 50b⁶c⁸d⁴: 25b²c⁴d⁴→ 50:25 = 2, b⁶:b² = b⁴, c⁸:c⁴ = c⁴ e d⁴:d⁴ = 1, ou seja, 2b⁴c⁴
c) 4mn¹⁰: mn²→ 4 : 1 = 4, m:m = 1 e n¹⁰:n² = n⁸, ou seja, 4n⁸

Potenciação de monômios
Antes de darmos continuidade ao tema, vale lembrar as seguintes propriedades da potência a fim de facilitarmos o cálculo de potências de monômios.
(a^m)ⁿ = a^m.n 
(a . b)^m = a^m . b^m
a) (4x³)²→ 4²= 16 e x² = x⁶, ou seja, 16x⁶;
b) (-3 . wz³)³→ (-3)³. w³ . z^3.3 = -27w³z⁹;

Exemplo:
Encontrar o quadrado do monômio -11a⁴ → (-11a⁴)² = (-11)² . a^4.2 = 121a⁸.

Retomando: Monômios são expressões algébricas que possuem multiplicações entre números e incógnitas (letras que representam algum número desconhecido).
Assim, uma expressão não é monômio quando apresenta pelo menos uma adição ou subtração ou ainda quando possui alguma divisão por incógnita.

Exemplos monômios
a) 3x
b) –2y²
c) 5
d) 2xy

Monômios e suas operações
01) Esta figura é uma representação de um retângulo, cujas medidas dos lados, expressas em unidades de comprimento, são x e y.
a) Qual é a expressão algébrica que representa a área desse retângulo?
Resolução:
A = x . y

b) Qual é a expressão algébrica que representa o perímetro do retângulo da figura?
Resolução:
P = 2x + 2y ou P = x + y + x + y

c) Entre as duas expressões algébricas que você escreveu nos itens a e b, existe uma diferença. Qual é essa diferença?
Resolução:
A diferença está relacionada ao número de termos presentes e na operação realizada em cada expressão algébrica.

Em (a) temos 2 termos e aplicamos a multiplicação
Em (b) temos 4 termos e aplicamos a soma

Retomada: Um monômio é uma expressão algébrica com apenas um termo. Esse termo pode ser formado por uma constante, uma variável ou o produto de uma constante por uma ou mais variáveis.

Exemplos de monômios
a) 3x
b) -2y²
c) 5
d) 2xy

Observação: Geralmente, um monômio é formado por duas partes: um número, chamado de coeficiente do monômio, e uma variável ou uma multiplicação de variáveis (considerando inclusive seus expoentes), achada de parte literal.

Grau de um Monômio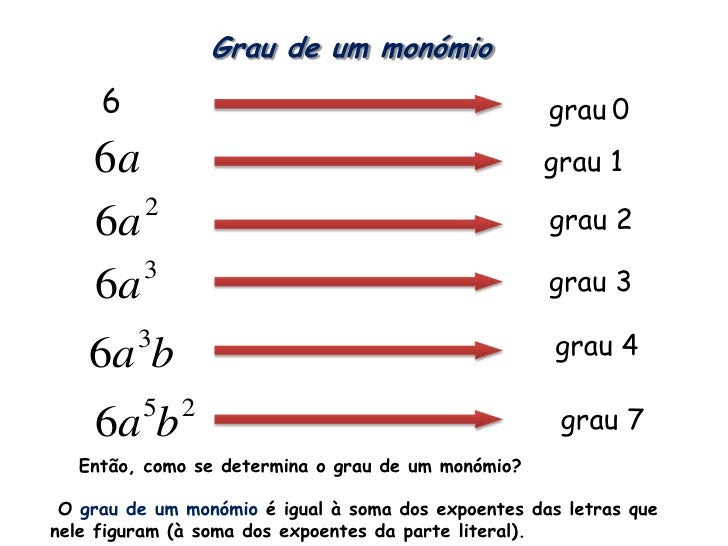
Com coeficiente não nulo e dado pela soma dos expoentes das variáveis.

Exemplos:
a) O monômio 2x³y² e do 5º grau
b) O monômio 13x²y é do 3º grau

Casos Especais: O grau de um monômio também pode ser dado em relação a uma de suas variáveis.
Nesse caso, o grau do monômio corresponde ao expoente da variável considerada.

Exemplos:
a) O monômio 2x³y2 é do 3º grau em relação a variável x
b) O monômio 13x²y é do 1º grau em relação a variável y.

Quando dois ou mais monômios apresentam a mesma parte literal, eles são denominados semelhante ou termos semelhantes.

Exemplos:
a) 10x²y e -2x²y
b) 13x³y³ e 25x³y³
c) 2x²y² / 3x²y²

QUESTÕES RESOLVIDAS
02) Identifique os coeficientes de cada monômio a seguir:
a) 5x²y → 5
b) - 12x² → -12
c) 32x³y² → 32
d) √2x² → √2
e) x²y / 3 → 1/3

03) Qual é o valor expressão 7,5a²b^xc⁵ que se deve colocar no lugar do expoente x para que o monômio  seja do 10º grau?
(A) 2
(B) 3
(C) 4
(D) 5
(E) 6
Resolução:
O grau de um monômio é dado pela soma:
2 + x + 5 = 10
2 + 3 + 5 = 10
Com o x valendo 3, teremos como 10 a soma dos coeficientes.
Alternativa C

04) É correto falar que os monômios 2x²y e 2x² são semelhantes? Justifique.
Resolução:
Não, pois a parte literal dos monômios é diferente.
Ou seja, um é x²y e o outro é apenas x²

05) Para gastar 100 calorias, Caio deve correr x minutos em um terreno plano ou fazer ginástica aeróbica por y minutos. Se Caio quiser perder 800 calorias, qual é o monômio que representa o tempo, em minutos, que ele deve:
a) correr em um terreno plano?
Resolução:
800x/100 = 8x

b) fazer ginástica aeróbica?
Resolução:
800y/100 = 8y

Monômios e suas operações II
06) Observe a figura a seguir formada por dois retângulos, A e B.
a) Qual é a área da figura A?
b) Qual é a área da figura B?
c) Qual é a soma das áreas das figuras A e B?
Resolução:
a) 30 . 5x = 150x cm²
b) 20 . 3x = 60x cm²
c) 150x cm² + 60x cm² = 210x cm²

Adição e Subtração de monômios de partes literal semelhantes
Ao adicionarmos ou subtrairmos monômios devemos levar em consideração as partes literais semelhantes, adicionando ou subtraindo os coeficientes e preservando a parte literal.

Exemplos:
a) 5ax + 7ax = 12ax
b) 5ax – 7ax = –2ax
c) 17x³ + 20x³ = (17 + 20)x³ = 37x³
b) 2ax² + 10b – 6ax² – 8b = (2 – 6)ax² + (10 – 8)b = –4ax² + 2b
e) –4xy + 6xy – 5xy = (–4 + 6 –5)xy = – 3xy
f) 5b³ + 7c³ + 6b³ – 2c³ = (5 + 6)b³ + (7 – 2)c³ = 11b³ + 5c³

07) Resolva as expressões a seguir:
a) 2a² + 2a² + 3a² = 7a²
b) 4x + 10x + 5x = 19x
c) 25y – 12y = 13y
d) 48k + 23k – 13k = 58k

Na multiplicação de monômios devemos multiplicar coeficiente por coeficiente e parte literal por parte literal. Observe que: ao multiplicar partes literais iguais, aplique a multiplicação de potências de bases iguais: somar os expoentes e repetir a base.

Exemplos:
a) 2x . 3x =
(3 . 2) . (x . x) =
6 . x² =
6x²

b) 4x . 6z =
(4 . 6) . (x . z) =
24 . xz =
24xz

c) 5b² . 10b² . c³ =
(5 . 10) . (b² . b² . c³) =
50 . b4c³ =
50b4c³

d) 4a²x³ . (–5ax²) =
[4.(–5)] . (a²x³ . ax²) =
–20 .a³x5 =
–20a³x5"

07) Efetue a multiplicação dos monômios a seguir observado cada caso
a) 6x . 2x = 12x²
b) 2x³ . 3xy³ = 6x³y³
c) – 2x³ . 3y³ = 6x³y³

09) Resolva as expressões a seguir:
a) (3x³) . (45x) = 134x⁴
b) (28x²) . (7x) = 196x³
c) (125a²) . (2a³) = 250a⁵
d) (16x²y⁴) . (4xy³) = 64x³y⁷

10) Se A = x + 2y; B = 5x – 4 e C = 7 – 8x, resolva as expressões indicadas por: 
a) A + B = 6x + 2y – 4
b) C – A = –9x – 2y +7
c) B – C = 13x – 11
d) A + B + C = –2x + 2y + 3

11) Qual a expressão algébrica que representa o volume do bloco retangular a seguir?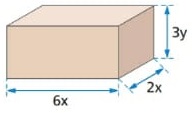
Resolução:
(6x) . (2x) . (3y) = 6 . 2 . 3 . x . x . y = 36x²y

Observações:

Divisão de monômios
Na divisão de monômios devemos dividir coeficiente por coeficiente e parte literal por parte literal. Ao dividir partes literais iguais, aplique a divisão de potências de bases iguais: subtrair os expoentes e repetir a base.

Exemplos:
a) 16x⁵ / 4x² = 4x³ → (16:4) e (x5 : x²)
b) 20a²x³ / (–5ax²) = –4ax → [20 / (–5)] e (a²x³ : ax²)
c) 81x / 9x = 9
d) 144x³b² / 2xb = 72x²b

12) Marcos efetuou a divisão 10x²y por 2 e obteve como resposta 5xy. A resposta de Marcos está correta? Justifique.
Resolução:

Não, pois a expressão da divisão é:

13) Se você dividir o cubo da soma (–7y + 10y + 2y) pela soma (10y² + 15y²), que monômio encontrará?
Resolução:
 

14) Calcule o quociente dos monômios:
a) (32abc) ÷(+8ac) = 4b
b) (40x⁷y²) ÷ (10x⁴y²) = 4x³
c) (100a³) ÷ (25a³) = 4
d) (55a⁴bc² ) ÷ (11a²bc) = 5a²c

15) Multiplique o monômio 40ax pelo monômio 0,5ax². A seguir, divida o resultado pelo monômio 10ax. Qual é o monômio que você vai obter?
Resolução:
Efetuando a multiplicação temos:
40ax . 0,5ax² = 20ax²
Agora, efetuando a divisão temos:
20ax² ÷ 10ax = 2ax²
Resposta: 2ax²

16) Quanto vale (2x²y³)³?
Resolução:
2³ . (x²)³ . (y³)³ = 8x⁶y⁹

Potenciação de monômios
Na potenciação de monômios devemos novamente utilizar uma propriedade da potenciação:
(I) (a . b)^m = a^m . b^m
(II) (am)ⁿ = a^m.n
Exemplos:
(-5x²b⁶)² aplicando a propriedade (I).
(-5)² . (x²)² . (b⁶)² aplicando a propriedade (II)
25 . x⁴ . b¹²
25x⁴b¹²

17) Resolva as subtrações abaixo:
a)25x– 42x =
    3
Resolução:
Para solucionar esse exercício, devemos inicialmente encontrar o MMC (3, 1):
3, 1| 3
1, 1|
MMC (3, 1) = 3
Agora devemos reduzir as frações ao mesmo denominador.
25x – 126x =
  3        3 
Como as frações possuem o mesmo denominador, podemos agora subtrair os coeficientes que estão no numerador.
101 x
   3
Sendo assim: 
25x – 42x = – 101 x
  3                     3

b)– 102ax²+ 202ax² =
Resolução:
A parte literal que compõe os monômios é idêntica. Devemos, então, subtrair os coeficientes:
(– 102 + 202) . ax² = + 100ax²
Sendo assim:
 – 102ax² + 202ax² = + 100ax²

c)12by – 7by =
Resolução:
Observe que a parte literal em ambos os monômios é idêntica (by), logo, podemos subtrair os coeficientes:
(12 – 7) . by = 5by
Sendo assim:
12by – 7by = 5by

18) Utilizando o agrupamento, resolva as expressões numéricas abaixo:
a)2x²+ 20y³ – 15y³ – 36x² =
Resolução:
Para resolver essa expressão, devemos agrupar os coeficientes que possuem a mesma parte literal.
2x² – 36x² + 20y³ – 15y³
Agora que os termos semelhantes estão agrupados, resolvemos:
2x² – 36x² e + 20y³ – 15y³
34x² + 5y

b) 6x²- 7 x² + 28 x² =
              10
Resolução:
Como o denominador é 10 para todos os monômios do numerador, não é necessário fazer o MMC. Observe que a parte literal é a mesma, assim, precisamos somente efetuar as operações com os coeficientes e conservar a parte literal.
(6 - 7 + 28) . x² =
 10 
 + 27x² =
10
2,7x²

Adição e Subtração de monômios
19) Faça o agrupamento dos monômios abaixo:
a) 3ax + 5bx – 12 ax – 15 bx + 4x =
Resolução:
Agrupe os termos semelhantes:
3ax – 12ax + 5bx – 15bx + 4x =
- 9ax – 10 bx + 4x =
Para obtermos a forma reduzida dessa expressão, coloque o x em evidência:
x (– 9a – 10b + 4)

b) 15y – 4z + 3x + 12y – 20z =
Resolução:
Agrupe os termos semelhantes:
15y + 12y – 4z – 20z + 3x =
27y – 24z + 3x

c) 24aw + 6x – 12aw – 6x =
Resolução:
Agrupe os termos semelhantes:
24aw – 12aw + 6x – 6x =
12aw + 0 =
12aw

20) Resolva as adições de monômios abaixo:
a) 15ax + 6ax =
Resolução:
A parte literal dos dois monômios é idêntica. Com isso, devemos somar os coeficientes e conservar a parte literal.
(15 + 6) . ax = 21ax
Sendo assim:
15ax + 6ax =
21ax

b) 1by+ 15by =
     2         6
Resolução:
Inicialmente teremos que fazer o MMC de 2 e 6. MMC (2, 6)
2, 6| 2
1, 3| 3
1, 1|  
MMC (2,6) = 2 . 3 = 6
Agora devemos reduzir as frações ao mesmo denominador.
3by + 15by =
  6        6
Como as frações possuem o mesmo denominador, podemos somar os coeficientes dos monômios que estão no numerador:
18by =
6
Dividindo 18 por 6, obteremos como resultado:
3by
Sendo assim: 
1by + 15by = 3by
  2        6

c) 32cz³ + 24cz³=
Resolução:
Como a parte literal dos dois monômios é idêntica, devemos somar os coeficientes e conservar a parte literal.
(32 + 24) . cz³ = 56cz³
Sendo assim:
32cz³ + 24cz³ = 56cz³

21) Resolva as subtrações abaixo:
a)25x– 42x =
      3
Resolução:
Para solucionar esse exercício, devemos inicialmente encontrar o MMC (3, 1):
3, 1| 3
1, 1|  
MMC (3, 1) = 3
Agora devemos reduzir as frações ao mesmo denominador.
 25x – 126x =
   3        3 
Como as frações possuem o mesmo denominador, podemos agora subtrair os coeficientes que estão no numerador.
 – 101 x
      3
Sendo assim: 
25x – 42x = – 101 x
  3                     3

b)– 102ax²+ 202ax² =
Resolução:
A parte literal que compõe os monômios é idêntica. Devemos, então, subtrair os coeficientes:
(– 102 + 202) . ax² = + 100ax²
Sendo assim:
– 102ax² + 202ax² = + 100ax²

c)12by – 7by =
Resolução:
Observe que a parte literal em ambos os monômios é idêntica (by), logo, podemos subtrair os coeficientes:
(12 – 7) . by = 5by
Sendo assim:
12by – 7by = 5by

22) Utilizando o agrupamento, resolva as expressões numéricas abaixo:
a)2x²+ 20y³ – 15y³ – 36x² =
Resolução:
Para resolver essa expressão, devemos agrupar os coeficientes que possuem a mesma parte literal.
2x² – 36x² + 20y³ – 15y³
Agora que os termos semelhantes estão agrupados, resolvemos: 
2x² – 36x² e + 20y³ – 15y³
34x² + 5y

b) 6x²- 7 x² + 28 x² =
              10
Resolução:
Como o denominador é 10 para todos os monômios do numerador, não é necessário fazer o MMC. Observe que a parte literal é a mesma, assim, precisamos somente efetuar as operações com os coeficientes e conservar a parte literal.
(6 - 7 + 28) . x² =
         10 
27x² =
  10
2,7x²

23)  Reduza os termos semelhantes na expressão 4x² – 5x -3x + 2x². Depois calcule o seu valor numérico da expressão.
Resolução:
4x² – 5x - 3x + 2x² reduzindo os termos semelhantes.
4x² + 2x² – 5x - 3x
6x² - 8x os termos estão reduzidos, agora vamos achar o valor numérico dessa expressão.
Para calcularmos o valor numérico de uma expressão devemos ter o valor de sua incógnita, que no caso do exercício é a letra x.
Vamos supor que x = - 2, então substituindo no lugar do x o -2 termos:
6x² - 8x
6 . (-2)² – 8 . (-2) =
6 . 4 + 16 =
24 + 16
40
 

Continua...