Professor Diminoi MAGENETISMO
MAGENETISMO
É a parte da física que estuda os fenômeno magnéticos (atração ou repulsão) entre determinados corpos, chamados ímãs, entre ímãs e certas substâncias magnéticas (como ferro, cobalto ou níquel) e também entre ímãs e condutores que estejam conduzindo correntes elétricas.
Os primeiros estudos realizados nessa área foram feitos no século VI a.C. por Tales de Mileto na Grécia antiga, em uma cidade chamada Magnésia. Ele observou a capacidade de algumas pedrinhas, que hoje são chamadas de magnetita, de atraírem umas às outras e também ao ferro.
 Ímãs
Ímãs
São objetos capazes de produzir um campo magnético ao seu redor, possuindo dois polos principais: um de atração e outro de repulsão. Também conhecido por magneto, o ímã é constituído por um material ferromagnético e a sua ação magnética se forma devido a constante movimentação dos elétrons em seu interior.
Os ímãs são objetos dipolos, ou seja, possuem dois polos que atraem ou repelem outros materiais ferromagnéticos e alguns paramagnéticos. PROPRIEDADES DE UM ÍMÃ
PROPRIEDADES DE UM ÍMÃ
Atração
Capacidade de atrair os objetos de ferro parece estar concentrada em dois pontos. Regiões extremas – Chamadas de polo norte magnético e polo sul magnético;
Regiões extremas – Chamadas de polo norte magnético e polo sul magnético;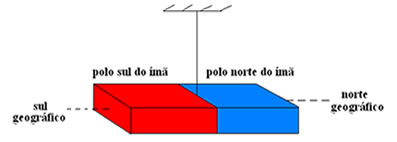 Atração e Repulsão entre os Polos Magnéticos
Atração e Repulsão entre os Polos Magnéticos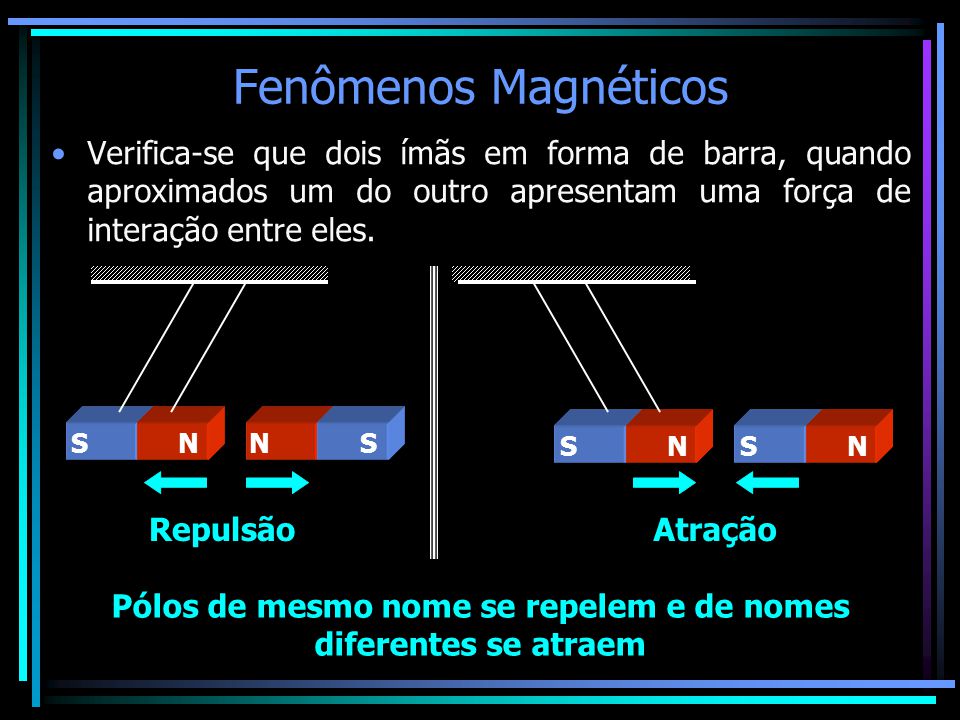 Inseparabilidade dos polos - Ao dividir um ímãs em várias partes, cada parte será um novo ímã com dois polos.
Inseparabilidade dos polos - Ao dividir um ímãs em várias partes, cada parte será um novo ímã com dois polos. Alinhamento espontâneo – Um ímã aponta sempre para a mesma direção (próxima ao norte geográfico da Terra) se for deixado suspenso ou de modo a se mover livremente, sem influência externa.
Alinhamento espontâneo – Um ímã aponta sempre para a mesma direção (próxima ao norte geográfico da Terra) se for deixado suspenso ou de modo a se mover livremente, sem influência externa.
Polos do ímãs e polos da Terra
Já a primeira aplicação prática do magnetismo foi encontrada pelos chineses: a bússola, que se baseia na interação do campo magnético de um imã (a agulha da bússola) com o campo magnético terrestre. No século VI, os chineses já dominavam a fabricação de imãs. Os estudos sobre o magnetismo somente ganharam força a partir do século XIII, quando alguns trabalhos e observações foram feitos sobre a eletricidade e o magnetismo, que ainda eram considerados fenômenos completamente distintos. Essa teoria foi aceita até o século XIX.
Os estudos sobre o magnetismo somente ganharam força a partir do século XIII, quando alguns trabalhos e observações foram feitos sobre a eletricidade e o magnetismo, que ainda eram considerados fenômenos completamente distintos. Essa teoria foi aceita até o século XIX.
Os estudos experimentais na área foram feitos pelos europeus. Pierre Pelerin de Maricourt, em 1269, descreveu uma grande quantidade de experimentos sobre magnetismo. Devem-se a ele as denominações polo norte e polo sul às extremidades do imã, bem como a descoberta de que a agulha da bússola apontava exatamente para o norte geográfico da Terra.
O polo norte do ímã é atraído pelo polo magnético sul da Terra, enquanto que o polo sul do ímã está relacionado com o polo norte geográfico.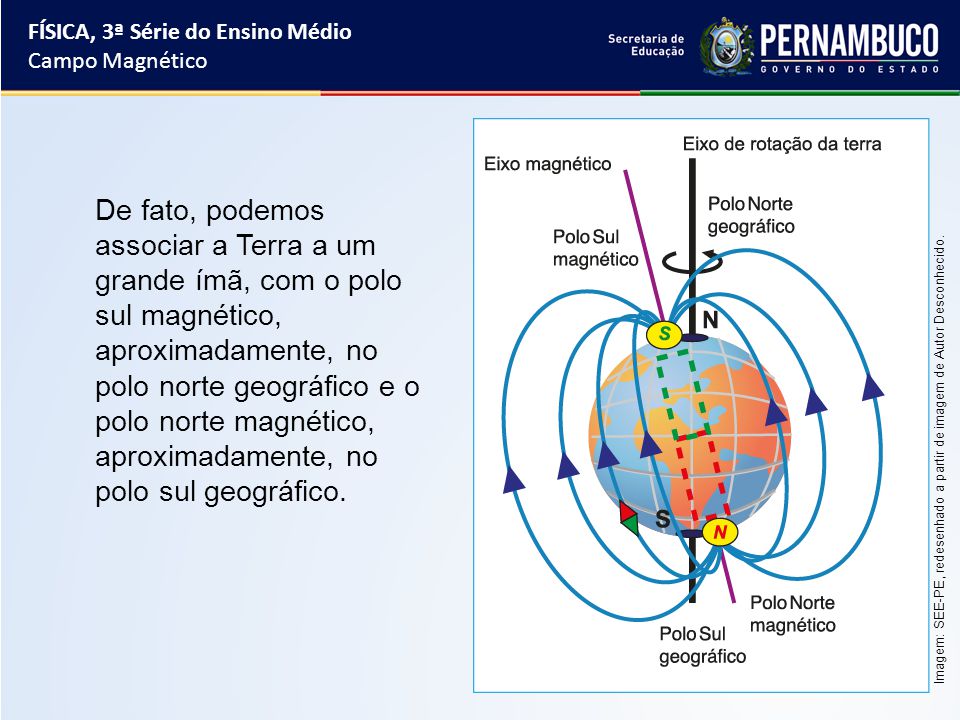
RESOLVIDAS – CARACTERÍSTICAS DOS ÍMÃS
01) Marque a afirmativa correta:
(A) Todos os imãs possuem dois polos, o polo norte e o sul. O polo sul é o positivo de um imã, enquanto o norte é negativo.
(B) Ao quebrar um imã, os seus polos são separados, passando a existir um imã negativo e outro positivo.
(C) Ao aproximar os polos iguais de um imã, eles repelem-se. Quando polos diferentes aproximam-se, eles atraem-se.
(D) Os materiais ferromagnéticos são os que não podem ser atraídos por imãs.
Resolução:
A alternativa correta é a letra c, pois, polos iguais de um imã repelem-se e os diferentes atraem-se.
Vejamos por que as demais afirmações estão incorretas:
A letra a está incorreta porque afirma que o polo sul do imã é positivo e o norte, negativo. O certo é que o polo norte é positivo e o sul, negativo.
A alternativa b está incorreta porque afirma que, quando um imã é quebrado, os seus polos são separados. De acordo com o princípio da inseparabilidade dos polos magnéticos, não é possível encontrar um imã apenas com o polo norte ou sul.
A opção d está incorreta porque os materiais ferromagnéticos podem ser atraídos por imãs.
Alternativa: C
02) (FGV-SP) Da palavra 'aimant', que traduzido do francês significa amante, originou-se o nome ímã, devido à capacidade que esses objetos têm de exercer atração e repulsão.
Sobre essas manifestações, considere as proposições:
I. assim como há ímãs que possuem os dois tipos de polos, sul e norte, há ímãs que possuem apenas um;
II. o campo magnético terrestre diverge dos outros campos, uma vez que o polo norte magnético de uma bússola é atraído pelo polo norte magnético do planeta;
III. os pedaços obtidos da divisão de um ímã são também ímãs que apresentam os dois polos magnéticos, independentemente do tamanho dos pedaços.
Está correto o contido em:
(A) I, apenas.
(B) III, apenas.
(C) I e II, apenas.
(D) II e III, apenas.
(E) I, II e III.
Resolução:
A proposição I é incorreta, pois não existem imãs que possuem apenas um polo magnético.
A proposição II é incorreta, pois o campo magnético da Terra comporta-se como o de qualquer imã, sendo o polo norte magnético da bússola atraído pelo polo sul magnético do planeta, que coincide com o norte geográfico.
Já a proposição III é correta.
Alternativa: B
03) A Terra é considerada um imã gigantesco, que tem as seguintes características:
(A) O polo norte geográfico está exatamente sobre o polo sul magnético, e o sul geográfico está na mesma posição que o norte magnético.
(B) O polo norte geográfico está exatamente sobre o polo norte magnético, e o sul geográfico está na mesma posição que o sul magnético.
(C) O polo norte magnético está próximo do polo sul geográfico, e o polo sul magnético está próximo ao polo norte geográfico.
(D) O polo norte magnético está próximo do polo norte geográfico, e o polo sul magnético está próximo do polo sul geográfico.
(E) O polo norte geográfico está defasado de um ângulo de 45º do polo sul magnético, e o polo Sul geográfico está defasado de 45º do polo norte magnético.
Resolução:
O polo norte magnético está próximo ao polo sul geográfico, e o polo sul magnético está próximo ao sul geográfico. Os polos magnéticos e geográficos não se coincidem, estando afastados 11,5º um do outro.
Alternativa: C
04) Uma bússola é colocada na proximidade do imã da figura sobre o ponto A: Sabendo que o vermelho corresponde ao polo norte da bússola, qual será a orientação da agulha sobre o ponto A:
Sabendo que o vermelho corresponde ao polo norte da bússola, qual será a orientação da agulha sobre o ponto A:
Resolução:
Sobre esse ponto, a bússola está em equilíbrio, sendo que o polo sul da bússola fica próximo ao polo norte do imã, e o polo norte da agulha próximo ao polo sul do imã.
Alternativa: A
05 (Udesc) Analise as proposições relacionadas às linhas de campo elétrico e às de campo magnético.
I. As linhas de força do campo elétrico se estendem apontando para fora de uma carga pontual positiva e para dentro de uma carga pontual negativa.
II. As linhas de campo magnético não nascem nem morrem nos ímãs, apenas os atravessam, ao contrário do que ocorre com os corpos condutores eletrizados que originam os campos elétricos.
III. A concentração das linhas de força do campo elétrico ou das linhas de campo magnético indica, qualitativamente, onde a intensidade do respectivo campo é maior.
Assinale a alternativa correta.
(A) Somente as afirmativas I e III são verdadeiras.
(B) Somente a afirmativa II é verdadeira.
(C) Somente as afirmativas II e III são verdadeiras.
(D) Somente as afirmativas I e II são verdadeiras.
(E) Todas as afirmativas são verdadeiras.
Resolução:
Todas as afirmações são verdadeiras.
Alternativa: E
06 (Unesp) Um ímã em forma de barra, com seus polos Norte e Sul, é colocado sob uma superfície coberta com partículas de limalha de ferro, fazendo com que elas se alinhem segundo seu campo magnético. Se quatro pequenas bússolas, 1, 2, 3 e 4, forem colocadas em repouso nas posições indicadas na figura, no mesmo plano que contém a limalha, suas agulhas magnéticas orientam-se segundo as linhas do campo magnético criado pelo ímã..jpg) Desconsiderando o campo magnético terrestre e considerando que a agulha magnética de cada bússola seja representada por uma seta que se orienta na mesma direção e no mesmo sentido do vetor campo magnético associado ao ponto em que ela foi colocada, assinale a alternativa que indica, correta e respectivamente, as configurações das agulhas das bússolas 1, 2, 3 e 4 na situação descrita.
Desconsiderando o campo magnético terrestre e considerando que a agulha magnética de cada bússola seja representada por uma seta que se orienta na mesma direção e no mesmo sentido do vetor campo magnético associado ao ponto em que ela foi colocada, assinale a alternativa que indica, correta e respectivamente, as configurações das agulhas das bússolas 1, 2, 3 e 4 na situação descrita.
(A) ![]()
(B)![]()
(C)![]()
(D)![]()
(E)![]()
Resolução:
As linhas de campo magnético saem do polo norte e entram no polo sul. Seguindo a orientação das linhas de norte para sul, podemos identificar o sentido do campo magnético em cada ponto indicado.
Alternativa: C
07) A respeito do desenvolvimento dos estudos relacionados com o magnetismo, marque V para as afirmações verdadeiras e F para as falsas.
( ) Os primeiros estudos realizados na área do magnetismo foram feitos por Aristóteles no século VI a.C. O filósofo analisou a atração entre pedras de um minério denominado de magnetita.
( ) A utilização da bússola provavelmente foi a primeira aplicação prática do magnetismo.
( ) A relação entre magnetismo e eletricidade só foi aceita no século XX com os estudos de Michael Faraday.
( ) O experimento de Oersted, realizado no século XIX, abriu caminho para os estudos relacionados ao eletromagnetismo.
(A) F, V, V, V
(B) V, V, V, V
(C) V, F, V, F
(D) F, F, F, F
(E) F, V, F, V
Resolução:
Falsa – Os primeiros estudos realizados na área do magnetismo foram feitos por Tales de Mileto.
Verdadeira.
Falsa – A relação entre magnetismo e eletricidade foi comprovada ainda no século XIX a partir das contribuições de Oersted.
Verdadeira.
Alternativa: E
08) Indique a única afirmação incorreta:
(A) A primeira aplicação prática do magnetismo foi desenvolvida pelos chineses: a bússola.
(B) As denominações polo norte e polo sul foram dadas por Pierre Pelerin de Maricourt.
(C) Os estudos sobre magnetismo iniciaram-se a partir da percepção de que materiais atritados poderiam atrair-se mutuamente.
(D) O experimento de Oersted abriu caminho para os estudos referentes ao eletromagnetismo.
(E) As bases teóricas sólidas entre a relação de campos magnéticos e campos elétricos foram feitas por Maxwell.
Resolução:
Os estudos iniciados a partir da percepção da atração mútua que ocorre após o atrito de determinados materiais voltavam-se para as propriedades elétricas dos objetos. Os estudos do magnetismo iniciaram-se a partir da observação do comportamento da magnetita, minério de ferro que é um ímã natural.
Alternativa C
10) Com relação aos estudos sobre as propriedades do ímã, podemos dizer que o polo sul de um ímã natural:
(A) atrai o polo sul de outro ímã, desde que ele seja artificial
(B) repele o polo norte de um ímã também natural
(C) atrai o polo norte de todos os ímãs, sejam naturais ou artificiais
(D) atrai o polo sul de outro ímã, sejam naturais ou artificiais
(E) não interage com um eletroímã em nenhuma hipótese
Resolução:
De acordo com as propriedades do ímã, polos de mesmo nome se repelem e polos de nomes contrários se atraem, portanto, o polo sul de um ímã natural irá atrair o polo norte de qualquer ímã, seja ele um ímã natural ou um ímã artificial.
Alternativa: C
12) (PUC-MG) Uma bússola pode ajudar uma pessoa a se orientar devido à existência, no planeta Terra, de:
(A) um mineral chamado magnetita
(B) ondas eletromagnéticas
(C) um campo polar
(D) um campo magnético
(E) um anel magnético
Resolução:
É possível uma bússola orientar-se graças à existência do campo magnético terrestre.
Alternativa: D
A TERRA E A BÚSSOLA
A Terra e a bússola - O polo norte da agulha de uma bússola é atraído pelo polo sul magnético da Terra, e o polo sul da bússola é atraído pelo polo norte magnético da Terra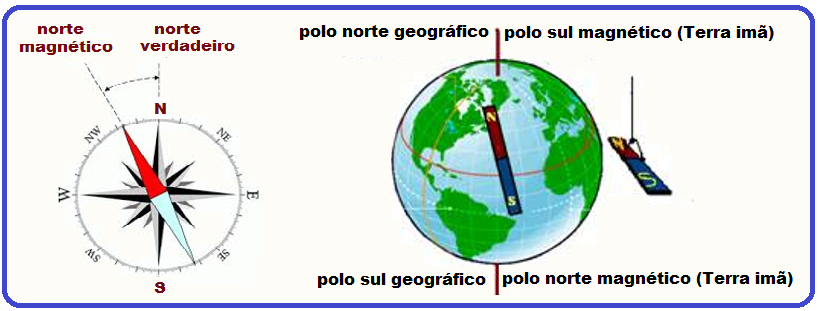 Bussola:
Bussola: Ímãs naturais e artificiais - A magnetita é o ímã que se encontra na natureza: é o ímã natural. Mas, podemos fazer com que os corpos que normalmente não são ímãs se tornem ímãs. Os ímãs obtidos desse modo são chamados ímãs artificiais. Chamamos corpo neutro àquele que não tem propriedade magnética: corpo imantado àquele que se tornou ímã.
Ímãs naturais e artificiais - A magnetita é o ímã que se encontra na natureza: é o ímã natural. Mas, podemos fazer com que os corpos que normalmente não são ímãs se tornem ímãs. Os ímãs obtidos desse modo são chamados ímãs artificiais. Chamamos corpo neutro àquele que não tem propriedade magnética: corpo imantado àquele que se tornou ímã. CAMPO MAGNÉTICO
CAMPO MAGNÉTICO  Campo magnético - É a região que sofre a ação da força de um ímã.
Campo magnético - É a região que sofre a ação da força de um ímã.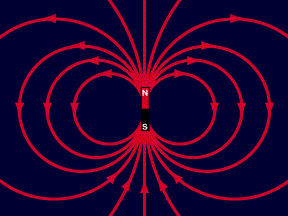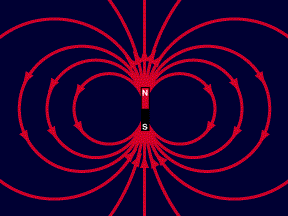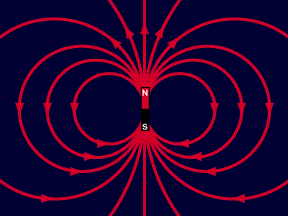
Representação de um campo magnético:
Campo magnético e corrente elétrica - A corrente elétrica em um fio condutor está associada ao campo magnético existente ao redor desse fio. Esse fenômeno demostra a interação entre eletricidade e magnetismo e dai surge eletromagnetismo.
As aplicações práticas e os desenvolvimentos tecnológicos que surgiram a partir daí, bem como suas implicações na vida das pessoas, como no caso do motor e do gerador elétricos.
No caso do motor elétrico simples, é necessário que uma corrente elétrica passe por um fio condutor para que surja um campo magnético ao seu redor e o fio se torne um ímã artificial (ou eletroímã), a fim de que possa interagir com o ímã natural fixo que está perto dele.
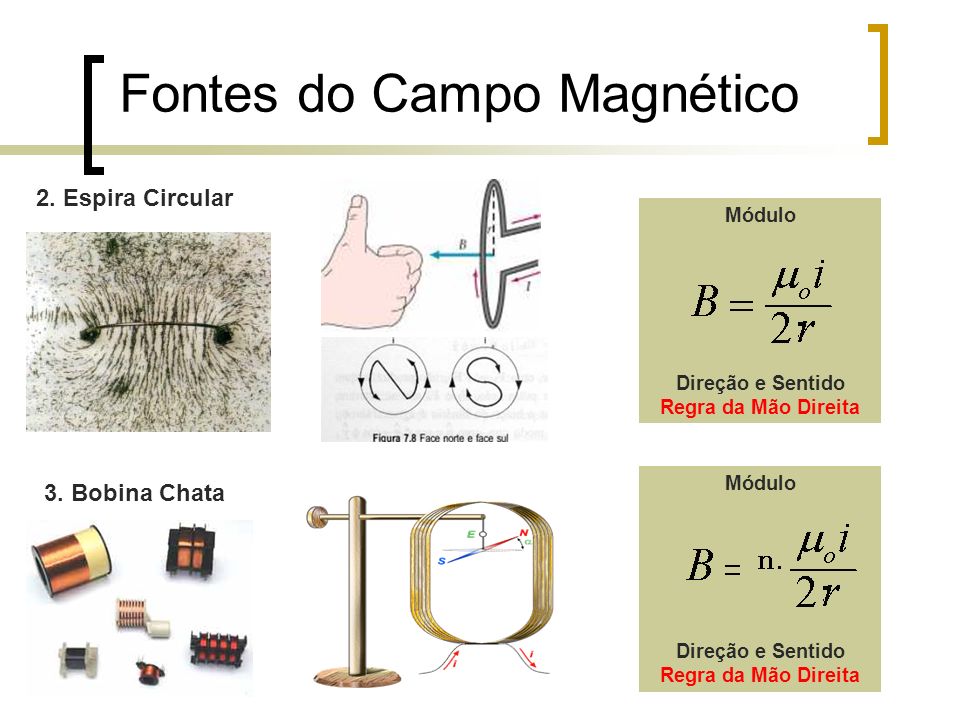 Vetor indução magnética - O campo magnético pode ser definido tomando como base os campos elétricos e gravitacionais, que determinam as modificações no espaço em razão da presença de cargas elétricas ou de massa. Sendo assim, o campo magnético é a região do espaço na qual um ímã manifesta sua ação.
Vetor indução magnética - O campo magnético pode ser definido tomando como base os campos elétricos e gravitacionais, que determinam as modificações no espaço em razão da presença de cargas elétricas ou de massa. Sendo assim, o campo magnético é a região do espaço na qual um ímã manifesta sua ação.
Representa-se o campo magnético em um ponto no espaço por um vetor denominado vetor indução magnética ou, simplesmente, vetor campo magnético, representado por B. No (SI), a unidade de intensidade do vetor B denomina-se tesla (símbolo T).
Sentido do vetor indução magnético - As linhas saem do polo norte e entram no polo sul.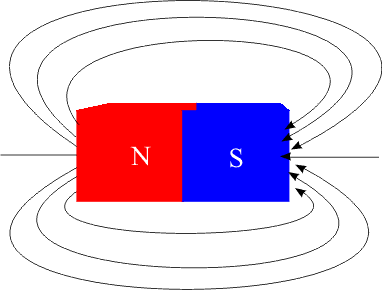
Representação do vetor indução magnética entrando e saindo do plano: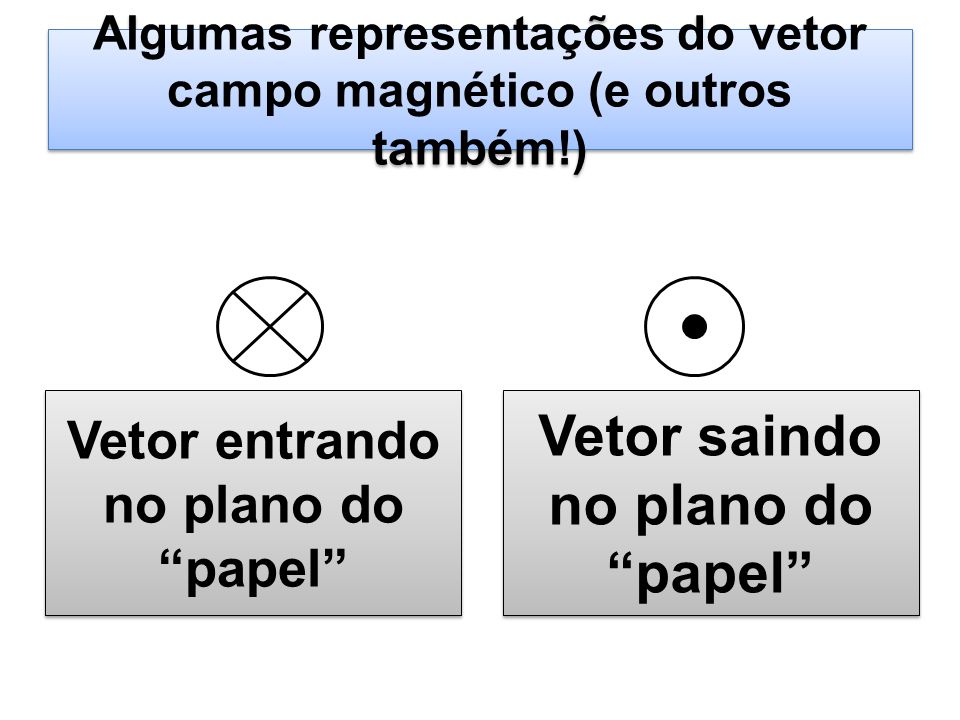 RESOLVIDOS - CAMPO MAGNÉTICO
RESOLVIDOS - CAMPO MAGNÉTICO
01) Marque a alternativa que melhor representa o vetor indução magnética B no ponto P, gerado pela corrente elétrica que percorre o condutor retilíneo da figura abaixo.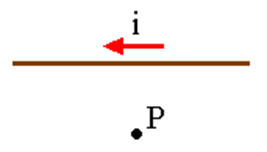 (A)
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
Resolução:
De acordo com a regra da mão direita, posicionamos o polegar no sentido da corrente elétrica e os demais dedos representam o vetor indução magnética. No ponto P, pela regra, temos o vetor saindo.
Alternativa: B
02) Vamos supor que uma corrente elétrica de intensidade igual a 5 A esteja percorrendo um fio condutor retilíneo. Calcule a intensidade do vetor indução magnética em um ponto localizado a 2 cm do fio. Adote μ= 4π.10-7 T.m/A.
(A) B = 2 . 10-5 T
(B) B = 5 . 10-7 T
(C) B = 3 . 10-7 T
(D) B = 5 . 10-5 T
(E) B = 2,5 . 10-5 T
Resolução:
Sabemos que a intensidade do vetor indução magnética no ponto P, devido à corrente elétrica i, é dada pela seguinte relação:![]()
Retirando os dados fornecidos pelo exercício e substituindo-os na equação acima, temos:
i = 5 A, R = 2 cm = 0,02 = 2 . 10-2 m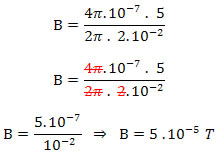
Alternativa: D
03) Para a figura abaixo, determine o valor do vetor indução magnética B situado no ponto P e marque a alternativa correta. Adote μ = 4π.10-7T.m/A, para a permeabilidade magnética.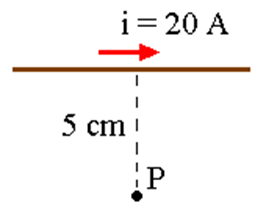 (A) B = 4 . 10-5 T
(A) B = 4 . 10-5 T
(B) B = 8 . 10-5 T
(C) B = 4 . 10-7 T
(D B = 5 . 10-5 T
(E) B = 8 . 10-7 T
Resolução:
Podemos determinar o valor do vetor indução magnética através da seguinte relação:![]()
Da figura podemos retirar o raio e a intensidade da corrente elétrica. Assim, temos:
R= 5 cm = 0,05 m = 5 . 10-2 m e i = 20 A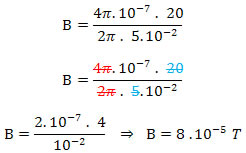
Alternativa: B
04) Na figura abaixo temos a representação de uma espira circular de raio R e percorrida por uma corrente elétrica de intensidade i. Calcule o valor do campo de indução magnética supondo que o diâmetro dessa espira seja igual a 6πcm e a corrente elétrica seja igual a 9 A. Adote μ = 4π.10-7T.m/A.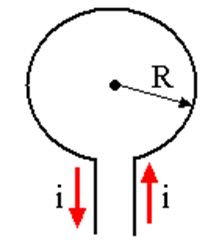 (A) B = 6 . 10-5 T
(A) B = 6 . 10-5 T
(B) B = 7 . 10-5 T
(C) B = 8 . 10-7 T
(D) B = 4 . 10-5 T
(E) B = 5 . 10-7 T
Resolução:
Podemos determinar o vetor campo indução magnética no interior de uma espira circular através da seguinte equação:![]()
Dados do exercício:
i = 9 A
μ = 4π.10-7 T.m/A
R = 3π . 10-2 m
(o diâmetro é duas vezes o raio, portanto, basta dividirmos o valor do diâmetro por 2). Para passar o valor do raio para metro dividimos por 100.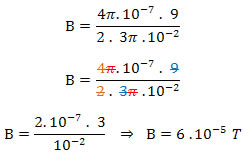
Alternativa: A
ELETROMAGNETISMO
É uma área da física na qual é foco é a relação entre a eletricidade e o magnetismo. Essa teoria, unificada e desenvolvida pelo físico e matemático James Clerk Maxwell, tem como base o conceito de campo eletromagnético para explicar a relação entre essas duas forças. O campo magnético é gerado a partir dos movimentos de cargas elétricas e o campo elétrico é resultado da variação do fluxo magnético. Ramo da física, seus conceitos e aplicações.
Ramo da física, seus conceitos e aplicações.
Antigamente, acreditava-se que o magnetismo e a eletricidade faziam parte de fatos distintos. Os estudos de pesquisadores importantes, como William Gilbert, Otto von Guericke e Stephen Gray, durante os séculos XVII e XVIII, tinham como objetivo explicar estes fenômenos de forma separada. Os experimentos realizados pelos cientistas tiveram resultados lógicos, que contribuíram para a evolução das pesquisas. Mesmo com a diferenciação entre estes dois fenômenos, acreditava-se que havia alguma relação entre eles.
Cargas elétricas em movimento geram campo magnético. Variação de fluxo magnético produz campo elétrico.
Variação de fluxo magnético produz campo elétrico. Durante muito tempo, acreditou-se que eletricidade e magnetismo eram o mesmo fenômeno. Foi somente em 1600 que o médico e físico inglês Gilbert escreveu um livro distinguindo as duas teorias. Apesar dessa diferenciação entre os dois fenômenos, havia fortes indícios de que existia alguma relação entre eles.
Durante muito tempo, acreditou-se que eletricidade e magnetismo eram o mesmo fenômeno. Foi somente em 1600 que o médico e físico inglês Gilbert escreveu um livro distinguindo as duas teorias. Apesar dessa diferenciação entre os dois fenômenos, havia fortes indícios de que existia alguma relação entre eles.
Qual é a relação entre Eletricidade e Magnetismo?
Essa relação foi descoberta pelo dinamarquês Hans Christian Oesterd em 1820, o que só foi possível graças à invenção dos geradores elétricos, que permitiam a geração de correntes elétricas duradouras e estáveis necessárias para o estudo dos fenômenos. Os seja: todo fio percorrido por uma corrente elétrica cria ao seu redor um campo magnético, Oersted demonstrou a existência dessa interação a partir de um simples experimento. Ele colocou uma agulha magnética próxima a um condutor de eletricidade. Para isso, ele utilizou uma bússola e um fio de platina em um circuito. O fio de platina, ao ser percorrido pela corrente elétrica, ficava incandescente, o que garantia uma corrente suficientemente intensa. Quando o fio era aproximado da bússola, sua agulha magnética sofria deflexão.
Oersted demonstrou a existência dessa interação a partir de um simples experimento. Ele colocou uma agulha magnética próxima a um condutor de eletricidade. Para isso, ele utilizou uma bússola e um fio de platina em um circuito. O fio de platina, ao ser percorrido pela corrente elétrica, ficava incandescente, o que garantia uma corrente suficientemente intensa. Quando o fio era aproximado da bússola, sua agulha magnética sofria deflexão.
Experimento de Oesterd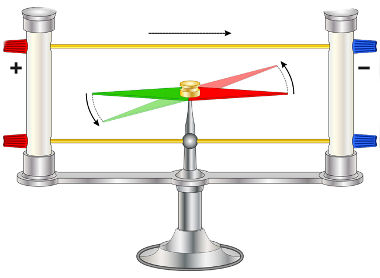 O experimento de Oersted mostrava que a corrente elétrica gerava campo magnético. Porém, em 1831, Michael Faraday, na Inglaterra, utilizou um núcleo de ferro e duas bobinas A e B para mostrar que a variação do fluxo magnético também gerava corrente elétrica. Faraday percebeu que, nos momentos em que conectava ou desconectava a bobina A na fonte, passava uma corrente elétrica na bobina B, mas essa corrente aparecia somente nesses instantes.
O experimento de Oersted mostrava que a corrente elétrica gerava campo magnético. Porém, em 1831, Michael Faraday, na Inglaterra, utilizou um núcleo de ferro e duas bobinas A e B para mostrar que a variação do fluxo magnético também gerava corrente elétrica. Faraday percebeu que, nos momentos em que conectava ou desconectava a bobina A na fonte, passava uma corrente elétrica na bobina B, mas essa corrente aparecia somente nesses instantes.
Experimento de Faraday
A partir dessa experiência, ele concluiu que essa corrente elétrica ocorria em virtude da variação do campo magnético, que aparecia quando a bobina A era ligada e desaparecia quando essa mesma bobina era desligada. Esse fenômeno ficou conhecido como indução magnética ou Lei de Faraday.
Os fenômenos eletromagnéticos foram descritos por um conjunto de leis formulado por James Clerck Maxwell, cientista que foi tão importante para o Eletromagnetismo como Isaac Newton foi para a Mecânica. James C. Maxwell teve importância sem igual para os estudos sobre Eletromagnetismo
James C. Maxwell teve importância sem igual para os estudos sobre Eletromagnetismo
Vários aparelhos indispensáveis atualmente só existem em face da evolução nos estudos sobre o Eletromagnetismo. Entre eles, podemos citar: cartões magnéticos, transformadores de tensão, motores elétricos, antenas de transmissão de dados, forno micro-ondas, entre outros.
Hans Christian Oersted (1777 - 1851) - Em 1820. Ele descobriu que fenômenos elétricos e magnéticos estão inter-relacionados. De acordo com essa teoria, denominada eletromagnetismo, cargas elétricas em movimento geram campo magnético, e campo magnético em movimento gera corrente elétrica. Esses estudos foram finalizados por Maxwell que estabeleceu bases teóricas sólidas sobre a relação entre o campo elétrico e o magnético, ou seja, as ondas eletromagnéticas. CAMPO MAGNÉTICO
CAMPO MAGNÉTICO 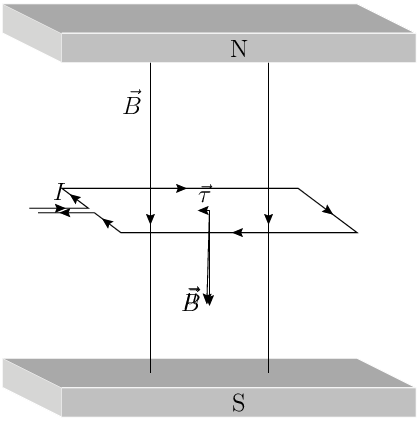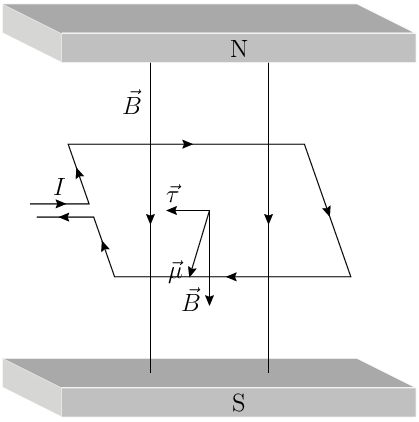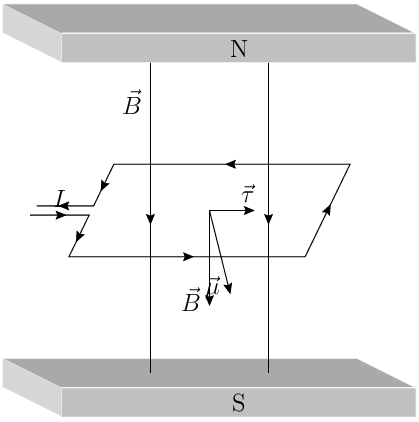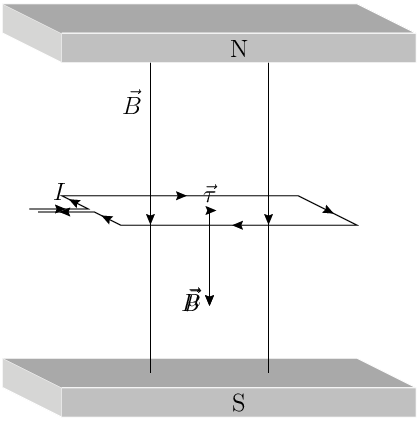
Condutor Retilíneo (fio Fino)
Espira Circular
Solenoide
Bobina Chata
CONDUTOR RETILÍNEO EM UM FIO FINO
Campo Magnético formado por um Fio Condutor - Quando um fio retilíneo é percorrido com uma corrente elétrica i, ele gera ao seu redor um campo magnético, cujas as linhas do campo são circunferências concêntricas pertencentes ao plano perpendicular ao fio e com centro comum em um ponto dele. d = distância do ponto ao condutor (m)
d = distância do ponto ao condutor (m)
i = corrente elétrica (A)
B = campo magnético (T)
μ = permeabilidade magnética no vácuo → 4π . 10-7 T.m/A
Observação: Para sabermos qual o sentido do campo magnético deste fio utilizamos a regra da mão direita. Coloca-se polegar direito no mesmo sentido que a corrente, assim a direção que os demais dedos curvados nos mostrará será o sentido do campo. A direção e sentido do vetor serão dadas pela regra da mão direita.
Regra da Mão Direita i = corrente elétrica (A)
i = corrente elétrica (A)
FORÇA MAGNÉTICA
Ao colocarmos um determinado fio percorrido por uma corrente elétrica dentro de um campo magnético, verifica-se que ele sofre a ação de uma força, que chamamos de força magnética, representada pela letra F.
Regra da Mão Esquerda 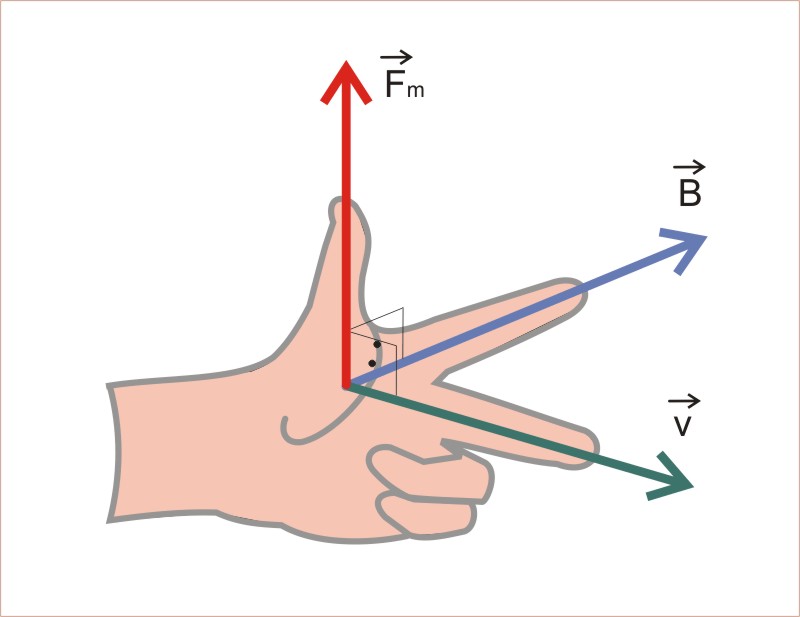
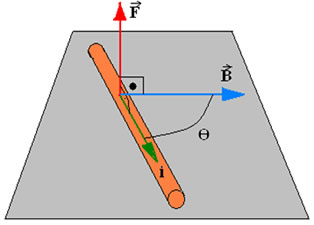


Força magnética
É o resultado da interação entre dois corpos dotados de propriedades magnéticas, como ímãs ou cargas elétricas em movimento. Característica da força magnética – As características desta força magnética foram determinadas pelo físico Hendrick Antoon Lorentz (1853-1920) e diz que a força magnética depende do movimento da carga.
Característica da força magnética – As características desta força magnética foram determinadas pelo físico Hendrick Antoon Lorentz (1853-1920) e diz que a força magnética depende do movimento da carga. 
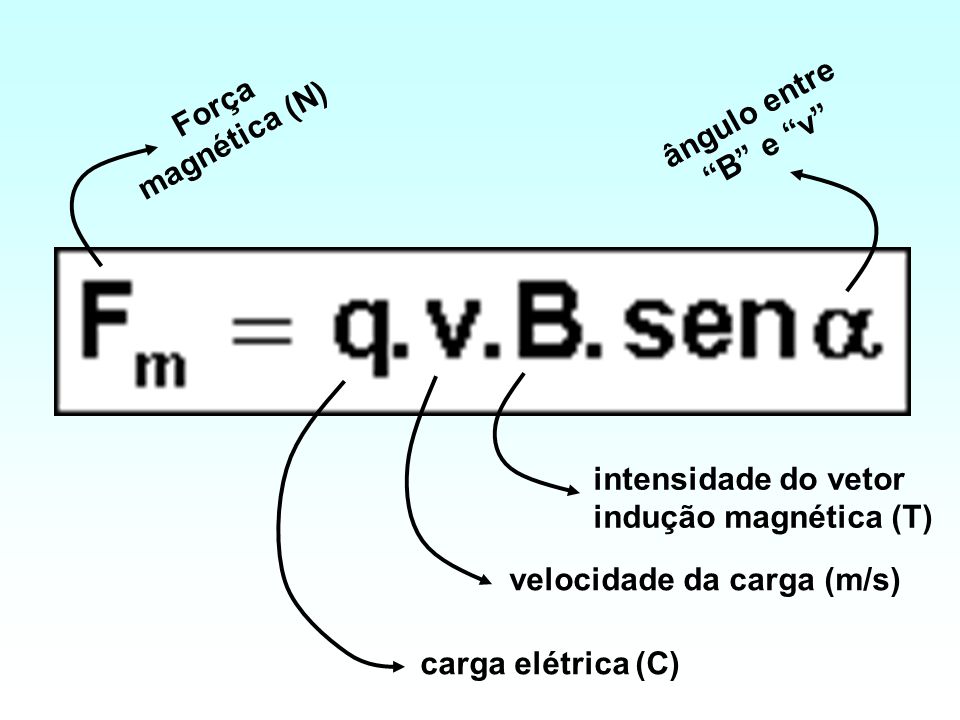
FORÇA MAGNÉTICA
A força magnética e a direção do movimento da carga elétrica
Um campo magnético é o responsável pelas forças magnéticas que atuam em uma carga em movimento. No caso de um condutor percorrido por corrente elétrica e submetido à presença de um campo magnético, também teremos a ação de uma força magnética, já que a corrente representa um movimento ordenado de cargas elétricas. Nesse caso o sentido é dado pela regra da mão esquerda, com a observação de que o dedo médio indicará o sentido convencional da corrente (lembrando sempre que o sentido da força depende do sentido da corrente).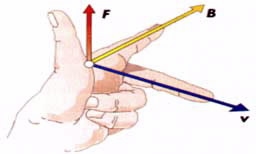 Sentido das linha de indução de um ímã
Sentido das linha de indução de um ímã
As linhas de campo saem do polo norte e entram no polo sul; são semelhantes às linhas de campo elétrico de um dipolo elétrico, mas a diferença é que as linhas de campo magnético não terminam no polo sul, nem começam no polo norte, mas são linhas fechadas que passam pelos dois polos.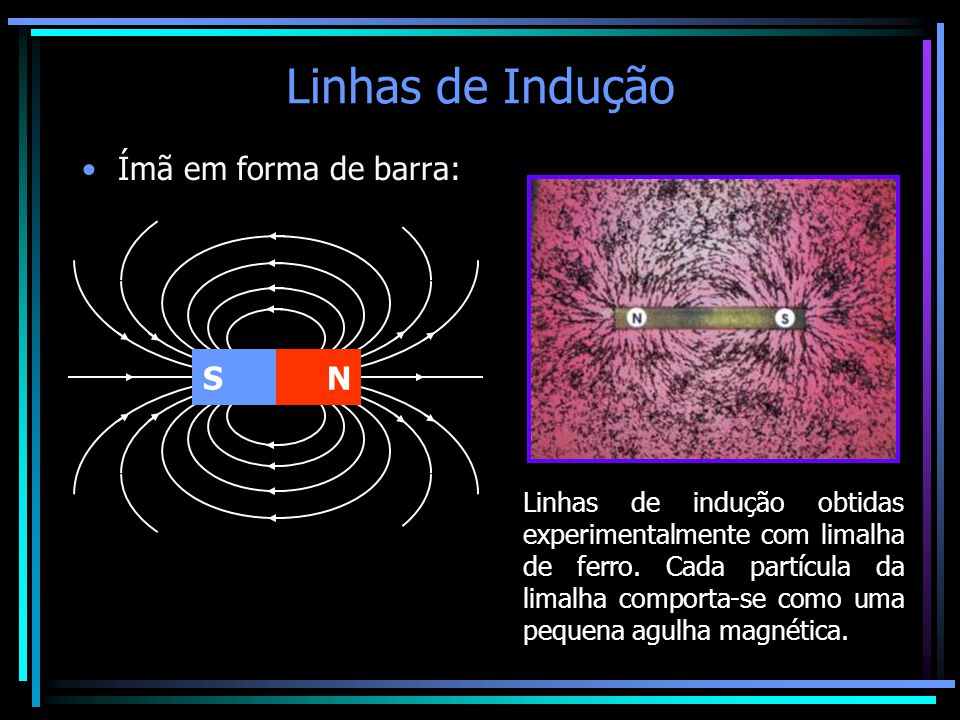
Movimento de uma partícula em um campo uniforme
Quando uma partícula eletrizada é lançada em um campo magnético uniforme, ela poderá descrever no interior desse campo diversos tipos de movimento, conforme a direção de sua velocidade em relação ao campo magnético.

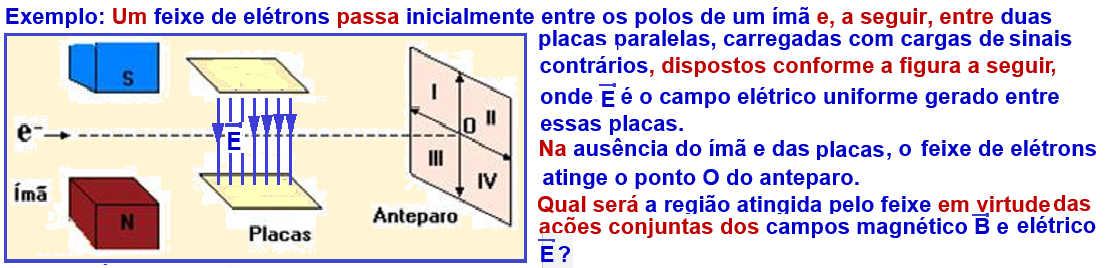
Intensidade da força elétrica em um fio retilíneo
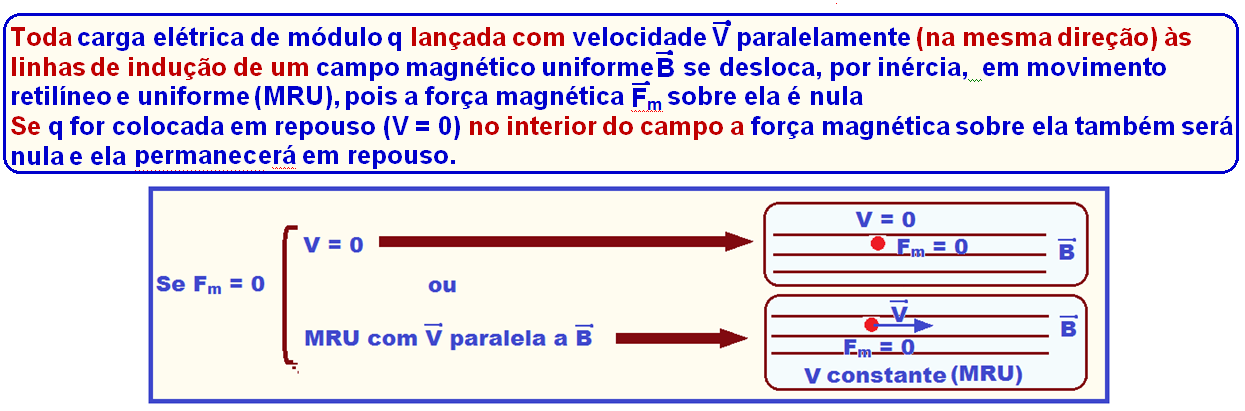
Considere um fio retilíneo de tamanho L conduzindo uma corrente elétrica i dentro de uma região de campo magnético uniforme B. Sobre cada carga elétrica que percorre o condutor atua uma força magnética. Pode-se mostrar que a intensidade da força magnética total exercida sobre o fio é dado por: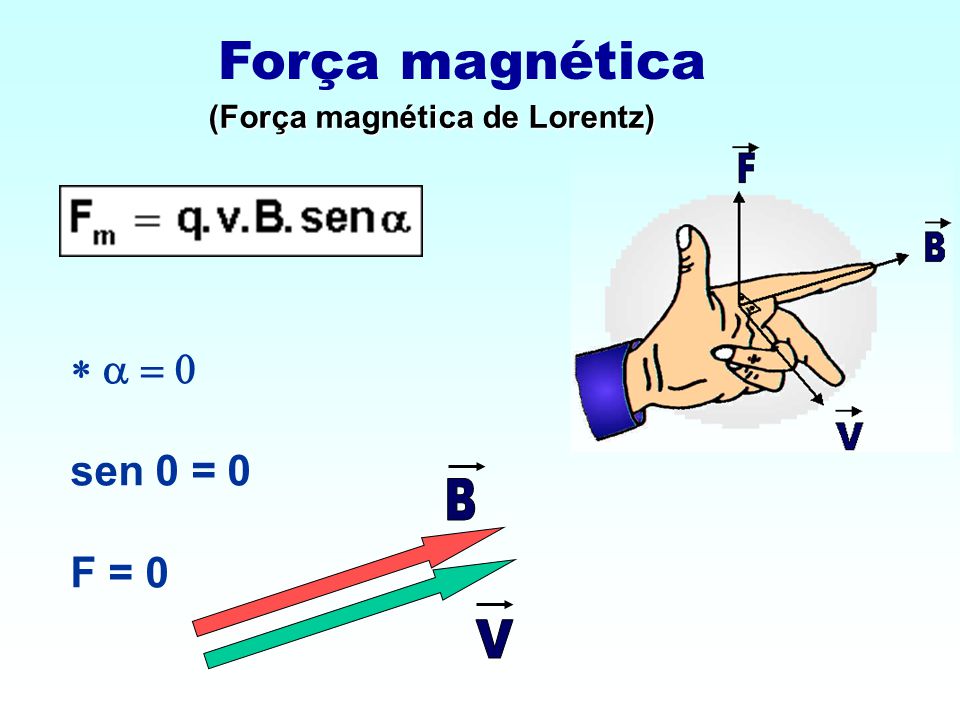


Força Magnética e Corrente Elétrica formada entre Dois Fios
Dois fios condutores retos em paralelo e próximos um do outro, quando passa pelos dois fios correntes elétricas no mesmo sentido, eles se atraem mutuamente e que quando passa pelos dois fios correntes elétricas de sentidos contrários, eles se repelem mutuamente.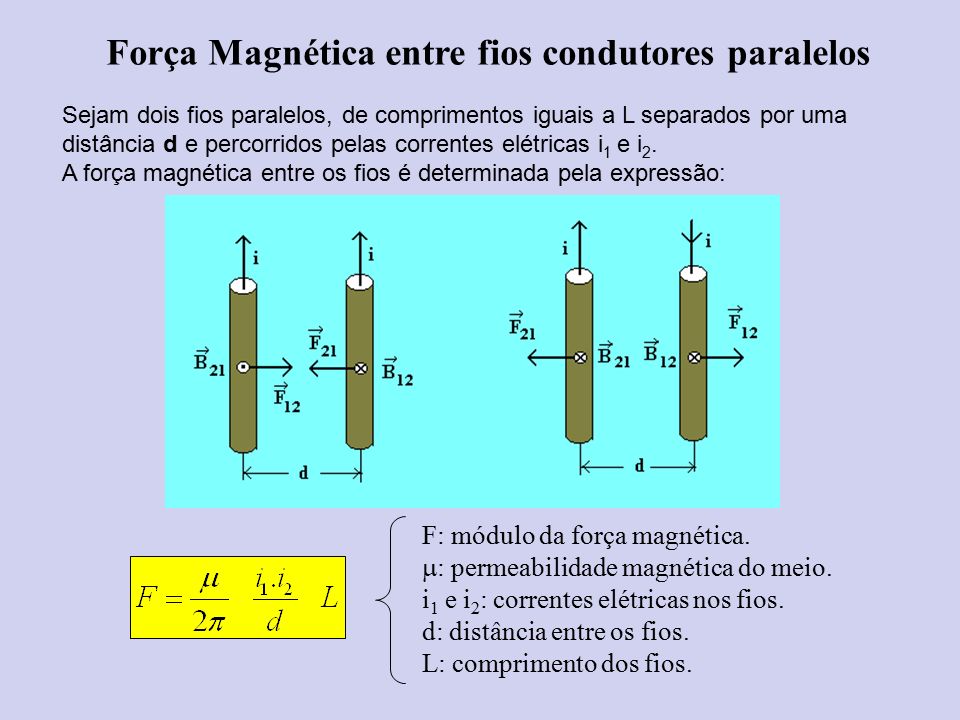
RESOLVIDAS - FORÇA MAGNÉTICA FORMADA POR FIO(S) FINO(OS)
02) (PUC) Vamos supor que uma corrente elétrica de intensidade igual a 5A esteja percorrendo um fio condutor retilíneo.
Calcule a intensidade do vetor indução magnética em um ponto localizado a 2cm do fio.
Adote μ= 4π.10-7 T.m/A.
(A) B = 2 . 10-5T
(B) B = 5 . 10-7T
(C) B = 3 . 10-7 T
(D) B = 5 . 10-5 T
(E) B = 2,5 . 10-5 T
Resolução:
Sabemos que a intensidade do vetor indução magnética no ponto P, devido à corrente elétrica i, é dada pela seguinte relação:
Retirando os dados fornecidos pelo exercício e substituindo-os na equação acima, temos:
i = 5 A,
R = 2 cm = 0,02 = 2 . 10-2 m
Alternativa: D
04) (UFES) A figura a seguir representa dois fios muito longos, paralelos e perpendiculares ao plano da página. Os fios são percorridos por correntes iguais e no mesmo sentido, saindo do plano da página. O vetor campo magnético no ponto P, indicado na figura, é representado por:
O vetor campo magnético no ponto P, indicado na figura, é representado por:
(A) ←
(B) →
(C)↓
(D) ↑
(E) |B| = 0
Resolução:
O campo magnético ao redor do fio é circular, e a sua determinação é feita por meio da aplicação da regra da mão direita. Na imagem abaixo, o vetor B representa o campo magnético gerado no ponto p pelo fio da esquerda, e o vetor B' representa o campo magnético gerado pelo fio da direita no mesmo ponto p. A partir da soma vetorial, podemos definir que o campo resultante no ponto p é horizontal para a esquerda. Alternativa: A
Alternativa: A
05) (UECE) A figura representa dois fios bastantes longos (1 e 2), perpendiculares ao plano do papel e percorridos por correntes de sentido contrário, i1 e i2, respectivamente. A condição para que o campo magnético resultante, no ponto P, seja zero é:
A condição para que o campo magnético resultante, no ponto P, seja zero é:
(A) i1 = i2
(B)i1 = 2i2
(C) i1 = 3i2
(D) i1 = 4i2
Resolução:
Os campos magnéticos gerados pelos fios no ponto P devem ter o mesmo módulo e sentidos opostos para que o campo resultante seja nulo. Portanto, aplicando a equação do campo magnético para os fios 1 e 2 e igualando essas equações, temos:
BFIO 1 = BFIO 2
μ0 . i1 = μ0 . i2
2 . π . r1 2 . π . r2
i1 = i2
2d d
i1 = i2
2
i1 = 2i2
Alternativa: B
07) (UFAM) As primeiras observações experimentais de fenômenos magnéticos foram realizadas pelos gregos em uma região da Ásia Menor denominada de Magnésia. Eles verificaram que certo tipo de pedra denominada de magnetita (ou ímã natural) era capaz de atrair pedaços de ferro. Em 1820, o dinamarquês Hans Christian Oersted (1777-1851) observou que uma corrente elétrica percorrendo um fio condutor também produz campo magnético. Essa descoberta deu início à unificação dos fenômenos elétricos e magnéticos, originando o ramo da física denominado de eletromagnetismo. Para o caso de um fio condutor retilíneo percorrido por uma corrente elétrica, o campo magnético produzido em um ponto P, em torno do fio condutor, depende da permeabilidade magnética do meio, da intensidade da corrente elétrica e da distância do fio condutor ao ponto P. Considere a situação em que dois condutores retilíneos e paralelos são percorridos por corrente elétrica de intensidades i1 = 2A e i2 = 4A, conforme mostra a figura a seguir: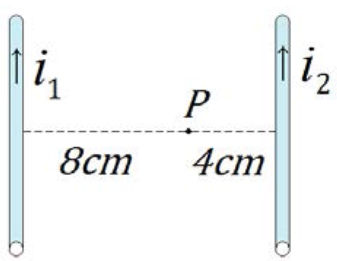 Podemos afirmar que a razão entre as intensidades dos campos magnéticos B1/B2, produzidos pelos dois condutores retilíneos no ponto P, vale:
Podemos afirmar que a razão entre as intensidades dos campos magnéticos B1/B2, produzidos pelos dois condutores retilíneos no ponto P, vale:
(A) 0,25
(B) 0,5
(C) 1
(D) 2
(E) 4
Resolução:
Aplicando a equação do campo magnético para o fio retilíneo para cada um dos fios, teremos: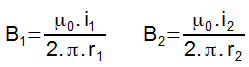
Dividindo B1 por B2, teremos: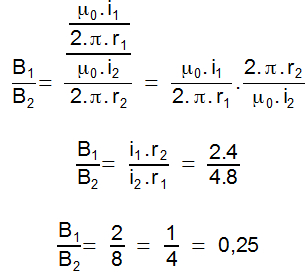
Alternativa: A
09) Um fio retilíneo conduz corrente elétrica de 2 A. Marque a alternativa correta a repeito dos valores e características dos campos magnéticos criados em pontos próximos ao fio.
(A) A uma distância de 5 cm do fio, o campo magnético possui intensidade de 6 μT.
(B) O campo magnético gerado por um fio possui a mesma direção e o mesmo sentido do deslocamento das cargas elétricas.
(C) O campo magnético gerado pelo fio possui formato circular e vale 8 μT a uma distância de 15 cm do fio.
(D) O campo magnético gerado pelo fio possui formato circular e vale 8,5 μT a uma distância de 10 cm do fio.
(E) Todas as afirmações anteriores estão incorretas.
Resolução:
A) Errada. Aplicando a equação do campo magnético gerado pelo fio retilíneo, a intensidade do campo magnético nas circunstâncias propostas seria de 8 μT.
B) Errada. O campo magnético tem formato circular.
C) Errada. O campo de 8 μT será gerado a 5 cm do fio.
D) Errada. A 10 cm do fio, o campo magnético será de 8 μT.
E) Correta.
Alternativa: E
10) Leia as afirmações a respeito de campos magnéticos gerados por fios retilíneos.
I – O campo magnético gerado por um fio retilíneo é diretamente proporcional à corrente elétrica e inversamente proporcional ao quadrado da distância de um ponto qualquer ao fio;
II – O campo magnético do fio retilíneo sempre é circular e no sentido horário;
III – O campo magnético gerado por um fio retilíneo é diretamente proporcional à corrente elétrica e inversamente proporcional à distância de um ponto qualquer ao fio;
IV – O campo magnético do fio retilíneo sempre é circular. O sentido da corrente elétrica define se o campo magnético ocorre no sentido horário ou anti-horário.
Está correto o que se afirma em
(A) I e II
(B) I e III
(C) II e IV
(D) I e IV
(E) III e IV.
Resolução:
I – Errada. O campo magnético gerado por um fio retilíneo é diretamente proporcional à corrente elétrica e inversamente proporcional à distância de um ponto qualquer ao fio.
II – Errada. O campo magnético do fio retilíneo sempre é circular. O sentido da corrente elétrica define se o campo magnético ocorre no sentido horário ou anti-horário.
III – Correta.
IV – Correta.
Alternativa: E
ESPIRA CIRCULAR
Campo Magnético formado por uma Espira Circular
Uma espira é um fio condutor dobrado em forma de círculo de raio R que quando percorrido por uma corrente elétrica, cria ao seu redor um campo magnético e as linhas do campo magnético irão acompanhar o formato da espira.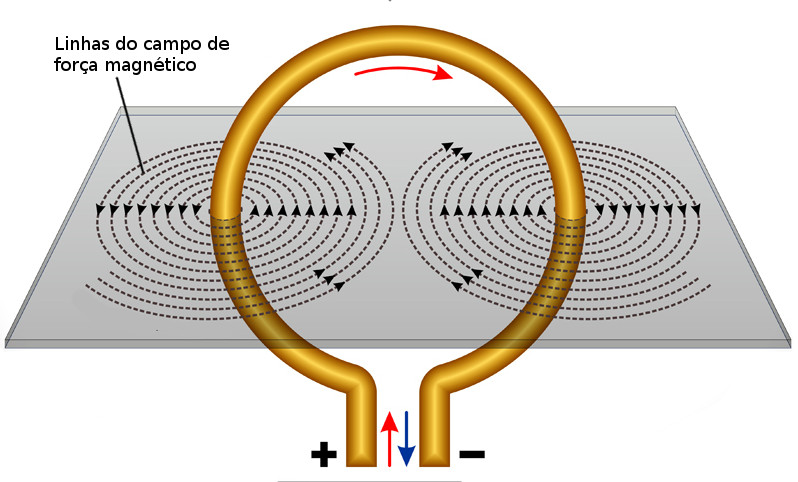
 R= raio da aspira (m)
R= raio da aspira (m)
i = corrente elétrica (A)
B = campo magnético (T)
μ = permeabilidade magnética no vácuo → 4π . 10-7 T.m/A RESOLVIDAS – CAMPO MAGNÉTICO CRIADO POR UMA ESPIRA CIRCULAR
RESOLVIDAS – CAMPO MAGNÉTICO CRIADO POR UMA ESPIRA CIRCULAR
01) (PUC-RS) Para uma espira circular condutora, percorrida por uma corrente elétrica de intensidade i, é registrado um campo magnético de intensidade B no seu centro. Alterando-se a intensidade da corrente elétrica na espira para um novo valor ifinal, observa-se que o módulo do campo magnético, no mesmo ponto, assumirá o valor 5B.
Qual é a razão entre as intensidades das correntes elétricas final e inicial (ifinal / i)?
(A) 1/5
(B) 1/25
(C) 5
(D) 10
(E) 25
Resolução:
O campo magnético gerado por uma espira é diretamente proporcional à corrente elétrica que a percorre, portanto, a corrente final também é cinco vezes maior que a corrente inicial. Desse modo, a razão entre as correntes final e inicial é 5.
Alternativa: C
02) (Unimontes-MG) Duas espiras circulares, 1 e 2, coplanares e concêntricas, possuem raios R1 e R2 e são percorridas por correntes I1 e I2, respectivamente (veja a figura). Sendo R2 = 2 R1 e I2 = 3 I1, a razão entre os módulos dos campos magnéticos criados pelas espiras 2 e 1 no centro O, B2/B1, a direção e o sentido do campo magnético resultante no centro O das espiras são, respectivamente: (A) 1,5, perpendicular à folha e apontando para fora dela.
(A) 1,5, perpendicular à folha e apontando para fora dela.
(B) 1,5, perpendicular à folha e apontando para dentro dela.
(C) 2/3, perpendicular à folha e apontando para fora dela.
(D) 2/3, perpendicular à folha e apontando para dentro dela.
Resolução:
A partir da equação do campo magnético para a espira circular, podemos escrever:.jpg) O campo magnético B2 é 1,5 vezes maior que B1. O campo resultante possui o mesmo sentido que o campo 2, que, nesse caso, em razão da aplicação da regra da mão direita para a espira, aponta para fora da página.
O campo magnético B2 é 1,5 vezes maior que B1. O campo resultante possui o mesmo sentido que o campo 2, que, nesse caso, em razão da aplicação da regra da mão direita para a espira, aponta para fora da página.
Alternativa: A
03) (PUC) Leia as afirmações a respeito do campo magnético gerado por uma espira circular.
I – O módulo do campo magnético gerado por uma espira é diretamente proporcional ao seu raio;
II – Se a corrente elétrica que flui por uma espira for dobrada, o campo magnético gerado por ela será duas vezes maior;
III – O sentido da corrente elétrica não interfere na direção e sentido do vetor indução magnética.
Está correto o que se afirma em:
(A) I e II
(B) II e III
(C) I e III
(D) Apenas III
(E) Apenas II
Resolução:
I – Falsa: O módulo do campo magnético gerado por uma espira é inversamente proporcional ao raio.
II – Correta.
III – Falsa. O sentido da corrente elétrica define a direção do campo magnético gerado pela espira.
Alternativa: E
04) (Vunesp) Uma espira circular, quando percorrida por uma corrente elétrica de intensidade i, gera um campo magnético que possui como módulo o dobro do valor referente à corrente.
Determine o valor do raio da espira sabendo que μ0 = 4.π x 10 – 7 T.m/A (utilize π = 3).
(A) 3 x 10 – 7 m
((B) 6 x 10 – 7 m
(C) 3 x 10 – 4 m
(D) 3 x 10 – 6 m
(E) 2 x 10 – 7 m
Resolução:
Isolando o raio na equação que define o campo magnético da espira e sabendo que esse é o dobro do valor da corrente, temos:
Alternativa: A
05) (Unicamp – SP) Um condutor homogêneo de resistência 8,0 Ω tem a forma de uma circunferência. Uma corrente I = 4,0 A chega por um fio retilíneo ao ponto A e sai pelo ponto B por outro fio retilíneo perpendicular, conforme a figura..jpg) As resistências dos fios retilíneos podem ser consideradas desprezíveis.
As resistências dos fios retilíneos podem ser consideradas desprezíveis.
a) calcule a intensidade das correntes nos dois arcos de circunferência compreendidos entre A e B.
b) calcule o valor da intensidade do campo magnético B no centro O da circunferência.
Resolução: (a)
São dados no problema:
I = 4,0A
R = 8,0 Ω
A figura a seguir representa esquematicamente o enunciado do problema:.jpg)
Sendo 8,0 Ω, a resistência em toda a circunferência, concluímos que o trecho correspondente a 1/4 da circunferência têm resistência:
R1 = 2,0 Ω
E o outro trecho, correspondente a 3/4 da circunferência tem resistência
R2 = 6,0 Ω
Como a diferença de potencial é igual para cada resistor, temos:
U1 = U2
R1.i1 = R2.i2
2,0.i1 = 6,0.i2
i1 = 3,0.i2
A corrente I chega pelo fio no ponto A e divide-se em i1 e i2, assim:
I = i1 + i2, sabendo que I = 4,0 A e que i1 = 3,0.i2,
temos que:
4,0 = 3,0i2 + i2
4,0 = 4,0.i2
i2 = 1,0 A
Portanto,
i1 = 3,0A
Resolução: (b)
A corrente elétrica i1 origina no centro O um campo B1, entrando na tela (regra da mão direita)..jpg)
A corrente elétrica i2 origina no centro O um campo B2, saindo da tela (regra da mão direita)..jpg)
Podemos concluir então que B1 = B2, portanto, o campo resultante é
Bresultante = 0
06) Duas espiras iguais, cada uma com raio de 2π cm, são colocadas com centros coincidentes em planos perpendiculares. Sendo percorridas pelas correntes i1 = 4,0 A e i2 = 3,0 A, caracterize o vetor indução magnética resultante no seu centro O.
(Dado: μ0 = 4μ . 10-7 T.m/A).
Resolução:
O campo magnético gerado pela corrente i1 = 4,0 A na espira 1 é:.jpg)
O campo gerado pela corrente i2 = 3,0 A na espira 2 é:.jpg)
Como as espiras estão dispostas perpendicularmente, o campo resultante é:.jpg)
08) (PUC) Duas espiras concêntricas de raios R e 2R conduzem correntes elétricas de sentidos opostos. Sabendo que o campo magnético no centro das espiras é nulo, marque a alternativa que relaciona corretamente o valor das correntes das espiras.
(A) A corrente da menor espira deve ser quatro vezes maior.
(B) A corrente da maior espira deve ser três vezes menor.
(C) A corrente da maior espira deve ser duas vezes maior.
(D) A corrente deve ser a mesma nas espiras.
(E) A corrente da espira maior deve ser 40% menor.
Resolução:
Para que o campo magnético no centro das espiras seja nulo, as correntes devem circular em sentidos opostos e os campos gerados pelas espiras devem ser iguais. Sabendo que B é o campo magnético, i é a corrente e μ0 éa permissividade magnética, temos:
BESPIRA MENOR = BESPIRA MAIOR
μ0 . iMENOR = μ0 . iMAIOR
2R 2. 2R
iMENOR = iMAIOR
2
2 iMENOR = iMAIOR
08) (Metodista) A figura abaixo mostra duas espiras concêntricas que conduzem correntes elétricas nos sentidos indicados pelas setas. Determine o módulo, a direção e o sentido do campo magnético resultante no ponto O, sabendo que a corrente que passa pela espira maior corresponde ao triplo da corrente que circula a espira menor.
Determine o módulo, a direção e o sentido do campo magnético resultante no ponto O, sabendo que a corrente que passa pela espira maior corresponde ao triplo da corrente que circula a espira menor.
(A) O campo em O corresponde à quinta parte do campo da maior espira e sai do plano da página.
(B) O campo em O corresponde à metade do campo da maior espira e entra no plano da página.
(C) O campo em O corresponde à sexta parte do campo da maior espira e sai do plano da página.
(D) O campo em O corresponde à metade do campo da menor espira e entra no plano da página.
(E) O campo em O corresponde ao triplo do campo da menor espira e sai do plano da página.
Resolução:
A partir da equação que determina o campo magnético para as espiras, encontraremos o campo para cada uma das espiras da figura. Pela regra da mão direita, sabemos que o campo magnético da espira maior (B) entra no plano da página e que o campo da espira menor (B') sai do plano da página.
B' = μ0 . i
2R
B = μ0 . 3i
2 . 2R
B = 3 μ0 . i
2 . 2R
B= 3 B'
2
O campo resultante em O será dado pela subtração de B por B' e terá o sentido de B, já que ele é o maior campo.
BRESULTANTE = B – B'
BRESULTANTE = 3 B' – B'
2
BRESULTANTE =1,5 B' – B'
BRESULTANTE = 0,5 B'
O campo resultante entra no plano da página e vale 0,5 B'.
SOLENOIDE
Campo Magnético formado por um Solenoide
É um fio condutor, longo, enrolado, que forma uma bobina em espiral. Essa bobina ao ser percorrido pela corrente i, surge no interior do solenoide um campo magnético cujas linhas de indução são praticamente paralelas. O campo magnético no interior do solenoide é praticamente uniforme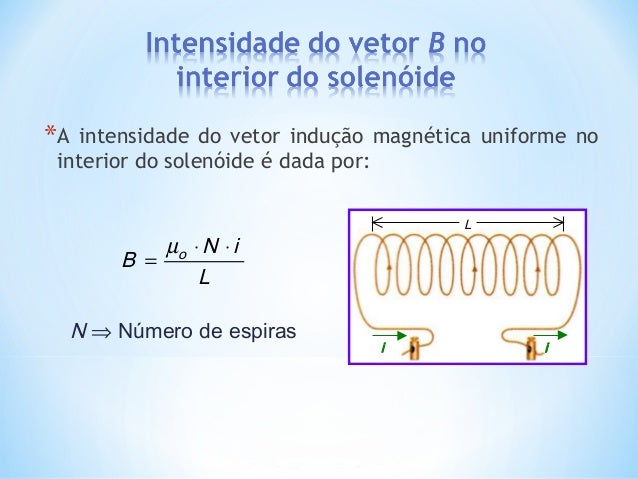 N = número de espiras
N = número de espiras
L = comprimento do solenoide (m)
i = corrente elétrica (A)
B = campo magnético (T)
μ = permeabilidade magnética no vácuo → 4π . 10-7 T.m/A RESOLVIDAS – CAMPO MAGNÉTICO FORMADO POR UM SOLENOIDE
RESOLVIDAS – CAMPO MAGNÉTICO FORMADO POR UM SOLENOIDE
01) (Unicesumar-SP) Um solenoide de 30 cm de comprimento, contendo 800 espiras e resistência elétrica de 7,5Ω , é conectado a um gerador de força eletromotriz igual a 15V e resistência interna de 2,5 Ω . Determine, em tesla (T) , o módulo do vetor indução magnética no interior do solenoide. Considere a permeabilidade magnética do meio que constitui o interior do solenoide igual a 4π.10–7 T.m.A–1 e π = 3. (A) 0,0048
(A) 0,0048
(B) 0,0064
(C) 0,0192
(D) 0,000048
(E) 0,000064
Resolução:
A corrente elétrica será determinada pela equação do gerador.
R = Resistência do solenoide = 7,5 Ω;
r = Resistência interna = 2,5 Ω;
ε = Força eletromotriz = 15 V;
Primeira lei de Ohm: U = R.i
Aplicando a equação para o campo magnético do solenoide, teremos:

Alternativa: A
02) (Udesc) Considere um longo solenoide ideal composto por 10.000 espiras por metro, percorrido por uma corrente contínua de 0,2A.
O módulo e as linhas de campo magnético no interior do solenoide ideal são, respectivamente:
(A) nulo, inexistentes.
(B) 8π.10 – 4 T, circunferências concêntricas.
(C) 4π.10 – 4 T, hélices cilíndricas.
(D) 8π.10 – 3T, radiais com origem no eixo do solenoide.
(R) 8π.10 – 4 T, retas paralelas ao eixo do solenoide.
Resolução:
Considerando que o solenoide tenha apenas 1m, o número de espiras a ser considerado é de 10.000 (104).
Assim, o campo magnético para esse solenoide é igual a:

As linhas de campo magnético são paralelas ao eixo do solenoide, saindo do lado referente ao polo norte (N) e entrando no lado referente ao polo sul (S).
Alternativa: E
03) Qual deve ser o número de espiras de um solenoide de 1m de comprimento para que o campo magnético gerado tenha intensidade de 2,4 . 10 – 3T quando percorrido por uma corrente elétrica de 2A? Considere a permeabilidade magnética do meio que constitui o interior do solenoide igual a 4π.10–7 T.m.A–1e π = 3.
(A) 10.000
(B) 100
(C) 1000
(D) 2000
(E) 20.000
Resolução:
Aplicando a equação do campo magnético do solenoide e isolando o número de espiras, teremos:
Alternativa: C
04) Marque a alternativa correta a respeito das características do campo magnético gerado por um solenoide.
(A) O campo magnético gerado por um solenoide é inversamente proporcional ao número de espiras.
(B) O campo magnético gerado por um solenoide é inversamente proporcional ao comprimento do solenoide.
(C) As linhas de campo magnético de um solenoide são circulares.
(D) As linhas de campo magnético de um solenoide são perpendiculares ao sentido da corrente.
(E) Todas as alternativas estão incorretas.
Resolução:
A) Errada. O campo magnético gerado por um solenoide é diretamente proporcional ao número de espiras.
B) Correta.
C) Errada. As linhas de campo magnético são paralelas ao eixo do solenoide, saindo do lado referente ao polo norte (N) e entrando no lado referente ao polo sul (S).
D) Errada.
E) Errada.
Alternativa: B
05) Determine a relação entre o número de espiras e o comprimento de um solenoide, por onde flui uma corrente elétrica de 2,2A que produz um campo magnético de 26,4 x 10 – 4 T.
Dado: Considere π = 3 e μ0 = 4π.10–7 T.m.A–1
(A) 102
(B) 103
(C) 104
(D) 101
(E) 100
Resolução:
A relação entre o número de espiras e o comprimento do solenoide pode ser isolada a partir da equação que define o campo magnético de um solenoide.

Alternativa: B
06) Um solenoide de comprimento 12 cm (0,12 m), percorrido por uma corrente elétrica de intensidade 2A, precisaria ser formado por quantas espiras para possuir um campo magnético de módulo igual a 100 T?
Dado: Considere π = 3 e μ0 = 4π.10–7 T.m.A–1
(A) 500
(B) 5000
(C) 5000.000
(D) 5000.000.000
(E) 5500.000.000
Resolução:
O número de espiras deve ser isolado a partir da equação que determina o campo magnético de um solenoide.
Alternativa: C
07) (Udesc) Considere um longo solenoide ideal composto por 10.000 espiras por metro, percorrido por uma corrente contínua de 0,2A.
O módulo e as linhas de campo magnético no interior do solenoide ideal são, respectivamente:
(A) nulo, inexistentes.
(B) 8π x 10– 4T, circunferências concêntricas.
(C) 4π x 10– 4T, hélices cilíndricas.
(D) 8π x 10– 3T, radiais com origem no eixo do solenoide.
(E) 8π x 10– 4T, retas paralelas ao eixo do solenoide.
Resolução:
Considerando que o solenoide tenha apenas 1 m, o número de espiras a ser considerado é de 10.000 (104). Assim, o campo magnético para esse solenoide é:
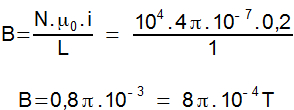
As linhas de campo magnético de um solenoide formam linhas paralelas ao eixo do solenoide, saindo do polo norte (N) e entrando no polo sul (S).
Alternativa: E
BOBINA CHATA
Campo Magnético formado por uma Bobina Chata
Para representar esse campo, precisamos ter em mente que uma bobina chata representa um conjunto de n espiras que estão justapostas. Lembrando que essas espiras são todas iguais, apresentando assim, o mesmo raio R.  N = número de espiras
N = número de espiras
i = corrente elétrica (A)
B = campo magnético (T)
R = raio da espiara (m)
μ = permeabilidade magnética no vácuo → 4π . 10-7 T.m/A
RESOLVIDAS – BOBINA CHATA
01) Uma bobina chata é formada de 100 espiras circulares de raio 0,2m. Sabendo que as espiras são percorridas por uma corrente de 8 A, determine B.
Dado: No= 4π. 10(-7) T.m/a
Resolução:
B = N . ( μ . i ) / 2 . R
B é a intensidade do vetor campo magnético , R é a raio descrito pelo campo , μ é a permissividade magnética do meio , i é a intensidade da corrente e N o número de espiras abordada na questão.
B = N . ( μ . i ) / 2 . R
ou então substituindo o valor de pi , temos :
RESUMO - FONTES DE CAMPOS MAGNÉTICOS
Condutor retilíneo
Um condutor percorrido por uma corrente elétrica gera um campo magnético ao seu redor. A configuração desse campo pode ser determinada colocando-se pequenas agulhas magnéticas em pontos dessa região. A equação que nos fornece o campo magnético gerado por um condutor retilíneo percorrido por uma corrente elétrica é a seguinte:![]()
Espira circular
O campo magnético gerado por uma espira circular percorrida por corrente elétrica pode ser determinado pela seguinte equação:![]() As linhas de indução do campo magnético são circunferências perpendiculares ao plano da espira, concêntricas com o condutor.
As linhas de indução do campo magnético são circunferências perpendiculares ao plano da espira, concêntricas com o condutor.
Bobina chata
Se considerarmos n espiras iguais justapostas, de modo que a espessura do enrolamento seja menor que o diâmetro de cada espira, teremos a chamada bobina chata. Podemos determinar a intensidade do vetor campo magnético no centro da bobina através da equação:![]() Solenoide
Solenoide
Chamamos de solenoide um condutor longo e enrolado que forma um tubo constituído de espiras igualmente espaçadas. A intensidade do vetor campo magnético no interior de um solenoide é determinada pela seguinte equação:![]()
Onde N/L representa o número de espiras por unidade de comprimento. E, em relação à equação acima, μ representa a permeabilidade magnética do condutor.
EQUIPAMENTO DE MEDIÇÃO
Galvanômetro - é um instrumento que pode medir correntes eléctricas de baixa intensidade, ou a diferença de potencial eléctrico entre dois pontos. Multímetro analógico - É o principal instrumento de teste e reparo de circuitos eletrônicos, consiste basicamente de um galvanômetro, ligado a uma chave seletora, uma bateria e vários resistores internos, para optarmos pelo seu funcionamento como amperímetro, ohmímetro ou voltímetro.
Multímetro analógico - É o principal instrumento de teste e reparo de circuitos eletrônicos, consiste basicamente de um galvanômetro, ligado a uma chave seletora, uma bateria e vários resistores internos, para optarmos pelo seu funcionamento como amperímetro, ohmímetro ou voltímetro. Observação: multímetros com galvanômetro - são chamados de multímetros analógicos, em oposição aos multímetros digitais, que possuem um mostrador de cristal líquido.
Observação: multímetros com galvanômetro - são chamados de multímetros analógicos, em oposição aos multímetros digitais, que possuem um mostrador de cristal líquido.
MOTORES ELÉTRICOS
Motores elétricos de corrente contínua - Alguns motores operam com corrente contínua (CC / DC) e podem ser alimentados quer por pilhas/baterias quer por fontes de alimentação adequadas, outros requerem corrente alternada (CA / AC) e podem ser alimentados diretamente pela rede elétrica domiciliar. Há até mesmo motores que trabalham, indiferentemente, com esses dois tipos de correntes.
 INDUÇÃO MAGNÉTICA
INDUÇÃO MAGNÉTICA
A indução magnética é o nome que se dá ao fenômeno no qual um campo magnético variável produz num circuito uma corrente elétrica, chamada de corrente induzida. Esse fenômeno foi descoberto em 1831 por dois cientistas, Michael Faraday, na Inglaterra, e Joseph Henry, nos Estados Unidos, porém, de forma independente.
Michael Faraday dedicou muito tempo na realização de pesquisas. Utilizando uma barra de ferro onde havia duas bobinas enroladas, ele percebeu que, ao ligar ou desligar uma das bobinas na bateria, na outra passava uma corrente elétrica, além disso, essa corrente durava pouco tempo, ou seja, desaparecia em instantes. Ou seja: a corrente induzida ocorre devido à variação do fluxo magnético em um circuito fechado.Foi assim que Faraday percebeu que ao variar o campo magnético, ligando ou desligando a bobina, surgia uma corrente elétrica na outra bobina, que é chamada de corrente induzida. Depois dessa descoberta, ele ainda realizou vários estudos até formular a lei que hoje recebe seu nome, a Lei de Faraday.
Observação: para que surja a corrente induzida, é necessário haver uma variação do fluxo magnético em certo intervalo de tempo.
Imantação – É o processo pelo qual um corpo neutro se torna imantado. Teoricamente, qualquer corpo pode se tornar um ímã. Mas a maioria dos corpos oferece uma resistência muito grande à imantação. Os corpos que se imantam com grande facilidade são o ferro e certas ligas de ferro usadas na fabricação de ímãs permanentes.
Os principais processos de imantação são:
Indução magnética: fenômeno pelo qual o ferro se imanta quando fica próxima de um ímã sendo atraído por ele. Atrito: quando uma barra de ferro neutra é atritada com um ímã, ela se imanta. É necessário que sejam atritados sempre no mesmo sentido, porque o atrito num sentido desfaz a ímantação obtida no outro.
Atrito: quando uma barra de ferro neutra é atritada com um ímã, ela se imanta. É necessário que sejam atritados sempre no mesmo sentido, porque o atrito num sentido desfaz a ímantação obtida no outro.
Corrente elétrica: Suponhamos que um condutor seja enrolado em uma barra de ferro e percorrido por uma corrente elétrica; a barra de ferro se torna um ímã.
ELETROÍMÃS
É um dispositivo formado por um núcleo de ferro envolto por um solenoide (bobina). Quando uma corrente elétrica passa pelas espiras da bobina, cria-se um campo magnético, o qual faz com que os imãs elementares do núcleo de ferro se orientem, ficando assim imantado e, consequentemente, com a propriedade de atrair outros materiais ferromagnéticos. Na figura abaixo temos um eletroímã e um imã com suas respectivas linhas de campo.
Na figura abaixo temos um eletroímã e um imã com suas respectivas linhas de campo..jpg) Observe que no eletroímã as linhas de campo entram em uma extremidade e saem na outra, já no imã, elas entram em um polo (polo sul) e saem no outro (polo norte) de maneira praticamente igual. Foi por esse motivo, de apresentar comportamento semelhante ao de um imã quando percorrido por uma corrente elétrica, que esse dispositivo ficou conhecido como eletroímã.
Observe que no eletroímã as linhas de campo entram em uma extremidade e saem na outra, já no imã, elas entram em um polo (polo sul) e saem no outro (polo norte) de maneira praticamente igual. Foi por esse motivo, de apresentar comportamento semelhante ao de um imã quando percorrido por uma corrente elétrica, que esse dispositivo ficou conhecido como eletroímã.
O fato de ter um núcleo (barra de ferro) no interior da bobina gera um campo magnético muito intenso e devido a essa propriedade os eletroímãs têm muitas aplicações, dentre elas, podemos destacar: nos motores, nas campainhas, nos telefones, na indústria de construção naval e no guindaste eletromagnético.
Como fazer um eletroímã? Acesse os endereços abaixo
GERADORES
Geradores de corrente alternada - São equipamento que converte energia mecânica em energia elétrica. Seu funcionamento é baseado na indução de força eletromotriz: o modelo mais simples é composto por uma espira (tipo de circuito elétrico que produz um campo magnético e eletricidade).

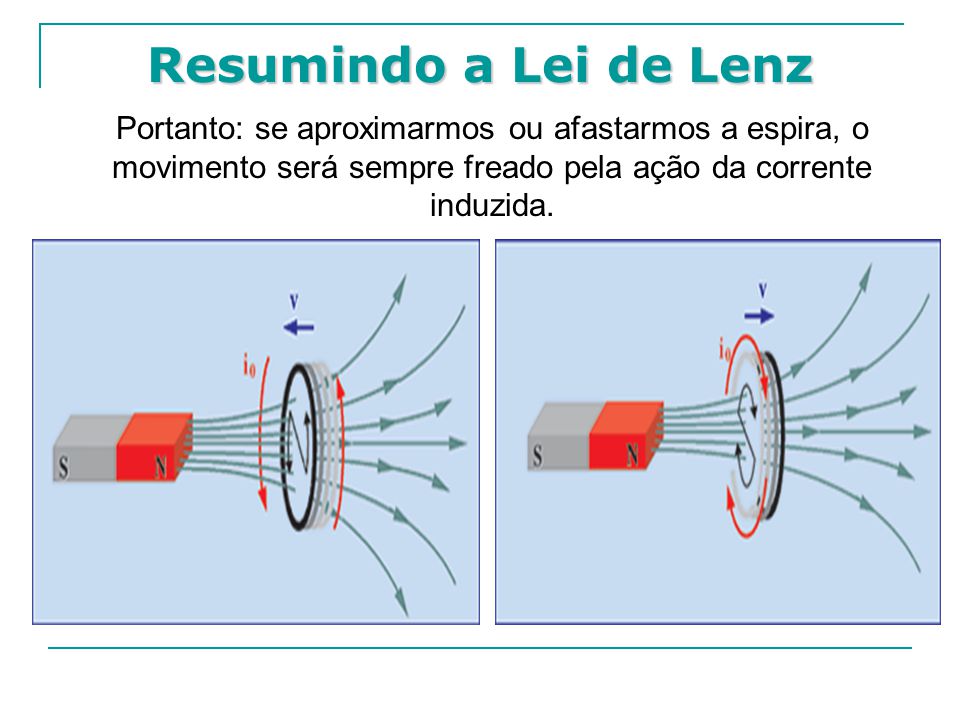
Lei de Lenz
O sentido da corrente elétrica induzida é tal que o campo magnético por ela produzido sempre se opõe á variação do campo magnético que a originou.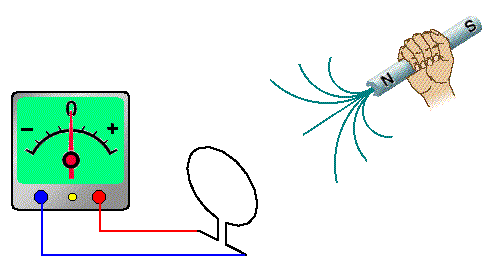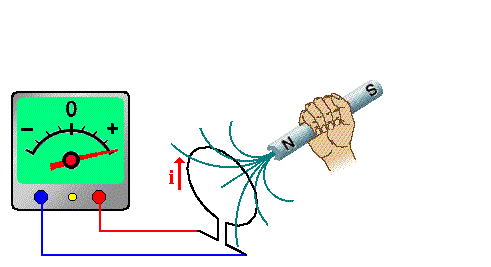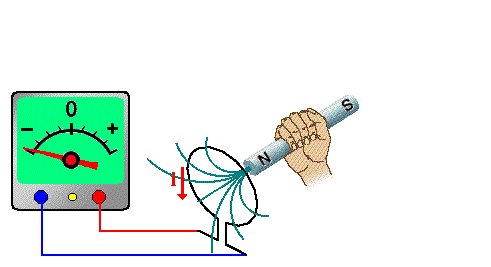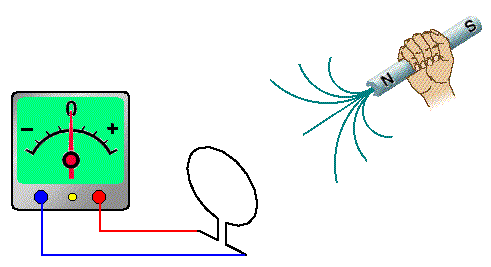
 Campo elétrico induzido – Um campo magnético variável no tempo produz um campo elétrico (induzido).
Campo elétrico induzido – Um campo magnético variável no tempo produz um campo elétrico (induzido).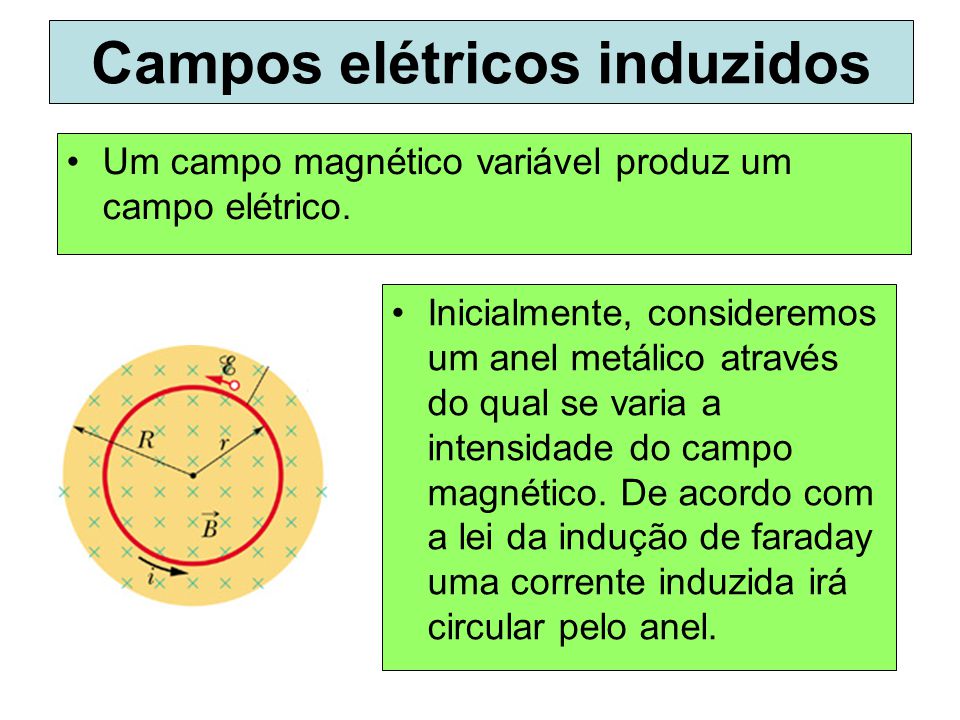
 Campo magnético induzido – Um campo elétrico variável produz um campo magnético induzido
Campo magnético induzido – Um campo elétrico variável produz um campo magnético induzido
Leis de Maxwell:
O escocês James Clerck Maxwell (1831 – 1879) é considerado um dos maiores físicos de todos os tempos em face dos seus estudos na área do eletromagnetismo. Maxwell baseou-se nas teorias de Gauss, Ampére e Faraday para formular um conjunto de quatro equações que descreve todos os fenômenos eletromagnéticos e para encontrar a equação dessas ondas no vácuo.
Apesar de todos os seus estudos, Maxwell morreu sem conseguir produzir ou detectar ondas eletromagnéticas, o que comprovaria suas teorias. Somente oito anos após sua morte que Heirinch Hertz provou experimentalmente as previsões feitas por Maxwell. As contribuições de Maxwell para o eletromagnetismo equiparam-no a físicos como Isaac Newton e Albert Einstein.
Observação: as equações de Maxwell firmam-se nas teorias de Gauss, Ampére e Faraday para fundamentar o eletromagnetismo, relacionando o campo elétrico é o campo magnético
Lei de Gauus para a eletricidade
A primeira das quatro equações de Maxwell e recebe esse nome em homenagem ao seu criador, o físico Carl Friederick Gauss. Ela estabelece a relação entre carga elétrica e campo elétrico que diz:
“O fluxo do campo elétrico através de uma superfície fechada no vácuo é igual à soma das cargas internas à superfície dividida pela permissividade elétrica do vácuo”.
Lei de Gauss para o magnetismo – Diz que:
“O fluxo magnético resultante no interior de uma superfície fechada é zero”
Essa lei evidencia a impossibilidade de existência de monopolos magnéticos, ou seja, não existe polo sul ou polo norte isolado. Além disso, afirma que as linhas de campo magnético são contínuas, ao contrário das linhas de campo elétrico que se iniciam nas cargas positivas e terminam nas cargas negativas.
Esta simulação mostra que o fluxo elétrico de uma carga puntiforme independe da forma da superfície gaussiana.
Lei de Ampére
Assim denominada em homenagem a André Marie Ampere, essa lei relaciona o campo magnético com o movimento de cargas elétricas ou corrente elétrica:
“Uma corrente elétrica de intensidade i ou a variação de fluxo do campo elétrico podem dar origem a um campo magnético.” Lei de Faraday
Lei de Faraday
Estabelece a relação entre campo magnético e elétrico e diz que:
“A variação do fluxo do campo magnético gera um campo elétrico”
Observação importante: não foi utilizada a descrição matemática para representar essas leis, uma vez que é necessário o conhecimento de conceitos avançados de Matemática que somente são estudados em cursos superiores.
MOTOR ELÉTRICO
O funcionamento dos motores elétricos está baseado nos princípios do eletromagnetismo, mediante os quais, condutores situados num campo magnético e atravessados por corrente elétrica, sofrem a ação de uma força mecânica, força essa chamada de torque. 
Existem vários tipos de motores elétricos, dos quais os principais são os de corrente contínua e de corrente alternada. Os motores de corrente contínua são mais caros, pois é necessário um dispositivo que converte a corrente alternada em corrente contínua. Já os motores de corrente alternada são mais baratos e os mais utilizados, pois a energia elétrica é distribuída em forma de corrente alternada, reduzindo assim seu custo.
TIPO DE CORRENTES ELÉTRICAS
Corrente contínua
Corrente na qual possui fluxo contínuo e ordenado de elétrons sempre na mesma direção. 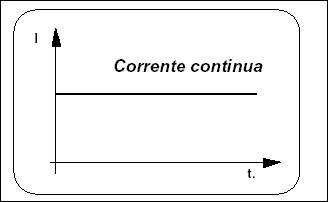
Corrente alternada
É uma corrente cuja magnitude e direção varia ciclicamente. Ou seja, há variação de corrente elétrica, ao contrário da corrente contínua.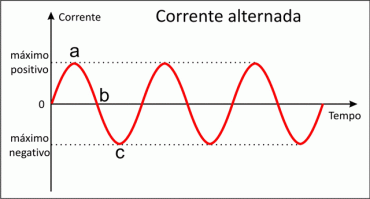
MOTOR ELÉTRICO
O que São e Como Fazer Um Motor Elétrico 

Capacitância e tensão elétrica
A capacitância ou capacidade é a grandeza elétrica de um capacitor, que é determinada pela quantidade de energia elétrica que pode ser armazenada em si por uma determinada tensão e pela quantidade de corrente alternada que atravessa o capacitor numa determinada freqüência.
Sua unidade é dada em farad (símbolo F), que é o valor que deixará passar uma corrente de 1 ampere quando a tensão estiver variando na razão de 1 volt por segundo.
A capacitância pode ser medida pela seguinte fórmula: C=Q / U, onde q é a quantidade de carga, dada em Coulomb e U é o potencial eletroestático, dado em Volts.
Quanto maior for o material, maior capacitância ele terá.
Tensão elétrica ou diferencial de potencial (ddp)
A tensão elétrica pode ser definida como a diferença de potencial entre dois pontos. Ou seja, a quantidade de energia gerada para movimentar uma carga elétrica, portanto, o gerador necessita liberar energia elétrica para movimentar uma carga eletrizada.
A partir daí, a fórmula para calcular a tensão é:
U = Eel / Q
Onde:
U = Tensão elétrica
Eel = Energia elétrica
Q = Quantidade de carga eletrizada
Outra fórmula para calcular a tensão elétrica é a partir da energia elétrica utilizada e quantidade de carga:
V = J / C
Onde:
J = Joule
C = Coulomb
A unidade de tensão será dada em J/C
Também é possível calcular a tensão elétrica de um circuito tendo as grandezas de corrente e resistência:
V= I.R
Onde:
V = tensão elétrica
I = corrente elétrica
R = resistência elétrica
Se analisarmos mais profundamente para calcular a tensão, poderemos calcular também através da potência elétrica:
V= P/IOnde: P = potência elétrica I = corrente elétrica Energia potencial elétrica armazenada por um capacitor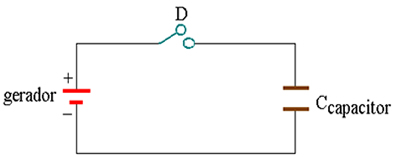 Para que consigamos armazenar energia em um capacitor é necessário realizar um trabalho que se transforma em energia potencial elétrica. Sendo assim, vamos considerar a figura acima, onde temos um circuito elétrico com capacitor plano. Caso fechemos a chave D do circuito, o capacitor irá carregar-se. Desta forma, sua capacitância é dada por C = Q / U , que resulta que a carga do capacitor é, em cada instante, diretamente proporcional à sua diferença de potencial.Podemos expressar esse resultado através do gráfico Q x U mostrado abaixo. O gerador, ao carregar o capacitor, forneceu-lhe energia potencial elétrica. Essa energia armazenada pelo capacitor é dada, numericamente, pela área A representada na figura abaixo.
Para que consigamos armazenar energia em um capacitor é necessário realizar um trabalho que se transforma em energia potencial elétrica. Sendo assim, vamos considerar a figura acima, onde temos um circuito elétrico com capacitor plano. Caso fechemos a chave D do circuito, o capacitor irá carregar-se. Desta forma, sua capacitância é dada por C = Q / U , que resulta que a carga do capacitor é, em cada instante, diretamente proporcional à sua diferença de potencial.Podemos expressar esse resultado através do gráfico Q x U mostrado abaixo. O gerador, ao carregar o capacitor, forneceu-lhe energia potencial elétrica. Essa energia armazenada pelo capacitor é dada, numericamente, pela área A representada na figura abaixo.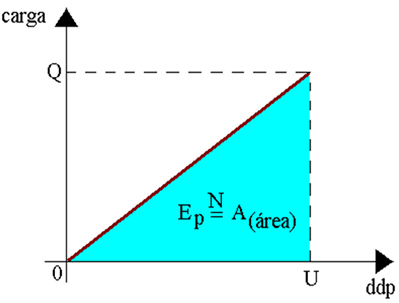 EP= área sombreada
EP= área sombreada![]()
![]() Em resumo temos:
Em resumo temos:![]() QUESTÕES RESOLVIDAS
QUESTÕES RESOLVIDAS
01)(Enem/2014) Do funcionamento dos geradores de usinas elétricas baseia-se no fenômeno da indução eletromagnética, descoberto por Michael Faraday no século XIX. Pode-se observar esse fenômeno ao se movimentar um ímã e uma espira em sentidos opostos com módulo da velocidade igual a v, induzindo uma corrente elétrica de intensidade i, como ilustrado na figura.
A fim de se obter uma corrente com o mesmo sentido da apresentada na figura, utilizando os mesmos materiais, outra possibilidade é mover a espira para a
(A) a esquerda e o ímã para a direita com polaridade invertida.
(B) direita e o ímã para a esquerda com polaridade invertida.
(C) esquerda e o ímã para a esquerda com mesma polaridade.
(D) direita e manter o ímã em repouso com polaridade invertida.
(E) esquerda e manter o ímã em repouso com mesma polaridade.
Resolução:
Na situação dada, de acordo com a Lei de Lenz, surge na face da espira, próxima ao ímã, um polo sul que se opõe ao afastamento relativo entre o ímã e a espira. Se houver a aproximação relativa entre o ímã e a espira e se a polaridade do ímã for invertida, também surge na face da espira, próxima ao ímã, um polo sul que se opõe à aproximação do polo sul do ímã. Assim, devemos mover a espira para a esquerda e o ímã para a direita com polaridade invertida.
Resposta: A
02) (Enem/2013) Desenvolve-se um dispositivo para abrir automaticamente uma porta no qual um botão, quando acionado, faz com que uma corrente elétrica i = 6 A percorra uma barra condutora de comprimento L = 5 cm, cujo ponto médio está preso a uma mola de constante elástica k = 5 x 10−2N/cm. O sistema mola-condutor está imerso em um campo magnético uniforme perpendicular ao plano. Quando acionado o botão, a barra sairá da posição do equilíbrio a uma velocidade média de 5m/s e atingirá a catraca em 6 milisegundos, abrindo a porta.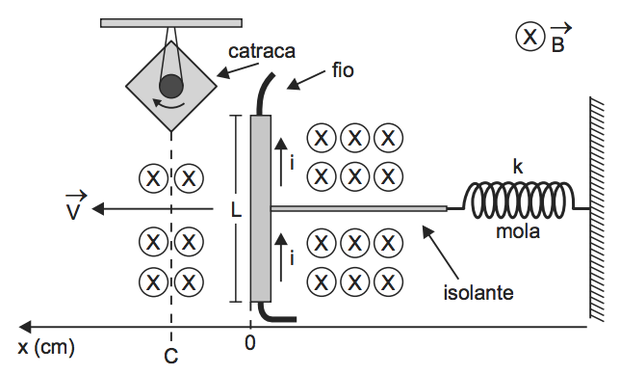 A intensidade do campo magnético, para que o dispostivo funcione corretamente, é de
A intensidade do campo magnético, para que o dispostivo funcione corretamente, é de
(A) 5 x 10−1
(B) 5 x 10−2
(C) 5 x 101
(D) 2 x 10−2
(E) 2 x 100
Resolução
Primeiramente, calculamos o comprimento do segmento OC:
OC = Vm ⋅ ∆t
OC = 5 . 6 . 10−3 m
OC = 30 . 10−3 m
OC= 3 . 10−2 m = 3 cm
Depois, calculamos a intensidade da força elástica:
Fel = k⋅xmáx
Fel = k ⋅ OC
Fel = 5 . 102 . 3 (N)
Fel = 15⋅10−2 N
Esquema da Foto Qi
O próximo passo é descobrir a força magnética na haste percorrida pela corrente: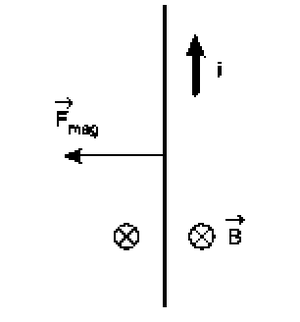 Usando a regra da mão direita, descobrimos que seu sentido é pela esquerda.
Usando a regra da mão direita, descobrimos que seu sentido é pela esquerda.
Módulo:
Fmag = B⋅i⋅L
Fmag = 6 . 5 . 10−2
Após atingir a posição C, devemos assumir a suposição de que as forças magnética e elástica devem equilibrar-se, o que não está explicitado no enunciado.
Fmag = Fel
B ⋅ 30 ⋅ 10−2 = 15 ⋅ 10−2
B = 15⋅10−23 ⋅ 10−1
B = 5 . 10−1T
Alternativa: A
03) (PUC RJ) Cientistas creem ter encontrado o tão esperado “bóson de Higgs” em experimentos de colisão próton-próton com energia inédita de 4 TeV(tera elétron-Volts) no grande colisor de hádrons, LHC. Os prótons, de massa 1,7x10–27 kg e carga elétrica 1,6x10–19 C, estão praticamente à velocidade da luz (3x108 m/s) e se mantêm em uma trajetória circular graças ao campo magnético de 8 Tesla, perpendicular à trajetória dos prótons.
Com estes dados, a força de deflexão magnética sofrida pelos prótons no LHC é em Newton:
(A) 3,8x10–10
(B) 1,3x10–18
(C) 4,1x10–18
(D) 5,1x10–19
(E) 1,9x10–10
Resolução:
Aplicando a equação de força magnética, temos:
FM = q . v . B . senα
FM = 1,6 . 10–19. 3 . 108. 8 . sen90°
FM = 3,84 . 10 – 10 N
Alternativa: A
04) (UNIFOR CE) Os cientistas que estudam a física das partículas necessitam estudar o comportamento e as propriedades do núcleo atômico. Para estudar os componentes dos prótons no maior acelerador do mundo, recentemente inaugurado na Suíça “LHC (Large Hadron Collider)”, prótons de massa ‘m’ e carga positiva ‘q’ são disparados em colisão frontal, com velocidades perpendiculares a Campos Magnéticos Uniformes, sofrendo ação de forças magnéticas. Os Campos Magnéticos utilizados são uniformes e atuam perpendicularmente à velocidade destas partículas. Podemos afirmar que estas forças magnéticas: (A) Mantêm as velocidades escalares dos prótons constantes, mas os colocam em trajetórias circulares.
(A) Mantêm as velocidades escalares dos prótons constantes, mas os colocam em trajetórias circulares.
(B) Mantêm as velocidades escalares dos prótons constantes, mas os colocam em trajetórias helicoidais.
(C) Aumentam as velocidades escalares dos prótons e mantêm suas trajetórias retilíneas.
(D) Diminuem as velocidades escalares dos prótons e mantêm suas trajetórias retilíneas.
(E) Não alteram as velocidades escalares dos prótons nem alteram as suas trajetórias.
Resolução:
A força magnética, neste caso, aponta para o centro da trajetória circular, atuando então como força centrípeta. Como ela é perpendicular à velocidade, não sofre alteração.
Alternativa: A
05) (MACK SP) Uma partícula alfa (q = 3,2.10–19 C e m = 6,7.10–27 kg), animada de velocidade v = 2,0.107 m/s, paralela ao plano xOy, é lançada numa região onde existe um campo de indução magnética uniforme, de mesma direção orientada que o eixo y e de intensidade 8,0.10–1 T. As ações gravitacionais e os efeitos relativísticos são desprezados. No instante em que esta partícula chega à região em que existe o campo, fica sujeita à ação de uma força de intensidade: (A) 2,56.10–12N e direção orientada igual a do eixo z.
(A) 2,56.10–12N e direção orientada igual a do eixo z.
(B) 2,56.10–12N e direção igual a do eixo z, porém de sentido contrário ao dele.
(C) 4,43.10–12N e direção orientada igual a do eixo z.
(D) 4,43.10–12N e direção igual a do eixo z, porém, de sentido contrário ao dele.
(E) Nula.
Resolução:
Aplicando a equação de força magnética, temos:
FM = q . v . B . senα
FM = 3,2 .10–19 . 2,0 . 107 . 8,0 . 10–1 . sen150°
FM = 2,56 . 10 – 12 N
A direção da força magnética deve ser perpendicular à direção da velocidade e à direção do campo magnético, sendo portanto, neste caso, a direção z.
Alternativa: A
06) Um elétron de massa m entra em uma região entre duas placas carregadas com velocidade v. Em razão da ação dos campos elétrico e magnético, sendo o campo magnético perpendicular ao plano da página, a carga passa por entre as placas sem sofrer desvios. Determine a velocidade do elétron em termos do campo magnético B e do campo elétrico E e o sentido do campo magnético. (A) v = B/E e o campo magnético entra no plano da página
(A) v = B/E e o campo magnético entra no plano da página
(B) v = B/E e o campo magnético sai do plano da página
(C) v = B + E e o campo magnético entra no plano da página
(D) v = E/B e o campo magnético sai do plano da página
Resolução:
Como o peso da carga foi desprezado, as forças que atuam sobre ela são a força elétrica, vertical e para baixo, e a força magnética, que é definida pela regra da mão direita, é vertical e para cima. Igualando essas duas forças, teremos:
FELÉTRICA = FMAGNÉTICA
q . E = q . v . B . senα
E = v . B . sen90°
E = v . B
Alternativa: D
07) (FGV-SP) Da palavra 'aimant', que traduzido do francês significa amante, originou-se o nome ímã, devido à capacidade que esses objetos têm de exercer atração e repulsão. Sobre essas manifestações, considere as proposições:
I. assim como há ímãs que possuem os dois tipos de polos, sul e norte, há ímãs que possuem apenas um;
II. o campo magnético terrestre diverge dos outros campos, uma vez que o polo norte magnético de uma bússola é atraído pelo polo norte magnético do planeta;
III. os pedaços obtidos da divisão de um ímã são também ímãs que apresentam os dois polos magnéticos, independentemente do tamanho dos pedaços.
Está correto o contido em:
(A) I, apenas.
(B) III, apenas.
(C) I e II, apenas.
(D) II e III, apenas.
(E) I, II e III.
Resolução:
A proposição I é incorreta, pois não existem imãs que possuem apenas um polo magnético.
A proposição II é incorreta, pois o campo magnético da Terra comporta-se como o de qualquer imã, sendo o polo norte magnético da bússola atraído pelo polo sul magnético do planeta, que coincide com o norte geográfico.
Já a proposição III é correta.
Alternativa: B
08) A Terra é considerada um imã gigantesco, que tem as seguintes características:
(A) O polo norte geográfico está exatamente sobre o polo sul magnético, e o sul geográfico está na mesma posição que o norte magnético.
(B) O polo norte geográfico está exatamente sobre o polo norte magnético, e o sul geográfico está na mesma posição que o sul magnético.
(C) O polo norte magnético está próximo do polo sul geográfico, e o polo sul magnético está próximo ao polo norte geográfico.
(D) O polo norte magnético está próximo do polo norte geográfico, e o polo sul magnético está próximo do polo sul geográfico.
(E) O polo norte geográfico está defasado de um ângulo de 45º do polo sul magnético, e o polo Sul geográfico está defasado de 45º do polo norte magnético.
Resolução:
O polo norte magnético está próximo ao polo sul geográfico, e o polo sul magnético está próximo ao sul geográfico. Os polos magnéticos e geográficos não se coincidem, estando afastados 11,5º um do outro
Alternativa: C
09) Uma bússola é colocada na proximidade do imã da figura sobre o ponto A: Sabendo que o vermelho corresponde ao polo norte da bússola, qual será a orientação da agulha sobre o ponto A:
Sabendo que o vermelho corresponde ao polo norte da bússola, qual será a orientação da agulha sobre o ponto A:
Resolução:
Sobre esse ponto, a bússola está em equilíbrio, sendo que o polo sul da bússola fica próximo ao polo norte do imã, e o polo norte da agulha próximo ao polo sul do imã.
Alternativa: A
10) (MED - ITAJUBÁ)
I. Uma carga elétrica submetida a um campo magnético sofre sempre a ação de uma força magnética.
II. Uma carga elétrica submetida a um campo elétrico sofre sempre a ação de uma força elétrica.
III. A força magnética que atua sobre uma carga elétrica em movimento dentro de um campo magnético é sempre perpendicular à velocidade da carga.
Aponte abaixo a opção correta:
(A) Somente I está correta.
(B) Somente II está correta.
(C) Somente III está correta.
(D) II e III estão corretas.
(E) Todas estão corretas.
Resolução:
A afirmação I está incorreta pelo fato de a carga elétrica nem sempre sofrer ação de uma força magnética. Para uma carga elétrica lançada paralelamente as linhas de campo a força magnética será nula.
A afirmação II está correta, pois cargas elétricas lançadas em campos elétricos sempre sofrem a ação de uma força elétrica.
A afirmação III está correta, pois a força magnética é sempre perpendicular à velocidade da carga. Essa comprovação pode ser realizada através da regra do tapa.
Alternativa: D
11) (PUC) Um elétron num tubo de raios catódicos está se movendo paralelamente ao eixo do tubo com velocidade 107 m/s.
Aplicando-se um campo de indução magnética de 2T, paralelo ao eixo do tubo, a força magnética que atua sobre o elétron vale:
(A) 3,2 . 10-12N
(B) nula
(C) 1,6 . 10-12 N
(D) 1,6 . 10-26 N
(E) 3,2 . 10-26 N
Resolução:
Se a direção do deslocamento da carga elétrica for paralela à direção do vetor indução magnética B, o ângulo θ será tal que sen θ = 0, pois θ = 0º ou θ = 180º, a força magnética será igual a zero. Aplicando a equação podemos provar:
Fmag=|q|.v.B.sen00
Fmag=0
Alternativa: B
12) (Enem) O manual de funcionamento de um captador de guitarra elétrica apresenta o seguinte texto: Esse captador comum consiste de uma bobina, fios condutores enrolados em torno de um imã permanente. O campo magnético do imã induz o ordenamento dos pplos magnéticos na corda da guitarra, que está próxima a ele. Assim, quando a corda é tocada, as oscilações produzem variações, com o mesmo padrão, no fluxo magnético que atravessa a bobina. Isso induz uma corrente elétrica na bobina, que é transmitida até o amplificador e, daí, para o alto-falante.
Esse captador comum consiste de uma bobina, fios condutores enrolados em torno de um imã permanente. O campo magnético do imã induz o ordenamento dos pplos magnéticos na corda da guitarra, que está próxima a ele. Assim, quando a corda é tocada, as oscilações produzem variações, com o mesmo padrão, no fluxo magnético que atravessa a bobina. Isso induz uma corrente elétrica na bobina, que é transmitida até o amplificador e, daí, para o alto-falante.
Um guitarrista trocou as cordas originais de sua guitarra, que eram feitas de aço, por outras feitas de náilon. Com o uso dessas cordas, o amplificador ligado ao instrumento não emitia mais som, porque a corda de náilon:
(A) isola a passagem de corrente elétrica da bobina para o alto-falante.
(B) varia seu comprimento mais intensamente do que ocorre com o aço.
(C) apresenta uma magnetização desprezível sob a ação do imã permanente.
(D) induz correntes elétricas na bobina mais intensas que a capacidade do captador.
(E) oscila com uma frequência menor do que a que pode ser percebida pelo captador.
Resolução
A guitarra é uma aplicação tecnológica do eletromagnetismo. Para que a guitarra funcione, é necessário haver o ordenamento dos polos magnéticos na corda da guitarra. Quando as cordas de aço são trocadas pelas de náilon, esse ordenamento dos polos não ocorre porque o náilon não apresenta magnetização.
Alternativa: C
13) (Unicamp) Um solenóide ideal, de comprimento 50 cm e raio 1,5 cm, contém 2000 espiras e é percorrido por uma corrente elétrica de 3,0 A. O campo de indução magnética B é paralelo ao eixo do solenóide e sua intensidade é dada por B = µ0 . n . i, onde n é o número de espiras por unidade de comprimento e i é a corrente elétrica. Sendo µ0 = 4π . 10-7 N/A2:
a) Qual é o valor de B ao longo do eixo do solenóide?
b) Qual é a aceleração de um elétron lançado no interior do solenóide, paralelamente ao eixo?
Resolução
a) o valor de n é dado por:
n = 2000 / 0,5
n = 4000 = 4.103 espiras / metro
logo,
B = µ0. n . i
4π . 10-7. 103. 3
B = 150 x 10-4
B = 1,5 . 10-2 T
Resposta: B = 1,5 . 10-2 T
b) Como a velocidade é paralela ao campo, a força magnética é nula, portanto:
a = 0
Resposta: a = 0
Continua...








.jpg)