PRODUTOS NOTAVIES

PRODUTOS NOTAVIES

Professor Diminoi
Produtos notáveis: o que são e como estudá-los?
Produtos notáveis são casos de expressões da Álgebra que envolvem padrões de multiplicação entre os termos. Isso quer dizer que eles apresentam um esquema de organização particular das fórmulas de Matemática, construído de acordo com determinadas regras.

Quais são os 5 casos dos produtos notáveis?
Existem cinco casos básicos de produtos notáveis. Aprender devidamente cada um deles ajuda a simplificar o cálculo de equações complexas e fornece caminhos possíveis para resolvê-las. Por isso, os produtos notáveis são grande auxílio nas questões de matematica do Enem e do vestibular.

Cinco casos do produtos notavies.

Primeiro caso
Quadrado da soma entre dois termos

O primeiro caso é bastante simples. Nele, temos uma expressão na qual a soma de dois termos a e b está elevada à segunda potência.
(a + b)² = (a + b) × (a + b)

Sempre que for esse o caso, a distribuição do produto notável vai resultar na seguinte expressão:
(a + b) × (a + b) = a² + 2ab + b²

Segundo caso
Quadrado da diferença entre dois termos

O segundo caso é idêntico ao primeiro. Todavia, em vez da soma entre dois termos a e b, é a diferença entre eles que está elevada à segunda potência.
(a – b)² = (a – b) × (a – b)

O resultado da distribuição será quase idêntico, com uma pequena diferença.
(a – b) × (a – b) = a² – 2ab + b²

Terceiro caso
Produto da soma entre dois termos pela diferença entre dois termos.
O terceiro caso é muito tranquilo, pois parte do produto entre os termos vai se anular.
(a + b) × (a – b) = a² – ab + ab – b² = a² – b²

Quarto caso
Cubo da soma entre dois termos
A partir do quarto caso, as coisas ficam mais complexas. Mas não se preocupe, basta entender bem de que modo uma expressão algébrica pode ser decomposta em fatores de multiplicação.

Ao elevar uma soma de termos à terceira potência.
(a + b)³ = (a + b) × (a + b) × (a + b) = a³ + 3a²b + 3ab² + b³

Portanto, em qualquer lugar que você encontrar a expressão (a + b)3, ela pode ser reduzida imediatamente a³ + 3a²b + 3ab² + b³, simplificando o cálculo.

Quinto caso
Cubo da diferença entre dois termos
(a – b)³ = (a – b) × (a – b) × (a – b) = a³ – 3a²b + 3ab² – b³

Resumo
Exemplo:
01) Desenvolva o seguinte produto notável (x + y)²
Resolucao
(x + y)²= x² + 2.x.y + y²

02) Desenvolva o seguinte produto notável (2a + b)²
Resolucao
(2a + b)²= (2a)² + 2.2a.b + b²= 4a² + 4ab + b²

03) Desenvolva o seguinte produto notável (x – 5y)²
Resolucao
(x – 5y)² = x² – 2.x.5y + (5y)² = x² – 10xy + 25y²

04) Desenvolva (3x + y)²
Resolucao
(3x + y)² = (3x)² + 2 . 3x . y + y² = 9x² + 6xy + y²
05) Desenvolva (2x + 3y)³
Resolucao
(2x + 3y)³ = (2x)³ + 3 . (2x)² . 3y + 3 . 2x . (3y)² + (3y)³ = 8x³ + 36x²y + 54xy² + 27y³

06) Desenvolva (5 + x)²
Resoluao
(5 + x)² = 5² + 2 . 5.x + x² = 25 + 10x + x²

07) Desenvolva (𝑥 + 3)³
(𝑥+3)³ = (𝑥 + 3) ∙ (𝑥 + 3)²

08) Simplifique as expressões: (x – y)² – (x + y)²
Resolucao
Primeiro
(x – y)² = x² – 2xy + y²
(x + y)² = x² + 2xy + y².
Assim,
(x – y)² – (x + y)²
x² – 2xy + y² – (x² + 2xy + y²)
x² – 2xy + y² – x² – 2xy – y²
x² – x² – 2xy – 2xy + y² – y²
-2xy – 2xy
-4xy

09 Efetue as multiplicações: (x – 2).(x – 5)
Resolucao
(x – 2) . (x-5)
xx + x(-5) + (-2)x + (-2) . (-5)
x² + ((-2) + (-5))x + (-2) . (-5)
x² – 7x + 10

10) Efetue as multiplicações: (x + 15).(x – 4)
Resolucao
(x + 15)(x – 4)
xx + x(-4) + 15x + 15(-4)
x² + (15 + (-4))x + 15.(-4)
x² + 11x – 60

11) (Faetec) Ao entrar na sua sala de aula, Pedro encontrou as seguintes anotações no quadro:
a + b = 6
a . b = 4
a² + b² = ?
Usando seus conhecimentos sobre produtos notáveis, Pedro determinou corretamente o valor da expressão
a² + b². Esse valor é:
(A) 26
(B) 28
(C) 32
(D) 36
Resolucao
Para encontrar o valor da expressão, vamos usar o quadrado da soma de dois termos, ou seja:
(a + b)² = a² + 2.a.b + b²
Como queremos encontrar o valor a a² + b², isolaremos esses termos na expressão anterior, então temos:
a² + b² = (a + b)² - 2.a.b
Substituindo os valores dados:
a² + b² = 6² - 2.4
a² + b² = 36 - 8
a² + b² = 28
Portanto, Pedro determinou corretamente o valor da expressão a² + b², que é 28.
Alternativa B

12) (UFRGS) Se x + y = 13 e x . y = 1, então x² + y² é
(A) 166
(B) 167
(C) 168
(D) 169
(E) 170
Resolucao
Lembrando do desenvolvimento do quadrado da soma de dois termos, temos:
(x + y)² = x² + 2 . x . y + y²
Como queremos encontrar o valor a x² + y², isolaremos esses termos na expressão anterior, então temos:
x² + y² = (x + y)² - 2.x.y
Substituindo os valores dados:
x² + y² = 13² - 2.1
x² + y² = 169 - 2
x² + y² = 167
Portanto, x² + y²= 167.
Alternativa B

13) (Espm) O número que se deve somar a 456.788² para se obter 456.789² é:
(A) 456.789
(B) 1
(C) 456.788
(D) 913.579
(E) 913.577
Resolucao
Veja que temos que somar um número x ao número dado para encontrar o resultado.
x + 456788² = 456789²
Note que podemos isolar o x, passando o número para o outro lado. Com isso, teremos:
x = 456789² – 456788²
Observe que chegamos a um produto notável, que será o produto da soma pela diferença. Lembrando:
a² – b² = (a + b) . (a – b)
Reescrevendo a equação que encontramos nesse mesmo molde:
x= (456789 + 456788) . ( 456789 – 456788)
x = (456789 + 456788) . 1
x = 913577
Alternativa E

14) (IFSC) Considere x o resultado da operação 525² – 523². Assinale a alternativa CORRETA, que representa a soma dos algarismos de x.
(A) 18
(B) 13
(C) 02
(D) 17
(E) 04
Resolucao
Repare que teremos o mesmo produto notável do exercícios anterior:
525² – 523²
(525 + 523) . (525 – 523)
(525 + 523) . 2
1048 . 2
2096
x = 2 + 0 + 9 + 6
x = 17
Alternativa D

15) (UFGRS) Se x + y = 13 e x . y = 1, então x² + y² é
(A) 166.
(B) 167.
(C) 168.
(D) 169.
(E) 170.
Resolucao
Como queremos descobrir o resultado de x² + y², vamos pegar a primeira equação dada (x + y = 13) e elevá-la ao quadrado:
(x + y)² = (13)²
Aplicando o produto notável do quadrado da soma:
x² + 2xy + y² = 169
Repare no enunciado mais uma vez: sabemos que x . y = 1, ou seja, podemos trocar:
x² + 2 + y² = 169
x² + y² = 167
Alternativa B

16) Analisando as alternativas a seguir, marque aquela que contém de forma correta a solução do produto notável (x – 5)²:
(A) x² + 25
(B) x² – 25
(C) x² – 10x + 25
(D) x² + 10x – 25
(E) x² + 10
Resolucao
Note que estamos calculando o quadrado da diferenca. Nesse produto notável, temos como resposta:
(x – 5)² = x² – 2 · 5 · x + 5²
(x – 5)² = x² – 10x + 25
Alternativa C

17) Durante as aulas de matemática, o professor Raul decidiu revisar com os estudantes os produtos notáveis. Então, ele escreveu no quadro as seguintes expressões:
I → (x – 2) (x + 2)
II → (x + 3)²
III → (x – 2)³
Os produtos notáveis listados pelo professor são conhecidos, respectivamente, como:
(A) Quadrado da diferença, quadrado da soma e cubo da diferença.
(B) Produto da soma pela diferença, quadrado da soma e cubo da diferença.
(C) Trinômio quadrado perfeito, cubo da soma, cubo da diferença.
(D) Quadrado da soma, produto da soma pela diferença e cubo da diferença.
(E) Produto da soma pela diferença, quadrado do cubo, cubo da diferença.
Resolucao
I → produto da soma pela diferenca
II → quadrado da soma
III → cubo da diferenca
Alternativa B

18) Realizando a simplificação da expressão algébrica a seguir, encontraremos:

(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
Resolucao
Podemos observar que, no numerador, temos um produto da soma pela diferença, então, temos que: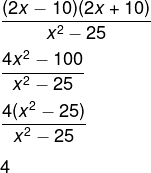

Alternativa D

19) Simplificando a expressão (x + 5)² – x (x + 10), encontraremos:
(A) 25
(B) 30
(C) 50
(D) 75
(E) 100
Resolucao
Calculando, temos que:
(x + 5)² – x(x + 10)
x² + 10x + 25 – x² – 10x
25
Alternativa A

20) Resolvendo os produtos notáveis da expressão (2x – 5) (2x + 5) – (2x – 5)² e simplificando, encontraremos como resultado o polinômio:
(A) 20x
(B) 20x – 50
(C) 8x³ + 2x²
(D) 50
(E) 2x – 25
Resolucao
Resolvendo os produtos notaveis, temos que:
(2x – 5) (2x + 5) – (2x – 5)²
4x² – 25 – (4x² – 20x + 25)
4x² – 25 – 4x² + 20x – 25
20x – 50
Alternativa B

21) Durante os estudos de cálculo 1, um matemático se deparou com a seguinte expressão: (g + a) (g – a), vendo-se diante de um produto notável conhecido como o produto da soma pela diferença. A solução desse produto notável é sempre igual ao:
(A) quadrado do primeiro termo, mais duas vezes o primeiro, vezes o segundo termo, mais o quadrado do segundo termo.
(B) quadrado do primeiro termo, menos duas vezes o primeiro, vezes o segundo termo, mais o quadrado do segundo termo.
(C) quadrado do primeiro termo menos o segundo termo.
(D) quadrado do primeiro termo mais o quadrado do segundo termo.
(E) quadrado do primeiro termo menos o quadrado do segundo termo.
Resolucao
Temos um caso de produto da soma pela diferença, que tem como resposta o quadrado do primeiro termo menos o quadrado do segundo termo.
Alternativa D

21) Ao desenvolver o produto (2x + 4)², encontramos como solução o polinômio:
(A) 4x² + 16x + 16
(B) 4x + 16
(C) 4x² + 16
(D) 2x² + 8x + 8
(E) 4x + 8
Resolucao
Calculando o produto notável conhecido como quadrado da soma, temos como resultado:
(2x + 4)² = 4x² + 16x + 16
Alternativa A

22) Das alternativas a seguir, marque aquela que contém um produto notável:
(A) x² + 25
(B) (x² – 3)
(C) (a – 3)²
(D) (x + 2) (x – 4)
(E) (x – 1) (x – 2) (x + 3)
Resolucao
Note que, na alternativa C, temos o cubo da diferença, que é um produto notável; as demais não são produtos notáveis.
Alternativa C

23) Sobre os produtos notáveis, julgue as afirmativas a seguir:
I → A multiplicação de dois polinômios é sempre um produto notável.
II → O produto (a + b)³ é um produto notável.
III → O produto da soma pela diferença é sempre igual à soma do quadrado do primeiro e segundo termos.
Marque a alternativa correta:
(A) Somente a afirmativa I é falsa.
(B) Somente a afirmativa II é falsa.
(C) Somente a afirmativa III é falsa.
(D) Todas as afirmativas são falsas.
(E) Todas as afirmativas são verdadeiras.
Resolucao
I → A multiplicação de dois polinomios é sempre um produto notável. (falsa)
Nem sempre uma multiplicação é um produto notável.
II → O produto (a + b)³ é um produto notável. (verdadeiro)
Verdadeira, pois trata-se do cubo da soma.
III → O produto da soma pela diferença é sempre igual à soma do quadrado do primeiro e segundo termos. (verdadeira)
Sempre que encontramos um produto da soma pela diferença, ele será igual ao quadrado do primeiro termo menos o quadrado do segundo termo.
Alternativa A

24) (UFRGS) Se x + y = 13 e x . y = 1, então, x² + y² é:
(A) 166
(B) 167
(C) 168
(D) 169
(E) 170
Resolucao
Calculando o quadrado da soma, temos que:
(x + y)² = x² + 2xy + y²
Sabemos que x + y = 13 e que xy = 1:
(13)² = x² + 2 · 1 + y²
169 = x² + 2 + y²
169 – 2 = x² + y²
167 = x² + y²
Alternativa B

25) A diferença entre (1522² – 1520²) é igual a:
(A) 2000
(B) 2340
(C) 5040
(D) 6084
(E) 7320
Resolucao
Transformando essa operação em um produto da soma pela diferença, temos que:
(1522 + 1520) (1522 – 1520)
34420 · 2
6084
Alternativa D

26) (IMNEC) A diferença entre o quadrado da soma e o quadrado da diferença entre dois números reais é igual:
(A) à diferença dos quadrados dos dois números.
(B) à soma dos quadrados dos dois números.
(C) à diferença dos dois números.
(D) ao dobro do produto dos números.
(E) ao quádruplo do produto dos números.
Resolucao
Seja a e b dois números, sabemos que:
(a + b)² =a² + 2ab + b²
Por outro lado, o quadrado da diferença é dado por:
(a – b)² = a² – 2ab + b²
Então, queremos a diferença do quadrado da soma e o quadrado da diferença:
a² + 2ab + b² – (a² – 2ab + b²)
a² + 2ab + b² – a² + 2ab – b²
4ab
Alternativa E

27) (UFRGS) Se x + y = 13 e x . y = 1, então x² + y² é
(A) 166
(B) 167
(C) 168
(D) 169
(E) 170
Resolucao
Lembrando do desenvolvimento do quadrado da soma de dois termos, temos:
(x + y)² = x² + 2.x.y + y²
Como queremos encontrar o valor a x² + y², isolaremos esses termos na expressão anterior, então temos:
x² + y² = (x + y)² - 2.x.y
Substituindo os valores dados:
x² + y² = 13² - 2.1
x² + y² = 169 - 2
x² + y² = 167
Portanto, x² + y²= 167.
Alternativa B

28) (Faetec) Ao entrar na sua sala de aula, Pedro encontrou as seguintes anotações no quadro: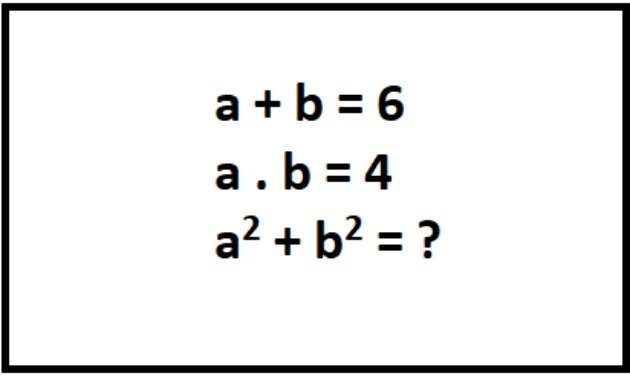
Usando seus conhecimentos sobre produtos notáveis, Pedro determinou corretamente o valor da expressão a² + b². Esse valor é:
(A) 26
(B) 28
(C) 32
(D) 36
Resolucao
Para encontrar o valor da expressão, vamos usar o quadrado da soma de dois termos, ou seja:
(a + b)² = a² + 2 . a . b + b²
Como queremos encontrar o valor a a² + b², isolaremos esses termos na expressão anterior, então temos:
a² + b² = (a + b)² - 2.a.b
Substituindo os valores dados:
a² + b² = 6² - 2.4
a² + b² = 36 - 8
a² + b² = 28
Portanto, Pedro determinou corretamente o valor da expressão a² + b², que é 28.
Alternativa B

29) (Aprendiz de Marinheiro) O produto (√3 - (√2) . (√3 + (√2) é igual a
(A) 6
(B) 1
(C) 0
(D) - 1
(E) – 6
Resolucao
Para resolver esse produto, podemos aplicar o produto notável do produto da soma pela diferença de dois termos, ou seja:
(a + b) . (a - b) = a² - b²
Assim:
(√3 - (√2) . (√3 + (√2) =
(√3 - (√2)² . (√3 + (√2)² =
3 – 2 = 1
Portanto, o produto é igual a 1.
Alternativa B

QUESTOES DIRETAS - RESOVIDOS
01) Calcule

a) (3 + x)² = 9 + 6x +x²

b) (x + 5)² = x² + 10x + 25

c) ( x + y)² = x² + 2xy +y²

d) (x + 2)² = x² + 4x + 4

e) ( 3x + 2)² = 9x² + 12x +4

f) (2x + 1)² = 4x² + 4x + 1

g) ( 5+ 3x)² = 25 + 30x + 9x²

h) (2x + y)² = 4x² + 4xy + y²

i) (r + 4s)² = r² + 8rs + 16s²

j) ( 10x + y)² =1 00x² + 20xy + y²

l) (3y + 3x)² = 9y² + 18xy + 9x²

m) (-5 + n)² = 25 -10n + n²

n) (-3x + 5)² = 9x² - 30x + 25

o) (a + ab)² = a² + 2a²b + a²b²

p) (2x + xy)² = 4x² + 4x²y + x²y²

q) (a² + 1)² = (a²)² + 2a² + 1

r) (y³ + 3)² = (y³)² + 6y³ + 9

s) (a² + b²)² = (a²)² + 2a²b² + (b²)²

t) ( x + 2y³)² = x² + 4xy³ + 4(y³)²

u) ( x + ½)² = x² +x + 1/4

v) ( 2x + ½)² = 4x² + 2x + 1/4

x) ( x/2 +y/2)² = x²/4 + 2xy/4 + y²/4

2) Calcule

a) ( 5 – x)² = 25 – 10x + x²

b) (y – 3)² = y² - 6y + 9

c) (x – y)² = x² - 2xy + y²

d) ( x – 7)² = x² - 14x + 49

e) (2x – 5) ² = 4x² - 20 x + 25

f) (6y – 4)² = 36y² - 48y + 16

g) (3x – 2y)² = 9x² - 12xy + 4y²

h) (2x – b)² = 4x² - 4xb + b²

i) (5x² - 1)² = 25(x²)² - 10x² + 1

j) (x² - 1)² = x⁴ - 2x² + 1

l) (9x² - 1)² = 81x⁴- 18x² + 1

m) (x³ - 2)² = x⁶ - 4x³ + 4

n) (x – 5y³)² = x² - 10xy³ +25x⁶

o) (1 - mx)² = 1 -2mx +m²x²

p) (3x + 5)² = 9x² + 30 x + 25

03) Calcule o produto da soma pela diferença de dois termos:

a) (x + y) . ( x - y) = x² - y²

b) (y – 7 ) . (y + 7) = y² - 49

c) (x + 3) . (x – 3) = x² - 9

d) (2x + 5 ) . (2x – 5) = 4x² - 25

e) (3x – 2 ) . ( 3x + 2) = 9x² - 4

f) (5x + 4 ) . (5x – 4) = 25x² - 16

g) (3x + y ) (3x – y) = 9x² - y²

h) ( 1 – 5x) . (1 + 5x) = 1 - 25x²

i) (2x + 3y) . (2x – 3y) = 4x² - 9y²

j) (7 – 6x) . ( 7 + 6x) = 49 - 36x²

l) (1 + 7x²) . ( 1 – 7x²) = 1 - 49x⁴

m) (3x² - 4 ) ( 3x² + 4) = 9x² - 16

n) (3x² - y²) . ( 3x² + y²) = 9x⁴ - y⁴

o) (x + 1/2 ) . ( x – 1/2 ) = x² - 1/4

p)(x – 2/3) . ( x + 2/3) = x² - 4/6

q)( x/4 + 2/3) . ( x/4 – 2/3) = x²/16 - 4/9

4) Desenvolva os seguintes produtos notáveis abaixo:

a) (2a + 3)² = 4a² + 12a + 9

b) (2 + 9x)² = 4 + 36x + 81x²

c) (6x - y)² = 36 x² - 12xy + y²

d) (a - 2b)² = a² - 4ab+ 4b²

e) (7a +1) (7a - 1) = 49 a² -1

f) (10a - bc) (10a + bc) = 100a² - b²c²

g) (x² + 2a)² = x⁴ + 4x²a + 4a²

h) (x - 5) (x + 5) = x² - 25

i) (9y + 4 ) (9y - 4) = 81y² -16

j) (m - n)² = m² - 2mn + n²

Quadrado da soma de dois termos
05) (x + 3)² = x² + 2 . x . 3 + 3² = x² + 6x + 9

06) (2x + 1)² = (2x)² + 2 . 2x . 1 + 1² = 4x² + 4x + 1

07) (x³ + 2)² = (x³)² + 2 . x³ . 2 + 2² = x6 + 4x³ +4

Quadrado da diferença de dois termos
08) (a – b) . (a – b) = a . a – a . b – b . a + b . b = a² – 2ab + b²

09) (x – 4)² = (x – 4) . (x – 4) = x . x – 4 . x – 4 . x + 4 .4 = x² – 8x + 16

10) (2y – 5)² = (2y – 5) . (2y – 5) = 2y . 2y – 2y . 5 – 5 . 2y + 5 . 5 = 4y² – 20y + 25

11) (5a – 2b)² = (5a – 2b) . (5a – 2b) = 5ª . 5a – 5ª . 2b – 2b . 5a + 2b . 2b = 25a² – 20ab + 4b²

Utilizando a regra prática na expressão (a – b)².
O quadrado do primeiro termo menos, duas vezes o primeiro termo vezes o segundo termo, mais o quadrado do segundo termo.

12) (y – 6)² = (y)² – 2 . y . 6 + (6)² = y² – 12y + 36

13) (4b – 9)² = (4b)² – 2 . 4b . 9 + (9)² = 16b² – 72b + 81

14) (7y – 6x)² = (7y)² – 2 . 7y . 6x + (6x)² = 49y² – 84xy + 36x²

15) (10x – 2z)² = (10x)² – 2 . 10x . 2z + (2z)² = 100x² – 40xz + 4z

Produto da soma pela diferença
16) (2x + 4)(2x – 4) = 2x . 2x – 2x . 4 + 4 . 2x – 4 . 4 = 4x² – 8x + 8x – 16 = 4x² – 16

17) (7x + 6)(7x – 6) = 7x . 7x – 7x . 6 + 6 . 7x – 6 . 6 = 49x² – 42x + 42x – 36 = 49x² – 36

18) (10x³ – 12)(10x³ + 12) = 10x³ . 10x³ + 10x³ . 12 – 12 . 10x³ –12 . 12 = 100x6 + 120x³ – 120x³ – 144 = 100x⁶ – 144

19) (20z + 10x)(20z – 10x) = 20z . 20z – 20z . 10x + 10x .20z – 10x . 10x = 400z² – 200zx + 200xz – 100x² = 400z² – 100x²

Aplicando a regra prática
A aplicação da regra prática se dá através da seguinte situação: “o primeiro termo elevado ao quadrado menos o segundo termo elevado ao quadrado”

20) (4x + 7)(4x – 7) = (4x)² – (7)² = 16x² – 49

21) (12x + 8)(12x – 8) = (12x)² – (8)² = 144x² – 64

22) (11x² – 5x)(11x² + 5x) = (11x²)² – (5x)² = 121x⁴ – 25x²

23) (20b – 30)(20b + 30) = (20b)² – (30)² = 400b² – 900

Continua...