Professor Diminoi
Equação do 1º grau com uma incógnita
Utilizamos uma equação para calcular o valor de um termo desconhecido, que geralmente é representado por uma letra.
As equações possuem sinais operatórios como adição, subtração, multiplicação, divisão, radiciação e igualdade. O sinal de igualdade divide a equação em dois membros, os quais são compostos de elementos de dois tipos:
Elemento de valor constante: representado por valores numéricos;
Elemento de valor variável: representado pela união de números e letras.
Exemplos de equações do primeiro grau com uma incógnita:
a) x + 1 = 6
b) 2x + 7 = 18
c) 4x + 1 = 3x – 9
d) 10x + 60 = 12x + 52
Símbolos usados
Nas expressões numéricas usamos parênteses ( ), colchetes [ ] e chaves { }.
A ordem de prioridade na resolução dos símbolos são:
1º) Primeiro, as operações que estão dentro do parêntese ( ).
2º) Depois, as operações que estão entre colchetes [ ].
3º) Por fim, as operações que estão entre chaves { }.
Ordem de prioridade na resolução nas operações são:
Devemos resolver as operações que aparecem em uma expressão numérica, na seguinte ordem:
1º) Potenciação e Radiciação (deve-se começar com a operação que aparece primeiro da esquerda para a direita)
2º) Multiplicação e Divisão (deve-se começar com a operação que aparece primeiro da esquerda para a direita)
3º) Soma e Subtração (deve-se começar com a operação que aparece primeiro da esquerda para a direita)
QUESTÕES RESOLVIDAS PASO-A-PASSO
01) Resolva as expressões numéricas 174 + 64 . 3 - 89 =
Resolução:
1º passo: resolvemos a multiplicação.
174 + 64 . 3 - 89 = 174 + 192 - 89
2º passo: como soma e subtração são de mesma prioridade, resolvemos a soma primeiro, pois aparece antes da subtração.
174 + 192 - 89 = 366 - 89
3º passo: resolvemos a última operação, que é a subtração.
366 - 89 = 277
Portanto, 174 + 64 . 3 - 89 = 277
02) 33 + 23 - 3 . 2 =
Resolução:
1º passo: resolvemos as potências.
33 + 23 - 3 . 2 = 27 + 8 - 3 . 2
2º passo: resolvemos a multiplicação.
27 + 8 - 3 . 2 = 27 + 8 - 6
3º passo: como soma e subtração são de mesma prioridade, resolvemos a soma primeiro, pois aparece antes da subtração.
27 + 8 - 6 = 35 - 6
4º passo: resolvemos a última operação, que é a subtração.
35 - 6 = 29
Portanto, 33 + 23 - 3 x 2 = 29
03) 378 - 52 . √400 : √25 =
Resolução:
1º passo: resolvemos a radiciação.
378 - 52 . √400 : √25 = 378 - 52 . 20 : 5
2º passo: como multiplicação e divisão são de mesma prioridade, resolvemos primeiro a multiplicação, pois aparece antes da divisão.
378 - 52 . 20 : 5 = 378 - 1040 : 5
3º passo: resolvemos a divisão.
378 - 1040 : 5 = 378 - 208
4º passo: resolvemos a última operação, que é a subtração.
378 - 208 = 170
Portanto, 378 - 52 . √400 : √25 = 170
04) Encontre o valor das expressões numéricas 900 - 4 . 2 . ( 3 + 5 ) =
Resolução:
1º passo: resolvemos a operação dentro dos parênteses.
900 - 4 . 2 . ( 3 + 5 ) = 900 - 4 . 2 . 8
2º passo: resolvemos as multiplicações.
900 - 4 . 2 .8 = 900 - 8 . 8 = 900 - 64
3º passo: resolvemos a última operação, que é a subtração.
900 - 64 = 836
Portanto, 900 - 4 . 2 . ( 3 + 5 ) = 836
05) 24 + [ 25 . ( 23 - 22 ) ] =
Resolução:
1º passo: resolvemos as potências e, em seguida, a subtração dentro parênteses.
24 + [ 25 . ( 23 - 22 ) ] = 24 + [ 25 . (8 - 4) ] = 24 + [ 25 . 4 ]
2º passo: resolvemos a potência e, posteriormente, a multiplicação dentro dos colchetes.
24 + [ 25 . 4 ] = 24 + 32 . 4 = 24 + [ 32 . 4 ] = 24 + 128
3º passo: resolvemos a potência.
24 + 128 = 16 + 128
4º passo: resolvemos a última operação, que é a adição.
16 + 128 = 144
Portanto, 24 + [ 25 . ( 23 - 22 ) ] = 144
06) 1440 : { 30 . [ 20 + ( 49 - 35 ) . 2 ] } =
Resolução:
1º passo: resolvemos a operação dentro dos parênteses.
1440 : { 30 . [ 20 + ( 49 - 35 ) . 2 ] } = 1440 : { 30 . [ 20 + 14 . 2 ] }
2º passo: resolvemos as operações dentro dos colchetes, começando pela multiplicação e, depois, a adição.
1440 : { 30 . [ 20 + 14 . 2 ] } = 1440 : { 30 . [ 20 + 28] } = 1440 : { 30 . 48 }
3º passo: resolvemos a multiplicação dentro das chaves.
1440 : { 30 . 48 } = 1440 : 1440
4º passo: resolvemos a última operação, que é a divisão.
1440 : 1440 = 1
Portanto, 1440 : { 30 . [ 20 + ( 49 - 35 ) . 2 ] } = 1
01)
8 ÷ 4(2 + 2) =
8 ÷ 4(4) =
4(4)
16
07)
5 . ( 64 - 12 : 4 ) =
5 . ( 64 - 3 ) =
5 . 61 =
305
08)
480 : { 20 . [ 86 - 12 . (5 + 2 ) ] 2 } =
480 : { 20 . [ 86 - 12 . 7 ] 2 } =
480 : { 20 . [ 86 - 84 ] 2 } =
480 : { 20 . [ 2 ] 2 } =
480 : { 20 . 4 } =
480 : 80 =
6
09)
- [ - 12 - ( - 5 + 3 ) ] =
- [ - 12 - ( - 2 ) ] =
- [ - 12 + 2 ] =
- [ - 10] =
+ 10
QUESTOES RESOLVIDAS - CONTINUAÇÃO
01) Resolva a equação 4x + 2 = 8 – 2x
Resolução:
4x + 2x = 8 – 2
6x = 6
x = 6
6
x = 1
02) Resolva a equação 10x – 9 = 21 + 2x + 3x
Resolução:
10x – 9 = 21 + 2x + 3x
10x – 2x – 3x = 21 + 9
10x – 5x = 30
5x = 30
x = 30
5
x = 6
03) Resolva a equação 3x – 2x + 10 = 10 + 5x – 40
Resolução:
3x – 2x + 10 = 10 + 5x – 40
3x – 2x – 5x = 10 – 40 – 10
3x – 7x = –40
– 4x = – 40
Nos casos em que a parte da variável é negativa, precisamos multiplicar os membros por –1.
– 4x = – 40 . (–1)
4x = 40
x = 40
4
x = 10
04) Resolva a equação 10 – (8x – 2) = 5x + 2(– 4x + 1)
Resolução:
10 – (8x – 2) = 5x + 2(– 4x + 1)
Nesse caso devemos aplicar a propriedade distributiva da multiplicação:
10 – 8x + 2 = 5x – 8x + 2
– 8x – 5x + 8x = + 2 – 10 – 2
– 13x + 8x = – 10
– 5x = – 10 . (–1)
5x = 10
x = 10
5
x = 2
05) O dobro de um número subtraído de 20 é igual a 100. Qual é o número?
Resolução:
Um número: x
O dobro do número: 2x
Como estamos subtraindo 2x de 20 a equação será:
20 – 2x = 100
Resolvendo a equação
20 – 2x = 100
– 2x – 20 + 20 = 100 – 20 (adicionamos 20 aos dois lados da equação)
– 2x = 80 (– 1)
2x = – 80
x = – 80
2
x = – 40
Conclusão: o número é igual a – 40.
06) O triplo de um número adicionado ao seu dobro resulta em 600. Qual é o número?
Resolução:
Um número: x
O triplo deste número: 3x
O dobro deste número: 2x
O triplo de um número adicionado ao seu dobro resulta em 600: 3x + 2x = 600
Resolvendo a equação:
3x + 2x = 600
5x = 600
x = 600/5
x = 120
Conclusão: temos que o número é igual a 120.
07) Que número eu sou? O dobro de meu antecessor, menos 3, é igual a 25.
Resolução:
Um número: x
Antecessor: x – 1
O dobro de meu antecessor menos 3: 2(x – 1) – 3 = 25
Resolvendo a equação
2(x – 1) – 3 = 25 (aplicar o método da distribuição)
2x – 2 – 3 = 25
2x – 5 = 25
2x = 25 + 5
2x = 30
x = 30/2
x = 15
Conclusão: o número é igual a 15.
08) Carlos tinha certa quantia em dinheiro, foi ao shopping e gastou 1/3 da quantia na compra de uma revista, gastou 1/4 da quantia na compra de um CD e ainda ficou com R$ 25,00. Qual era a quantia que Carlos possuía?
Resolução:
Quantia: x
Um terço da quantia: 1/3x
Um quarto da quantia: 1/4x
Equação do problema: (1/3)x + (1/4)x + 25 = x
MMC (3,4) = 12
(4/12)x + (3/12)x + 300 = (12/12)x (simplificando os denominadores)
4x + 3x + 300 = 12x
12x – 4x – 3x = 300
12x – 7x = 300
5x = 300
x = 300/5
x = 60
Conclusão: Carlos possuía a quantia de R$ 60,00.
09) Os 44 alunos da 7ª série A de uma escola representam 40% de todos os alunos da 7ª série dessa mesma instituição. Quantos são os alunos da 7ª série dessa escola?
Resolução:
Alunos: x
40% = 40/100 = 2 / 5 dos alunos
2 / 5 de x
( 2 / 5 )x = 44
2x = 44 . 5
2x = 220
x = 220/2
x = 110
Conclusão: a escola possui 110 alunos cursando a 7ª série.
10) Sabe-se que o triplo do preço do skate com o preço da bola (R$ 50,00) dá um valor de R$ R$ 650,00. Ajude Daniel, encontre o valor unitário do skate.
Resolução:
Chamemos de x o preço skate; 3x é o triplo do preço do skate; R$ 50,00 é preço da bola; R$ 650,00 é a soma de 3x com R$50,00.
Montando a equação:
3x + 50 = 650
3x = 650 – 50
3x = 600
x = 600 : 3
x = 200
Conclusão: o valor do skate é R$ 200.
11) A soma das idades de André e Carlos é 22 anos. Descubra as idades de cada um deles, sabendo-se que André é 4 anos mais novo do que Carlos.
Resolução:
Primeiro passamos o problema para a linguagem matemática. Vamos tomar a letra c para a idade de Carlos e a letra a para a idade de André, logo a = c -4.
Assim:
c + a = 22 c + (c - 4)
22 2c - 4 = 22 2c - 4 + 4
22 + 4 2c
26 c = 13.
Questões de equações do 1º grau
a) Qual a raiz da equação 20 – 80 + 2x =1 0
2x = 10 - 20 +80
2x = -10 + 80
2x = 70
x = 70/2
x = 35
b) Resolva a equação 23x - 16 = 14 - 17x
23x = 14 - 17x + 16
23x + 17x = 30
40x = 30
x = 30/40 = 3/4
c) Encontre o valor de x na equação [ 2( x – 5 ) + 4( 1 - 2x ) ] / 20 = 5 ( 3 – x ) / 20
2x - 10 + 4 - 8x = 15 - 5x
-6x - 6 = 15 - 5x
-6x + 5x = 15 + 6
-x = 21 . (-1)
x = -21
Conclusão: Carlos tem 13 anos e André tem 13 -4 = 9 anos
12) Um relógio que custa R$ 250,00 está sendo vendido com o seguinte plano de pagamento: R$ 30,00 de entrada e o restante em 4 prestações iguais, sem juros.
Qual é o valor de cada prestação?
Resolução:
R$ 250 – R$ 30 = R$ 220
Equação
30 + 4x = 250
4x = 250 – 30
4x = 220
x = 220/4
x = 55
Conclusão: o valor de cada prestação é R$ 55,00.
13) Sabendo que o triplo de um número somado com 8 é igual ao número somado com 10, descubra qual é o número?
Resolução:
Um número: x
Triplo do número: 3x
Equação
3x + 8 = x + 10
3x – x = 10 – 8
2x = 2
x = 2/2
x = 1
Conclusão: número é igual a 1.
14) Um número adicionado ao seu dobro e ao seu quádruplo resulta em 84. Qual é o número?
Resolução:
Um número: x
Dobro: 2x
Quádruplo: 4x
Equação
x + 2x + 4x = 84
7x = 84
x = 84/7
x = 12
Conclusão: o número é igual a 12.
15) (ENEM) O Salto Triplo é uma modalidade do atletismo em que o atleta dá um salto em um só pé, uma passada e um salto, nessa ordem. Sendo que o salto com impulsão em um só pé será feito de modo que o atleta caia primeiro sobre o mesmo pé que deu a impulsão; na passada ele cairá com o outro pé, do qual o salto é realizado.
Um atleta da modalidade Salto Triplo, depois de estudar seus movimentos, percebeu que, do segundo para o primeiro salto, o alcance diminuía em 1,2 m, e, do terceiro para o segundo salto, o alcance diminuía 1,5 m. Querendo atingir a meta de 17,4 m nessa prova e considerando os seus estudos, a distância alcançada no primeiro salto teria de estar entre
(A) 4,0 m e 5,0 m.
(B) 5,0 m e 6,0 m.
(C) 6,0 m e 7,0 m.
(D) 7,0 m e 8,0 m.
(E) 8,0 m e 9,0 m.
Resolução:
Fazendo-se as considerações que:
- o alcance do segundo salto é 1,2 m menor que do primeiro salto
- o alcance do terceiro salto é 1,5 m menor que do segundo salto
- a distância alcançada no primeiro salto é x
Logo, para atingir a meta de 17,4 m, tem-se:
x + (x – 1,2) + (x – 1,2 – 1,5) = 17,4 ⇔3x = 21,3 ⇔ x = 7,1
Alternativa: D
16) (UNIRIO - RJ) Um grupo de amigos vai acampar num final de semana. Sabendo-se que numa certa hora da manhã de domingo, o equivalente a um terço desse grupo está envolvido com o preparo do almoço, o equivalente à metade do grupo cuida da limpeza do acampamento, o equivalente à décima parte desses dois subgrupos colhe flores nas redondezas e um elemento do grupo deleita-se com um livro de crônicas de Zuenir Ventura, quantos elementos tem esse grupo de amigos?
Resolução:
Considerando:
X - a parte do grupo envolvida com o preparo do almoço
Y - a parte do grupo que cuida da limpeza do acampamento
Z - a parte do grupo que colhe flores
V - total do grupo
Então, sabemos:
X = 1/3 V
Y = 1/2 V
Z = 1/10 (X + Y)
V = X + Y + Z + 1
(Este 1 é o elemento do grupo que está a ler)
Agora é só substituir.
V = 1/3 V + 1/2 V + 1/10 [ (1/3 V) + (1/2 V) ] + 1
V = 1/3 V + 1/2 V + 1/30 V + 1/20 V + 1 (reduzindo os termos com "V" ao mesmo denominador)
V = 20/60 V + 30/60 V + 2/60 V + 3/60 V + 1
V = 55/60 V + 1
V - 55/60V = 1 (reduzindo novamente os termos com "V" ao mesmo denominador)
60/60 V - 55/60V =1
5/60 V = 1
5 V = 60
V = 60/5
Resposta: V = 12
17) Num campeonato de futebol, os dois melhores artilheiros pertencem ao mesmo time vencedor. Durante o campeonato, só esses dois jogadores marcaram 32 gols. Se o segundo artilheiro marcou um terço do número de gols do primeiro, quantos gols marcou cada jogador?
Resolução:
1º jogador = x
2º jogador = y
eles juntos marcaram 32, então x + y = 32
o 2º. marcou 1/3 do 1º. , então y = x/3
isolando x na 2ª. equação, fica x = 3y
volte na 1ª. e troque x por 3y
3y + y = 32
4y = 32
y = 8
x = 3y
x = 3.8
x = 24
Conclusão: o 1º. jogador marcou 24 gols e o 2º 8 gols.
18) Em um concurso os participantes devem responder a um total de 20 questões. Para cada resposta correta o candidato ganha 3 pontos e para cada resposta errada perde 2 pontos. Determine o número de acertos e erros que um candidato obteve considerando que ele totalizou 35 pontos.
Resolução:
Acertos: representados pela letra x.
Erros: representados por 20 − x.
Portanto:
3 . x – 2 . (20 – x) = 35
3x – 40 + 2x = 35
5x = 35 + 40
5x = 75
x = 75/5
x = 15
Conclusão: o candidato obteve 15 acertos e 5 erros.
19) (PUC – RJ) 3/5 de um número somados a ½ é igual a 2/3 desse mesmo número. Indique a opção que apresenta esse número.
(A) 0
(B) 1
(C) 20/33
(D) 33/20
(E) 15/2
Resolução:
Como desconhecemos o número procurado no exercício, podemos identificá-lo como a incógnita x. Sendo assim, podemos escrever a expressão literal “3/5 de um número somados a ½ é igual a 2/3 desse mesmo número” como:
3.x + 1 = 2. x
5 2 3
Calculando o mínimo múltiplo comum entre os denominadores 2, 3 e 5, teremos:
6.3x + 15.1 = 10.2x
30 30
18x + 15 = 20x
15 = 20x – 18x
15 = 2x
2x = 15
x = 15
2
Alternativa: E
20) Resolva a equação do 1° grau: 4.(x + 3) – x = 24 + x
Resolução:
Aplicando a propriedade distributiva ao primeiro membro da equação do 1° grau, temos:
4.(x + 3) – x = 24 + x
4x + 12 – x = 24 + x
Ao organizar a equação, manteremos todos os elementos que possuem a incógnita no lado esquerdo da equação e todos aqueles que não estão acompanhados da incógnita x permanecerão no lado direito:
4x – x – x = 24 – 12
2x = 12
x = 12
2
x = 6
Conclusão: o valor da incógnita x é 6.
21) Encontre a raiz da equação do 1° grau: 9x + 75 = 34
x
Resolução:
Para identificar a raiz da equação, inicialmente vamos trocar de membro a incógnita x. Dessa forma, ela irá para o segundo membro da equação através de uma multiplicação:
9x + 75 = 34
x
9x + 75 = 34x
75 = 34x – 9x
75 = 25x
25x = 75
x = 75
25
x = 3
Conclusão: a raiz da equação é 3.
22) (Unicamp) Um copo cheio de água pesa 385 g; com 2/3 da água pesa 310 g. Pergunta-se:
a) Qual é o peso do copo vazio?
Resolução:
Se o copo cheio pesa 385 g e, com 2/3 de água, pesa 310 g, podemos encontrar o peso do copo através da diferença entre o peso do copo cheio pelo peso do copo parcialmente preenchido, isto é, se x representa o peso da água, então:
x – 2.x = 385 – 310
3
1.x = 75
3
x = 75.3
x = 225 g
Seja y o peso do copo. Retirando 225 g de água do peso do copo cheio (385 g), teremos:
y = 385 – 225
y = 160 g
Conclusão: o copo vazio pesa 160 g.
b)Qual é o peso do copo com 3/5 da água?
Resolução:
Já sabemos que o peso do copo vazio é de 160 g e que a quantidade de água suficiente para encher o copo é de 225 g. Basta então calcular o valor correspondente a 3/5 dessa quantidade de água e adicioná-lo ao peso do copo. Seja z o peso do copo com 3/5 da água:
z = 3.225 + 160
5
z = 675 + 160
5
z = 135 + 160
z = 295 g
Conclusão: quando o copo está preenchido com 3/5 da água, seu peso é de 295 g.
23) (ENEM) Um grupo de 50 pessoas fez um orçamento inicial para organizar uma festa, que seria dividido entre elas em cotas iguais. Verificou-se ao final que, para arcar com todas as despesas, faltavam R$ 510,00, e que 5 novas pessoas haviam ingressado no grupo. No acerto foi decidido que a despesa total seria dividida em partes iguais pelas 55 pessoas. Quem não havia ainda contribuído pagaria a sua parte, e cada uma das 50 pessoas do grupo inicial deveria contribuir com mais R$ 7,00.
De acordo com essas informações, qual foi o valor da cota calculada no acerto final para cada uma das 55 pessoas?
(A) R$ 14,00.
(B) R$ 17,00.
(C) R$ 22,00.
(D) R$ 32,00.
(E) R$ 57,00.
Resolução:
De acordo com o enunciado da questão, 50 pessoas já haviam pagado sua parte da despesa total, por isso não consideraremos o valor total para elas, apenas o valor de R$ 7,00 adicional, que deverá ser multiplicado por 50 pessoas. Além desse pessoal, outros cinco juntaram-se ao grupo e precisam pagar sua parte, um valor que não conhecemos e, portanto, podemos identificar como x. Somando-se o valor que essas pessoas pagarão ao valor acrescentado ao restante do grupo, teremos um recolhimento de R$ 510,00. Podemos então montar uma equação do 1° grau:
(50 · 7) + (5 · x) = 510
350 + 5x = 510
5x = 510 – 350
5x = 160
x = 32
Conclusão: cada um pagou o valor total de R$ 32,00.
Alternativa: D
24) (ENEM) O Salto Triplo é uma modalidade do atletismo em que o atleta dá um salto em um só pé, uma passada e um salto, nessa ordem. Sendo que o salto com impulsão em um só pé será feito de modo que o atleta caia primeiro sobre o mesmo pé que deu a impulsão; na passada ele cairá com o outro pé, do qual o salto é realizado.
Um atleta da modalidade Salto Triplo, depois de estudar seus movimentos, percebeu que, do segundo para o primeiro salto, o alcance diminuía em 1,2 m, e, do terceiro para o segundo salto, o alcance diminuía 1,5 m. Querendo atingir a meta de 17,4 m nessa prova e considerando os seus estudos, a distância alcançada no primeiro salto teria de estar entre
(A) 4,0 m e 5,0 m.
(B) 5,0 m e 6,0 m.
(C) 6,0 m e 7,0 m.
(D) 7,0 m e 8,0 m.
(E) 8,0 m e 9,0 m.
Resolução:
Podemos interpretar o enunciado da questão como:
No primeiro salto, ele atinge uma distância desconhecida, que pode ser chamada de x m;
No segundo salto, a distância diminui 1,2 m em relação ao primeiro salto, logo a distância é de ( x – 1,2) m;
No terceiro salto, a distância reduz ainda 1,5 m em relação ao anterior, portanto a distância é ( x – 1,2 – 1,5 ) m, que equivale a( x – 2,7 ) m.
Se o atleta pretende alcançar a distância total de 17,4 m, somando as distâncias em cada salto, teremos a seguinte equação do 1° grau:
x + (x – 1,2) + (x – 2,7) = 17,4
x + x – 1,2 + x – 2,7 = 17,4
3x – 3,9 = 17,4
3x = 17,4 + 3,9
3x = 21,3
x = 21,3
3
x = 7,1
Conclusão: o valor de alcance do primeiro salto é 7,1 m. Esse valor está entre 7,0 m e 8,0 m.
Alternativa: D
25) (ENEM) Uma escola recebeu do governo uma verba de R$ 1000,00 para enviar dois tipos de folhetos pelo correio. O diretor da escola pesquisou que tipos de selos deveriam ser utilizados. Concluiu que, para o primeiro tipo de folheto, bastava um selo de R$ 0,65 enquanto para folhetos do segundo tipo seriam necessários três selos, um de R$ 0,65, um de R$ 0,60 e um de R$ 0,20. O diretor solicitou que se comprassem selos de modo que fossem postados exatamente 500 folhetos do segundo tipo e uma quantidade restante de selos que permitisse o envio do máximo possível de folhetos do primeiro tipo.
Quantos selos de R$ 0,65 foram comprados?
(A) 476
(B) 675
(C) 923
(D) 965
(E) 1 538
Resolução:
Para que fossem enviados 500 selos do segundo tipo, mais x selos do primeiro tipo, totalizando um valor igual ou inferior a R$ 1000,00, tem-se:
x.(0,65)+500(0,65+060+0,20) ≤ 1000.
x≤423,07. Logo, x=423 selos primeiro tipo.
Assim, o total de selos de R$ 0,65 que foram comprados é de 923.
Alternativa: C
26) (ENEM) O Salto Triplo é uma modalidade do atletismo em que o atleta dá um salto em um só pé, uma passada e um salto, nessa ordem. Sendo que o salto com impulsão em um só pé será feito de modo que o atleta caia primeiro sobre o mesmo pé que deu a impulsão; na passada ele cairá com o outro pé, do qual o salto é realizado.
Um atleta da modalidade Salto Triplo, depois de estudar seus movimentos, percebeu que, do segundo para o primeiro salto, o alcance diminuía em 1,2 m, e, do terceiro para o segundo salto, o alcance diminuía 1,5 m. Querendo atingir a meta de 17,4 m nessa prova e considerando os seus estudos, a distância alcançada no primeiro salto teria de estar entre:
(A) 4,0 m e 5,0 m.
(B) 5,0 m e 6,0 m.
(C) 6,0 m e 7,0 m.
(D) 7,0 m e 8,0 m.
(E) 8,0 m e 9,0 m.
Resolução:
Sendo x o valor do primeiro salto, (x - 1,2) será o valor do segundo salto e (x – 2,7) o valor do terceiro salto, logo para que o atleta alcance a meta de 17,4m no salto triplo
x + (x- 1,2)+(x - 2,7) terá que ser igual a 17,4, tem-se:
x + (x- 1,2)+(x - 2,7) = 17,4 , x=7,1m.
Logo, considerando os seus estudos, terá que alcançar 7,1m no primeiro salto para atingir a meta de 17,4 m.
Alternativa: D
27) (ENEM) Um grupo de 50 pessoas fez um orçamento inicial para organizar uma festa, que seria dividido entre elas em cotas iguais. Verificou-se ao final que, para arcar com todas as despesas, faltavam R$ 510,00, e que 5 novas pessoas haviam ingressado no grupo. No acerto foi decidido que a despesa total seria dividida em partes iguais pelas 55 pessoas. Quem não havia ainda contribuído pagaria a sua parte, e cada uma das 50 pessoas do grupo inicial deveria contribuir com mais R$ 7,00.
De acordo com essas informações, qual foi o valor da cota calculada no acerto final para cada uma das 55 pessoas?
(A) R$ 14,00.
(B) R$ 17,00.
(C) R$ 22,00.
(E) R$ 32,00.
(E) R$ 57,00.
Resolução:
A despesa pode ser escrita de duas formas de acordo com o valor x que será pago por cada uma das 55 pessoas no acerto final. Nesse acerto, a despesa (D) pode ser escrita por D = 55x. No acerto inicial, cada uma das 50 pessoas estava pagando (x - 7) reais e estava faltando 510 reais para completar o valor da despesa, assim D = 50 (x - 7) + 510. Igualando-se às duas equações e realizando a distributiva, tem-se que: 50x – 350 + 510 = 55x.
Logo 5x = 160, x = 32 reais.
Alternativa: D
28) (ENEM) Em quase todo o Brasil existem restaurantes em que o cliente, após se servir, pesa o prato de comida e paga o valor correspondente, registrado na nota pela balança. Em um restaurante desse tipo, o preço do quilo era R$12,80. Certa vez a funcionária digitou por engano na balança eletrônica o valor R$18,20 e só percebeu o erro algum tempo depois, quando vários clientes já estavam almoçando. Ela fez alguns cálculos e verificou que o erro seria corrigido se o valor incorreto indicado na nota dos clientes fosse multiplicado por:
(A) 0,54
(B) 0,65
(C) 0,70
(D) 1,28
(E) 1,42
Resolução:
Montando a equação temos
18,20 x = 12,80
x = 0.70
Logo x = 0,70
Alternativa: C
29) (Enem – PPL) Uma indústria automobilística está testando um novo modelo de carro. Cinquenta litros de combustível são colocados no tanque desse carro, que é dirigido em uma pista de testes até que todo o combustível tenha sido consumido. O segmento de reta no gráfico mostra o resultado desse teste, no qual a quantidade de combustível no tanque é indicada no eixo y (vertical), e a distância percorrida pelo automóvel é indicada no eixo x (horizontal).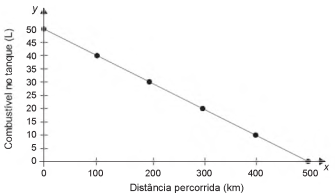 A expressão algébrica que relaciona a quantidade de combustível no tanque e a distância percorrida pelo automóvel é:
A expressão algébrica que relaciona a quantidade de combustível no tanque e a distância percorrida pelo automóvel é:
(A) y = - 10x + 500
(B) y = - x/10 + 50
(C) y = - x/10 + 500
(D) y = x/10 + 50
(E) y = x/10 + 500
Resolucao
Sabemos que essa situação é uma funcao do 1º grau, já que o gráfico é uma reta. Além disso, o ponto em que a reta toca o eixo y é o ponto (0,50).
Então, seja f(x) = ax + b:
f(0) = 50
50 = a · 0 + b
b = 50
Sendo b = 50, para encontrar o valor de a, basta encontrar outro ponto no gráfico. Usaremos o ponto (0,500):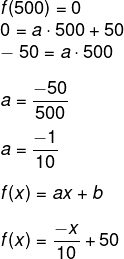
Alternativa B
30) (Encceja) Uma prestadora de serviços cobra pela visita à residência do cliente e pelo tempo necessário para realizar o serviço na residência.
O valor da visita é R$ 40 e o valor da hora para realização do serviço é R$ 20.
Uma expressão que indica o valor a ser pago (P) em função das horas (h) necessárias à execução do serviço é:
(A) P = 40h
(B) P = 60h
(C) P = 20 + 40h
(D) P = 40 + 20h
Resolucao
A funcao é descrita por P = ah + b, em que b é a taxa fixa, que, no caso, é o valor da visita, que é R$ 40. Já o coeficiente a é a taxa que depende do número de horas, no caso, R$ 20. Substituindo, temos que:
P = 20h + 40
P = 40 + 20h
Alternativa D
31) (Enem) Uma cisterna de 6 000 L foi esvaziada em um período de 3 h. Na primeira hora foi utilizada apenas uma bomba, mas nas duas horas seguintes, a fim de reduzir o tempo de esvaziamento, outra bomba foi ligada com a primeira. O gráfico, formado por dois segmentos de reta, mostra o volume de água presente na cisterna, em função do tempo.
O gráfico, formado por dois segmentos de reta, mostra o volume de água presente na cisterna, em função do tempo.
Qual é a vazão, em litro por hora, da bomba que foi ligada no início da segunda hora?
(A) 1 000
(B) 1 250
(C) 1 500
(D) 2 000
(E) 2 500
Resolucao
No primeiro momento até a primeira hora, o volume vai de 6000 litros para 5000 litros, ou seja, ocorre uma diferença de 1000 litros, logo, a vazão da primeira bomba é de 1000 L/h. Agora, após ligar a segunda bomba, note que ela foi inteiramente esvaziada, ou seja, nas outras 2 horas, foi possível retirar 5000 L. Realizando a divisão 5000 : 2 = 2500, a soma das vazões das bombas foi de 2500 L/h.
Sabemos que a primeira bomba tem vazão de 1000 L/h, então, para descobrir a vazão da segunda, temos que: 2500 – 1000 = 1500 L.
Alternativa C
32) (UFSM) Sabe-se que o preço a ser pago por uma corrida de táxi inclui uma parcela fixa, que é denominada bandeirada, e uma parcela variável, que é função da distância percorrida. Se o preço da bandeirada é de R$ 4,60 e o quilômetro rodado é R$ 0,96, a distância percorrida pelo passageiro que pagou R$ 19 para ir de sua casa ao shopping é de:
(A) 5 km
(B) 10 km
(C) 15 km
(D) 20 km
(E) 25 km
Resolucao
Seja d a distância percorrida em quilômetros, sabemos que:
19 = 0,96d + 4,6
Isolando a incógnita, temos que:
19 – 4,6 = 0,96d
14,4 = 0,96d
d = 14,4 : 0,96
d = 15
Alternativa C
33) Uma determinada espécie de pimenta, ao atingir 20 centímetros de altura, começa a crescer de forma linear. A cada dia que se passa, essa planta aumenta 2,5 centímetros. Assim, é possível descrever essa situação como uma função do 1º grau, em que a altura h(d) está em função dos dias, cuja lei de formação é:
(A) h(d) = 2,5d
(B) h(d) = 2,5d + 20
(C) h(d) = 20d + 2,5
(D) h(d) = 20d
(E) h(d) = 2,5d – 20
Resolucao
Seja h(d) = ad + b uma função afim, sabemos que b é a taxa fixa, no caso, 20 cm, e que, além disso, a cada dia, ela aumenta 2,5 cm, ou seja, 2,5 d. Dessa forma, a lei de formação que melhor descreve essa situação é:
h(d) = 2,5d + 20
Alternativa B
34) Um fazendeiro resolveu investir em uma colheitadeira para facilitar o serviço na plantação. Sabendo que o valor pago foi de R$ 300.000 no ano da compra, é bastante comum que máquinas desse porte percam o seu valor V ao decorrer dos anos t. Supondo que a taxa de depreciação de uma máquina desse porte é de R$ 22.000 por ano, devido ao seu constante uso, podemos afirmar que o valor da colheitadeira, ao final de 7 anos, será de:
(A) R$ 154.000
(B) R$ 246.000
(C) R$ 146.000
(D) R$ 174.000
(E) R$ 210.000
Resolucao
A função que descreve o valor em função do tempo possui a lei de formação:
V(t) = -22.000t + 300.000
Como o tempo foi de 7 anos, então faremos t = 7.
V(7) = -22.000 · 7 + 300.000
V(7) = -154.000 + 300.000
V(7) = 146.000
Alternativa C
35) O uso de aplicativos para realizar viagens é cada vez mais comum no cotidiano. Supõe-se que, para calcular o valor da viagem em um aplicativo, há um valor fixo mais um total de R$ 1,40 por quilômetros rodado. Sabendo que um cliente pagou R$ 15,60 ao final da viagem, a quantidade de quilômetros rodados foi de 8 km, então o valor fixo da viagem foi de:
(A) R$ 2
(B) R$ 2,50
(C) R$ 3,60
(D) R$ 4,40
(E) R$ 5
Resolucao
Sabemos que o valor pago é calculado por:
V(q) = 1,40q + T
Sendo T a taxa fixa e q os quilômetros rodados, substituindo os valores conhecidos, temos:
15,60 = 1,40 · 8 + T
15,60 = 11,20 + T
15,60 – 11,20 = T
T = 4,40
Alternativa D
36) Dada a função afim f(x) = ax + b, sabendo-se que f(3) = 6 e f (-2) = -3, o valor do coeficiente angular dessa função é:
(A) 9/5
(B) 5/9
(C) 3
(D) 3/5
(E) 5/3
Resolucao
Sabemos que f(x) = ax + b.
Substituindo os valores conhecidos, temos que:
f(3) = 6
f(3) = 3a + b → 3a + b = 6
f(-2) = -3
f(-2) = -2a + b → -2a + b = -3
Dessa foma, vamos resolver o sistema de rquacao:
3a + b = 6
-2a + b = -3
Realizando a subtração do primeiro pelo segundo sistema, temos que:
5a = 9
a = 9/5
Alternativa A
37) Podemos afirmar que o zero da função f(x) = -2x + 5 é igual a:
(A) 2
(B) 2,5
(C) -2,5
(D) -3
(E) 3
Resolucao
Para encontrar o zero da função, vamos igualar a função a zero e resolver a equação, então, temos que:
-2x + 5 = 0
-2x = -5
x = (-5) : (-2)
x = 2,5
Alternativa B
39) Seja f(x) e g(x), funções cujas leis de formação são, respectivamente, f(x) = 2x -5 e g(x) = -x + 2, podemos afirmar que o valor de f(g(2)) – g(-3) é igual a:
(A) 0
(B) 5
(C) -5
(D) -10
(E) -12
Resolucao
Sabendo que:
f(x) = 2x -5 e que g(x) = -x + 2, vamos calcular o valor da expressão: f(g(2)) – g(-3). Para isso calcularemos os valores separados.
Primeiro g(2):
g(2) = -2 + 2 = 0
Então, f(g(2)) = f(0):
f(g(2)) = f(0) = 2 · 0 – 5 = -5
Por fim, vamos calcular o valor de g(-3):
g(-3) = - (-3) + 2 = 3 + 2 = 5
Sendo assim, temos que:
f(g(2)) – g(-3) = -5 – 5 = -10
Alternativa D
40) Julgue as afirmativas a seguir sobre a função f(x) = 2x – 3. Podemos afirmar que:
I – O coeficiente angular é 2.
II – O coeficiente linear é 3.
III – A imagem da função para x = 1 é -1.
De acordo com o julgamento das afirmativas, é correto afirmar que:
(A) Somente I é verdadeira.
(B) Somente I e II são verdadeiras.
(C) Somente III é verdadeira.
(D) Somente I e III são verdadeiras.
(E) Todas são verdadeiras.
Resolucao
I → Verdadeira, pois o coeficiente angular é o termo que acompanha a incógnita x, que, no caso, é igual a 2.
II → Falsa, pois o coeficiente linear é o termo independente, que, nesse caso, é -3.
III → Verdadeira, pois f(1) = 2 · 1 – 3 = 2 – 3 = -1.
Então, podemos concluir que I e III são verdadeiras e que II é falsa.
Alternativa D
41) Sobre o comportamento da função f(x) = 4x – 3, marque a alternativa correta:
(A) f(x) é crescente, pois seu coeficiente angular é positivo e igual a 4.
(B) f(x) é decrescente, pois seu coeficiente angular é positivo e igual a 4.
(C) f(x) é decrescente, pois seu coeficiente angular é positivo e igual a -3.
(D) f(x) é crescente, pois seu coeficiente angular é negativo e igual a -3.
(E) f(x) é decrescente, pois o seu coeficiente linear é negativo e igual a -3.
Resolucao
Para saber se a função é crescente ou decrescente, basta olhar o coeficiente angular. Se ele for positivo, a função é crescente, se for negativo, ela será decrescente. Nesse caso a = 4, então, a função é crescente, pois seu coeficiente angular é positivo e igual a 4.
Alternativa A
42) A respeito da resolução de expressões numéricas, assinale a alternativa correta:
(A) As operações devem ser feitas na ordem em que aparecem.
(B) É necessário calcular primeiro todas as operações no interior dos parênteses na ordem em que elas aparecem.
(C) A pessoa que realiza os cálculos escolhe a ordem mais oportuna para eles.
(D) Não existe ordem para realização dos cálculos em uma expressão numérica.
(E) As adições e subtrações são os últimos cálculos na lista de prioridades das expressões numéricas.
Resolução:
a) Falsa!
As operações devem ser feitas na seguinte ordem: potências e raízes, multiplicações e divisões e, por fim, adições e subtrações.
b) Falsa!
Embora realmente seja necessário calcular primeiro as operações no interior de parênteses, a ordem de realização das operações é: potências e raízes, multiplicações e divisões e, por fim, adições e subtrações.
c) Falsa!
A ordem para realização das operações é predefinida: potências e raízes, multiplicações e divisões e, por fim, adições e subtrações.
d) Falsa!
Na realidade, existe uma ordem de realização dos cálculos, como já dito.
e) Verdadeira!
Alternativa: E
43) Qual das alternativas a seguir representa um quinto do resultado desta expressão numérica:
[(64 – 16·4) + (48·10 – 180)]·5
(A) 270
(B) 300
(C) 350
(D) 400
(E) 410
Resolução:
Para resolver esse problema, lembre-se da ordem de resolução das expressões numéricas. Primeiramente, deve-se resolver o interior dos parênteses; em seguida, os colchetes e, nos casos em que aparecerem, as chaves. Já as operações matemáticas devem ser resolvidas com a seguinte prioridade: primeiramente, as raízes e potências (na ordem em que aparecerem); depois, multiplicações e divisões (na ordem em que aparecerem) e, por fim, adições e subtrações (na melhor ordem possível).
Dessa maneira, faremos:
[(64 – 16·4) + (48·10 – 180)]·5 =
[(64 – 64) + (480 – 180)]·5 =
[0 + 300]·5 =
300·5 =
1500
Como o exercício pede um quinto desse resultado, será necessário dividi-lo por 5:
1500:5 = 300
Alternativa: B
44) Analise a solução da expressão algébrica abaixo e assinale a alternativa correta:
{(10·10 + 4·11):12 – [(20 + 19·10):39 + 15]} + 50 =
{(100 + 44):12 – [(39·10):39 + 15]} + 50 =
{144:12 – [390:39 + 15]} + 50 =
{12 – [10 + 15]} + 50 =
{12 – 25} + 50 =
– 13 + 50 =
37
(A) A resolução está correta, nenhum erro foi cometido.
(B) A resolução está correta, mas por coincidência, pois alguns erros foram cometidos.
(C) A resolução está incorreta, o verdadeiro resultado é 50.
(D) A resolução está incorreta, pois foi feita uma soma em vez de dar prioridade a uma multiplicação.
(E) A resolução está incorreta, pois as multiplicações devem ser feitas sempre depois das divisões.
Resolução:
a) Incorreta!
A resolução está incorreta e um erro foi cometido.
b) Incorreta!
A resolução está incorreta.
c) Incorreta!
O resultado não é 50.
d) Correta!
Observe que, logo no início, houve esta soma: 20 + 19 = 39. O correto seria primeiramente multiplicar 19·10 e, depois, somar 20 ao resultado.
e) Incorreta!
Não existe prioridade entre multiplicações e divisões.
Alternativa: D
45) Margarida viu no quadro-negro algumas anotações da aula anterior um pouco apagadas, conforme mostra a figura a seguir. Qual número foi apagado?
(A) 9
(B) 10
(C) 12
(D) 13
(E) 15
Resolução:
Primeiramente, trocaremos x por ·, para representar a multiplicação, e o espaço apagado por y, para representar o número que queremos descobrir. Posteriormente, multiplicaremos ambos os lados da igualdade pelo mesmo número para obter:
2 . 12 – x = 5
3
2 . 12 – x = 5·3
2 . 12 – x = 15
24 – x = 15
Agora, pense em um número que subtraído de 24 resulte em 15, ou seja, um número que somado com 15 resulte em 24. Esse número é 9.
Alternativa: A
Continua...





