Professor Diminoi

RAZORES TRIGONOMETRICAS

Catetos e hipotenusa
Em um triângulo, chamamos o lado oposto ao ângulo reto de hipotenusa e os lados adjacentes de catetos.
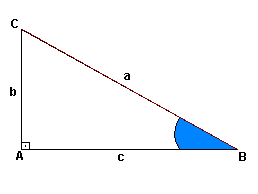
Observe a figura: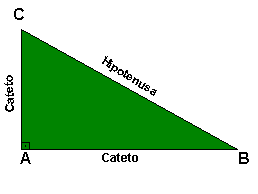

Hipotenusa = BC

Catetos = AC e AB

Veremos a seguir as razões trigonométricas existentes em um triângulo desse tipo.

Seno e cosseno
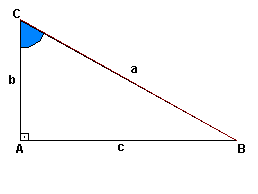
Considere um triângulo retângulo BAC: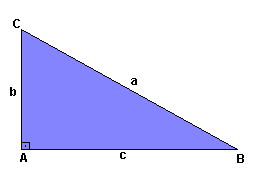
Hipotenusa =   BC

Catetos =  CA e AB  

Ângulos são:     A, B e C

Tomando por base os elementos desse triângulo, podemos definir as seguintes razões trigonométricas:
Seno de um ângulo agudo é a razão entre a medida do cateto oposto a esse ângulo e a medida da hipotenusa.

Assim:

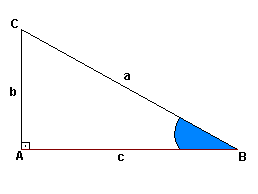
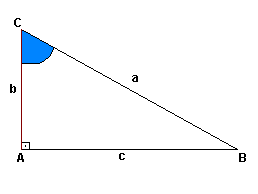
Cosseno de um ângulo agudo é a razão entre a medida do cateto adjacente a esse ângulo e a medida da hipotenusa.
Assim:

Tangente
Tangente de um ângulo agudo é a razão entre a medida do cateto oposto e a medida do cateto adjacente a esse ângulo.

Assim:




Exemplo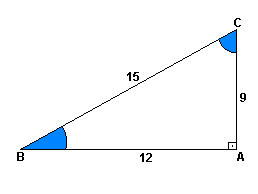



 

 

 



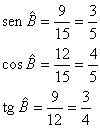
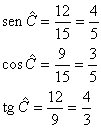
Observações:
a -  A tangente de um ângulo agudo pode ser definida como a razão entre o seno deste ângulo e o seu cosseno.
Assim: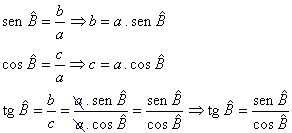

b - A tangente de um ângulo agudo é um número real positivo.
c - O seno e o cosseno de um ângulo agudo são sempre números reais positivos menores    que 1, pois qualquer cateto é empre menor que a hipotenusa.

As razões trigonométricas de 30º, 45º e 60º
Considere as figuras: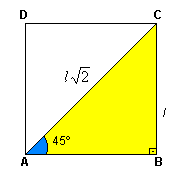
Quadrado de lado l e diagonal

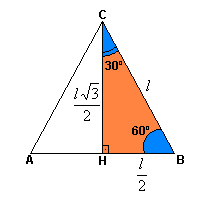
Triângulo equilátero de lado I e altura

Seno, cosseno e tangente de 30º
Aplicando as definições de seno, cosseno e tangente para os ângulos de 30º, temos: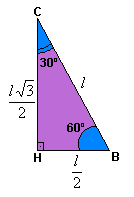

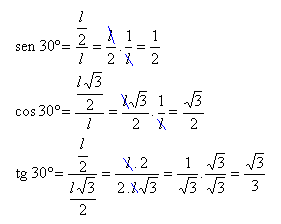
Seno, cosseno e tangente de 45º
Aplicando as definições de seno, cosseno e tangente para um ângulo de 45º, temos: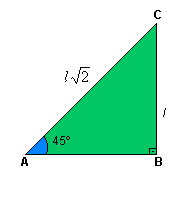

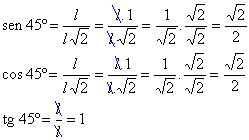
Seno, cosseno e tangente de 60º
Aplicando as definições de seno, cosseno e tangente para um ângulo de 60º, temos: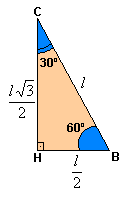

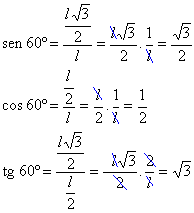
Quadros resumo: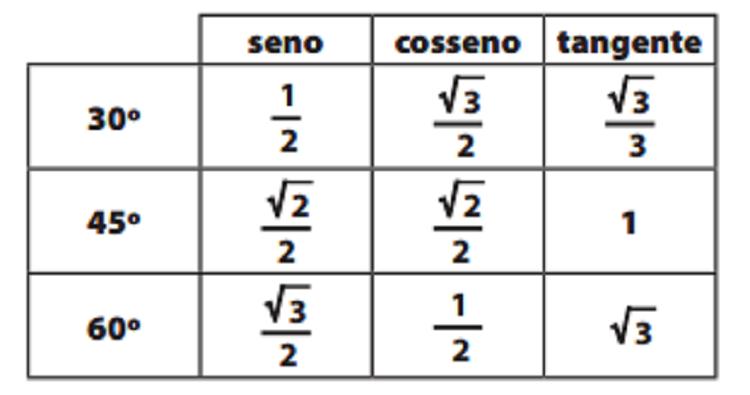


Continua ...