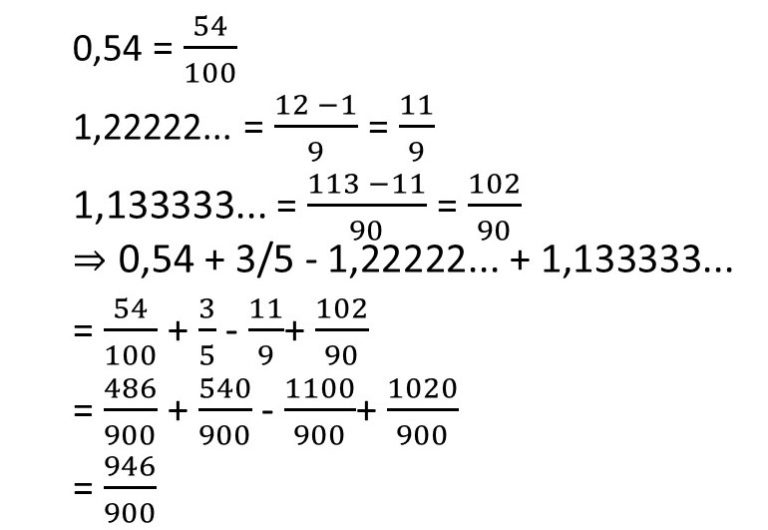Professor Diminoi
Fração geratriz
Para tratarmos do assunto referente à fração geratriz, precisamos relembrar os conceitos de: dízima, dízima periódica simples e dízima não periódica. Isso porque a fração geratriz é obtida por meio das dízimas periódicas.
Dízima é toda fração cuja divisão não resulta em um número decimal exato, ou seja, a divisão da fração irá gerar um número com infinitas casas decimais.
Exemplos:
0,34567...
2,33333...
0,345345...
0,222222...
A dízima periódica simples é dada pela repetição de termos numéricos nas casas decimais. Sendo assim, uma dízima periódica apresenta repetições de termos numéricos depois da vírgula, esses termos determinam o período.
Exemplos:
2,555... Período igual a 5
1,235235... Período igual a 235
0,323232... Período igual a 32
Já a dízima não periódica não possui período.
Observe:
2,326598..... Não possui período
25,12032569.... Não possui período
0,02069875... Não possui período
Vamos agora explicar um método prático para encontrar a fração geratriz. Caso tenha interesse em aprender o método tradicional clique aqui: Geratriz de uma dízima periódica.
Para utilizar esse método prático o primeiro passo é identificar o período da dízima periódica.
Exemplo:
Dízima periódica: 0,222...
Período igual a 2
No segundo passo devemos montar a fração geratriz. O numerador será o valor numérico do período, já o denominador será 9. A quantidade de noves no denominador é determinada pela quantidade de termos numéricos que compõem o período.
A dízima periódica 0,222... possui um período, então o numerador da fração será o numero 2 e o denominador possuirá somente um 9, porque temos somente um algarismo que representa o numerador. Logo:
0,222...= 2
9
A fração encontrada é a geratriz, ou seja, quando dividimos 2 por 9 geramos o valor de 0,222....
Vamos fazer mais alguns exemplos para que fique bem entendido.
A fração geratriz, quando representada na forma decimal, produz dízimas periódicas simples ou compostas. Portanto, toda dízima periódica (número decimal) deve possuir uma forma fracionária, por isso demonstraremos como transformar números decimais em frações geratrizes. Primeiro vamos observar alguns exemplos de números racionais com períodos:
0,33333333... , período 3 (um algarismo)
0,23232323..., período 23 (dois algarismos)
0,562562562..., período 562 (três algarismos)
Exemplo 1: Encontrar a fração geratriz da seguinte dízima periódica: x = 0,333333...
Resolução:
1º passo
Relacionar a dízima periódica com uma incógnita
x = 0,333333...
2º passo
Multiplicar os dois lados da igualdade por um múltiplo de 10, de acordo com a quantidade de algarismos do período, por exemplo:
um algarismo, multiplicar por 10
dois algarismos, multiplicar por 100
três algarismos, multiplicar por 1000, e assim sucessivamente.
x = 0,333333 ... * 10
10x = 3,3333 ...
3º passo
Subtrair a segunda igualdade da primeira igualdade
10x = 3,3333
– x = 0,3333
9x = 3
9x = 3
x = 3/9
Exemplo 2: Encontrar a fração geratriz da seguinte dízima periódica: 0,232323... .
Resolução:
1º passo
x = 0,232323....
2º passo
x = 0,232323 ... * 100
100x = 23,23
3º passo
100x = 23,23
– x = 0,23
99x = 23
99x = 23
x = 23/99
Exemplo 3: Determinar a fração geratriz do número racional 0,562562...
Resolução:
1º passo
x = 0,562562...
2º passo
x = 0,562562... * 1000
1000x = 562,562
3º passo
1000x = 562,562
– x = 0,562
999x = 562
x = 562/999
Encontre a fração geratriz das dízimas periódicas abaixo.
01) 0,3333...
Resolução:
período: 3
Numerador: 3
Denominador: 9, pois o numerador é representado por somente um algarismo.
Fração geratriz: 3
9
O número e o denominador são divisíveis por 3. Podemos então simplificar a fração geratriz:
3 : 3 = 1
9 : 3 3
Caso queira verificar se 1/3 é, de fato, a fração que gera o número decimal 0,333... basta dividir 1 por 3.
02) Dízima periódica: 0,120120...
Resolução:
período: 120
Numerador: 120
Denominador: 999, pois o numerador é representado por 3 algarismos.
Fração geratriz: 120
999
O numerador e o denominador são divisíveis por 3. Simplificando a fração geratriz por 3 temos que:
120 = 40
999 333
03) Dízima periódica: 2,3737...
Resolução:
Essa dízima periódica possui um número inteiro que é 2. Para encontrar a fração geratriz dessa dízima basta separarmos a parte inteira da decimal numa soma e aplicarmos o método prático para encontrar a fração geratriz na parte decimal.
2,3737... = 2 + 0,3737... =
Período: 37
Numerador: 37
Denominador: 99, pois o numerador é representado por 2 algarismos.
Fração geratriz: 37
99
Agora substituímos, na soma, o valor decimal pela fração geratriz:
2,3737... = 2 + 0,3737... = 2 + 37
99
Faça com que os termos da soma tenha o mesmo denominador, em seguida some os numeradores.
2,3737... = 2 + 0,3737... = 2 x 99+ 37 = 198 + 37 = 235
1 x 99 99 99 99
A fração geratriz para a dízima periódica 2,3737... é:
2,3737... = 235
99
Método Prático
Para encontrar a fração geratriz de uma dízima periódica, podemos também utilizar um método prático.
Quando a dízima for simples, o numerador será igual a parte inteira com o período menos a parte inteira, e no denominador, a quantidades de "noves" igual ao número de algarismo do período.
Exemplos 1
Qual a fração geratriz da dízima periódica 0,222...?
Resolução
Método prático para dízima periódica simples adotamos o seguinte: parte inteira e período menos a parte inteira dividido pelo período (para algarismo que compõem o período substitui-se por 9).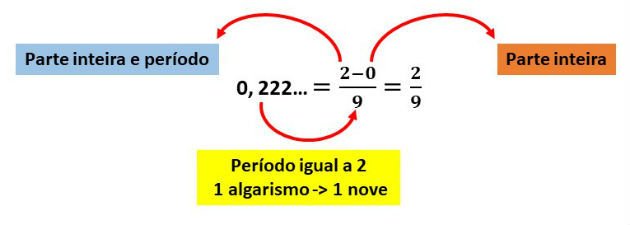
Exemplos 2
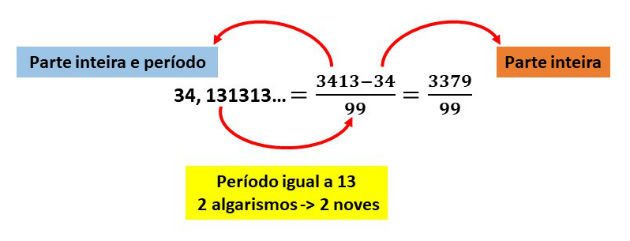
Qual a fração geratriz da dízima periódica 34,131313...?
Resolução
Método prático para dízima periódica simples adotamos o seguinte: parte inteira e período menos a parte inteira dividido pelo período (para algarismo que compõem o período substitui-se por 9).
Exemplos 3
Qual a fração geratriz da dízima periódica 6,3777...?
Resolução
Método prático para dízima periódica composta adotamos o seguinte: parte inteira e números que não se repetem e período menos a parte inteira e número que não se repetem dividido pelo período (para algarismo que compõem o período substitui-se por 9) e para cada número que não se repete adote zero.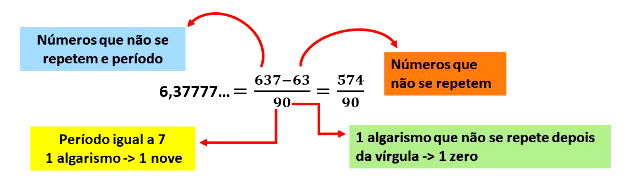
Exercícios resolvido:
Exercícios 1:
Calcule a fração geratriz de cada uma das dízimas periódicas simples: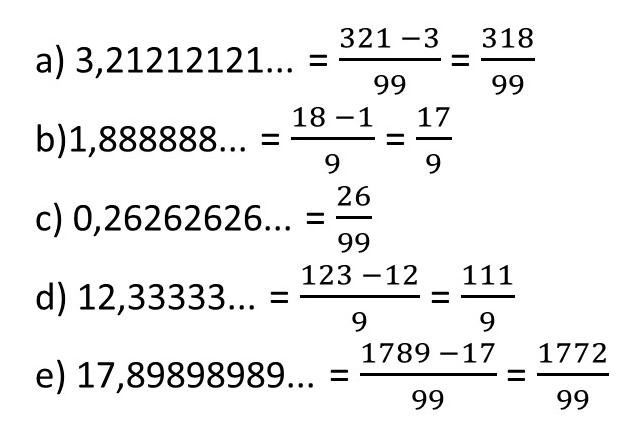
QUESTÕES RESOLVIDAS:
Exercícios 2
Calcule a fração geratriz de cada uma das dízimas periódicas compostas:
Exercícios 3:
Encontre a fração geratriz para realizar as seguintes operações entre números decimais:
Exercícios 4:
Utilizando fração geratriz, encontre o resultado da seguinte operação:
(1,0131313… – 0, 0141414…)
Exercícios 5:
Por meio de fração geratriz, encontre o resultado da seguinte operação:
0,54 + 3/5 – 1,22222… + 1,133333…