Professor Diminoi
MMC
O MMC (Mínimo Múltiplo Comum) é usado quando o enunciado da questão indica a ideia de tempo, encontro ou coincidência.
O MDC (Máximo Divisor Comum) é usado quando o enunciado indica a ideia de divisão, repartir em partes iguais ou do maior tamanho possível.
O MMC é o menor número que é múltiplo de dois ou mais números, ou seja, é o menor número que pode ser dividido por todos os números sem sobrar resto. J
O MDC é o maior número que divide dois ou mais números ao mesmo tempo.
O MMC e o MDC são ferramentas utilizadas para resolver questões de vários assuntos matemáticos, como matemática financeira, cálculo de frações e simplificação de expressões algébricas.
São também cobrados em provas tais como: Prova Paulista, Provão Paulista, Prova Brasil, Senai, ETEC, Termomecânica, ENEM, Concurso Públicos entre outros.
Para calcular o MMC e o MDC, é preciso decompor os valores originais em fatores ou em números primos.
MMC
Mínimo múltiplo comum (MMC) é o menor número múltiplo de dois ou mais números. Esse cálculo é muito comum ao fazer-se somas e subtrações entre frações.
Conhecemos como MMC o mínimo múltiplo comum de dois ou mais números. Encontrar o MMC entre dois números é procurar o menor número múltiplo de dois ou mais números simultaneamente. Para encontrar o MMC entre dois números, podemos fazer uma lista dos múltiplos de cada um deles até achar um que seja comum a ambos, ou então utilizar o método de decomposição em fatores primos ou até mesmo o de fatoração sucessiva.
Existem propriedades importantes para o mínimo múltiplo comum.
O que é o MMC?
Conhecemos como MMC o mínimo múltiplo comum entre dois ou mais números. Encontrar o MMC entre dois números é identificar o menor numero inteiro diferente de zero e múltiplo de ambos simultaneamente. Para compreender o que é o MMC, é fundamental saber o que são os múltiplos de número.
Conhecemos como multiplos de um número o produto obtido quando multiplicamos um número natural por outro número natural.
Exemplo 1:
M(12) = {0, 12, 24, 36, 48, 60, 72, 84, 96…}
Note que o conjunto dos números múltiplos de 12 é formado pelos resultados de 12 vezes 0, 12 vezes 1, 12 vezes 2, e assim sucessivamente. O conjunto de múltiplos é infinito.
Exemplo 2:
Vejamos agora os múltiplos de 14:
M(14) = {0, 14, 28, 42, 56, 70, 84, 98, 112…}
Podemos encontrar o mínimo múltiplo comum entre esses dois números (12, 14), para isso, basta analisar as duas listas de múltiplos e procurar o menor número inteiro diferente de zero e que seja múltiplo dos dois.
MMC(12, 14)
M(12) = {0, 12, 24, 36, 48, 60, 72, 84, 96…}
M(14) = {0, 14, 28, 42, 56, 70, 84, 98, 112…}
MMC(12, 14) = 84
Como calcular o MMC?
Para calcular o MMC entre dois ou mais números, existem vários métodos. Os que mais se destacam são três, apresentados a seguir.
1º método - comparação dos múltiplos
O primeiro deles é o que nós utilizamos anteriormente para encontrar o MMC entre 12 e 14: escrever a lista de múltiplo de cada um dos números e encontrar o menor múltiplo em comum entre eles.
Exemplo
MMC(10, 15)
M(10) = {0, 10, 20, 30…}
M(15) = {0, 15, 30…}
MMC(10, 15) = 30
Acontece que esse método é pouco prático quando há mais números, ou então, quando os números são maiores, muitas vezes encontrar o MMC escrevendo a lista de múltiplos de cada um dos números pode ser bastante trabalhoso.
2º método - decomposição em fatores primos
O método de decompor os números em fatores primos facilita encontrar os múltiplos em comum quando os números são maiores.
Os números que não são primos podem ser escritos como o produto entre numeros primos. Esse método consiste em reescrever os números na forma fatorada e multiplicar os fatores com os seus maiores expoentes.
Exemplo:
Encontre o MMC(36, 40):
Primeiro vamos escrever esses números na sua forma fatorada:
36 = 2² · 3²
40 = 2³ · 5
Os fatores encontrados na decomposição foram 2, 3 e 5. Vamos realizar a multiplicação entre eles com os seus respectivos exponentes. Note que o 2 apareceu em ambos, nesse caso, escolhemos o maior expoente:
MMC(36, 40) = 2³ · 3² · 5
MMC(36, 40) = 8 · 9 · 5
MMC(36, 40) = 360
3º método - método das divisões sucessivas
O terceiro método é o mais utilizado e é conhecido como método prático do MMC ou método das divisões sucessivas. Como o nome sugere, nele se realiza divisões sucessivas com esses números simultaneamente para encontrar os fatores cujo o produto será o MMC.
Exemplo:
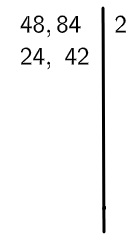
Calcule MMC(48, 84).
1º passo: montar o algoritmo e encontrar o menor número primo que divide pelo menos um dos dois números. 
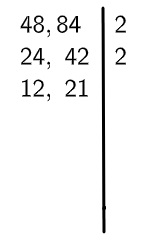
3º passo: com os resultados encontrados, repetiremos o processo, dividindo-os novamente por 2:
4º passo: note que 2 não divide o 21, mas ainda divide o 12, então escreveremos o 2 como fator, mas realizaremos somente a divisão que tem resultado inteiro, repetindo o processo até que não tenha mais nenhum número divisível por 2.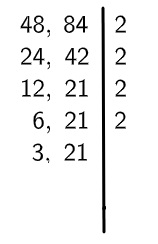
5º passo: encontraremos agora o próximo número primo que divide qualquer um dos dois números, que, no caso, é o 3, e realizaremos a divisão.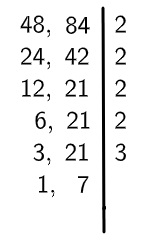
6º passo: como 3 não divide mais nenhum dos dois números, então encontraremos o próximo número que divide qualquer um dos dois números, que no caso é 7.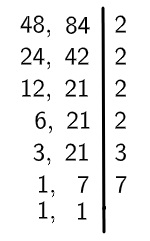
7º passo: agora que não é mais possível dividir, calculamos o produto entre os números encontrados para encontrar o MMC.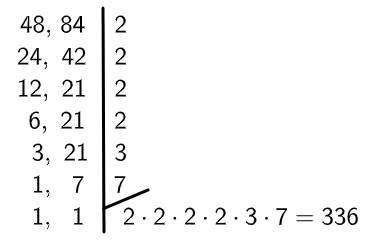
Então, o MMC(48, 84) = 336.
Propriedades do MMC
Existem algumas propriedades importantes do MMC:
1ª propriedade: o MMC entre dois números primos entre si é igual ao produto entre esses dois números.
Exemplo
MMC(10, 9)
Note que os divisores de 10 são D(10) = {1, 2, 5, 10} e os divisores de 9 são {1, 3, 9}. Sendo assim, não existe nenhum divisor comum entre esses números, logo, temos que:
MMC(10, 9) = 10 × 9 = 90
2ª propriedade: quando um dos números de que queremos encontrar o MMC é múltiplo do outro, então o MMC entre esses números será o maior deles.
Exemplo
MMC(4, 12)
M(6) = {0, 4, 8, 12 , 18...}
M(18) = {0, 12…}
MMC(4, 12) = 12
MMC em frações
Utilizamos o MMC para igualar os denominadores de fracoes, a fim de que seja possível calcular a adição ou a subtração entre duas frações.
Para calcular a soma de duas frações com denominadores distintos, é necessário calcular o mínimo múltiplo comum dos denominadores, a fim de escrever fracoes equivalentes que possuam o mesmo denominador e, assim, ser possível realizar a soma.
Exemplo:
![]()
Primeiro encontraremos o MMC(9, 5). Como eles são primos entre si, basta multiplicar 9 × 5 = 45, então, temos que: MMC(9, 5) = 45
Encontrado o MMC, agora precisamos analisar as frações. Na primeira, para que o denominador seja igual a 45, é necessário multiplicar por 5 tanto o numerador quanto o denominador.
Já na segunda fração, como o denominador igual a 5, é necessário multiplicar o numerador e o denominador por 9.
Após igualar os denominadores, é possível realizar a soma entre as frações:
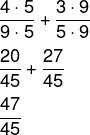
Diferença entre MMC e MDC
Conhecemos o mínimo múltiplo comum (MMC), mas existe também o máximo divisor comum MDC). Como o nome sugere, o máximo divisor comum é o maior número divisor de dois ou mais números ao mesmo tempo.
Exemplo
MDC(18, 27)
Dessa vez, escreveremos a lista de divisores de cada um desses números:
D(18) = {1, 2, 3, 6, 9, 18}
D(27) = {1, 3, 9, 27}
QUESTOES RESOLVIDAS - MMC
01) (IFG) Antônio realiza atividades físicas regularmente, entre as modalidades de corrida, ciclismo e natação. Ele corre a cada três dias, pedala dia sim e dia não, e nada de quatro em quatro dias. Certa vez, coincidiu de realizar essas três atividades físicas no mesmo dia. É correto afirmar que essa coincidência voltará a ocorrer daqui a
(A) 06 dias.
(B) 08 dias.
(C) 10 dias.
(D) 12 dias.
Resolução
Queremos o MMC(2, 3, 4).
Listando os múltiplos de cada um deles até encontrar o primeiro que seja comum aos três, temos que:
M(2) = {0, 2, 4, 6, 8, 10, 12...}
M(3) = {0, 3, 6, 9, 12...}
M(4) = {0, 4, 8, 12…}
Então, o MMC(2, 3, 4) = 12.
Alternatiuva D
02) Em um conselho regional, o presidente é eleito a cada 4 anos, o secretário, a cada 3 anos, e o coordenador geral, a cada 2 anos. Se em 2020 houve eleições para os três cargos simultaneamente, das opções abaixo, em que ano isso ocorrerá novamente?
(A) 2028
(B) 2030
(C) 2032
(D) 2034
Resolução
Calculando o MMC(4, 3, 2), temos que:
M(4) = {0, 4, 8, 12…}
M(3) = {0, 3, 6, 9, 12…}
M(2) = {0, 2, 4, 6, 8, 10, 12…}
Então, temos que: MMC(4, 3, 2) = 12.
Desse modo, a eleição para esses 3 cargos ocorrerá simultaneamente em 12 anos, 2020 + 12 = 2032.
Alternativa C
03) Qual é o mínimo múltiplo comum entre os números 90, 150 e 20?
(A) 90
(B) 150
(C) 20
(D) 900
(E) 450
Resolucao
ara realizar esse cálculo, basta utilizar o método prático: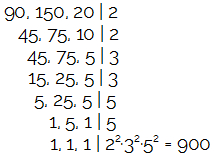
Alternativa D
04) Uma loja de aviamentos vende prendedores de cabelo em embalagens com 15 unidades e lacinhos em embalagens com 6 unidades cada uma. Uma pessoa que deseja comprar a mesma quantidade de lacinhos e de prendedores de cabelo deverá comprar quantas embalagens no total?
Resolucao
MMC entre 15 e 6 dirá exatamente quantas embalagens devem ser compradas no total.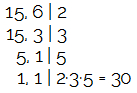
05) (UEM PR/2009 - adaptada)
Considerando os números 60, 110 e 126, assinale o que for correto.
01. 2 é o único divisor positivo par de 110.
02. A soma dos números primos positivos que são simultaneamente divisores de 60 e de 126 é igual a 5.
04. A soma dos divisores positivos do número 110 é igual a 216.
08. O mínimo múltiplo comum entre 60 e 110 é 6600.
16. O máximo divisor comum entre 60 e 126 é 6.
Qual é a soma dos números referentes às alternativas corretas?
(A) 22
(B) 23
(C) 31
(D) 11
(E) 14
Resolucao
1. Incorreta!
10 também é um divisor par de 110.
2. Correta!
3. 2 e 3, cuja soma é 5, são primos positivos que são, simultaneamente, divisores de 60 e 126.
4. Correta!
Os divisores do número 110 são: 1, 2, 5, 11, 10, 22, 55 e 110, e a soma entre eles é: 1 + 2 + 5 + 10 + 11 + 22 + 55 + 110 = 216
8. Incorreta!
O MMC entre 60 e 110 é:
O MDC entre 60 e 126 é: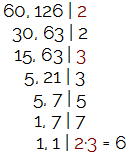
Altenativa A
06) (PUC MG/2001)
O Mínimo Múltiplo Comum dos números 23, 3n e 7 é 1512. O valor de n é:
(A) 3
(B) 4
(C) 5
(D) 6
Resolucao
O Mínimo Múltiplo Comum também pode ser calculado a partir da decomposição em fatores primos de um número. Para resolver esse exercício, portanto, podemos decompor o número 1512 em fatores primos, sabendo que ele é MMC de 23, 3n e 7, podemos ter certeza de que os fatores primos que aparecerão serão exatamente esses com o expoente do número 3. Observe: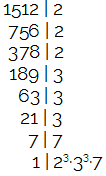
A decomposição em fatores primos é igual ao produto apresentado no texto do exercício. Assim, podemos escrever a igualdade abaixo e concluir que o valor de n é:
23 . 3n .7 = 23 . 3 . 7
n = 3
Alternativa A
07) (Aprendiz de Marinheiro) Seja A = 120, B = 160, x = mmc (A,B) e y = mdc (A,B), então o valor de x + y é igual a:
(A) 460
(B) 480
(C) 500
(D) 520
(E) 540
Resolucao
Para encontrar o valor da soma de x com y, é necessário primeiro encontrar esses valores.
Desta forma, vamos fatorar os números em fatores primos e depois calcular o mmc e o mdc entre os números dados.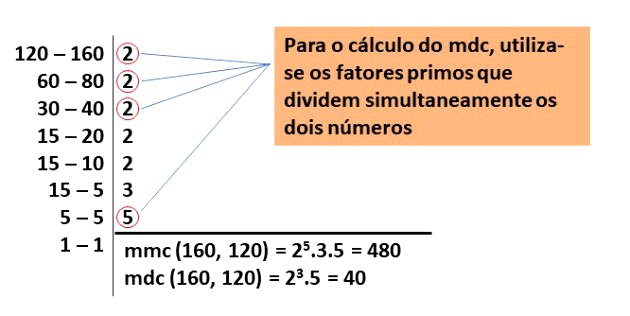 Agora que já conhecemos o valor de x (mmc) e de y (mdc), podemos encontrar a soma:
Agora que já conhecemos o valor de x (mmc) e de y (mdc), podemos encontrar a soma:
x + y = 480 + 40 = 520
Alternativa D
08) (Unicamp) A tabela abaixo informa alguns valores nutricionais para a mesma quantidade de dois alimentos, A e B.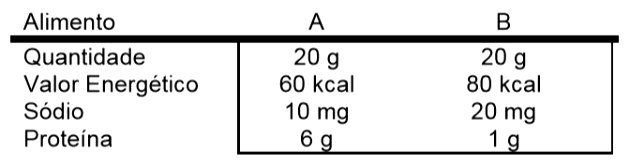 Considere duas porções isocalóricas (de mesmo valor energético) dos alimentos A e B. A razão entre a quantidade de proteína em A e a quantidade de proteína em B é igual a
Considere duas porções isocalóricas (de mesmo valor energético) dos alimentos A e B. A razão entre a quantidade de proteína em A e a quantidade de proteína em B é igual a
(A) 4.
(B) 6.
(C) 8.
(D) 10.
Resolucao
Para encontrar porções isocalóricas dos alimentos A e B, vamos calcular o mmc entre os valores energéticos respectivos.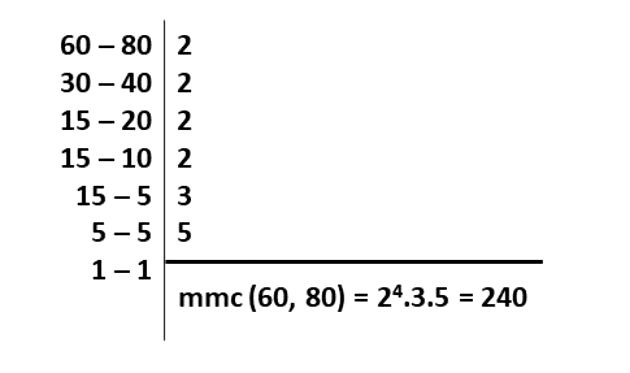
Então, devemos considerar a quantidade necessária de cada alimento para obter o valor calórico.
Considerando o alimento A, para ter um valor calórico de 240 Kcal é necessário multiplicar as calorias iniciais por 4 ( 60 . 4 = 240). Já para o alimento B, é necessário multiplicar por 3 (80 . 3 = 240).
Assim, a quantidade de proteína do alimento A será multiplicada por 4 e a do alimento B por 3:
Alimento A : 6 . 4 = 24 g
Alimento B : 1 . 3 = 3 g
Desta forma, temos que a razão entre essas quantidades será dada por:
24 /3 = 8g
Alternativa C
09) (UERJ) Na tabela abaixo, estão indicadas três possibilidades de arrumar n cadernos em pacotes: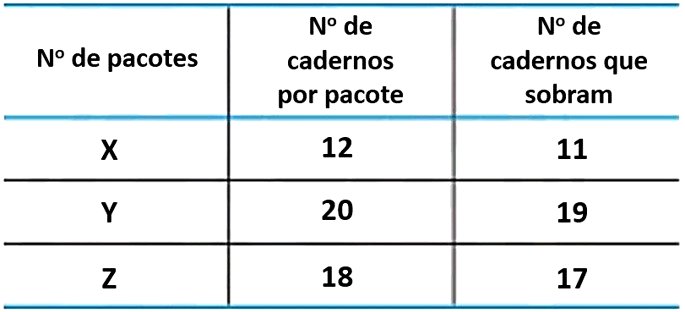 Se n é menor do que 1200, a soma dos algarismos do maior valor de n é:
Se n é menor do que 1200, a soma dos algarismos do maior valor de n é:
(A) 12
(B) 17
(C) 21
(D) 26
Resolucao
Considerando os valores informados na tabela, temos as seguintes relações:
n = 12 . x + 11
n = 20 . y + 19
n = 18 . z + 17
Note que se somássemos 1 livro ao valor de n, deixaríamos de ter resto nas três situações, pois formaríamos mais um pacote:
n+ 1 = 12 . x + 12
n+ 1 = 20 . x + 20
n+ 1 = 18 . x + 18
Sendo assim, n + 1 é múltiplo comum de 12, 18 e 20, então, se encontrarmos o mmc (que é o menor múltiplo comum), podemos, a partir daí, encontrar o valor de n+1.
Calculando o mmc: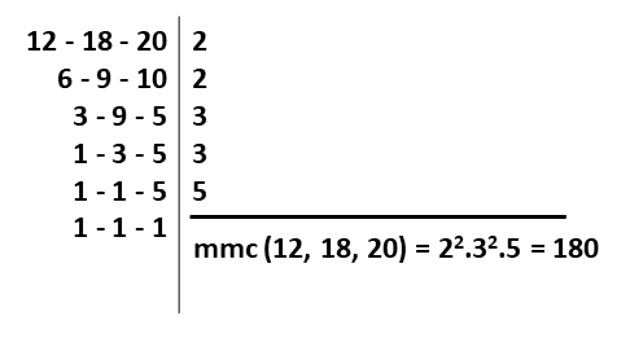
Então, o menor valor de n + 1 será 180. Entretanto, queremos encontrar o maior valor de n menor que 1200. Assim, vamos procurar um múltiplo que satisfaça essas condições.
Para isso, vamos multiplicar o 180 até encontrar o valor desejado:
180 . 2 = 360
180 . 3 = 540
180 . 4 = 720
180 . 5 = 900
180 . 6 = 1 080
180 . 7 = 1 260 (esse valor é maior que 1 200)
Portanto, podemos calcular o valor de n:
n + 1 = 1 080
n = 1080 - 1
n = 1079
Sendo que a soma dos seus algarismos será dada por:
1 + 0 + 7 + 9 = 17
Alternativa B
MDC
O máximo divisor comum (MDC) é o maior número que divide dois ou mais números ao mesmo tempo. Ele é utilizado para resolver várias situações-problema da Matemática.
O que é o MDC?
MDC é o máximo divisor comum entre dois ou mais números, ou seja, o maior número que dividi dois ou mais números simultaneamente. Dados dois números, como o 8 e o 16, sabemos que eles possuem divisores em comum, a saber: 1, 2, 4 e 8, que dividem tanto o 8 quanto o 16 ao mesmo tempo, logo:
MDC (8,16) = 8, que é o maior deles.
Como calcular o MDC?
Existem diferentes métodos para calcular o MDC entre dois ou mais números. Os mais comuns são o método da comparação entre os divisores, a decomposição em fatores primos e a decomposição simultânea.
Método da comparação
O método da comparação consiste em escrever a lista dos divisores de cada um dos números e encontrar qual é o maior divisor em comum entre eles.
Exemplo
Encontre o MDC de 20 e 16.
Por comparação, vamos escrever os divisores de 20 e os divisores de 16.
D(20) = {1,2,4,5,10,20}
D(12) = {1,2,4,8,16}
Existem alguns divisores em comum, que são os números {1,2,4}. O MDC é o maior deles.
MDC (20,16) = 4
O problema é que esse método nem sempre é conveniente, pois, se os números forem muito grandes, encontrar os divisores de cada um deles pode não ser uma tarefa fácil.
O método da decomposição consiste em decompor os numeros em fatores primos e procurar quais são os fatores em comum entre esses dois números.
Exemplo:
Encontre o MDC entre 120 e 150.
Primeiro encontraremos a decomposição em fatores primos de cada um desses números: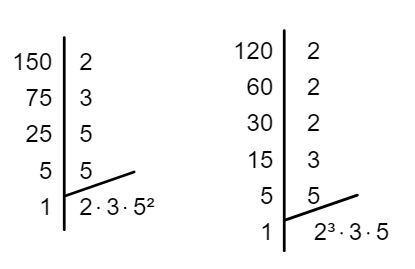
Agora vamos encontrar os fatores que são comuns aos dois e calcular o produto entre eles.
Note que, em 150, aparece o fator 2 e, em 120, aparece 2³. Nesse caso, sempre escolhemos o fator com o menor expoente, ou seja, 2 é um fator em comum. O mesmo acontece com o 3 e com o 5.
MDC (150, 120) = 2 · 3 · 5 = 30
Decomposição simultânea
Semelhantemente ao método anterior, a ideia é encontrar os fatores em comum aos dois números quando realizamos a decomposição; porém, faremos essa decomposição dos dois números ao mesmo tempo.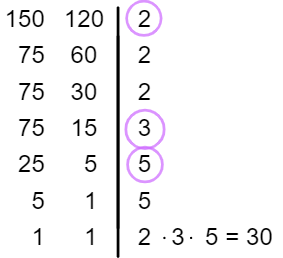
Propriedades do MDC
O máximo divisor comum possui propriedades importantes que nos auxiliam a encontrar de forma mais rápida o MDC entre dois números.
1ª propriedade: o MDC entre dois números consecutivos é sempre igual a 1.
MDC (10, 11) = 1
2ª propriedade: quando temos dois ou mais números e um dos números é divisor dos demais, então ele é o MDC.
MDC (5,10,15)
Sabemos que o 5 é divisor de 10 e de 15, então:
MDC (5,10,15) = 5
QUESTOES RESOLVIDAS - MDC
01) (Enem) O gerente de um cinema fornece anualmente ingressos gratuitos para escolas. Este ano, serão distribuídos 400 ingressos para uma sessão vespertina e 320 ingressos para uma sessão noturna de um mesmo filme. Várias escolas podem ser escolhidas para receberem ingressos. Há alguns critérios para a distribuição dos ingressos:
1) cada escola deverá receber ingressos para uma única sessão;
2) todas as escolas contempladas deverão receber o mesmo número de ingressos;
3) não haverá sobra de ingressos (ou seja, todos os ingressos serão distribuídos).
O número mínimo de escolas que podem ser escolhidas para obter ingressos, segundo os critérios estabelecidos, é:
(A) 2.
(B) 4.
(C) 9.
(D) 40.
(E) 80.
Resolução
Calculando o MDC entre 320 e 400, temos que:
Para encontrar o MDC, vamos multiplicar os números que são divisores tanto de 320 quanto de 400:
MDC (400, 320) = 24 · 5 = 16 · 5 = 80
Cada escola receberá 80 ingressos, logo 720 : 80 = 9 escolas.
Alternativa C.
02) A Câmara de Vereadores de um município é composta por 16 mulheres e 12 homens, que serão divididos no maior número possível de comissões de tal forma que cada comissão tenha o mesmo número de membros. O número de membros em cada comissão é igual a:
(A) 8.
(B) 7.
(C) 6.
(D) 5.
(E) 4.
Resolução
Encontrando o MDC entre 16 e 12, temos que:
D(16) = {1, 2, 4, 8, 16}
D(12) = {1, 2, 3, 4, 6, 12}
Analisando as listas, o maior divisor em comum entre esses números é 4.
MDC(16, 12) = 4
Então, cada comissão terá um total de 4 pessoas.
Alternativa E
03) (EPCAR-2001)
Uma abelha rainha dividiu as abelhas de sua colmeia nos seguintes grupos para exploração ambiental: um composto de 288 batedoras e outro de 360 engenheiras. Sendo você a abelha rainha e sabendo que cada grupo deve ser dividido em equipes constituídas de um mesmo e maior número de abelhas possível, então você redistribuiria suas abelhas em:
(A) 8 grupos de 81 abelhas.
(B) 9 grupos de 72 abelhas.
(C) 24 grupos de 27 abelhas.
(D) 2 grupos de 324 abelhas.
Resolucao
Para resolver essa questão devemos fatorar 288 e 360 simultaneamente. Depois da fatoração iremos obter o seu MDC.
360, 288| 2
180, 144| 2
90, 72| 2
45, 36| 2
45, 18| 2
45, 9| 3
15, 3| 3
5, 1| 5
1, 1|
MDC = 2 x 2 x 2 x 3 x 3 = 72
Então cada grupo terá 72 abelhas. Para saber a quantidade de grupos basta dividir o total de abelhas por 72. Veja:
288 + 360 = 648 (Total de abelhas)
648 : 72 = 9
A alternativa B
04) (Concurso Correios) O piso de uma sala retangular, medindo 3,52 m × 4,16 m, será revestido com ladrilhos quadrados, de mesma dimensão, inteiros, de forma que não fique espaço vazio entre ladrilhos vizinhos. Os ladrilhos serão escolhido de modo que tenham a maior dimensão possível. Na situação apresentada, o lado do ladrilho deverá medir:
(A) mais de 30 cm.
(B) menos de 15 cm.
(C) mais de 15 cm e menos de 20 cm.
(D) mais de 20 cm e menos de 25 cm.
(E) mais de 25 cm e menos de 30 cm.
Resolucao
Para resolvermos essa questão devemos primeiro converter as medidas 3,52 m × 4,16 m para centímetros (cm).
3,52 x 100 = 352 cm
4,16 x 100 = 416 cm
Para escolher a dimensão adequada do ladrilho que irá revestir o piso retangular devemos fazer o MDC de 352 e 416.
352, 416| 2
176, 208| 2
88, 104| 2
44, 52| 2
22, 26| 2
11, 13| 11
1, 13| 13
1, 1|
MDC = 2 x 2 x 2 x 2 x 2 = 32
O ladrilho quadrado que irá revestir a sala retangular terá 32 cm x 32 cm de dimensão.
Alternativa A
05) Encontre o número que será o maior divisor comum dos números 12, 32, 64 e 120.
Resolucao
Para encontrar o número que é o maior divisor de 12, 32, 64 e 120; devemos fatorar todos os números simultaneamente.
12, 32, 64,120| 2
6, 16, 32, 60| 2
3, 8, 16, 30| 2
3, 4, 8, 15| 2
3, 2, 4, 15| 2
3, 1, 2, 15| 2
3, 1, 1, 15| 3
1, 1, 1, 5| 5
1, 1, 1, 1|
Agora que fatoramos, devemos encontrar o MDC que será o maior divisor para 12, 32, 64 e 120.
MDC (12, 32, 64,120) = 2 . 2 = 4
06) O professor de história precisa dividir uma turma de alunos em grupos, de modo que cada grupo tenha a mesma quantidade de alunos. Nessa turma temos 24 alunas e 16 alunos. Quantos componentes terá cada grupo?
Resolucao
Inicialmente devemos verificar qual o MDC de 24 e 16.
24, 16| 2
12, 8| 2
6, 4| 2
3, 2| 2
3, 1| 3
1, 1|
MDC (24,16) = 2 . 2 . 2 = 8
A resposta final para essa questão é: Cada grupo terá 8 alunos.
07) Joana está preparando kits de doces para distribuir entre alguns convidados. Há 36 brigadeiros e 42 cajuzinhos. Ela quer separá-los em pratos de modo a ocupar a menor quantidade de pratos mas, que todos os pratos tenham a mesma quantidade de doces e sem misturá-los. A quantidade de doces que Joana deverá colocar em cada prato, será
(A) 21.
(B) 12.
(C) 6.
(D) 8.
(E) 5.
Resolucao
Para encontrar a menor quantidade de pratos a serem utilizados, será necessário colocar a maior quantidade de doces em cada prato, mas fazendo com que todos os pratos tenham a mesma quantidade de doces e, sem misturar brigadeiros e cajuzinhos.
Para isso, é necessário encontrar o maior divisor comum entre 36 e 42. Fazendo a fatoração: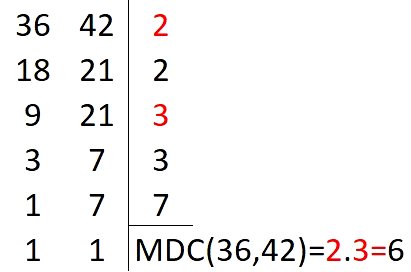
A quantidade de doces em cada prato será de 6 doces.
Alternativa C
08) Um evento de corrida de equipes irá acontecer no próximo final de semana e, o período para as inscrições de participantes terminou hoje. Ao total, 88 pessoas se inscreveram, sendo 60 mulheres e 28 homens. Para as duas modalidades, feminina e masculina, as equipes devem possuir sempre, o mesmo e o maior número e atletas possível sem misturar homens e mulheres em uma mesma equipe. Desta forma o número de atletas em cada equipe será de
(A) 10.
(B) 8.
(C) 6.
(D) 4.
(E) 2.
Resolucao
Para saber o maior número de atletas possível em cada equipe, de modo que todas tenham o mesmo número de atletas, sem misturar homens e mulheres em uma mesma equipe, devemos dividir a quantidade de inscritos, homens e mulheres, pelo Maior Divisor Comum entre os dois.
Para determinar o MDC(28,60), fazemos a fatoração.
Alternativa D
09) (Correios – Cespe) O piso de uma sala retangular, medindo 3,52 m × 4,16 m, será revestido com ladrilhos quadrados, de mesma dimensão, inteiros, de forma que não fique espaço vazio entre ladrilhos vizinhos. Os ladrilhos serão escolhidos de modo que tenham a maior dimensão possível.
Na situação apresentada, o lado do ladrilho deverá medir
(A) mais de 30 cm.
(B) menos de 15 cm.
(C mais de 15 cm e menos de 20 cm.
(D) mais de 20 cm e menos de 25 cm.
(E) mais de 25 cm e menos de 30 cm
Resolucao
Note que os dados da questão estão em metros e as respostas em centímetros. Sendo assim, vamos passar os valores da questão para centímetros.
3,52 m = 352 cm
4,16 m = 416 cm
Como o piso é quadrado, todos os lados devem possuir a mesma medida. Por isso, a medida do lado deve ser um divisor comum para 352 e 416.
Vamos determinar o Maior Divisor Comum em 352 e 416.
Desta forma, a resposta é a letra a, o ladrilho deverá medir mais que 30 cm.
Alternativa A
10) (Professor de Matemática da Educação Básica) Um ferreiro vai confeccionar pedaços de barras de ferro de mesma medida. Ele dispõe de 35 barras de 270 cm, 18 de 540 cm e 6 de 810 cm, todas de igual largura. Ele pretende cortar as barras em pedaços de mesmo comprimento, sem deixar sobras, de modo que esses pedaços fiquem o maior possível, mas de comprimento menor que 1 m. Quantas pedaços de barra de ferro o ferreiro pode produzir?
(A) 89.
(B) 178.
(C) 267.
(D) 524.
(E) 801.
Resolucao
O comprimento dos novos pedaços devem dividir de forma exata as barras já disponíveis, de modo que todas tenham o mesmo e o maior comprimento mas, menores que 1 m.
Para isso, devemos fatorar as medidas.
O MDC é 270 cm. No entanto, é preciso que os novos pedaços sejam menores que 100 cm.
Se retirarmos o fator 2, e multiplicarmos os que restaram em destaque na fatoração, teríamos:
3.3.3.5 = 135 cm, ainda maior que 100 cm.
Retirando um fator 3, e multiplicarmos os que restaram em destaque na fatoração, teríamos:
2.3.3.5 = 90 cm
Sendo assim, os novos pedaços devem possuir 90 cm. Para saber a quantidade, devemos dividir cada medida de barra já disponível por 90 e multiplicar pelas quantidades de cada.
270cm / 90 cm = 3
Como há 35 barras de 270, fazemos a multiplicação:
35 . 3 = 105 barras
540 cm / 90cm = 6
Como há 18 barras de 540, fazemos a multiplicação:
18 . 6 = 108 barras
810cm / 90cm = 9
Como há 18 barras de 540, fazemos a multiplicação:
6 . 9 = 54 barras
Somando as quantidades individuais
105 + 108 + 54 = 267.
Portanto, ferro o ferreiro pode produzir 267 pedaços de barra de ferro.
Alternativa C
11) (Prefeitura de Areial Professor B - Matemática) O gerente de uma loja de aparelhos eletrônicos, apaixonado por matemática, propõe que o preço de um determinado celular seja dado em reais pela expressão mdc (36,42). mmc (36,42).
Neste caso, é CORRETO afirmar que o valor do celular, em reais, é igual a:
(A) R$ 1,812,00
(B) R$ 1,612,00
(C) R$ 1,712,00
(D) R$ 2,112,00
(E) R$ 1,512,00
Resolucao
Primeiro vamos calcular o MDC(36,42).
Para isso, basta fatorar os números e multiplicar os fatores que dividem, simultaneamente, as duas colunas.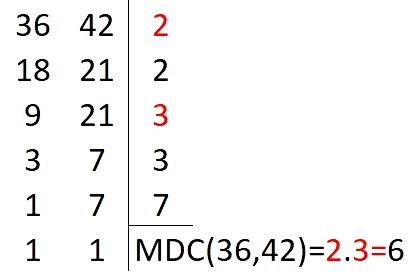
Para o cálculo do MMC, basta multiplicarmos todos os fatores.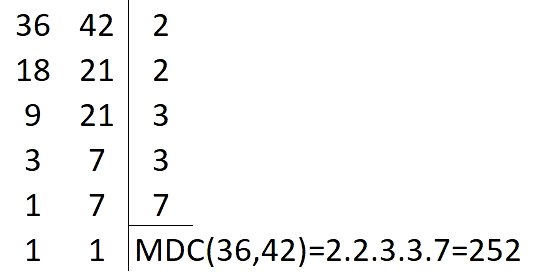
Agora, basta multiplicar os dois resultados.
252 . 6 = 1512
O valor do celular, em reais, é igual a R$ 1512,00.
Alternativa E
12) (Prefeitura de Irati - SC - Professor de Inglês) Em uma caixa, há 18 bolinhas azuis, 24 bolinhas verdes e 42 bolinhas vermelhas. Marta quer organizar as bolinhas em sacolas, de modo que cada sacola tenha o mesmo número de bolinhas e cada cor fique igualmente distribuídas nas sacolas e que possa usar a quantidade máxima de sacolas possíveis para isso. Qual a soma das bolinhas azuis, verdes e vermelhas que ficaram em cada sacola?
(A) 7
(B) 14
(C) 12
(D) 6
Resolucao
Resposta correta: b) 14.
Primeiramente, vamos determinar o maior divisor comum aos três números;
Agora, basta dividir a quantidade de bolinhas de cada cor por 6 e, somar o resultado.
18 / 6 = 3
24 / 6 = 4
42 / 6 = 7
Somando os resultados temos: 3 + 4 + 7 = 14
13) (PUC-PR Medicina 2015) Um estagiário recebeu a tarefa de organizar documentos em três arquivos. No primeiro arquivo, havia apenas 42 contratos de locação; no segundo arquivo, apenas 30 contratos de compra e venda; no terceiro arquivo, apenas 18 laudos de avaliação de imóveis. Ele foi orientado a colocar os documentos em pastas, de modo que todas as pastas devem conter a mesma quantidade de documentos. Além de não poder mudar algum documento do seu arquivo original, deveria colocar na menor quantidade possível de pastas. O número mínimo de pastas que ele pode usar é:
(A) 13.
(B) 15.
(C) 26.
(D) 28.
(E) 30.
Resolucao
Calculamos o MDC(18,30,42)
Agora, dividimos as quantidades de documentos em cada arquivo por 6 e, somamos o resultado.
18 / 6 = 3
30 / 6 = 5
42 / 6 = 7
Somando os resultados temos: 3 + 5 + 7 = 15
Desse modo, 15 é o número mínimo de pastas que ele pode usar.
Alternativa B
DIFERENCAS ENTRE MDC e MMC
Além do máximo divisor comum, existe também o minimo multiplo comum, conhecido como MMC, que é o menor múltiplo em comum que dois ou mais números possuem.
As diferenças entre eles é que, no MDC, estamos calculando o maior divisor em comum; já no MMC, estamos trabalhando com o menor múltiplo em comum.
Exemplo 1:
Dados os números 32 e 24, encontre o MDC entre eles.
1º passo: vamos listar os divisores de 32 e os divisores de 24.
D(32) = {1,2,4,8,16, 32}
D(24) = {1,2,3,4,6,8, 12, 24}
2º passo: agora encontraremos o maior número que divide ambos ao mesmo tempo.
MDC (32,24) = 8
Oito é o maior número que divide 32 e 24 ao mesmo tempo.
Exemplo 2
Dados os números 24 e 32, encontre o MMC entre eles.
Vamos listar os MULTIPLOS de 24 e de 32 até encontrar um que seja comum aos dois.
M(24) = {0, 24, 48, 72, 96 ...}
M(32) = {0, 32, 64, 96 …}
MMC(24,32) = 96
QUESTOES RESOLVIDAS envonvedo MMC e MDC
01) Encontre os múltiplos de 10 e 20 compreendidos entre 1 e 200 e responda:
a) quais são múltiplos de 10 que também são múltiplos de 20?
Resolucao
Entre 1 e 200, os múltiplos de 10 e de 20 são: 20, 40, 60, 100, 140, 160, 180 e 200.
b) qual é o menor múltiplo comum entre eles?
Resolucao
O menor múltiplo comum entre eles é o 20.
02) Calcule o mínimo múltiplo comum entre 4 e 18
Resolucao
4 e 18
4, 18 | 2
2, 9 | 2
1, 9 | 3
1, 3 | 3
1, 1 ⇒ MMC (4, 18) = 2.2.3.3 = 36
03) Calcule o mínimo múltiplo comum entre 10 e 25
Resolucao
10 e 25
10, 25 | 2
5, 25 | 5
1, 5 | 5
1, 1 ⇒ MMC (10, 25) = 2.5.5 = 50
04) Calcule o mínimo múltiplo comum entre 6, 9 e 24
Resolucao
6, 9 e 24
6, 9, 24 | 2
3, 9, 12 | 2
3, 9, 6 | 2
3, 9, 3 | 3
1, 3, 1 | 3
1, 1 , 1 ⇒ MMC (6, 9, 24) = 2.2.2.3.3 = 72
05) Para um trabalho de inglês, os alunos de uma turma podem ser agrupados de 5 em 5 alunos ou de 7 em 7. Quantos alunos há na turma?
Resolucao
O número de alunos da turma é o MMC entre 5 e 7.
5, 7 | 5
1, 7 | 7
1, 1 ⇒ MMC (5, 7) = 5.7 = 35
Portanto, há 35 alunos na turma de inglês.
06) Sem fazer contas, responda qual é o MMC entre:
Sem fazer contas, responda qual é o MMC entre: 6 e 30.
Resolucao
Como 30 é um múltiplo de 6, então, o MMC entre 6 e 30 é 30.
07) Sem fazer contas, responda qual é o MMC entre: 45 e 15.
Resolucao
Como 45 é um múltiplo de 15, então, o MMC entre 45 e 15 é 45.
08) Sem fazer contas, responda qual é o MMC entre: 8 e 32.
Resolucao
Como 32 é um múltiplo de 8, então, o MMC entre 8 e 32 é 32.
09) Um alarme dispara a cada 15 minutos e outro alarme dispara a cada 40 minutos. Qual é, em horas, o menor intervalo de tempo entre dois disparos simultâneos entre os alarmes?
Resolucao
O MMC entre 15 e 40 é 120. Então, o menor intervalo de tempo é de 120 minutos, que equivale a 2 horas.
10) (PM SE – IBFC) Um comerciante vende balas em pacotinhos, sempre com a mesma quantidade. Ao fazer isso, percebeu que dentre as balas que possuía poderia colocar 8, 12 ou 20 balas em cada pacote. Nessas condições, assinale a alternativa que apresenta o número mínimo de balas que o comerciante dispunha:
(A) 120
(B) 240
(C) 360
(D) 60
Resolução
Observe que a quantidade mínima de balas que o comerciante dispunha é múltiplo de 8, 12 e 20, ou seja, basta calcular o MMC dos três números.
8 = 2³
12 = 2².3
20 = 2².5
MMC(8, 12, 20) = 2³.3.5 = 120
Alternativa A
11) (PM PI – Nucepe) No alto de uma torre de uma emissora de televisão duas luzes “piscam” com frequências diferentes. A primeira, “pisca“ 12 vezes por minuto e a segunda, “pisca“ 15 vezes por minuto. Se num certo instante as luzes piscam simultaneamente, após quantos segundos elas voltarão a piscar simultaneamente?
(A) 10 segundos.
(B) 20 segundos.
(C) 15 segundos.
(D) 40 segundos.
(E) 30 segundos.
Resolução
A que pisca 12 vezes por minuto pisca de 5 em 5 segundos.
Ela pisca em 0, 5, 10, 15, 20…
A que pisca 15 vezes por minuto pisca de 4 em 4 segundos.
Ela pisca em 0, 4, 8, 12, 16, 20…
O que estamos fazendo na verdade é calcular o mmc de 4 e 5 que é 20.
Alternativa B
12) (PM SP – Vunesp) No estoque de uma papelaria, há uma caixa com várias borrachas iguais e, para facilitar as vendas, o dono dessa papelaria decidiu fazer pacotinhos, todos com a mesma quantidade de borrachas. Ao fazer isso, notou que era possível colocar 3 ou 4 ou 5 borrachas em cada pacotinho e, assim, não sobraria borracha alguma na caixa. O menor número de borrachas que essa caixa poderia conter era:
(A) 80.
(B) 65.
(C) 60.
(D) 70.
(E) 75.
Resolução
A questão fala de uma caixa com várias borrachas, onde o vendedor consegue dividir em caixas com 3, 4 ou 5 borrachas.
Estamos tratando de mmc (mínimo múltiplo comum), ou seja, a quantidade de borrachas pode ser dividida por 3, 4 ou 5 e tem que ser a menor possível.
Como não existem fatores primos em comum, o mmc(3, 4, 5) = 3.4.5 = 60
Alternativa C
13) (SAP SP) Uma pizzaria funciona todos os dias da semana e sempre tem promoções para seus clientes. A cada 4 dias, o cliente tem desconto na compra da pizza de calabresa; a cada 3 dias, na compra de duas pizzas, ganha uma mini pizza doce, e uma vez por semana tem a promoção de refrigerantes. Se hoje estão as três promoções vigentes, esse ocorrido voltará a acontecer daqui a quantas semanas?
(A) 40.
(B) 12.
(C) 84.
(D) 22.
(E) 7.
Resolução
Veja que os descontos acontecem a cada, 4, 3 e 7 dias.
Hoje é o dia da coincidência. Queremos saber quando acontecerá novamente.
Na verdade estamos querendo saber qual o menor múltiplo comum de 4, 3 e 7, ou seja, o mmc e 4, 3 e 7, que é 84.
Para descobrirmos a semana, obviamente basta dividir por 7:
84/7 = 12
14) (Detran SP – Vunesp) Uma coleção de miniaturas de brinquedos é formada por 328 carrinhos, 256 motos e 192 caminhões. Os brinquedos serão organizados em grupos com a mesma quantidade, de modo que cada grupo seja formado pelo mesmo tipo de miniatura. Desejando-se que cada grupo tenha o maior número possível de miniaturas, então o número de brinquedos em cada grupo e a quantidade de grupos formados com motos são, respectivamente,
(A) 6 e 67.
(B) 8 e 41.
(C) 6 e 53.
(D) 8 e 32.
(E) 6 e 41.
Resolução
A questão está pedindo para dividirmos os números 328, 256 e 192 pelo mesmo número e que seja maior número possível.
Perceba que é justamente a definição de MDC (máximo divisor comum).
Sabendo que MDC(328, 256, 192) = 8, temos:
328/8 = 41 grupos com 8 carrinhos cada
256/8 = 32 grupos com 8 motos cada
192/8 = 24 grupos com 8 caminhões cada
Alternativa D
15) Qual é o MDC entre os números (15,16,17)?
(A) 10
(B) 5
(C) 2
(D) 1
(E) 15
Resolução
Como estamos trabalhando com três números consecutivos, sabemos que o MDC entre ele é sempre igual a 1.
Alternativa D
16) Em um jogo para duas ou mais pessoas, existem 36 peças triangulares e 60 peças quadradas. Sabendo que, para jogar esse jogo, as peças precisam ser igualmente distribuídas e não pode sobrar nenhuma delas, qual é o máximo de participantes possíveis no jogo?
(A) 12
(B) 9
(C) 8
(D) 6
(E) 4
Resolução
Queremos encontrar o MDC entre 36 e 60.
Fatorando 36 e 60, temos que:
36 = 2 · 2 · 3 · 3
60 = 2 · 2 · 3 · 5
MDC (36,60) 2 · 2 · 3 = 12
Alternativa A
17) (Enem) Um arquiteto está reformando uma casa. De modo a contribuir com o meio ambiente, decide reaproveitar tábuas de madeira retiradas da casa. Ele dispõe de 40 tábuas de 540 cm, 30 de 810 cm e 10 de 1 080 cm, todas de mesma largura e espessura. Ele pediu a um carpinteiro que cortasse as tábuas em pedaços de mesmo comprimento, sem deixar sobras, e de modo que as novas peças ficassem com o maior tamanho possível, mas de comprimento menor que 2 m.
Atendendo o pedido do arquiteto, o carpinteiro deverá produzir
(A) 105 peças.
(B) 120 peças.
(C) 210 peças.
(D) 243 peças.
(E) 420 peças.
Resolucao
Como é pedido que as peças tenham o mesmo comprimento e o maior tamanho possível, vamos calcular o mdc (máximo divisor comum).
Vamos calcular o mdc entre 540, 810 e 1080: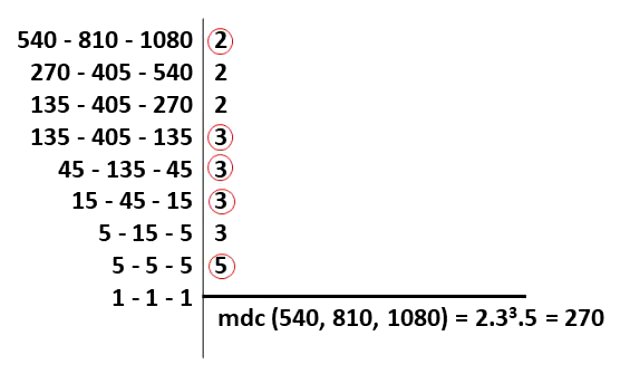
Entretanto, o valor encontrado não poderá ser usado, pois existe a restrição do comprimento ser menor que 2 m.
Assim, vamos dividir 2,7 por 2, pois o valor encontrado também será um divisor comum de 540, 810 e 1080, visto que o 2 é o menor fator primo em comum desses números.
Então, o comprimento de cada peça será igual a 1,35 m (2,7 : 2). Agora, precisamos calcular quantas peças teremos de cada tábua. Para isso, faremos:
5,40 : 1,35 = 4 peças
8,10 : 1,35 = 6 peças
10,80 : 1,35 = 8 peças
Considerando a quantidade de cada tábua e somando, temos:
40 . 4 + 30 . 6 + 10 . 8 = 160 + 180 + 80 = 420 peças
Alternativa E
18) (Enem) O gerente de um cinema fornece anualmente ingressos gratuitos para escolas. Este ano serão distribuídos 400 ingressos para uma sessão vespertina e 320 ingressos para uma sessão noturna de um mesmo filme. Várias escolas podem ser escolhidas para receberem ingressos. Há alguns critérios para a distribuição dos ingressos: cada escola deverá receber ingressos para uma única sessão;
todas as escolas contempladas deverão receber o mesmo número de ingressos;
não haverá sobra de ingressos (ou seja, todos os ingressos serão distribuídos).
O número mínimo de escolas que podem ser escolhidas para obter ingressos, segundo os critérios estabelecidos, é
(A) 2.
(B) 4.
(C) 9.
(D) 40.
(E) 80.
Resolucao
Para descobrir o número mínimo de escolas, precisamos conhecer o número máximo de ingressos que cada escola poderá receber, considerando que este número deverá ser igual nas duas sessões.
Desta maneira, iremos calcular o mdc entre 400 e 320:
O valor do mdc encontrado representa o maior número de ingressos que cada escola irá receber, de modo que não haja sobras.
Para calcular o número mínimo de escolas que podem ser escolhidas, devemos ainda dividir a quantidade de ingressos de cada sessão pelo número de ingressos que cada escola receberá, assim temos:
400 : 80 = 5
320 : 80 = 4
Portanto, o número mínimo de escolas será igual a 9 (5 + 4).
Alternativa C
19) (EPCAR) Um agricultor fará uma plantação de feijão em canteiro retilíneo. Para isso, começou a marcar os locais onde plantaria as sementes. A figura abaixo indica os pontos já marcados pelo agricultor e as distâncias, em cm, entre eles.
Esse agricultor, depois, marcou outros pontos entre os já existentes, de modo que a distância d entre todos eles fosse a mesma e a maior possível. Se x representa o número de vezes que a distância d foi obtida pelo agricultor, então x é um número divisível por
(A) 4
(B) 5
(C) 6
(D) 7
Resolucao
Para resolver a questão, precisamos encontrar um número que divide ao mesmo tempo os números apresentados. Como é pedido que a distância seja a maior possível, vamos calcular o mdc entre eles.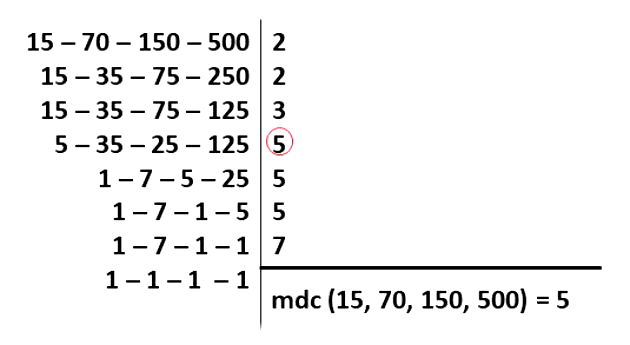
Desta forma, a distância entre cada ponto será igual a 5 cm.
Para encontrar o número de vezes que essa distância foi repetida, vamos dividir cada segmento original por 5 e somar os valores encontrados:
15 : 5 = 3
70 : 5 = 14
150 : 5 = 30
500 : 5 = 100
x = 3 + 14 + 30 + 100 = 147
O número encontrado é divisível por 7, pois 21.7 = 147
Alternativa D
20) Calcule o MMC e o MDC dos numeros 18 e 60
Resolucao
Primeiramente, vamos calcular o Mínimo Múltiplo Comum (MMC) entre 18 e 60 pela decomposição simultânea dos dois números. Sempre dividindo os números pelo menor número primo possível:
18, 60 | 2
9, 30 | 2
9, 15 | 3
3, 5 | 3
1, 5 | 5
1, 1 |
Vamos multiplicar todos os números que ficaram à direita: 2 x 2 x 3 x 3 x 5 = 180. Portanto, MMC (18, 60) = 180.
18, 60 | 2
9, 30 | 2
9, 15 | 3
3, 5 | 3
1, 5 | 5
1, 1 |
Mas desses números à direita, os únicos que dividem o 18 e o 60, simultaneamente, são os números destacados: 2 e 3. Multiplicando-os, encontramos o resultado 6. Logo, o MDC (18, 60) = 6.
21) Calcule o MMC e o MDC dos numeros 210 e 462
Resolucao
Vamos calcular o MMC (210, 462) através da decomposição simultânea dos dois números:
210, 462 | 2
105, 231 | 3
35, 77 | 5
7, 77 | 7
1, 11 | 11
1, 1 |
Basta multiplicar todos os números que ficaram à direita : 2 . 3 . 5 . 7 x 11 = 2.310. Portanto, MMC (210, 462) = 2.310.
210, 462 | 2
105, 231 | 3
35, 77 | 5
7, 77 | 7
1, 11 | 11
1, 1 |
Para encontrarmos o MDC, procuramos à direita os números que dividiram o 210 e o 462 simultaneamente, 2, 3 e 7. Multiplicando-os, encontramos o resultado 42. O MDC (210, 462) = 42.
22) (Fuvest – SP) No alto da torre de uma emissora de televisão, duas luzes “piscam” com frequências diferentes. A primeira “pisca” 15 vezes por minuto e a segunda “pisca” 10 vezes por minuto. Se num certo instante, as luzes piscam simultaneamente, após quantos segundos elas voltarão a “piscar simultaneamente”?
(A) 12
(B) 10
(C) 20
(D) 15
(E) 30
Resolucao
Como o exercício nos questiona “após quantos segundos elas voltarão a 'piscar simultaneamente'”, precisamos converter as informações dadas para medidas de “segundos”. Portanto, se a primeira torre “pisca” 15 vezes por minuto, sabendo que um minuto equivale a 60 segundos, podemos fazer 60 : 15 = 4, pois as luzes da primeira piscam de 4 em 4 segundos. Equivalentemente, os cálculos para a segunda torre são 60 : 10 = 6, o que nos indica que as luzes da segunda torre piscam de 6 em 6 segundos.
4, 6 | 2
2, 3 | 2
1, 3| 3
1, 1 | 3 . 2 . 2 = 12
Multiplicando os números que dividem o 4 e o 6, temos 2 x 1 x 3 = 12. Portanto, MMC (4,6) = 12.
Alternativa A
23) (Mackenzie – SP) Nas últimas eleições, três partidos políticos tiveram direito, por dia, a 90s, 108s e 144s de tempo gratuito de propaganda na televisão, com diferentes números de aparições. O tempo de cada aparição, para todos os partidos, foi sempre o mesmo e o maior possível. A soma do número das aparições diárias dos partidos na TV foi de:
Resolucao
Para resolver essa questão, precisamos recorrer à ideia do Máximo Divisor Comum, pois queremos que o tempo de cada aparição seja o maior possível.
Façamos então a fatoração simultânea dos tempos de aparição de cada político:
90, 108, 144 | 2
45, 54, 72 | 2
45, 27, 36 | 2
45, 27, 18 | 2
45, 27, 9 | 3
15, 9, 3 | 3
5, 3, 1 | 3
5, 1, 1 | 5
1, 1, 1 |
Já que estamos procurando o MDC, vamos procurar aqueles números que dividiram os três números ao mesmo tempo. Fazendo a multiplicação deles, temos: 2 x 3 x 3 = 18.
Encontramos o tempo de aparição de cada político, 18 segundos. Precisamos agora descobrir quantas aparições cada um deles realizou. Vejamos:
90: 18 = 5 aparições
108/18 = 6 aparições
144 : 18 = 8 aparições
Somando as aparições de cada um, encontramos 5 + 6 + 8 = 19 aparições.
24) José possui um supermercado e pretende organizar de 100 a 150 detergentes, de três marcas distintas, na prateleira de produtos de limpeza, agrupando-os de 12 em 12, de 15 em 15 ou de 20 em 20, mas sempre restando um. Quantos detergentes José tem em seu supermercado?
Resolucao
Se José arruma os detergentes em grupos de múltiplos de 12, 15 ou 20, e sobra 1, vamos então encontrar o mínimo múltiplo comum entre esses números e adicionaremos 1 ao resultado. Vejamos:
12, 15, 20 | 2
6 , 15 , 10 | 2
3 , 15 , 5 | 3
1 , 5 , 5 | 5
1 , 1 , 1 |
Temos que multiplicar os números que apareceram à direita: 2 x 2 x 3 x 5 = 60. Todos os múltiplos de 60 serão também múltiplos comuns a 12, 15 e 20. Vejamos os múltiplos de 60:
M(60) = {0, 60, 120, 180, 240, ...}
Você pode observar que o único dos múltiplos de 60 que se encaixa na quantidade de detergentes do supermercado de José é o 120. Mas falta ainda acrescentarmos aquele detergente que sempre restava, portanto, podemos concluir que no supermercado de José havia 121 detergentes.
Continuacao...





