Professor Diminoi
RAZÃO E PROPORÇÃO
Razão e proporção são utilizadas em situações que envolvem grandezas. Razão é a comparação entre dois números por meio de uma fração; proporção, a igualdade entre duas razões.
A proporção é a igualdade entre duas razões.
Razão e proporção são conceitos utilizados para resolver situações-problema do nosso cotidiano. Conhecemos como razão a comparação entre dois números por meio de um quociente. Sabendo o que é razão, definimos como proporção a igualdade entre duas razões, ou seja, são razões que possuem o mesmo resultado.
Existem grandezas que são formadas pela razão de outras duas grandezas, como a densidade, que é:
A razão entre a massa e o volume; a velocidade, que é a razão entre distância e tempo; entre outras.
Já a proporção é constantemente utilizada em receitas, produção, regra de três, entre outras situações.
A propriedade fundamental da proporção é que o produto dos extremos é igual ao produto dos meios.
Resumo sobre razão e proporção
- A razão é a comparação entre dois números por meio de uma fração.
- A proporção é a igualdade de duas razões.
- Existem propriedades importantes na proporção.
- Utilizamos razão e proporção para resolver situações-problema cotidianas.
O que é razão?
A razão é uma comparação entre dois números por meio de uma divisão. Podemos expressar a razão como uma fração ou até mesmo como o quociente desses dois números.
Exemplo:
Neste caso, temos a razão entre a e b. Exemplo:
Exemplo:
Em uma empresa de produção de parafusos, foram produzidos 90 parafusos, sendo que 6 deles são defeituosos. Qual a razão entre a quantidade de parafusos defeituosos e o total de parafusos produzidos?
Resolução:
Montando a razão, temos que:![]() Isso significa que temos 6 parafusos defeituosos em um total de 90 parafusos. Podemos simplificar a razão, dividindo o numerador por 6 e o denominador por 6.
Isso significa que temos 6 parafusos defeituosos em um total de 90 parafusos. Podemos simplificar a razão, dividindo o numerador por 6 e o denominador por 6.![]() Essa razão diz que 1 a cada 15 parafusos produzidos é defeituoso.
Essa razão diz que 1 a cada 15 parafusos produzidos é defeituoso.
Existem alguns casos de razão entre grandezas que geram novas grandezas
Exemplo:
- Densidade é a razão entre a massa e o volume.
- Velocidade é a razão entre a distância e o tempo.
- Probabilidade é a razão entre o número de elementos do conjunto evento e o número de elementos no conjunto universo.
- Consumo do automóvel é a razão entre a distância e o volume de combustível gasto.
- Densidade demográfica é a razão entre a área e o número de habitantes.
O que é proporção?
A proporção é uma comparação entre duas ou mais quantidades ou medidas que indica como essas grandezas se relacionam entre si. Duas grandezas podem ou não se relacionar de forma proporcional.
Quando se relacionam de forma proporcional, essas grandezas podem ser diretamente proporcionais ou inversamente proporcionais. A proporção é utilizada para calcular valores desconhecidos por meio da igualdade de razões.
Podemos destacar 4 propriedades da proporção:
1ª propriedade da proporção
A propriedade fundamental da proporção diz que, dada a igualdade de duas razões, o produto dos meios é sempre igual ao produto dos extremos, o que nos permite multiplicar cruzado em uma igualdade de frações:
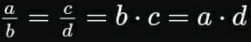
2ª propriedade da proporção
Dadas duas razões proporcionais, a soma entre os numeradores e denominadores dessas frações também gerará uma nova razão proporcional às duas anteriores.
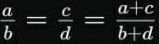
3ª propriedade da proporção
Dadas duas razões proporcionais, a diferença entre os numeradores e denominadores dessas frações também gerará uma nova razão proporcional às duas anteriores.

4ª propriedade da proporção
A adição do numerador com o denominador dividida pelo valor do numerador da primeira proporção é equivalente à adição do numerador com o denominador dividida pelo valor do numerador da segunda proporção.

Como se calcula razão e proporção?
Para calcular o valor desconhecido de uma grandeza utilizando razão e proporção, utilizamos as propriedades da proporção, principalmente a propriedade fundamental da proporção, que foi a primeira propriedade apresentada.
QUESTÕES DE RAZÃO E PROPORÇÃO
01) Represente a razão entre 2 e 4 na forma fracionária, decimal e percentual.
Resolução:
Para determinar a forma fracionária, 2 e 4, basta realizar a divisão do numerador pelo denominador.
2/4
Simplificando a fração temos:
1/2
Representação decimal da razão dos números 2 e 4, basta efetuar a divisão
2 ÷ 4 = 0,5
Representando a razão dos números 2 e 4 na forma percentual, temos que efetuar a divisão e multiplicar por 100.
0,5 · 100 = 50%
02) Determine o valor de x sabendo que:
9 = x
3 27
Resolução:
3x = 9 . 29
3x = 243
x = 243
3
x = 81
03) Verifique se os números 2, 3, 10 e 15 são proporcionais nessa ordem.
Resolução:
Para isso, devemos montar a razão entre esses números e, em seguida, multiplicar cruzado. Se encontrarmos uma igualdade verdadeira, então eles serão proporcionais, caso contrário, eles não serão proporcionais.
2 = 10
3 15
Multiplicando em “cruz” tem
2 . 15 = 3 . 10
30 = 30
Os números 2, 3 10 e 15 são proporcionais.
04) (UEPB — Adaptada) A razão entre a massa de uma pessoa na Terra e sua massa em Netuno é 5/7. Dessa forma, se uma pessoa tem uma massa de 60 kg na Terra, qual sua massa em Netuno?
(A) 45 kg
(B) 54 kg
(C) 67 kg
(D) 74 kg
(E) 84 kg
Resolução:
De acordo com o texto, tem-se a seguinte proporção:
5 = 60
7 x
5x = 7 . 60
5x = 420
x = 420
5
x = 84
05) Qual o valor de x na proporção abaixo?
1 = 12
3 x
Resolução:
3 . 12 = x
x = 36
06) Para fazer 250 mL de café, são necessários 8g de pó de café. Caso uma pessoa queira fazer 875 mL, a quantidade de pó de café necessária é de quanto?
Resolução:
Sendo x a quantidade de pó de café em gramas necessária para fazer 875 mL de café, temos que:
250 = 875
8 x
Multiplicando cruzado:
250x = 875 . 8
250x = 7000
x = 7000
250
x = 28
Então são necessários 28 gramas.
07) (ENEM) Uma mãe recorreu à bula para verificar a dosagem de um remédio que precisava dar a seu filho. Na bula, recomendava-se a seguinte dosagem: 5 gotas para cada 2 kg de massa corporal a cada 8 horas.
Se a mãe ministrou corretamente 30 gotas do remédio a seu filho a cada 8 horas, então a massa corporal dele é de:
(A) 12 kg
(B) 16 kg
(C) 24 kg
(D) 36 kg
(E) 75 kg
Resolução:
Sabemos que
5 = 30
2 x
Então temos que:
5x = 2 . 30
5x = 60
x = 60
5
x = 12
Alternativa A
08) (ENEM) Cerca de 20 milhões de brasileiros vivem na região coberta pela Caatinga, em quase 800 mil km² de área. Quando não chove, o homem do Sertão e sua família precisam caminhar quilômetros em busca da água dos açudes. A irregularidade climática é um dos fatores que mais interferem na vida do sertanejo.
Segundo este levantamento, a densidade demográfica da região coberta pela Caatinga, em habitantes por km², é de:
(A) 250
(B) 25
(C) 2,5
(D) 0,25
(E) 0,025
Resolução:
Calculando a razão:
20 000 000 = 25
800 000
Alternativa: B
09) Para melhorar os processos administrativos dentro de uma empresa, foi feita uma pesquisa com os 5 funcionários do setor para averiguar a produtividade de cada um deles.
Funcionário I → 25 processos em 6 dias
Funcionário II → 18 processos em 4 dias
Funcionário III → 20 processos em 5 dias
Funcionário IV → 14 processos em 3 dias
Funcionário V → 22 processos em 5 dias
Supondo que a produtividade desses funcionários continue a mesma, o funcionário menos produtivo desse setor é:
(A) I
(B) II
(C) III
(D) IV
(E) V
Resolução:
Para analisar a produtividade de cada funcionário, calcularemos a razão entre o número de processos e o número de dias:
Funcionário I → 25 : 6 = 4,166...
Funcionário II → 18 : 4 = 6
Funcionário III → 20 : 5 = 4
Funcionário IV → 14 : 3 = 4,66...
Funcionário V → 22 : 5 = 4,4
O menos produtivo é o funcionário III.
Alternativa: C
10) Em uma loja, há 2300 vendedores e 46 supervisores. A razão entre o número de vendedores e o número de supervisores é igual a:
(A) 1 supervisor a cada 46 vendedores
(B) 46 supervisores a cada 50 vendedores
(C) 50 supervisores para cada vendedor
(D) 1 supervisor para cada 50 vendedores
Resolução:
Calculando a razão, temos que 2300 : 46 = 50, logo, há 1 supervisor para cada 50 vendedores.
Alternativa: D
11) Duas cidades A e B estão a uma distância de 204 km. Para sair da cidade A, ir até a cidade B e voltar novamente para a cidade A, foram necessários 48 litros de combustível. Então o desempenho desse veículo foi de:
(A) 4,25 km/L
(B) 6,50 km/L
(C) 7,00 km/L
(D) 7,75 km/L
(E) 8,50 km/L
Resolução:
O consumo do veículo é a razão entre a distância percorrida e o volume de combustível necessário. Note que ele foi e voltou da cidade A até a cidade B, então, foram 204 + 204 = 408 km rodados. Dessa forma, calcularemos a razão entre 408 e 48.
408 : 48 = 8,5 km/L
Alternativa: E
12) Em uma fábrica de parafusos, é comum que, em meio à produção, alguns parafusos saiam defeituosos. Nessa fábrica há 4 máquinas, e a que tem pior desempenho será substituída. Sabendo que o tempo gasto para a produção foi o mesmo, retirou-se uma amostra de produção de cada máquina.
Máquina 1 → produziu 1200 parafusos, sendo 15 defeituosos.
Máquina 2 → produziu 1020 parafusos, sendo 12 defeituosos.
Máquina 3 → produziu 900 parafusos, sendo 9 defeituosos.
Máquina 4 → produziu 612 parafusos, sendo 6 defeituosos.
Analisando a produção das máquinas, a que será substituída será a:
(A) máquina 1
(B) máquina 2
(C) máquina 3
(D) máquina 4
Resolução:
Calcularemos a razão entre a quantidade de parafusos produzidos e a quantidade de parafusos defeituosos, o que nos dará a quantidade de parafusos produzidos para que se tenha 1 parafuso defeituoso.
Máquina 1 → 1200 : 15 = 80
Máquina 2 → 1020 : 12 = 85
Máquina 3 → 900 : 9 = 100
Máquina 4 → 612 : 6 = 102
A máquina que tem pior desempenho é a 1, pois, a cada 80 parafusos produzidos, 1 é defeituoso.
Alternativa: A
13) O desempenho de um técnico de futebol é de 15 vitórias em 25 jogos. Então, a razão entre o número de partidas perdidas e o número de partidas disputadas é:
(A) 2/5
(B) 3/5
(C) 4/5
(D) 5/3
(E) 5/4
Resolução:
Se houve 15 vitórias, então houve 25 – 15 = 10 derrotas. A razão entre o número de derrotas e o total de partiras é 10/25.
Note que é possível realizar a simplificação dividindo por 5 tanto o numerador quanto o denominador, resultando na fração 2/5.
Alternativa: A
14) (ENEM) O esporte de alta competição da atualidade produziu uma questão ainda sem resposta: qual é o limite do corpo humano? O maratonista original, o grego da lenda, morreu de fadiga por ter corrido 42 quilômetros. O americano Dean Karnazes, cruzando sozinho as planícies da Califórnia, conseguiu correr dez vezes mais em 75 horas.
Um professor de Educação Física, ao discutir com a turma o texto sobre a capacidade do maratonista americano, desenhou na lousa uma pista reta de 60 centímetros, que representaria o percurso referido.
Se o percurso de Dean Karnazes fosse também em uma pista reta, qual seria a escala entre a pista feita pelo professor e a percorrida pelo atleta?
(A) 1:700
(B) 1:7 000
(C) 1:70 000
(D) 1:700 000
(E) 1:7 000 000
Resolução:
Sabemos que o atleta percorreu uma distância 10 vezes maior que 42 km, logo, ele percorreu 420 km. Sabendo que 420 km = 42 000 000 cm e construindo a razão, temos que:
60 ÷ 42 000 000
Note que é possível simplificar a divisão por 60, então teremos a seguinte escala:
1 ÷ 700 000
Alternativa: D
15) (ENEM) Cerca de 20 milhões de brasileiros vivem na região coberta pela caatinga, em quase 800 mil km2 de área. Quando não chove, o homem do sertão e sua família precisam caminhar quilômetros em busca da água dos açudes. A irregularidade climática é um dos fatores que mais interferem na vida do sertanejo.
Segundo este levantamento, a densidade demográfica da região coberta pela caatinga, em habitantes por km², é de:
(A) 250
(B) 25
(C) 2,5
(D) 0,25
(E) 0,025
Resolução:
Para encontrar a densidade demográfica, vamos dividir a área pelo total de pessoas, ou seja, 20 000 000 por 800.000:
20 000 000 ÷ 800.000 = 25 habitantes por km²
Alternativa: B
16) (ENEM) No monte de Cerro Armazones, no deserto de Atacama, no Chile, ficará o maior telescópio da superfície terrestre, o Telescópio Europeu Extremamente Grande (E-ELT). O E-ELT terá um espelho primário de 42 m de diâmetros, “maior olho do mundo voltado para o céu”.
Ao ler esse texto em uma sala de aula, uma professora fez uma suposição de que o diâmetro do olho humano mede aproximadamente 2,1 cm.
Qual a razão entre o diâmetro aproximado do olho humano, suposto pela professora, e o diâmetro do espelho primário do telescópio citado?
(A) 1:20
(B) 1:100
(C) 1:200
(D) 1:1 000
(E) 1:2 000
Resolução:
Sabemos que 42 metros equivalem a 4200 cm, então:
2,1 : 4200
Dividindo por 2,1 dos dois lados, temos que a escala será de:
1:2000
Alternativa: E
17) (ENEM) Em um certo teatro, as poltronas são divididas em setores. A figura apresenta a vista do setor 3 desse teatro, no qual as cadeiras escuras estão reservadas e as claras não foram vendidas. A razão que representa a quantidade de cadeiras reservadas do setor 3 em relação ao total de cadeiras desse mesmo setor é
A razão que representa a quantidade de cadeiras reservadas do setor 3 em relação ao total de cadeiras desse mesmo setor é
(A) 17/70.
(B) 17/53.
(C) 53/70.
(D) 53/17.
(E) 70/17.
Resolução:
Há 17 cadeiras ocupadas entre as 70 cadeiras do setor, logo, calculando a razão entre o número de cadeiras ocupadas e o total de cadeiras, faremos 17/70.
Alternativa: A
18) (Unisinos-RS) Sabendo que a distância entre duas cidades num mapa, na escala 1 : 1 600 000, é de 8 cm, qual é a distância real entre elas?
(A) 2 km
(B) 12,8 km
(C) 20 km
(D) 128 km
(E) 200 km
Resolução:
Do enunciado temos a escala 1 : 1 600 000, ou seja, cada 1 centímetro no mapa corresponde a 1 600 000 centímetros na realidade. Interpretando tal escala como sendo a razão entre 1 e 1 600 000, devemos determinar a media real de uma distância de 8 centímetros no mapa, logo:
1/1600 000 = 8/d
1d = 8 . 1 600 000
d = 12 800 000cm
Alternativa: D
19) A razão entre a idade de duas pessoas é de 12 para 11. Sabe-se que a soma das idades é 115, determine a idade de cada uma dessas pessoas.
Resolução:
Como desconhecemos a idade das duas pessoas, vamos nomeá-las a e b. Como a razão entre essas idades é de 12 para 11, podemos montar uma proporção:
a/b = 12/11
11a = 12b
Sabemos que a soma das idades é 115, logo:
a + b = 115
a = 115 – b
Substituindo o valor de a na primeira equação, teremos:
11 . a = 12 . b
11 · (115 – b) = 12 . b
1 . 265 – 11b = 12b
1.265 = 12b + 11b
1 . 265 = 23b
b = 1.265 ÷ 23
b = 55
Como a = 115 – b, então:
a = 115 – 55
a = 60
Portanto, essas pessoas possuem, respectivamente, 60 anos e 55 anos.
20) (ENEM) A taxa de urbanização de um município é dada pela razão entre a população urbana e a população total do município (isto é, a soma das populações rural e urbana).
Os gráficos apresentam, respectivamente, a população urbana e a população rural de cinco municípios (I, II, III, IV, V) de uma mesma região estadual. Em reunião entre o governo do estado e os prefeitos desses municípios, ficou acordado que o município com maior taxa de urbanização receberá um investimento extra em infraestrutura.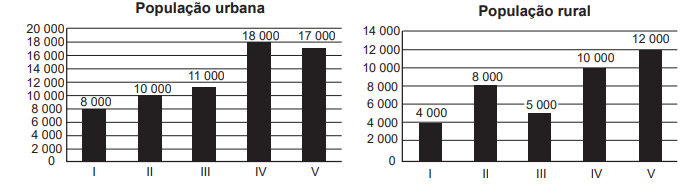 Segundo o acordo, qual município receberá o investimento extra?
Segundo o acordo, qual município receberá o investimento extra?
(A) I.
(B) II.
(C) III.
(D) IV.
(E) V.
Resolução
Como a taxa de urbanização de um município é a razão entre a população urbana e a população total do município, há as seguintes taxas de urbanização:
Logo, o município III é o que possui a maior taxa de urbanização e, consequentemente, é o que receberá o investimento extra.
Alternativa: C.





