EF II - EQUACAO DO 2º GRAU

Professor Diminoi
EQUACAO DO 2º GRAU

O que é uma equação do 2º grau?
Denomina-se equação do 2º grau na incógnita x, toda equação da forma:
ax2 + bx + c = 0; a, b, c    IR e (a diferente de 0)

Exemplos:
a) x² - 5x + 6 = 0(é um equação do 2º grau)
a = 1
b = -5
c = 6.

b) 6x²- x - 1 = 0(é um equação do 2º grau)
a = 6
b = -1
c = -1.

c) 7x²- x = 0 (é um equação do 2º grau com)
a = 7
b = -1 
c = 0.

d) x²- 36 = 0(é um equação do 2º grau)
a = 1
b = 0
c = -36.

Nas equações escritas na forma ax² + bx + c = 0 (forma normal ou forma reduzida de uma equação do 2º grau na  incógnita x) chamamos a, b e c de coeficientes.
a  = o coeficiente de  x²
b  =  o coeficiente de x,
c  = o coeficiente ou termo independente.

Equações completas e incompletas
Uma equação do 2º grau é completa quando b e c são diferentes de zero.

Exemplos:
a) x² - 9x+ 20 = 0
b) -x² + 10x- 16 = 0

Observação (a) e (b) Ambas são equações completas.
Uma equação do 2º grau é incompleta quando b ou c é igual a zero, ou ainda quando ambos são iguais a zero.

Exemplos
a) x² – 36 =0
(b = 0)

b) x² – 10 = 0
(c = 0)

c) 4x² = 0
(b = c = 0)

Raízes de uma equação do 2º grau
Resolver uma equação do 2º grau significa determinar suas raízes.
Raiz é o número real que, ao substituir a incógnita de uma equação, transforma-a numa sentença verdadeira.

O conjunto formado pelas raízes de uma equação denomina-se conjunto verdade ou conjunto solução.

Exemplos
a) Dentre os elementos do conjuntos A= {-1, 0, 1, 2}, quais são raízes da equação x² - x- 2 = 0?
Resolucao
Substituímos a incógnita x da equação por cada um dos elementos do conjunto e verificamos quais as sentenças verdadeiras.
Para x = -1
(-1)² - (-1) - 2 = 0
1 + 1 - 2 = 0
0 = 0
(V)
Para x = 0
0² - 0 - 2 = 0
0 - 0 -2 = 0
-2 = 0
(F)
Para x = 1
1² - 1 - 2 = 0
1 - 1 - 2 = 0
- 2 = 0
(F)
Para x = 2
2² - 2 - 2 = 0
4 - 2 - 2 = 0
0 = 0
(V)
Logo, -1 e 2 são raízes da equação.

b) Determine psabendo que 2 é raiz da equação (2p- 1) x² - 2px - 2 = 0.
Resolucao
Substituindo a incógnita  x por 2, determinamos o valor de p.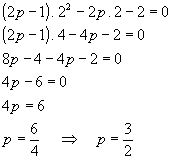


 

 

 

 

Logo, o valor de p é
Resolução de equações incompletas
Resolver uma equação significa determinar o seu conjunto verdade. Na resolução de uma equação incompleta, utilizamos as técnicas da fatoração e duas importantes propriedades dos números reais:
1ª Propriedade:  
2ª Propriedade: 

1º Caso: equação do tipo ax² + bx = 0.

Exemplo:
Determine as raízes da equação 
x² – 8x = 0
sendo U = R
Resolucao
Inicialmente, colocamos x em evidência:
x.(x – 8) = 0
Para o produto ser igual a zero, basta que um dos fatores também o seja.
Assim:
x = 0
ou
x – 8 = 0
x = 8
Obtemos dessa maneira duas raízes que formam o conjunto verdade:
 V = (0, 8)
De modo geral, a equação do tipo ax² + bx = 0  tem para soluções x = 0 e
2º Caso: equação do tipo ax² + c = 0 
Exemplos:
Determine as raízes da equação 2x² – 72 = 0, sendo U = IR.
Resolucao
De modo geral, a equação do tipo ax² + c = 0 possui duas raízes reais. 
Se for um número positivo, não tendo raiz real caso

Seja um número negativo.

Resolução de equações completas
Para solucionar equações completas do 2º grau utilizaremos a fórmula de Bhaskara. A partir da equação ax² + bx + c = 0, em que a, b, c     IR e (a diferente de 0), desenvolveremos passo a passo a dedução da fórmula de Bhaskara (ou fórmula resolutiva).

1º passo: multiplicaremos ambos os membros por 4ª
(4a).(ax² + bx + c) = 0.(4a)
4a²x² + 4abx = 0

2º passo: passar 4ac par o 2º membro. 

4a²x² + 4abx = - 4ac

3º passo: adicionar  aos dois membros.
4º passo: fatorar o 1º elemento. 
(2ax + b)² = b² – 4ac

5º passo: extrair a raiz quadrada dois membros.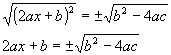

6º passo: passar b para o 2º membro.

7º passo: dividir os dois membros por 2a (a diferente 0)
Assim, encontramos a fórmula resolutiva da equação do 2º grau:
Podemos representar as duas raízes reais por x' e x", assim: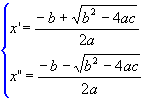


 

 

 
Exemplos:
Resolva a equação: 7x² + 13X – 2 = 0 .
Valores dos termos a, b e c.
a = 7
b = 13
c = -2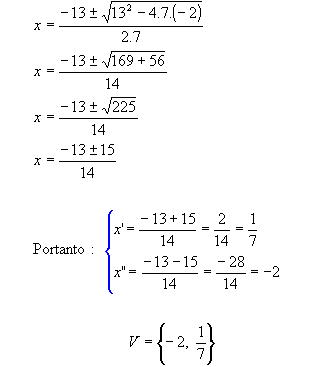

Discriminante
Denominamos discriminante o radical b²-4ac que é representado pela letra grega
(delta).
Podemos agora escrever deste modo a fórmula de Bhaskara:
De acordo com o discriminante, temos três casos a considerar:

1º caso: o discriminante é positivo 
O valor de  é real e a equação tem duas raízes reais diferentes, assim representadas:
Exemplo:
Para quais valores de k a equação x² - 2x + k- 2 = 0 admite raízes reais e desiguais?
Resolucao
Para que a equação admita raízes reais e desiguais, devemos ter

Logo, os valores de k devem ser menores que 3.

2º caso: o discriminante é nulo
O valor de  é nulo e a equação tem duas raízes reais e iguais, assim representadas:
Exemplo:
Determine o valor de p, para que a equação x² - (p - 1) x + p-2 = 0 possua raízes iguais.
Resolucao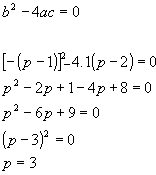
Para que a equação admita raízes iguais, é necessário que
Logo, o valor de p é 3.

3º caso: o discriminante é negativo

O valor de  não existe em IR, não existindo portanto raízes reais.
As raízes da equação são número complexos.
Exemplo:
Para quais valores de m a equação 3x² + 6x + m = 0 não admite nenhuma raiz real?
Resolucao
Para que a equação não tenha raiz real, devemos ter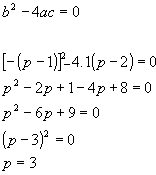 
Logo, os valores de m devem ser maiores que 3.

Resumo
Dada a equação ax² + bx + c = 0,  temos:
Com (a equação tem duas raízes reais diferentes)
Com  (a equação tem duas raízes reais iguais)
Com  (a equação não tem raízes reais)

Equações literais
As equações do 2º grau na variável x que possuem alguns coeficientes ou alguns termos independentes indicados por outras letras são denominadas equações literais.
As letras que aparecem em uma equação literal, excluindo a incógnita, são denominadas parâmetros.

Exemplos:
ax²+ bx + c = 0                        incógnita: x     parâmetros:a, b, c
ax² - (2a + 1) x + 5 = 0            incógnita: x     parâmetro: a

Equações literais incompletas
A resolução de equações literais incompletas segue o mesmo processo das equações numéricas. Observe os exemplos:
Resolva a equação literal incompleta 3x² - 12m² = 0, sendo x a variável.
Resolucao
3x² - 12m² = 0
3x² = 12m²
x² = 4m²
x= 
Logo, temos:
V = (-2m + 2m)
Resolva a equação literal incompleta my² - 2aby = 0, com m 0, sendo y a variável.
Resolucao
my² - 2aby = 0
y(my - 2ab) = 0
Temos, portanto, duas soluções:
y = 0
ou
my - 2ab = 0
my = 2ab
y = 

Assim: 
Na solução do último exemplo, teríamos cometido um erro grave se tivéssemos assim resolvido:
my² - 2aby= 0
my² =  2aby
my = 2ab
Desta maneira, obteríamos apenas a solução

O zero da outra solução foi "perdido" quando dividimos ambos os termos por y.
Esta é uma boa razão para termos muito cuidado com os cancelamentos, evitando desta maneira a divisão por zero, que é um absurdo.

Equações literais completas
As equações literais completas podem ser também resolvidas pela fórmula de Bhaskara.

Exemplo
Resolva a equação: x² - 2abx - 3a²b², sendo x a variável.
Resolucao
Temos 
a = 1
b = - 2ab
c = - 3a²b²
Portanto: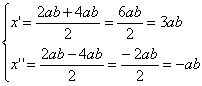

Assim, temos: V= { - ab, 3ab}

Relações entre os coeficientes e as raízes
Considere a equação ax² + bx + c = 0, com a  0 e sejam x'e x'' as raízes reais dessa equação.
Logo: 
Observe as seguintes relações:
Soma das raízes (S)

Produto das raízes (P)               
Como 

temos:


Denominamos essas relações de relações de Girard. Verifique alguns exemplos de aplicação dessas relações.

Exemplo
Determine a soma e o produto das raízes da equação 10x²  + x - 2 = 0. 
Resolucao
Nesta equação, temos:
A = 10
b = 1
c = - 2
A soma das raízes é igual a.

O produto das raízes é igual a

Assim:

 Assim:


Exemplo
Determine o valor de k na equação x² + ( 2k - 3)x + 2 = 0, de modo que a soma de suas raízes seja igual a 7.
Resolucao
Nesta equação, temos:
a = 1
b = 2k
c = 2
S = x₁ + x₂ = 7

Logo, o valor de k é -2.

Composição de uma equação do 2º grau, conhecidas as raízes
Considere a equação do 2º grau ax² + bx + c = 0 
Dividindo todos os termos por a 

Obtemos:
Como

podemos escrever a equação desta maneira.
x² – Sx + P = 0

Exemplos:
Componha a equação do 2º grau cujas raízes são -2 e 7.
Resolucao
A soma das raízes corresponde a:
S= x₁ + x₂ = -2 + 7 = 5
O produto das raízes corresponde a:
P= x₁ . x₂ = ( -2) . 7 = -14
A equação do 2º grau é dada por x² - Sx + P = 0, onde S = 5 e P = -14.
Logo, x² - 5x - 14 = 0 é a equação procurada.
Formar a equação do 2º grau, de coeficientes racionais, sabendo-se que uma das raízes é 
Resolucao:
Se uma equação do 2º grau, de coeficientes racionais, tem uma raiz,  A outra raiz será
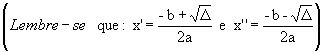Portanto;
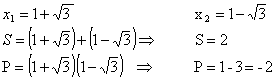Logo, x² - 2x - 2 = 0 é a equação procurada.

Forma fatorada
Considere a equação ax² + bx + c = 0. 
Colocando a em evidência, obtemos: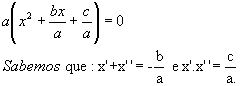


 

Então, podemos escrever: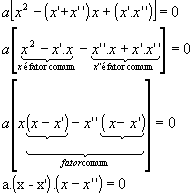


Logo, a forma fatorada da equação ax² + bx + c = 0 é:
a.(x – x`) . (x –x”) = 0

Exemplos:
Escreva na forma fatorada a equação x² - 5x + 6 = 0.
esolucao
alculando as raízes da equação x² - 5x + 6 = 0, obtemos x₁ = 2 e x₂ = 3.
Sendo
a = 1
x₁ = 2
x₂= 3, a forma fatorada de x² - 5x + 6 = 0 pode ser assim escrita: (x-2).(x-3) = 0

Exemplo
Escreva na forma fatorada a equação 2x² - 20x + 50 = 0.
Resolucao
Calculando as raízes da equação 2x² - 20x + 50 = 0, obtemos duas raízes reais e iguais a 5.
Sendo a= 2,
x₁ = x₂ = 5, a forma fatorada de 2x² - 20x + 50 = 0 pode ser assim escrita:

2.(x - 5) (x - 5) = 0 
ou
(x - 5)²= 0
Escreva na forma fatorada a equação x² + 2x + 2 = 0.
Resolucao
Como o
A equação não possui raízes reais.
Logo, essa equação não possui forma fatorada em IR.

Equações biquadradas
Observe as equações:
a) x⁴- 13x²+ 36 = 0
b) 9x⁴- 13x²+ 4 = 0
c) x⁴- 5x² + 6 = 0
Note que os primeiros membros são polinômios do 4º grau na variável x, possuindo um termo em x⁴, um termo em x² e um termo constante.
Os segundos membros são nulos.
Denominamos essas equações de equações biquadradas.
Ou seja, equação biquadrada com uma variável x é toda equação da forma:
ax⁴ + bx² + c = 0
Exemplos:
a) x⁴- 5x²+ 4 = 0
b) x⁴- 8x²= 0
c) 3x⁴- 27 = 0

Tome muito cuidado!
As equações abaixo não são biquadradas, pois em uma equação biquadrada a variável x só possui expoentes pares.
a) x⁴- 2x³+ x² + 1 = 0
b) 6x⁴ + 2x³ - 2x = 0
c) x⁴ - 3x = 0

Resolução de uma equação biquadrada
Na resolução de uma equação biquadrada em IR, devemos substituir sua variável, transformando-a numa equação do 2º grau.
Observe agora o procedimento que deve ser utilizado.

Sequência prática:
1- Substitua x⁴ por y² (ou qualquer outra incógnita elevada ao quadrado) e x² por y.
2- Resolva a equação ay² + by + c = 0.
3 - Determine a raiz quadrada de cada uma da raízes ( y'e y'') da equação ay² + by + c = 0.
Essas duas relações indicam-nos que cada raiz positiva da equação ay² + by + c = 0 dá origem a duas raízes simétricas para a biquadrada: a raiz negativa não dá origem a nenhuma raiz real para a mesma.

Exemplos
a) Determine as raízes da equação biquadrada x⁴- 13 x²+ 36 = 0.
Resolucao
Substituindo x⁴ por y² e x² por y,
temos:
y² - 13y + 36 = 0
Resolvendo essa equação, obtemos:
y' = 4     e      y'' = 9
Como x²= y, temos: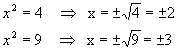
Logo, temos para conjunto verdade:
V = { -3, -2, 2, 3}.

b) Determine as raízes da equação biquadrada x⁴+ 4x²- 60 = 0.
Resolucao
Substituindo x⁴ por y² e x² por y,
Temos:
y² + 4y - 60 = 0
Resolvendo essa equação, obtemos:
y' = 6   e  y' '= -10
Como x² = y, temos: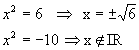
Logo, temos para o conjunto verdade:
c) Determine a soma das raízes da equação
Resolucao
Utilizamos o seguinte artifício:
Assim:
y² - 3y = -2
y² - 3y + 2 = 0
y' = 1  e  y' '= 2

Substituindo y, determinamos: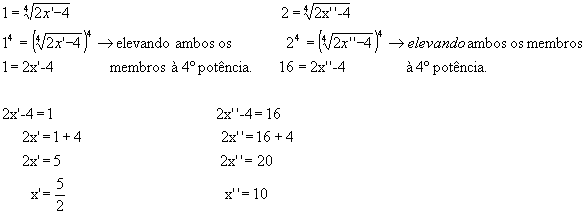

Logo, a soma das raízes é dada por:
Resolução de equações da forma: ax²ⁿ  +  bxⁿ  + c = 0
Esse tipo de equação pode ser resolvida da mesma forma que a biquadrada. Para isso, substituimos xⁿ por y, obtendo:
ay² + by + c = 0, que é uma equação do 2º grau.
Exemplo:
Resolva a equação x⁶ + 117x³ - 1.000 = 0.
Resolucao
Fazendo x³ = y, temos:
y² + 117y - 1.000 = 0
Resolvendo a equação, obtemos:
y'= 8  e  y''= - 125
Então: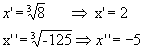
Logo, V = {-5, 2 }.

Composição da equação biquadrada
Toda equação biquadrada de raízes reais x₁, x₂, x₃ e x₄ pode ser composta pela fórmula:
(x – x₁) . (x – x₂) . (x – x₃) . (x – x₄) = 0
Exemplo
Compor a equação biquadrada cujas raízes são
Resolucao de a
(x – 0) . (x – 0) . (x + 7) . (x – 7) = 0
x²(x² – 49) = 0
x⁴ – 49x² = 0
Resolucao de b
(x + a) . (x – a) . (x + b) . (x – b) = 0
(x² – a²) . (x² – b²) = 0
x⁴ – (a² + b²) x² + a²b² = 0

Propriedades das raízes da da equação biquadrada
Consideremos a equação ax⁴ + bx² + c = 0, cujas raízes são x₁, x₂, x₃ e x₄ e a equação do 2º grau
ay² + by + c = 0, cujas raízes são y' e y''
De cada raiz da equação do 2º grau, obtemos duas raízes simétricas para a biquadrada.
Assim: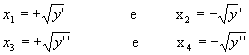
Do exposto, podemos estabelecer as seguintes propriedades:
1ª propriedade: a soma das raízes reais da equação biquadrada é nula.
X₁ + x₂ + x₃ + x₄ = 0

2ª propriedade: a soma dos quadrados das raízes reais da equação biquadrada é igual a

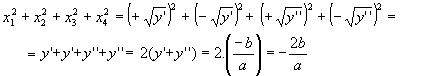
3ª propriedade: o produto das raízes reais e não-nulas da equação biquadrada é igual a

Equações irracionais
Considere as seguintes equações:

Observe que todas elas apresentam variável ou incógnita no radicando. Essas equações são irracionais. 
Ou seja:     
Equação irracional é toda equação que tem variável no radicando. 

Resolução de uma equação irracional
A resolução de uma equação irracional deve ser efetuada procurando transformá-la inicialmente numa equação racional, obtida ao elevarmos ambos os membros da equação a uma potência conveniente.
Em seguida, resolvemos a equação racional encontrada e, finalmente, verificamos se as raízes da equação racional obtidas podem ou não ser aceitas como raízes da equação irracional dada (verificar a igualdade).
É necessária essa verificação, pois, ao elevarmos os dois membros de uma equação a uma potência, podem aparecer na equação obtida raízes estranhas à equação dada. Observe alguns exemplos de resolução de equações irracionais no conjunto dos reais.
a) 
Resolucao

Logo, V= {58}.

b) 
Resolucao

Logo, V= { -3}; note que 2 é uma raiz estranha a essa equação irracional.

c) 
Resolucao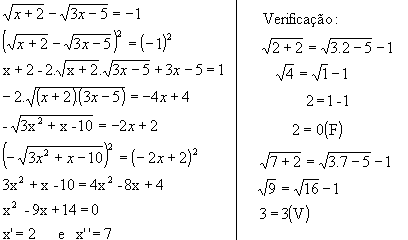

Logo, V= { 7 }; note que 2 é uma raiz estranha a essa equação irracional.

d) 
Resolucao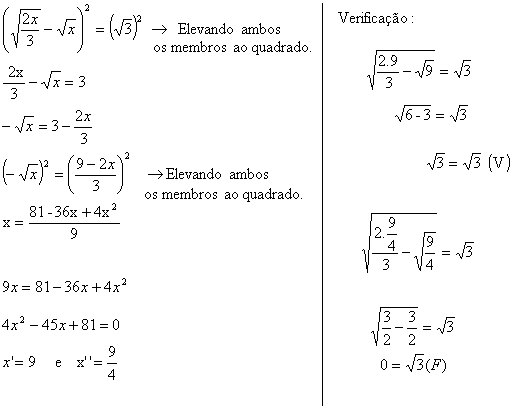

Logo, V = {9}; note que 9/4 é uma raiz estranha a essa equação irracional.

Sistemas de equações do 2º grau
Observe o seguinte problema:
Uma quadra de tênis tem a forma da figura, com perímetro de 64 m e área de 192 m².
Determine as medidas x e y indicadas na figura.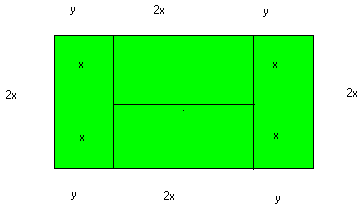
Resolucao
De acordo com os dados, podemos escrever:
Perímetro: 8x + 4y = 64
Área: 2x . ( 2x + 2y) = 192    4x² + 4xy = 192
Simplificando, obtemos:
2x + y = 16        (1)
x² +xy = 48       (2)
Temos aí um sistema de equações do 2º grau, pois uma das equações é do 2º grau.
Podemos resolvê-lo pelo método da substituição:
Assim:    2x + y = 16       (1)
                   y = 16 - 2x
Substituindo y em (2), temos:
x² + x ( 16 - 2x) = 48
x ² + 16x - 2x² = 48
- x²  + 16x - 48 = 0 
Multiplicando ambos os membros por -1.
x² - 16x + 48 = 0
x'=4       e        x''=12
Determinando y para cada um dos valores de x, obtemos:
y' = 16 - 2 . 4 = 8
y'' = 16 - 2 . 12 = - 8
As soluções  do sistema são os pares ordenados (4,8) e ( 12, -8). Desprezando o par ordenado que possui ordenada negativa, teremos para dimensões da quadra:
Comprimento = 2x + 2y = 2.4 + 2.8 = 24m
Largura = 2x = 2. 4 = 8m
Verifique agora a solução deste outro sistema: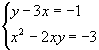

Isolando y na primeira equação:
y - 3x = -1   y = 3x - 1
Substituindo na segunda:
x²  - 2x(3x - 1)  = -3
x² - 6x² + 2x    = -3   
-5x² + 2x + 3    = 0     Multiplicando ambos os membros por -1.
5x² - 2x - 3     = 0
x'=1       e    x''= 3/-5
Determinando y para cada um dos valores de x, obtemos: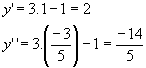

As soluções do sistema são os pares ordenados ( 1, 2) e
Logo, temos para conjunto verdade:

Problemas do 2º grau
Para resolução de problemas do 2º grau, devemos seguir etapas:

Sequência prática:
1- Estabeleça a equação ou sistema de equações que traduzem o problema para a linguagem matemática.
2- Resolva a equação ou o sistema de equações.
3- Interprete as raízes encontradas, verificando se são compatíveis com os dados do problema.
Observe agora, a resolução de alguns problemas do 2º grau:

a) Determine dois números inteiros consecutivos tais que a soma de seus inversos seja 13/41
Resolucao
Representamos um número por x, e por x + 1 o seu consecutivo. Os seus inversos serão representados por
Temos então a equação:
Resolvendo-a: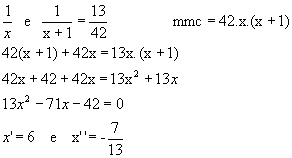


b) Observe que a raiz -7/13não é utilizada, pois não se trata de número inteiro.
Resposta:
Os números pedidos são, portanto, 6 e o seu consecutivo 7.

c) Um número de dois algarismos é tal que, trocando-se a ordem dos seus algarismos, obtém-se um número que o excede de 27 unidades. Determine esse número, sabendo-se que o produto dos valores absolutos dos algarismos é 18.
Resolucao
Representamos um número por 10x + y, e o número com a ordem dos algarismos trocada por 10y + x.
Observe:
Número
10x + y
Número com a ordem dos algarismos trocada:
10y + x.
Temos, então, o sistema de equações:

Resolvendo o sistema, temos: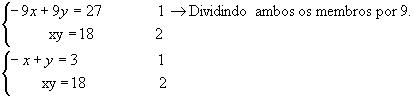

Isolando y na primeira equação:
-x + y = 3    y= x + 3
Substituindo y na segunda equação:
xy   =  18
x ( x + 3) = 18
x² + 3x = 18
x² + 3x - 18   =   0
x' = 3  e  x''  -6
Determinando y para cada um dos valores de x, obtemos:
y' = 3 + 3 = 6
y'' = -6 + 3 = -3
Logo, o conjunto verdade do sistema é dado por: V= { (3,6), ( -6, -3)}.

Desprezando o par ordenado de coordenadas negativas, temos para solução do problema o número 36 ( x = 3  e y = 6).
Resposta: O número procurado é 36.

Outros exemplos de problemas do 2º grau
a) Duas torneiras enchem um tanque em 6 horas. Sozinha, uma delas gasta 5 horas mais que a outra. Determine o tempo que uma delas leva para encher esse tanque isoladamente.
Resolucao
Consideremos x o tempo gasto para a 1ª torneira encher o tanque e x+5 o tempo gasto para a 2ª torneira encher o tanque.
Em uma hora, cada torneira enche a seguinte fração do tanque:
Em uma hora, as duas torneiras juntas encherão 1/6do tanque; observe a equação correspondente:
Resolvendo-a, temos:
6( x + 5 ) + 6x = x ( x + 5 )
6x + 30 + 6x = x² + 5x
x² - 7x - 30 = 0
x'= - 3      e   x''=10
Como a raiz negativa não é utilizada, teremos como solução x = 10.
Resposta: A 1ª torneira enche o tanque em 10 horas e a 2ª torneira, em 15 horas.

b) Num jantar de confraternização, seria distribuído, em partes iguais, um prêmio de R$ 24.000,00 entre os convidados. Como faltaram 5 pessoas, cada um dos presentes recebeu um acréscimo de R$ 400,00 no seu prêmio. Quantos pessoas estavam presentes nesse jantar?
Resolucao
Podemos representar por:

Resolvendo-a:

Resposta:  Nesse jantar deveriam estar presentes 20 pessoas. Como faltaram 5, então 15 pessoas estavam presentes no jantar.
 

Continua ...