Professor Diminoi DINÂMICA
DINÂMICA
É área de conhecimento da Física que estuda a causa dos movimentos, analisando-os e descrevendo-os de acordo com as forças que são responsáveis por produzi-los.
A dinâmica é, portanto, uma das áreas da mecânica, juntamente com a cinemática e a estática.
VAMOS ESTUDAR OS TEMAS ABAIXO:
- Leis de Newton,
- Energias mecânica,
- Energia Cinética
- Energia Mecânica
- Energia Potencial Gravitacional
- Leis de Hook
- Gravitação Universal
- Leis de Kepler
- Força Peso
- Força Resultante
- Trabalho de uma Força
- Força de Atrito
- Força Centrípeta
- Potência
- Rendimento
LEIS DE NEWTON
1ª Lei de Newton
A Primeira Lei de Newton é também chamada de "Lei da Inércia" ou "Princípio da Inércia". Inércia é a tendência dos corpos de permanecerem em repouso ou em movimento retilíneo uniforme (MRU).
Assim, para um corpo sair do seu estado de repouso ou de movimento retilíneo uniforme é necessário que uma força passe a atuar sobre ele.
Apesar de ser uma lei qualitativa, podemos esquematizá-la da seguinte forma:![]()
2ª Lei de Newton
A Segunda Lei de Newton é o "Princípio Fundamental da Dinâmica". Nesse estudo, Newton constatou que a força resultante (soma vetorial de todas as forças aplicadas) é diretamente proporcional ao produto da aceleração de um corpo pela sua massa: Δv = variação da velocidade (m/s)
Δv = variação da velocidade (m/s)
3ª Lei de Newton
A Terceira Lei de Newton é chamada de "Lei da Ação e Reação" ou "Princípio da Ação e Reação" no qual toda força de ação é correspondida por uma força de reação.
Dessa maneira, as forças de ação e reação, que atuam em pares, não se equilibram, uma vez que estão aplicadas em corpos diferentes.
Caso essas forças apresentam a mesma intensidade, mesma direção e sentidos opostos.
Temos:![]()
QUESTÕES RESOLVIDAS
01) (ENEM 2013) Uma pessoa necessita da força de atrito em seus pés para deslocar-se sobre uma superfície. Logo, uma pessoa que sobe uma rampa em linha reta será auxiliada pela força de atrito exercida pelo chão em seus pés.
Em relação ao movimento dessa pessoa, quais são a direção e o sentido da força de atrito mencionada no texto?
(A) Perpendicular ao plano e no mesmo sentido do movimento.
(B) Paralelo ao plano e no sentido contrário ao movimento.
(C) Paralelo ao plano e no mesmo sentido do movimento.
(D) Horizontal e no mesmo sentido do movimento.
(E) Vertical e no sentido para cima.
Resolução:
Para andarmos, empurramos o chão para trás. Por causa do atrito com o chão, somos empurrados para a frente. Logo, a força de atrito, nesse caso, tem a mesma direção e o mesmo sentido do movimento."
Alternativa: C
02) (PUC-RIO) A primeira Lei de Newton afirma que, se a soma de todas as forças atuando sobre o corpo for zero, o corpo …
(A) terá um movimento uniformemente variado
(B) apresentará velocidade constante
(C) apresentará velocidade constante em módulo, mas sua direção poderá ser alterada.
(D) será desacelerado
(E) apresentará um movimento circular uniforme.
Resolução:
De acordo com a primeira Lei de Newton, se a resultante das forças que atuam sobre um corpo for zero, ele permanecerá em repouso ou em movimento retilíneo uniforme, ou seja, com velocidade constante.
Alternativa: B
03) Um ônibus com passageiros viaja em trajetória retilínea. Ao se deparar com uma vaca que cruza repentinamente a estrada, o motorista freia bruscamente e as pessoas são "lançadas para frente". O que acontece é que as pessoas continuam em movimento em relação ao ônibus, agora parado. Este fenômeno acontece porque
(A) elas têm uma força resultante não nula que as impulsiona para frente.
(B) elas têm uma força de inércia que as mantém em movimento retilíneo uniforme.
(C)elas têm uma força de atrito com o ar que as empurra para frente.
(D) elas têm uma força de reação do ônibus que as lança para frente.
(E) elas têm uma tendência natural de resistir à mudança do seu estado de movimento devido à inércia.
Resolução:
Elas têm uma tendência natural de resistir à mudança do seu estado de movimento devido à inércia.
Conforme a primeira lei de Newton, os corpos possuem a tendência de manter suas trajetórias em movimento retilíneo uniforme devido sua inércia.
Alternativa: E
04) Relacione as três leis de Newton com os respectivos enunciados.
1ª lei de Newton
2ª lei de Newton
3ª lei de Newton
( ) parêntese esquerdo espaço espaço espaço espaço espaço espaço parêntese direito Determina que a força resultante é igual ao produto da massa pela aceleração do corpo.
( ) parêntese esquerdo espaço espaço espaço espaço espaço espaço parêntese direito Enuncia que a toda ação existe uma reação de mesma intensidade, mesma direção e sentido oposto.
( ) parêntese esquerdo espaço espaço espaço espaço espaço espaço parêntese direito Indica que um corpo tende a permanecer em seu estado de repouso ou em movimento retilíneo uniforme, a menos que uma força resultante passe a atuar sobre ele.
Resolução:
Lei da inércia (1ª lei de Newton): indica que um corpo tende a permanecer em seu estado de repouso ou em movimento retilíneo uniforme, a menos que uma força resultante passe a atuar sobre ele.
Lei fundamental da dinâmica (2ª lei de Newton): determina que a força resultante é igual ao produto da massa pela aceleração do corpo.
Lei da ação e reação (3ª lei de Newton): enuncia que a toda ação existe uma reação de mesma intensidade, mesma direção e sentido oposto.
Resposta: (2ª), (3ª) e (1ª)
05) Uma folha de massa igual 0,3 g cai de uma árvore com velocidade constante. Determine a força resultante sobre essa folha, sabendo que ela está sujeita à força de resistência do ar.
Dado: a aceleração da gravidade tem valor igual a 9,8 m/s².
Resolução:
Como a folha cai com velocidade constante, sua aceleração é igual a zero (a = 0).
Pela segunda lei de Newton, temos: Fr = m . a, logo nesse caso Fr = 0
06) Um bloco de massa 50 kg é empurrado sobre uma superfície horizontal por uma força F = 220 N. Sabendo que o coeficiente de atrito cinético (μc) entre o bloco e a superfície é igual a 0,2, calcule a aceleração sofrida pelo bloco.
Resolução:
A força de atrito (fat) pode ser calcula assim:
fat = μc . N
e N é a força normal que é igual ao seu peso, nesse caso: N = m . g
fat = μc . m . g
fat = 0,2 . 50 . 10
fat = 100 N
Pela segunda Lei de Newton, temos que Fr = m. A
Fr = F – fat
Fr = 220 – 100
Fr = 120 N
Agora substituímos esse valor em: Fr = m . a
120 = 50 . a
a = 2,4 m/s²
07) (Unespar-PR) Um corpo com massa de 5 kg é lançado sobre um plano horizontal liso, com velocidade de 40 m/s. Determine o módulo da intensidade da força que deve ser aplicada sobre o corpo contra o sentido do movimento, para pará-lo em 20 s.
(A) 200 N
(B) 20 N
(C) 10 N
(D) 40 N
(E) 8 N
Resolução:
Se essa força parar o corpo, sua velocidade será zero.
Podemos usar a função horária da velocidade para calcular o módulo da aceleração sofrida pelo corpo.
V = Vo + a . t
0 = 40 + 20 . a
a = - 40/20
a = - 2 m/s²
Em módulo a = 2 m/s²
Logo, a força necessária para isso será:
F = m . a
F = 5 . 2
F = 10 N
Alternativa: C
08) (PUC-MG) Um automóvel, com uma massa de 1200 kg, tem uma velocidade de 72 km/h quando os freios são acionados, provocando uma desaceleração constante e fazendo com que o carro pare em 10 s, a força aplicada ao carro pelos freios vale, em newtons:
(A) 3600
(B) 2400
(C) 1800
(D) 900
Resolução:
72 km/h : 3,6 = 20 m/s
V = Vo + a .t
0 = 20 + 10 a
a = - 2 m/s², e módulo: 2 m/s²
Fr = m . a
Fr =1200 . 2
Fr = 2400 N
Alternativa: B
09) (UFRJ) A figura abaixo mostra um sistema constituído por fios inextensíveis e duas roldanas, todos de massa desprezível. A roldana A é móvel, e a roldana B é fixa. Calcule o valor da massa m1 para que o sistema permaneça em equilíbrio estático.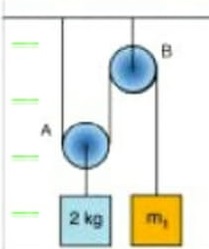 Resolução:
Resolução:
Como a roldana A é móvel, a força de tração que equilibra a força peso será dividida por dois. Assim, a força de tração em cada fio será metade da força peso. Portanto, a massa m1 deverá ser igual a metade de 2kg.
Assim m1 = 1 kg
10) (UERJ) No interior de um avião que se desloca horizontalmente em relação ao solo, com velocidade constante de 1000 km/h, um passageiro deixa cair um copo. Observe a ilustração abaixo, na qual estão indicados quatro pontos no piso do corredor do avião e a posição desse passageiro.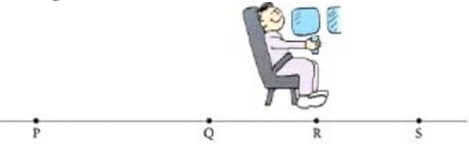 O copo, ao cair, atinge o piso do avião próximo ao ponto indicado pela seguinte letra:
O copo, ao cair, atinge o piso do avião próximo ao ponto indicado pela seguinte letra:
(A) P
(B) Q
(C) R
(D) S
Resolução:
Alternativa: C
ENERGIA CINÉTICA
Energia cinética é a quantidade de energia armazenada em qualquer corpo de massa m que se move com velocidade v, como se vê na fórmula a seguir:
Ec = mv2
2
Ec = energia cinética (J)
m = massa (kg)
v = velocidade (m/s)
QUESTÕES RESOLVIDAS
00) Determine o módulo da energia cinética associada ao movimento de um homem e sua motocicleta, cuja massa é igual a 350 kg e velocidade igual a 72 km/h.
(A) 75.000 J
(B) 150.000 J
(C) 10,5 J
(D) 70.000 J
Resolução:![]()
Alternativa: D
11) Se um corpo permanece deslocando-se em movimento uniforme, podemos afirmar que:
(A) há realização de trabalho sobre o corpo.
(B) sua energia cinética permanece constante.
(C) sua energia cinética aumenta de maneira uniforme.
(D) sua energia cinética aumenta de acordo com o quadrado de sua velocidade.
(E) sua energia cinética diminui de acordo com o quadrado de sua velocidade.
Resolução:
Se um corpo desenvolve um movimento uniforme, sua velocidade permanece constante, bem como sua energia cinética, uma vez que não há realização de trabalho sobre o corpo.
Alternativa: B
12) Uma partícula de massa m se desloca com velocidade v. A partir de certo instante, essa partícula passa a se mover com o dobro dessa velocidade. Em relação à energia cinética dessa partícula, assinale a alternativa correta.
(A) A energia cinética da partícula é reduzida a um quarto de seu valor original.
(B) A energia cinética da partícula é reduzida oito vezes.
(C) A energia cinética da partícula torna-se quatro vezes maior que seu valor original.
(D) A energia cinética da partícula não se altera.
(E) A energia cinética da partícula aumenta em oito vezes.
Resolução:
Para resolver esse exercício, é necessário lembrar que a energia cinética é uma grandeza proporcional ao quadrado da velocidade, portanto, reduzindo-se a velocidade à metade, a energia cinética será igual a um quarto de seu módulo original.
![]()
Alternativa: A
13) Determine qual é a velocidade em que se move um corpo de 20 kg cuja energia cinética é igual a 400 J.
(A) √5 m/s
(B) √10 m/s
(C) 2√10 m/s
(D) 4√2 m/s
Resolução:
Para responder ao exercício, vamos fazer uso da fórmula da energia cinética e substituir as informações fornecidas no enunciado; em seguida, para determinarmos a velocidade, vamos fatorar o número 40.
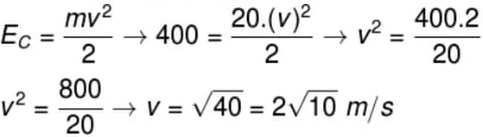
Alternativa: C
14) Assinale a alternativa que represente corretamente a energia cinética de um veículo de 1000 kg de massa que se move a uma velocidade constante de 3 m/s.
(A) 450 J
(B) 9000 J
(C) 4500 J
(D) 900 J
(E) 300 J
Resolução:
Para resolver a questão, basta usarmos a fórmula de energia cinética e substituir os dados informados no enunciado do exercício.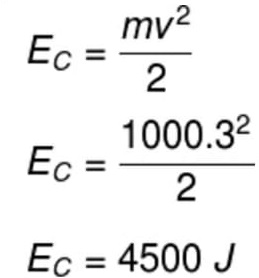
Alternativa: C
15) Sabe-se que a energia cinética de um corpo é de 2000 J e que a sua massa é de 10 kg. Determine a velocidade com que esse corpo se move e assinale a alternativa correta.
(A) 20 m/s
(B) 40 m/s
(C) 200 m/s
(D) 3 m/s
(E) 10 m/s
Resolução:
Para resolvermos o exercício, basta aplicarmos os dados informados na fórmula de energia cinética: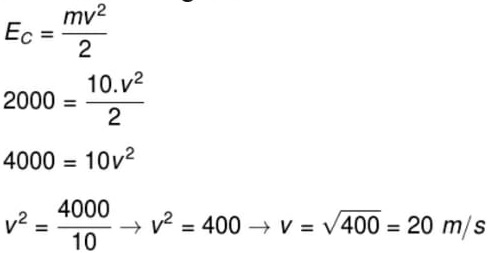
Alternativa: A
16) Um móvel apresenta energia cinética E e velocidade v. Em determinado instante, a velocidade desse móvel passa a ser 3v e sua massa permanece constante. A alternativa que apresenta a nova energia cinética desse móvel é:
(A) 3 E
(B) 9 E
(C) 4,5 E
(D) 10 E
(E) E/3
Resolução:
Como sabemos, a energia cinética depende do quadrado da velocidade, desse modo, quando a velocidade é triplicada, essa energia deve aumentar em um fator de nove vezes."
Alternativa: B
17) Um corpo que se desloca 1,0 m ao longo de uma superfície horizontal, sofrendo a ação de uma força de 100 N que forma um ângulo de 60º com essa direção. Determine o módulo do trabalho exercido por essa força sobre o bloco e assinale a alternativa correspondente.
Dados:
sen60º = √3/2
cos60º = 0,5
(A) 50√3 J
(B) 100√3 J
(C) 50 J
(D) 150 J
(E) 200 J
Resolução:![]()
Para calcularmos o módulo do trabalho exercido sobre o bloco pela força de 100N, é necessário utilizarmos a definição de trabalho, que é definida pela equação mostrada a seguir:
T = trabalho (J)
f = força (N)
d = distância (m)
α = ângulo entre F e d
Dessa forma, opós subtraímos os dados na fórmula, basta resolver o seguinte cálculo:![]()
Portanto, de acordo com o cálculo, o trabalho realizado por essa força fio de 50J
Alternativa: C
18) Sobre um objeto de 10 kg em repouso, é realizado um trabalho de 320 J. Determine o módulo da velocidade final desse objeto após a aplicação dessa força e assinale a alternativa correspondente.
(A) 10 m/s
(B) 2 m/s
(C) 4 m/s
(D) 8 m/s
(E) 15 m/s
Resolução:
Para calcularmos o módulo do trabalho exercido sobre o bloco pela força de 100 N, é necessário utilizarmos a definição de trabalho, que é definida pela equação mostrada a seguir:
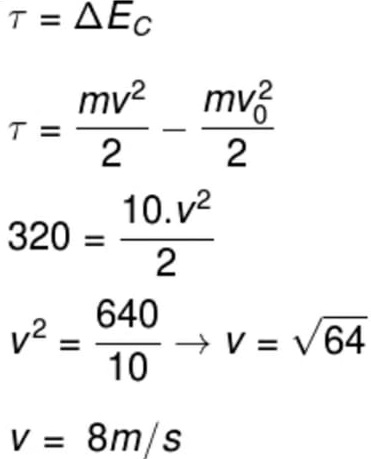
τ = Trabalho
F = Força
d = distância
θ = ângulo entre F e d
Dessa forma, após substituirmos os dados na fórmula, basta resolver o seguinte cálculo:
Portanto, de acordo com o cálculo, o trabalho realizado por essa força foi de 50 J.
Alternativa: C
19) Se o trabalho de uma força resultante sobre um corpo for positivo, podemos dizer que
(A) sua energia cinética permanece constante.
(B) sua energia potencial aumenta.
(C) sua energia cinética aumenta.
(D) sua velocidade diminui.
(E) sua aceleração diminui.
Resolução:
Quando o trabalho da força resultante é positivo, a energia cinética do corpo aumenta.
Alternativa: C
20) Em um movimento circular, a força centrípeta de 50 N forma um ângulo de 90º em relação ao deslocamento de um corpo que se move uma distância de 2,0 m. Assinale a alternativa que apresenta o módulo do trabalho exercido sobre esse corpo.
(A) 100 J
(B) 0 J
(C) 25 J
(D) -100 J
(E) -25 J
Resolução:
Para resolvermos esse exercício, precisamos nos lembrar da definição de trabalho:![]()
Para que o trabalho exercido pela força seja não-nulo, é necessário que o ângulo formado entre a força F e o deslocamento d seja diferente de 90º, dessa forma, a força centrípeta descrita no exercício não realiza trabalho sobre o corpo, já que o cosseno de 90º vale 0.
Alternativa: B
21) (Enem) Uma análise criteriosa do desempenho de Usain Bolt na quebra do recorde mundial dos 100 metros rasos mostrou que, apesar de ser o último dos corredores a reagir ao tiro e iniciar a corrida, seus primeiros 30 metros foram os mais velozes já feitos em um recorde mundial, cruzando essa marca em 3,78 segundos. Até se colocar com o corpo reto, foram 13 passadas, mostrando sua potência durante a aceleração, o momento mais importante da corrida. Ao final desse percurso, Bolt havia atingido a velocidade máxima de 12 m/s.
Supondo que a massa desse corredor seja igual a 90 kg, o trabalho total realizado nas 13 primeiras passadas é mais próximo de:
(A) 5,4.102 J
(B) 6,5.103 J
(C) 8,6.102 J
(D) 1,3.104 J
(E) 3,2.104 J
Resolução:
Vamos resolver o exercício por meio do teorema do trabalho e energia cinética, dessa forma, devemos fazer o seguinte cálculo: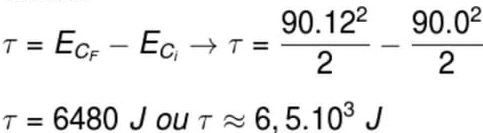
Alternativa: B
22) Um corpo de massa M e energia cinética E, move-se com velocidade V, reduzindo a velocidade desse corpo a um terço de seu valor original. Qual deverá ser a sua nova energia cinética E'?
(A) E/3
(B) E/9
(C) 9E
(D) 3E
(E) 16E
Resolução
Para resolver esse exercício, basta utilizarmos a fórmula de energia cinética, atribuindo à nova velocidade o valor v/3, observe:![]()
Alternativa: B
ENERGIA MECANICA
Energia mecânica diz respeito a toda energia relativa ao movimento de um corpo ou sistema de corpos. A energia mecânica é igual à soma da energia cinética com a energia potencial.
Em = EC + EP
EM = energia mecânica (J)
EC = energia cinética (J)
EP = energia potencial gravitacional (J)
QUESTÕES RESOLVIDAS
21) Um caminhão de 1500 kg desloca-se, a 10 m/s, sobre um viaduto de 10 m, construído acima de uma avenida movimentada. Determine o módulo da energia mecânica do caminhão em relação à avenida.
Dados: g = 10 m/s²
(A) 1,25.104 J
(B) 7,25.105 J
(C) 1,5105 J
(D) 2,25.105 J
(E) 9,3.103 J
Resolução:
Para calcularmos a energia mecânica do caminhão, somaremos a energia cinética com a energia potencial gravitacional, observe:
Com base no cálculo anterior, descobrimos que a energia mecânica desse caminhão em relação ao chão da avenida é igual a 2,25.105 J.
Alternativa: D
22) Uma caixa d'água cúbica, de 10.000 l, está preenchida até a metade de seu volume total e posicionada a 15 m de altura em relação ao solo. Determine a energia mecânica dessa caixa d'água.
(A) 7,5.105 J
(B) 1,5.105 J
(C) 1,5.106 J
(D) 7,5.103 J
(E) 5,0.102 J
Resolução:
Uma vez que a caixa d'água está preenchida até a metade de seu volume e sabendo que 1 l de água corresponde à massa de 1 kg, faremos o cálculo da energia mecânica da caixa d'água. Dessa forma, é importante perceber que, quando em repouso, a energia cinética do corpo é igual a 0, e, por isso, sua energia mecânica será igual à sua energia potencial.
Alternativa: A
23) A respeito da energia mecânica de um sistema conservativo, livre de forças dissipativas, assinale a alternativa correta:
(A) Na presença de atrito, ou de outras forças dissipativas, a energia mecânica de um corpo em movimento aumenta.
(B) A energia mecânica de um corpo que se move livre da ação de quaisquer forças dissipativas mantém-se constante.
(C) Para que a energia mecânica de um corpo permaneça constante, é necessário que, quando houver aumento de energia cinética, também haja aumento de energia potencial.
(D) A energia potencial é a parte da energia mecânica relacionada à velocidade com o que o corpo desloca-se.
(E) A energia cinética de um corpo que se move livre da ação de quaisquer forças dissipativas mantém-se constante.
Resolução:
Vamos analisar as alternativas:
a) FALSO – na presença de forças dissipativas, a energia mecânica diminui.
b) VERDADEIRO
c) FALSO – caso ocorra aumento da energia cinética, a energia potencial deverá diminuir, para que a energia mecânica permaneça constante.
d) FALSO – a energia cinética é a parte da energia mecânica relacionada ao movimento.
e) FALSO – nesse caso, a energia cinética sofrerá decréscimos por conta das forças dissipativas."
Alternativa: B
24) (UEM-Adaptada) Segue abaixo algumas questões que envolvem a energia mecânica e a conservação de energia. De tal modo, assinale a alternativa incorreta.
(A) Denomina-se energia cinética a energia que um corpo possui, por este estar em movimento.
(B) Pode-se denominar de energia potencial gravitacional a energia que um corpo possui por se situar a uma certa altura acima da superfície terrestre.
(C) A energia mecânica total de um corpo é conservada, mesmo com a ocorrência de atrito.
(D) A energia total do universo é sempre constante, podendo ser transformada de uma forma para outra; entretanto, não pode ser criada e nem destruída.
(E) Quando um corpo possui energia cinética, ele é capaz de realizar trabalho.
Resolução:
A energia mecânica total de um corpo é conservada, mesmo com a ocorrência de atrito.
Alternativa: C
25) (UFSM) Um ônibus de massa m anda por uma estrada de montanha e desce uma altura h. O motorista mantém os freios acionados, de modo que a velocidade é mantida constante em módulo durante todo o trajeto. Considerando as afirmativas a seguir, assinale se são verdadeiras (V) ou falsas (F).
( ) A variação da energia cinética do ônibus é nula.
( ) A energia mecânica do sistema ônibus-Terra se conserva, pois a velocidade do ônibus é constante.
( ) A energia total do sistema ônibus-Terra se conserva, embora parte da energia mecânica se transforme em energia interna.
A sequência correta é:
(A) V, V, F
(B) V, F, V
(C) F, F, V
(D) V, V, V
(E) F, F, V
Resolução:
V, F, V
Alternativa: B
26) (Enem) Os carrinhos de brinquedo podem ser de vários tipos. Dentre eles, há os movidos a corda, em que uma mola em seu interior é comprimida quando a criança puxa o carrinho para trás. Ao ser solto, o carrinho entra em movimento enquanto a mola volta à sua forma inicial. O processo de conversão de energia que ocorre no carrinho descrito também é verificado em:
(A) um dínamo.
(B) um freio de automóvel.
(C) um motor a combustão.
(D) uma usina hidroelétrica.
(E) uma atiradeira (estilingue).
Resolução:
Uma atiradeira (estilingue).
Alternativa: E
ENERGIA POTENCIAL GRAVITACIONAL
Energia potencial gravitacional diz respeito à quantidade de energia que é armazenada em um corpo de massa m, quando elevado a uma altura h a partir do solo, em uma região onde a aceleração da gravidade é igual a g.
EP = . m . g . h
Ep = energia potencial (J)
m = massa (kg)
g = aceleração da gravidade (m/s2)
h = altura (h)
QUESTÕES RESOLVIDAS
42) Um vaso de 2,0kg está pendurado a 1,2m de altura de uma mesa de 0,4m de altura. Sendo g = 10m/s², determine a energia potencial gravitacional do vaso em relação à mesa e ao solo.
Resolução:
m = 2kg
hvm = 1,2m
hms = 0,4m
hvs = hvm + hms = 1,6m
g = 10m/s²
A energia potencial gravitacional do vaso com relação à mesa.
Epg = m . g . hvm
Epg = 2.10.1,2 = 20.1,2 = 24J
A energia potencial gravitacional do vaso com relação ao solo.
Epg = m . g . hvs
Epg = 2.10.1,6 = 20.1,6 = 32J
43) (FUVEST – SP) No rótulo de uma lata de leite em pó lê-se “valor energético: 1509kj por 100g (361kcal)”. Se toda energia armazenada em uma lata contendo 400g de leite fosse utilizada para levantar um objeto de 10kg, a altura máxima atingida seria de aproximadamente (g = 10m/s²)
Resolução:
100g equivalem a 1509kJ
1509 . 4 = 6036kJ = 6036.10³J que equivalem a 400g
m = 10kg
g = 10m/s²
Como toda energia do leite será utilizada para elevar o objeto, podemos dizer que toda ela será convertida em energia potencial gravitacional.
Eleite = Epotencial
Eleite = m . g . h
6036.10³ = 10 . 10 . h
h = 6036.10
h = 60,36.10³m
h = 60,36km
44) Um bloco de massa igual a 1kg encontra-se preso sobre uma mola vertical que está deformada 10cm com relação à sua posição de equilíbrio. Após o bloco ser solto, ele é arremessado verticalmente para cima. Sendo o sistema livre de forças dissipativas e a constante elástica da mola equivalente à 50N/m, determine a altura máxima que o bloco alcançará em cm. (obs.: considere a massa da mola desprezível).
Resolução:
Quando o bloco atingir a altura máxima, toda energia potencial elástica terá sido convertida em energia potencial gravitacional.
Epel = Epg
K.x² = m.g.h
2
50.0,1² = 1.10.h
2
0,25 = 10.h
h = 0,25
10
h = 0,025m
h = 2,5cm
45) Calcule o módulo da energia potencial gravitacional de um corpo de massa igual a 4,0 kg que se encontra em uma altura de 50,0 cm em relação ao solo. Adote g = 10 m/s².
Resolução:
Para calcularmos o módulo da energia potencial gravitacional desse corpo, fazemos o seguinte cálculo:
Lembre-se de que é necessário que a altura esteja definida em metros (50,0 cm equivalem a 0,5 m).

46) Qual é o valor da massa de uma pedra que apresenta, em um dado instante, energia potencial gravitacional igual a 3500 J e se encontra a uma altura de 200,0 m em relação ao solo? Considere o valor da aceleração da gravidade igual a 10 m/s2
Resolução:
Epg = 3500 J
h = 200,0 m
g = 10 m/s2
Substituindo os valores em
Epg = m.g.h
3500 = m . 200.10
3500 / 2000 = m
m = 1,75 kg
48) Qual o valor da energia potencial gravitacional de um corpo de 120 kg posicionado a uma altura de 50 m acima do solo? Considere a aceleração da gravidade como 10ms2.
(A) 6 J
(B) 60 J
(C) 600 J
(D) 6000 J
(E) 60 000 J
Resolução:
Epg = m . g . h
Epg = 120 . 10 . 50
Epg = 60000J
Alternativa: E
49) (IFSP) Um atleta de salto com vara, durante sua corrida para transpor o obstáculo à sua frente, transforma a sua energia _____________ em energia ____________ por causa do ganho de altura e, consequentemente, ao/à _____________ de sua velocidade.
As lacunas do texto acima são, correta e respectivamente, preenchidas por:
(A) potencial – cinética – aumento
(B) térmica – potencial – diminuição
(C) cinética – potencial – diminuição
(D) cinética – térmica – aumento
(E) térmica – cinética – aumento
Resolução:
Nesse caso, a energia cinética se converte em energia potencial gravitacional."
Alternativa: C
LEI DE HOOKE
Força Elástica
A lei de Hooke é a equação matemática usada para determinar o sentido e calcular o módulo da força elástica que é produzida por molas caso elas estejam comprimidas ou esticadas.
Fel = k . x
Fel = força elástica (N)
k = constante elástica (N/m)
x = deformação da mola (m)
QUESTÕES RESOLVIDAS
27) Uma mola tem constante elástica k = 2,5kN/m. Quando ela for comprimida de 12cm, qual será a força elástica dela?
Resolução:
Pela lei de Hooke:
Fel = k .x
Fel = 2500 . 0,12
Fel = 300N
28) Determine o módulo da deformação sofrida por uma mola de constante elástica de 200 N/m, quando sujeita a uma força de 50 N.
(A) 10,0 m
(B) 0,50 m
(C) 0,25 m
(D) 0,10 m
Resolução:
Vamos utilizar a lei de Hooke para calcular a deformação sofrida por essa mola.
Com base no cálculo feito na figura acima, é possível perceber que a deformação sofrida pela mola é de 0,25 m.
Alternativa: C
29) Uma mola sofre uma deformação de 10 cm (0,1 m) quando comprimida por uma força de 200 N. Determine a constante elástica dessa mola.
(A) 50 N/m
(B) 20 N/m
(C) 2000 N/m
(D) 500 N/m
Resolução:
Vamos calcular a constante elástica da mola com a lei de Hooke.
Com base no resultado obtido, descobrimos que a constante elástica da mola é igual a 2000 N/m.
Alternativa: D
30) Uma mola de constante elástica de 500 N/m é pressionada por uma força de 50 N. Com base nessas informações, calcule qual deverá ser, em centímetros, a deformação sofrida pela mola em razão da aplicação dessa força.
(A) 100
(B) 15
(C) 0,1
(D) 10
Resolução:
Para calcular a deformação da mola, é necessário utilizar a lei de Hooke e substituir os dados fornecidos no enunciado do exercício. Observe:
Uma vez que o exercício pediu que determinássemos a deformação da mola em centímetros, após termos encontrado o resultado de 0,1 m, tivemos que multiplicá-lo por 100, uma vez que 1 metro tem 100 centímetros. Fazendo isso, descobrimos que a deformação foi de 10 cm.
Alternativa: D
31) (Unicamp) Assinale as afirmativas verdadeiras e as afirmativas falsas.
( ) As molas são distendidas uniformemente por forças que variam com a distância.
( ) A expressão da força que distende a mola de constante K é F = k . x, onde x é o alongamento da mola.
( ) A mola do item anterior reage sempre com força F′ = −k . x , onde x é o alongamento da mola.
( ) Os dinamômetros são equipamentos destinados a medir forças.
( ) Nos sistemas conservativos, a energia mecânica é conservada.
Resolução:
V – V – V – V – V
Todas as alternativas são verdadeiras.
Alternativa:
32) Uma mola com uma constante elástica que vale 250 N/cm é deformada em 5 cm , a partir disso, determine qual deve ser a força elástica aplicada sobre ela.
(A) 1,25 N
(B) 12 500 N
(C) 1250 N
(D) 125 N
(E) 12,5 N
Resolução:
Nesse caso, não há necessidade de converter a unidade de medida da elongação, já que a constante da mola também está em centímetros. Então, calcularemos a força elástica através da sua fórmula:
Fel = k . x
Fel = 250 . 5
Fel = 1250 N
Alternativa: C
33) Qual a força elástica sofrida por uma mola de constante elástica 100 N/m quando é comprimida em 10 cm ?
(A) 7 N
(B) 8 N
(C) 9 N
(D) 10 N
(E) 11 N
Resolução:
Primeiramente, converteremos a elongação de centímetro para metro:
10cm = 0,1m
Vamos calcular a força elástica através da sua fórmula:
Fel = k . x
Fel = 100 . 0,1
Fel = 10 N
Alternativa: D
34) Sabendo que, na Física, muitas vezes nomeamos equações, unidades de medida e leis para homenagear grandes físicos ainda que eles não as tenham desenvolvido, responda: quem foi o físico responsável pela fórmula da força elástica?
(A) Robert Hooke.
(B) Galileu Galilei.
(C) Giordano Bruno.
(D) Robert Boyle.
(E) Isaac Newton.
Resolução:
A fórmula da força elástica, também chamada de lei de Hooke, foi desenvolvida por Robert Hooke.
Alternativa: A
35) Quais proposições apresentam a unidade de medida correspondente à grandeza física estudada em força elástica?
I. A constante elástica é medida em Newton.
II. A força elástica é medida em Newton.
III. A elongação da mola é medida em Joule.
III. O trabalho da força elástica é medida em Joule.
IV. A aceleração é medida em metros por segundo.
(A) Alternativas I e II.
(B) Alternativas III e IV.
(C) Alternativas I e V.
(D) Alternativas II e III.
(E) Alternativas II e IV.
Resolução:
A constante elástica é medida em Newton. (falso)
A constante elástica é medida em Newton por metros.
A força elástica é medida em Newton.(verdadeiro)
III. A elongação da mola é medida em Joule. (falso)
A elongação da mola é medida em metros.
O trabalho da força elástica é medida em Joule.(verdadeiro)
A aceleração é medida em metros por segundo.(falso)
A aceleração é medida em metros por segundo ao quadrado.
Alternativa: E
ENERGIA POTENCIAL ELÁSTICA
A Energia potencial elástica é a forma de energia que é adquirida por corpos elásticos capazes de retornarem ao seu formato original após sofrerem algum tipo de deformação.
A energia potencial elástica depende da constante elástica do corpo, bem como do tamanho da deformação sofrida por ele.
E = kx2
2
E = Energia potencial elástica (J)
k = constante elástica (N/m)
x = deformação sofrida pela mola (m)
36) (FUND. CARLOS CHAGAS) Uma mola elástica ideal, submetida a ação de uma força de intensidade F = 10N, está deformada de 2,0 cm. A energia elástica armazenada na mola é de:
(A) 0,10J
(B) 0,20J
(C) 0,50J
(D) 1,0J
(E) 2,0J
Resolução:
F = 10 N
X = 2 cm = 0,02 m
Para calcular a energia potencial elástica, utilizamos a equação:
E = kx2
2
Como o exercício não forneceu o valor da constante elástica da mola (k), devemos utilizar a equação da força elástica (F = kx) e reescrever a equação da energia da seguinte forma:
E = F . x
2
Substituindo os dados, temos:
E = 10 . 0,02
2
E = 0,1 J
Alternativa: A
ENERGIA POTECIAL GRAVITACIONAL
Energia potencial gravitacional é uma grandeza escalar, medida em joules, que mensura a quantidade de energia atribuída a um corpo de certa massa que se encontre a uma determinada altura em relação ao chão. A fórmula utilizada para calculá-la é obtida a partir da lei da gravitação universal de Isaac Newton, por isso faz parte das equações usadas para descrever todos os tipos de interações gravitacionais.
E = m . g . h
E = Energia potencial gravitacional (J)
m = massa (kg)
h = altura (m)
g = aceleração da gravidade do local (m/s2)
37) Um corpo de massa de 6 kg está posicionado a uma altura de 30m. Calcule a energia potencial gravitacional desse corpo.
Resolução:
E = m . g . h
E = 6 . 10 . 30
E = 1800 J
38) (FATEC) Um bloco de massa 0,60kg é abandonado, a partir do repouso, no ponto A de uma pista no plano vertical. O ponto A está a 2,0m de altura da base da pista, onde está fixa uma mola de constante elástica 150 N/m. São desprezíveis os efeitos do atrito e adota-se g=10m/s². A máxima compressão da mola vale, em metros:
(A) 0,80
(B) 0,40
(C) 0,20
(D) 0,10
(E) 0,05
Resolução:
M = 0,60 Kg
HA = 2,0m
K = 150 N/m
g = 10 m/s2
A energia potencial gravitacional transforma-se em energia potencial elástica, portanto, elas são iguais e pode-se utilizar a expressão:
Epot = Eel
mgh = kx2
2
Substituindo os dados, temos:
0,6.10.2 = 150.x2
2
12 = 75x2
x2 = 12
75
x2 = 0,16
x = 0,4 m
Alternativa: B
39) Calcule a energia potencial elástica armazenada em uma mola, cuja constante elástica é 100 N/m, que está comprimida, apresentando uma deformação de 45 cm.
Resolução:
K = 100 N/m
X = 45 cm = 0,45 m
E = k . x2
2
E = (100 . 0,452)/2
E = 10,125 J
40) Uma mola de constante elástica igual a 200 N/m tem comprimento de 20 cm. Quando submetido a uma força externa, o comprimento dessa mola passa a ser de 15 cm. Determine o módulo da força elástica que é exercida pela mola, quando comprimida em 15 cm.
(A) 40 N/m
(B) 10 N/m
(C) 30 N/m
(D) 15 N/m
(E) 25 N/m
Resolução:
A deformação da mola é medida pela diferença entre o seu comprimento original e o seu tamanho quando sujeita a uma força externa. Nesse caso, a elongação da mola é de 5 cm ou 0,05 m. Com base nisso, vamos fazer os cálculos:
Fel = k . x
Fel = 200 . 0,05
Fel = 10 n/m
Alternativa: B
41) Quando comprimida por uma força de 4 N, uma mola tem o seu comprimento alterado em 1,6 cm (0,016 m). A constante elástica dessa mola, em N/m, vale cerca de:
(A) 6,4 N/m
(B) 500 N/m
(C) 250 N/m
(D) 256 N/m
(E) 12,8 N/m"
Resolução:
Aplicando o cálculo de acordo com a lei de Hooke:
Fel = k . x
4 = k . 0,016
k = 4/0,016
k = 250 n/m
Alternativa: C
GRAVITAÇÃO UNIVERSAL
É a área da dinâmica que estuda o movimento dos corpos celestes. Além da lei da gravitação universal, que é utilizada para calcular a força e atração que um corpo exerce sobre outro, há também as leis de Kepler, usadas para descrever as órbitas planetárias.
FORÇA GRAVITAÇÃO UNIVERSAL
Gravitação Universal
A gravitação universal é uma lei que permite calcular a força gravitacional exercida entre duas massas separadas com certa distância.
A Lei da Gravitação Universal estabelece que, se dois corpos possuem massa, eles sofrem a ação de uma força atrativa proporcional ao produto de suas massas e inversamente proporcional a sua distância.
Resumo sobre a Lei da Gravitação Universal
- Todos os corpos do universo atraem-se mutuamente com uma força proporcional ao produto de suas massas e inversamente proporcional ao quadrado de sua distância;
A Lei da Gravitação Universal é definida em termos da Constante de Gravitação Universal, cujo módulo é igual a G = 6,67408.10-11 N.m²/kg².
- A Lei da Gravitação Universal foi descoberta e desenvolvida pelo físico inglês Isaac Newton e foi capaz de prever os raios das órbitas de diversos astros, bem como explicar teoricamente a lei empírica descoberta por Johannes Kepler que relaciona o período orbital ao raio da órbita de dois corpos que se atraem gravitacionalmente.
Fórmula da Gravitação Universal
A principal fórmula utilizada na gravitação universal estabelece que o módulo da força gravitacional entre duas massas é proporcional ao produto de suas massas e inversamente proporcional ao quadrado da distância entre elas. A expressão utilizada para o cálculo da força gravitacional é esta:
|F| = GMn
d2
|F| = módulo da força de atração gravitacional (N)
G = constante de gravitação universal (6,67408.10-11 N.kg²/m²)
M = massa gravitacional ativa (kg)
m = massa gravitacional passiva (kg)
d = distância entre as massas (m)
A força peso, ou simplesmente o peso de um corpo sujeito a uma gravidade de módulo g, é dada por:
P = n . g
P = módulo da força peso (N)
m = massa gravitacional passiva (kg)
g = aceleração da gravidade local (m/s²)
QUESTÕES RESOLVIDAS
01) A Terra, por exemplo, possui massa de 5,972.1024 kg e raio médio de 6371 km (6,371.106 m), logo, podemos calcular o valor médio da gravidade na sua superfície:
Resolução:
g = GM
d2
g = (6,67408 . 10-11) . (5,975 . 1024)
(6, 371 . 106)2
g = 9,82 m/s2
Gravitação Universal e a Terceira Lei de Kepler
Um dos indicadores de sucesso da Lei da Gravitação Universal foi a sua capacidade de reproduzir a famosa relação matemática descoberta empiricamente por Johannes Kleper, conhecida como Lei Harmônica:
T2 = constante
R3
Para tanto, basta recordar que a força de atração gravitacional aponta sempre na direção que liga os dois corpos, tratando-se, portanto, de um tipo de força central, assim como a força centrípeta, que atua nos corpos em movimento circular. Assim:
F garv = F centr
GMm = mv2
d2 d
com v = ωd = 2π
T
Temos:
T2 = = 4π2
d3 GM
v = velocidade de translação do corpo (m/s – metros por segundo)
ω = velocidade angular (rad/s – radianos por segundo)
T = período de translação (s – segundos)
G = constante de gravitação universal (6,67408.10-11 N.kg²/m²)
QUESTÕES RESOLVIDAS
02) A lua é um satélite natural que orbita o planeta Terra pela ação da grande força gravitacional exercida pela gravidade terrestre. Sendo a massa da Terra igual a 5,972.1024 kg, a massa da lua 7,36.1022 kg e a distância média entre a Terra e a Lua igual a 384.400 km (3,84.108 m), determine:
Dados: G = 6,67408.10-11 N.m²/kg²
a) a força gravitacional que a Terra exerce sobre a Lua
b) a força gravitacional que a Lua exerce sobre a Terra
c) o módulo da aceleração adquirida pela Lua e pela Terra
Resolução
a) Para calcular a atração gravitacional que a Terra exerce sobre a Lua, usaremos a Lei da Gravitação Universal:
|F| = GMn
d2
F = (6,67408 . 10-11) .(5,957 . 1014) . (7,36 `1022)
(3,84 . 108)2
F = 29 . 1019 N
b) De acordo com a Terceira Lei de Newton, a Lei da Ação e Reação, se a Terra exerce uma força de ação sobre a Lua, esta deve exercer uma força atrativa sobre a Terra de mesmo módulo e direção, porém, no sentido oposto, logo, a força que a Lua faz sobre a Terra também é de 20.1019
Resolução
Terra = FR m . a
20 . 1019 = 5,072 . 1024 . a
a = 20 . 1019
5,972 . 1024
a = 3,35 . 10-5 m/s
c) Se nos lembrarmos da Segunda Lei de Newton, que nos diz que o módulo da força resultante sobre um corpo é igual ao produto de sua massa pela sua aceleração, podemos calcular a aceleração adquirida pela Lua e pela Terra facilmente.
Resolução:
Lua = FR m . a
20 . 1019 = 7,36 . 1022 . a
a = 20 . 1019
7,36 . 1022
a = 2,71 . 10-3 m/s
LEIS DE KEPLER
Leis de Kepler afirmam que as órbitas são elípticas, que a velocidade aureolar dos planetas é constante, e que a razão entre o cubo do período e o quadrado do raio é constante.
Leis de Kepler sobre o movimento planetário foram desenvolvidas entre 1609 e 1619 pelo astrônomo e matemático alemão Johannes. As três leis de Kepler, usadas para descrever as órbitas dos planetas do Sistema Solar, foram construídas com base em medidas astronômicas precisas, obtidas pelo astrônomo dinamarquês Tycho Brahe.
Introdução às leis de Kepler
A resolução dos problemas inexplicáveis pelo modelo planetário de Copérnico veio somente no século XVII, pelas mãos de Johannes Kepler. Para tanto, Kepler admitiu que as órbitas planetárias não eram perfeitamente circulares, mas sim elípticas. Por meio das leis de Kepler é possível determinar a forma das órbitas planetárias
Por meio das leis de Kepler é possível determinar a forma das órbitas planetárias
Leis de Kepler
As leis do movimento planetário de Kepler são conhecidas como: lei das órbitas elípticas, lei das áreas e lei dos períodos. Juntas estas explicam como funciona o movimento de qualquer corpo orbitando algum astro massivo, como planetas ou estrelas.
1ª lei de Kepler: lei das órbitas
A primeira Lei de Kelper afirma que a órbita dos planetas que giram em torno do Sol não é circular, mas sim elíptica.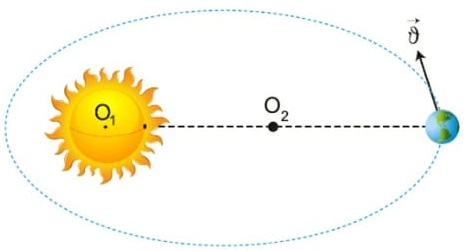 “A órbita dos planetas é uma elipse em que o Sol ocupa um dos focos.”
“A órbita dos planetas é uma elipse em que o Sol ocupa um dos focos.”
A figura (fora de escala) mostra que a órbita da Terra é elíptica e que o Sol está em um dos focos.
2ª lei de Kepler: lei das áreas
A segunda lei de Kepler afirma que a linha imaginária que liga o Sol aos planetas que o orbitam varre áreas em intervalos de tempo iguais. Em outras palavras, essa lei afirma que a velocidade com que as áreas são varridas é igual, isto é, a velocidade aureolar das órbitas é constante.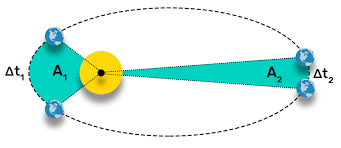 “A linha imaginária que liga o Sol aos planetas que o orbitam varre áreas iguais em intervalos de tempos iguais.”
“A linha imaginária que liga o Sol aos planetas que o orbitam varre áreas iguais em intervalos de tempos iguais.”
De acordo com a lei das áreas, para o mesmo intervalo de tempo, as áreas A1 e A2 são iguais.
3ª lei de Kepler: lei dos períodos ou lei da harmonia
A terceira lei de Kepler afirma que o quadrado do período orbital (T²) de um planeta é diretamente proporcional ao cubo de sua distância média ao Sol (R³). Além disso, a razão entre T² e R³ tem exatamente a mesma magnitude para todos os astros que orbitam essa estrela.
“A razão entre o quadrado do período e o cubo do raio médio da órbita de um planeta é constante.”
A expressão usada para o cálculo da terceira lei de Kepler é mostrada a seguir, confira:![]() T = período orbital
T = período orbital
R = raio médio da órbita
Observe a próxima figura, nela mostramos os semieixos maior e menor de uma órbita planetária em torno do Sol: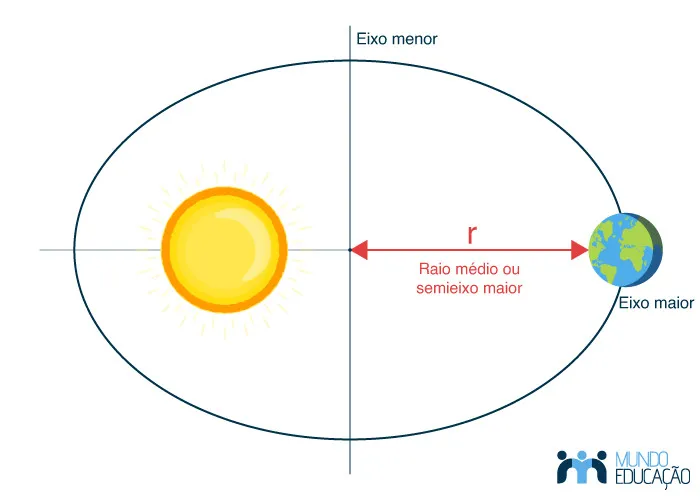 O raio médio da órbita, utilizado no cálculo da terceira lei de Kepler, é dado pela média entre os raios máximo e mínimo. As posições mostradas na figura, que caracterizam a maior e a menor distância da Terra em relação ao Sol, são chamadas de afélio e periélio, respectivamente.
O raio médio da órbita, utilizado no cálculo da terceira lei de Kepler, é dado pela média entre os raios máximo e mínimo. As posições mostradas na figura, que caracterizam a maior e a menor distância da Terra em relação ao Sol, são chamadas de afélio e periélio, respectivamente.
![]() O raio médio é calculado pela média entre os raios do periélio e afélio.
O raio médio é calculado pela média entre os raios do periélio e afélio.
Quando a Terra aproxima-se do periélio, sua velocidade orbital aumenta, uma vez que a aceleração gravitacional do Sol intensifica-se. Dessa maneira, a Terra tem máxima energia cinética quando nas proximidades do periélio.
Aproximando-se do afélio, ela perde energia cinética, tendo assim a sua velocidade orbital reduzida à sua menor medida.
Observe que a razão entre T² e R³ é determinada exclusivamente por duas constantes, o número pi e a constante da gravitação universal, e também pela massa do Sol:
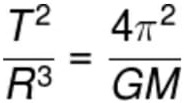
G = constante da gravitação universal (6,67.10-11 N.m²/kg²)
M = massa do Sol (1,989.1030 kg)
Observe o cálculo seguinte, nele se mostra como é possível obter, com base na lei da gravitação universal, a expressão geral da terceira lei de Kepler:
MOVIMENTO PLANETÁRIO
Periélio - No periélio, a Terra encontra-se mais próxima do Sol, mantendo-se a aproximadamente 147 milhões de quilômetros. A velocidade nesse ponto da órbita é maior.
Afélio - No afélio, a Terra encontra-se mais afastada do Sol, mantendo-se a aproximadamente 152 milhões de quilômetros. A velocidade nesse ponto da órbita é menor.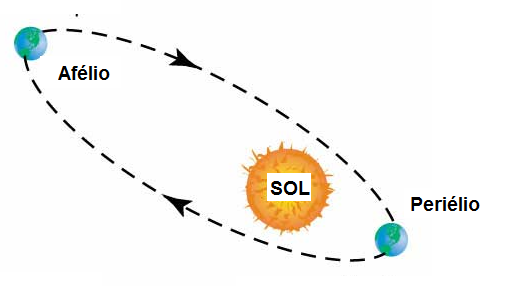
Primeira Lei de Kepler
A primeira lei de Kepler, chamada lei das órbitas elípticas, estabelece o seguinte: num referencial fixo no Sol, as órbitas dos planetas são elipses e o Sol ocupa um dos focos.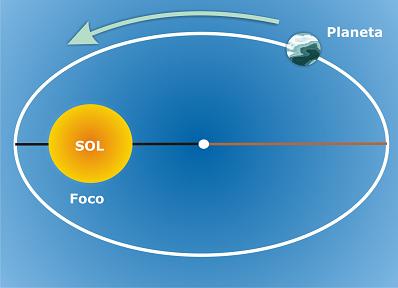
Segunda Lei de Kepler
A segunda lei de Kepler, chamada lei das áreas, estabelece o seguinte: num referencial fixo no Sol, a reta que une o planeta ao Sol varre áreas iguais em tempos iguais.
Terceira Lei de Kepler
A terceira lei de Kepler, chamada lei harmônica, estabelece o seguinte: num referencial fixo no Sol, o quadrado do período de revolução de um planeta ao redor do Sol é proporcional ao cubo do semi-eixo maior da elipse que representa a órbita do planeta.
Matematicamente:
Em que k tem, aproximadamente, o mesmo valor para todos os planetas.
Observação:
A velocidade média em que a Terra realiza o movimento de translação é de aproximadamente 107.000 km/h. Apesar de ser uma velocidade elevada, ela não é sentida aqui na Terra.
Duração - O movimento de translação dura 365 dias, 5 horas e 48 minutos, tempo esse que foi convencionado no ano civil, cuja duração é de 365 dias. A cada quatro anos, tendo em vista o tempo exato do movimento, o ano possui 366 dias, sendo chamado de ano bissexto.
MOVIMENTO PLANETÁRIO RESOLIVDOS
50) (ITA) Uma estação espacial, Kepler, estuda um exoplaneta cujo satélite natural tem órbita elíptica de semieixo maior a0 e período T0, sendo d = 32a0 a distância entre a estação e o exoplaneta. Um objeto que se desprende de Kepler é atraído gravitacionalmente pelo exoplaneta e inicia um movimento de queda livre a partir do repouso em relação a esse. Desprezando a rotação do exoplaneta, a interação gravitacional entre o satélite e o objeto, bem como as dimensões de todos os corpos envolvidos, calcule em função de T0 o tempo de queda do objeto.
Resolução:
Se levarmos em conta que a excentricidade da trajetória elíptica que o objeto descreverá é aproximadamente igual a 1, podemos assumir que o raio da órbita do objeto será igual à metade da distância entre a estação espacial Kepler e o planeta. Desse modo, calcularemos qual deve ser o tempo em que o objeto aproxima-se do planeta, a partir de sua posição inicial. Para tanto, devemos encontrar o período da órbita, e o tempo de queda, por sua vez, será igual à metade desse tempo: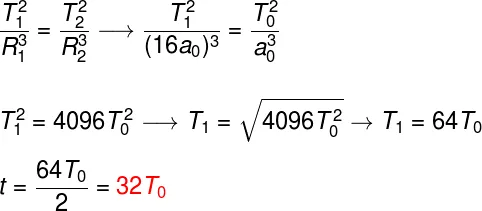
Depois de termos aplicado a terceira lei de Kepler, dividimos o resultado por 2, uma vez que o que calculamos foi o período orbital, em que, na metade do tempo, o objeto cai em direção ao planeta, e na outra metade, afasta-se. Desse modo, o tempo de queda, em termos de T0, é igual a 32T0.
51) (Udesc) Analise as proposições com relação às leis de Kepler sobre o movimento planetário.
I. A velocidade de um planeta é maior no periélio.
II. Os planetas movem-se em órbitas circulares, estando o Sol no centro da órbita.
III. O período orbital de um planeta aumenta com o raio médio de sua órbita.
IV. Os planetas movem-se em órbitas elípticas, estando o Sol em um dos focos.
V. A velocidade de um planeta é maior no afélio.
Assinale a alternativa correta.
(A) Somente as afirmativas I, II e III são verdadeiras.
(B) Somente as afirmativas II, III e V são verdadeiras.
(C) Somente as afirmativas I, III e IV são verdadeiras.
(D) Somente as afirmativas III, IV e V são verdadeiras.
(E) Somente as afirmativas I, III e V são verdadeiras.
Resolução:
Vamos analisar as alternativas:
I – VERDADEIRO. Quando o planeta aproxima-se do periélio, sua velocidade translacional aumenta, em razão do ganho de energia cinética.
II – FALSO. As órbitas planetárias são elípticas, com o Sol ocupando um de seus focos.
III – VERDADEIRO. O período orbital é proporcional ao raio da órbita.
IV – VERDADEIRO. Essa afirmação é confirmada pelo enunciado da primeira lei de Kepler.
V – FALSO. A velocidade de um planeta é maior nas proximidades do periélio.
Alternativa: C
52) (UFJF) Muitas teorias sobre o Sistema Solar sucederam-se, até que, no século XVI, o polonês Nicolau Copérnico apresentou uma versão revolucionária. Para Copérnico, o Sol, e não a Terra, era o centro do Sistema. Atualmente, o modelo aceito para o Sistema Solar é, basicamente, o de Copérnico, feitas as correções propostas pelo alemão Johannes Kepler e por cientistas subsequentes.
Sobre gravitação e as leis de Kepler, considere as afirmativas, a seguir, verdadeiras (V) ou falsas (F).
I. Adotando-se o Sol como referencial, todos os planetas movem-se descrevendo órbitas elípticas, tendo o Sol como um dos focos da elipse.
II. O vetor posição do centro de massa de um planeta do Sistema Solar, em relação ao centro de massa do Sol, varre áreas iguais em intervalos de tempo iguais, não importando a posição do planeta em sua órbita.
III. O vetor posição do centro de massa de um planeta do Sistema Solar, em relação ao centro de massa do Sol, varre áreas proporcionais em intervalos de tempo iguais, não importando a posição do planeta em sua órbita.
IV. Para qualquer planeta do Sistema Solar, o quociente do cubo do raio médio da órbita pelo quadrado do período de revolução em torno do Sol é constante.
Assinale a alternativa CORRETA.
(A) Todas as afirmativas são verdadeiras.
(B) Apenas as afirmativas I, II e III são verdadeiras.
(C) Apenas as afirmativas I, II e IV são verdadeiras.
(D) Apenas as afirmativas II, III e IV são verdadeiras.
(E) Apenas as afirmativas I e II são verdadeiras.
Resolução:
I. VERDADEIRA.A afirmação é o próprio enunciado da primeira lei de Kepler.
II. VERDADEIRA. A afirmação coincide com a definição da segunda lei de Kepler.
III. FALSA. A determinação da segunda lei de Kepler, que decorre do princípio da conservação do momento angular, implica que as áreas varridas são iguais para intervalos de tempos iguais.
IV. VERDADEIRA. A afirmativa reproduz o enunciado da terceira lei de Kepler, também conhecida como lei dos períodos.
Alternativa: C
53) (UNIFESP-SP) A Massa da Terra é aproximadamente 80 vezes a massa da Lua e a distância entre os centros de massa desses astros é aproximadamente 60 vezes o raio da Terra. A respeito do sistema Terra-Lua pode-se afirmar que:
(A) a Lua gira em torno da Terra com órbita elíptica e em um dos focos dessa órbita está o centro de massa da Terra.
(B) a Lua gira em torno da Terra com órbita circular e o centro de massa da Terra está no centro dessa órbita.
(C) a Terra e a Lua giram em torno de um ponto comum, o centro de massa do sistema Terra-Lua, localizado no interior da Terra.
(D) a Terra e a Lua giram em torno de um ponto comum, o centro de massa do sistema Terra-Lua, localizado no meio da distância entre os centros de massa da Terra e da Lua.
(E) a Terra e a Lua giram em torno de um ponto comum, o centro de massa do sistema Terra-Lua, localizado no interior da Lua.
Resolução:
O centro de massa é um ponto que se comporta como se toda a massa do sistema estivesse concentrada nele. Como a massa da Terra é muito maior que a massa da Lua, o centro de massa do sistema Terra-Lua deve ser um ponto localizado na Terra.
Alternativa: C
54) (UEPB) O astrônomo alemão J. Kepler (1571-1630), adepto do sistema heliocêntrico, desenvolveu um trabalho de grande vulto, aperfeiçoando as ideias de Copérnico. Em consequência, ele conseguiu estabelecer três leis sobre o movimento dos planetas, que permitiram um grande avanço no estudo da astronomia. Um estudante ao ter tomado conhecimento das leis de Kepler concluiu, segundo as proposições a seguir, que:
I. Para a primeira lei de Kepler (lei das órbitas), o verão ocorre quando a Terra está mais próxima do Sol, e o inverno, quando ela está mais afastada.
II. Para a segunda lei de Kepler (lei das áreas), a velocidade de um planeta X, em sua órbita, diminui à medida que ele se afasta do Sol.
III. Para a terceira lei de Kepler (lei dos períodos), o período de rotação de um planeta em torno de seu eixo, é tanto maior quanto maior for seu período de revolução.
Com base na análise feita, assinale a alternativa correta:
(A) apenas as proposições II e III são verdadeiras
(B) apenas as proposições I e II são verdadeiras
(C) apenas a proposição II é verdadeira
(D) apenas a proposição I é verdadeira
(E) todas as proposições são verdadeiras
Resolução:
I : As estações do ano não têm relação com as posições de periélio e afélio.
II: VAFÉLIO < VPERIÉLIO
III: A terceira lei de Kepler não faz referência ao movimento de rotação do planeta.
Alternativa: C
55) (UFRGS) A elipse, na figura abaixo, representa a órbita de um planeta em torno de uma estrela S. Os pontos ao longo da elipse representam posições sucessivas do planeta, separadas por intervalos de tempos iguais. As regiões alternadamente coloridas representam as áreas varridas pelo raio da trajetória nesses intervalos de tempo. Na figura, em que as dimensões dos astros e o tamanho da órbita não estão em escala, o segmento de reta SH representa o raio focal do ponto H de comprimento p.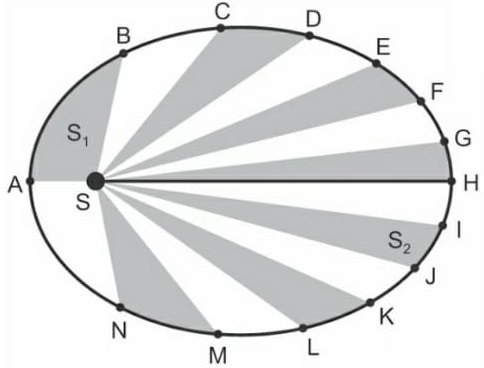 Considerando que a única força atuante no sistema estrela-planeta seja a força gravitacional, são feitas as seguintes afirmações:
Considerando que a única força atuante no sistema estrela-planeta seja a força gravitacional, são feitas as seguintes afirmações:
I. As áreas S1e S2, varridas pelo raio da trajetória, são iguais.
II. O período da órbita é proporcional a p3.
III. As velocidades tangenciais do planeta nos pontos A e H, VA e VH são tais que VA > VH.
Quais estão corretas?
(A) Apenas I
(B) Apenas I e II
(C) Apenas I e III
(D) Apenas II e III
(E) I, II e III
Resolução:
Vamos analisar as alternativas:
I – VERDADEIRO
II – FALSO. O quadrado do período da órbita é proporcional ao cubo do raio médio, de acordo com a 3ª lei de Kepler.
III – VERDADEIRO
Alternativa: C
56) (Acafe) Foi encontrado pelos astrônomos um exoplaneta (planeta que orbita uma estrela que não o Sol) com uma excentricidade muito maior que o normal. A excentricidade revela quão alongada é sua órbita em torno de sua estrela. No caso da Terra, a excentricidade é 0,017, muito menor que o valor 0,96 desse planeta, que foi chamado HD 20782.
Nas figuras a seguir, pode-se comparar as órbitas da Terra e do HD 20782.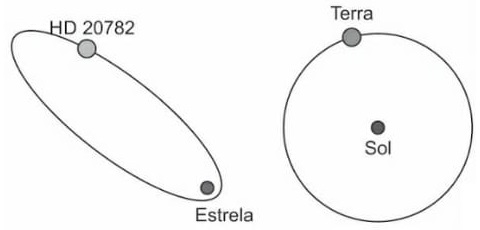 Nesse sentido, assinale a alternativa correta:
Nesse sentido, assinale a alternativa correta:
(A) As leis de Kepler não se aplicam ao HD 20782 porque sua órbita não é circular como a da Terra.
(B) As leis de Newton para a gravitação não se aplicam ao HD 20782 porque sua órbita é muito excêntrica.
(C) A força gravitacional entre o planeta HD 20782 e sua estrela é máxima quando ele está passando no afélio.
(D) O planeta HD 20782 possui um movimento acelerado quando se movimenta do afélio para o periélio.
Resolução:
No periélio, o planeta está na menor distância até o Sol, por isso, está sujeito à maior atração gravitacional que sua órbita permite.
Alternativa: D
57) (UFSM) Os avanços nas técnicas observacionais têm permitido aos astrônomos rastrear um número crescente de objetos celestes que orbitam o Sol. A figura mostra, em escala arbitrária, as órbitas da Terra e de um cometa (os tamanhos dos corpos não estão em escala). Com base na figura, analise as afirmações: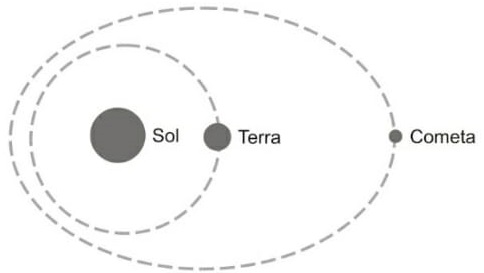 I. Dada a grande diferença entre as massas do Sol e do cometa, a atração gravitacional exercida pelo cometa sobre o Sol é muito menor que a atração exercida pelo Sol sobre o cometa.
I. Dada a grande diferença entre as massas do Sol e do cometa, a atração gravitacional exercida pelo cometa sobre o Sol é muito menor que a atração exercida pelo Sol sobre o cometa.
II. O módulo da velocidade do cometa é constante em todos os pontos da órbita.
III. O período de translação do cometa é maior que um ano terrestre.
Está(ão) correta(s):
(A) apenas I
(B) apenas III
(C) apenas I e II
(D) apenas II e III
(E) I, II e III
Resolução:
Vamos analisar as alternativas:
I – FALSA. De acordo com a terceira lei de newton, essas forças devem ter intensidades iguais.
II – FALSA. Nas trajetórias elípticas, o movimento é acelerado quando o astro aproxima-se do Sol.
III – VERDADEIRA
Alternativa: B
57A) (ITA) Uma estação espacial, Kepler, estuda um exoplaneta cujo satélite natural tem órbita elíptica de semieixo maior a0 e período T0, sendo d = 32a0 a distância entre a estação e o exoplaneta. Um objeto que se desprende de Kepler é atraído gravitacionalmente pelo exoplaneta e inicia um movimento de queda livre a partir do repouso em relação a esse. Desprezando a rotação do exoplaneta, a interação gravitacional entre o satélite e o objeto, bem como as dimensões de todos os corpos envolvidos, calcule em função de T0 o tempo de queda do objeto.
Resolução;
Se levarmos em conta que a excentricidade da trajetória elíptica que o objeto descreverá é aproximadamente igual a 1, podemos assumir que o raio da órbita do objeto será igual à metade da distância entre a estação espacial Kepler e o planeta. Desse modo, calcularemos qual deve ser o tempo em que o objeto aproxima-se do planeta, a partir de sua posição inicial. Para tanto, devemos encontrar o período da órbita, e o tempo de queda, por sua vez, será igual à metade desse tempo: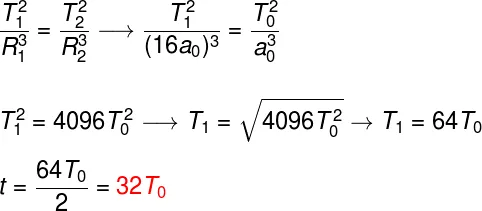
57B) (Udesc) Analise as proposições com relação às leis de Kepler sobre o movimento planetário.
I. A velocidade de um planeta é maior no periélio.
II.Os planetas movem-se em órbitas circulares, estando o Sol no centro da órbita.
III. O período orbital de um planeta aumenta com o raio médio de sua órbita.
IV. Os planetas movem-se em órbitas elípticas, estando o Sol em um dos focos.
V. A velocidade de um planeta é maior no afélio.Assinale a alternativa correta.
(A) Somente as afirmativas I, II e III são verdadeiras.
(B) Somente as afirmativas II, III e V são verdadeiras.
(C) Somente as afirmativas I, III e IV são verdadeiras.
(D) Somente as afirmativas III, IV e V são verdadeiras.
(E) Somente as afirmativas I, III e V são verdadeiras.
Resolução:
Vamos analisar as alternativas:
I – VERDADEIRO. Quando o planeta aproxima-se do periélio, sua velocidade translacional aumenta, em razão do ganho de energia cinética.
II – FALSO. As órbitas planetárias são elípticas, com o Sol ocupando um de seus focos.
III – VERDADEIRO. O período orbital é proporcional ao raio da órbita.
IV – VERDADEIRO. Essa afirmação é confirmada pelo enunciado da primeira lei de Kepler.
V – FALSO. A velocidade de um planeta é maior nas proximidades do periélio.
Alternativa: C
57C) (UFJF) Muitas teorias sobre o Sistema Solar sucederam-se, até que, no século XVI, o polonês Nicolau Copérnico apresentou uma versão revolucionária. Para Copérnico, o Sol, e não a Terra, era o centro do Sistema. Atualmente, o modelo aceito para o Sistema Solar é, basicamente, o de Copérnico, feitas as correções propostas pelo alemão Johannes Kepler e por cientistas subsequentes.
Sobre gravitação e as leis de Kepler, considere as afirmativas, a seguir, verdadeiras (V) ou falsas (F).
I. Adotando-se o Sol como referencial, todos os planetas movem-se descrevendo órbitas elípticas, tendo o Sol como um dos focos da elipse.
II. O vetor posição do centro de massa de um planeta do Sistema Solar, em relação ao centro de massa do Sol, varre áreas iguais em intervalos de tempo iguais, não importando a posição do planeta em sua órbita.
III. O vetor posição do centro de massa de um planeta do Sistema Solar, em relação ao centro de massa do Sol, varre áreas proporcionais em intervalos de tempo iguais, não importando a posição do planeta em sua órbita.
IV. Para qualquer planeta do Sistema Solar, o quociente do cubo do raio médio da órbita pelo quadrado do período de revolução em torno do Sol é constante.
Assinale a alternativa CORRETA.
(A) Todas as afirmativas são verdadeiras.
(B) Apenas as afirmativas I, II e III são verdadeiras.
(C) Apenas as afirmativas I, II e IV são verdadeiras.
(D) Apenas as afirmativas II, III e IV são verdadeiras.
(E) Apenas as afirmativas I e II são verdadeiras.
Resolução:
I. VERDADEIRA. A afirmação é o próprio enunciado da primeira lei de Kepler.
II. VERDADEIRA. A afirmação coincide com a definição da segunda lei de Kepler.
III. FALSA. A determinação da segunda lei de Kepler, que decorre do princípio da conservação do momento angular, implica que as áreas varridas são iguais para intervalos de tempos iguais.
IV. VERDADEIRA. A afirmativa reproduz o enunciado da terceira lei de Kepler, também conhecida como lei dos períodos."
Alternativa: C
57D) (UFSC) Sobre as leis de Kepler, assinale a(s) proposição(ões) verdadeira(s) para o sistema solar.
(01) O valor da velocidade de revolução da Terra em torno do Sol, quando sua trajetória está mais próxima do Sol, é maior do que quando está mais afastada dele.
(02) Os planetas mais afastados do Sol têm um período de revolução em torno dele maior que os mais próximos.
(04) Os planetas de maior massa levam mais tempo para dar uma volta em torno do Sol, devido à sua inércia.
(08) O Sol está situado em um dos focos da órbita elíptica de um dado planeta.
(16) Quanto maior for o período de rotação de um dado planeta, maior será o seu período de revolução em torno do Sol.
(32) No caso especial da Terra, a órbita é exatamente uma circunferência.
Resolução:
01 + 02 + 08 = 11
(01) Verdadeira. De acordo com a segunda lei de Kepler, o segmento de reta traçado pelo Sol até qualquer planeta varre áreas iguais em intervalos de tempos iguais. Portanto, para que isso seja verdade, quando a distância até o sol é menor, a velocidade dos planetas é maior.
(02) Verdadeira, pois a 3ª Lei de Kepler diz que os períodos dependem das distâncias dos planetas ao Sol. Assim, conforme a distância, os períodos aumentam.
(04) Falsa, pois os períodos não dependem das massas.
(08) Verdadeira. De acordo com a primeira Lei de Kepler, os planetas movem-se em órbitas elípticas e o Sol está localizado em um dos focos.
(16) Falsa. Os movimentos de rotação e translação não dependem um do outro.
(32) Falsa. O movimento da Terra ao redor do Sol possui uma pequena excentricidade.
57E) (Cefet-PR) Dois satélites artificiais giram em torno da Terra em órbitas de mesma altura. O primeiro tem massa m1, e o segundo, massa 3m1. Se o primeiro tem período de 6 h, o período do outro será, em horas, igual a:
(A) 18
(B) 2
(C) 6
(D) 6√3
(E) 3√2
Resolução:
O período orbital depende apenas da altura da órbita. Como os dois satélites apresentam órbitas de mesma altura, seus períodos devem ser iguais. O período não depende da massa.
Alternativa: C
57F) O planeta Mercúrio está distante 5,8 . 1010 m do Sol. Sabendo-se que a Terra está a uma distância de 1,5 . 1011 m do Sol e que o seu período de revolução é de 3,2 . 107s, calcule o período de revolução de Mercúrio.
Resolução:
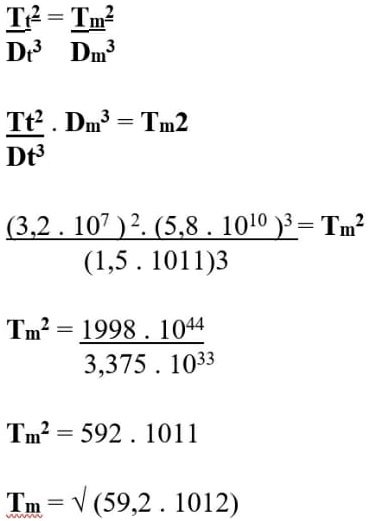
57G) Sobre as Leis de Kepler e o movimento dos planetas, marque a alternativa correta:
(A) A velocidade de Revolução dos planetas é constante.
(B) Quanto maior a distância de um planeta ao Sol, mais rápido ele se movimenta.
(C) A velocidade de rotação de um planeta não depende da sua distância ao Sol.
(D) Quanto menor a distância de um planeta ao Sol, mais rápido ele se movimenta.
(E) A velocidade de rotação dos planetas depende unicamente de suas massas.
Resolução:
De acordo com a segunda Lei de Kepler, um planeta em órbita descreve áreas iguais em intervalos iguais de tempo. Para que isso seja possível, ele adquire uma maior velocidade quando a distância ao Sol é menor.
Alternativa: D
57H) O ônibus espacial Atlantis foi lançado ao espaço com cinco astronautas a bordo e uma câmera nova, que iria substituir uma outra danificada por um curto-circuito no telescópio Hubble. Depois de entrarem em órbita a 560 km de altura, os astronautas se aproximaram do Hubble. Dois astronautas saíram da Atlantis e se dirigiram ao telescópio. Ao abrir a porta de acesso, um deles exclamou: “Esse telescópio tem a massa grande, mas o peso é pequeno.” Considerando o texto e as leis de Kepler, pode-se afirmar que a frase dita pelo astronauta
Considerando o texto e as leis de Kepler, pode-se afirmar que a frase dita pelo astronauta
(A) se justifica porque o tamanho do telescópio determina a sua massa, enquanto seu pequeno peso decorre da falta de ação da aceleração da gravidade.
(B) se justifica ao verificar que a inércia do telescópio é grande comparada à dele próprio, e que o peso do telescópio é pequeno porque a atração gravitacional criada por sua massa era pequena.
(C) não se justifica, porque a avaliação da massa e do peso de objetos em órbita tem por base as leis de Kepler, que não se aplicam a satélites artificiais.
(D) não se justifica, porque a força-peso é a força exercida pela gravidade terrestre, neste caso, sobre o telescópio e é a responsável por manter o próprio telescópio em órbita.
(E) não se justifica, pois a ação da força-peso implica a ação de uma força de reação contrária, que não existe naquele ambiente. A massa do telescópio poderia ser avaliada simplesmente pelo seu volume.
Resolução:
Devemos afirmar que a frase dita pelo astronauta é falsa. O telescópio sofre a ação da força gravitacional da Terra e é essa força que vai mante-lo em uma orbita circular, caracterizando um movimento circular. Nesse movimento circular, a força gravitacional corresponde a força centrípeta, logo, a aceleração gravitacional corresponde a aceleração centrípeta. Para um corpo (uma pessoa) dentro desse telescópio, o dito “peso aparente” tem valor nulo devido a distancia com a superfície e por isso o astronauta flutua dentro do telescópio.
Alternativa: D
Velocidade de escape
A velocidade de escape é a velocidade mínima necessária que um objeto necessita ter para conseguir escapar da atração gravitacional de um corpo celeste. A velocidade de escape é a velocidade mínima necessária para que um corpo escape da atração gravitacional de um corpo celeste, como a Terra.
A velocidade de escape é a velocidade mínima necessária para que um corpo escape da atração gravitacional de um corpo celeste, como a Terra.
Ao lançar objetos da superfície, eles são atraídos de volta para o chão devido à atração gravitacional. No entanto, é possível chegar a uma velocidade mínima que possa vencer essa atração gravitacional, o que chamamos de velocidade de escape.
A velocidade de escape não depende da massa do objeto que tenta escapar, mas se relaciona com a massa do planeta ou estrela (M) de onde se quer escapar, com o raio desse corpo celeste (R) e com a constante de gravitação universal (G), que possui valor de 6,67.10 -11 N.m2/kg2.
Assim, para encontrar a velocidade de escape, chegamos à fórmula a seguir:![]() G = 6,67.10-11 N.m2/kg2
G = 6,67.10-11 N.m2/kg2
M = massa do planeta (kg)
R = raio do corpo celeste (m)
Observação: A unidade de medida de Velocidade de escapo (Ve) é (km/s).
QUESTÕES RESOLVIDAS
01) Qual a velocidade mínima que um corpo precisa ter para escapar do campo gravitacional de um planeta Terra?.
Resolução:
Dados:
G = 6,67.10-11 N.m2/kg2
M = 5,98.1024 kg
R = 6,38.106 m![]()
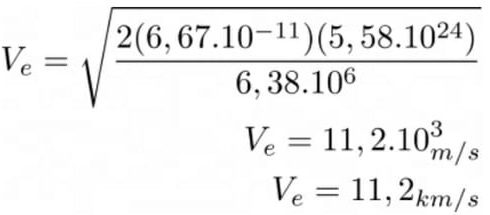
02) (Fuvest) A velocidade de escape de um corpo celeste é a mínima velocidade que um objeto deve ter nas proximidades da superfície desse corpo para escapar de sua atração gravitacional. Com base nessa informação e em seus conhecimentos sobre a interpretação cinética da temperatura, considere as seguintes afirmações a respeito da relação entre a velocidade de escape e a atmosfera de um corpo celeste.
I. Corpos celestes com mesma velocidade de escape retêm atmosferas igualmente densas, independentemente da temperatura de cada corpo.
II. Moléculas de gás nitrogênio escapam da atmosfera de um corpo celeste mais facilmente do que moléculas de gás hidrogênio.
III. Comparando corpos celestes com temperaturas médias iguais, aquele com a maior velocidade de escape tende a reter uma atmosfera mais densa.
Apenas é correto o que se afirma em:
(A) I.
(B) II.
(C) III.
(D) I e II.
(E) I e III
Resolução
A temperatura do planeta interfere na densidade de sua atmosfera. Então, quanto maior a temperatura, menor a densidade da atmosfera e vice-versa.
Corpos mais leves (menos densos) possuem uma maior facilidade para escapar dos corpos celestes, pois sua energia cinética é menor. Com isso, apenas a alternativa III é correta, já que o nitrogênio é mais pesado que o hidrogênio e a temperatura altera a densidade.
Alternativa: C
03) A velocidade mínima para que um corpo possa sair da superfície de um corpo celeste é denominada velocidade de escape. Determine a velocidade de escape para que uma sonda consiga escapar da superfície da Lua, em m/s.
Dados:
Massa da Lua: 7,36.1022
Constante de gravitação universal: 6,67.10-11 N.m2/kg2
Raio da Lua: 1,74.106
(A) 5,64.106
(B) 2,37.103
(C) 2,82.106
(D) 3,13.106
Resolução:![]() Para descobrir a velocidade de escape, utilizaremos a equação a seguir:
Para descobrir a velocidade de escape, utilizaremos a equação a seguir:
Substituindo com as informações apresentadas no enunciado: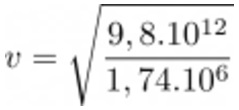
Resolvendo a multiplicação:![]()
Resolvendo a divisão:![]()
Tirando o valor da raiz:
Alternativa: B
FORÇA PESO
A força peso (P) é um tipo de força que atua na direção vertical sob a atração da gravitação da Terra.
Em outras palavras, é a força que existe sobre todos os corpos, sendo exercida sobre eles por meio do campo gravitacional da Terra.
P = m . g
P = força peso (N)
m = massa (Kg)
g = aceleração da gravidade (m/s2)
QUESTÕES RESOLVIDAS
58) Qual a força mínima que deve ser feita para levantar um automóvel com massa 800kg?
A força deve ser maior ou igual à força peso, então: Adote g = 10m/s2
Resolução:
F = P . m . g
F = P = m . g
F = P 800 . 10
F = P = 8000N
59) Qual a massa de um corpo com peso 12000kgf? Adote g = 9,8m/s2
Resolução:
P = m . g
12000 = m . 9,8
12000/9,8 = m
M =1224,5 kg
60) Um corpo com massa de 60 kg está na superfície do planeta Marte, onde a aceleração da gravidade é 3,71 m/s2. De acordo com esses dados, responda:
a) Qual é o peso desse corpo na superfície de Marte?
Resolução:
Na superfície de Marte:
P = m . g
P = 60 . 3,71
P = 222,6 N
b) Suponha que esse mesmo objeto seja trazido para a Terra, onde g = 9,78 m/s2, qual será o seu peso?
Resolução:
Na Terra:
P = m . g
P = 60 . 9,78
P = 586,8 N
FORÇA RESULTANTE
A força resultante pode ser obtida por meio do cálculo vetorial. De acordo com a 2ª lei de Newton, ela é igual ao produto entre a massa do corpo e sua aceleração.
FR = m . a
F = força (N)
m = massa (kg)
a = aceleração (m/s2)
Cálculo da força resultante pela soma vetorial
As direções e os sentidos nos indicam quais operações devemos realizar a fim de determinar a força resultante. Se as forças atuam com a mesma direção e o mesmo sentido, elas devem ser somadas; se estão na mesma direção, mas em sentidos opostos, devem ser subtraídas. As setas são os vetores que representam as forças.
Mesma direção e mesmo sentido:
Os módulos são somados.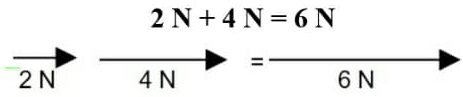 Mesma direção, mas em sentidos opostos:
Mesma direção, mas em sentidos opostos:
Os módulos são subtraídos.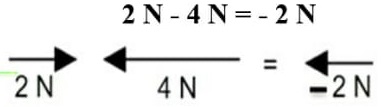 O sinal negativo se refere ao sentido. Adotando o sentido para a direita como positivo, a resultante aponta para a esquerda.
O sinal negativo se refere ao sentido. Adotando o sentido para a direita como positivo, a resultante aponta para a esquerda.
Soma de vetores perpendiculares (90º)
Caso duas forças perpendiculares atuem em um corpo, seu módulo é determinado pelo Teorema de Pitágoras.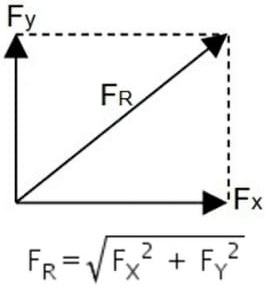 Forças oblíquas
Forças oblíquas
Forças oblíquas são forças em que suas direções realizam um certo ângulo entre si, que difira de 90º. Quando forças oblíquas atuam sobre o corpo, determinamos seu módulo, sua direção e seu sentido pela regra do paralelogramo.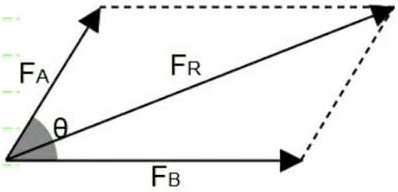 As forças A e B atuam em um mesmo ponto material, com suas direções fazendo um ângulo.
As forças A e B atuam em um mesmo ponto material, com suas direções fazendo um ângulo.
Para determinar direção e sentido, traçamos retas paralelas à cada vetor de força, como as linhas pontilhadas na figura. O vetor resultante começa no ponto de atuação das forças e termina na interseção das linhas paralelas.
QEUSTÕES RESOLVIDAS
61) Um corpo com a massa de 5 kg cai de uma janela do terceiro andar de um prédio. Este corpo se mantém com uma aceleração de 9,81 m/s². Qual a intensidade, a direção e o sentido da força que produz o movimento?
Resolução:
O movimento se mantém na direção vertical com sentido apontado para o centro da Terra. A força que age sobre o corpo é a força da gravidade. Desprezando a resistência do ar, a gravidade é a única força que atua no movimento, sendo a força resultante.
Resolução:
A intensidade da força pode ser calculada pela segunda Lei de Newton:
FR = m . a
FR = 5 . 9,81
FR = 49,05N
62) Em uma competição esportiva estudantil, dois times disputam a prova do cabo de guerra. Os times puxam uma corda na mesma direção, mas em sentidos contrários. O objetivo é trazer um ponto demarcado na corda até um certo referencial.
Suponha que o time A esteja produzindo uma força de 110 N, para a esquerda; enquanto o time B, 105 N para a direita. Calcule a força resultante e determine qual é o time vencedor.
Resolução:
Como as forças atuam em mesma direção e em sentidos opostos, parte da força produzida pelos times é anulada, e a resultante possui como módulo a subtração entre 110 N e 105 N.
FR = 110 – 105
FR = 5N
Como o time A está produzindo a força de maior módulo para a esquerda, é neste sentido que a corda se movimentará. Podemos caracterizar a força resultante como:
Módulo de 5 N, direção horizontal (igual a corda) e sentido para a esquerda. Assim, o time A é o vencedor.
63) Uma criança brinca puxando um carrinho de brinquedo preso por um barbante. O carrinho se movimenta pelo chão enquanto a força produzida pela criança atua na direção do barbante. Suponha que as competentes vertical e horizontal da força sejam conhecidas e iguais a 0,3 N e 0,4 N. Determine o módulo da força resultante produzida pela criança.
Resolução: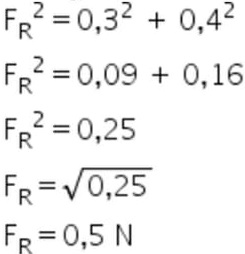
As forças horizontais e verticais são perpendiculares, ou seja, fazem 90º entre si. O módulo da força resultante, neste caso, pode ser calculado pelo uso do Teorema de Pitágoras.
Assim, o módulo da força resultante que atua no carrinho é de 0,5 N.
64) Uma bola de boliche de massa igual a 5 kg é arremessada em direção aos pinos. Ao sair das mãos do jogador, ela desenvolve uma aceleração de 0,75 m/s². Qual o módulo da força resultante aplicada à bola?
Resolução:
O módulo da força resultante pode ser calculado pela segunda Lei de Newton.
FR = m . a
FR = 5 . 0,75
FR = 3,75 N
65) Considere as seguintes forças aplicadas a um corpo:![]() Qual é a força resultante aplicada?
Qual é a força resultante aplicada?
Resolução:
Módulo: 5N -3 N = 2N
Direção e sentido: O mesmo da força maior em módulo (5N)
62) Uma força de 50N é aplicada a um corpo de massa 100kg que se encontra em repouso. Sendo esta a única força que atua no corpo, qual a velocidade alcançada após 10s da aplicação da força?
Resolução:
Conhecendo a aceleração do corpo podemos calcular sua velocidade:
V = Vo + at
V = 0 + 0,5 . 10
V 5m/s
66) Uma força horizontal de intensidade F = 10 N é aplicada no bloco A, de 6 kg, o qual está apoiado em um segundo bloco B, de 4 kg. Os blocos deslizam sobre um plano horizontal sem atrito. Determine:  a) a aceleração do conjunto.
a) a aceleração do conjunto.
Resolução:
A aceleração de conjunto é equivalente a 1m/s².
F - Fab = 6a
10 - Fab = 6a
Fab = - 6a + 10
(que é a força que a exerce em b)
Fab = 4a
-6a + 10 = 4a
10a = 10
a = 10/10
b) a intensidade da força que um bloco exerce no outro.
Resolução:
A intensidade da força que um bloco exerce no outro é equivalente a 4 Newton (quatro Newton).
Fab = 4a
Fab = 4 N ewton, que é o valor exato da força exercida por a sobre o bloco B.
c) a intensidade da força resultante em Ae em B
Resolução:
A intensidade da força resultante em a e em b é equivalente a 6 N (seis Newton).
F - Fab
10 - 4 = 6 Newton.
67) Três blocos A, B e C, de massa mA = 5 kg, mB = 2 kg e mC = 3 kg, estão numa superfície horizontal sem atrito. Aplica-se ao bloco A uma força de 20 N, constante, como indicado na figura.  Determine:
Determine:
a) a aceleração do conjunto;
Resolução:
Podemos afirmar que a aceleração do conjunto é equivalente a 2 m/s² (dois metros por segundo ao quadrado).
F = m.a
20 = (5 + 2 + 3) . a
20 = 10a
a = 2 m/s²
b)a intensidade da força que B exerce em C
Resolução:
Podemos afirmar que a intensidade da força que B exerce em C é equivalente a 6 N (seis Newton).
B exerce em c a força necessária pra movimentá-lo a 2m/s²:
F = 3 . 2
F = 6 Newton
c)a intensidade da força que A exerce em B
Resolução:
Podemos afirmar que a intensidade da força que A exerce em B é equivalente a 10 N (dez Newton).
A exerce a força necessária pra mover os corpos B e C:
F = (2 + 3) . 2
F = 5 . 2
F = 10 Newton.
68) Dois blocos de massas mA = 5 kg e mB = 3 kg estão numa superfície horizontal sem atrito e ligados por um fio de massa desprezível. A força horizontal F tem intensidade constante igual a 4 N. Determine a tração no fio que liga os corpos  Resolução:
Resolução:
F = (mA + mB) . a
4 = (5 + 3) . a
a = 0,5 m/s²
Corpo B
F - T = mB.a
4 - T = 3.0,5
T = 2,5 N
69) (FEI-SP)Sabendo-se que a tração no fio que une os dois blocos vale 100 N, qual é o valor do módulo da força F? Não há atritos.  Resolução:
Resolução:
bloco maior
F - T = 10.a (I)
bloco menor
T = 5.a (II)
T = 100N
a = 20m/s²
substituindo na equação I os valores.
F - 100 = 200
F = 300
70) (UFRJ) Dois blocos de massa igual a 4 kg e 2 kg, respectivamente, estão presos entre si por um fio inextensível e de massa desprezível. Deseja-se puxar o conjunto por meio de uma força F cujo módulo é igual a 3 N sobre uma mesa horizontal e sem atrito. O fio é fraco e corre o risco de romper-se. Qual é o melhor modo de puxar o conjunto sem que o fio se rompa: pela massa maior ou pela menor? Justifique sua resposta.  Resolução:
Resolução:
Vamos aplicar a segunda lei de newton em ambas as caixas e em ambos os casos.
Aplicando 3 N na caixa de 4 Kg e aplicando a segunda lei de newton em ambas as caixas, temos:
F – T = 4 . a
T = 2 . a
F - 2a = 4a
F = 6a
3 = 6a
a =1 /2 m/s ²
T = 1/2.2
T = 1 N
Temos uma tração de 1 N, aplicando a força F de 3 N na caixa de 4.
Fazendo a mesma coisa, só que na de 2 kg.
F - T= 2 .a
T = F - 2a
T = 4a
4a = F- 2a
6a = 3
a = 1/2 m/s²
T = 4 . a
T = 4 . 1/2
T = 2 N
Conclui-se, que ao puxar pela caixa maior, a tração será menor.
71) No arranjo experimental da figura não há atrito algum e o fio tem massa desprezível, os blocos tem massas mA = 2 kg e mB = 3 kg. Adote g = 10 m/s². 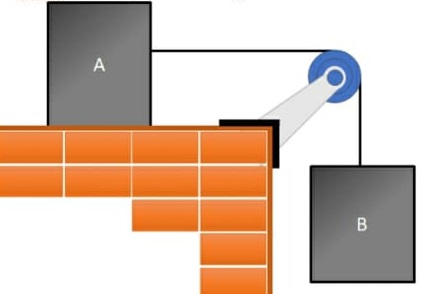 Determine:
Determine:
a) a aceleração do corpo.
Resolução:
mB= 3 kg
mA= 2 kg
peso de B = Pb
Pb= m . g
Pb =3 .10
Pb = 30 N = F
cálculo da aceleração do conjunto = a
F = ( mA + mB)a
30 = (2 + 3)a
30 = 5a
A = 30/5
A = 6m/s²
b) a tração no fio.
Resolução:
Tração no fio = Tf
Tf = mA . a
Tf = 2 . 6
Tf = 12 N
72) Na situação indicada na figura, os fios têm massa desprezível e passam pelas polias sem atrito. Adote g = 10 m/s2.  Determine:
Determine:
a) a aceleração do conjunto;
Resolução:
I) PA - T = mA . a
II)T - PB = mB .a
PA - PB = (ma + mb + mc) a
200 - 100 = 40a
100 = 40 a
a = 100 /40
a = 2.5m/s²
b) a tração no fio que liga A B.
Resolução:
Tração do fio A e B de I temos:
I) PA - T = m a
200 - T = 50
-T = -150
T = 150N
c) a tração no fio que liga Ba C.
Resolução:
a tração no fio que liga B e C.
T = PB + mB . a
T = 100 + 10 . 2,5
T = 100 + 25
T = 125N
73) Os corpos A e B têm massas mA = 1 kg e mB = 3 kg. O corpo C, pendurado pelo fio, tem massa mC = 1 kg. O fio é inextensível e tem massa desprezível. Adote g = 10 m/s² e suponha que A e B deslizam sem atrito sobre o plano horizontal.  Calcule:
Calcule:
a) a aceleração do corpo C
Resolução:
A aceleração de um corpo, primeiro é necessário achar a força resultante do corpo.
Fr = m . a
Considerando que o corpo está em repouso, já que no exercício diz que ele apenas está pendurado, enquanto A e B deslizam, podemos considerar que:
Para corpos em equilíbrio, utilizamos:
Somatório das forças = 0
T- P = 0
T= tração
P= Peso
Logo:
T = P = Força resultante
Portanto, basta aplicar a fórmula da força resultante, igualando-a ao peso
P = Fr
m.g = m.a
g = a = 10m/s²
b) a intensidade da força que o corpo B exerce em A.
Resolução:
A intensidade de uma força é adotada pela relação:
Fr = m.a
m = quilos (Kg)
a = aceleração (m/s²)
logo:
Fr = 3kg . 10m/s²
Fr = 30N
74) No arranjo experimental da figura os fios e a polia têm massas desprezíveis. O fio é inextensível e passa sem atrito pela polia. Adotando g = 10 m/s2, determine:  a) a aceleração dos corpos;
a) a aceleração dos corpos;
Resolução:
Como o bloco A possui 3kg então o seu peso é 30N, pois:
P = m . a
P = 3 . 10
P = 30
E o bloco B possui 1kg, então seu peso é de 10N:
P = 1 . 10
P = 10
Como o peso do bloco A é maior, a tendência é de que o movimento da corda seja puxando o bloco B para cima e o bloco A para baixo.
Para o bloco B temos:
T1 - 10 = 1 . a
Para o bloco A temos:
30 - T1 = 3 . a
b) as trações T1 e T2.
Resolução:
Juntando em um sistema:
T1 - 10 = 1 x a
30 - T1 = 3 x a
20 = 4 . a
a = 20/4
a = 5m/s²
De posse da aceleração, podemos usá-la em alguma das fórmulas obtidas:
T1 - 10 = 1 . a
T1 - 10 = 1 . 5
T1 = 15N
Como o fio que passa pela roldana será puxado por 15N pelos dois lados, T2 terá o valor de 30N, pois a roldana precisa se manter parada, e tudo o que está em cima é igual tudo o que está para baixo.
75) (Olimpíada Paulista de Física) Um homem de 70 kg está em cima de uma balança dentro de um elevador. Determine qual é a indicação da balança, nas seguintes situações:
a) O elevador subindo acelerado com aceleração de 3 m/s².
Resolução:
N - P = m.a
N - mg = m.a
N – 70 . 10 = 70 . 3
N = 210 + 700
N = 910 N
b) O elevador subindo com velocidade constante de 2 m/s.
Resolução:
O elevador sobe com velocidade constante
a = 0m/s²
Fn = m . g
Fn = 70 . 10
Fn = 700 N
c) O elevador descendo acelerado com aceleração de 1 m/s².
Resolução:
O elevador desce com a = 1m/s²
70kg .10m/s² - Fn = 70kg .1m/s²
700N - 70N = Fn
Fn = 630N
d) O elevador caindo em queda livre.
Resolução:
O elevador cai em queda livre
a = g = 10m/s²
Fn = m (a - g)
Fn = m (10 - 10g)
Fn = m . 0
Fn = 0
Considere a balança graduada em newtons e adote: g = 10 m/s².
76) (Efoa-MG) No esquema representado na figura abaixo, o bloco C tem massa 0,5 kg e está em repouso sobre o plano inclinado de 37w com a horizontal, preso pelo fio AB. Não há atrito entre o bloco e o plano.  a) Qual é a tração exercida pelo fio?
a) Qual é a tração exercida pelo fio?
Resolução:
A atração exercida pelo fio e a aceleração adquirida pelo bloco é: 3N e 6m/s², respectivamente.
Vamos aos dados/resoluções:
Os corpos que se encontram em cima do plano inclinado acabam apresentando três forças que atuam sobre ele, que são:
- Força Peso (P): É a força associada a gravidade da terra sobre os corpos que apresentam massa;
- Força Normal (N): Essa já é a força de reação contrária a força peso;
- Força de Atrito (Fat): Se encontra como a força de contato entre os materiais sendo esta proporcional à força normal e ao coeficiente de atrito entre os materiais.
T = Pt
T = P.sen37º
T = m . g . sen37º
T = 0,5 . 10 . 0,6
T = 3N
b) Cortando-se o fio, qual é a aceleração adquirida pelo bloco?
(Dados: g = 10 m/s²;
sen 37º = cos 53º = 0,6;
sen 53º = cos 37º = 0,8)
Resolução:
Fr = Pt
M . a = m . g . sen37º
a = 10 . 0,6
a = 6 m/s².
77) Determine a aceleração dos corpos na situação esquematizada abaixo. Adote g = 10 m/s². O fio e a polia têm massa desprezível. Não há atrito (dado: sen 30º = 0,5).  Resolução:
Resolução:
A 2ª lei de Newton é o princípio fundamental da dinâmica (PFD), pois é uma fórmula que explica a causa da movimentação ou não de um corpo. Ela diz que a resultante das forças que atuam sobre um corpo é igual ao produto entre sua massa e sua aceleração:
F = m . a
F = força resultante
m = massa do corpo
a = aceleração do corpo
As unidades de medida no Sistema Internacional (SI) são:
Força = Newton (N)
Massa = quilograma (kg)
Aceleração = metro por segundo ao quadrado (m/s²)
No nosso caso
O bloco sobre o plano inclinado está sob a ação de duas forças:
A tração do fio que o arrasta para cima: T
A componente x de seu peso (ver figura):
Px = P . cos60º
O bloco na vertical também está sujeito a duas forças:
O seu peso que o puxa para baixo = P
A tração que o sustenta = T
Aplicando a 2ª lei de Newton para os dois
Somando as expressões membro a membro (cancela T)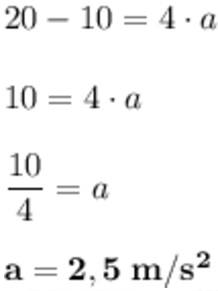
78) (Uerj 2013) Um bloco de madeira encontra-se em equilíbrio sobre um plano inclinado de 45º em relação ao solo. A intensidade da força que o bloco exerce perpendicularmente ao plano inclinado é igual a 2,0 N. Entre o bloco e o plano inclinado, a intensidade da força de atrito, em newtons, é igual a:
(A) 0,7
(B) 1,0
(C) 1,4
(D) 2,0
Resolução:
A intensidade da força de atrito é de 1,4 N.
Sabemos que a força normal que o plano faz sobre o bloco é de 2 N, isso quer dizer que a força peso do bloco também é 2 N. Na direção do plano inclinado, temos que a componente horizontal da força normal e a força de atrito são iguais, já que o bloco está em equilíbrio, ou seja:
P . sen(45°) = Fat
M . g . sen(45°) = u . m . g . cos(45°)
u = m . g . sen(45°)/m . g . cos(45°)
Como sen(45°) = cos(45°), temos:
u = 1
A força de atrito vale:
Fat = m . g . cos(45°)
Fat = 2 . cos(45°)
Fat = 1,4 N
Alternativa: C
79) (G1 – cftmg) Na figura, estão indicadas as forças atuantes em uma caixa de peso P = 60 N que sobe uma rampa áspera com velocidade constante sob a ação de uma força F = 60 N.  Nessas circunstâncias, o coeficiente de atrito cinético entre a rampa e esse bloco vale
Nessas circunstâncias, o coeficiente de atrito cinético entre a rampa e esse bloco vale
(A) 0,1.
(B) 0,2.
(C) 0,3.
(D) 0,5.
Resolução:
1. Como o movimento é retilíneo e uniforme, as forças (ou componentes) equilibram-se nos dois eixos, x e y.
2. Como os ângulos α e θ têm cada lado de um perpendicular a cada lado do outro, eles são congruentes: α = θ
Eixo y: N = Py ⇒ N = Pcosθ
Eixo y: Fa + Px = F ⇒ μ N + P senθ = F, substituindo N:
μ Pcosθ + P senθ = F, isolando P:
P(μ cosθ + senθ) = F, substituindo os valores de P e F:
60(μ cosθ + senθ) = 60, simplificando os dois valores "60"
μ cosθ + senθ = 1, isolando μ:
μ = (1 - senθ)/cosθ
μ = (1 - sen37°)/cos37°
μ = (1 - 0,6)/0.8
μ = 0,4/0.8
μ = 0,5
Alternativa: D
80) Na figura, os fios e as polias são ideais e não há atrito entre o corpo A e o plano horizontal. Os corpos A e B, de massas mA = 0,5 kg e mB = 2,0 kg, respectivamente, são abandonados do repouso. Determine os módulos das acelerações de A e de B. (Use g = 10 m/s²)
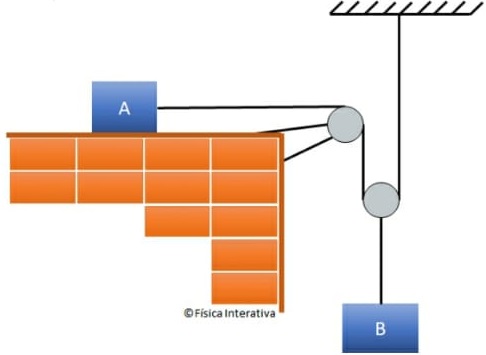 Resolução:
Resolução:
Como a massa do corpo B é maior que a do corpo A, os blocos vão ser puxados para baixo pela força gravitacional. A força resultante no sistema é nula. Ou seja, as força agentes em A são iguais e contrárias e B.
P = m.g
Em A, temos apenas a tensão da corda que liga ao corpo B.
T = mₐ.a (1)
Em B, temos a tensão aplicada no cabo que liga os corpos e a força gravitacional.
P - T = mᵇ . a (2)
Somando as duas equações
mᵇ . g = mₐ . a + mᵇ . a
coloca a em evidência
10 = 2,5 . a
2,5a = 20
a = 8 m/s²
TRABALHO DE UMA FORÇA
O trabalho exercido por uma força constante pode ser calculado por meio do produto entre a força aplicada e a distância percorrida pelo corpo.
Ao empurrarmos um carro, realizamos um trabalho que ocasiona o movimento do carro. Trabalho de uma força?
Trabalho de uma força?
Para calcularmos o trabalho exercido por uma força constante, é necessário que se multiplique o módulo dessa força pela distância percorrida e pelo cosseno do ângulo que é formado entre a força (F) e a distância T = trabalho (J)
T = trabalho (J)
F = força (N)
d = distância (m)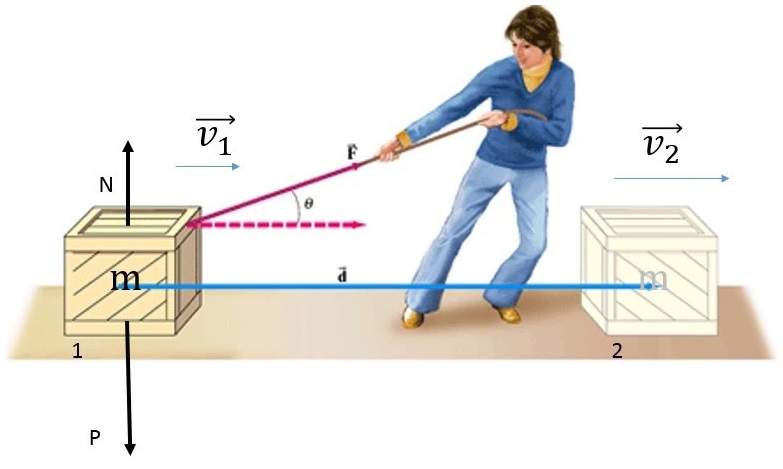 T = F . d . cos (ânguloº)
T = F . d . cos (ânguloº)
T = trabalho (J)
F = força (N)
d = deslocamento (m)
cos = ângulo (º)
QUESTÕES RESOLVIDAS
81) Uma pessoa quer mudar a posição de um armário e para isso o empurra fazendo uma força constante e paralela ao chão, com intensidade de 50N, conforme figura abaixo. Sabendo que o deslocamento sofrido pelo armário foi de 3 m, determine o trabalho realizado pela pessoa sobre o armário, nesse deslocamento. Resolução:
Resolução:
Para encontrar o trabalho da força, podemos substituir diretamente na fórmula os valores informados. Observando que o ângulo θ será igual a zero, pois a direção e o sentido da força e do deslocamento são os mesmos.
Calculando o trabalho:
T = 50 . 3 . cos 0º
T = 150 J
Trabalho motor e trabalho resistente
Trabalho motor é nome que se dá ao trabalho que é realizado a favor do movimento de um corpo, dotando-lhe de energia cinética. Em contrapartida, o trabalho resistente é aquele em que se aplica uma força contrária ao movimento, fazendo com que o corpo tenha sua energia cinética reduzida e/ou transformada em outros tipos de energia, tais como energia potencial gravitacional ou energia térmica, para o caso em que atue uma força dissipativa.
Trabalho da força peso
O trabalho exercido pela força peso corresponde à quantidade de energia necessária para elevar um corpo de massa m até uma altura h em relação ao solo, em uma região onde a gravidade vale g.
T = m . g .h
T = trabalho (J)
m = massa do corpo (kg)
g = gravidade (m/s²)
h = altura (m)
QUESTÕES RESOLVIDAS
82) Um corpo de massa igual a 4 kg é abandonado do alto de um prédio a uma altura de 12 m. Considerando o valor da aceleração da gravidade local igual a 9,8 m/s2, determine o trabalho produzido pela força peso no deslocamento do corpo até o chão.
Resolução:
Para calcular o trabalho da força peso, basta multiplicar os valores indicados no enunciado. Como a força peso atua na mesma direção e sentido da deslocamento, o trabalho será positivo.
T = m . g . h
T = 4 . 9,8 . 12
T = 470,4 J
Trabalho da força elétrica
O cálculo do trabalho da força elétrica pode ser feito a partir do produto entre o módulo da carga e a diferença de potencial elétrico, em volts, a que essa carga é submetida.
T = q . ΔU
T = trabalho (J)
q = carga elétrica (C)
ΔU = diferença de potencial (V)
Trabalho de uma força variável
O trabalho de uma força variável pode ser calculado a partir de um gráfico que relacione a força com o deslocamento sofrido pelo corpo. Nesse caso, o módulo do trabalho realizado é numericamente igual à área abaixo da curva.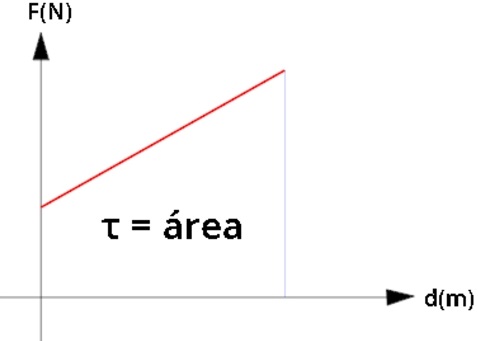
QUESTÕES RESOLVIDAS
83) No gráfico abaixo, representamos a força motora que age no movimento de um carro. Determine o trabalho desta força que atua na direção do movimento do carro, sabendo que o mesmo partiu do repouso. Resolução:
Resolução:
Na situação apresentada, o valor da força não é constante em todo o deslocamento. Sendo assim, vamos calcular o trabalho através do cálculo da área da figura, que nesse caso é um trapézio.
Assim, no deslocamento a força motora fez um trabalho de 540 kJ.
TRABALHO DA FORÇA ELÁSTICA
Quando esticamos ou comprimimos uma mola, verificamos que surge uma força que tenta fazer com que a mola volte a sua posição de equilíbrio.
Essa força, chamada de força elástica, não é constante e sua intensidade varia em função da deformação. Abaixo apresentamos o gráfico da força elástica: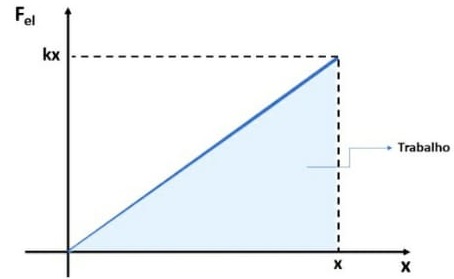 Assim, o módulo do trabalho da força elástica será igual a área da figura, que neste caso é um triângulo. Sendo expresso por:
Assim, o módulo do trabalho da força elástica será igual a área da figura, que neste caso é um triângulo. Sendo expresso por: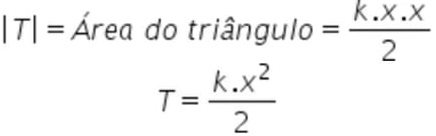 T = trabalho (J)
T = trabalho (J)
k = constante elástica da mola (N/m)
x = deformação da mola (m)
O trabalho da força elástica, assim como o trabalho da força peso, também não depende da trajetória. Forças que possuem essa característica são chamadas de conservativas.
Teorema do trabalho e da energia cinética
O teorema do trabalho e da energia cinética relaciona a quantidade de trabalho que é exercida sobre um corpo ou sobre um sistema de corpos de acordo com a variação de sua energia cinética. Em outras palavras, toda realização de trabalho vem acompanhada de uma variação de energia cinética.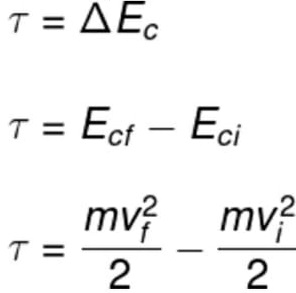 De forma resumida, dizemos que o trabalho exercido é igual à variação da energia cinética:
De forma resumida, dizemos que o trabalho exercido é igual à variação da energia cinética:
QUESTÕES RESOLVIDAS
84) Uma força de intensidade 1000 N, aplicada sobre um objeto de 500 g, arrasta-o por uma distância de 0,5 m. Marque a alternativa que caracteriza de forma correta a grandeza trabalho e que fornece o trabalho da força de F.
(A) O trabalho é uma grandeza vetorial; 500 J.
(B) O trabalho é a energia gasta na execução de uma tarefa; 250 J.
(D) O trabalho é uma grandeza escalar; 500 J.
(D) O trabalho é uma grandeza adimensional; 250 J.
(E) O trabalho é medido em kgf; 550 N.
Resolução:
O trabalho é dado pelo produto da força pelo deslocamento:
T = F.d
T = 1000 . 0,5
T = 500 J
O trabalho é a quantidade de energia gasta na execução de uma tarefa. Por ser energia, é grandeza escalar.
Alternativa: C
85) (Espcex) Um bloco, puxado por meio de uma corda inextensível e de massa desprezível, desliza sobre uma superfície horizontal com atrito, descrevendo um movimento retilíneo e uniforme. A corda faz um ângulo de 53° com a horizontal e a tração que ela transmite ao bloco é de 80 N. Se o bloco sofrer um deslocamento de 20 m ao longo da superfície, o trabalho realizado pela tração no bloco será de:
(Dados: sen 53° = 0,8 e cos 53° = 0,6)
(A) 480 J
(B) 640 J
(C) 960 J
(D) 1280 J
(E) 1600 J
Resolução:
Para respondermos a essa questão, é necessário utilizar a fórmula do trabalho, mas também identificar os dados pertinentes no enunciado, que são a força, a distância e o cosseno do ângulo. Em seguida, é necessário fazer o cálculo a seguir: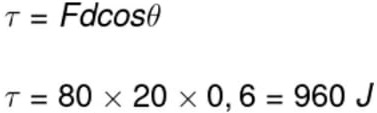
Alternativa: C
86) (CPS) Para transportar terra adubada retirada da compostagem, um agricultor enche um carrinho de mão e o leva até o local de plantio aplicando uma força horizontal, constante e de intensidade igual a 200 N. Se durante esse transporte, a força resultante aplicada foi capaz de realizar um trabalho de 1800 J, então a distância entre o monte de compostagem e o local de plantio foi, em metros:
(A) 6
(B) 9
(C) 12
(D) 16
(E) 18
Resolução:
A questão pede que calculemos a distância e, para tanto, nos é informado o módulo da quantidade de trabalho, bem como da força. Dessa maneira, devemos fazer o seguinte cálculo: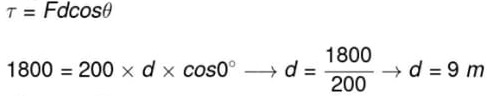
Alternativa: B
87) (Mackenzie) Na Olimpíada Rio 2016, nosso medalhista de ouro em salto com vara, Thiago Braz, de 75,0 kg, atingiu a altura de 6,03 m, um recorde mundial, caindo a 2,80 m do ponto de apoio da vara. Considerando o módulo da aceleração da gravidade g = 10 m/s², o trabalho realizado pela força peso durante a descida foi aproximadamente de:
(A) 2,10 kJ
(B) 2,84 kJ
(C) 4,52 kJ
(D) 4,97 kJ
(E) 5,10 kJ
Resolução:
A resposta dessa questão requer que calculemos uma quantidade de trabalho. Para tanto, precisamos saber os valores da massa, da gravidade e da altura. Em posse desses valores, basta fazermos o cálculo: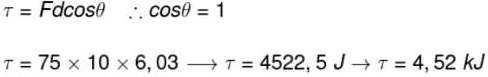
Alternativa: C
88) (Enem) Uma análise criteriosa do desempenho de Usain Bolt na quebra do recorde mundial dos 100 metros rasos mostrou que, apesar de ser o último dos corredores a reagir ao tiro e iniciar a corrida, seus primeiros 30 metros foram os mais velozes já feitos em um recorde mundial, cruzando essa marca em 3,78 segundos. Até se colocar com o corpo reto, foram 13 passadas, mostrando sua potência durante a aceleração, o momento mais importante da corrida. Ao final deste percurso, Bolt havia atingido a velocidade máxima de 12 m/s.
Supondo que a massa desse corredor seja igual a 90 kg, o trabalho total realizado nas 13 primeiras passadas é mais próximo de:
(A) 5,4 .×102 J
(B) 6,5×103 J
(C) 8,6×103 J
(D) 1,3×104 J
(E) 3,2×104 J
Resolução:
Para resolver a questão, basta utilizar o teorema da energia cinética, pois queremos descobrir o valor do trabalho e temos o valor da velocidade. Como queremos calcular para as 13 primeiras passadas, a velocidade inicial é igual a zero, portanto:![]()
Alternativa: B
89) (UERJ) Uma pessoa empurrou um carro por uma distância de 26 m, aplicando uma força F de mesma direção e sentido do deslocamento desse carro. O gráfico abaixo representa a variação da intensidade de F, em newtons, em função do deslocamento d, em metros.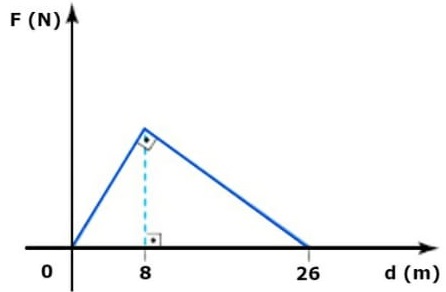 Desprezando o atrito, o trabalho total, em joules, realizado por F, equivale a:
Desprezando o atrito, o trabalho total, em joules, realizado por F, equivale a:
(A) 117
B) 130
(C) 143
(D) 156
Resolução:
Para calcular o trabalho de uma força variável, devemos encontrar a área da figura, que neste caso é um triângulo.
A = (b.h) /2
Como não conhecemos o valor da altura, podemos usar a relação trigonométrica: h2 = m . n. Então:
H2 = 8.18 = 144
h = 12m
T = (12.26)/2
T = 156 J
Alternativa: D
90) O primeiro satélite geoestacionário brasileiro foi lançado ao espaço em 2017 e será utilizado para comunicações estratégicas do governo e na ampliação da oferta de comunicação de banda larga. O foguete que levou o satélite ao espaço foi lançado do Centro Espacial de Kourou, na Guiana Francesa. A massa do satélite é constante desde o lançamento até a entrada em órbita e vale m = 6,0.103 kg. O módulo de sua velocidade orbital é igual a vor = 3,0.103 m/s.
Desprezando a velocidade inicial do satélite, em razão do movimento de rotação da Terra, o trabalho da força resultante sobre o satélite para levá-lo até a sua órbita é igual a:
(A) 2 MJ
(B) 18 MJ
(C) 27 GJ
(D) 54 GJ
Resolução
O trabalho exercido sobre o satélite é igual à sua variação de energia cinética, portanto:
Alternativa: C
91) Marque a alternativa correta:
(A) O trabalho de uma força independe de o corpo entrar em movimento.
(B) Trabalho é uma grandeza vetorial.
(C) O trabalho é definido como motor caso a força e o deslocamento tenham o mesmo sentido.
(D) O trabalho de uma força é diretamente proporcional à força aplicada sobre ele e inversamente proporcional à distância percorrida.
(E) Quando o trabalho é efetuado pela força peso, depende apenas da trajetória percorrida pelo objeto.
Resolução:
O trabalho é definido como motor caso a força e o deslocamento tenham o mesmo sentido. Vejamos por que as demais estão incorretas:
Alternativa “a” está incorreta porque o trabalho é definido como a relação entre força e o deslocamento. Portanto, se não há deslocamento, não foi realizado nenhum trabalho.
Alternativa “b” está incorreta porque o trabalho é uma grandeza escalar. Grandezas vetoriais são aquelas que possuem módulo, direção e sentido. O trabalho possui apenas módulo, portanto, não pode ser caracterizado como grandeza vetorial.
A alternativa “d” é incorreta porque, de acordo com equação T = F . d, podemos perceber que o trabalho é diretamente proporcional à força e ao deslocamento.
A alternativa “e” está incorreta, pois o trabalho independe da trajetória percorrida.
Alternativa: C
92) Um bloco de massa igual a 7 Kg é levantado a uma altura de 10 m. Calcule o trabalho realizado pela força peso sabendo que a gravidade no local é 10m/s2.
Resolução:
Se o objeto está sendo levantado, o trabalho realizado sobre ele é negativo:
T = - m . g . h
T = - 7 . 10 . 10
T = - 700 J
93) (PUC-MG) Não realiza trabalho:
(A) a força de resistência do ar;
(B) a força peso de um corpo em queda livre;
(C) a força centrípeta em um movimento circular uniforme;
(D) a força de atrito durante a frenagem de um veículo;
(E) a tensão no cabo que mantém um elevador em movimento uniforme.
Resolução:
A força que não realiza trabalho é a centrípeta, pois é perpendicular ao movimento.
Alternativa: C
94) (PUC-BA) A força F de módulo 30N atua sobre um objeto formando um ângulo constante de 60o com a direção do deslocamento do objeto. Dados: sen 60o= √3/2, cos 60o=1/2. Se d=10m, o trabalho realizado pela força F, em joules, é igual a:
(A) 300
(B) 150√3
(C) 150
(D) 125
(E) 100
Resolução:
T = F . d . cosα
T = 30 . 10 . ½
T = 150 J
Alternativa: C
95) (FGV SP) Mantendo uma inclinação de 60º com o plano da lixa, uma pessoa arrasta sobre esta a cabeça de um palito de fósforos, deslocando-o com velocidade constante por uma distância de 5 cm, e ao final desse deslocamento, a pólvora se põe em chamas. Se a intensidade da força, constante, aplicada sobre o palito é 2 N, a energia empregada no acendimento deste, desconsiderando-se eventuais perdas, é:
Se a intensidade da força, constante, aplicada sobre o palito é 2 N, a energia empregada no acendimento deste, desconsiderando-se eventuais perdas, é:
Dados: ![]()
(A) 5√3 x 10-2 J
(B) 5 x 10-2 J
(C) 2√3 x 10-2 J
(D) 2 x 10-2 J
(E) √3 x 10-2 J
Resolução:
Como o exercício nos orienta a desprezar eventuais perdas, podemos supor que toda energia será transferida para o palito.
Vamos utilizar a expressão do trabalho realizado pela força. A força realiza trabalho sobre o palito, esse trabalho é igual à variação da energia cinética do próprio palito.
T = F . d . cos θ
Logo: T = 2 x 0,05 x 0,5 = 0,05 J.
Expressando esse resultado em notação científica, temos:
T = 5 . 10-2J.
Alternativa: B
96) (Mackenzie SP) Uma caixa de massa m é abandonada do repouso, do topo do plano inclinado liso da figura. Essa caixa passa pelo ponto B e, devido ao atrito existente no trecho horizontal, para no ponto C. O coeficiente de atrito no trecho BC pode ser dado por:
O coeficiente de atrito no trecho BC pode ser dado por:
(A) μ = x
h
(B) μ = h
x
(C) μ = 2h
x
(D) μ = x
h2
(E) μ = 2x
h
Resolução:
Fazendo: Energia mecânica em A : Ea = Mgh
Energia mecânica em B: Eb = MVb²/2
temos que
Ea = Eb, logo: Mgh = MVb²/2.
Dividindo os dois lados da equação por M e passando o 2 multiplicando, temos: Vb² = 2gh.
Sabendo que de B até C o movimento será retilíneo variado, podemos fazer:
Vb² = Vc² - 2α x (Equação de Torricelli)
2gh = 2αx, então α = -gh/x
Pela segunda lei de Newton temos que Fr = m.α, mas a partir do ponto B, a única força que atua sobre o bloco é a força de atrito cinético. Logo:
-μN = M.(-gh/x), onde N é força normal, que é perpendicular à superfície BC, e nesse caso tem módulo igual ao do peso Mg da caixa.
μ.Mg = Mgh/x
Então: μ = h/x.
Alternativa: B
97) Imagine a seguinte situação: um operário da construção civil precisa carregar um saco de cimento de 50 kg. Ele levanta esse saco de cimento e se desloca por 20 metros na horizontal. Adote g = 10 m/s². Calcule o trabalho realizado pela força do operário sobre o cimento.
(A) 1000 J
(B) 2500 J
(C) 0 J
(D) 10000J
(E 50 J
Resolução:
A resposta é zero. Embora o operário exerça uma força em módulo igual ao peso do saco de cimento, que é de 500 N, essa força é na vertical, enquanto seu deslocamento é na horizontal, ou seja, o ângulo entre a força e o deslocamento é 90°. Quando a força e o deslocamento formam um ângulo igual a 90°, o trabalho realizado por essa força é nulo. Veja: T = F . d . cos θ
θ = 90°, logo cos 90° = 0, então T = 0.
Alternativa: C
98) Um objeto de massa 5 kg é deixado cair de uma determinada altura. Ele chega ao solo com energia cinética igual 2000 J. Determine a altura que o objeto foi abandonado. Despreze o atrito com o ar e considere g = 10 m/s²
Resolução:
Pela conservação da energia mecânica (E) temos:
Einicial = Efinal
No início só temos energia potencial gravitacional, pois o objeto é abandonado do repouso. No final , ao chegar no solo, toda energia potencial gravitacional se converteu em energia cinética. Então:
m .g. h = 2000, logo 5 . 10 . h = 2000
h = 2000/50
h = 40 m
99) Um corpo com massa de 5 kg é submetido a uma força de intensidade 25N. Qual é a aceleração que ele adquire?
Resolução:
F = m . a
a = F/m
a = 25/5
a = 5 m/s2
100) (UFRGS) Aplica-se uma força de 20 N a um corpo de massa m. O corpo desloca-se em linha reta com velocidade que aumenta 10 m/s a cada 2 s. Qual o valor, em kg, da massa m?
(A) 5.
(B) 4.
(C) 3.
(D) 2.
(E) 1.
Resolução:
Para encontrar o valor da massa, vamos aplicar a segunda lei de Newton. Para isso, precisamos primeiro calcular o valor da aceleração.
Como a aceleração é igual ao valor da variação da velocidade dividido pelo intervalo de tempo, temos:
a= 10/2
a= 5 m/a2
Aplicando
F = m . a
20 = m . 5
m = 20/5
m = 4
Alternativa: B
101) Um corpo de massa igual a 2,0 kg move-se sobre um piso horizontal e sem atrito com velocidade inicial de 36,0 km/h quando submetido a uma força de 4,0 N, durante um intervalo de tempo de 3,0 s. Sobre o movimento desse corpo, determine:
a) A aceleração do corpo.
Resolução:
Para calcularmos a aceleração do corpo, utilizamos a Segunda Lei de Newton:![]()
De acordo com os dados informados pelo enunciado, teremos uma aceleração igual a:![]()
b) A velocidade do corpo ao final dos 3,0 s.
Resolução:
Para calcularmos a velocidade final do corpo, usaremos a própria definição de aceleração:![]()
Substituindo os valores informados pelo exercício, percebemos que será necessário transformar a velocidade inicial do corpo para m/s, dividindo o valor de 36 km/h pelo fator 3,6. Dessa forma, teremos:
c) O espaço percorrido pelo corpo ao final dos 3,0 s.
Resolução:
Podemos calcular o espaço percorrido pelo corpo por meio da equação de Torricelli. Observe:
102) Observe o sistema de blocos representado na figura abaixo. Os dois blocos da figura, de massas ma = 2,0 kg e mb = 3,0 kg, movem-se juntos em razão de uma força externa de 20,0 N, orientada da esquerda para a direita, exercida sobre o bloco A."A respeito do sistema de corpos mostrado acima, determine:
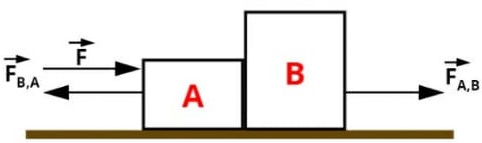 a) A aceleração do conjunto.
a) A aceleração do conjunto.
Resolução:
Para calcularmos a aceleração do sistema de corpos acima, devemos utilizar a Segunda Lei de Newton:
Como temos dois corpos, devemos aplicar a lei acima para cada um dos blocos individualmente, prestando atenção em quais forças atuam em cada um dos corpos. Dessa forma, montamos o sistema de forças, como mostrado abaixo:
(Neste exercício, orientamos o sentido esquerda-direita como o sentido positivo para as forças.)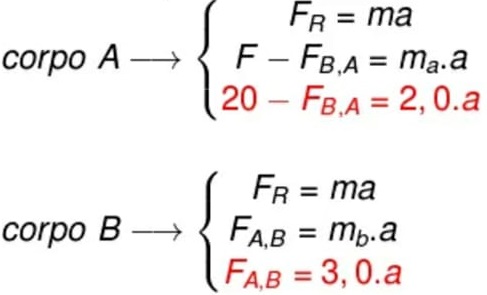
Em seguida, somamos as duas equações em vermelho. Lembre-se de que FA,B e FB,A constituem um par de ação e reação, portanto, têm módulos iguais, cancelando-se em decorrência da diferença de sinais: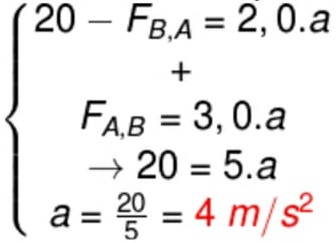
b) A força que o bloco A exerce sobre o bloco B (FA,B).
Resolução:
A força que o corpo A exerce sobre o corpo B pode ser calculada apenas substituindo o valor encontrado, no item acima, para a aceleração:
Como as forças que A faz em B e B faz em A são pares de ação e reação, as duas têm o mesmo módulo.
c) A força que o bloco B exerce sobre o bloco A (FB,A).
Resolução:
FB,A = 12,0 N
d) Considerando que o sistema de blocos encontra-se inicialmente em repouso, calcule seu deslocamento após um tempo de 5,0 s. Desconsidere o tamanho dos blocos.
Resolução:
Podemos calcular o deslocamento sofrido pelos corpos por meio da função horária da posição, Para tanto, devemos considerar que o sistema de blocos parte do repouso: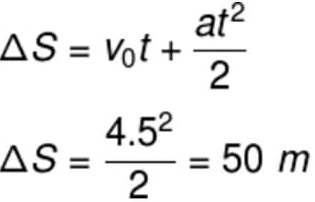
103) (PUC) Quando a resultante das forças que atuam sobre um corpo é 10N, sua aceleração é 4m/s2. Se a resultante das forças fosse 12,5N, a aceleração seria de:
(A) 2,5m/s2
(B) 5,0m/s2
(C) 7,5 m/s2
(D) 2 m/s2
(E) 12,5 m/s2
Resolução:
Inicialmente devemos encontrar a massa desse corpo. Como são dadas a aceleração e a distância, podemos usar a equação:
FR1 = m . a
m = FR1/a
m = 10/4
m = 2,5 Kg
Possuindo o valor da massa e a força, utilizaremos novamente a expressão acima para calcular a aceleração:
FR2 = m . a'
a' = FR2
m
a' = 12,5
2,5
a' = 5 m/s2
Alternativa: B
104) Uma folha de massa igual 0,3 g cai de uma árvore com velocidade constante. Determine a força resultante sobre essa folha, sabendo que ela está sujeita à força de resistência do ar.
Dado: a aceleração da gravidade tem valor igual a 9,8 m/s².
Resolução:
Como a folha cai com velocidade constante, sua aceleração é igual a zero (a = 0).
Pela segunda lei de Newton, temos: Fr = m . a, logo nesse caso Fr = 0
105) Um bloco de massa 50 Kg é empurrado sobre uma superfície horizontal por uma força F = 220 N. Sabendo que o coeficiente de atrito cinético (μc) entre o bloco e a superfície é igual a 0,2, calcule a aceleração sofrida pelo bloco.
Resolução:
A força de atrito (fat) pode ser calcula assim:
fat = μc . N
e N é a força normal que é igual ao seu peso, nesse caso: N = m . g
fat = μc . m . g
fat = 0,2 x 50 x 10
fat = 100 N
Pela segunda Lei de Newton, temos que Fr = m . a
Fr = F – fat
Fr = 220 – 100
Fr = 120 N
Agora substituímos esse valor em: Fr = m . a
120 = 50 . a
a = 2,4 m/s²
106) (Unespar-PR) Um corpo com massa de 5 kg é lançado sobre um plano horizontal liso, com velocidade de 40 m/s. Determine o módulo da intensidade da força que deve ser aplicada sobre o corpo contra o sentido do movimento, para pará-lo em 20 s.
(A) 200 N
(B) 20 N
(C) 10 N
(D) 40 N
(E) 8 N
Resolução:
Se essa força parar o corpo, sua velocidade será zero.
Podemos usar a função horária da velocidade para calcular o módulo da aceleração sofrida pelo corpo.
V = Vo + a . t
0 = 40 + 20 . a
a = - 40/20
a = - 2 m/s², em módulo a = 2 m/s²
Logo, a força necessária para isso será:
F = m . a
F = 5 . 2
F = 10 N
Alternativa: C
107) (PUC-MG) Um automóvel, com uma massa de 1200 kg, tem uma velocidade de 72 km/h quando os freios são acionados, provocando uma desaceleração constante e fazendo com que o carro pare em 10 s, a força aplicada ao carro pelos freios vale, em newtons:
(A) 3600
(B) 2400
(C) 1800
(D) 900
Resolução:
72 km/h : 3,6 = 20 m/s
V = Vo + a . t
0 = 20 + 10 a
a = - 2 m/s², e módulo: 2 m/s²
Fr = m . a
Fr =1200 . 2
Fr = 2400 N
Alternativa: D
FORÇA DE ATRITO
A força de atrito corresponde a força exercida entre duas superfícies que estão em contato.
Dessa forma, a força atrito possui direção, sentido e módulo, sendo uma força de oposição à tendência do escorregamento.
Portanto, a força atrito é uma força que se opõe ao movimento do corpo ou dos objetos, tentando impedi-lo. A força de atrito surge das irregularidades entre duas superfícies que estejam em contato.
Logo, quanto maior às rugosidades apresentadas nas superfícies, maior será a força de atrito. Importante destacar que por mais lisa que seja determinada superfície, ela terá uma força atrito.
A expressão utilizada para calcular a força atrito é:
Fat = µ . N
Fat = força de atrito
µ = coeficiente de atrito
N = força normal
O coeficiente de atrito (µ) é uma propriedade do material e do estado das superfícies que estão em contato.
Além disso, trata-se de um valor numérico adimensional, ou seja, não possui unidade. Por sua vez, a força normal, indicada pela letra N, designa a reação da pressão exercida sobre a superfície e depende diretamente do peso do objeto.
TIPOS DE ATRITO
Dependendo da superfície e do corpo, há dois tipos de força atrito: atrito estático e o atrito dinâmico.
Note que a força de atrito será ligeiramente maior quando o corpo está a ponto de se deslocar (atrito estático) do que quando ela está em movimento (atrito cinemático ou dinâmico).
Nesse sentido, vale observar que o coeficiente (µ) do atrito estático será sempre maior que o coeficiente do atrito dinâmico (µe> µd):
ATRITO ESTÁTICO
Ocorre quando os dois corpos permanecem imóveis, ou seja, quando não há deslizamento, gerando uma maior força de atrito, por exemplo, empurrar uma pedra muito pesada.
Para calcular a força do atrito estático, utiliza-se a expressão:
Fate = µe . N
µe = coeficiente do atrito estático;
N = forca norml.
ATRITO DINÂMICO
Também chamado atrito cinético, o atrito dinâmico ocorre quando a força do atrito estático for superada, de modo que os dois corpos entram em movimento, gerando assim, uma menor força de atrito, por exemplo, empurrar a pedra depois que ela entrou em movimento.
Para calcular a força do atrito dinâmico, utiliza-se a expressão:
Fatd = µd . N
µd = coeficiente de atrito dinâmico;
N = força normal.
PLANO INCLINADO
Corpos apoiados sobre superfícies inclinadas têm a sua força peso dividida em componentes. Essas componentes, chamadas de componente horizontal (PX) e componente vertical (PY), podem ser calculadas por meio da decomposição do vetor força peso, confira como: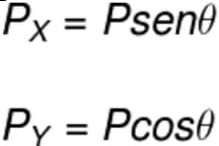 PX = componente horizontal do peso (N)
PX = componente horizontal do peso (N)
PY = componente vertical do peso (N)
QUESTÕES RESOLVIDAS
108) Qual o coeficiente de atrito de um bloco de 10kg que alcança 2m/s em um deslocamento de 10m, partindo do repouso? Sendo que a força que é aplicada a ele é 10N. Podemos calcular a aceleração do bloco utilizando a equação de Torricelli:
Podemos calcular a aceleração do bloco utilizando a equação de Torricelli:
Resolução:
V2 = Vo2 + 2aΔS
22 = 02 + 20a
4 = 20a
a = 4/20
a = 0,2m/s2
Pelo princípio da dinâmica, onde a Força resultante é proporcional à massa e aceleração:
F – Fat = m . a
10 – Fat = 10 . 0,2
10 – 2 = Fat
Fat = 8N
Conhecendo o módulo da força de atrito é possível calcular seu coeficiente de atrito:
Fat = µ . N
Fat = µ . N . g
8 = µ . 10 . 10
µ = 8/100
µ = 0,08
109) Uma força F é aplicada a um bloco de 15kg que desliza sobre um superfície onde o coeficiente de atrito dinâmico é 0,25. O corpo tem aceleração constante de 1m/s². Qual a força aplicada no corpo?
Resolução:
Pelo princípio da dinâmica:
F – Fat = m . a
F – µ . N = m . a
F – 0,25 . 15 . 10 = 15 . 1
F – 37,5 = 15
F = 15 + 37,5
F = 52,5N
110) (Fatec-SP) Um motorista conduzia seu automóvel de massa 2 000 kg que trafegava em linha reta, com velocidade constante de 72 km/h, quando avistou uma carreta atravessada na pista. Transcorreu 1 s entre o momento em que o motorista avistou a carreta e o momento em que acionou o sistema de freios para iniciar a frenagem, com desaceleração constante igual a 10 m/s2. Antes de o automóvel iniciar a frenagem, pode-se afirmar que a intensidade da resultante das forças horizontais que atuavam sobre ele era
(A) nula, pois não havia forças atuando sobre o automóvel.
(B) nula, pois a força aplicada pelo motor e a força de atrito resultante atuavam em sentidos opostos com intensidades iguais.
(C) maior do que zero, pois a força aplicada pelo motor e a força de atrito resultante atuavam em sentidos opostos, sendo a força aplicada pelo motor a de maior intensidade.
(D) maior do que zero, pois a força aplicada pelo motor e a força de atrito resultante atuavam no mesmo sentido com intensidades iguais.
(E) menor do que zero, pois a força aplicada pelo motor e a força de atrito resultante atuavam em sentidos opostos, sendo a força de atrito a de maior intensidade.
Resolução:
Como a velocidade do automóvel era constante, ele se encontrava em equilíbrio dinâmico, e a soma de todas as forças que atuavam sobre ele era nula. A força aplicada pelo motor foi anulada pela força de atrito entre os pneus e o chão e pelo atrito com o ar. Para que sejam anuladas, essas forças devem ter a mesma intensidade e sentidos opostos.
Alternativa: B
111) (PUC-RS) Sobre uma caixa de massa 120 kg, atua uma força horizontal constante F de intensidade 600 N. A caixa encontra-se sobre uma superfície horizontal em um local no qual a aceleração gravitacional é 10 m/s2. Para que a aceleração da caixa seja constante, com módulo igual a 2 m/s2, e tenha a mesma orientação da força F, o coeficiente de atrito cinético entre a superfície e a caixa deve ser de
(A) 0,1
(B) 0,2
(C) 0,3
(D) 0,4
(E) 0,5
Resolução:
O coeficiente de atrito é determinado pela segunda lei de Newton.
Considere que:
Peso: P = m.g
O objeto está sobre uma superfície horizontal, logo, o peso é igual à força normal;
FAT = μ . N;
Para que a aceleração tenha a mesma orientação da força aplicada sobre a caixa, esta deve ser maior que a força de atrito (F > FAT).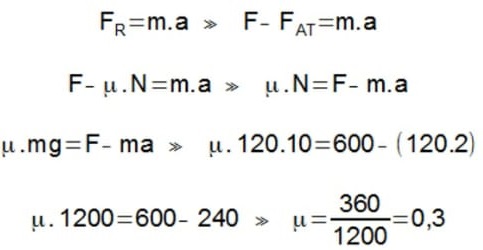
Alternativa: B
112) Marque a alternativa correta a respeito da força de atrito.
(A) A força de atrito sempre é oposta ao movimento dos objetos.
(B) O coeficiente de atrito estático é menor que o coeficiente de atrito dinâmico (cinético).
(C) Se um objeto estiver em uma superfície horizontal, a força de atrito será determinada pelo produto do coeficiente de atrito pelo valor do peso do corpo.
(D) Se um objeto estiver parado sobre um plano inclinado, a força de atrito será igual à componente da força peso escrita sobre o eixo x e determinada por PX = P. cos θ.
(E) Todas as alternativas estão incorretas.
Resolução:
a) Errada. Quando caminhamos, o chão é empurrado para trás, de modo que o atrito impulsiona-nos para frente. Nesse caso, movimento e atrito possuem mesmo sentido.
b) Errada. O coeficiente de atrito estático é maior que o coeficiente de atrito dinâmico (cinético).
c) Correta.
d) Errada. Se um objeto estiver parado sobre um plano inclinado, a força de atrito será igual à componente da força peso escrita sobre o eixo x e determinada por PX= P. sen θ.
e) Errada.
Alternativa: C
113) Um homem puxa um objeto de 40 kg ao longo de uma calçada plana e totalmente horizontal e aplica sobre ela uma força de 80 N. Sabendo que o objeto move-se com velocidade constante, determine o coeficiente de atrito cinético entre a caixa e o solo.
Dados: Adote a aceleração da gravidade como 10 m/s2.
(A) 0,1
(B) 0,2
(C) 0,4
(D) 0,6
(E) 0,8
Resolução:
Para que o objeto movimente-se com velocidade constante, a força aplicada pelo homem deve ser igual e oposta à força de atrito. Sabendo que a força normal é igual ao peso do objeto, pois a superfície é horizontal, podemos escrever: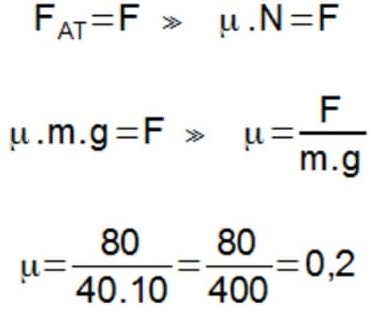
Alternativa: B
114) (Fatec) O bloco da figura, de massa 5 kg, move-se com velocidade constante de 1,0 m/s em um plano horizontal, sob a ação da força F, constante e horizontal. Se o coeficiente de atrito entre o bloco e o plano vale 0,20 e a aceleração da gravidade, 10 m/s2, então o módulo da força F, em Newtons, vale:
Se o coeficiente de atrito entre o bloco e o plano vale 0,20 e a aceleração da gravidade, 10 m/s2, então o módulo da força F, em Newtons, vale:
(A) 25
(B) 20
(C) 15
(D) 10
(E) 5
Resolução:
Primeiramente, devemos identificar as forças atuando sobre o bloco. Nele, há a força F e a força de atrito. Como ele está se movimentando, a força F é maior que a força de atrito, portanto calcularemos F por meio da fórmula da força resultante:
FR = F - Fat
A aceleração será nula, porque a velocidade é constante. Falta o valor da força normal, que é igual à força peso:
N = P
N = m . g
N = 5 . 10
N = 50 N
Substituindo todos os valores na fórmula da força resultante, encontraremos a força F:
FR = F - Fat
m . a = F - µd . N
5 . 0 = F – 0,5 . 50
0 = F - 10
F = 10 N
Alternativa: D
115) (Enem) Uma pessoa necessita da força de atrito em seus pés para se deslocar sobre uma superfície. Logo, uma pessoa que sobe uma rampa em linha reta será auxiliada pela força de atrito exercida pelo chão em seus pés. Em relação ao movimento dessa pessoa, quais são a direção e o sentido da força de atrito mencionada no texto?
(A) Perpendicular ao plano e no mesmo sentido do movimento.
(B) Paralela ao plano e no sentido contrário ao movimento.
(C) Paralela ao plano e no mesmo sentido do movimento.
(D) Horizontal e no mesmo sentido do movimento.
(E) Vertical e sentido para cima.
Resolução:
Ao pisarmos no chão, fazemos uma força para trás, e o atrito faz uma força para frente. Então, a força de atrito possui direção paralela ao movimento, sendo horizontal e com o mesmo sentido do movimento, contrária à força dos pés.
Alternativa: C
16) Uma pessoa se move em uma bicicleta em uma pista que possui um coeficiente de atrito cinético igual a 0,7. Determine a força de atrito entre a bicicleta e a pista, sabendo que a força normal aplicada sobre elas é de 100 N.
(A) 60 N
(B) 70 N
(C) 80 N
(D) 90 N
(E) 100 N
Resolução:
Como a caixa ainda não se moveu, a força de atrito é estática, e a calcularemos usando a fórmula:
Fat = µd . N
Fat = 0,7 . 100
Fat = 70 N
Alternativa: B
117) Dois colegas estão se mudando de casa e organizando as caixas. Eles tentam mover uma caixa de 20 kg. Sabendo que o atrito estático entre a caixa e a superfície é de 0,3 e a força normal sobre a caixa é de 50 N, qual é a força de atrito que a superfície está fazendo e impedindo que a caixa se mova?
(A) 13 N
(B) 14 N
(C) 15 N
(D) 16 N
(E) 17 N
Resolução:
Como a caixa ainda não se moveu, a força de atrito é estática, e a calcularemos por meio da fórmula:
Fat = µd . N
Fat = 0,5 . 50
Fat = 15 N
Alternativa: C
118) Qual das alternativas abaixo corresponde aos fatores que influenciam na força de atrito?
(A) A força normal e o coeficiente de atrito.
(B) A força peso e o coeficiente de atrito.
(C) A força normal e a força peso.
(D) O coeficiente de atrito estático e o cinético.
(E) A força de normal e a força de tração.
Resolução:
Os fatores que influenciam na força de atrito são a força normal e o coeficiente de atrito, como podemos identificar na sua fórmula:
Fat = µd . N
Alternativa: A
119) Uma pessoa faz uma força F de 200 N sobre três blocos que estão apoiados sobre uma superfície plana e horizontal, como podemos ver na imagem abaixo. Sabendo que as massas dos blocos são 5 kg, 10 kg e 15 kg e que eles se movem a uma aceleração de 4 m/s2, qual é a intensidade da força de atrito sobre eles?
Sabendo que as massas dos blocos são 5 kg, 10 kg e 15 kg e que eles se movem a uma aceleração de 4 m/s2, qual é a intensidade da força de atrito sobre eles?
(A) 60 N
(B) 70 N
(C) 80 N
(D) 90 N
(E) 100 N
Resolução:
Como os blocos estão se movimentando, a força F aplicada sobre eles é maior que a força de atrito. Portanto, calcularemos a força de atrito por meio da fórmula da força resultante:
FR = F - Fat
a . m = F - Fat
(5 + 10 + 15) . 4 = 200 - Fat
30 . 4 = 200 - Fat
120 = 200 - Fat
Fat = 200 - 120
Fat = 80 N
Alternativa: C
FORCA CENTRÍPETA
A força centrípeta é a força que age sobre os corpos no movimento circular em determinada trajetória curvilínea.
Através dela, é possível mudar a direção da velocidade de um corpo em uma trajetória circular, atraindo-o para o centro.![]() FCP = força centrípeta (N)
FCP = força centrípeta (N)
m = massa (kg)
v = velocidade (m/s)
R = raio da curva (m)
A força centrípeta também pode ser escrita em termos da velocidade angular (ω), confira:![]()
Por tratar-se de uma força, a centrípeta é uma grandeza vetorial, medida em newtons (N ou kg.m/s²). Além disso, de acordo com a 2ª lei de Newton, por tratar-se da resultante das forças, a centrípeta pode ser igualada ao produto da massa do corpo por sua aceleração. Desse modo, podemos definir uma fórmula para o cálculo da aceleração centrípeta:![]() acp = aceleração centrípeta (m/s²)
acp = aceleração centrípeta (m/s²)
QUESTOES RESOLVIDAS
120) Um carro de 1000 kg de massa entra, a 30 m/s, em uma curva de raio igual a 300 m, contida em uma superfície horizontal. Determine o módulo do coeficiente de atrito estático entre os pneus do carro e o asfalto, para que esse veículo não derrape.
(A) 0,5
(B) 3
(C) 0,3
(D) 0,2
(E) 0,8
Resolução:
Para fazermos esse cálculo, é necessário notar que a força de atrito entre os pneus e o solo desempenha o papel da força centrípeta. Depois disso, é necessário que nos lembremos da relação entre a força normal e o peso: essas forças têm a mesma intensidade quando em superfícies planas, desse modo, basta que façamos o seguinte cálculo: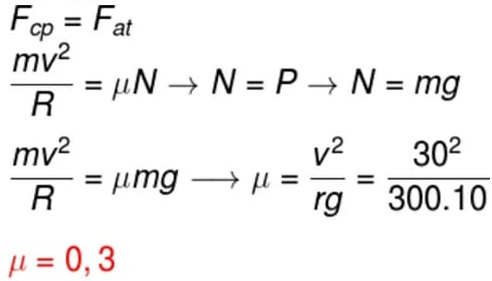
Alternativa: C
121) Um carrinho de brinquedo de 50 g é preso a uma corda de 0,05 m de comprimento e colocado para girar em torno de um prego que se encontra fixo a uma superfície perfeitamente horizontal. Sabendo que a velocidade do carrinho é de 0,1 m/s, determine a intensidade da força de tração que é feita pela corda, desconsidere a ação de quaisquer forças dissipativas.
(A) 1,0.10-2 N
(B) 5,0.10-3 N
(C) 1,0.10-4 N
(D) 6,0.10-1 N
(E) 1,0.10-3 N
Resolução:
Neste exercício, a força centrípeta é desempenhada pela força de tração exercida pela corda, desse modo, basta que façamos o seguinte cálculo:
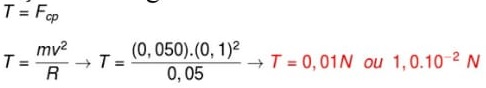
Alternativa: A
122) Um ciclista treina em uma pista circular, executando um movimento circular e uniforme, com velocidade igual a 20 m/s. Sendo o raio da pista igual a 80 m, determine o valor da aceleração centrípeta.
Resolução:
Como a aceleração centrípeta é dada por:![]()
Além disso, temos v = 20 m/s e R = 80 m, agora basta fazermos as substituições na expressão e calcular o valor da aceleração centrípeta ac.
123) Um objeto realiza um movimento circular e uniforme em uma circunferência com raio igual a 100 cm e com uma aceleração centrípeta de 4 m/s2. Determine sua velocidade.
Resolução:
A aceleração centrípeta é dada por:![]()
No exercício, temos:
4 m/s2
R = 100 cm = 1 m
v = ?
Substituindo na equação:
V=2 m/s.
124) (UFSM) A figura representa dois atletas numa corrida, percorrendo uma curva circular, cada um em uma raia. Eles desenvolvem velocidades lineares com módulos iguais e constantes, num referencial fixo no solo. Atendendo à informação dada, assinale a resposta correta.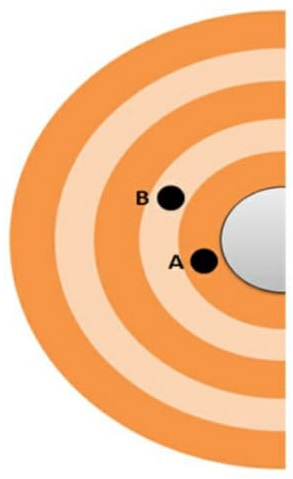 (A) Em módulo, a aceleração centrípeta de A é maior do que a aceleração centrípeta de B.
(A) Em módulo, a aceleração centrípeta de A é maior do que a aceleração centrípeta de B.
(B) Em módulo, as velocidades angulares de A e B são iguais.
(C) A poderia acompanhar B se a velocidade angular de A fosse maior do que a de B, em módulo.
(D) Se as massas dos corredores são iguais, a força centrípeta sobre B é maior do que a força centrípeta sobre A, em módulo.
(E) Se A e B estivessem correndo na mesma raia, as forças centrípetas teriam módulos iguais, independentemente das massas.
Resolução:
A expressão matemática da aceleração centrípeta é dada abaixo. Nota-se que ela é diretamente proporcional ao quadrado da velocidade e inversamente proporcional ao raio. ![]()
Uma informação tirada do enunciado da questão é que a velocidade linear é a mesma para o ciclista A e para o ciclista B. Além disso, observando a figura, percebe-se que a curvatura de A é menor que a de B, isto é, o raio de A é menor que o de B. Assim, conclui-se que a aceleração centrípeta de A é maior que a de B.
Alternativa: A
125) Um carro de corrida percorre uma pista circular com velocidade constante de 180 km/h e aceleração centrípeta de 25 m/s2. Com base nessas informações, podemos afirmar que o raio dessa pista é igual a:
(A) 1296 m
(B) 925 m
(C) 1200 m
(D) 800 m
(E) 100 m
Resolução:
Os dados da questão são:![]()
Observe que a velocidade estava em k/h e a aceleração em m/s2. Como nos foi pedido o raio da pista e as respostas estão em metros (m), passamos a velocidade que estava em k/h para m/s, para isso dividimos 180 km/h por 3,6.
Agora vamos substituir os valores na expressão da aceleração centrípeta para calcularmos o valor do raio da pista.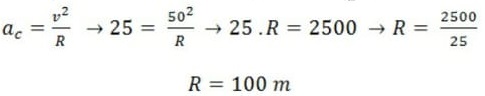
Alternativa: E
126) (Enem) O Brasil pode se transformar no primeiro país das Américas a entrar no seleto grupo das nações que dispõem de trens-bala. O Ministério dos Transportes prevê o lançamento do edital de licitação internacional para a construção da ferrovia de alta velocidade Rio-São Paulo. A viagem ligará os 403 quilômetros entre a Central do Brasil, no Rio, e a Estação da Luz, no centro da capital paulista, em 1 hora e 25 minutos.
Devido à alta velocidade, um dos problemas a serem enfrentados na escolha do trajeto que será percorrido pelo trem é o dimensionamento das curvas. Considerando-se que uma aceleração lateral confortável para os passageiros e segura para o trem seja de 0,1 g, em que g é a aceleração da gravidade (considerada igual a 10 m/s2) e que a velocidade do trem mantenha-se constante em todo o percurso, seria correto prever que as curvas existentes no trajeto deveriam ter raio de curvatura minimo de, aproximadamente:
(A) 80 m
(B) 430 m
(C) 800 m
(D) 1600 m
(E) 6400 m
Resolução:
Pede-se que encontremos o raio mínimo da curva que o trem precisa percorrer para que os passageiros não se sintam desconfortáveis. Para isso, devemos calcular a velocidade escalar do trem:
Alternativa: E
127) Um carro de fórmula 1 entra em uma curva a 108 km/h (30 m/s). Sabendo que o raio da curva em questão é de 90,0 m, a aceleração centrípeta sentida pelo piloto é igual a:
(A) 5 m/s²
(B) 10 m/s²
(C) 3 m/s²
(D) 8 m/s²
(E) 3 m/s²
Resolução:
Para fazermos o cálculo, utilizamos a fórmula da aceleração centrípeta.
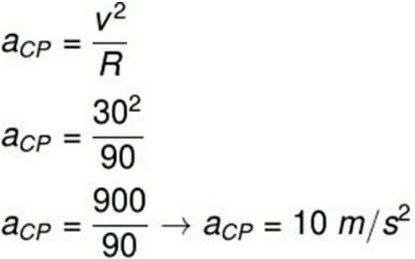
De acordo com os cálculos realizados, a aceleração centrípeta percebida pelo piloto é de 10 m/s², o equivalente a 1g (10 m/s², o módulo da aceleração da gravidade).
Alternativa: B
PETÊNCIA DE UMA FORÇA DURANTE UM PERCUSO
A potência é uma grandeza física que mensura a rapidez em que um equipamento executa um trabalho por meio da transformação de uma das formas de energia. Ela pode ser calculada pela sua fórmula geral, que é a variação de trabalho dividida pela variação de tempo.![]() Pot = potêncai (W)
Pot = potêncai (W)
T = trabalho (J)
Δt = tempo (s)
QUESTÕES RESOLVIDAS
128) Qual a potência média desenvolvida por uma força de intensidade 100N, durante um percurso de 20m durante um intervalo de tempo igual a 2s?
Resolução:![]()
129) Um bloco de massa 1kg tem aceleração constante de 3m/s². Sendo que esta parte do repouso, qual a potência instantânea do bloco após 10s?
Resolução:
Para fazermos este cálculo, é necessário saber a Força exercida sobre o bloco e a velocidade no instante pedido.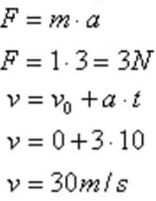
Conhecendo a Força e a velocidade instantânea:![]()
130) (FGV) Depois de anos investigando o funcionamento de nossas pernas, um grupo de cientistas construiu uma traquitana simples, mas extremamente sofisticada, que é capaz de diminuir o consumo de energia de uma caminhada em até 10%.
Uma pessoa caminhando, sem a traquitana, gasta 80 cal a cada metro. Utilizando o equipamento e reduzindo em 10% seu consumo de energia, essa pessoa percorreu uma distância D com velocidade média igual a 7,0 km/h e gastou energia correspondente a um prato de feijoada de 504 kcal. Os valores da distância D e da potência P consumida na caminhada são, respectivamente,
Dado: 1 cal = 4 J
(A) 5,7 km e 700 W.
(B) 6,3 km e 155 W.
(C) 6,3 km e 622 W.
(D) 7,0 km e 140 W.
(E) 7,0 km e 560 W.
Resolução:
Com o uso da traquitana, o gasto de energia para cada metro caminhado é 10% menor. Como o consumo de energia sem o equipamento é de 80 cal por metro andado, com a ajuda do dispositivo, o consumo cai para 72 cal por metro andado.
A energia consumida corresponde a 504 kcal = 504. 1000 cal = 504.000 cal. Se para cada 1 metro de deslocamento, a energia consumida é de 72 cal, a distância percorrida com 504.000 cal é:![]()
A energia total utilizada pode ser transformada em joules. Se cada caloria é equivalente a 4 J, podemos escrever que:![]()
A potência da caminhada é definida pela energia total, em J, e o tempo de 1 h. Sabendo que a velocidade de deslocamento é de 7 km/h e que o deslocamento executado foi de 7 km, definimos que o tempo gasto foi de 1 h, que equivale a 3600 s.![]()
Alternativa: E
131) (Enem) Um carro solar é um veículo que utiliza apenas a energia solar para a sua locomoção. Tipicamente, o carro contém um painel fotovoltaico que converte a energia do Sol em energia elétrica, que, por sua vez, alimenta um motor elétrico. A imagem mostra o carro solar Tokai Challenger, desenvolvido na Universidade de Tokai, no Japão, e que venceu o World Solar Challenge de 2009, uma corrida internacional de carros solares, tendo atingido uma velocidade média acima de 100 km/h. Considere uma região plana onde a insolação (energia solar por unidade de tempo e de área que chega à superfície da Terra) seja de 1 000 W/m2, que o carro solar possua massa de 200 kg e seja construído de forma que o painel fotovoltaico em seu topo tenha uma área de 9,0 m2 e rendimento de 30%.
Considere uma região plana onde a insolação (energia solar por unidade de tempo e de área que chega à superfície da Terra) seja de 1 000 W/m2, que o carro solar possua massa de 200 kg e seja construído de forma que o painel fotovoltaico em seu topo tenha uma área de 9,0 m2 e rendimento de 30%.
Desprezando as forças de resistência do ar, o tempo que esse carro solar levaria, a partir do repouso, para atingir a velocidade de 108 km/h é um valor mais próximo de
(A) 1,0 s.
(B) 4,0 s.
(C) 10 s.
(D) 33 s.
(E) 300 s.
Resolução:
A cada 1 m2, a potência disponível é de 1000 W, portanto, para os 9 m2 das placas solares do carro, a potência disponível é de 9000 W. Como o rendimento é de apenas 30% (0,3), somente 2700 W serão efetivamente utilizados (9000. 0,3 = 2700). A partir da equação da potência de uma força, teremos:![]()
A energia utilizada é a energia cinética, que se refere à velocidade de 108 km/h (30 m/s).
Alternativa: D
132) Um homem comeu uma refeição que totalizou 600 Kcal. Ao se exercitar, o indivíduo só conseguiu queimar a energia adquirida com a refeição depois de 6 h de atividade. Determine a potência, em W, aproximada desenvolvida pelo homem.
Dados: 1 cal = 4J; 1 h = 3600 s; 1 Kcal = 1000 cal.
(A) 102
(B) 122
(C) 152
(D) 202
(E) 112
Resolução:
A energia total consumida pelo homem em joules é de 2.400.000 J (600 Kcal = 600. 1000 = 60.0000 cal. 4 = 2.400.000 J). A partir da definição de potência e sabendo que 6 h correspondem a 21.600 s (6 x 3600s = 21.600 s), teremos: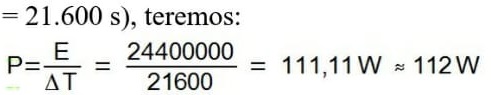
Alternativa: E
133) Um objeto é empurrado por uma força de intensidade 100 N que forma um ângulo de 60º com a horizontal. Sabendo que a velocidade do objeto durante a atuação da força é de 2 m/s, determine a potência média desenvolvida.
(A) 50 W
(B) 100 W
(C) 150 W
(D) 200 W
(E) 250 W
Resolução:
A potência pode ser definida em termos da força aplicada e da velocidade do objeto.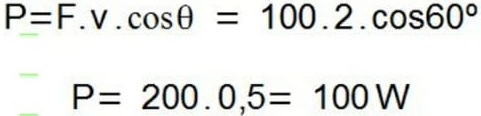
Alternativa: B
RENDIMENTO
Rendimento é uma importante variável para o estudo de sistemas não conservativos, isto é, que apresentam perdas de energia, como nos casos não ideais do nosso dia a dia. Todas as máquinas e aparelhos que conhecemos são sistemas incapazes de aproveitar toda a potência fornecida a eles.
Rendimento pode ser dada pela divisão da potência útil pela potência total recebida durante algum processo: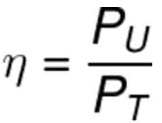 η = rendimento (%)
η = rendimento (%)
PU = potência útil (W)
PT = potência total (W)
QUESTÕES DE POTÊNCIA E RENDIMENTO
134) (FCM-PB) Em uma cachoeira aproveitada para mover uma roda d’água, a potência disponível é de 300 kW. Qual a potência útil para essa roda d’água cujo rendimento é de 50%?
(A) 150 kW
(B) 450 kW
(C) 50 kW
(D) 100 kW
(E) 200 kW
Resolução:
O rendimento é obtido pela razão entre a potência útil e a potência total. Sendo assim, podemos escrever: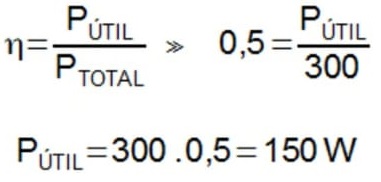
Alternativa: A
135) (Uncisal) No filme “De volta para o futuro” (Universal Pictures, USA, 1985), o protagonista cria uma máquina do tempo utilizando um automóvel modelo DeLorean DMC 1981. Para isso, o seu motor foi modificado para que fosse capaz de produzir uma potência de 1,21 GW. Supondo o rendimento do motor de 50%, a massa do automóvel igual a 1.210 Kg e desprezando a resistência do ar, um DeLorean com uma potência de 1,21 GW atingiria de 0 a 100 Km/h (100 Km/h ↓≈ 27 m/s) em um tempo de:
(A) 223,1 μs.
(B) 364,5 μs..
(C) 441,0 μs.
(D) 605,0 μs.
(E) 729,0 μs.
Resolução:
O trabalho realizado pelo motor corresponde à variação da energia cinética sofrida pelo carro.
A potência do veículo deve ser multiplicada por 0,5, uma vez que o rendimento do supercarro é de 50%. Dessa forma, ao utilizar a equação do rendimento, temos que: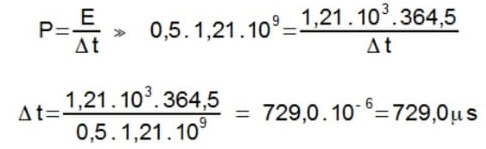
Alternativa: E
136) Leia as seguintes afirmações a respeito das grandezas potência e rendimento.
I – O rendimento é resultado da razão entre a potência total disponível e a potência efetivamente utilizada.
II – Cavalo-vapor é uma unidade de medida de potência maior que a unidade horse-power.
III – Se uma máquina que possui rendimento de 40% apresentar potência total de 500 W, a potência efetivamente utilizada será de 200 W.
Está correto o que se afirma em:
(A) I e II
(B) II e III
(C) I e III
(D) Apenas I
(E) Apenas III.
Resolução:
I – Falsa: O rendimento é o resultado da razão entre a potência útil e a potência total.
II – Falsa: A unidade horse-power é ligeiramente maior que a unidade cavalo-vapor.
III – Verdadeira: O rendimento corresponde à porcentagem efetivamente utilizada pela máquina. Portanto, nesse caso, a potência útil corresponde a 40 % da potência total, ou seja, 200 W.
Alternativa: E
137) Um homem empurra um objeto fazendo uma força de 100 N por uma distância de 25 m. Sabendo que o tempo gasto na execução da atividade foi de 50 s, determine a potência do homem.
(A) 250 W
(B) 150 W
(C) 100 W
(D) 50 W
(E) 25 W
Resolução:
A energia gasta pelo homem pode ser definida pela equação do trabalho de uma força.![]()
Sabendo que a potência é resultado da razão entre a energia consumida e o tempo gasto, temos: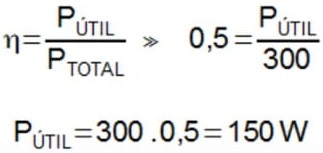
Alternativa: D
138) Leia as seguintes afirmações a respeito das grandezas potência e rendimento.
I – O rendimento é resultado da razão entre a potência total disponível e a potência efetivamente utilizada.
II – Cavalo-vapor é uma unidade de medida de potência maior que a unidade horse-power.
III – Se uma máquina que possui rendimento de 40% apresentar potência total de 500 W, a potência efetivamente utilizada será de 200 W.
Está correto o que se afirma em:
(A) I e II
(B) II e III
(C) I e III
(D) Apenas I
(E) Apenas III.
Resolução:
I – Falsa: O rendimento é o resultado da razão entre a potência útil e a potência total.
II – Falsa: A unidade horse-power é ligeiramente maior que a unidade cavalo-vapor.
III – Verdadeira: O rendimento corresponde à porcentagem efetivamente utilizada pela máquina. Portanto, nesse caso, a potência útil corresponde a 40 % da potência total, ou seja, 200 W.
Alternativa: E
139) (FCM-PB) Em uma cachoeira aproveitada para mover uma roda d’água, a potência disponível é de 300 kW. Qual a potência útil para essa roda d’água cujo rendimento é de 50%?
(A) 150 kW
(B) 450 kW
(C) 50 kW
(D) 100 kW
(E) 200 kW
Resolução:
O rendimento é obtido pela razão entre a potência útil e a potência total. Sendo assim, podemos escrever: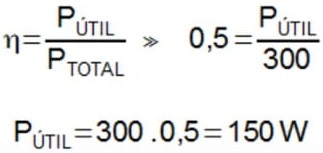
Alternativa: A
QUESTÕES RESOLVIDAS -SEDUC-SP/2025
OS PRINCÍPIOS DA DINÂMICA
Força
Força é um agente físico que pode vir a alterar o estado de repouso ou de movimento de um objeto.
Grandezas escalares - São aquelas que necessitam apenas de intensidade para serem definidas.
Grandezas vetoriais - Precisam, além da intensidade, de direção (horizontal, vertical, inclinada etc.) e sentido (para a direita, para a esquerda, para cima etc.).
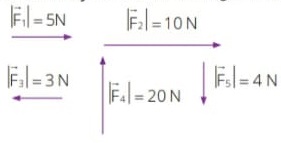
Força resultante - Corresponde à soma (vetorial) de todas as forças que atuam em um corpo. Em muitos casos, é conveniente trocarmos todas essas forças pela resultante, pois, assim, o problema fica mais simples de ser resolvido.
Força na mesma direção e no mesmo sentido
FR = F1 + F2
Forças na mesma direção e sentido contrário
FR = F1 - F2
Forças perpendiculares
RF = √F12 + F22
01) (Livro do Aluno/2025-SEDUC-SP) Classifiquem as grandezas físicas a seguir em escalares ou vetoriais.
1 Volume.....................................................(Escalar)
2 Força........................................................(Vetorial)
3 Área.........................................................(Escalar)
4 Energia....................................................(Escalar)
5 Potência...................................................(Escalar)
6 Velocidade...............................................(Vetorial)
7 Temperatura.............................................(Escalar)
8 Densidade................................................(Escalar)
9 Aceleração...............................................(Vetorial)
10 Comprimento.........................................(Escalar)
11 Deslocamento........................................(Vetorial)
12 Tempo....................................................(Escalar)
02) (Livro do Aluno/2025-SEDUC-SP) A intensidade da força resultante da figura a seguir é igual a:
(A) 15 N
(B) 20 N
(C) 25 N
(D) 30 N
(E) 42 N
Resolução:
Forças na horizontal:

Alternativa: B
03) (Livro do Aluno/2025-SEDUC-SP) Assinale a alternativa que contém apenas grandezas vetoriais.
(A) Massa, tempo e temperatura.
(B) Velocidade, volume e área.
(C) Aceleração, força e velocidade.
(D) Densidade, força e aceleração.
(E) Energia, potência e impulso.
Alternativa: C
04) (Livro do Aluno/2025-SEDUC-SP) A partir do diagrama abaixo, assinale a alternativa que corresponde à intensidade e ao sentido de F4, para que a resultante das quatro forças apresentadas seja igual a zero.
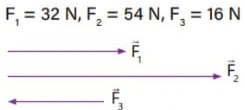
(A) F4 = 70 N para a direita.
(B) F4 = 70 N para a esquerda.
(C) F4 = 102 N para a direita.
(D) F4 = 102 N para a esquerda.
Resolução:

Alternativa: B
1ª LEI DE NEWTON
1ª Lei de Newton ou Princípio da Inércia
Formulada por Isaac Newton em seu trabalho publicado em 1687, Princípios matemáticos da Filosofia Natural, pode ser enunciada da seguinte forma: “Todo corpo continua em seu estado de repouso ou de movimento retilíneo uniforme, a menos que seja forçado a mudar aquele estado por forças imprimidas sobre ele”.
Observe o esquema abaixo:
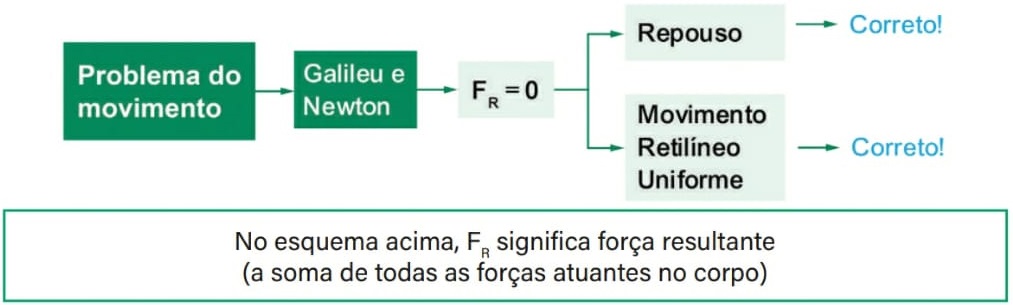
05) (Livro do Aluno/2025-SEDUC-SP) Na imagem a seguir, uma pessoa puxa rapidamente uma toalha que está sobre a mesa, sem derrubar os utensílios em cima dela. Essa é uma experiência frequentemente vista em demonstrações, na qual algumas pessoas afirmam que o fato de os objetos não caírem se deve à primeira lei de Newton. Você concorda com essa afirmação? Se sim, explique com mais detalhes. Caso contrário, identifique um aspecto que não esteja em conformidade com essa lei e explique de que maneira diverge da primeira lei de Newton.
Resolução:
A afirmação de que o fato de os objetos não caírem ao puxar rapidamente a toalha se deve à primeira lei de Newton não é correta. Na verdade, a retirada da toalha provoca um pequeno deslocamento dos objetos, como podemos observar na imagem.
As pessoas acreditam que o fenômeno pode ser explicado pela primeira lei de Newton porque a retirada é feita em um curto intervalo de tempo. Isso minimiza a interação por atrito entre os objetos e a toalha, fazendo com que o seu efeito seja menos perceptível e permitindo que os utensílios não caiam.
06) (Livro do Aluno/2025-SEDUC-SP - UPF 2023) O cinto de segurança é um item indispensável quando se trata da segurança em um veículo em movimento. Seu uso, que é obrigatório no Brasil, está relacionado com a 1ª lei de Newton. Sobre essa lei, é correto afirmar que:
(A) quando a resultante das forças que atuam sobre um corpo é igual a zero, esse corpo somente pode estar em repouso.
(B) um corpo permanece em movimento apenas enquanto houver uma força atuando sobre ele.
(C) um corpo tende a permanecer em aceleração constante.
(D) a inércia de um objeto independe de sua massa.
(E) um corpo tende a permanecer em repouso ou em movimento retilíneo uniforme quando a resultante das forças que atuam sobre ele é nula.
Resolução:
O Princípio da Inércia, ou 1ª lei de Newton, diz que um corpo tende a permanecer em repouso ou em movimento retilíneo uniforme quando a resultante das forças que atuam sobre ele é nula.
Alternativa: E
07) (Livro do Aluno/2025-SEDUC-SP - IFSUL 2017) Leia com atenção o texto abaixo:
Galileu fez outra grande descoberta. Ele mostrou que Aristóteles estava também errado quando considerava que fosse necessário exercer forças sobre os objetos para mantê-los em movimento. Embora seja necessária uma força para dar início ao movimento, Galileu mostrou que, uma vez em movimento, nenhuma força é necessária para manter em movimento – exceto a força necessária para sobrepujar o atrito. Quando o atrito está ausente, em um objeto em movimento, mantém-se em movimento sem a necessidade de qualquer força. O texto refere-se a uma questão central no estudo do movimento dos corpos na Mecânica Newtoniana, que é a propriedade dos corpos de manter seu estado de movimento.
Essa propriedade é conhecida como:
(A) força.
(B) massa.
(C) inércia.
(D) velocidade.
Resolução:
A propriedade dos corpos de manter seu estado de movimento é chamada de inércia.
Alternativa: C
08) (Livro do Aluno/2025-SEDUC-SP) Sabendo que um determinado objeto realizou um movimento retilíneo percorrendo 1000 metros e levando para isso um intervalo de tempo de 50 segundos, calcule sua velocidade escalar média em m/s e km/h.
Resolução:
![]()
09) (Livro do Aluno/2025-SEDUC-SP) Um motorista numa estrada retilínea percebe que está acima do limite de velocidade e reduz sua velocidade de 30 m/s (108 km/h) para 25 m/s (90 km/h) em 4 segundos. Calcule a aceleração escalar média do motorista em m/s2.
Resolução:
![]()
10) (Livro do Aluno/2025-SEDUC-SP - UNICAMP 2017) Em 2016 foi batido o recorde de voo ininterrupto mais longo da história. O avião Solar Impulse 2, movido a energia solar, percorreu quase 6480 km, em aproximadamente 5 dias, partindo de Nagoya no Japão até o Havaí nos Estados Unidos da América. A velocidade escalar média desenvolvida pelo avião foi de aproximadamente:
(A) 54 km/h
(B) 15 km/h
(C) 1296 km/h
(D) 198 km/h
Resolução:

Alternativa: A
11) (Livro do Aluno/2025-SEDUC-SP) O guepardo é considerado um dos animais terrestres mais rápidos do mundo. Ele consegue atingir uma incrível velocidade máxima de 120 km/h. Considerando que, numa caça, ele parte do repouso e atinge a velocidade máxima em 3 s, calcule sua aceleração escalar média em m/s2
Resolução:
O cálculo da aceleração requer que a unidade esteja em m/s2. Logo, temos que passar a velocidade máxima de km/h para m/s. Então: 120 km/h ‑ 3 6, , 33 33 m/s = 33,33 m/s

12) (Livro do Aluno/2025-SEDUC-SP - UERJ 2024) A Agência Espacial Europeia realizou a primeira transmissão “ao vivo” de Marte ao receber imagens do planeta capturadas pelos equipamentos de uma sonda espacial. Cada captura de imagem foi recebida na Terra com um atraso temporal Δt.
Admita que essa transmissão ocorreu através de ondas eletromagnéticas que se propagaram no vácuo com velocidade constante de 3∙105 km/s. Admita, também, que a distância entre a sonda espacial e a Terra seja igual a 3,24∙108 km. Determine, em minutos, o intervalo de tempo Δt entre cada captura de imagem.
Resolução:
Cálculo do intervalo de tempo:
Conversão de segundo para minuto:

13) (Livro do Aluno/2025-SEDUC-SP - PUC-RIO 2008) A primeira lei de Newton afirma que, se a soma de todas as forças atuando sobre o corpo é zero, o mesmo:
(A) terá um movimento uniformemente variado.
(B) apresentará velocidade constante.
(C) apresentará velocidade constante em módulo, mas sua direção pode ser alterada.
(D) será desacelerado.
(E) apresentará um movimento circular uniforme.
Alternativa: B
2ª LEI DE NEWTON
A segunda lei de Newton, também conhecida como princípio fundamental da dinâmica, estabelece que a força resultante que atua sobre um corpo é igual ao produto da massa do corpo pela sua aceleração. Em outras palavras, a aceleração de um objeto é diretamente proporcional à força resultante que atua sobre ele e inversamente proporcional à sua massa.
A relação entre estas três grandezas, massa (considerada constante), força resultante e aceleração, é dada pela segunda lei de Newton:
FR = m . a
A unidade de Força no Sistema Internacional de Unidades é o newton (N). Ela é obtida, segundo a equação acima, quando expressamos a massa em kg e a intensidade da aceleração em m/s2.
14) (Livro do Aluno/2025-SEDUC-SP) Um automóvel de massa 1000 kg está trafegando em uma estrada a uma velocidade constante de 20 m/s. Quando, de repente, se depara com uma onça pintada atravessando a estrada. Com medo de atropelá-la, o motorista aciona os freios, parando o seu carro em 5 segundos. Considerando que a força aplicada pelos freios foi constante durante a frenagem, determine a intensidade dessa força.
Resolução:
Inicialmente, vamos calcular a aceleração sofrida pelo automóvel após o intervalo de tempo de 5 segundos. Para isso, faremos:
![]()
Em seguida, vamos calcular a intensidade da força (F).
Então:
FR = m . a
FR = 1000 ⋅ 4
FR = 4000 N
16) (Livro do Aluno/2025-SEDUC-SP) Sabendo que um objeto de massa 20 kg está sujeito a uma força resultante de 50 N, e que tem direção horizontal e sentido para a direita, determine:
1. A intensidade da aceleração que atua sobre esse corpo.
Resolução:
Aplicando a segunda lei de Newton, temos:
FR = m ∙ a
50 = 20 ∙ a
a = 2,5 m/s²
2. A direção e o sentido dessa aceleração.
Resolução:
A direção e o sentido da aceleração são os mesmos da força resultante. Assim, a aceleração tem direção horizontal e sentido para a direita.
15) ((Livro do Aluno/2025-SEDUC-SP - UFSCAR/UNICAMP 2023) Um objeto de 2 kg sofre a ação de várias forças (ilustradas pelo diagrama de corpo livre da figura a seguir). A aceleração do objeto é:
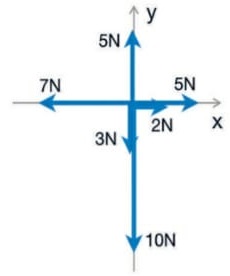
(A) positiva na direção x e tem magnitude igual a 5 m/s2
(B) positiva na direção y e tem magnitude igual a 2,5 m/s2
(C) negativa na direção x e tem magnitude igual a 3,5 m/s2
(D) negativa na direção y e tem magnitude igual a 4 m/s2
Resolução:

Alternativa: D
Resumo
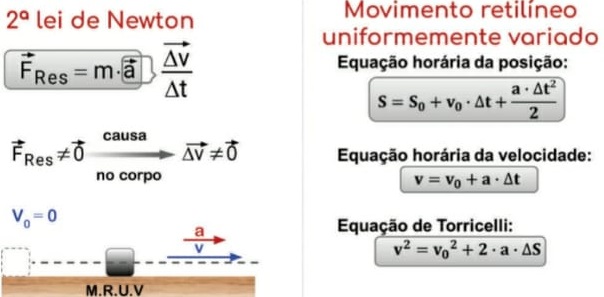
16) (Livro do Aluno/2025-SEDUC-SP) Um objeto de massa de 2 kg sofre a ação de uma força resultante de 8 newtons. Sabendo que ele parte do repouso, calcule:
1. A velocidade que ele terá após 5 segundos.
Resolução

2. O seu deslocamento escalar nesse intervalo de tempo.
Resolução:

17) (Livro do Aluno/2025-SEDUC-SP - UECE 2020) Considere um objeto cúbico, de massa de 1 kg, que repousa sobre uma mesa horizontal sem atrito. Pela ação de uma força constante, o objeto sai do repouso e atinge uma velocidade de 3 m/s, em módulo, após se deslocar por uma distância de 1,5 m. O módulo da força resultante atuando no objeto, em N, é:
(A) 4,5
(B) 2
(C) 3
(D) 1,5
Resolução:

Alternativa: C
18) (Livro do Aluno/2025-SEDUC-SP - UFU 2020) Um dos procedimentos utilizados na indústria automobilística para verificar a segurança dos automóveis é o teste de impacto. Ele é realizado produzindo colisão de um automóvel contra uma barreira rígida. Em um dado teste de impacto, utilizam-se dois diferentes materiais e configurações, designados de sistema A e de sistema B, que são montados na região sujeita ao contato na colisão, em um mesmo automóvel, que possui massa total de 1000 kg. Durante o teste, este automóvel colide com uma barreira fixa e indeformável a 54 km/h (15 m/s), atingindo o repouso sem haver mudanças na direção do movimento inicial. Utilizando-se o sistema A, a colisão dura 0,1 s e o deslocamento do centro de massa do automóvel é de 75 cm; já utilizando-se o sistema B, o tempo de colisão reduz para 0,075 s.
a) Qual é o módulo da força média, considerada constante durante toda a colisão, exercida pela barreira sobre o automóvel, utilizando-se o sistema A e o sistema B? Demonstre com cálculos.
Resolução:

19) (Livro do Aluno/2025-SEDUC-SP - UNICAMP 2024 - Adaptada) Um corpo em queda nas proximidades da superfície terrestre sofre a ação da força gravitacional FG e da força de resistência do ar Far, sendo que essa última atua em sentido oposto à força gravitacional. Nos primeiros instantes, Far = 0, se o corpo parte do repouso.
À medida que a velocidade aumenta, Far também aumenta. Com isso, a aceleração do corpo diminui gradativamente, tornando-se praticamente nula a partir de certo momento. Desse ponto em diante, o corpo passa a cair com velocidade constante, chamada de velocidade terminal. Um objeto de massa m = 200 g é solto a partir de certa altura e atinge a velocidade terminal após determinado tempo. Qual é o módulo da força de resistência do ar depois que o objeto atinge a velocidade terminal?
Dado: a força gravitacional pode ser calculada pela expressão FG = m ∙ g, onde m é a massa do corpo (em kg) e g é a aceleração da gravidade (g = 10 m/s²).
(A) 0,20 N
(B) 2,0 N
(C) 200 N
(D) 2000 N
Resolução:
Uma vez que a velocidade terminal é constante, podemos aplicar a 1ª lei de Newton, igualando a força de resistência do ar com a força gravitacional:
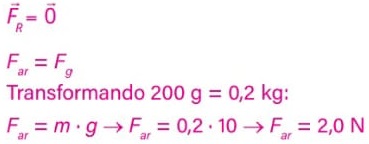
Alternativa: B
20) (Livro do Aluno/2025-SEDUC-SP - UNICAMP 2013 - Adaptada) Em agosto de 2012, a Nasa anunciou o pouso da sonda Curiosity na superfície de Marte. A sonda, de massa m = 1000 kg, entrou na atmosfera marciana a uma velocidade v0 = 6000 m/s. Ela atingiu o repouso, na superfície de Marte, 7 minutos após a sua entrada na atmosfera.
Calcule o módulo da força resultante média de desaceleração da sonda durante a sua descida.
Resolução:
Utilizando a 2ª lei de Newton, temos:

21) (Livro do Aluno/2025-SEDUC-SP - UFMG 2010) Nesta figura, está representado um balão dirigível, que voa para a direita, em altitude constante e com velocidade v, também constante: Sobre o balão, atuam as seguintes forças: o peso P, o empuxo E, a resistência do ar R e a força M, que é devida à propulsão dos motores.
Assinale a alternativa que apresenta o diagrama de forças em que estão mais bem representadas as forças que atuam sobre esse balão.
Resolução:
Considerando o enunciado, segundo o qual o dirigível voa em velocidade constante, sabemos, pela 1ª lei de Newton, que todas as forças que atuam sobre ele se anulam.
Alternativa: D
22) (Livro do Aluno/2025-SEDUC-SP - FUVEST 2017) Objetos em queda sofrem os efeitos da resistência do ar, a qual exerce uma força que se opõe ao movimento desses objetos, de tal modo que, após um certo tempo, eles passam a se mover com velocidade constante. Para uma partícula de poeira no ar, caindo verticalmente, essa força pode ser aproximada por v Fa = b - v , sendo v a velocidade da partícula de poeira e b uma constante positiva. O gráfico mostra o comportamento do módulo da força resultante sobre a partícula, FR, como função de v, o módulo de v.
O valor da constante b, em unidades de N.s/m, é:
Note e adote: o ar está em repouso.
(A) 1,0 ∙ 10–14
(B) 1,5 ∙ 10–14
(C) 3,0 ∙ 10–14
(D) 1,0 ∙ 10–10
(E) 3,0 ∙ 10–10
Resolução:

Alternativa: E
3ª LEI DE NEWTON
A Terceira Lei de Newton, também conhecida como Princípio da Ação e Reação, afirma que para cada ação (força) existe uma reação (força) de igual magnitude e direção, mas em sentido oposto.
23) (Livro do Aluno/2025-SEDUC-SP) Joaquim aplica, em uma parede, uma força horizontal, apontando para a direita, de 50 N. A força que a parede aplica sobre Joaquim é:
(A) horizontal, para a direita, e tem intensidade igual a 50 N.
(B) horizontal, para a direita, e tem intensidade maior do que 50 N.
(C) horizontal, para a esquerda, e tem intensidade igual a 50 N.
(D) horizontal, para a esquerda, e tem intensidade maior do que 50 N.
Resolução:
A 3ª lei de Newton diz que um par ação-reação tem as mesmas intensidade e direção, e sentidos opostos.
Alternativa: C
24) (Livro do Aluno/2025-SEDUC-SP - ENEM 2012) Durante uma faxina, a mãe pediu que o filho a ajudasse, deslocando um móvel para mudá-lo de lugar. Para escapar da tarefa, o filho disse ter aprendido na escola que não poderia puxar o móvel, pois a terceira lei de Newton define que se puxar o móvel, o móvel o puxará igualmente de volta, e assim não conseguirá exercer uma força que possa colocá-lo em movimento.
Qual argumento a mãe utilizará para apontar o erro de interpretação do garoto?
(A) A força de ação é aquela exercida pelo garoto.
(B) A força resultante sobre o móvel é sempre nula.
(C) As forças que o chão exerce sobre o garoto se anulam.
(D) A força de ação é um pouco maior do que a força de reação.
(E) O par de forças de ação e reação não atua em um mesmo corpo.
Resolução:
A 3ª lei de Newton diz que um par de forças de ação-reação sempre atua em corpos distintos.
Alternativa: E
25) As duas forças representadas abaixo podem formar um par ação-reação? Justifique.
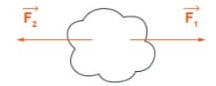
Resolução:
Não, pois estão aplicadas em um mesmo corpo.
26) (Livro do Aluno/2025-SEDUC-SP) - UFV 2018 - Adaptada) Observe as tirinhas.

As leis de Newton que melhor explicam as situações das tirinhas I, II e III, respectivamente, são:
(A) Segunda, Primeira e Terceira.
(B) Primeira, Segunda e Terceira.
(C) Terceira, Segunda e Primeira.
(D) Segunda, Terceira e Primeira.
Alternativa: A
Força peso
A força peso é a força de atração gravitacional que atua entre um corpo e a Terra (ou qualquer outro corpo celeste). Essa força está relacionada com a interação entre a massa do corpo e a aceleração da gravidade no local onde ele se encontra.
Para calcular a força peso, podemos utilizar a seguinte expressão:

Um objeto em queda livre descreve um movimento retilíneo uniformemente variado, apresentando uma aceleração escalar igual à gravidade, representada pela letra g, que, para nossos estudos, é considerada constante.
Para um corpo qualquer que é abandonado no vácuo a uma altura h, são válidas as seguintes expressões:
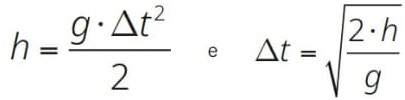
Na superfície da Terra, a aceleração da gravidade é de aproximadamente 10 m/s2.
27) (Livro do Aluno/2025-SEDUC-SP) Um objeto é abandonado no vácuo de uma altura de 20 m. Calcule seu tempo de queda até atingir o chão, sabendo que g = 10 m/s2
Resolução:

28) (Livro do Aluno/2025-SEDUC-SP - UPF 2022) Luiza, uma estudante do Ensino Médio, depois de ouvir as explanações de seu professor de Física sobre a queda dos corpos, resolve fazer alguns testes soltando um mesmo objeto de diferentes andares de seu prédio.
Em seus experimentos, Luiza abandona o objeto da sacada de um andar que está a 20 metros do solo e logo depois abandona o mesmo objeto de uma sacada que está a 60 metros do solo.
Desprezando a resistência do ar e considerando a aceleração gravitacional 10 m/s², Luiza obtém uma diferença de tempo entre a queda do objeto do primeiro para o segundo experimento, em segundos, aproximadamente, de:
(A) 2,8
(B) 3,5
(C) 0,8
(D) 1,5
(E) 0,3
Resolução:

Alternativa: D
Força normal
A força normal é a força que uma superfície exerce sobre um objeto que está em contato com ela. Essa força é sempre perpendicular à superfície de contato.
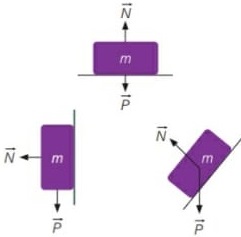
Características:
Direção: perpendicular à superfície de contato.
Magnitude: pode variar dependendo da inclinação da superfície.
A força de tração é a força transmitida por meio de uma corda, um cabo ou um fio, quando é puxada por forças em sentidos opostos.
Representação das forças em um fio ideal e sua respectiva equação
Direção: ao longo do fio, da corda ou do cabo.
Magnitude: geralmente, é a mesma em todos os pontos ao longo de um fio ideal.
Fio ideal – Em mecânica é um conceito teórico que simplifica a análise de problemas mecânicos e é caracterizado por ser:
Massa desprezível: Sua massa é tão pequena que pode ser ignorada na análise do sistema.
Inextensível: Não se estica sob tensão.
Flexível: Permite a transmissão de força de uma extremidade à outra sem resistência.
29) (Livro do Aluno/2025-SEDUC-SP) A figura a seguir mostra um bloco de 8 kg pendurado em repouso no teto por um fio ideal. Determine o valor da tração no fio. Considere g = 10 m/s².

Resolução:
As forças que atuam sobre o bloco estão marcadas a seguir:

30) (Livro do Aluno/2025-SEDUC-SP) Considere que um elevador está subindo com aceleração de intensidade 2 m/s2. Sobre o piso do elevador há uma pessoa de 60 kg. Considerando g = 10 m/s2, calcule a intensidade da força normal que o piso do elevador exerce sobre a pessoa:
Quando o elevador acelera para cima.
Resolução:
1. Sendo a aceleração para cima, da 2ª lei de Newton vem:
FR = m ⋅ a
FN − P = m ⋅ a
FN − 60 ⋅ 10 = 60 ⋅ 2
FN = 720 N
2. Quando o elevador acelera para baixo.
Resolução:
Sendo a aceleração para baixo, da 2ª lei de Newton vem:
FR = m ⋅ a
P − FN = m ⋅ a
60 ⋅ 10 − FN = 60 ⋅ 2
FN = 480 N
31) (Livro do Aluno/2025-SEDUC-SP - UFRGS 2024) Na figura abaixo, estão representados dois corpos de massas M e m, com M > m, unidos por um fio inextensível e de massa desprezível que passa por uma polia, também de massa desprezível e sem atrito.
Sendo g o módulo da aceleração da gravidade local, o módulo da aceleração de qualquer um dos dois corpos é dado por
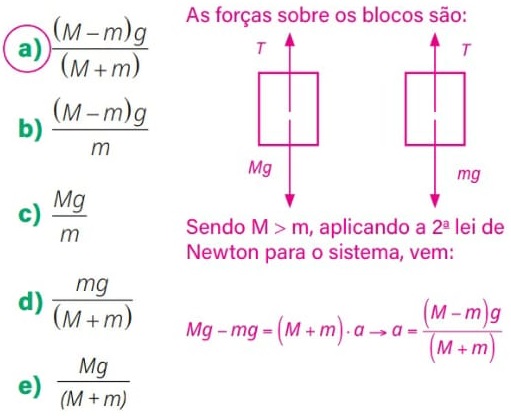
Alternativa: A
Força elástica
A lei de Hooke descreve o comportamento elástico de certos materiais quando submetidos a uma força. Ela estabelece que a força elástica necessária para deformar um material é proporcional à deformação causada, dentro do limite de elasticidade do material.
Matematicamente, a lei de Hooke pode ser expressa por:
![]()
Nessa equação, k é a constante da mola, e x é a deformação da mola.
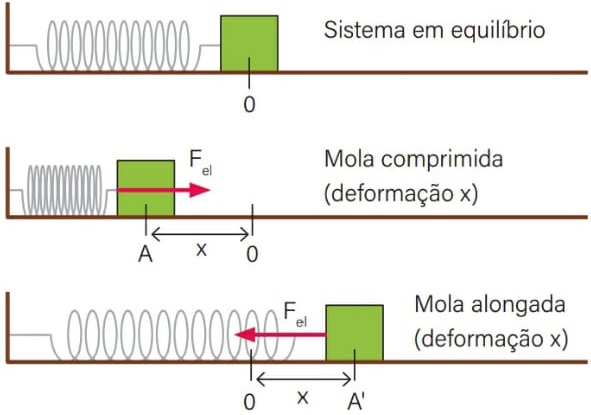
32) (Livro do Aluno/2025-SEDUC-SP - UERN 2013) A tabela apresenta a força elástica e a deformação de 3 molas diferentes.
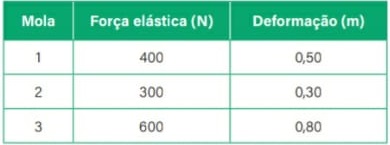
Comparando-se as constantes elásticas destas 3 molas, tem-se que:
(A) K1 > K2 > K3
(B) K2 > K1 > K3
(C) K2 > K3 > K1
(D) K3 > K2 > K1
Resolução:
Aplicando a lei de Hooke para cada mola, podemos determinar os valores do k de cada uma:
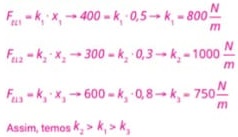
Alternativa: B
33) (Livro do Aluno/2025-SEDUC-SP - UERN 2013) A tabela apresenta a força elástica e a deformação de 3 molas diferentes.
Comparando-se as constantes elásticas destas 3 molas, tem-se que:
(A) K1 > K2 > K3
(B) K2 > K1 > K3
(C) K2 > K3 > K1
(D) K3 > K2 > K1
Resolução:
Aplicando a lei de Hooke para cada mola, podemos determinar os valores do k de cada uma:
Alternativa: B
33) (Livro do Aluno/2025-SEDUC-SP - UNICAMP 2023) A pele humana detecta simultaneamente, com uma sensibilidade
que sistemas artificiais não conseguem reproduzir, vibrações, forças estáticas, textura e escorregamento de objetos sobre sua superfície. Sensores tácteis que apresentassem respostas análogas à pele humana seriam muito desejáveis. A figura a seguir ilustra um modelo simples, utilizado no estudo da resposta da pele humana. Na referida figura, estão representados o peso P do bloco, a força normal N, a força de atrito fat aplicada pela superfície da pele no bloco de massa m e uma força externa F aplicada na mola.
A constante de mola é k = 10 N/m, e a massa do bloco é m = 4 g. Na iminência de movimento, a deformação da mola é ∆x = 3 mm em relação ao seu comprimento de equilíbrio. Qual é o coeficiente de atrito estático entre o bloco e a pele?
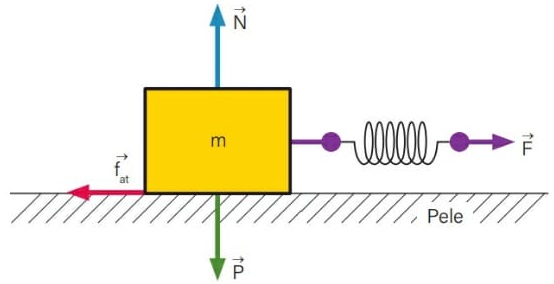
(A) 8,8 ∙ 10–7
(B) 1,1 ∙ 10–6
(C) 7,5 ∙ 10–1
(D) 1,3 ∙ 100
Resolução:
Na iminência do movimento do bloco, o módulo da força exercida pela mola, F, é igual ao módulo da força de atrito estático máxima.
k ∙ ∆x = μE∙ N
10 ∙ 3 ∙ 10–3 = μE ∙ 4 ∙ 10–3 ∙ 10
μE = 7,5 ∙ 10–1
Alternativa: C
Força de atrito
A força de atrito é uma força de contato que surge entre duas superfícies quando há deslizamento ou uma tendência de deslizamento entre elas. Essa força atua no sentido oposto ao escorregamento ou à tendência de escorregamento, do corpo em análise.
Chamamos de atrito estático a força que impede o deslizando de um corpo.
À medida que a intensidade de uma força externa aplicada a um corpo aumenta, a força de atrito também cresce, igualando-se a essa força. Isso continua até que a força de atrito atinja seu valor máximo, conhecido como atrito estático máximo, que representa o limite que a força de atrito pode alcançar sem permitir que o corpo escorregue.
Na eminência de escorregamento do corpo, a intensidade da força de atrito é dada por:
FatE = μE ∙ N
Nessa equação, N representa a força normal e μE o coeficiente de atrito estático, um valor constante que depende das superfícies em contato.
34) (Livro do Aluno/2025-SEDUC-SP) (UNICAMP 2021) A força de atrito cinético entre a agulha e um disco de vinil tem módulo FAT = 8 ∙ 10-3 N.
Sendo o módulo da força normal N = 2 ∙ 10-2 N, o coeficiente de atrito cinético μC, entre a agulha e o disco, é igual a:
(A) 1,6 ∙ 10-5
(B) 5 ∙ 10-2
(C) 4,0 ∙ 10-1
(D) 2,5 ∙ 100
Resolução:
Sendo o atrito dinâmico, temos:
FAT D = μD ∙ N
8 ∙ 10-3 = μD ∙ 2 ∙ 10-2
μD = 4 ∙ 10-1
Alternativa: C
35) (Livro do Aluno/2025-SEDUC-SP - ENEM PPL 2015) Num sistema de freio convencional, as rodas do carro travam e os pneus derrapam no solo, caso a força exercida sobre o pedal seja muito intensa. O sistema ABS evita o travamento das rodas, mantendo a força de atrito no seu valor estático máximo, sem derrapagem. O coeficiente de atrito estático da borracha em contato com o concreto vale μE = 1,0 e o coeficiente de atrito cinético para o mesmo par de materiais é μD = 0,75.
Dois carros, com velocidades iniciais iguais a 108 km/h, iniciam a frenagem numa estrada perfeitamente horizontal de concreto no mesmo ponto. O carro 1 tem sistema ABS e utiliza a força de atrito estática máxima para a frenagem; já o carro 2 trava as rodas, de maneira que a força de atrito efetiva é a cinética. Considere g = 10 m/s2.
As distâncias, medidas a partir do ponto em que iniciam a frenagem, que os carros 1 (d1) e 2 (d2) percorrem até parar são, respectivamente,
(A) d1 = 45 m e d2 = 60 m
(B) d1 = 60 m e d2 = 45 m
(C) d1 = 90 m e d2 = 120 m
(D) d1 = 5,8 ∙ 102 m e d2 = 7,8 ∙ 102 m
(E) d1 = 7,8 ∙ 102 m e d2 = 5,8 ∙ 102 m
Resolução:

Alternativa: A
PLANO INCLINADO E FORÇA DE ATRITO
Quando um corpo desliza sem atrito em um plano inclinado, como ilustrado na figura a seguir, muitas vezes é útil decompor a força peso em duas componentes.
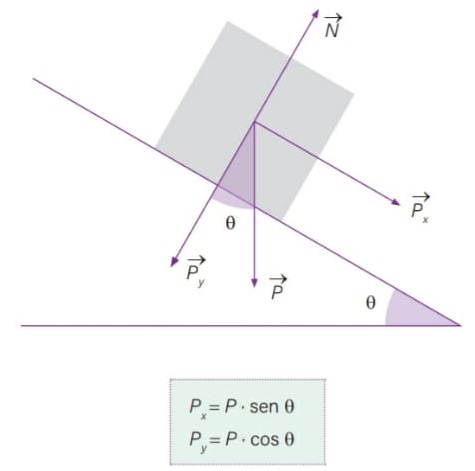
Na situação ilustrada na imagem acima, a aceleração da caixa que desliza no plano inclinado sem atrito é dada por:

36) (Livro do Aluno/2025-SEDUC-SP - UECE 2019 – Adaptada) Suponha que uma caixa de aço desce deslizando, sem atrito, um plano inclinado. Pode-se afirmar corretamente que, em relação ao movimento da caixa, sua aceleração:
(A) aumenta e sua velocidade diminui.
(B) e velocidade aumentam.
(C) é constante e sua velocidade aumenta.
(D) e velocidade permanecem constantes.
Resolução:
Quando uma caixa desce deslizando umplano inclinado sem atrito, ela o faz com uma aceleração constante que vale a = g ∙ sen θ. Por possuir aceleração no mesmo sentido do movimento da caixa, sua velocidade aumenta.
Alternativa: C
37) (Livro do Aluno/2025-SEDUC-SP - IFSUL 2018) Uma caixa encontra-se em repouso sobre um plano inclinado, o qual forma um ângulo θ com a horizontal. Sabe-se que a caixa está submetida à ação de uma força F, indicada na figura ao lado, cujo módulo é igual a 25 N, e que existe atrito entre a superfície de contato da caixa e do plano.
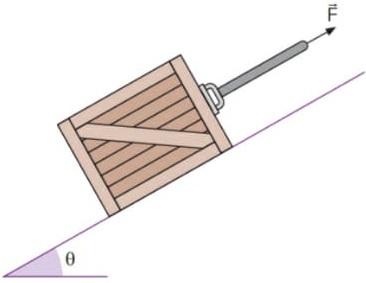
Considere a aceleração da gravidade igual a 10m/s², o coeficiente de atrito estático entre as superfícies de contato igual a 0,5, cos θ = 0,8, sen θ = 0,6 e a massa da caixa igual a 10 kg.
A força de atrito estático entre as superfícies de contato do corpo e do plano tem módulo igual a:
(A) 35 N e mesmo sentido da força F.
(B) 35 N e sentido contrário ao da força F.
(C) 40 N e mesmo sentido da força F.
(D) 40 N e sentido contrário ao da força F.
Resolução:

Alternativa: A
PLANO INCLINADO E FORÇA DE ATRITO
Resumo

38) (Livro do Aluno/2025-SEDUC-SP Um bloco de massa 2 kg é lançado para cima com velocidade inicial v0 = 10 m/s em um plano inclinado com atrito, cuja inclinação em relação à horizontal é θ. Sabendo que g = 10 m/s², que o coeficiente de atrito dinâmico μD = 0,5, e que sen θ = 0,6 e cos θ = 0,8, calcule:
1. A intensidade da força normal sobre o bloco.
Resolução:

2. A aceleração que atua sobre o bloco.
Resolução:
O bloco descreve um MUV. Da equação horária da velocidade, sabendo que no ponto mais alto da subida a velocidade v é nula, temos:
![]()
3. O tempo que o bloco leva para atingir o ponto mais alto do plano, considerando que ele para nesse momento.
Resolução:
O bloco descreve um MUV. Da equação horária da velocidade, sabendo que no ponto mais alto da subida a velocidade v é nula, temos:
![]()
4. A distância percorrida até chegar ao ponto mais alto.
Resolução:
Aplicando a equação de Torricelli para a subida, temos:
![]()
5. A altura máxima atingida em relação ao lançamento.
Resolução:
Aplicando a relação trigonométrica na figura abaixo:
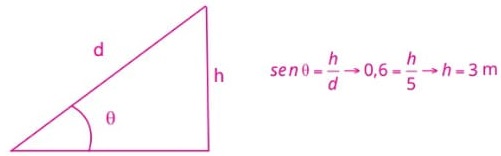
6. A intensidade da força resultante que atua sobre o bloco.
Resolução:
Da 2ª lei de Newton:
![]()
39) (Livro do Aluno/2025-SEDUC-SP) Considere o sistema formado pelos 2 blocos abaixo.
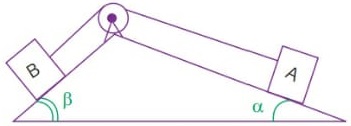
Sabendo que mA = 5 kg; mB = 3 kg; sen α = 0,6; sen β = 0,8; cos α = 0,8; cos β = 0,6 e g = 10m/s2, e que não há atrito sobre o bloco A, calcule o valor da força de atrito que atua sobre o bloco B para que o sistema se mantenha em equilíbrio estático.
Resolução:
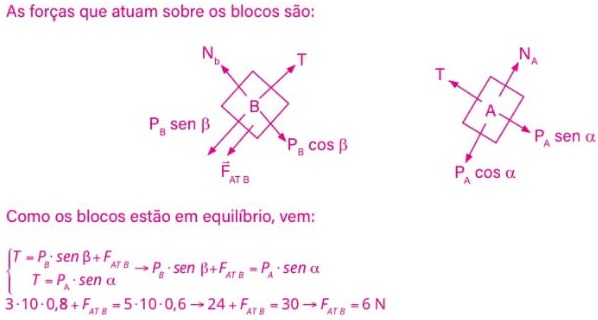
40) (Livro do Aluno/2025-SEDUC-SP - EEAR 2020) Um corpo de massa m está apoiado sobre um plano inclinado, que forma um ângulo de 30º em relação à horizontal, conforme a figura a seguir.
O valor do coeficiente de atrito estático que garante a condição de iminência de movimento desse corpo é?
(A) 1/3
(B) √2/2
(C) √3/2
(D) √3/4
Resolução:
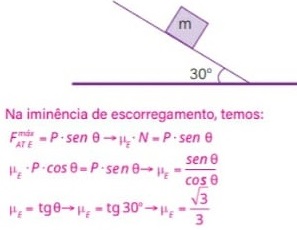
Alternativa: D
41) (Livro do Aluno/2025-SEDUC-SP - EEAR 2021) Uma mola ideal está presa a parede e apoiada sobre um plano inclinado. Quando um bloco de massa igual a 5 kg é preso a extremidade dessa mola, esta sofre uma distensão de 20 cm, conforme o desenho. Considerando que o módulo da aceleração da gravidade no local vale 10 m/s² e desprezando qualquer tipo de atrito, qual o valor da constante elástica da mola em N/m?
(A) 50
(B) 100
(C) 125
(D) 250
Resolução:
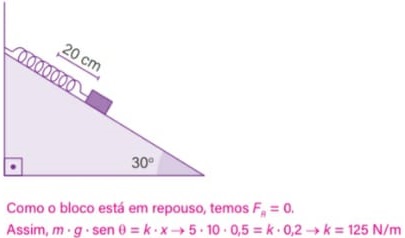
Alternativa: C
Continua,,,,





