EM - PROGRESSAO

Professor Diminoi

PROGRESSAO

Sequências
Observe a sequência dos anos em foram realizadas Olimpíadas, a partir de 1996:
(1996, 2000, 2004, 2008, 2012, 2016...)

Os parênteses sugerem que estamos trabalhando com um conjunto de números colocados numa certa ordem. Esses elementos são chamados de termos da sequência. Costuma-se representar cada termo de uma sequência por uma letra qualquer, normalmente a, acompanhada de um índice que dá a sua posição ou ordem.
(a₁, a₂, a₃, a₄, a₅, ..., n_a, ...)

Por exemplo, na sequência (1996, 2000, 2004, 2008, ...), temos:
primeiro termo = a₁ = 1996;
segundo termo = a₂ = 2000;
terceiro termo = a₃ = 2004;
quarto termo = a₄ = 2008;
... (e assim sucessivamente).

O enésimo termo a_n pode representar qualquer termo da sequência. Por exemplo, se n = 50, temos a_n = a₅₀ e estamos nos referindo ao 50º termo da sequência.

Definição de sequencia
Matematicamente, denomina-se sequência qualquer função f cujo domínio é N*.

Exemplo
 definida por f(n) = 2n
Substituindo-se n pelos números naturais 1, 2, 3, ... temos:

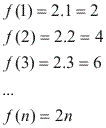
Portanto, a sequência pode ser escrita como (2, 4, 6, ..., 2n, ...).

Observe que há uma lei de formação dos termos de uma sequência. A partir de agora, vamos estudar duas formas diferentes de definir uma sequência: pelo termo geral e por recorrência.

Sequencia definida pelo Termo Geral
Cada termo a_n é calculado em função de sua posição n na sequência.

Exemplo
Os três primeiros termos da sequência cujo termo geral é a_n = n + 7 são: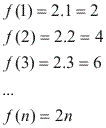

Assim, a sequência que tem como termo geral a_n = n + 7, é (8, 9, 10, ...) 

Sequência definida por recorrência
Cada termo da sequência é calculado em função do termo anterior.

Exemplo
Na sequência definida por a_n+1 = a_n+3    em que a₁ = 4, cada termo, exceto o primeiro, é igual ao anterior adicionado a 3.


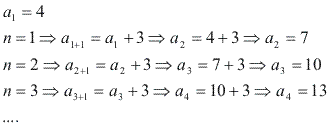
Portanto, a sequência pode ser escrita como (4, 7, 10, 13, ...).

Progressão aritmética
Observe a sequência dos números naturais ímpares:
(1, 3, 5, 7, ...)

Observe que cada termo, exceto o primeiro, equivale ao anterior adicionado a um número fixo: 2.
Sequências como essa são chamadas de progressões aritméticas.

Progressão aritmética (PA) é toda sequência numérica em que cada um de seus termos, a partir do segundo, é igual ao anterior somado a uma constante r, denominada razão da progressão aritmética.

Exemplo
(2, 5, 8, 11, 14, ...) é uma PA de razão 3;
(10, 8, 6, 4, 2, 0, ...) é uma PA de razão -2.

Uma sequência (a₁, a₂, a₃, a₄, a₅, ... n_a, ...) é uma PA quando:


Genericamente:

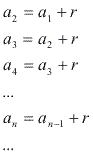
Note que em uma PA, subtraindo-se de cada termo o seu antecessor, obtemos a razão r:


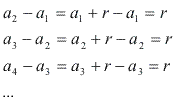
Genericamente:
a₂ – a₁ = a₃ – a₂ = ... = n_a -n_a-1 = r
Assim, para descobrimos qual é a razão de uma PA, basta subtrairmos um termo qualquer de seu antecessor:

Exemplo 1
Qual a razão da PA
?
Resolução
A razão da PA é a diferença entre um termo qualquer e seu antecessor. Vamos calcular a diferença entre o 3º e o 2º termos:

Portanto, a razão dessa PA é -1/2 

Exemplo
A sequência (-2, 1, 4, 8) é uma PA?
Resolução
A sequência é uma PA se, subtraindo de cada termo o seu antecessor, o resultado for constante.
1 – (-2) = 3
4 – 1 = 3
8 – 4 = 4
Portanto, a sequência (-2, 1, 4, 8) não é uma PA.

Exemplo
Determine x na PA
Resolução
A razão da PA é a diferença entre um termo qualquer e seu antecessor. Sendo assim, fazemos:

Logo, 


Classificação de uma PA
Uma PA pode ser:
Formula do termo de uma PA
Já sabemos que numa PA:

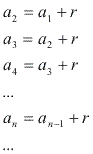
Note que podemos escrever todos os termos de uma PA em função de a₁ e r:

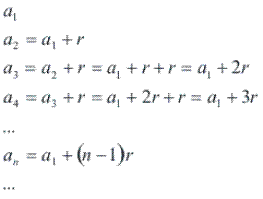
Portanto, o termo geral da PA será dado pela fórmula:

a₁ = primeiro termo
a_n = enésimo termo
r = razão
n = números de termos

Exemplo
Determine o termo geral da PA (-19, -15, -11, ...):
Resolução

O termo geral da PA (-19, -15, -11, ...) é a_n = 4n – 23  

Exemplo
Determine o 16º termo da PA (3, 9, 15, ...):

Resolução


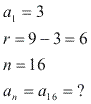
Portanto, o 16º termo da PA (3, 9, 15, ...) é 93.

Exemplo
Interpole seis meios aritméticos entre -8 e 13:
Resolução
Do enunciado temos que:




Encontrada a razão, basta interpolar os meios aritméticos: (-8, -5, -2, 1, 4, 7, 10, 13).

Exemplo
Quantos múltiplos de 5 há entre 101 e 999?
Resolução
O primeiro múltiplo de 5 depois de 101 é 105, portanto a₁ = 105;
O último múltiplo de 5 antes de 999 é 995, portanto a_n = 995;
A razão é 5, pois estamos nos referindo a múltiplos de 5.
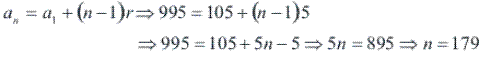Assim, concluímos que existem 179 múltiplos de 5 entre 101 e 999.

Exemplo
Sabendo que numa PA o 2º termo é 9 e o 11º termo é 45, escreva essa PA:
Resolução
Vamos escrever esses termos em função de a₁ e r:


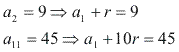
Montamos um sistema de equações: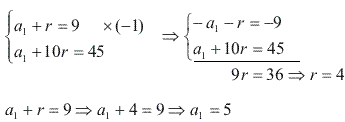


Portanto, a PA é (5, 9, 13, 17, ...).

Soma do n termos de uma PA
Considere a PA finita:
(5, 7, 9, 11, 13, 15, 17, 19).
Note que:
5 e 19 são extremos;
7 e 17 são termos equidistantes dos extremos;
9 e 15 são termos equidistantes dos extremos;
11 e 13 são termos equidistantes dos extremos.

Observe:
5 + 19 = 24 → soma dos extremos
7 + 17 = 24 → soma de dois termos equidistantes dos extremos
9 + 15 = 24 → soma de dois termos equidistantes dos extremos
11 + 13 = 24 → soma de dois termos equidistantes dos extremos

Baseada nessa ideia, existe a seguinte propriedade:

Numa PA finita, a soma de dois termos equidistantes dos extremos é igual a soma dos extremos.
Através dessa propriedade, podemos descobrir a fórmula para a soma dos n termos de uma PA:
Vamos considerar a PA finita  (a₁, a₂, a₃, ... n_a-2, n_a-1, a_n)
Podemos representar por  S_n a soma dos termos dessa PA.

Como a soma de dois termos equidistantes dos extremos é igual a soma dos extremos, a soma da PA é dada pela soma dos extremos vezes a metade do número de termos  n^(n:2), pois em cada soma estão envolvidos dois termos.

Assim, temos a fórmula da soma dos n termos de uma PA: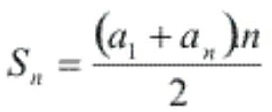
S_n = soma dos n termos
a₁ = primeiro termo
a_n = enésimo termo
n = numero de termo
Observação: Através dessa fórmula, podemos calcular a soma dos n primeiros termos de uma PA qualquer, basta determinarmos o número de termos que queremos somar.

Exemplo
Qual a soma dos 10 primeiros termos da PA  (1, 4, 7, ...) ?
Resolução
Primeiramente, temos de descobrir qual é o 10º termo dessa PA:




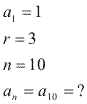
Conhecendo o valor do 10º termo, podemos calcular a soma dos 10 primeiros termos dessa PA: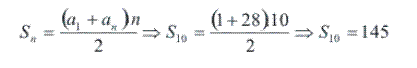

Portanto, a soma dos 10 primeiros termos da PA (1, 4, 7, ...) é 145.

Exemplo
A soma dos n primeiros números pares positivos de uma PA é 132. Encontre o valor de n.
Resolução
Primeiramente, vamos descobrir qual é o enésimo termo a_n:
a₁ = 2
r = 2
Substituindo na fórmula da soma dos termos:

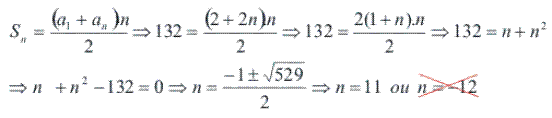
Portanto, a soma dos 11 primeiros números pares positivos é 132.

Progressão Geometria
Podemos definir progressão geométrica, ou simplesmente P.G., como uma sucessão de números reais obtida, com exceção do primeiro, multiplicando o número anterior por uma quantidade fixa q, chamada razão.

Podemos calcular a razão da progressão, caso ela não esteja suficientemente evidente, dividindo entre si dois termos consecutivos.
Por exemplo, na sucessão (1, 2, 4, 8,...), temos q = 2.

Cálculo do termo geral
Numa progressão geométrica de razão q, os termos são obtidos, por definição, a partir do primeiro, da seguinte maneira:   
Assim, podemos deduzir a seguinte expressão do termo geral, também chamado enésimo termo, para qualquer progressão geométrica.
a_n = a₁ . q^n-1

Portanto, se por exemplo, a₁ = 2 e q = 1/2, então:
a_n = 2 . (1/2)^n-1

Se quisermos calcular o valor do termo para n = 5, substituindo-o na fórmula, obtemos:
a₅ = 2 . (1/2)^5-1 = 2 . (1/2)⁴ = 1/8

A semelhança entre as progressões aritméticas e as geométricas é aparentemente grande. Porém, encontramos a primeira diferença substancial no momento de sua definição. Enquanto as progressões aritméticas formam-se somando-se uma mesma quantidade de forma repetida, nas progressões geométricas os termos são gerados pela multiplicação, também repetida, por um mesmo número. As diferenças não param aí.

Observe que, quando uma progressão aritmética tem a razão positiva, isto é, r > 0, cada termo seu é maior que o anterior. Portanto, trata-se de uma progressão crescente. Ao contrário, se tivermos uma progressão aritmética com razão negativa, r < 0, seu comportamento será decrescente. Observe, também, a rapidez com que a progressão cresce ou diminui. Isto é consequência direta do valor absoluto da razão, |r|. Assim, quanto maior for r, em valor absoluto, maior será a velocidade de crescimento e vice-versa.

Soma dos n primeiros termos de uma PG
Seja a PG (a₁, a₂, a₃, a₄, ... , a_n , ...) . Para o cálculo da soma dos n primeiros termos S_n, vamos considerar o que segue:
S_n = a₁ + a₂ + a₃ + a₄ + ... + a_n-1 + a_n

Multiplicando ambos os membros pela razão q, temos:
S_n.q = a₁ . q + a₂ .q + .... + a_n-1 . q + a_n .q

Conforme a definição de PG, podemos reescrever a expressão como:
S_n . q = a₂ + a₃ + ... + a_n + a_n . q

Observe que a₂ + a₃ + ... + a_n é igual a S_n - a₁. Logo, substituindo, vem:
S_n . q = S_n - a₁ + a_n . q

Daí, simplificando convenientemente, chegaremos à seguinte fórmula da soma:
Se substituirmos a_n = a₁ . q^n-1, obteremos uma nova apresentação para a fórmula da soma, ou seja:
Exemplo
Calcule a soma dos 10 primeiros termos da PG (1,2,4,8,...)
Temos:
Observe que neste caso a₁ = 1.

Soma dos termos de uma PG infinita
Considere uma PG ilimitada (infinitos termos) e decrescente. Nestas condições, podemos considerar que no limite teremos a_n = 0. Substituindo na fórmula anterior, encontraremos:

Por exemplo, resolva a equação:
x + x/2 + x/4 + x/8 + x/16 + ... = 100

O primeiro membro é uma PG de primeiro termo x e razão 1/2. Logo, substituindo na fórmula, vem:

Dessa equação encontramos como resposta x = 50.
 

Continua ...