TRANSFORMAÇÃO GASOSA

Professor Diminoi

TRANSFORMAÇÃOES GASOSAS

Gases são corpos muito especiais. São facilmente comprimidos ou expandidos. Além disso, as moléculas de corpos gasosos estão mais distantes e sempre mais agitadas do que nos sólidos e líquidos.

Um gás é caracterizado por três grandezas físicas: temperatura, volume e pressão. São as chamadas variáveis de estado, que definem o estado termodinâmico de um gás.

Para facilitar o estudo dos gases, os físicos adotam um modelo científico que trata o gás como um gás ideal.

Gás perfeito

Um gás perfeito, também chamado de gás ideal, é um conjunto de moléculas ou átomos que se movem constantemente e aleatoriamente. As moléculas não interagem entre si e as colisões entre elas são perfeitamente elásticas.

Características de um gás perfeito

- As moléculas se movem em movimento desordenado e rápido

- As velocidades médias das moléculas estão relacionadas com a temperatura

- As forças de coesão entre as moléculas são extremamente fracas

- O volume da molécula é desprezível quando comparado ao volume do gás

- Não há interação gravitacional entre as moléculas

- As colisões entre as moléculas são perfeitamente elásticas, ou seja, há total conservação da energia cinética

Variáveis de estado

As grandezas físicas temperatura (T), volume (V) e pressão (P) de um gás perfeito são o que chamamos de variáveis de estado, que, em conjunto, definem o comportamento macroscópico do gás.

Unidades correspondentes nas equações;

P = pressão (Pa)

V = volume (m³)

R = constante universal dos gases ideais (0,082 atm.l/mol.K ou 8,3 J/mol.K)

T₁ = temperatura em Kelvin (K)

T₂ = temperatura em Kelvin (K)

V_i = volume inicial volume (m³)

V_f= volume final volume (m³)

K = Não depende da natureza do gás. K = 1,38 . 10^-23 J/K

Transformação isotérmica ou A lei de Boyle-Mariotte

Ocorre quando a temperatura é constante, mas a pressão e o volume variam.

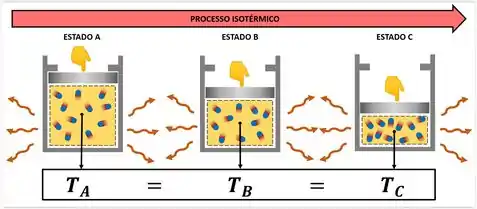
PV = K ou Pi .Vi = Pf . Vf

01) Certa quantidade de um gás ocupa um volume de 120 L em pressão de 700 mmHg e temperatura de 20 ºC. Qual será a pressão quando o volume for apenas de 30 L, mantendo-se a temperatura constante?

Resolução:

P1 . V1 = P2 . V2

P₂= P₁ . V₁
V₂
P₂= 700 . 120
30
P₂= 2800 mmHg

02) (PUC-RJ) A cada 10 m de profundidade a pressão sobre um mergulhador aumenta 1 atm com relação à pressão atmosférica. Sabendo-se disso, qual seria o volume de 1 L de ar (comportando-se como um gás ideal) inspirado pelo mergulhador ao nível do mar, quando ele estivesse a 30 m de profundidade?

Resolução:

P1 . V1 = P2 . V2

1 atm . 1 L = 4 atm . V2

4V2 = 1

V2 = 1/4

V2 = 0,25 L = 250 mL

Transformação isobárica ou primeira lei de Charles/Gay-Lussac

Ocorre quando a pressão é constante, enquanto o volume e a temperatura variam. O trabalho na transformação isobárica.

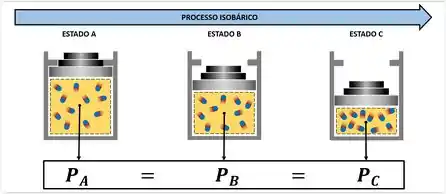
V = K ou Vi = Vf

T Ti Tf

03) Um gás no estado 1 apresenta volume de 14 L, pressão de 5 atm e temperatura de 300 K. Qual será o volume do gás em um estado 2 se a temperatura for dobrada à pressão constante?

Resolução:

V1 = V2

T1 T2

14 L /300 = 600/V₂

300 . V₂ = 14 . 600

V₂ = 8400/300

V₂ = 28 L

04) Em uma pressão constante, um gás é aquecido até que seu volume inicial de 150 L dobre. Se a temperatura inicial do gás era de 20ºC, qual deve ser a temperatura final na escala kelvin?

Resolução:

150 T_final = 300. 293

50 . T_final = 293 . 300

T_final = 87900/150

T_final = 586 K

Segunda lei de Charles/Gay-Lussac ou Transformação isovolumétrica ou isométrica ou ainda isocórica

Ocorre quando o volume é constante e sofre alteração de pressão e temperatura

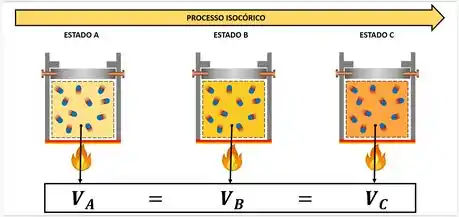
Pi = Pf

Ti Tf

05) Um gás no estado 1 apresenta volume de 14 L, pressão de 5 atm e temperatura de 300 K. Qual será a pressão do gás em um estado II se o volume permanecer igual a 14 L, mas a temperatura passar para 273 K?

Resolução:

P_inicial = P_final
T_inicialT_final

P_final = P_inicial . T_finalT_inicial

P_final = 5 atm . 273 K
300 K

P_final = 4,55 atm

06) (UEPG-PR) Um recipiente fechado de volume “V” contém certa massa gasosa à temperatura de 27°C, exercendo uma pressão de 760 mmHg. Após aquecimento, verificou-se que o novo valor da pressão era de 2 atm.

Supondo desprezível a variação de volume, a nova temperatura, em °C, do sistema será:

Resolução:

P_inicial = P_final
T_inicialT_final

T_final = T_inicial. P_finalP_inicial

T_final = 300 K. 2 atm
1 atm

T_final = 600 K = 600 – 273 = 327 ºC.

Lei Geral dos Gases

Quando uma certa massa de gás perfeito passa por uma transformação em que as três variáveis de estado – pressão (p), volume (V) e temperatura absoluta (T) – se alteram, podemos relacionar essas três variáveis por meio da Lei Geral dos Gases, dada pela seguinte expressão:

Pi . V1 = P2 . V2

T1 T2

05) Em um recipiente fechado, certa massa de gás ideal ocupa um volume de 12 litros a 293k. Se este gás for aquecido até 302k, sob pressão constante, seu volume será

Resolução:

V₁ = V₂

T₁ T₂

12 = V₂

293 302

293 V² = 12 . 302

293V₂ = 6324

V₂ = 3624

293

V₂= 12,37 L

07) (Uneb-BA) Em condições tais que um gás se comporta como ideal, as variáveis de estado assumem os valores 300 K, 2,0 m³ e 4,0 x 10⁴ Pa, num estado A. Sofrendo certa transformação, o sistema chega ao estado B, em que os valores são 450 K, 3,0 m³ e p. O valor de p, em Pa, é:

Resolução:

Pi . V1 = P2 . V2

T1 T2

4 . 10⁴ . 2 = p_B . 3

300 450

8 . 10⁴ = 3p_B

300 450

3600 . 10⁴ = 900p_B

p_B= 4 . 10⁴ p_a

Equação de Clapeyron

Os resultados encontrados nas experiências podem ser explicados pela Equação de Clapeyron, que descreve a relação entre pressão, volume, número de partículas e temperatura, em um gás ideal.

P . V = n . R . T

08) Determine o volume molar de um gás ideal, cujas condições estejam normais, ou seja, a temperatura à 273K e a pressão a 1 atm. (Dado: R = 0,082 atm.L/mol.K)

Resolução:

pV = nRT

1.V = 1. 0,082. 273

V = 22,4 L

09) Determine o número de mols de um gás que ocupa volume de 90 litros. Este gás está a uma pressão de 2 atm e a uma temperatura de 100K. (Dado: R = 0,082 atm.L/mol.K)

Resolução:

pV = nRT

90 = n. 0,082. 100
180 = n. 8,2

n = 180/8,2

n = 21,95 mols

O trabalho na transformação isobárica:

τ = F . d

τ = F . ΔV

10) Um cilindro contém 2 litros de um gás a uma temperatura de 27°C. Se o gás sofre uma transformação isobárica e a temperatura se eleva para 127°C, determine o volume final do gás.

Resolução:

V₁ = V₂

T₁ T₂

2 /300,15 = 400 V₂

V₂. 300,15 = 2 . 400,15

V₂ 300,15 = 800,3

V2 = 800,3/300,15

V₂ = 2,6

11) Em uma transformação isobárica um gás que preenche um recipiente de 3,0 l e está inicialmente com uma temperatura de 450 K. O estado final do gás indica que sua temperatura diminuiu para 300 K. Qual o volume do gás ao término da transformação?

Resolução:

V₁ = V₂

T₁ T2

3,01/400 = 300

450V₂ = 3,01 . 300

450V₂= 903

V₂= 903/450

V₂ = 2,0

Sinais da variação da energia interna (ΔU).

Variação da energia interna do gás positiva (ΔU > 0), o gás terá recebido energia.

Variação da energia interna do gás negativa (ΔU< 0), o gás cede parte de sua energia.

EXERCÍCIOS GERAIS

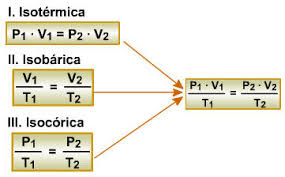
01) Observe o gráfico abaixo:

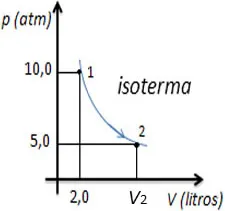
A isoterma de uma quantidade de gás que é levado de um estado 1 para um estado 2. O volume do estado 2, em litros, é:

Resolução:

P₁ . v₁ = P₂ . V₂

10 . 2 = p₂ . V₂

20 = 5V₂

20/5 = V₂

V₂ = 4L

02) (PUC-SP) Um certo gás, cuja massa vale 140g, ocupa um volume de 41 litros, sob pressão 2,9 atmosferas a temperatura de 17°C. O número de Avogadro vale 6,02. 1023 e a constante universal dos gases perfeitos R= 0,082 atm.L/mol.K. Nessas condições, o número de moléculas continuadas no gás é aproximadamente de:

Resolução:

pV = nRT

2,9. 41 = n. 0,082. 290

n = 5 mols

Usaremos regra de três simples para calcularmos o valor das moléculas

1 mol _______ 6,02 .1023 moléculas

5 mols ______ x

x ≈ 3,00. 1024 moléculas (note que este é um valor aproximado: houve a utilização da regra de arredondamento.)

03) Com base nas características de um gás ideal, analise as afirmações a seguir:

I. As partículas de um gás ideal ocupam um volume desprezível em relação ao volume total do recipiente.

II. As forças de atração e repulsão entre as partículas de um gás ideal são consideradas nulas, exceto durante as colisões.

III. As colisões entre as partículas de um gás ideal e as paredes do recipiente são inelásticas, resultando em perda de energia cinética.

IV. As partículas de um gás ideal movem-se em trajetórias retilíneas e uniformes entre as colisões.

(A) Apenas as afirmativas I e II estão corretas.

(B) Apenas as afirmativas II e III estão corretas.

(D) Todas as afirmativas estão corretas.

(E) Nenhuma das afirmativas está correta

Resolução:

Afirmativa I: Correta. A característica de "partículas pontuais" significa que o volume ocupado pelas próprias partículas é considerado desprezível em relação ao volume total do recipiente.

Afirmativa II: Correta. A ausência de interações intermoleculares, exceto durante colisões elásticas, é uma característica fundamental dos gases ideais.

Afirmativa III: Incorreta. As colisões em um gás ideal são perfeitamente elásticas, ou seja, não há perda de energia cinética durante as colisões.

Afirmativa IV: Correta. Entre as colisões, as partículas de um gás ideal movem-se em linha reta e com velocidade constante, devido à ausência de forças atuando sobre elas.

Alternativa: C

04) A equação de estado dos gases perfeitos, PV = nRT, relaciona diversas grandezas que descrevem o comportamento de um gás ideal. Considerando essa equação e os conceitos relacionados aos gases perfeitos, assinale a alternativa incorreta:

(A) Aumentando a temperatura de um gás ideal a volume constante, a pressão também aumenta.

(B) Diminuindo o volume de um gás ideal a temperatura constante, a pressão aumenta.

(D) A equação de estado dos gases perfeitos é válida para qualquer gás, independentemente das condições de pressão e temperatura.

(E) O número de mols (n) de um gás é diretamente proporcional ao volume ocupado por ele, a pressão e a temperatura constantes.

Resolução:

Alternativa b) Correta: A lei de Boyle estabelece que o produto da pressão pelo volume de um gás ideal é constante, a temperatura constante. Portanto, ao diminuir o volume, a pressão aumenta para manter o produto constante.

Alternativa c) Correta: A constante universal dos gases perfeitos é uma constante física que tem o mesmo valor para todos os gases ideais.

Alternativa d) Incorreta: A equação de estado dos gases perfeitos é uma idealização e não descreve o comportamento de todos os gases em todas as condições. A altas pressões e baixas temperaturas, as interações intermoleculares se tornam significativas e o modelo do gás perfeito se torna menos preciso.

Alternativa e) Correta: A lei de Avogadro estabelece que volumes iguais de gases diferentes, nas mesmas condições de temperatura e pressão, contêm o mesmo número 1 de moléculas. Portanto, o número de mols é diretamente proporcional ao volume, a pressão e a temperatura constantes.

Alternativa: D

05) Analise as afirmações a seguir, que tratam das transformações gasosas isotérmica, isocórica e adiabática, e marque V para as alternativas verdadeiras e F para as alternativas falsas.

I. Em uma transformação isotérmica, a temperatura do gás permanece constante, mas sua pressão e volume podem variar.

II. Em uma transformação isocórica, o volume do gás permanece constante, o que implica que não há trabalho realizado pelo gás ou sobre ele.

III. Durante uma transformação adiabática, ocorre troca de calor entre o gás e o ambiente, mas a temperatura do gás não varia.

IV. Na transformação isotérmica, o trabalho realizado pelo gás é igual à variação de sua energia interna.

V. Em uma transformação adiabática, o calor trocado com o meio é zero, mas a energia interna pode variar devido à realização de trabalho.

(A) V, V, F, F, V

(B) F, F, F, F, V

(D) V, V, F, F, V

(E) V, V, V, F, V

Resolução:

I. V – Na transformação isotérmica, a temperatura é constante, mas a pressão e o volume podem variar conforme a equação P vezes V igual a c o n s t a n t e

IIV – Na transformação isocórica, o volume é constante, e, portanto, W=0 (não há trabalho realizado).

III. F – Em uma transformação adiabática, não há troca de calor com o ambiente (Q=0), mas a temperatura pode variar devido à compressão ou expansão do gás.

IV. F – Na isotérmica, a variação de energia interna é zero (ΔU=0), e o trabalho realizado pelo gás é igual ao calor trocado (Q=W).

V. V – Na transformação adiabática, o calor trocado é zero (Q=0), mas a energia interna pode variar em função do trabalho realizado pelo gás ou sobre ele.

Alternativa: D

06) Uma massa gasosa está confinada em um recipiente com volume inicial de 8,0 L, a uma temperatura de 300 K e submetida a uma pressão inicial de 2,0 atm. O gás sofre uma transformação onde a pressão é aumentada para 3,0 atm e o volume diminui para 6,0 L.

Com base nesses dados, a nova temperatura do gás após e a transformação são

(A) 225,5 k e a transformação Isotérmica.

(B) 270,5 k e a transformação Isocórica

(D) 362,5 k e a transformação Adiabática

(E) 432,5 k e a transformação Isobárica

Resolução:

Usar a equação geral dos gases para calcular a nova temperatura.

A equação geral dos gases é:

Pi . V1 = P2 . V2

T1 T2

2 . 8/300 = 3 . 6T₂

16/300 = 18T²

16T₂ = 18 . 300

16T₂ = 5400

T₂ = 5400/16

T₂ = 377,5

Alternativa: C

07) Analise as alternativas abaixo e assinale a resposta que contém somente alternativas verdadeiras.

I – Transformações isotérmicas são aquelas em que a temperatura do gás é mantida constante.

II – Transformações adiabáticas envolvem trocas de calor entre o gás e o meio externo.

III – Transformação isocórica é aquela em que a pressão do gás é mantida constante.

IV – Transformações isobáricas acontecem com pressão constante.

São corretas:

(A) I e II.

(B) I, II e III.

(D) I e IV.

Resolução:

As alternativas II e III estão erradas, uma vez que as transformações adiabáticas não envolvem trocas de calor, e as transformações isocóricas são aquelas que acontecem em volumes constantes.

Alternativa: D

08) Um gás ideal sofre uma transformação rápida, de modo que sua temperatura, pressão e volume sofrem variações bruscas em um curto intervalo de tempo. De acordo com os seus conhecimentos sobre as transformações gasosas, a transformação sofrida pelo gás foi:

(A) isotérmica.

(B) isobárica.

(D) isovolumétrica.

Resolução:

As transformações adiabáticas ocorrem de forma rápida, de modo que não há tempo para que o gás realize trocas de calor com o meio externo. Nesse tipo de transformação, os parâmetros de pressão, volume e temperatura mudam de forma abrupta.

Alternativa: C

08) Vinte litros de gás hidrogênio foram medidos a 27ºC e 700 mmHg de pressão. Qual será o novo volume do gás a 87ºC e 600 mmHg de pressão?

Resolução:

P₁. V₁ =P₂. V₂
T₁T₂

V₂ = P_{1 .}V₁ . T₂
P₂ . T₁

V₂ = 700 . 20 . 360
600 . 300

V₂ = 28 L

09) Foram medidos 38 L de cloro a 127 ºC e a 720 mmHg de pressão. Qual será o volume que esse gás ocupará se ele for reduzido às condições normais de temperatura e pressão (CNTP)?

Resolução:

P₁. V₁ = P ₂. V₂
T₁T₂

V₂ = P₁.V₁ . T₂
P₂. T₁

V₂ = 720 . 38 . 273
760 . 400

V₂ = 24,57 L

10) (Cesgranrio-RJ) Você brincou de encher, com ar, um balão de gás, na beira da praia, até um volume de 1 L e o fechou. Em seguida, subiu uma encosta próxima carregando o balão, até uma altitude de 900m, onde a pressão atmosférica é 10% menor que a pressão ao nível do mar. Considerando que a temperatura na praia e na encosta seja mesma, o volume de ar no balão após a subida, será de:

Resolução:

P₁.V₁ = P₂.V₂

P₁. 1 = (0,90 . P₁) . V₂

V₂= 1 P₁
(0,90 . P₁)

V₂= 1
0,90

V₂= 1,1L

11) (UFU-MG) A atmosfera é composta por uma camada de gases que se situa sobre a superfície da Terra. Imediatamente acima do solo localiza-se uma região da atmosfera conhecida por troposfera, na qual ocorrem as nuvens, os ventos e a chuva. Ela tem uma altura aproximada de 10 km, a temperatura do seu topo é cerca de -50 °C e sua pressão é de 0,25 atm. Se um balão resistente a altas pressões, cheio com gás hélio até um volume de 10 L, a 1,00 atm e 27 °C, for solto, o volume deste balão, quando chegar ao topo da troposfera, será de:

Resolução:

P₁. V₁ = P ₂. V₂

T₁ T₂

V2 = P1.V1 . T2

P2. T1

V2 = 1,00 . 10 . 223

0,25 . 300

V2 = 29,7 L

12) Um gás ideal ocupa 6 litros em um recipiente, a pressão dentro do frasco é de 3 atm. Suponha que o gás sofra uma expansão isotérmica e passe a ocupar 9 litros. Qual será a pressão dentro do frasco?
Resolução:
P₁V₁ = P₂V₂

3 . 6 = P₂ . 9

18 = 9P₂

P2 = 18/2

P2 = 2 atm

13) Considerando a pressão de um gás ideal constante, o volume ocupado por ele é de 3 litros e a temperatura varia de 400 K para 800 K. Qual o volume final que este gás ocupa no frasco?
Resolução:

P₁V₁ = P₂V₂

3/400 = V_2/800

400V₂ = 3 . 800

400V₂ = 2400

V₂ = 2400/400

V₂ = 6 litros

topo