SIMULADO SARESP 9ºANO - MATEMÁTICA

Professor Diminoi

SAREP - 9º ANO

01) (SIMULADO SARESP – 9º ANO) O número 3 também pode ser representado por
(A) 13
(B) 1/3
(C) 6/2
(D) √6
Resolução:

Alternativa:

02) (SIMULADO SARESP – 9º ANO) João comprou uma pizza de 8 fatias e comeu 5 pedaços.
A fração que indica corretamente o total consumido é
(A) 5/1
(B) 1/5
(C) 8/5
(D) 5/8
Resolução:

Alternativa: D

03) (SIMULADO SARESP – 9º ANO) Qual o valor da expressão abaixo:

(A) 3/4
(B) – 3/4
(C) – 7/45
(D) – 31/45
Resolução:


Alternativa: D

04) (SIMULADO SARESP – 9º ANO) A soma do polinômio 4x2 + 2x + 1 com o polinômio x2 – 2x + 1 resulta no polinômio
(A) 5x2 + 1
(B) 5x2 + 2
(C) 5x4 + 2
(D) 5x4 – 4x + 1
Resolução: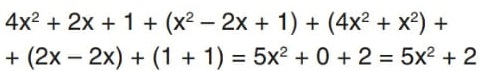

Alternativa: B

05) (SIMULADO SARESP – 9º ANO) Assinale a alternativa que representa corretamente a simplificação da expressão abaixo:

(A) 4x + 24x
(B) 16x + 6x
(C) 4 + 6x
(D) 4x + 6
Resolução:

Alternativa: D

06) (SIMULADO SARESP – 9º ANO) Dois irmãos compraram um bolo. Henrique comeu 1/4 do bolo e Leonardo comeu 1/2. Qual o total consumido do bolo?
(A) 2/6
(B) 1/6
(C) 1/4
(D) 3/4
Resolução:

Alternativa: D

07) (SIMULADO SARESP – 9º ANO) No 5º ano existem 50 alunos e 60% da turma é de meninas; sendo assim, quantos meninos há no 5º ano?
(A) 10
(B) 20
(C) 30
(D) 40
Resolução:

Total de alunos – número de meninas = número de meninos 50 – 30 = 20
Alternativa: B

08) (SIMULADO SARESP – 9º ANO) José viajou para um estado à direita do Mato Grosso, abaixo da Bahia, acima de São Paulo e que faz fronteira à esquerda com o Rio de Janeiro. José viajou para qual estado?
(A) Goiás.
(B) Tocantins.
(C) Minas Gerais.
(D) Espírito Santo.
Resolução:
MG está localizado à esquerda de MT, faz fronteira à esquerda com o RJ e está acima de SP e abaixo da BA.
Alternativa: C

09) (SIMULADO SARESP – 9º ANO) A imagem a seguir possui a base na forma geométrica de: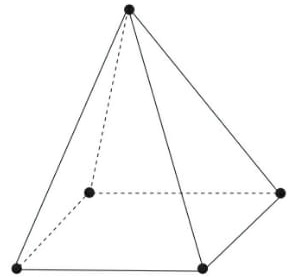
(A) pirâmide.
(B) triângulo.
(C) retângulo.
(D) quadrado.
Resolução:
Com a parte superior apresentando 4 triângulos iguais, podemos concluir que a base da pirâmide é um paralelogramo com lados iguais. Devido ao número de faces apresentado trata-se de um quadrado.
Alternativa: D

10) (SIMULADO SARESP – 9º ANO) No plano cartesiano abaixo, podemos representar os seguintes pontos: K(2,3), L(–1,4), Z(3,3) e R(–2,–1).
Dentre esses pontos, o mais distante do ponto (1,1) é
(A) K.
(B) L.
(C) Z.
(D) R.
Resolução:
(1, 1) – (–3, –1) = ((1 + 3), (1 + 1)) = (4, 2)
Alternativa: D

11) (SIMULADO SARESP – 9º ANO) Qual é a área em unidades² do paralelogramo abaixo localizado no centro da malha quadriculada?
(A) 16 u².
(B) 18 u².
(C) 20 u².
(D) 25 u².
Resolução:
B x h = 5 unidades x 4 unidades = 20 u2
Alternativa: B

12) (SIMULADO SARESP – 9º ANO) Uma quadra de futebol, de 40 metros de comprimento e 20 metros de largura, está sendo utilizada pelo 9º ano A e pelo 9º ano B, cada classe em uma metade.
Qual é a área da quadra destinada a cada turma do 9º ano?
(A) 120 m².
(B) 200 m².
(C) 400 m².
(D) 800 m².
Resolução:
4 unidades + 4 unidades = 8 u + 5 u = 18 unidades
Alternativa: B

13) (SIMULADO SARESP – 9º ANO) Uma quadra de futebol, de 40 metros de comprimento e 20 metros de largura, está sendo utilizada pelo 9º ano A e pelo 9º ano B, cada classe em uma metade.
Qual é a área da quadra destinada a cada turma do 9º ano?
(A) 120 m².
(B) 200 m².
(C) 400 m².
(D) 800 m².
Resolução:

Alternativa: C

14) (SIMULADO SARESP – 9º ANO) A cor da camisa de um time de futebol da escola foi posta em votação. O gráfico a seguir mostra o resultado dos votos.
Qual é a cor foi mais rejeitada na votação?
(A) Azul.
(B) Roxa.
(C) Branca.
(D) Vermelha.
Resolução:
Cor vencedora: vermelha com 15 votos.
Diferença azul para vermelha: 5 votos
Diferença roxa para vermelha: 11 votos
Diferença branca para vermelha: 15 votos
Maior diferença cor branca, logo a cor que foi mais
rejeitada na votação foi branca.
Alternativa: C

15) (SIMULADO SARESP – 9º ANO) Em uma universidade com cursos de exatas há 1 000 alunos, separados conforme o gráfico.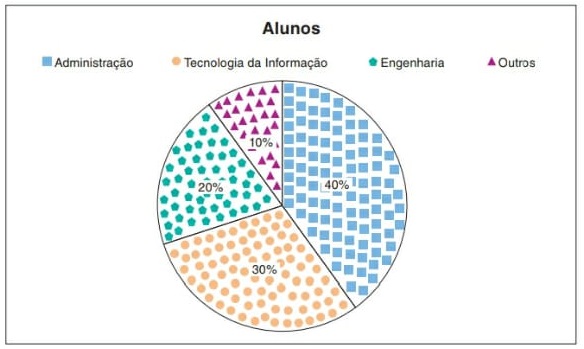
Quando somamos os alunos de Tecnologia da Informação com os de Engenharia, temos que a soma representará
(A) 30% do gráfico.
(B) 50% do gráfico.
(C) 60% do gráfico.
(D) 70% do gráfico.
Resolução:
TI = 20% de alunos da universidade, ENG = 30%.
20% + 30% = 50% do gráfico.
Alternativa: B

16) (SIMULADO SARESP – 9º ANO) Qual é a resposta correta para a raiz quadrada de √23, com aproximação até centésimos?
(A) 4,7
(B) 479
(C) 4,79
(D) 4,795
Resolução:
√23 = 4,7958 → aproximação para a casa de centésimos = 4,79
Alternativa: C

17) (SIMULADO SARESP – 9º ANO) A fração que melhor representa o ponto A na reta numérica é
(A) 1/6
(B) 2/3
(C) 3/2
(D) 6/10
Resolução:

Alternativa: B

18) (SIMULADO SARESP – 9º ANO) Observe o plano cartesiano a seguir.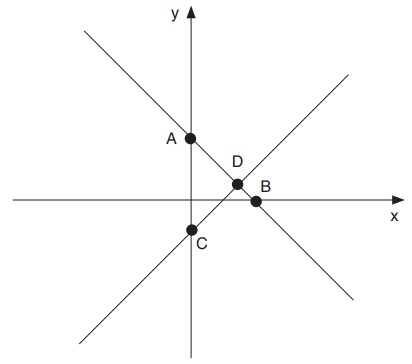
As retas da figura representam graficamente um sistema de duas equações do 1º grau com duas incógnitas, cuja solução pode ser representada pelo ponto
(A) A.
(B) B.
(C) C.
(D) D
Resolução:
Independente das equações que o sistema apresentar, se houver um ponto de intersecção entre as retas, ela será o resultado dos sistemas.

As retas são concorrentes no ponto (D)
Alternativa: D

19) (SIMULADO SARESP – 9º AO) Qual é a área do círculo abaixo, utilizando pí = 3,1?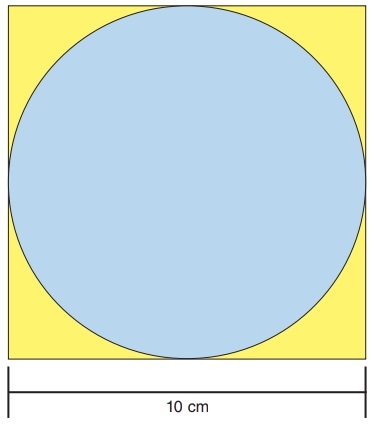
(A) 40 cm².
(B) 124 cm².
(C) 310 cm².
(D) 77,5 cm².
Resolução: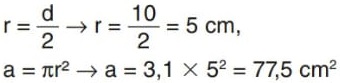

Alternativa:

20) (SIMULADO SARESP – 9º ANO) Considerando que um objeto em queda livre percorre a distância d, que é proporcional ao quadrado do tempo t x 6, a função que representa essa relação é
(A) d = 6 . t2
(B) d = 2 . t6
(C) d = 6 . t
(D) d = 6 . 2t
Resolução:
d = (t . t) 3 6 → d = 6 . t2
Alternativa: A

21) (SIMULADO SARESP – 9º ANO) Considerando que Tiago gastou 3/7 da metade de sua mesada para comprar uma camiseta no valor de R$ 42,00, qual é o valor da mesada que Tiago ganha?
(A) R$ 49,00.
(B) R$ 84,00.
(C) R$ 98,00.
(D) R$ 196,00.
Resolução: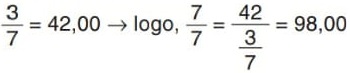

Os 7/7 representam a metade do valor da mesada, basta agora multiplicar por 2 para se obter o valor total da mesada. 98,00 3 2 = R$ 196,00
Alternativa: D

22) (SIMULADO SARESP – 9º ANO) O x no sistema linear abaixo
é igual a
(A) 2
(B) 6
(C) 8
(D) 10
Resolução:

Alternativa: C

23) (SIMULADO SARESP – 9º ANO) Um triângulo retângulo possui catetos de mesma medida; logo os ângulos agudos desse triângulo
(A) medem 45°.
(B) somam 180°.
(C) medem 30° e 60°.
(D) medem 40° e 50°.
Resolução:
Sabendo que a soma dos ângulos internos de um triângulo resulta em 180°, subtrai-se 90° por se tratar de um triângulo retângulo. Sobram 90° para que os catetos formem a hipotenusa, porém, se os catetos possuem medidas iguais, obrigatoriamente seus ângulos deverão ser iguais.
Logo, 90/2 = 45° cada ângulo.
Alternativa: A

24) (SIMULADO SARESP – 9º ANO) Em relação aos triângulos da figura a seguir, pode-se afirmar que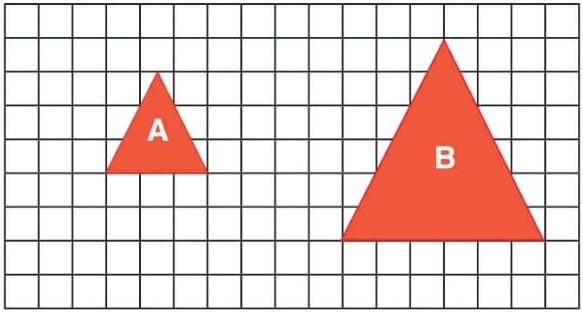
(A) o triângulo B é seis vezes mais alto que o triângulo A.
(B) o triângulo A é três vezes mais baixo que o triângulo B.
(C) o triângulo B é duas vezes mais alto que o triângulo A.
(D) o triângulo A é duas vezes mais alto que o triângulo B.
Resolução:
Triângulo maior = B, triângulo menor = A

Triângulo maior B = 2 vezes o menor triângulo A.
Alternativa: C

25) (SIMULADO SARESP – 9º ANO) Uma bola de futebol oficial possui raio de aproximadamente 11 centímetros, logo uma bola oficial possui diâmetro de
(A) 14,14 centímetros.
(B) 22 centímetros.
(C) 5,5 centímetros.
(D) 34,54 centímetros.
Resolução:
Considerando que o raio é a metade do diâmetro, temos

diâmetro = 11 . 2 = 22 cm
Alternativa: B

26) (SIMULADO SARESP – 9º ANO) O proprietário de uma chácara decide construir uma piscina de 5 metros de largura por 6 metros de comprimento. Sabendo que a água ficará a 10 cm de transbordar e a altura total é de 1,3 m, qual volume de água a piscina terá?
(A) 30 m³.
(B) 36 m³.
(C) 39 m³.
(D) 42 m³.
Resolução:
1 m = 100 cm; portanto 10 cm = 0,1 metro

Vol. = 5 m . 6 m . 1,2 m = 36 m3
Alternativa: B

27) (SIMULADO SARESP – 9º ANO) Um aro de basquete não oficial, colocado no colégio de Antônio, possui o diâmetro de 46 centímetros. Qual é a área interna do aro?
(A) 1 661 cm².
(B) 3 322 cm².
(C) 6 644 cm².
(D) 144,4 cm².
Resolução:

Alternativa: A

28) (SIMULADO SARESP – 9º ANO) A medida da ponta de um prédio até o final de sua sombra é igual a 40 metros e a sombra forma um ângulo de 50° em relação ao solo.
Utilizando 0,8 para sen 50°, assinale a alternativa que corresponde à altura H do prédio.
(A) 32 m.
(B) 50 m.
(C) 62,5 m.
(D) 90 m.
Resolução:

cateto op. = sen 50° . 40 = 0,8 . 40 = 32 m
Alternativa: A

29) (SIMULADO SARESP – 9º ANO) Em um aquário com dimensões de três metros de comprimento, dois metros de largura e com a água a uma profundidade de um metro e meio, foi feito um estudo para colocar uma espécie de peixe. Considerando que a cada metro cúbico cabem dois peixes confortavelmente, quantos peixes dessa espécie caberiam nesse aquário?
(A) 6
(B) 9
(C) 12
(D) 18
Resolução:

3 m . 2 m = 6 m2 . 1,5 m = 9 m3, sendo 2 peixes por m3
Alternativa: D

30) (SIMULADO SARESP – 9º ANO) Em um lançamento de dado a probabilidade de cair em uma face cujo número seja par é
(A) 1/2
(B) 1/3
(C) 1/6
(D) 3/1
Resolução:
Um dado possui seis lados, sendo três deles de números pares. Sendo eles 2, 4 e 6.

Alternativa: A

31) (SIMULADO SARESP – 9º ANO) As variáveis y e z assumem valores de acordo com a tabela a seguir.
A relação y e z é obtida pela expressão
(A) y2 = z – 2
(B) z2 = y – 2
(C) z2 = y + 2
(D) y2 = z + 2
Resolução:
y2 = z + 2
12 = – 1 + 2 → 1 = 1
22 = 2 + 2 → 4 = 4
32 = 7 + 2
9 = 9
42 = 14 + 2
16 = 16
Logo a expressão é y2 = z + 2
Alternativa: D

32) (SIMULADO SARESP – 9º ANO) Na liga de basquete, os times ganham 2 pontos a cada vitória, 1 ponto por empate e não pontuam quando são derrotados. O time do colégio Alpha participou de 40 jogos e fez 60 pontos, empatando 10 jogos. Adote como G o número de jogos ganhos pelo colégio Alpha, E para o número de jogos em que houve empate e P para os jogos que foram perdidos.
O sistema de equações que representa corretamente a situação do colégio Alpha na liga é

Resolução:
número de vitórias = 60 – 10 (empates) = 50/2 = 25 vitórias número de perdas = 40 – 25 – 10 = 5 jogos perdidos número de jogos disputados é igual à soma das perdas, vitórias e empates → G + E + P = 40, sendo P = 5, G = 25 e E = 10
Portanto, a expressão que representa o total de jogos é esta:
G + E + 5 = 40
E a expressão que representa os pontos ganhos é esta:
2G + 1E + 0P = 60 ou 2G + 1E = 60
Alternativa: B

33) (SIMULADO SARESP – 9º ANO) Qual expressão algébrica representa a área total da figura?
(A) x² + y²
(B) (x + y)²
(C) (x + y) 3 x 2
(D) (x + y) 3 x 4
Resolução:
(x + y)2 = x2 + 2xy + y2
x2 = área do quadrado maior.
2xy = área dos dois retângulos
y2 = área do quadrado menor
Sendo assim, a somatória das áreas corresponde à área do quadrado formado.
Alternativa: B

34) (SIMULADO SARESP – 9º ANO) A dimensão média de uma molécula de oxigênio é de 0,0000003 milímetros.
Esse número, escrito em notação científica, corresponde a
(A) 3 . 3.108 mm.
(B) 3 . 3.10–8 mm.
(C) 0,3 .3.106  mm.
(D) 0,3 . 3.10–6 mm.
Resolução:
0,000 000 3 → 6 casas de zero após a vírgula

Para indicar a divisão, o número que eleva o dez é multiplicado por –1.
Alternativa: D

35) (SIMULADO SARESP – 9º ANO) A área do quadrado a seguir é igual a 64 cm².
Com base nas informações acima, no texto e na imagem, qual é o valor do perímetro desse quadrado?
(A) 16
(B) 20
(C) 25
(D) 32
Resolução:
a = 12 → lado = y + 3, área = 64.
64 = (y + 3)2 → y = √64 – 3 → y = 5
perímetro = lado + lado + lado + lado = 4 3 lado
p = 4 3 (y + 3) → p = 4 3 (5 + 3) → p = 32
Alternativa: D

36) (SIMULADO SARESP – 9º ANO) Um veículo consome 12 litros de etanol a cada 84 quilômetros. Considerando que o preço do litro é R$ 2,30, quantos quilômetros o carro percorre sabendo-se que foi abastecido com R$ 103,50?
(A) 315 km.
(B) 399 km.
(C) 540 km.
(D) 1 008 km.
Resolução:
O primeiro passo é determinar o valor de litros de etanol abastecido.
2,30 – 1 litro
103,50 – x litros = 45 litros no tanque Em seguida, determinamos a quantidade de quilômetros percorrida. Se 12 litros fazem 84 km, 45 fazem x.

Alternativa: A

37) (SIMULADO SARESP – 9º ANO) Quando encaixamos quatro triângulos retângulo isósceles iguais, unindo as laterais de 45° e os ângulos de 90° no centro, formamos o polígono
(A) retângulo.
(B) quadrado.
(C) hexágono.
(D) pentágono.
Resolução:

4 triângulos retângulo isósceles geram um polígono de 4 lados. Como dois dos lados são iguais, formarão um
quadrado regular.
Alternativa: B

38) (SIMULADO SARESP – 9º ANO) João caminhava na parte da manhã em direção ao nascer do Sol, quando virou a 90° à direita e seguiu caminhando. Após alguns minutos, João se virou a 180° e notou que caminhava na direção
(A) Sul.
(B) Leste.
(C) Norte.
(D) Oeste.
Resolução:
Na parte da manhã o Sol está a Leste, quando João vira a 90° à direita, toma a posição Sul e, após virar 180° da posição Sul, inverte seu curso para o Norte
Alternativa: C

39) (SIMULADO SARESP – 9º ANO) Qual é o número de diagonais do polígono regular cuja soma dos ângulos internos é igual 720°?
(A) 4
(B) 5
(C) 6
(D) 9
Resolução:

Alternativa: D

40) (SIMULADO SARESP – 9º ANO) Sabendo que os triângulos abaixo são semelhantes, calcule o valor de z.
(A) 19
(B) 19,5
(C) 27
(D) 30
Resolução:

Alternativa: D

41) (SIMULADO SARESP – 9º ANO) Um recipiente cilíndrico com 17 centímetros de altura e 8 centímetros de diâmetro possui volume interno de
(A) 200 cm³.
(B) 427 cm³.
(C) 854 cm³.
(D) 3 416 cm³.
Resolução:

Alternativa: C

42) (SIMULADO SARESP – 9º ANO) Em um mapa a escala marcada é 1 mm: 1 km. Roberta mediu a distância de 8 centímetros com uma régua, o que em medida real corresponde a
(A) 8 km.
(B) 80 km.
(C) 0,8 km.
(D) 800 km
Resolução:

Alternativa: B

43) (SIMULADO SARESP – 9º ANO) Observe a imagem a seguir.
A medida h é igual a
(A) 6
(B) 9
(C) 13
(D) 18
Resolução:
a2 = b2 + c2
102 = 82 + h2
102 – 82 = h2
h = √100 - √64
h = √36
h = 6
Alternativa: A

44) (SIMULADO SARESP – 9º ANO) Um veículo percorreu 400 quilômetros, metade em duas horas e metade em uma hora e meia. Pode-se afirmar que a velocidade média, em quilômetros por hora, foi de
(A) 100 km/h.
(B) 114 km/h.
(C) 116 km/h.
(D) 133 km/h.
Resolução:

Alternativa: C

45) (SIMULADO SARESP – 9º ANO) Márcio irá jogar três dados em sequência. Quantas possíveis combinações existem para que os três dados caiam apenas em números ímpares sem repetir os números anteriores?
(A) 6
(B) 9
(C) 27
(D) 120
Resolução:
1º lance . 2 lance . 3º lance
3 . (3 – 1) . (3 – 2) = 6
Alternativa: A

46) (SIMULADO SARESP – 9º ANO) João foi comprar uma mala de viagem, e o vendedor lhe disse que o preço da mala multiplicado pelo seu triplo daria 432.
A equação que expressa o valor da mala é    
(A) x + 3x = 432.  
(B) x - 3x = 432.  
(C) x ∙ 3x = 432.  
(D) x2 + 3x = 432.
Resolução:
Chamando de x o preço da mala e que deve ser multiplicado pelo seu triplo para encontrar o número 432, tem-se, seguindo a leitura do texto que: x ∙ 3x = 432
Alternativa: C

47) (SIMULADO SARESP – 9º ANO) As raízes da equação x2− 5x + 6 = 0 são 
(A) 2 ou −3.  
(B) −2 ou 3.  
(C) 2 ou 3.  
(D) −2 ou −3.
Resolução:
Por Bhaskara, temos que: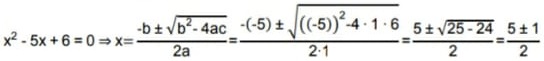

x1 = 3 e x2 = 2 
Por soma e produto:

De (I) e (II), temos que os únicos valores que satisfazem a igualdade, são os números 2 e 3. 
Podemos usar também a expressão x2 - Sx + P e calcular mentalmente.
Alternativa: C

48) (SIMULADO SARESP – 9º ANO) Se o produto de dois fatores é zero, necessariamente um deles é igual a zero. Assim, as raízes reais da equação (x + 2) ∙ (x - 6) = 0  são 
(A) 2 e −6.  
(B) −2 e 6.  
(C) 2 e −2.  
(D) 2 e 6.
Resolução:
Dada a equação: (x + 2) . (x - 6) = 0, Considerando a afirmação do enunciado têm – se: (x + 2) = 0 ou (x – 6) = 0
Donde: x = −2 e x = 6.
Logo, as raízes da equação estão no conjunto solução S = {−2, 6}
Alternativa: B

49) (SIMULADO SARESP – 9º ANO) Um vitral retangular colorido de dimensões 2m por 4m será emoldurado conforme indica a figura a seguir.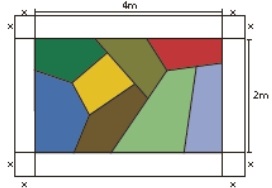 
Sabendo que a área total da moldura é de 7 m2, calcule a medida x do lado dos quadrados nos cantos da moldura, tendo em vista que os quatro cantos da moldura são quadrados idênticos. 
(A) 0,2 m.  
(B) 0,3 m.  
(C) 0,4 m.  
(D) 0,5 m.
Resolução:
Tem-se inicialmente que, a área do vitral (4m . 2m) é 8m2.
A dimensão dos lados da figura retangular com a moldura ficará acrescida de 2x.
Sendo (4 + 2x) e (2 + 2x).
A outra informação é que a área da moldura é 7m2.
Ao subtrair a área do vitral (8m2) da área total da figura (4 + 2x) . (2 + 2x), tem-se a área da moldura que é 7m2.
Assim: 
[(4 + 2x) . (2 + 2x) -8] = 7 (aplicando a propriedade distributiva)
(8 + 8x + 4x + 4x2) – 15 = 0 (agrupando os termos comuns) 4x2 + 12x – 7 = 0
Na equação, temos que:
a = 4
b = 12
c = −7

As raízes da equação serão:

(neste caso não se considera esta raiz)
Portanto a medida x, do lado do quadrado, conforme figura, é x = 0,5m.
Alternativa: D

50) (SIMULADO SARESP – 9º ANO) Em um retângulo, de 54cm2 de área, o comprimento é expresso por (x − 1) cm, enquanto a largura é expressa por (x − 4) cm. Nessas condições, o valor de x é: 
(A) −5.  
(B) 9.  
(C) 10.  
(D) 54.
Resolução:
Tendo a representação de um retângulo como citado no problema com dimensões (x − 1) cm e (x − 4) cm e área de 54 cm2
Então:
(x - 1) ∙ (x - 4) =54
x2 - 4x - x + 4 = 54
x2 - 5x + 4 = 54
x2 - 5x - 50 = 0
x1 = 10
x2 = -5 
Não considerando o valor −5, pois não existem medidas negativas, então o valor de x será 10 metros.
Alternativa: C

51) (SIMULADO SARESP – 9º ANO) Uma determinada revista canadense apresentou duas leis que representam a relação entre o número do sapato (n) e o comprimento do pé (c) de uma pessoa, em polegadas. Para as mulheres, a lei é n = 3c – 22 e para os homens, é n = 3c – 25. Assim, responda: Qual é o número do sapato de uma mulher cujo comprimento do pé é 11 polegadas e o de um homem com 15 polegadas, respectivamente? 
(A) 55 e 70  
(B) 20 e 11  
(C) 11 e 20  
(D) 11 e 15
Resolução:
Para resolver o problema proposto o aluno deverá identificar a natureza da variação entre duas grandezas. Nesta situação-problema as grandezas N e C, diretamente proporcionais. Então temos que:

Na caracterização dessa interdependência entre as duas grandezas, identificamos que uma pode variar livremente, que será a variável independente, a outra que foi determinada, será a variável dependente.
Alternativa: C

52) (SIMULADO SARESP – 9º ANO) Francisca e João fizeram um bolo. Cada um contribui com alguns ingredientes. No final da sua confecção, irão reparti-lo na razão de 3/2 .  Sabendo-se que o bolo pesa 1200 gramas, caberá a 
(A) Francisca 1080 gramas e João 120 gramas.  
(B) Francisca 400 gramas e João 600 gramas.  
(C) Francisca 600 gramas e João 600 gramas.  
(D) Francisca 720 gramas e João 480 gramas.
Resolução:
Se o bolo será repartido na razão de 3 para 2, conclui-se que ele será dividido em cinco partes iguais, ou seja, a razão de proporcionalidade direta é  1/5 , portanto cada parte do bolo equivale a uma massa de 240 g (1200/5). Desta forma caberá a Francisca 720g do bolo (240 . 3) e para João 480g do bolo (240 . 2).
Alternativa: D

53) (SIMULADO SARESP – 9º ANO) Dois sacos de ração alimentam 6 galinhas por semana. Sabendo que se trata de uma situação de proporcionalidade direta, os valores que preenchem corretamente as lacunas na tabela são, respectivamente.
(A) 9 e 11.  
(B) 12 e 14.  
(C) 9 e 9.  
(D) 10 e 12.
Resolução:
Verifica-se a partir da tabela que, se dois sacos de ração alimentam seis galinhas, um saco alimenta três galinhas. Logo os valores na tabela estão na razão de 1:3. Então, 3 sacos de ração alimentam 9 galinhas e, para alimentar 33 galinhas serão necessários 11 sacos de ração. Portanto, 9 e 11 são as quantidades respectivas às lacunas da tabela;
Alternativa: A

54) (SIMULADO SARESP – 9º ANO) Considere as grandezas “distância de casa” e “tempo percorrido” na seguinte situação: Paulo saiu de sua casa de automóvel para ir ao trabalho, mas o pneu furou. Depois de trocá-lo ele continuou o trajeto. Nessas condições o gráfico que representa corretamente essa situação é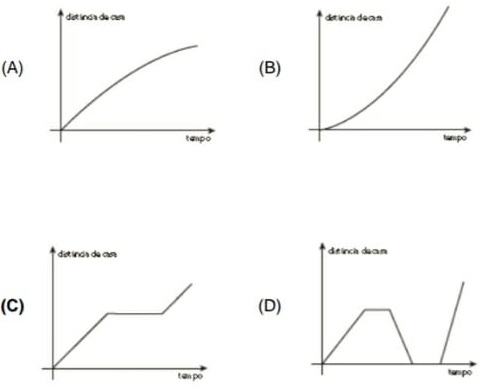

Resolução:
O gráfico correto é o da alternativa C. Pois, partindo de casa a distância inicial e o tempo são iguais a zero, por isso seu início é na origem. A medida que inicia o movimento, a distância aumenta com o passar do tempo, até o momento de trocar o pneu. A partir desse instante a distância permanece constante, ou seja, sem aumentar, porém, o tempo não para e determina um patamar no gráfico. Com o pneu trocado o movimento é retomado e novamente a distância volta a crescer com o passar do tempo, como se observa no gráfico:

Alternativa: C

55) (SIMULADO SARESP – 9º ANO) O valor a ser pago por uma pessoa para abastecer seu automóvel varia proporcionalmente em função da quantidade de litros de combustível utilizado. Tal função trata-se de uma relação de proporcionalidade direta.
A partir das informações apresentadas no gráfico, pode-se afirmar que: 
(A) a relação de (L) litros e Preço (P) é decrescente, ou seja, quanto maior a quantidade de litros menor o valor a ser pago.  
(B) a relação de (L) litros e Preço (P) é crescente, ou seja, quanto maior a quantidade de litros maior o valor a ser pago.   
(C) a relação de (L) litros e Preço (P) é crescente e sua constante de proporcionalidade é k = 3,5.   
(D) a relação de (L) litros e Preço (P) é decrescente e sua constante de proporcionalidade é k = −3,5.
Resolução:
O objetivo da questão é demonstrar a habilidade do estudante em identificar, no gráfico a relação de crescimento entre as grandezas envolvidas. Do gráfico, tem-se que a relação litros e preço é direta, e que o valor do litro do combustível em questão é R$ 2,50. Então a constante k de proporcionalidade é k = 2,5. Assim, P = k . L ou P= 2,5 . L e, portanto, quanto maior a quantidade de litros de combustível, maior o valor a ser pago.
Alternativa: B

56) (SIMULADO SARESP – 9º ANO) A maior parte da água doce existente no Brasil está na Amazônia. Na figura, a quantidade de copos com água representa a proporção de água doce na Amazônia e no restante do Brasil. Ou seja, 7 copos para a Amazônia e 3 para o resto do Brasil.
Considerando a água doce existente no Brasil, qual a porcentagem dela que está na Amazônia?         
(A) 7%. 
(B) 23,3%.  
(C) 30%.  
(D) 70%.
Resolução:
É necessário compreende o conceito de razão e porcentagem.
Alternativa: D

57) (SIMULADO SARESP – 9º ANO) Ao pesar 1/4 de quilograma de salame, a balança mostrou         
(A) 0,250 kg.  
(B) 0,125 kg.  
(C) 0,150 kg.  
(D) 0,500 kg.
Resolução:
O problema pede a representação decimal da fração 1/4 é realizando     1 ÷ 4 = 0,250 ou seja, a quarta parte de 1 kg é equivalente a 250 g.
Alternativa: A

58) (SIMULADO SARESP – 9º ANO) Na figura 1, tem-se um retângulo tomado como unidade de área. Na figura 2, está sombreada a quarta parte da unidade. Na figura 3, está sombreado um terço da unidade
Na figura 4, a unidade está dividida em partes iguais e a região sombreada (uma dessas partes) corresponde a
(A) 1/6 da unidade.  
(B) 1/12 da unidade.  
(C) 1/24 da unidade.  
(D) 1/36 da unidade.
Resolução:
Basta compreender a ideia de que fração e parte todo representada na figura.
Alternativa: B