Professor Diminoi
TERMOMECÂNICA
01) (Termomecânica) Uma nova marca de sabão em pó foi colocada no mercado em duas embalagens diferentes. A embalagem verde contém 500 g e é vendida por R$ 4,00, e a embalagem rosa contém 750 g e custa R$ 5,40. Na compra de 5 kg desse produto, o menor preço que uma pessoa poderá pagar é
(A) R$ 35,20.
(B) R$ 36,40.
(C) R$ 37,60.
(D) R$ 38,80.
(E) R$ 40,00.
Resolução:
Transformando todo em garmas:
1250g custa R$ 9,40
Aplicando regra de três temso:
1250 --- 9,4
5000 --- x
1250x = 9,4 . 5000
1250x = 47000
x = 47000 / 125 0
x = 37,6
Alternativa: B
02) (Termomecânica) Para chegar exatamente às 8 horas a uma reunião, um funcionário precisou dirigir seu automóvel a uma velocidade constante de 60 quilômetros por hora, demorando 1 hora e 10 minutos no trajeto de casa até o trabalho. Se ele houvesse feito o mesmo percurso, utilizando velocidade constante de 50 quilômetros por hora, teria chegado
(A) 14 minutos atrasado.
(B) 14 minutos adiantado.
(C) 24 minutos atrasado.
(D) 24 minutos adiantado.
(E) 48 minutos adiantado.
Resolução:
1 hora e 10 minutos = 70 minutos
Aplicando a regra de trê temos:
60 --- 70
50 --- x
Grandeza inversamente proporcional
60 --- x
50 --- 70
50x = 60 .70
50x = 4200
x = 4200 / 50
x = 84
Lavendo 60minutos ele chegou no horário se ele levar 84 minutos. Portanto, ele chagará 14 minutos atrasado.
Alternativa: A
03) (Termomecânica) A mensalidade paga pelos alunos de uma determinada escola é de R$ 240,00 e vence no dia 10 de cada mês. Após o dia do vencimento, cobra-se uma multa correspondente a 2,5% desse valor, por dia de atraso. Se o pagamento de uma mensalidade for feito no dia 17, o valor a ser pago será de
(A) R$ 264,00.
(B) R$ 276,00.
(C) R$ 282,00.
(D) R$ 342,00.
(E) R$ 360,00.
Resolução:
J = C . i . t / 100
J = juros simples
C = capital inicial
i = taxa de juros
t = tempo da aplicação
J = C . i . t / 100
J = 240 . 2,5 . 7 / 100
J = 4200 / 100
J = 42
O valor da mensalidade é R4 240,00 mais o juot de 7 dias;
240 + 42 = 282
Alternativa: C
04) (Termomecânica) O anúncio publicado em uma revista, sobre a venda de um apartamento, apresenta o esboço de uma planta desenhada em escala de 1:200, isto é, a cada centímetro do desenho correspondem 200 centímetros da medida real. Dessa forma, uma parede que tem comprimento de 5,5 m deve estar representada
no desenho por um traço de
(A) 75 cm.
(B) 55 cm.
(C) 27 cm.
(D) 5,5 cm.
(E) 2,75 cm.
Resolução:
1 --- 200
x --- 550
200x = 550
x = 550 / 200
x = 2,75
Alternativa: E
05) (Termomecânica) Uma pessoa aplica R$ 5.400,00 à taxa de 12,5% ao ano, em regime de juros simples. Para que esse capital seja duplicado, o tempo de aplicação deve ser de
(A) 6 meses.
(B) 8 meses.
(C) 7,5 anos.
(D) 8 anos.
(E) 8,5 anos.
Resolução:
J= C. i. n
J = ?
C = 5400
i = 12,5
Neste caso o juros deve ser igual ao capital
J = C . i . t
5400 = 5400 , 12,5 . t
5400 = 67500t
5400 = 67500t
0,08 = t
O juro é dividido por 100, portanto, neste caso para encontramos o tempo temos que multiplica-lo por 100:
0,08 . 100 = 8
Alternativa: D
06) (Termomecânica) João precisa pintar um total de 48 ripas de madeira. Na sexta-feira, ele pintou 3/8 desse total, no sábado, pintou 1/3 das ripas restantes, e, no domingo, pintou as demais, finalizando a pintura. Em relação ao número total de ripas de madeira, aquelas que foram pintadas no domingo correspondem à fração
(A) 1/3
(B) 1/6
(C) 1/8
(D) 1/4
(E) 1/5
Resolução
Sexta-feira
Quantidade de ripas pintadas
48 . 3 / 8 = 18
Quantidade de ripas restantes
48 – 18 = 30
Sábado
Quantidade de ripas pintadas
30 . 3 / 5 = 18
Quantidade de ripas restantes
30 – 18 = 12
Conclusão: João pintou 12 ripas no domingo.
12 / 48 = 1 / 4
Resposta: D
07) (Termomecânica) Um lote de livros será dividido em caixas, cada uma delas contendo o mesmo número de livros. Pode-se colocar em cada caixa 20 livros, mas também é possível colocar 24 livros em cada uma, ou 25 livros em cada uma, e qualquer que seja a opção, todos os livros do lote ficarão guardados não sobrando livro algum fora das caixas. O menor número de livros desse lote é
(A) 480
(B) 540
(C) 720
(D) 660
(E) 600
Resolução
A questão não informa a quantidade total de livros, porém sabemos que esses livros podem ser divididos em caixas com 20, 24 ou 25 livros, sem sobra.
Como a banca deseja saber “o menor número de livros desse lote”, basta calcularmos o MMC (mínimo múltiplo comum) de 20, 24 e 25.
MMC (20, 24, 25) = 600
Alternativa: E
08) (Termomecânica) Uma empresa possui em sua frota 36 veículos. Parte desses veículos são movidos somente a etanol e os demais são movidos somente a gasolina. A razão do número de veículos movidos somente a etanol para o número de veículos movidos somente a gasolina é 5/7. O número de veículos dessa frota movidos somente a gasolina é
(A) 21
(B) 18
(C) 12
(D) 15
(E) 9
Resolução
Sabendo que a razão entre o número de carros movidos a etanol e o número de carros movidos a gasolina é 5/7, podemos concluir que a cada 12 carros, 5 são movidos a etanol e 7 são movidos a gasolina.
Considerando que a frota possui 36 veículos, temos:
36 . 7 / 12 = 21
Alternativa: A
09) (Termomecânica) Uma empresa recebeu 1 200 currículos de candidatos interessados nas vagas oferecidas de emprego e selecionou 35% deles para realizarem uma prova. Sabendo que 15% dos candidatos que fizeram a prova foram contratados, então, o número de candidatos contratados foi
(A) 42
(B) 49
(C) 63
(D) 56
(E) 70
Resolução
Quantos participaram da prova:
1200 . 35/100 = 420
Quantos foram contratados:
420 . 15/100 = 63
Alternativa: C
10) (Termomecânica) O gráfico mostra algumas informações sobre o número de unidades vendidas do produto A em 5 dias de uma determinada semana.Sabendo que nesses 5 dias foram vendidas, em média, 30 unidades por dia, então, o número de unidades vendidas na quinta-feira foi
(A) 45
(B) 30
(C) 40
(D) 35
(E) 25
Resolução
Analisando o gráfico, e sabendo que a média é igual a 30 unidades, temos:
(30 + 25 + 20 + x + 40) / 5 = 30
115 + x = 30.5
115 + x = 150
x = 150 – 115
x = 35
Alternativa: D
11) (Termomecânica) Uma máquina, trabalhando sem interrupções, fabrica 30 peças iguais em 18 minutos. Essa mesma máquina, trabalhando sem interrupções por 2 horas e 48 minutos, irá fabricar uma quantidade de peças igual a
(A) 220
(B) 280
(C) 300
(D) 240
(E) 260
Resolução
2 horas e 48 minutos = 120 + 48 = 168 minutos
Regra de três
30 peças ————— 18 minutos
x peças —————- 168 minutos
18x = 30.168
18x = 5040
x = 5040/18
x = 280
Alternativa: B
12) (Termomecânica) Roberta recebeu determinado valor de abono salarial. Gastou, desse valor, 1/5 na farmácia e 1/3 no supermercado, restando ainda R$ 252,00. O valor do abono recebido por Roberta foi
(A) R$ 600,00.
(B) R$ 630,00.
(C) R$ 660,00.
(D) R$ 570,00.
(E) R$ 540,00.
Resolução
Calculando a fração que representa quanto Roberta gastou na farmácia e no supermercado:
1/5 + 1/3 = (3 + 5)/15 = 8/15
Considerando que x representa o valor do abono, temos:
x . 8/15 = 252
x = 252 . 15/8
x = 540
Alternativa: E
13) (Termomecânica) Ana e Bete trabalham como vendedoras em uma mesma loja de roupas. Certo dia elas venderam, no total, 54 camisetas. Sabendo que Ana vendeu 8 camisetas a mais do que Bete, então, o número de camisetas vendidas por Ana foi
(A) 29
(B) 30
(C) 31
(D) 28
(E) 27
Resolução
Sabendo que Ana vendeu 8 camisetas a mais do que Bete, considere que:
x = quantidade de camisas vendidas por Bete
x + 8 = quantidade de camisas vendidas por Ana
Considerando que, no total, foram vendidas 54 camisetas:
x + x + 8 = 54
2x = 54 – 8
2x = 46
x = 46/2
x = 23
Quantidade de camisetas vendidas por Ana:
x + 8 = 23 + 8 = 31
Alternativa: C
14) (Termomecânica) Um fio de cobre, com 2,7 m de comprimento, foi dividido em 5 pedaços. O 1o pedaço com 1,3 m de comprimento e os demais pedaços todos de comprimento iguais entre si, conforme mostra a figura.
(A) 65 cm.
(B) 75 cm.
(C) 85 cm.
(D) 105 cm.
(E) 95 cm.
Resolução
Sabendo que o comprimento total é de 2,7 metros e que o comprimento do primeiro pedaço é igual a 1,3 metros, podemos concluir que a soma dos demais é igual a:
2,7 – 1,3 = 1,4 metros
Como os demais pedaços possuem comprimentos iguais, temos que:
4x = 1,4
x = 1,4 / 4
x = 0,35 m
Calculando a diferença entre o comprimento do 1o pedaço e o comprimento do 2o pedaço:
1,3 – 0,35 = 0,95 m = 95 cm
Alternativa: E
15) (Termomecânica) Alfredo foi a uma loja de materiais elétricos para comprar alguns itens. A tabela mostra a quantidade comprada de cada item e seu respectivo valor unitário.O valor total gasto por Alfredo nessa compra foi
(A) R$ 90,00.
(B) R$ 92,80.
(C) R$ 87,50.
(D) R$ 80,00.
(E) R$ 83,20.
Resolução
Calculando o valor gasto com cada item:
Lâmpada
4 . 8,70 = 34,80
2 . 12,60 = 25,20
3 . 10,00 = 30,00
Total
34,80 + 25,20 + 30,00 = 90,00
Alternativa: A
16) (Termomecânica) Um terreno retangular ABCD, com 12 m de comprimento, teve 2/5 de sua área total, reservada para um canteiro de hortaliças, conforme mostra a figura, onde as medidas indicadas estão em metros.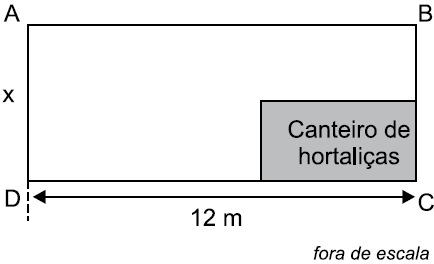 Sabendo que a área do canteiro de hortaliças é 24 m2, então, a medida do lado do terreno, indicada na figura pela letra x, é igual a
Sabendo que a área do canteiro de hortaliças é 24 m2, então, a medida do lado do terreno, indicada na figura pela letra x, é igual a
(A) 6,0 m.
(B) 5,5 m.
(C) 7,0 m.
(D) 5,0 m.
(E) 6,5 m.
Resolução
Área total da figura
A = 12x
Considerando que a área do canteiro é 24m2, e que isso representa 2/5 da área total, temos:
12x . 2/5 = 24
24x/5 = 24
x/5 = 1
x = 5
Alternativa: D
17) (Termomecânica) Uma região retangular foi totalmente cercada por tela. A figura mostra as medidas dos lados, em metros, dessa região.Se para cercar totalmente essa região foram utilizados 48 m de tela, a medida do lado maior é igual a
(A) 8 m
(B) 14 m
(C) 12 m
(D) 10 m
(E) 16 m
Resolução
Sabendo que o perímetro do retângulo mede 48 metros, temos:
x + x + x + 4 + x + 4 = 48
4x + 8 = 48
4x = 48 – 8
4x = 40
x = 40/4
x = 10 m
Medida do maior lado:
x + 4 = 10 + 4 = 14 m
Alternativa: B
18) (Termomecânica) A figura mostra as medidas internas, em centímetros, de um recipiente que tem a forma de um bloco retangular, com 30 cm de altura.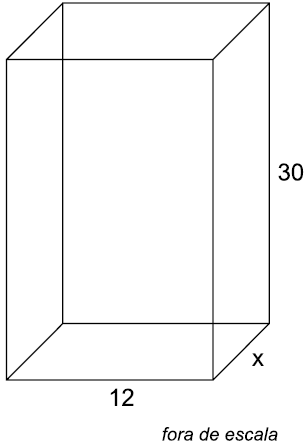 A capacidade total desse reservatório é 2,88 litros. Lembrando que 1 litro = 1 000 cm3 , então, a medida do lado do retângulo da base, indicado na figura pela letra x, é igual a
A capacidade total desse reservatório é 2,88 litros. Lembrando que 1 litro = 1 000 cm3 , então, a medida do lado do retângulo da base, indicado na figura pela letra x, é igual a
(A) 8 cm.
(B) 7 cm.
(C) 10 cm.
(D) 6 cm.
(E) 9 cm.
Resolução
Considerando que 1 litro = 1000 cm3, temos que 2,88 litros corresponde a 2880 cm3.
Calculando o volume do bloco retangular:
12.x.30 = 2880
360x = 2880
36x = 288
x = 288/36
x = 8 cm
Alternativa: A
19) (Termomecânica) Três amigos, Pedro, José e Caio marcaram de se encontrar na frente de um estádio de futebol, para assistirem a um jogo. Sabe-se que:
– Pedro não foi o último a chegar.
– Caio chegou antes que José.
– Pedro chegou depois de Caio.
Nessas condições, o 1o, o 2o e o 3o a chegar foram, respectivamente,
(A) Caio, José e Pedro.
(B) Pedro, Caio e José.
(C) Caio, Pedro e José.
(D) José, Pedro e Caio.
(E) Pedro, José e Caio.
Resolução
Como Pedro não foi o último a chegar, porém chegou depois de Caio, podemos concluir que ele foi o segundo a chegar.
Como Caio chegou antes de José, um foi o primeiro e o outro foi o último a chegar.
Ordem correta:
Caio, Pedro, José
Alternativa: C
Continua...





