Professor Diminoi
EXPRESSÕES NUMÉRICAS
Expressões numéricas são conjuntos de números que sofrem operações matemáticas com uma ordem de operações preestabelecida. Para que você aprenda a resolvê-las, primeiramente, destacaremos a prioridade que as operações matemáticas possuem.
Ordem das operações
As operações matemáticas estudadas no Ensino Fundamental são: adição, subtração, multiplicação, divisão, potenciação e radiciação.

Potenciação e radiciação
Em uma expressão numérica, sempre resolva primeiro as potências e raízes antes de qualquer outra operação matemática. A única exceção é para o caso em que aparecem colchetes, chaves ou parênteses. Vale ressaltar que, entre potências e raízes, não há prioridade.
Multiplicação e divisão
Em segundo lugar, quando não houver mais potências ou raízes, devem ser feitas as multiplicações e divisões. Entre essas duas, também não há prioridade. Realize aquela que aparecer primeiro ou que facilitará os cálculos.
Adição e subtração
Por último, realize as somas e diferenças. Também não há prioridade entre elas. Resolva-as na ordem em que aparecerem.
Ordem entre colchetes, chaves e parênteses
Em algumas expressões numéricas, uma parte da expressão pode ter prioridade em relação às outras. Essa parte deve ser separada com parênteses, chaves e/ou colchetes. A prioridade em que as operações devem ser feitas é a seguinte:
Parênteses
Em primeiro lugar, devem ser feitas todas as operações que estiverem dentro dos parênteses. Se houver muitas operações, a ordem que deve ser seguida é a das operações, dada anteriormente.
Colchetes
Em segundo lugar, as operações que estiverem dentro de colchetes deverão ser feitas também de acordo com a ordem das operações dada anteriormente.
Lembre-se apenas de que os parênteses aparecem sozinhos ou dentro de colchetes. Nesse caso, quando sobrar apenas um número dentro dos parênteses, estes podem ser eliminados.
Chaves
Por último, as operações dentro de chaves também devem ser realizadas de acordo com a ordem das operações.
Exemplo:
{15 + [(7 – 100:102) + (16:√4 – 4)]2 + 10} . 3
Observe que existem dois parênteses dentro de colchetes. Qualquer um dos dois pode ser feito primeiro ou ambos podem ser realizados ao mesmo tempo, desde que não se misturem os cálculos para cada um. Faremos na ordem em que aparecem. Isso é o mais indicado a ser feito.
Assim, para os primeiros parênteses, faremos a potência; depois, a divisão e, por fim, a subtração:
{15 + [(7 – 100:102) + (16:√4 – 4)]2 + 10}·3
{15 + [(7 – 100:100) + (16:√4 – 4)]2 + 10}·3
{15 + [(7 – 1) + (16:√4 – 4)]2 + 10}·3
{15 + [(6) + (16:√4 – 4)]2 + 10}·3
Nesse caso, os parênteses podem ser eliminados.
{15 + [6 + (16:√4 – 4)]2 + 10} . 3
Agora os parênteses seguintes. Primeiro, a raiz quadrada; depois, divisão e subtração.
{15 + [6 + (16:2 – 4)]2 + 10} . 3
{15 + [6 + (8 – 4)]2 + 10} . 3
{15 + [6 + (4)]2 + 10} . 3
{15 + [6 + 4]2 + 10} . 3
Note que, dentro dos colchetes, sobrou apenas uma adição. Depois de realizá-la, o número que sobrar deverá ser elevado ao quadrado. Assim, obteremos:
{15 + [10]2 + 10} . 3
{15 + 100 + 10} . 3
Agora, falta apenas realizar os cálculos dentro das chaves e multiplicar o resultado por 3:
{15 + 100 + 10} . 3
125 . 3
375
QUESTOES RESOLVIDAS
01) 87 + 7 . 85 - 120
Resolução:
87 + 7 . 85 - 120
87 + 595 - 120
682 - 120 = 562
02) 25 + 6 2 : 12 - √169 + 42
Resolução:
25 + 6 2 : 12 - √169 + 42
25 + 36 : 12 - 13 + 42
25 + 3 - 13 + 42
28 - 13 + 42
15 + 42 = 57
01) {15 + [(7 – 100:102) + (16:√4 – 4)]2 + 10} . 3
Resolucao
{15 + [(7 – 100:102) + (16:√4 – 4)]2 + 10} . 3
{15 + [(7 – 100:100) + (16:√4 – 4)]2 + 10} . 3
{15 + [(7 – 1) + (16:√4 – 4)]2 + 10} .3
{15 + [(6) + (16:√4 – 4)]2 + 10} . 3
Nesse caso, os parênteses podem ser eliminados.
{15 + [6 + (16:√4 – 4)]2 + 10}·3
Agora os parênteses seguintes. Primeiro, a raiz quadrada; depois, divisão e subtração.
{15 + [6 + (16:2 – 4)]2 + 10} . 3
{15 + [6 + (8 – 4)]2 + 10} . 3
{15 + [6 + (4)]2 + 10} . 3
{15 + [6 + 4]2 + 10} . 3
Note que, dentro dos colchetes, sobrou apenas uma adição. Depois de realizá-la, o número que sobrar deverá ser elevado ao quadrado. Assim, obteremos:
{15 + [10]2 + 10} . 3
{15 + 100 + 10} . 3
Agora, falta apenas realizar os cálculos dentro das chaves e multiplicar o resultado por 3:
{15 + 100 + 10}·3
125 . 3
375
02) Resolva as espresao a seguir
10 + 12 – 6 + 7
22 – 6 + 7
16 + 7
23
03) Resolva as espresao a seguir
40 – 9 x 4 + 23
40 – 36 + 23
4 + 23
27
04) Resolva as espresao a seguir
120 + 2 . 14 – 63
120 + 28 – 63
148 – 63
85
05) Resolva as espresao a seguir
76 + 81 : 3 – 39
76 + 27 – 39
103 – 39
64
06) Resolva as espresao a seguir
13 . 3 – 14 . 2
39 – 28
11
07) Resolva as espresao a seguir
123 + 120 – 65 + 39 . 3 – 83
243 – 65 + 117 – 83
178 + 117 - 83
295 - 83
212
08) Resolva as espresao a seguir
52 + 36 . 4 + 32 – 90
52 + 144 + 32 – 90
196 + 32 – 90
228 – 90
138
09) Resolva as espresao a seguir
138 – 15 . 6 +31 + 60 . 2
138 – 90 + 31 + 120
48 + 31 + 120
199
10) Resolva as espresao a seguir
( 4 .7 + 12) : ( 3 . 5 + 5)
( 4 x 7 + 12) : ( 3 x 5 + 5)
( 28 + 12) : ( 3 x 5 + 5)
40 : ( 3 x 5 + 5 )
40 : ( 15 + 5)
40 : 20
2
11) Resolva as espresao a seguir
15 + [(3 . 6 -2) -(10 - 6 : 2) + 1]
15+[(18 – 2) - (10 - 3)+1]
15+[16-7 +1]
15+[9 + 1]
15+10
25
12) Resolva as espresao a seguir
50 -{40 – 3 . [5 -(10 - 7)]}
50-{40-3x[5 - 3]}=
50-{40 - 3 x 2}=
50-{ 40 – 6 }=
50 - 34=
16
13) A respeito da resolução de expressões numéricas, assinale a alternativa correta:
(A) As operações devem ser feitas na ordem em que aparecem.
(B) É necessário calcular primeiro todas as operações no interior dos parênteses na ordem em que elas aparecem.
(C) A pessoa que realiza os cálculos escolhe a ordem mais oportuna para eles.
(D) Não existe ordem para realização dos cálculos em uma expressão numérica.
(E) As adições e subtrações são os últimos cálculos na lista de prioridades das expressões numéricas.
Resolucao
a) Falsa.
As operações devem ser feitas na seguinte ordem: potências e raízes, multiplicações e divisões e, por fim, adições e subtrações.
b) Falsa.
Embora realmente seja necessário calcular primeiro as operações no interior de parênteses, a ordem de realização das operações é: potências e raízes, multiplicações e divisões e, por fim, adições e subtrações.
c) Falsa.
A ordem para realização das operações é predefinida: potências e raízes, multiplicações e divisões e, por fim, adições e subtrações.
d) Falsa.
Na realidade, existe uma ordem de realização dos cálculos, como já dito.
e) Verdadeira.
Alternativa E
14) Calcule o valor numérico da expressão [(18 + 3 · 2) ÷ 8 + 5 · 3] ÷ 6.
Resolucao
A ordem em que uma expressão deve ser calculada é a seguinte: primeiro as operações dentro dos parênteses; depois, dentro dos colchetes e, por fim, dentro das chaves. Quanto às operações, o correto é realizar primeiramente as multiplicações e divisões e, posteriormente, as adições e subtrações. Portanto:
[(18 + 3 · 2) ÷ 8 + 5 · 3] ÷ 6
[(18 + 6) ÷ 8 + 5 · 3] ÷ 6
[(24) ÷ 8 + 5 · 3] ÷ 6
Quando sobrar apenas um número dentro dos parênteses, colchetes ou chaves, elimine essas marcações.
[(24) ÷ 8 + 5 · 3] ÷ 6
[24 ÷ 8 + 5 · 3] ÷ 6
[3 + 15] ÷ 6
[18] ÷ 6
18 ÷ 6
3
Logo, o valor numérico dessa expressão é 3.
15) Calcule o valor numérico da expressão {[(8 · 4 + 3) ÷ 7 + (3 + 15 ÷ 5) · 3] · 2 – (19 – 7) ÷ 6} · 2 + 12.
Resolucao
Primeiramente, devem ser calculadas as operações dentro dos parênteses. Mesmo dentro dos parênteses, a ordem correta de operações é multiplicação e divisão, depois adição e subtração.
{[(8 · 4 + 3) ÷ 7 + (3 + 15 ÷ 5) · 3] · 2 – (19 – 7) ÷ 6} · 2 + 12
{[(32 + 3) ÷ 7 + (3 + 3) · 3] · 2 – (12) ÷ 6} · 2 + 12
Agora realizaremos as somas dentro dos parênteses e eliminaremos os parênteses desnecessários.
{[(32 + 3) ÷ 7 + (3 + 3) · 3] · 2 – (12) ÷ 6} · 2 + 12
{[35 ÷ 7 + 6 · 3] · 2 – 12 ÷ 6} · 2 + 12
Eliminados os parênteses, partiremos para os cálculos dos colchetes:
{[35 ÷ 7 + 6 · 3] · 2 – 12 ÷ 6} · 2 + 12
{[5 + 18] · 2 – 12 ÷ 6} · 2 + 12
{[23] · 2 – 12 ÷ 6} · 2 + 12
{23 · 2 – 12 ÷ 6} · 2 + 12
Sem colchetes, realizaremos as operações presentes nas chaves, respeitando a ordem de operações:
{23 · 2 – 12 ÷ 6} · 2 + 12
{46 – 2} · 2 + 12
{44} · 2 + 12
44 · 2 + 12
Basta finalizar a expressão respeitando apenas a ordem entre as operações.
44 · 2 + 12
88 + 12
100
O valor numérico da expressão é 100.
16) (UniCESUMAR SP) Escrever um número na notação científica significa expressá-lo como o produto de dois números reais x e y, tais que: 1 ≤ x < 10 e y é uma potência de 10.
Assim, por exemplo, as respectivas expressões dos números 0,0021 e 376,4 na notação científica são
2,1 x 10–3 e 3,764 x 102.
Com base nessas informações, a expressão do número N na notação científica é:
N = 14,4·0,072
0,16·0,000027
(A) 7,2 x 103
(B) 2,4 x 104
(C) 2,4 x 105
(D) 3,6 x 104
(E) 3,6 x 103
Resolucao
N = 1,44 . 101 . 7,2 . 10-2
1,6·10-1· . 2,7·10-5
N = 1,44 . 7,2 . 101 . 10-2
1,6 . 2,7. 10-1. 10-5
N = 10,368 . 101-2
4,32 . 10-1-5
N = 10,368 . 10-1
4,32 . 10-6
N = 2,4 . 105
17) (UNAERP SP) Analisando as expressões:
I. [(+2)(– 3/4):(–2/3)]
II. (+2–3+1):(–2+2)
III. (+4–9):(–5+3)
IV. (2–3+1):(–7)
podemos afirmar que zero é o valor de:
(A) somente I, II e IV
(B) somente I e III
(C) somente IV
(D) somente II e IV
(E) somente II
Resolucao
Para resolver essa questão, é necessário resolver antes todas as expressões numéricas presentes.
I: [(+2)(–3)]:(–2)
4 3
(–6):(–2)
4 3
(–6) · 3
4 –2
18
8
Como 18 divido por 8 é um número próximo de 2, então a expressão I é diferente de zero.
II: (+2 – 3 + 1):(–2 + 2) = 0:0
Como não é possível dividir números por 0, então 0:0 não existe e, por isso, a expressão é diferente de zero.
III: (+ 4 – 9):(– 5 + 3) = (– 5):(– 2) = 2,5
2,5 é diferente de zero.
IV: (2 – 3 + 1):(–7) = 0:(–7) = 0
Essa expressão é a única que tem 0 como resultado
Alternativa C
18) (CREF SC – Quadrix) Qual é o valor da expressão numérica abaixo? [- (-2)³ – 2³]
(A) 0
(B) 1
(C) 8
(D) -8
(E) -16
Resolução
[- (-2)³ – 2³]
= [- (-8) – 2³]
= [8 – 2³]
= [8 – 8]
= 0
Alternativa A
19) (Bombeiros AC – Funcab) Calcule o valor da expressão: [2 + 3 x 4] ÷ 7 + 7.
(A) 9
(B) 7
(C) 4
(D) 12
(E) 1
Resolução
[2 + 3 x 4] ÷ 7 + 7
[2 + 12] ÷ 7 + 7
14 ÷ 7 + 7
2 + 7
9
Alternativa A
20) (PM AC – Funcab) Determine o valor da expressão: -1 + 6 x (7 – 4 ÷ 2)
(A) 7,5
(B) 29
(C) 8,5
(D) 24
(E) 32,5
Resolução
-1 + 6 x (7 – 4 ÷ 2)
-1 + 6 x (7 – 2)
-1 + 6 x 5
-1 + 30
29
Alternativa B
21) (TJ CE – ESAF) Simplifique: ( (0 ÷ 3) + (0,75 x 4) ) / ( 1 + 0,5).
(A) 1,5
(B) 2
(C) 4
(D) 5,5
(E) 6
Resolução
( (0 ÷ 3) + (0,75 x 4) ) / ( 1 + 0,5)
( 0 + 3) ) / 1,5
3) / 1,5
2
Alternativa B
22) A respeito da resolução de expressões numéricas, assinale a alternativa correta:
(A) As operações devem ser feitas na ordem em que aparecem.
(B) É necessário calcular primeiro todas as operações no interior dos parênteses na ordem em que elas aparecem.
(C) A pessoa que realiza os cálculos escolhe a ordem mais oportuna para eles.
(D) Não existe ordem para realização dos cálculos em uma expressão numérica.
(E) As adições e subtrações são os últimos cálculos na lista de prioridades das expressões numéricas.
Resolucao
a) Falsa!
As operações devem ser feitas na seguinte ordem: potências e raízes, multiplicações e divisões e, por fim, adições e subtrações.
b) Falsa!
Embora realmente seja necessário calcular primeiro as operações no interior de parênteses, a ordem de realização das operações é: potências e raízes, multiplicações e divisões e, por fim, adições e subtrações.
c) Falsa!
A ordem para realização das operações é predefinida: potências e raízes, multiplicações e divisões e, por fim, adições e subtrações.
d) Falsa!
Na realidade, existe uma ordem de realização dos cálculos, como já dito.
e) Verdadeira!
Alternativa E
23) Qual das alternativas a seguir representa um quinto do resultado desta expressão numérica: [(64 – 16 . 4) + (48·10 – 180)] . 5
(A) 270
(B) 300
(C) 350
(D) 400
(E) 410
Resolucao
Para resolver esse problema, lembre-se da ordem de resolução das expressões numéricas. Primeiramente, deve-se resolver o interior dos parênteses; em seguida, os colchetes e, nos casos em que aparecerem, as chaves. Já as operações matemáticas devem ser resolvidas com a seguinte prioridade: primeiramente, as raízes e potências (na ordem em que aparecerem); depois, multiplicações e divisões (na ordem em que aparecerem) e, por fim, adições e subtrações (na melhor ordem possível). Dessa maneira, faremos:
[(64 – 16·4) + (48·10 – 180)]·5 =
[(64 – 64) + (480 – 180)]·5 =
[0 + 300]·5 =
300·5 =
1500
Como o exercício pede um quinto desse resultado, será necessário dividi-lo por 5:
1500:5 = 300
Alternativa B
25) Margarida viu no quadro-negro algumas anotações da aula anterior um pouco apagadas, conforme mostra a figura a seguir. Qual número foi apagado?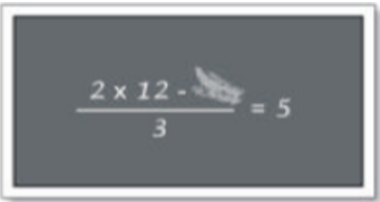 (A) 9
(A) 9
(B) 10
(C) 12
(D) 13
(E) 15
Resolucao
Primeiramente, trocaremos x por ·, para representar a multiplicação, e o espaço apagado por y, para representar o número que queremos descobrir. Posteriormente, multiplicaremos ambos os lados da igualdade pelo mesmo número para obter:
2·12 – x = 5
3
2·12 – x = 5·3
2·12 – x = 15
24 – x = 15
Agora, pense em um número que subtraído de 24 resulte em 15, ou seja, um número que somado com 15 resulte em 24. Esse número é 9.
Alternativa A
26) (CREF SC – Quadrix) Qual é o valor da expressão numérica abaixo? [- (-2)³ – 2³]
(A) 0
(B) 1
(C) 8
(D) -8
(E) -16
Resolução
[- (-2)³ – 2³]
= [- (-8) – 2³]
= [8 – 2³]
= [8 – 8]
= 0
Alternativa A
27) (Bombeiros AC – Funcab) Calcule o valor da expressão: [2 + 3 x 4] ÷ 7 + 7.
(A) 9
(B) 7
(C) 4
(D) 12
(E) 1
Resolução
[2 + 3 x 4] ÷ 7 + 7
[2 + 12] ÷ 7 + 7
14 ÷ 7 + 7
2 + 7
9
Alternativa A
28) (PM AC – Funcab) Determine o valor da expressão: -1 + 6 x (7 – 4 ÷ 2)
(A) 7,5
(B) 29
(C) 8,5
(D) 24
(E) 32,5
Resolução
-1 + 6 x (7 – 4 ÷ 2)
-1 + 6 x (7 – 2)
-1 + 6 x 5
-1 + 30
29
Alternativa B
29) (Guarda Civil SP) Qual o valor de x na expressão abaixo?
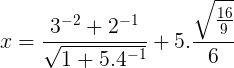
(A) 1/27
(B) 41/27
(C) 1/17
(D) 11/18
(E) 41/17
Resolução
Calcularemos por partes:
3-² + 2-¹ = 1/9 + 1/2 = (2 + 9)/18 = 11/18
√(1 + 5.4-¹) = √(1 + 5/4) = √[(4 + 5)/4] = √(9/4) = 3/2
5.√(16/9)/6 = 5.(4/3)/6 = 5.4/6.3 = 20/18 = 10/9
(11/18) / (3/2) = 11.2/18.3 = 22/54 = 11/27
11/27 + 10/9 = (11 + 30)/27 = 41/27
Alternativa B
30) (TJ CE – ESAF) Simplifique: ( (0 ÷ 3) + (0,75 x 4) ) / ( 1 + 0,5).
(A) 1,5
(B) 2
(C) 4
(D) 5,5
(E) 6
Resolução
((0 ÷ 3) + (0,75 x 4) ) / ( 1 + 0,5)
(0 + 3) ) / 1,5
3) / 1,5
2
Alternativa B
31) Qual é o resultado da expressão: 20 ÷ {√4 . [-9 + 17 ÷ (-2 + 5)]} – [7 . (-3) – 16 ÷ (-2) + 2]
(A) 9
(B) 10
(C) 11
(D) 12
(E) 13
Resolução
Primeiro vamos eliminar o parêntese:
20 ÷ {√4 . [-9 + 12 ÷ (-2 + 5)]} – [7 . (-3) – 16 ÷ (-2) + 2]
20 ÷ {√4 . [-9 + 12 ÷ (-2 + 5)]} – [7 . (-3) – 16 ÷ (-2) + 2]
20 ÷ {√4 · [-9 + 12 ÷ 3]} – [7 · (-3) – 16 ÷ (-2) + 2]
Agora eliminaremos os colchetes:
20 ÷ {√4 . [-9 + 12 ÷ 3]} – [7 . (-3) – 16 ÷ (-2) + 2]
20 ÷ {√4 . [-9 + 4]} – [7 . (-3) – 16 ÷ (-2) + 2]
20 ÷ {√4 . [-9 + 4]} – [7 . (-3) – 16 ÷ (-2) + 2]
20 ÷ {√4 . [-9 + 4]} – [-21 – 16 ÷ (-2) + 2]
20 ÷ {√4 . [-9 + 4]} – [-21 – 16 ÷ (-2) + 2]
20 ÷ {√4 . [-9 + 4]} – [-21 + 8 + 2]
20 ÷ {√4 . [-9 + 4]} – [-21 + 8 + 2]
20 ÷ {√4 . (-5)} – [-21 + 8 + 2]
20 ÷ {√4 . (-5)} – [-21 + 8 + 2]
20 ÷ {√4 . (-5)} – [-13 + 2]
20 ÷ {√4 . (-5)} – [-13 + 2]
20 ÷ {√4 . (-5)} – [-11]
20 ÷ {√4 . (-5)} + 11
Agora eliminaremos as chaves, respeitando a ordem de prioridade entre as operações:
20 ÷ {√4 . (-5)} + 11
20 ÷ {2 . (-5)} + 11
20 ÷ {2 . (-5)} + 11
20 ÷ (-10) + 11
Eliminando todos os símbolos, realizaremos, primeiro, a divisão e, depois, a adição:
20 ÷ (-10) + 11
-2 + 11
9
Alternativa A
32)– Analisando as expressões:
I. [8 : (8 × (-2) + 18)] – √16
II. [8 × (9 : 3 + 1)] + 2
III. {3² – [4 + (3 – 6 : 2)²]} – 5
As expressões que têm como resultado zero são:
(A) I, II e III
(B) somente I e II
(C) somente I e III
(D) somente II e III
(E) Nenhuma delas
Resolução
Resolvendo cada uma delas, temos que:
I.
[8 : (8 × (-2) + 18)] – √16
[8 : (-16 + 18)] – √16
[8 : 2] – √16
4 – √16
4 – 4
0
II.
[8 × (9 : 3 + 1)] + 2
[8 × (3 + 1)] + 2
[8 × 4] + 2
32 + 2
34
III.
{3² – [4 + (3 – 6 : 2)²]} – 5
{3² – [4 + (3 – 3)²]} – 5
{3² – [4 + 0²]} – 5
{3² – [4 + 0]} – 5
{3² – 4} – 5
{9 – 4} – 5
5 – 5
0
Alternativa C
33) (UNAERP SP/2006) Analisando as expressões:
I. [(+2)(–3/4)]:(–2/3)
II. (+2 – 3 + 1):(–2+2)
III. (+4–9):(–5+3)
IV (2–3+1):(–7)
Podemos afirmar que zero é o valor de:
(A) somente I, II e IV
(B) somente I e III
(C) somente IV
(D) somente II e IV
(E) somente II
Resolucao
A única forma de ter certeza do resultado é resolvendo todas as expressões numéricas presentes no exercício.
Lembre-se da ordem de resolução das expressões: primeiramente o que está no interior de parênteses, depois dentro de colchetes e, por fim, dentro de chaves. As operações encontradas devem ser feitas na seguinte ordem: radiciação ou potenciação, depois multiplicação ou divisão e, por fim, as adições ou subtrações.
I. Primeiramente o que está no interior dos parênteses:
[(+2)(–3/4)]:(–2/3)
[(+2)(–0,75)]:(–0,666...)
Observe que os parênteses dentro dos colchetes servem apenas para dizer que se trata de uma multiplicação entre um número positivo e um número negativo. Sendo assim, o resultado dessa multiplicação será negativo também. Portanto, teremos:
–1,5:(–0,666...)
Fazendo o jogo de sinais para a divisão acima, teremos:
1,5:0,666...
O resultado dessa divisão é 2,25, que é diferente de zeroII. Primeiramente, devemos resolver o que está no interior dos parênteses. É aconselhável somar números de sinais iguais quando a soma envolve três ou mais parcelas.
(+2 – 3 + 1):(–2+2)
(+3 – 3):(– 2+2)
0:0
A divisão encontrada, de zero por zero, não pode existir, pois, em uma divisão, o divisor é obrigatoriamente diferente de zero. Portanto, o resultado dessa divisão não é zero.
III. Novamente, é preciso fazer os cálculos no interior dos parênteses primeiro.
(+4–9):(–5+3)
(– 5):(– 2)
Fazendo o jogo de sinais, teremos:
5:2 = 2,5
Esse resultado é diferente de zero.
IV. Primeiramente, resolva as operações no interior dos parênteses.
(2–3+1):(–7)
(3 – 3):(–7)
0:(–7)
0
O único item que resulta em zero é o IV.
Alternativa C
34) (UEL PR) Considere dois números inteiros, a e b, consecutivos e positivos. Qual das expressões abaixo corresponde necessariamente a um número par?
(A) a + b
(B) 1 + ab
(C) 2 + a + b
(D) 2a + b
(E) 1 + a + b
Resolucao
Se a e b são consecutivos, um deles tem que ser par, e o outro, ímpar. Números pares podem ser escritos na forma 2n, e números ímpares, na forma 2n + 1. Supondo que a = 2n, b obrigatoriamente deve ser igual a 2n+1, pois 2n+1 é consecutivo de a.
Agora, é preciso analisar cada alternativa da questão.
a)
a + b =
2n + 2n + 1 =
4n + 1 =
2·(2n) + 1
É um número ímpar, pois é o sucessor de um número par.
b)
1 + ab
O produto entre um número par e um número ímpar é um número par. Somando esse resultado a um, obtemos um número ímpar.
c)
2 + a + b
A soma de um número par com um número ímpar sempre tem um número ímpar como resultado. Assim, 2 + a é um número par que, somado a b (ímpar), resulta em um número ímpar.
d)
2a + b
Qualquer multiplicação por 2 tem como resultado um número par. A soma de um número par (2a) com um número ímpar sempre resulta em um número ímpar.
e)
1 + a + b
A soma entre um número par e um número ímpar é igual a um número ímpar. Somando um número ímpar com um número ímpar, o resultado sempre será um número par.
Alternativa E
35) Os professores de determinada escola precisavam fazer a contagem dos alunos vencedores dos jogos internos a fim de adquirir as medalhas para premiação. No sexto ano, são 50 alunos no total. Apenas a quinta parte deles recebeu medalhas no vôlei, e a metade recebeu medalhas no futebol. No sétimo ano, com 30 alunos, apenas as meninas, que representam um terço dos alunos da sala, foram premiadas no vôlei e todos os meninos foram premiados no futebol. Já no oitavo ano, foram 7 medalhas de ouro, 4 de prata e 3 de bronze. Por fim, o nono ano não participou da competição.
Quantas medalhas foram compradas?
(A) 79
(B) 80
(C) 78
(D) 77
(E) 81
Resolucao
Primeiramente, é necessário montar a expressão numérica que representa a situação. A quinta parte de 50 é representada pela divisão 50:5 e a metade é 50:2. A situação do sétimo é de 30:3 meninas premiadas e 30-30:3 meninos premiados. Por fim, basta somar 7, 4 e 3 alunos do oitavo ano. Observe:
(50:5 + 50:2) + (30:3 + 30 – 30:3) + 7 + 4 + 3
Faça primeiro o interior dos parênteses, dando prioridade para multiplicações e divisões.
(50:5 + 50:2) + (30:3 + 30 – 30:3) + 7 + 4 + 3
(10 + 25) + (10 + 30 – 10) + 7 + 4 + 3
35 + 30 + 7 + 4 + 3
Agora realize as operações que sobraram.
35 + 30 + 7 + 4 + 3
65 + 7 + 4 + 3
72 + 4 + 3
76 + 3
79
O número de alunos premiados foi 79.
Alternativa A
36) Que número representa metade do resultado da expressão numérica abaixo?
[(4 . 5 – 6·3):(5 . 13 – 9 . 7)]:[(122:6 . 4):(6 . 8 – 6 . 7)]
(A) 1
(B) 2
(C) 0,5
(D) 1,5
(E) 2,5
Resolucao
A hierarquia de realização dos cálculos começa com o interior dos parênteses para depois o interior dos colchetes. Nas operações, a ordem correta é potenciação e radiciação, depois multiplicação e divisão e, por fim, adições e subtrações.
Seguindo essa ordem, teremos o seguinte:
[(4·5 – 6·3):(5·13 – 9·7)]:[(122:6·4):(6·8 – 6·7)]
[(20 – 18):(65 – 63)]:[(144:24):(48 – 42)]
[2:2]:[6:6]
1:1
1
O resultado da expressão numérica é 1, mas a questão pede metade desse resultado.
1/2 = 0,5
Alternativa C
37) Carla pensou em um número e a ele somou 4 unidades. Após isso, Carla multiplicou o resultado por 2 e somou o próprio número. Sabendo que o resultado da expressou foi 20, qual o número que Carla escolheu?
(A) 8
(B) 6
(C) 4
(D) 2
Resolucao
Vamos utilizar a letra x para representar o número que Carla pensou.
Primeiro, Carla somou 4 unidades a x, ou seja, x + 4.
Ao multiplicar o resultado por 2, temos 2(x+4) e, por fim, o próprio número pensado foi adicionado:
2(x+4) + x
Se o resultado da expressão é 20, podemos calcular o número que Carla escolheu da seguinte forma:
2(x + 4) + x = 20
2x + 8 + x = 20
3x = 20 - 8
3x = 12
x = 12/3
x = 4
Portanto, o número escolhido por Carla foi 4.
Alaternatica C
38) Paula montou o próprio negócio e resolveu vender dois tipos de bolo para começar. Um bolo de chocolate custa R$ 15,00 e um bolo de baunilha custa R$ 12,00. Sendo x a quantidade de bolo de chocolate vendida e y a quantidade de bolo de baunilha vendida, quanto Paula ganhará vendendo 5 unidades e 7 unidades, respectivamente, de cada tipo de bolo?
(A) R$ 210,00
(B) R$ 159,00
(C) R$ 127,00
(D R$ 204,00
Resolucao
Se cada bolo de chocolate é vendido por R$ 15,00 e a quantidade vendida é x, então Paula ganhará 15.x pelos bolos de chocolate vendidos.
Como o bolo de baunilha custa R$ 12,00 e são vendidos y bolos, então Paula ganhará 12.y pelos bolos de baunilha.
Unindo os dois valores temos que a expressão algébrica para o problema apresentado: 15x + 12y.
Substituindo os valores de x e y pelas quantidades apresentadas podemos calcular o total arrecadado por Paula:
15x + 12y =
= 15.5 + 12.7 =
= 75 + 84 =
= 159
Portanto, Paula ganhará R$ 159,00.
Alternatica B
39) Sabendo que a soma de três números consecutivos é igual a 18, escreva a expressão algébrica correspondente e calcule o primeiro número da sequência.
Resolucao
Vamos chamar o primeiro número da sequência de x. Se os números são consecutivos, então o próximo número da sequência tem uma unidade a mais que o anterior.
1º número: x
2º número: x + 1
3º número: x + 2
Sendo assim, a expressão algébrica que apresenta a soma dos três números consecutivos é:
x + (x + 1) + (x + 2)
Sabendo que o resultado da soma é 18, calculamos o valor de x da seguinte forma:
x + (x + 1) + (x + 2) = 18
x + x + x = 18 - 1 - 2
3x = 15
x = 15/3
x = 5
A resposta correta: x + (x+1) + (x+2) e x = 5.
Portanto, o primeiro número da sequência é 5.
Cntinua ...





