Professor Diminoi
MOVIMENTO UNIFORMENTE VARIADO – (MUV)
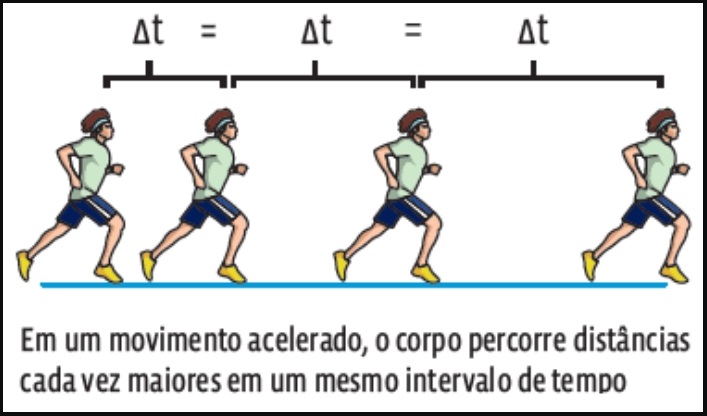
É um movimento no qual a mudança de velocidade, chamada de aceleração, ocorre a uma taxa constante.
O movimento uniformemente variado a velocidade varia no decorrer do tempo.
Aceleração média do MUV
![]()
am = aceleração média (m/s2)
Δv = variação da velocidade (m/s)
Δt = variação de tempo (s)
Função horária da velocidade no MUV:
![]()
v = velocidade final (m/s)
vo = velocidade inicial (m/s)
a = aceleração (m/s2)
t = tempo (s)
Função horária da posição no MUV
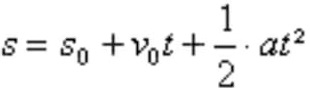
S = posição final (m)
So = posição inicial (m)
vo = velocidade inicial (m/s)
a = aceleração (m/s2)
t = tempo (s)
Equação de Torricelli
A equação de Torricelli é bastante útil quando precisamos resolver algum problema relacionado ao movimento uniformemente variado e não sabemos em qual intervalo de tempo ele ocorreu.
![]()
v = velocidade final (m/s)
vo = velocidade inicial (m/s)
a = aceleração (m/s2)
ΔS = distância (m)
Gráficos do MUV
Os gráficos do MUV são utilizados para relacionar grandezas como posição, velocidade e aceleração com um determinado instante de tempo.
Os gráficos do MUV são recursos utilizados para estudarmos a posição, a velocidade ou ainda a aceleração de um corpo que se move com aceleração constante durante um certo intervalo de tempo. Eles geralmente são feitos tendo como variável o tempo ao longo do eixo horizontal (eixo das abscissas).
A reta pode ser ainda paralela ao eixo horizontal, no caso em que a velocidade permanece constante durante certo intervalo de tempo. Além disso, nesse gráfico, a inclinação da reta (que pode ser calculada pela tangente) representa a aceleração do móvel.
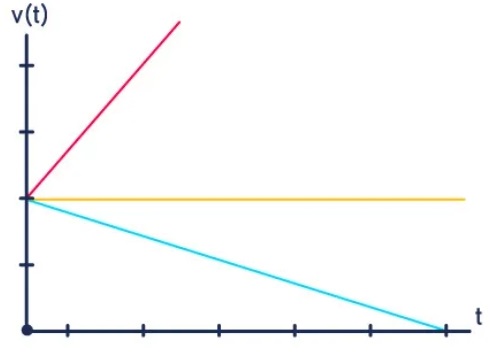
A figura a seguir mostra essas três situações ilustradas em um gráfico da velocidade em função do tempo v(t).
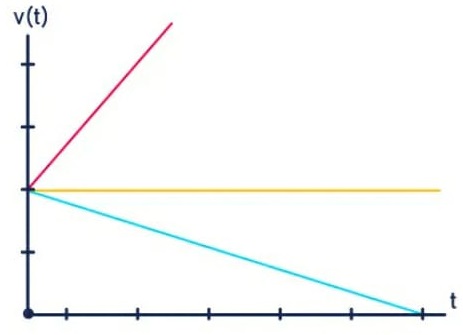
- 1º caso [reta vermelha] – movimento acelerado
- 2º caso [reta azul] – movimento retardado
- 3º caso [reta amarela] – movimento uniforme
A partir do gráfico de v(t), é possível determinar o espaço percorrido por uma partícula movendo-se em MRUV. Para tanto, calculamos a área abaixo do gráfico entre os instantes de tempo desejados.
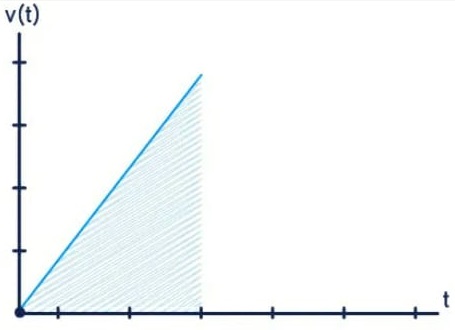
Gráfico do MUV: posição x tempo
Os gráficos da posição em função do tempo para o MUV são representados por parábolas, uma vez que as funções da posição no MUV são equação do 2º grau.
Um aspecto importante desses gráficos de posição é a concavidade das parábolas.
- Se a concavidade estiver voltada para cima, o movimento é acelerado.
- Se a concavidade estiver para baixo, o movimento é retardado.
Além disso, é importante perceber em qual ponto a curva cruza o eixo vertical. Essa informação serve para determinar qual é a posição inicial do móvel.
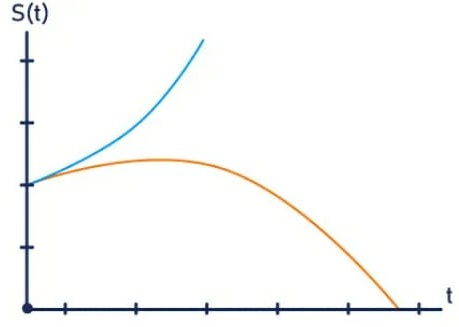
Nos gráficos de s(t), a inclinação da curva representa a velocidade em cada instante.
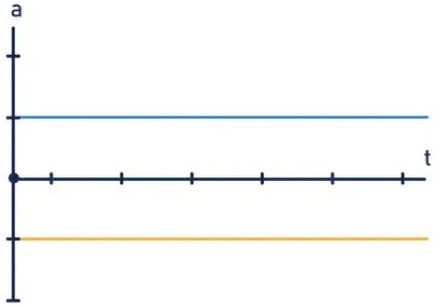
Gráficos do MUV: aceleração x tempo
Os gráficos do MUV que relacionam a aceleração com o tempo são bastante simples: trata-se de retas paralelas ao eixo horizontal. No caso em que o movimento é acelerado, a reta é desenhada acima do eixo das abscissas; caso contrário, ela é desenhada abaixo desse mesmo eixo.
QUESTÕES RESOLVIDAS – (MRV)
01) Um móvel desloca-se com velocidade inicial de 20 m/s, quando inicia um processo de frenagem, com desaceleração de 2,5 m/s². Determine o tempo necessário para que esse móvel inverta o seu sentido de movimento.
(A) 8,0 s
(B) 50,0 s
(C) 5,0 s
(D) 10,0 s
(E) 12,5 s
Resolução:
Para resolvermos esse exercício, faremos uso da função horária da velocidade. Nesse sentido, podemos afirmar que o móvel inverterá o sentido de seu movimento no instante seguinte àquele em que a sua velocidade torna-se nula. Desse modo, encontraremos o tempo necessário para que a velocidade final desse móvel seja de 0 m/s, sabendo que a sua velocidade inicial era de 20 m/s:
Nesse cálculo, utilizamos o sinal negativo para a aceleração devido ao fato de que o móvel tinha a sua velocidade diminuída a cada segundo, o que caracteriza um movimento retardado.
Alternativa: A
02) Um móvel tem a sua função horária de deslocamento dada por S = 5 + t². Assinale a alternativa que indica a velocidade inicial e a aceleração desse móvel, respectivamente:
(A) 5 m/s e 1 m/s²
(B) 0 m/s e 2 m/s²
(C) 1 m/s e 5 m/s²
(D) 5 m/s e 2 m/s²
(E) 3 m/s e 5 m/s²
Resolução:
Sabemos que as funções horárias de deslocamento seguem o formato ax² + bx +c = 0, mas também sabemos que o coeficiente b equivale à velocidade inicial do móvel e que o coeficiente a equivale à metade de sua aceleração. Desse modo, temos que: v0 = 0 e a = 2 m/s².
Alternativa: B
03) Em um gráfico de posição em função do tempo, observa-se que a curva descreve uma parábola com a sua concavidade voltada para baixo. Em relação a esse gráfico, assinale a alternativa correta:
(A) Trata-se de um movimento acelerado.
(B) Trata-se do gráfico de um movimento retrógrado.
(() Trata-se do gráfico de um movimento retardado.
(D) Trata-se de um gráfico de aceleração variável.
(E) Trata-se de um gráfico de velocidade crescente.
Resolução:
Quando o gráfico de posição em função do tempo tem o formato de uma parábola, sabemos que esse movimento apresenta aceleração constante. O que nos diz se o movimento representado pelo gráfico é retardado ou acelerado é a concavidade da parábola, que, nesse caso, é voltada para baixo. Portanto, o gráfico em questão representa um movimento retardado."
Alternativa: C
04) (Unicamp) A Agência Espacial Brasileira está desenvolvendo um veículo lançador de satélites (VLS) com a finalidade de colocar satélites em órbita ao redor da Terra. A agência pretende lançar o VLS em 2016, a partir do Centro de Lançamento de Alcântara, no Maranhão.
a) Considere que, durante um lançamento, o VLS percorre uma distância de 1200 km em 800 s. Qual é a velocidade média do VLS nesse trecho?
Resolução:
A primeira coisa que devemos fazer é lembrar da fórmula da velocidade média:
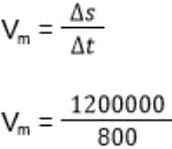
Vm = 1500 m/s
b) Suponha que no primeiro estágio do lançamento o VLS suba a partir do repouso com aceleração resultante constante de módulo aR. Considerando que o primeiro estágio dura 80 s, e que o VLS percorre uma distância de 32 km, calcule aR.
Resolução:
Se o corpo parte do repouso, temos que v0 = 0. E se a aceleração é constante, temos um MUV. Veja também que Δt = 80 e que Δs = 32000.
Temos que encontrar uma fórmula que contenha todas as grandezas pedidas. No caso, não sabemos apenas a aceleração. Portanto:
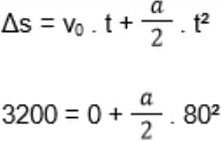
a = 10 m/s
05) (Pucrs) Muitos acidentes acontecem nas estradas porque o motorista não consegue frear seu carro antes de colidir com o que está à sua frente. Analisando as características técnicas, fornecidas por uma revista especializada, encontra-se a informação de que um determinado carro consegue diminuir sua velocidade, em média, 5,0 m/s a cada segundo. Se a velocidade inicial desse carro for 90,0 km/h (25,0 m/s), a distância necessária para ele conseguir parar será de, aproximadamente,
(A) 18,5 m
(B) 25,0 m
(C) 31,5 m
(D) 45,0 m
(E) 62,5 m
Resolução:
Repare: quando ele fala que o carro diminui sua velocidade, temos um Δv negativo. Nesse caso: Δv = -5 m/s. Já Δt = 1 s e v0 = 25 m/s. Note, agora, que ele nos diz que o carro vai parar, ou seja, a velocidade final será igual a zero (v = 0).
Vamos novamente buscar uma fórmula que atenda à nossa necessidade, que nesta questão é o Δs. Então, nosso primeiro passo será:
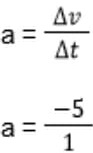
a = -5 m/s²
Veja que temos duas situações: as informações que utilizamos para calcular a aceleração não fazem parte da mesma situação dos outros dados que temos, incluindo o Δs que queremos encontrar.
Como não temos a grandeza tempo, podemos usar Torricelli:
v² = v0² 2 + 2. a . Δs
0 = 25 . 2 . (-5) . Δs
Δs = 62,5 m
Alternativa: E
06) (Uern) Seja o gráfico da velocidade em função do tempo de um corpo em movimento retilíneo uniformemente variado representado abaixo.
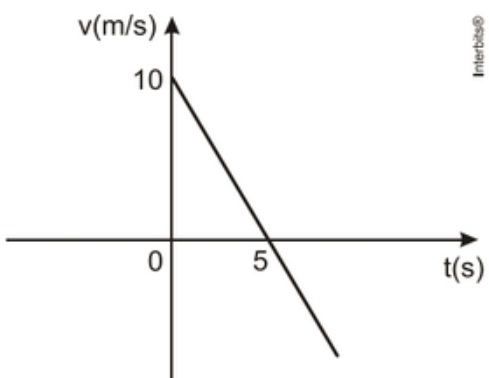
Considerando a posição inicial desse movimento igual a 46 m, então a posição do corpo no instante t = 8 s é
(A) 54 m.
(B) 62 m.
(C) 66 m.
(D) 74 m.
Resolução:
Vamos lembrar que a equação que nos dá a posição é:
![]()
Porém, ainda precisamos da aceleração para usar essa fórmula. Como não temos a posição (s), a fórmula que podemos utilizar para calcular a aceleração é:
![]()
Para isso, vou usar os dados que já tenho no gráfico. Repare que, como a aceleração é constante (MUV), o mesmo valor que posso calcular entre t = 0 e t = 5 s vale para o intervalo de t = 5 s a t = 8 s.
![]()
a = -2 m/s
Agora, basta substituir:
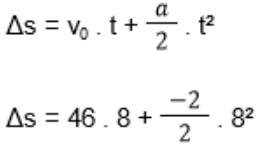
Δs = 62 m
07) Determine a velocidade escalar média entre os instantes t = 0 e t = T, para o movimento descrito pelo gráfico v x t abaixo.
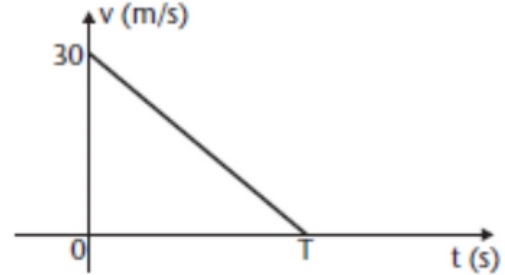
Resolução:
Vamos lembrar que temos duas maneiras de calcular a velocidade média:
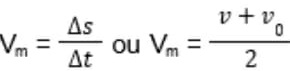
Essas fórmulas valem para um único MUV, como vemos no gráfico. Atenção: se o gráfico não possuir apenas uma reta, então há mais de um MUV.
Então, utilizado as informações que temos:
![]()
Vm = 15 m/s
08) (Fuvest-SP-modificada) Um corpo movimenta-se sobre o eixo X, com aceleração constante, de acordo com a função horária x = 2 + 2 . t – 2t², em que t é dado em segundos e x em metros.
a) Qual a velocidade escalar média entre t = 0 e t = 2 s?
Resolução:
Repare que em t = 0, temos que x0 = 2 m. Já para t = 2, basta usar a fórmula que ele nos deu:
x = 2 + 2 . 2 – 2 . 2²
x = -2 m
Agora:
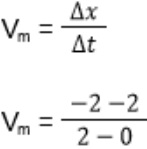
Vm = -2 m/s
b) Qual a velocidade no instante t = 2 s?
Resolução:
Veja que o que calculamos não é a velocidade instantânea final. Para isso, precisamos utilizar:
v = v0 + a . t
Veja que a fórmula que temos no enunciado nada mais é que:
![]()
Então, basta comparar essa equação com a do enunciado. Sabemos, portanto, que v0 = 2 m/s e que a/2 = -2, então a = -4 m/s². Agora basta voltar à equação da velocidade:
v = v0 + a . t
v = 2 – 4 . 2
v = -6 m/s
c) Em que instante esse corpo inverte o sentido do movimento? Em que posição ocorre essa inversão?
Inverter o sentido significa parar. Então, v = 0:
Resolução:
v = 2 – 4 . t
0 = 2 – 4 . t
t = 0,5 s
Para achar a posição de inversão, basta substituir na fórmula que a própria questão nos deus:
x = 2 + 2 . 0,5 – 2 . 0,5²
x = 2,5 m
09) Um móvel parte do repouso e desenvolve uma aceleração constante de 3 m/s² durante 4 segundos. O deslocamento desse móvel foi de:
(A) 12,0 m
(B) 24,0 m
(C) 22,0 m
(D) 18,0 m
(E) 30,0 m
Resolução:
A função horária da posição para o Movimento Uniformemente Variado é a apresentada a seguir:
![]()
De acordo com o enunciado do exercício, o móvel parte do repouso, portanto, sua velocidade inicial é igual a 0 m/s. Sua aceleração tem valor constante de 3 m/s². Esse corpo move-se durante um intervalo de tempo de 3 s, dessa forma:
![]()
O deslocamento do móvel foi de 24 m.
Alternativa: B
10) Um motorista dirige seu carro a uma velocidade de 108 km/h quando avista a placa de pare. Ao acionar os freios, ocorre uma desaceleração constante, e o carro leva um tempo de 3,0 s até parar completamente. A distância percorrida pelo automóvel até a frenagem total é de:
(A) 45,0 m
(B) 15,0 m
(C) 300,0 m
(D) 324,0 m
(E) 36,0 m
Resolução:
Sabemos que o deslocamento de um móvel com aceleração constante é determinado por:
De acordo com os dados fornecidos pelo enunciado, a velocidade inicial do carro é de 108 km/h. Esse valor deve ser expresso em unidades do Sistema Internacional, sendo necessária a sua conversão para km/h. Dessa forma, divide-se esse valor pelo fator 3,6, resultando em 30 m/s. Para calcular o deslocamento do carro, entretanto, é necessário saber o valor de sua aceleração (nesse caso, uma desaceleração.). Para tanto, utilizamos a definição de aceleração média:
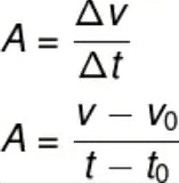
Com isso, a aceleração sofrida pelo automóvel tem valor igual a:
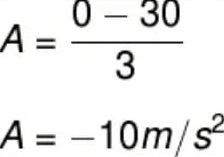
Seu deslocamento será, portanto:
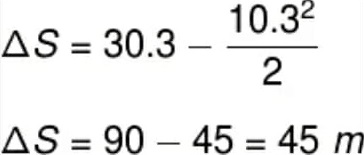
Logo, o carro sofrerá um deslocamento de 45 m antes de parar por completo.
Alternativa: A
11) A função horária da posição de um ponto material, dada em unidades do Sistema Internacional, que se move com aceleração constante é fornecida a seguir:
S = 15 + 10.t + 2.t²
Sua velocidade inicial, posição inicial e aceleração são respectivamente iguais a:
(A) S0 = 2 m, v0 = 15 m/s e a = 10 m/s2
(B) S0 = 10 m, v0 = 15 m/s e a = 2 m/s2
(C) S0 = 15 km, v0 = 10 km/h e a = 2 m/s2
(D) S0 = 15 m, v0 = 10 m/s e a= 4 m/s2
(E) S0 = 4 m, v0 = 10 m/s e a= 15 m/s2
Resolução:
A função horária da posição para móveis com aceleração constante é determinada por:
![]()
No entanto, o deslocamento ΔS é dado por ΔS = S – S0 (S é a sua posição final, e S0, sua posição inicial). Portanto, podemos reescrevê-la como:
![]()
Ao compararmos a equação acima com aquela fornecida pelo enunciado do exercício, observa-se que, em unidades do Sistema Internacional, sua posição inicial é de 15 m, sua velocidade inicial é de 10 m/s, e sua aceleração deve ser de 4 m/s², pois, na equação acima, a aceleração vem dividida por um fator 2.
Alternativa: D
12) Certo móvel, inicialmente na velocidade de 3 m/s, acelera constantemente a 2 m/s2 até se distanciar 4 m de sua posição inicial. O intervalo de tempo decorrido até o término desse deslocamento foi de:
(A) 4,0 s
(B) 1,0 s
(C) 3,0 s
(D) 5,0 s
(E) 2,5 s
Resolução:
A função horária da posição de um móvel cuja aceleração é constante é dada por:
De acordo com os dados do exercício, a velocidade inicial do móvel é de 3 m/s, sua aceleração é de 2 m/s2 e o seu deslocamento é de 4 m. A incógnita do exercício é o tempo necessário para que ocorra esse deslocamento, portanto:
![]()
Portanto, para encontrarmos o tempo, devemos resolver uma equação do segundo grau:
![]()
As raízes da equação acima são determinadas por:
![]()
Portanto, os possíveis valores de tempo são:
![]()
Como não admitimos a existência de tempo negativo, a resposta é t = 1,0s.
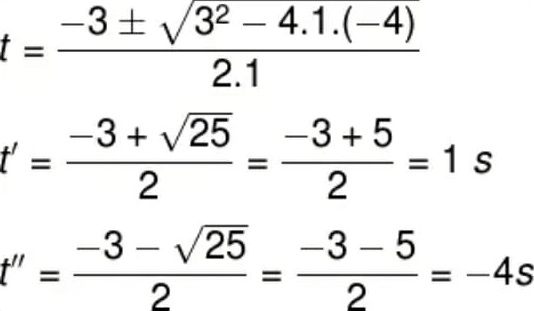
Alternativa: B
13) (UTF-PR) Um ciclista movimenta-se em sua bicicleta, partindo do repouso e mantendo uma aceleração aproximadamente constante de valor médio igual a 2,0 m/s². Depois de 7,0 s de movimento, atinge uma velocidade, em m/s, igual a:
(A) 49
(B) 14
(C) 98
(D) 35
(E) 10
Resolução:
Vamos resolver a questão e, para isso, utilizaremos os dados informados pelo exercício, bem como a função horária da posição.
v(t) = vo + at
V = 0 + 2 . 7 = 14m/s
Alternativa: B
14) (UFPR) Um motorista conduz seu automóvel pela BR-277 a uma velocidade de 108 km/h quando avista uma barreira na estrada, sendo obrigado a frear (desaceleração de 5 m/s²) e parar o veículo após certo tempo. Pode-se afirmar que o tempo e a distância de frenagem serão, respectivamente:
(A) 6 s e 90 m.
(B) 10 s e 120 m.
(C) 6 s e 80 m.
(D) 10 s e 200 m.
(E) 6 s e 120 m.
Resolução:
Primeiramente vamos determinar qual é o tempo de frenagem. Observe o cálculo a seguir, pois fazemos uso da função horária da velocidade:
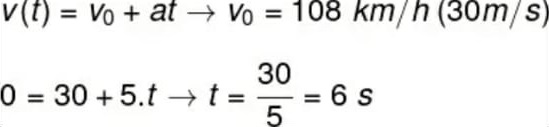
Para fazermos o cálculo acima, foi necessário transformar a unidade da velocidade, que estava em km/h, em m/s, dividindo-a pelo fator 3,6. O próximo cálculo diz respeito ao deslocamento do carro até a parada completa. Para fazê-lo, vamos usar a função horária da posição:
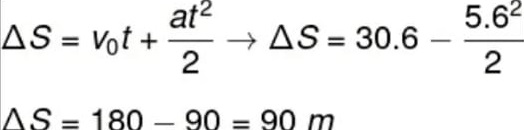
Com base no cálculo, descobrimos que o deslocamento do veículo, desde o início da frenagem até a parada completa, é de 90 m.
Alternativa: A





