Professor Diminoi
SEQUÊNCIA NUMÉRICA - PA & PG
A sequência numérica, como o nome sugere, é uma sequência de números e geralmente possui uma lei de recorrência, o que torna possível prever quais serão os próximos termos conhecendo os seus antecessores.
Podemos montar sequências numéricas com diferentes critérios, como:
- Sequência dos números pares;
- Sequência dos números divisíveis por 4;
- Sequência de números primos;
- Sequência dos quadrados perfeitos etc.
Enfim, existem várias possibilidades de sequências numéricas.
Observação: A sequência numérica nada mais é do que uma sequência de números.
Alguns exemplos de sequência numérica:
- Sequência de números pares (0,2,4,6,8…)
- Sequência dos naturais menores que 6 (1, 2, 3, 4, 5)
- Sequência de números primos (2,3,5,7,11,…)
Uma sequência pode ser finita ou infinita.
Finita: quando possui uma quantidade limitada de termos.
Infinita: quando possui uma quantidade ilimitada de termos.
Uma sequência pode ser crescente, descrente, constante ou oscilante.
Crescente: quando o termo é sempre menor que seu sucessor.
Decrescente: quando o termo é sempre maior que seu sucessor.
Constante: quando o termo é sempre igual ao seu sucessor.
Oscilante: quando há termos maiores e menores que o seu sucessor.
Observação: Existem casos especiais de sequência conhecidos como:
- Progressão aritmética
- Progressão geométrica.
Exemplo 1
Lei de ocorrência da sequência dos números múltiplos de 5:
(0, 5, 10, 15, 20, 25, …)
Exemplo 2:
Lei de ocorrência da sequência dos números primos:
(2,3,5,7,11,13,17,19,23 … )
Exemplo 3:
Lei de ocorrência dos inteiros negativos:
( – 1, – 2, – 3, – 4, – 5, – 6, – 7...)
Exemplo 4:
Sequência dos números ímpares positivos menores que 10:
(1, 3, 5, 7, 9)
Classificação da sequência numérica
Existem duas maneiras distintas de classificar uma sequência. A primeira delas é quanto à quantidade de termos, forma pela qual uma sequência pode ser finita ou infinita.
A outra maneira de classificar as sequências é quanto ao seu comportamento. Nesse caso, elas são classificadas como crescentes, decrescentes, constantes ou oscilantes.
Classificação da sequência numérica quanto ao comportamento
Sequência numérica crescente
A sequência é crescente se um termo for sempre maior que o seu antecessor.
Exemplos:
a) (1, 5, 9, 13, 17, ...)
b) (10, 11, 12, 13, 14, 15, ...)
Sequência numérica constante
A sequência é constante quando todos os termos possuem o mesmo valor.
Exemplos:
a) (1, 1, 1, 1, 1, 1, 1, ...)
b) (-1, -1, -1, -1, -1, ...)
Sequência numérica decrescente
A sequência é decrescente se os termos da sequência sempre são menores que os seus antecessores.
Exemplos:
a) (-1, -2, -3, -4, -5, ...)
b) (19, 16, 13, 10, 8, ...)
Sequência numérica oscilante
A sequência é oscilante se houver termos maiores que os seus antecessores e termos menores que seus antecessores de forma alternada.
Exemplos:
a) (1, -3, 9, -27, 81, ...)
b) (1, -1, 2, -2, 3, -3, 4, -4, ...)
Lei de formação da sequência numérica
Algumas sequências podem ser descritas por uma fórmula que gera os seus termos. Essa fórmula é conhecida como lei de formação.
Utilizamos a lei de formação para encontrar qualquer termo na sequência quando conhecemos o comportamento dela.
Exemplo 1:
A sequência a seguir é formada por quadrados perfeitos:
(0, 1, 4, 9, 16, 25, 36, 64, … )
Podemos descrever essa sequência pela lei de formação:
an = (n – 1)²
n = número do termo
an = o termo de posição n
Com essa fórmula, é possível saber, por exemplo, o termo que ocupa a posição número 10 na sequência:
a10 = ( 10 – 1) ²
a10 = 9²
a10 = 81
Exemplo
Liste os termos da sequência cuja lei de formação é an = 2n – 5.
Exemplos para encontrar os primeiros termos da sequência:
1º termo:
an = 2n – 5
a1 = 2·1 – 5
a1 = 2 – 5
a1 = – 3
2º termo:
an = 2n – 5
a2 = 2 . 2 – 5
a2 = 4 – 5
a2 = – 1
3º termo:
an = 2n – 5
a3 = 2·3 – 5
a3 = 6 – 5
a3 = 1
4º termo:
an = 2n – 5
a4 = 2·4 – 5
a4 = 8 – 5
a4 = 3
5º termo:
a5 = 2n – 5
a5 = 2·5 – 5
a5 = 10 – 5
a5 = 5
SECURENCIA RECURSIVA
Uma sequência é recursiva quando um termo depende dos termos anteriores.
Exemplos
A mais conhecida dessa classificação é a sequência de Fibonacci. Fibonacci, matemático italiano no século XIII, criou uma sequência com base na observação do crescimento de uma população de coelhos. Os números dessa sequência descrevem a quantidade de casais de coelhos após n meses, considerando as seguintes informações:
- no primeiro mês, temos um casal de coelhos que acabaram de nascer;
- um casal atinge a fase reprodutiva ao final de um mês;
- ao atingir a fase reprodutiva, cada casal gera outro casal de coelhos por mês;
- o período de gestação dura um mês;
- nenhum coelho morre durante o ano.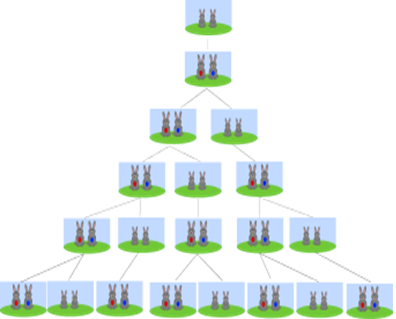 Daí temos que os números que compõem a sequência de Fibonacci são: 1,1,2,3,5,8,…
Daí temos que os números que compõem a sequência de Fibonacci são: 1,1,2,3,5,8,…
SEQUENCIAS NÃO RECURSIVAS
As sequências não recursivas são aquelas que não dependem de termos anteriores para que se determine o próximo termo, pode-se obter o valor de um elemento da sequência apenas pela sua posição.
Exemplos
a) Na sequência (7,14,21,28...), não é necessário saber o último termo para determinar o seguinte.
Resolução
Observando atentamente, essa sequência é formada pelos múltiplos de 7.
b) No caso da sequência (2,3,5,7,11..), percebe-se que ela é formada pelos números primos
(Currículo em Ação 2022) Nas sequências abaixo, classifique-as como recursivas ou não recursivas, justificando a sua resposta.
14) (11, 21, 31, 41, ...)
Resolução
Recursiva, pois ao termo anterior soma-se 10 unidades para se obter o próximo.
15) (8, 8, 13, 12, 13, 10, 9, ...)
Resolução
Não recursiva, pois não conseguimos estabelecer um padrão, uma regra para formação da sequência.
16) (2, 3, 5, 7, 11, 13, 17, ...)
Resolução
Não recursiva, pois não conseguimos estabelecer um padrão, uma regra para a formação.
17) (-6, -3, 0, 3, 6, ...)
Resolução
Recursiva, pois ao termo anterior soma-se 3 unidades para se obter o próximo.
QUESTÕES RESOLVIDAS - SEQUENCIA
(Currículo em Ação 2022) Descubra qual é a regra de formação e encontre até o oitavo termo de cada sequência.
18) (20, 15, 10, 5, ...)
Resposta
(20, 15, 10, 5, 0, -5, -10, -15)
Regra: para determinar o próximo termo, subtrai-se 5 unidades do termo anterior.
19) (6, 2, - 2, - 6, - 10, - 14, ...)
Resolução
(6, 2, -2, -6, -10, -14, -18, -22)
Regra: para determinar o próximo termo, subtrai-se 4 unidades do termo anterior.
03) (6, 2, -2, -6, -10, -14, -18, -22)
Resposta
Regra: para determinar o próximo termo, subtrai-se 4 unidades do termo anterior.
(1, 4, 9, 16, 25, 36, 64, 81)
Regra: sequência dos quadrados dos oito primeiros números naturais.
(Currículo em Ação 2022) Complete a sequência finita com 5 termos, descobrindo a regra de formação, e registre-a:
20 Adicione 4 ao termo anterior.
Resolução
(1, 5, 9, 13, 17)
21) Multiplique o termo anterior por 3 e subtraia 2.
Resolução
(2, 4, 10, 28, 82
(Currículo em Ação 2022) Complete a sequência finita com 5 termos, descobrindo a regra de formação, e registre-a:
22) Adicione 4 ao termo anterior. (1, 5, 9, 13, 17)
23) Multiplique o termo anterior por 3 e subtraia 2. (2, 4, 10, 28, 82)
24) Sequência dos números pares maiores que zero.
na = 2 . n
Observação: Vá substituindo o valor de n por: 1, 2, 3, 4, ....
Resolução
Note que ao substituir n por um número natural (1, 2, 3, 4, ...), encontraremos um número par:
a1 = 2 . 1= 2
a2 = 2 . 2 = 4
a3 = 2 . 3 = 6
a4 = 2 . 4 = 8
Então, temos uma fórmula que gera os termos da sequência formada por números pares maiores que zero: (2, 4, 6, 8, ...)
25) Sequência dos números naturais maiores que 4.
Observação: Vá substituindo valor de n por: 1, 2, 3, 4, ....
an = 4 + n
Resolução
Calculando os termos da sequência, temos que:
a1 = 4 + 1 = 5
a2 = 4 + 2 = 6
a3 = 4 + 3 = 7
a4 = 4 + 4 = 8
Escrevendo a lei de ocorrência:
(5, 6, 7, 8,…)
26) Currículo em Ação 2023) São chamadas de sequências recursivas quando determinado termo pode ser calculado em função de termos antecessores. Sequências não recursivas seus elementos não obedecem a nenhuma regra de formação.
Com base no texto responda as questões a seguir:
a) Sequência recursiva: (1, 4, 7, 10, 13, ...), escreva a regra de formação dessa sequência. Qual será o termo seguinte?
Resposta
O termo seguinte é a soma do termo anterior com 3 unidades.
b) Sequência não recursiva: (1, 1, 3, 4, 5, 2, 1, 3, 6, 2, 4). Para obter qualquer termo da sequência, não dependemos do termo anterior. Qual a regra de formação dessa sequência.
Resposta:
Os termos das sequências não obedecem a nenhuma regra de formação.
27) Veja as sequências de figuras. Quais são os três próximos termos? Explique a “regra de formação” que você utilizou.
a) 
Resolução
(boneco, coração, boneco) – padrão boneco, coração.
b) 
Resolução
(sol, lua, raio) – padrão raio, sol, lua.
28) Na sequência (1, 2, 3, 4, 5, 6…), indique quais serão os dois próximos termos e explique por quê.
Resolução
(1, 2, 3, 4, 5, 6, 7, 8…) Sequência dos números naturais. Padrão: soma-se uma unidade ao termo anterior para encontrar o próximo termo.
29 Escreva a sequência dos números naturais menores que 8 e classifique-a como finita ou infinita.
Resolução
(0, 1, 2, 3, 4, 5, 6, 7) Finita, pois possui uma quantidade determinada de termos.
30) Observe a sequência numérica infinita: (2, 5, 8, 11, 14,…). Qual é sua regra de formação?
Resolução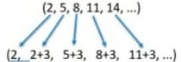
Note que podemos estabelecer uma regra de formação para definir seus termos: “a partir do primeiro termo obtemos os próximos somando 3 unidades”.
31) Sequência dos números pares maiores que zero.
na = 2n
Note que ao substituir n por um número natural (1, 2, 3, 4, ...), encontraremos um número par:
a1 = 2 . 1= 2
a2 = 2 . 2 = 4
a3 = 2 . 3 = 6
a4 = 2 . 4 = 8
Então, temos uma fórmula que gera os termos da sequência formada por números pares maiores que zero: (2, 4, 6, 8, ...)
32) Sequência dos números naturais maiores que 4.
an = 4 + n = 4
Calculando os termos da sequência, temos que:
a1 = 4 + 1 = 5
a2 = 4 + 2 = 6
a3 = 4 + 3 = 7
a4 = 4 + 4 = 8
Escrevendo a lei de ocorrência:
(5, 6, 7, 8,…)
33) Uma sequência numérica possui lei de formação igual a an = n2 + 1. Analisando essa sequência, podemos afirmar que o valor do 5º termo da sequência será:
(A) 6
(B) 10
(C) 11
(D) 25
(E) 26
Resolução:
Calculando o valor do 5º termo da sequência, temos que:
a5 = 52 + 1
a5 = 25 +1
a5 = 26
Alternativa E
34) Analise as sequências numéricas a seguir:
I. (1, -2, 3, -4, 5, -6, ...)
II. (13, 13, 13, 13, 13, ...)
III. (1, 2, 3, 4, 5, 6, ...)
Podemos afirmar que as sequências I, II e III são classificadas respectivamente como:
(A) crescente, oscilante e decrescente.
(B) decrescente, crescente e oscilante.
(C) oscilante, constante e crescente.
(D) decrescente, oscilante e constante.
(E) oscilante, decrescente e crescente.
Resolução:
Analisando as sequências, podemos afirmar que:
I. (1, -2, 3, -4, 5, -6, ...)
É oscilante, pois há termos que são maiores que seus antecessores e termos que são menores que os seus antecessores.
II. (13, 13, 13, 13, 13, ...)
É constante, pois os termos da sequência são sempre os mesmos.
III. (1, 2, 3, 4, 5, 6, ...)
É crescente, pois os termos são sempre maiores que os seus antecessores.
Alternativa C
35) Determine os três próximos números da sequência 0, 5, 10, 15, 20, …
Resolução
Perceba que temos uma PA com razão 5.
Portanto, podemos continuar desenvolvendo a sequência utilizando a fórmula do termo geral da PA.
an = a1 + (n – 1) . r
Assim, os três próximos termos são:
a6 = 0 + (6 – 1) . 5 = 0 + 5 . 5 = 25
a7 = 0 + (7 – 1) . 5 = 0 + 6 . 5 = 30
a8 = 0 + (8 – 1) . 5 = 0 + 7 . 5 = 35
Portanto, os três próximos termos da sequência são: 25, 30 e 35
0, 5, 10, 15, 20, 25, 30, 35, …
36 Escreve por extenso parte da sequência definida pela fórmula n² + 1, n ∈ N.
Resolução
Atribuindo números naturais a n, temos:
n = 0: 0² + 1 = 1
n = 1: 1² + 1 = 2
n = 2: 2² + 1 = 4 + 1 = 5
n = 3: 3² + 1 = 9 + 1 = 10
n = 4: 4² + 1 = 16 + 1 = 17
n = 5: 5² + 1 = 25 + 1 = 26
n = 6: 6² + 1 = 36 + 1 = 37
n = 7: 7² + 1 = 49 + 1 = 50
n = 8: 8² + 1 = 64 + 1 = 65
n = 9: 9² + 1 = 81 + 1 = 82
n = 10: 10² + 1 = 100 + 1 = 101
Então, temos parte da sequência: 1, 2, 5, 10, 17, 26, 37, 50, 65, 82, 101, …
37 Determine a soma dos dois próximos termos da sequência com ordem lógica 0, 2, 6, 2, 4, 12, 4, 6, 18, 6, …
Resolução
Veja que a sequência é formada pelos múltiplos de 6 e de 2.
Múltilos de 2 repetidos: _, 2, _, 2, 4, _, 4, 6, _, 6
Múltiplos de 6: _, _, 6, _, _, 12, _, _, 18, _, …
Então, podemos continuar a sequência:
0, 2, 6, 2, 4, 12, 4, 6, 18, 6, 8, 24, 8, 10, 30, 10, …
Os dois próximos números da sequência da questão são 8 e 24. Portanto,
24 + 8 = 32
38) Analisando a sequência (1, 4, 9, 16, 25, … ), podemos afirmar que os dois próximos números serão:
(A) 35 e 46.
(B) 36 e 49.
(C) 30 e 41.
(D) 41 e 66.
Resolução
Para encontrar os termos da sequência, é importante encontrar uma regularidade na sequência, ou seja, entender a sua lei de ocorrência. Note que, do primeiro termo para o segundo termo, somamos 3; do segundo para o terceiro termo, somamos 5; do terceiro para o quarto termo e do quarto para o quinto termo, somamos, respectivamente, 7 e 9, logo a soma aumenta duas unidades a cada termo da sequência, ou seja, no próximo, somaremos 11, depois 13, depois 15, depois 17 e assim sucessivamente.
Para encontrar o sucessor do 25, somaremos 11.
25 + 11 = 36.
Para encontrar o sucessor de 36, somaremos 13.
36 + 13 = 49
Então os próximos termos serão 36 e 49.
Alternativa B
39) (Instituto AOCP) A seguir, é apresentada uma sequência numérica, tal que os elementos dessa sequência foram dispostos obedecendo a uma lei (lógica) de formação, em que x e y são números inteiros: (24, 13, 22, 11, 20, 9, x, y). Observando essa sequência e encontrando os valores de x e de y, seguindo a lei de formação da sequência dada, é correto afirmar que
(A) x é um número maior que 30.
(B) y é um número menor que 5.
(C) a soma de x com y resulta em 25.
(D) o produto de x por y resulta em 106.
(E) a diferença entre y e x, nessa ordem, é um número positivo.
Resolução
Queremos encontrar o 7º e 8º termo dessa sequência.
Analisando a lei de ocorrência da sequência (24, 13, 22, 11, 20, 9, x, y), é possível perceber que existe uma lógica para os termos ímpares (1º termo, 3º termo, 5º termo … ). Note que o 3º termo é igual ao 1º termo menos 2, pois 24 – 2 = 22. Usando essa mesma lógica, o 7º termo, representado por x, será o 5º termo menos 2, ou seja, x = 20 – 2 = 18.
Existe lógica parecida para os termos pares (2º termo, 4º termo, 6º termo … ): o 4º termo é o 2º termo menos 2, pois 13 – 2 = 11, e assim sucessivamente. Queremos o 8º termo, representado por y, que será o 6º termo menos 2, então y = 9 – 2 = 7.
Logo, temos x = 18 e y = 7. Analisando as alternativas, temos que x + y = 25, ou seja, a soma de x com y resulta em 25."
Alternativa C
40) (Instituto Consulplan) Observe a sequência numérica: 12, 14, 17, 21, 26, 32, 39,.... A soma dos dois próximos números da sequência é:
(A) 99
(B) 101
(C) 103
(D) 105
Resolução:
Analisando a sequência, é necessário compreender qual é a lógica para identificação dos próximos termos. Note que o primeiro termo é 12 e nele foi adicionado 2.
12 + 2 = 14
Já ao termo 14 foi adicionado 3:
14 + 3 = 17
Ao 17, foi adicionado 4:
17 + 4 = 21
Continuando com essa mesma lógica, temos que:
21 + 5 = 26
26 + 6 = 32
32 + 7 = 39
Agora queremos encontrar os dois próximos termos:
39 + 8 = 47
47 + 9 = 56
Então a soma 47 + 56 = 103
Alternativa C.
41) Os números abaixo estão dispostos em uma sequência lógica: 1, 1, 2, 3, 5, 8, 13, A, B, 55, 89,...
Nesse caso, pode-se afirmar que A + B é igual a:
(A) 55
(B) 64
(C) 74
(D) 82
Resolução:
É possível perceber que a partir do 3º termo, para encontrar um próximo na sequência basta somar os dois antecessores ao número verificado:
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
5 + 3 = 8
Assim sucessivamente. Então, podemos afirmar que A + B = 55
Alternativa A
42) (BB – Cesgranrio) Uma sequência numérica infinita (e1, e2, e3,…, en,…) é tal que a soma dos n termos iniciais é igual a n² + 6n. O quarto termo dessa sequência é igual a
(A) 9
(B) 13
(C) 17
(D) 32
(E) 40
Resolução:
Calculando a soma dos 3 primeiros termos:
n² + 6n
3² + 6 . 3
9 + 18 = 27
Calculando a soma dos 4 primeiros termos:
n² + 6n
4² + 6.4
16 + 24 = 40
Logo, o quarto termo é 40 – 27 = 13
Alternativa B
43) (Banestes) A senha de meu cofre é dada por uma sequência de seis números, todos menores que 100, que obedece a determinada lógica. Esqueci o terceiro número dessa sequência, mas lembro-me dos demais. São eles: {32, 27, __, 30, 38, 33}. Assim, qual o terceiro número da sequência?
(A) 35
(B) 31
(C) 34
(D) 40
(E) 28
Resolução
Analisando a sequência, é possível verificar que o número 35 pode ser inserido na terceira posição, utilizando a lógica:
Ora subtrai-se 5, ora soma-se 8…
Observe:
32 – 5 = 27
27 + 8 = 35
35 – 5 = 30
30 + 8 = 38
38 – 5 = 33
Alternativa A
44) (IBGE) Considere a sequência infinita IBGEGBIBGEGBIBGEG… A 2016ª e a 2017ª letras dessa sequência são, respectivamente:
(A) BG;
(B) GE;
(C) EG;
(D) GB;
(E) BI.
Resolução
Perceba que a sequência sempre repete as 6 letras IBGEGB.
Dividindo 2016 por 6:
2016/6 = 336
Daí, a sequência se repetirá 336 vezes até a posição 2016.
De onde concluímos que a letra B ocupa a posição 2016 e a letra I ocupa a posição 2017.
Alternativa E
45) (TJ - SP) Observe a sequência de espaços identificados por letras
Cada espaço vazio deverá ser preenchido por um número inteiro e positivo, de modo que a soma dos números de três espaços consecutivos seja sempre igual a 15. Nessas condições, no espaço identificado pela letra g deverá ser escrito o número
(A) 6.
(B) 7.
(C) 3.
(D) 4.
(E) 5.
Resolução
Como a soma dos três espaços consecutivos é sempre 15, temos:
(1) 6 + b + c = 15
(2) b + c + d = 15
Fazendo (2) – (1):
b + c + d – 6 – b – c = 15 – 15
d – 6 = 0
d = 6
Agora que calculamos d, podemos utilizar o mesmo raciocínio para calcular g:
6 + e + f = 15
e + f + g = 15
Da mesma forma, temos que g = 6.
Alternativa A
PROGRESSÃO ARITMETICA & PROGRESSÃO GEOMÉTRICA
Existem casos especiais de sequências que são conhecidos como progressão aritmética e progressão geométrica.
Uma sequência é uma progressão quando existe uma razão de um termo para o seu sucessor.
PROGRESÃO ARITMETICA (PA)
Quando conhecemos o primeiro termo da sequência e, para encontrar o segundo, somamos o primeiro a um valor r e, para encontrar o terceiro termo, somamos o segundo a esse mesmo valor r, e assim sucessivamente, a sequência é classificada como uma progressão aritmética.
Exemplo:
(1, 5, 9, 13, 17, 21, …)
Essa é uma progressão aritmética de razão igual a 4 e primeiro termo igual a 1.
Note que, para encontrar o sucessor de um número na sequência, basta somar 4, por isso dizemos que 4 é a razão dessa progressão aritmética.
PROGRESSÃO GFEOMÉTRICA (PG)
Na progressão geométrica, também existe uma razão, mas, nesse caso, para encontrar o sucessor de um termo, devemos multiplicar o termo pela razão.
Exemplo:
(2, 6, 18, 54, 162, … )
Essa é uma progressão geométrica de razão igual a 3 e primeiro termo igual a 2.
Note que, para encontrar o sucessor de um número nessa sequência, basta multiplicar por 3, o que faz com que a razão dessa progressão geométrica seja 3.
QUESTÕES RESOLVIDAS - PG
46) Determine o décimo termo desta PG: 1, 6, 36, 216, 1296, …
Resolução
ara encontrarmos um termo qualquer de uma PG, utilizamos a fórmula do termo geral.
an = a1 x q(n -1)
Primeiro temos que calcular a razão desta PG. Para isso, podemos pegar qualquer termo e dividi-lo pelo seu antecessor na sequência, assim, temos que a razão desta PG é: 6, pois 36/6 = 6
Portanto, temos:
a10 = 1 . 69
a10 = 10077696
47) (PM - Maranhão) Para tornar uma mensagem secreta, uma palavra foi codificada de acordo com as instruções a seguir:
I. Você deve substituir cada letra pelo número correspondente da tabela a seguir: II. Se o número for múltiplo de 3, você deve subtrair duas unidades dele. Se não for, some uma unidade a ele;
II. Se o número for múltiplo de 3, você deve subtrair duas unidades dele. Se não for, some uma unidade a ele;
III. Substitua cada novo número pela letra correspondente.
Por exemplo, a palavra PAULO corresponde à sequência 25-10-30-21-24, que após ser modificada será 26-11-28-19-22, formando a palavra codificada QBSJM.
A palavra EGJBO está codificada. Decodificando-a, você obtém
(A) DILAN.
(B) DENIS.
(C) CELSO.
(D) FHKCM.
(E) DFKCO.
Resolução
Vamos fazer o inverso:
EGJBO corresponde a 14-16-19-11-24
Iremos analisar cada um desses números, sabendo que:
- se o número é do tipo múltiplo de três mais um, então ele era múltiplo de 3 e foram subtraídas duas unidades.
- se o número for múltiplo de três ou do tipo múltiplo de três mais dois, então foi somada uma unidade.
Observe o primeiro caso
14 = 3 . 4 + 2
Estamos percorrendo o caminho inverso, e o nosso objetivo é descobrir se o número anterior foi subtraído em duas unidades, ou teve uma unidade adicionada.
Retiramos duas unidades quando o número é múltiplo de 3, ou seja, não pode ser o 16, pois não é múltiplo de 3.
Adicionamos uma unidade quando não é múltiplo de 3, ou seja, 13 não é múltiplo de 3, que somado a 1, temos o número resultante 14.
Da mesma forma, temos os demais casos:
16 = 3.5 + 1, logo o número era 18
19 = 3.6 + 1, logo o número era 21
11 = 3.3 + 2, logo o número era 10
24 = 3.8, logo o número era 23
13-18-21-10-23 corresponde a DILAN
Alternativa A
48) (PM PB – IBFC) Os números estão dispostos em sequência lógica 0, 5, 50, 5, 10, 45, 10, 15, 40, 15,… Nessas condições a soma entre os dois próximos números dessa sequência é:
(A) 55
(B) 50
(C) 45
(D) 60
Resolução
Os termos múltiplos de 3 são uma PG cujo primeiro termo é 50 e a razão é 5.
_, _, 50, _, _, 45, _, _, 40, _, _, 35, …
Os demais termos possuem uma repetição de múltiplos de 5, que aparecem duas vezes.
_, 5, _, 5, 10, _, 10, 15, _, 15, 20, _, 20, 25, _…
Veja a continuação da sequência:
0, 5, 50, 5, 10, 45, 10, 15, 40, 15, 20, 35, 20, 25, 30…
Soma dos dois próximos termos:
20 + 35 = 55
Alternativa A
49) (TRT 2 – SP) Na sequência (5, 7, 9, 11, 6, 8, 10, 12, 7, 9, 11, 13, 8, 10, 12, 14, 9, 11, 13, 15, 10, 12, 14, 16, 11, . . .), o número 15 aparece pela primeira vez na 20a posição e aparecerá pela última vez na posição de número
(A) 44
(B) 41
(C) 43
(D) 42
(E) 40
Resolução
Perceba que temos uma sequência “formada” por 4 sequências, cada uma representada de uma cor diferente.
5, 7, 9, 11, 6, 8, 10, 12, 7, 9, 11, 13, 8, 10, 12, 14, 9, 11, 13, 15, 10, 12, 14, 16, 11, . . .
Veja que a sequência vermelha é a que começa com o menor número, ou seja, o número 15 aparecerá pela última vez nesta sequência.
Analisando a sequência vermelha:
5 – posição 1
6 – posição 5
7 – posição 9
8 – posição 13
9 – posição 17
10 – posição 21
11 – posição 25
12 – posição 29
13 – posição 33
14 – posição 37
15 – posição 41
Alternativa B
50) (GCM SP – IBADE) Considere a seguinte sequência:
0 – (1/3) – (-9) – (1/27) – …
O sétimo item da sequência é:
(A) -1/729
(B) 729
(C) -729
(D) 1/729
(E) 1/243
Resolução
Observe que:
- os números 3, 9, 27, …, são potências de 3;
- o sinal do expoente está se alternando entre negativo e positivo;
- o sinal de cada elemento da sequência também está alternando entre positivo e negativo.
Com essas informações, podemos listar os próximos termos da sequência:
0; (1/3); (-9); (1/27); (-81); (1/243); (-729)
Alternativa C
QUESTÕE SRESOLVIDAS DE PROGRESSÃO ARITMETICA
51) Analise as sequências a seguir:
A – (1, 4, 7, 10, 13)
B – (1, 1, 1, 1, 1, 1)
C – (9, 3, -3, -9, -15...)
D – (1, 0, -1, 2, -2, 3, -3)
Sobre as sequências, podemos afirmar que:
(A) Todas são progressões aritméticas.
(B) Somente A e C são progressões aritméticas.
(C) Somente D não é uma progressão aritmética.
(D) Somente B e D são progressões aritméticas.
(E) Nenhuma das sequências representa uma progressão aritmética.
Resolução
Para que uma sequência seja uma progressão a aritmética, a diferença de um termo com o seu antecessor tem que ser constante, essa diferença é o que chamamos de razão r.
Analisando cada uma delas, temos que:
A – (1, 4, 7, 10, 13) é uma progressão aritmética:
4 – 1 = 3
7 – 4 = 3
10 – 7 = 3
13 – 10 = 3
É fácil ver que, de um termo para o seu anterior, a diferença é sempre 3, o que faz com que essa seja uma PA de razão 3.
B – (1, 1, 1, 1, 1, 1) é uma progressão aritmética:
1 – 1= 0
Note que a diferença entre um termo e o outro é sempre igual a 0, logo, essa é uma progressão arimética de razão 0.
C – (9, 3, -3, -9, -15...) é uma progressão aritmética:
3 – 9 = -6
-3 – 3 = -6
-9 – (-3) = -9 + 3 = -6
-15 – (-9) = -15 + 9 = -6
Note que a diferença entre um termo e o outro é sempre igual a -6, logo, essa é uma progressão arimética de razão -6.
D – (1, 0, -1, 2, -2, 3, -3) não é uma progressão aritmética:
0 – 1 = -1
-1 – 0 = -1
2 – (-1) = 2 + 1 = 3
Já é possível perceber que essa sequência não é uma progressão aritmética, pois a diferença entre os termos não é constante.
Alternativa C
52) Os ganhos de uma empresa, ao decorrer do ano, foram de R$800.000 no primeiro mês, e, a cada mês, houve um aumento de R$15.000 em relação ao mês anterior. Caso essa tendência seja mantida durante todos os meses, o lucro mensal dessa empresa, em dezembro, será de:
(A) R$165.000
(B) R$180.000
(C) R$816.500
(D) R$965.000
(E) R$980.000
Resolução
Analisando a situação, é possível percebermos que o primeiro termo a1 = 800.000 e que a razão dessa progressão r = 15.000.
Utilizando a fórmula do termo geral de uma P.A., queremos encontrar os lucros no 12º mês (dezembro), ou seja, o termo a12.
Sabemos que:
an = a1 + (n – 1) r
Substituindo os valores conhecidos, temos que:
a12 = 800.000 + (12 – 1) 15.000
a12 = 800.000 + 11 · 15.000
a12 = 800.00 + 165.000
a12 = 965.000
Alternativa D
53) Cris decidiu ser uma influenciadora digital, e, para isso, ela criou uma conta nas redes sociais. Realizando a divulgação para os seus amigos mais próximos, logo no primeiro dia, ela conseguiu o marco de 40 seguidores. Após esse marco, no segundo dia, ela conseguiu mais 14 seguidores, no terceiro dia também, e assim sucessivamente durante toda a primeira semana. Se esse comportamento for mantido, ou seja, se ela conseguir 14 seguidores por dia, qual será a quantidade de seguidores ao final de 30 dias?
(A) 446
(B) 406
(C) 400
(D) 396
(E) 380
Resolução
A sequência formada pela quantidade de seguidores é uma P.A., cujo primeiro termo é 40 e cuja razão é 14. Queremos encontrar o termo a30.
De modo geral, sabemos que:
an = a1 + (n – 1) r
Substituindo pelos valores conhecidos, temos que:
a30 = 40 + (30 – 1) 14
a30 = 40 + 29 · 14
a30 = 40 + 406
a30 = 446
Alternativa A
54) Um atleta de alta performance tem se preparado para a disputa da Maratona do Rio, que possui atualmente um percurso de 42 km. Para isso, ele começou percorrendo 14 km no primeiro dia, e, a cada dia, ele acrescentou 5 km em relação ao dia anterior. A distância total percorrida por esse atleta durante uma semana de treino é de:
(A) 44 km
(B) 244 km
(C) 193 km
(D) 198 km
(E) 203 km
Resolução
Queremos calcular a soma dos termos de uma P.A. que é dada pela fórmula a seguir:![]()
Queremos, nesse caso, a soma dos sete primeiros termos da sequência, ou seja n = 7. Conhecido o valor de n, o valor inicial a1 = 14 e a razão r = 5, encontraremos o valor de a7.
an = a1 + (n – 1) r
a7 = 14 + (7 – 1) · 5
a7 = 14 + 6 · 5
a7 = 14 + 30 = 44
Agora é possível calcular S7: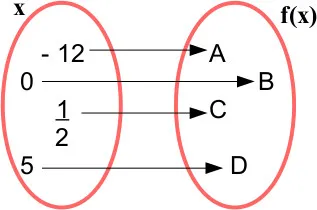
Na primeira semana, o atleta percorreu, ao todo, 203 km.
Alternativa E
55) No ano de 2020, infelizmente, as Olimpíadas foram adiadas devido à pandemia de COVID-19. Sabendo que as Olimpíadas ocorrem de 4 em 4 anos e supondo que, em 2021, tenhamos esse evento, e que, até 2100, ele não passe por um novo adiamento, a quantidade de Olimpíadas que terão acontecido nesse intervalo será de:
(A)18
(B)19
(C) 20
(D) 21
(E) 22
Resolução
Queremos o valor de n, tal que an seja igual a 2100 ou o valor que chegue mais próximo a ele.
Sabendo que:
an = 2100
a1 = 2021
r = 4
Sendo assim, faremos:
an = a1 + (n – 1) r
2100 = 2021 + (n – 1) · 4
2100 – 2021 = (n – 1) · 4
79 = (n – 1) · 4
79 = 4n – 4
79 + 4 = 4n
83 = 4n
n = 83/4
n = 20,75
Note que a parte inteira é o número de Olimpíadas que já ocorreram, logo, o número de Olimpíadas, nesse intervalo de tempo, é igual a 20.
Alternativa C
56) Sobre progressões aritméticas, julgue como verdadeiro ou falso as afirmativas a seguir:
I – Uma progressão aritmética é crescente quando sua razão é positiva.
II – Uma progressão aritmética é constante quando sua razão é zero.
III – Uma progressão aritmética é decrescente quando sua razão é negativa.
Marque a alternativa correta:
(A) Somente a afirmativa I é verdadeira.
(B) Somente a afirmativa II é verdadeira.
(C) Somente a afirmativa III é verdadeira.
(D) Todas as afirmativas são verdadeiras.
(E) Nenhuma das afirmativas é verdadeira.
Resolução
O comportamento de uma progressão arimética é dado de acordo com a sua razão, então temos três casos:
Se r positivo → a P.A. é crescente.
Se r igual a zero → a P.A. é constante.
Se r negativo → a P.A. é decrescente.
Sendo assim, todas as afirmativas são verdadeiras.
I – Verdadeira
II – Verdadeira
III – Verdadeira
Alternativa D
57) Uma empresa faturou R$150.000 no primeiro ano, R$ 148.000 no segundo ano, R$146.000 no terceiro ano, e assim sucessivamente. Durante a primeira década de existência dessa empresa, ela faturou um total de:
(A) 1.500.000
(B) 3.500.000
(C) 3.780.000
(D) 1.410.000
(E) 1.280.000
Resolução
É possível perceber que a sequência de faturamento comporta-se como uma P.A. de razão r igual a -2.000 e que o primeiro termo a1 = 150.000. Para realizar a soma dos dez primeiros termos dessa sequência, utilizaremos a fórmula da soma de uma P.A. finita, que é:
Para aplicar a fórmula, primeiro é necessário encontrarmos o termo a10.
an = a1 + (n – 1) r
a10 = 150.000 + (10 – 1) (-2.000)
a10 = 150.000 + 9 (-2.000)
a10 = 150.000 – 18.000
a10 = 132.000
Substituindo os valores conhecidos na fórmula da soma dos termos de uma P.A.:
Alternativa D
58) (Enem) O número mensal de passagens de uma determinada empresa aérea aumentou no ano passado nas seguintes condições: em janeiro foram vendidas 33.000 passagens; em fevereiro, 34.500; em março, 36.000. Esse padrão de crescimento manteve-se para os meses subsequentes. Quantas passagens foram vendidas por essa empresa em julho do ano passado?
(A) 38.000
(B) 40.500
(C) 41.000
(D) 42.000
(E) 48.000
Resolução
Analisando o comportamento da venda de passagens, percebe-se que, de janeiro para fevereiro, houve um aumento de 1.500, e o mesmo aconteceu de fevereiro para março. Dessa forma, se esse padrão for mantido, temos uma P.A. de razão 1.500 e primeiro termo 33.000. Queremos encontrar a quantidade de passagens vendidas em julho, que é o sétimo mês do ano, ou seja, vamos calcular o a7.
an = a1 + (n – 1) r
a7 = 33.000 + (7 – 1) · 1.500
a7 = 33.000 + 6 · 1.500
a7 = 33.000 + 9.000
a7 = 42.000
Alternativa D
59) (Enem) A prefeitura de um pequeno município do interior decide colocar postes para iluminação ao longo de uma estrada retilínea, que inicia em uma praça central e termina numa fazenda na zona rural. Como a praça já possui iluminação, o primeiro poste será colocado a 80 metros dela, o segundo, a 100 metros, o terceiro, a 120 metros, e assim sucessivamente, mantendo-se sempre uma distância de 20 metros entre os postes, até que o último poste seja colocado a uma distância de 1.380 metros da praça.
Se a prefeitura pode pagar, no máximo, R$ 8.000 por poste colocado, o maior valor que poderá gastar com a colocação desses postes é:
(A) R$512.000
(B) R$520.000
(C) R$528.000
(D) R$552.000
(E) R$584.000
Resolução
Primeiro é necessário encontrarmos a quantidade de postes que serão colocados. Note que a sequência que mede a distância do poste em relação à praça é uma P.A., pois, para cada poste em relação ao anterior, há um aumento de 20 metros nessa distância, logo, r = 20. Para saber a quantidade de postes necessários, vamos calcular o valor de n para an = 1380, que é a distância do último poste. Note que o primeiro termo da sequência é 80, então temos que:
an = a1 + (n – 1) r
1380 = 80 + (n – 1) · 20
1380 = 80 + 20n – 20
1380 – 80 + 20 = + 20n
1320 = 20n
1320 : 20 = n
n = 66
Como o valor máximo de um poste é R$ 8000, então 66 · 8000 = 528.000.
Alternativa C
60) (Ita) O valor de n que torna a sequência
2 + 3n, -5n, 1 – 4n
uma progressão aritmética pertence ao intervalo
(A) [-2, -1].
(B) [-1, 0].
(C) [0, 1].
(D) [1, 2].
(E) [2, 3].
Resolução
Para que essa sequência seja uma progressão arimética, sabemos que a2 – a1 = a3 – a2, pois a diferença de um termo com o seu antecessor é sempre constante.
Sendo assim, temos que:
O valor encontrado para n está entre -1 e 0.
Alternativa B
TERMO GERAL DA PG
A fórmula para calcular a soma dos números de uma PG![]()
sn= Soma dos números da PG
a1 = primeiro termo da sequência
q = razão
n = quantidade de elementos da PG
QUESTÕES SOBRE TERMOS GERAL DA PG
61) Determine o décimo termo de uma progressão geométrica cujo primeiro termo é 2 e a razão é 3.
(A) 10
(B) 29
(C) 30
(D) 39366
(E) 130000
Resolução
A fórmula usada para determinar um termo qualquer de uma PG é:
an = a1 . qn – 1
Substituindo os valores nessa fórmula, teremos:
an = a1 . qn – 1
a10 = 2 . 310 – 1
a10 = 2 . 39
a10 = 2 . 19683
a10 = 39366
Alternativa D
62) O oitavo termo de uma PG é 256 e o quarto termo dessa mesma PG é 16. Calcule seu primeiro termo.
(A) 1
(B) 2
(C) 3
(D) 4(E) 5
Resolução
Podemos considerar uma PG cujo primeiro termo é 16 e o quarto termo é 256. Isso porque do quarto até o oitavo existem quatro termos. Usando a fórmula do termo geral, fica fácil encontrar a razão dessa PG:
an = a1 . qn – 1
a8 = a4 . q8 – 4
256 = 16 . q4
256 = q4
16
16 = q4
Como 16 = 24, teremos:
24 = q4
Logo,
q = 2
Para encontrar o primeiro termo, basta usar a mesma fórmula, considerando que a PG possui oitavo termo igual a 256 e razão igual a 2:
an = a1 . qn – 1
256 = a1 . 28 – 1
256 = a1 . 27
256 = a1 .128
256 = a1
128
a1 = 2
Alternativa B
63) Qual é o décimo quinto termo da PG (1, 2, 4, 8, …)?
(A) 10000
(B) 12584
(C) 16384
(D) 20384
(E) 22004
Resolução
Para encontrar o 15º termo da PG, basta usar a fórmula do termo geral:
an = a1 . qn – 1
Note que a razão da PG é 2, pois esse é o resultado da divisão de qualquer termo por seu antecessor. Por exemplo, 2 : 1 = 2. Substituindo os valores na fórmula, teremos:
a15 = 1 . 215 – 1
a15 = 215 – 1
a15 = 214
a15 = 16384
Alternativa C
64) Considerando a PA de razão 2 e primeiro termo igual a 2, e a PG que possui mesma razão e mesmo primeiro termo, qual a diferença entre o décimo termo da PG e o décimo termo da PA?
(A) 20
(B) 1028
(C) 1208
(D) 1228
(E) 1004
Resolução
Substituindo as informações na fórmula do termo geral da PA teremos:
an = a1 + (n – 1)r
a10 = 2 + (10 – 1)·2
a10 = 2 + 9·2
a10 = 2 + 18
a10 = 20
Substituindo as informações na fórmula do termo geral da PG, teremos:
an = a1 . qn – 1
a10 = 2 . 210 – 1
a10 = 2 . 29
a10 = 2 . 512
a10 = 1024
A diferença entre o décimo termo da PG e o décimo termo da PA é:
1024 – 20 = 1004
Alternativa E
QEUSTÕES RESOLVIDAS - PG
65) A sequência seguinte é uma progressão geométrica, observe: (2, 6, 18, 54...). Determine o 8º termo dessa progressão.
Resolução
Razão da progressão: 6 : 2 = 3
an = a1 . q n–1
a8 = 2 . 38–1
a8 = 2 . 37
a8 = 2 . 2187
a8 = 4374
66) (Vunesp – SP – Adaptado) Várias tábuas iguais estão em uma madeireira. Elas deverão ser empilhadas respeitando a seguinte ordem: uma tábua na primeira vez e, em cada uma das vezes seguintes, tantas quantas já estejam na pilha. Por exemplo: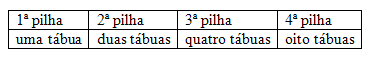 Determine a quantidade de tábuas empilhadas na 12ª pilha.
Determine a quantidade de tábuas empilhadas na 12ª pilha.
Resolução
As tábuas são empilhadas de acordo com uma progressão geométrica de razão 2. Então:
an = a1 . q n–1
a12 = 1 . 2 12–1
a12 = 1 . 2 11
a12 = 1 . 2048
a12 = 2048
Na 12ª pilha teremos 2048 tábuas.
67) (UE – PA) Um carro, cujo preço à vista é R$ 24 000,00, pode ser adquirido dando-se uma entrada e o restante em 5 parcelas que se encontram em progressão geométrica. Um cliente que optou por esse plano, ao pagar a entrada, foi informado que a segunda parcela seria de R$ 4 000,00 e a quarta parcela de R$ 1 000,00. Quanto esse cliente pagou de entrada na aquisição desse carro?
Resolução
an = a1 . q n–1
a2 = 4000
a4 = 1000
a2 = a1 . q
4000 = a1 . q
a1 = 4000 / q
a4 = a1 . q3
1000 = 4000 / q . q3
1000 / 4000 = q3 / q
1 / 4 = q2
√1/4 = √q2
q = 1/2
a1 = 4000 / 1/2
a1 = 4000 . 2
a1 = 8000
1ª prestação: R$ 8 000,00
2ª prestação: R$ 4 000,00
3ª prestação: R$ 2 000,00
4ª prestação: R$ 1 000,00
5ª prestação: R$ 500,00
Soma total das prestações: R$ 15 500,00
Entrada (valor do carro menos o total das prestações)
R$ 24 000,00 – R$ 15 500,00 = R$ 8 500,00
O valor da entrada foi de R$ 8 500,00
68) Sabendo que uma PG tem a1 = 4 e razão q = 2, determine a soma dos 10 primeiros termos dessa progressão.
Resolução![]()





