HIDROSTÁTICA

ONLINE

HIDROSTÁTICA

Professor Diminoi
HIDOSTÁTICA
É um ramo da Física que estuda as características dos fluidos em repouso. Em especial, estabelece relações com a pressão exercida sobre corpos imersos em fluidos como o ar atmosférico e a água.

Introdução à Hidrostática
A Hidrostática estuda as propriedades dos fluidos em repouso. Entre as propriedades físicas dos fluidos, podemos destacar como as mais importantes: densidade, pressão e força de empuxo. Entendemos como fluidos as substâncias capazes de assumir o formato de seu recipiente, mudando sua forma sob a ação de alguma força externa.

Densidade

A densidade é um parâmetro importante, já que essa propriedade mede a quantidade de matéria que um fluido apresenta em um determinado espaço. Segundo o Sistema Internacional de Unidades (SI), a densidade de um fluido é medida em quilogramas por metro cúbico (kg/m³).

Pressão hidrostática

A pressão hidrostática mede a força por unidade de área que um fluido em repouso é capaz de exercer contra uma superfície. Quanto maior for a profundidade de um corpo imerso em um fluido, maior será a pressão exercida sobre ele. A unidade de pressão no SI é o pascal (Pa), que equivale à pressão de 1 newton por metro quadrado (N/m²).

Empuxo

O empuxo, por sua vez, é a força que todo fluido exerce sobre os corpos nele imersos. A força de empuxo é responsável por expelir as bolhas de gás de bebidas gaseificadas. Além disso, faz com que uma cortiça, um navio ou um cubo de gelo flutue sobre a água. A força de empuxo é descrita pelo Teorema de Arquimedes, e sua unidade é o newton (N).

VASOS COMUNICANTES
São recipientes geralmente em formato de U que são utilizados para analisar as relações entre as densidades de líquidos imiscíveis e executar estudos sobre a pressão exercida por líquidos.
Nos vasos comunicantes, a pressão para pontos de mesma altura é a mesma

Lei de Stevin
A lei de Stevin propõe que a pressão exercida por um líquido depende apenas da densidade do líquido, da aceleração da gravidade e da altura da coluna de líquido existente acima do ponto analisado.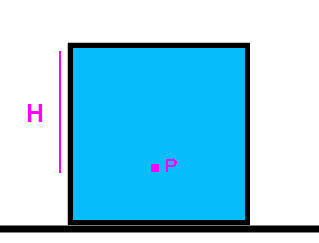
Lei de Stevin
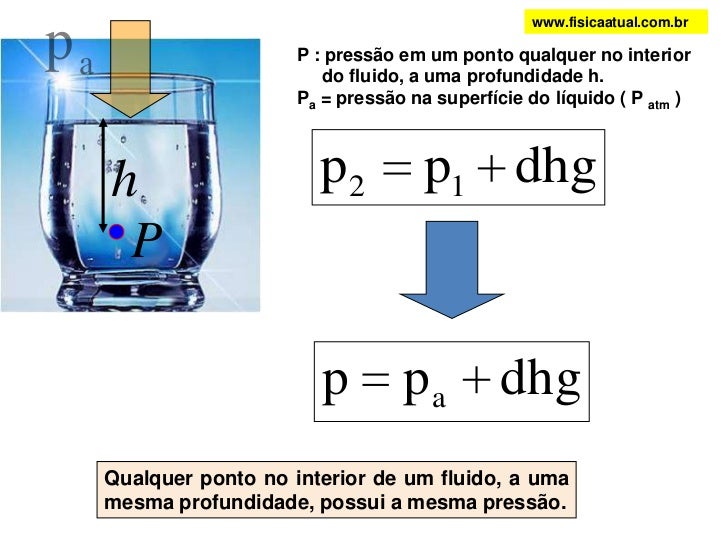P = pressão no ponto P (pa)
P_atm = pressão atmosférica (pa)
d = densidade do líquido (g/cm³) ou (kg/m³)
g = gravidade (m/s²)
h = altura da coluna de líquido acima do ponto analisado.

Por intermédio da lei de Stevin, pode-se observar que:

“a pressão exercida por um líquido não depende do formato ou do volume do recipiente no qual ele se encontra e que pontos de mesma altura possuem mesma pressão.”

Unidades de medida para a densidade
A unidade de medida da densidade, no Sistema Internacional de Unidades, é o quilograma por metro cúbico (kg/m³), embora as unidades mais utilizadas sejam o grama por centímetro cúbico (g/cm³) ou o grama por mililitro (g/mL). Para gases, ela costuma ser expressa em gramas por litro (g/L).
A imagem a seguir mostra um sistema de vasos comunicantes formados por recipientes de formas e volumes diferentes.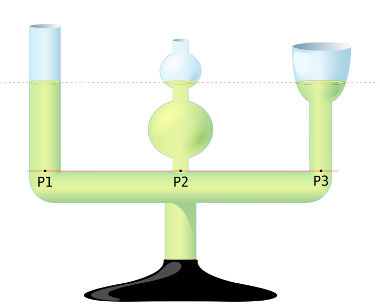
Repare que a altura da coluna de líquido e o tipo de líquido são exatamente iguais para os três recipientes. Sendo assim, pode-se concluir, por meio da lei de Stevin, que as pressões exercidas nos pontos 1, 2 e 3 são exatamente iguais (P₁ = P₂ = P₃).

Pressão
É uma grandeza escalar definida como o módulo da força aplicada dividida por unidades de área. A unidade de pressão no sistema internacional de unidades (SI) é o Pa(pascal), que equivale à aplicação de uma força de 1 Nsobre uma área de 1 m². A definição de pressão é comumente utilizada para descrever a influência sobre o comportamento de fluidos, como gases e líquidos.

Pressão hidrostática é o nome dado à pressão produzida por um determinado fluido em equilíbrio estático (repouso).

A unidade de pressão no sistema internacional de unidades (SI) é o pascal, que é equivalente à aplicação de uma força de 1 N em uma área de 1 m².

Pressão absoluta é o nome dado à soma da pressão hidrostática com a pressão atmosférica.

O que é pressão?
Pressão é a expressão de uma força aplicada sobre uma área. Pode ser expressa a partir da equação abaixo:
P = pressão
F = força aplicada
A = área

Para simplificação dos cálculos, é comum encontrarmos livros didáticos que trazem a informação de que 1 atm equivale a 1,01.10⁵ Pa ou a 760 mmHg.

1 atm = 1,01.10⁵ Pa = 760 mmHg

De acordo com o sistema internacional de unidades (SI), a unidade de pressão é o pascal (Pa). A pressão de 1 Pa equivale à aplicação de uma força de 1 N sobre uma área de 1 m²: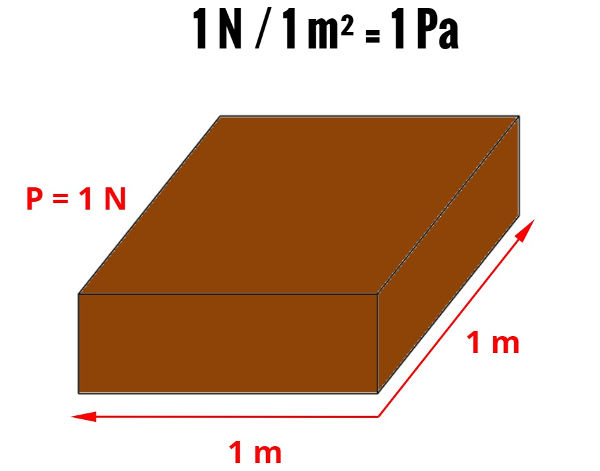
O bloco mostrado na figura acima tem peso de 1 N, e a área de sua superfície inferior é de 1 m². Logo, a pressão exercida por ele é de 1 Pa.

Pressão é uma variável importante em diversas situações, por exemplo: ao amolar uma faca, reduzimos sua área de contato, aumentando, assim, a pressão exercida, facilitando o corte. Quanto menor for a área de contato entre dois corpos, maior será a pressão exercida, independentemente se aumentarmos ou diminuirmos a força aplicada.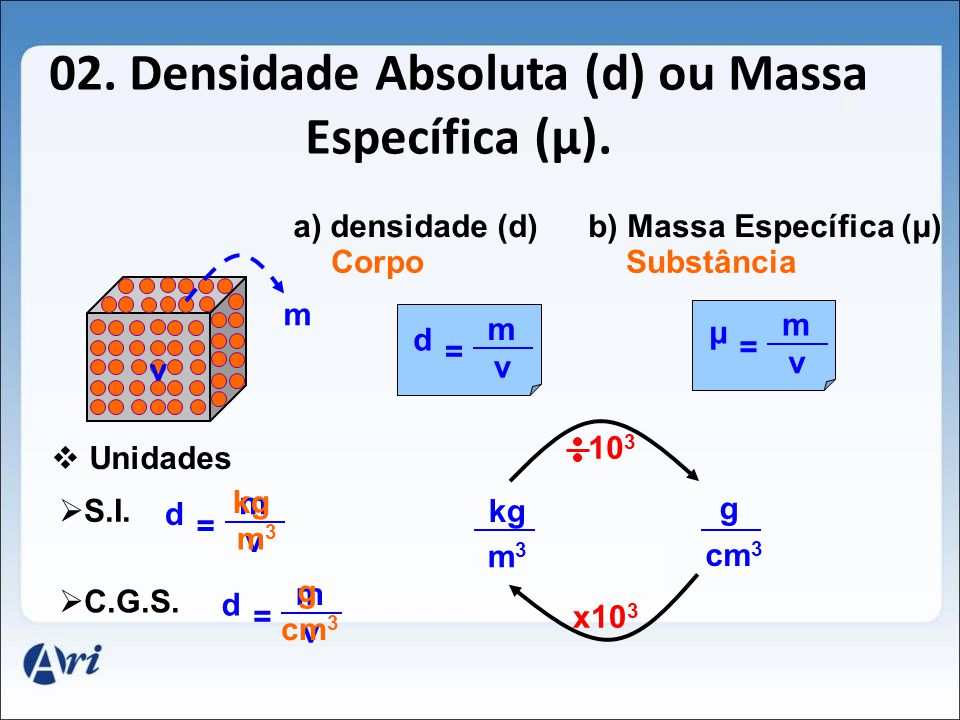

Pressão hidrostática
É a pressão exercida por fluidos em repouso. Para calcularmos essa pressão, utilizamos uma relação matemática um pouco diferente, porém mais útil para o estudo dos fluidos.

Imagine um cilindro de massa desprezível, completamente preenchido por um fluido qualquer, como mostra a figura abaixo:
A pressão exercida por esse fluido pode ser calculada por meio da relação clássica de pressão (P = F/A). Entretanto, se levarmos em conta que a massa do fluido (m) relaciona-se com outras duas propriedades do fluido, seu volume (V) e sua densidade (d), poderemos deduzir a seguinte fórmula de pressão hidrostática: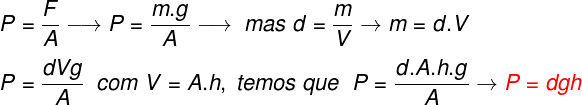

A pressão hidrostática, também conhecida como pressão manométrica, é dada pela expressão matemática

P = d . g . h
d = densidade do fluido (kg/m³)
V = volume do fluido (m³)
A = área da base do recipiente (m²)
h = altura do fluido que ocupa o recipiente (m)

De acordo com o cálculo acima, a pressão exercida por um fluido em equilíbrio estático é dada pela expressão P = dgh, ou seja, quanto maior for a profundidade de um fluido, maior será a pressão exercida por ele.

O que é pressão atmosférica?
Pressão atmosférica é a pressão exercida pela coluna de gases atmosféricos presente acima de nós durante todo o tempo.

À medida que nos encontramos mais altos em relação ao nível do mar, a densidade atmosférica tende a cair, e seus gases tornam-se cada vez mais rarefeitos até uma fronteira de centenas de quilômetros, quando se inicia o vácuo espacial.

Ao verter o conteúdo do tubo em um recipiente cheio de mercúrio, Torricelli percebeu que a altura do líquido dentro do tubo de vidro permanecia estática em 76 cm (760 mm).

Dessa forma, definiu que a pressão atmosférica era de módulo igual ao da pressão exercida por uma coluna de 760 milímetros de mercúrio.

Observação:

P₀ = 760 mmHg = 1 atm

P₀ = pressão atmosférica
atm = pressão exercida pela atmosfera terrestre ao nível do mar
mmHg = pressão exercida por uma coluna de mercúrio

Pressão absoluta
Pressão absoluta é a pressão total exercida sobre um corpo na superfície da Terra. Para calcularmos a pressão absoluta sobre um corpo, devemos levar em conta a atuação de duas pressões distintas: a pressão atmosférica e a pressão manométrica (exercida por um fluido).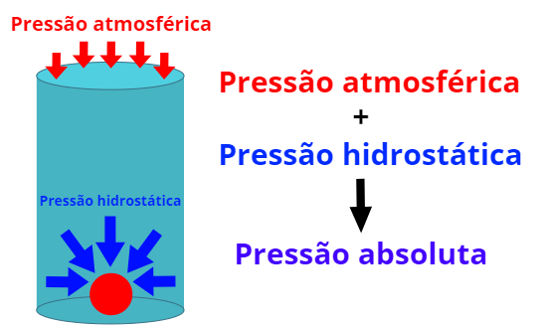

A pressão absoluta exercida sobre um corpo imerso em um fluido é a soma da pressão atmosférica com a pressão hidrostática.

A relação estabelecida entre a pressão atmosférica e a pressão hidrostática é chamada de Teorema de Stevin e é definida pela equação abaixo:

P = P₀ + d.g.h

P = pressão absoluta
P₀ = pressão atmosférica
dgh = pressão manométrica ou hidrostática

Fórmulas de pressão
Utilize a fórmula abaixo para calcular a pressão exercida sobre uma área:

P = pressão
F = força aplicada
A = área

A fórmula a seguir pode ser usada para determinar a pressão exercida por um fluido em equilíbrio estático.

Denominamos esse tipo de pressão como pressão hidrostática ou pressão manométrica

P = d. g . h

P = pressão hidrostática (Pa)
d = densidade do fluido (kg/m³)
g = gravidade local (m/s²)
h = altura do fluido(m)

Para calcular a pressão absoluta sobre um corpo que esteja imerso em um fluido sob a ação da pressão atmosférica, pode-se utilizar o

Teorema de Stevin:

P = P₀ + d.g.h

P = pressão absoluta
P₀ = pressão atmosférica
dgh = pressão manométrica ou hidrostática

Unidades de pressão

Existem muitas unidades utilizadas para medir a pressão em diferentes partes do mundo ou na realização de diferentes atividades. É importante conhecermos algumas delas e sabermos como convertê-las para a unidade padrão, o pascal:

Para simplificação dos cálculos, é comum encontrarmos livros didáticos que trazem a informação de que 1 atm equivale a 1,01.10⁵ Pa ou a 760 mmHg.

1 atm = 1,01.10⁵ Pa = 760 mmHg

Pressão arterial
É a pressão exercida pelo sangue contra as paredes das artérias. Para medirmos a pressão arterial, utilizamos um aparelho chamado esfigmomanômetro.

De acordo com a Sociedade Brasileira de Cardiologia (SBC), a razão dessas pressões considerada saudável é a de 120 mmHg de pressão sistólica por 80 mmHg de pressão diastólica, comumente denotado como uma pressão de 12:8 (doze por oito).

EXERCÍCIO – PRESSÃO/FORÇA/ÁREA
01) Um cubo maciço, assim como o da figura abaixo, de aresta 3,0 cm e massa igual a 10,0g encontra-se apoiado sobre uma superfície lisa e horizontal. Sendo a aceleração da gravidade local g = 10 m/s², calcule a pressão que esse objeto exerce sobre a superfície.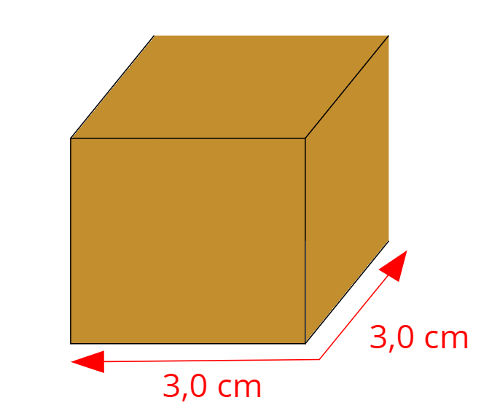
Resolução:
Começaremos dando atenção às unidades fornecidas pelo enunciado do exercício. Para tanto, devemos lembrar que todas elas devem ser expressas no sistema internacional de unidades(S.I.). Dessa forma, a aresta do cubo tem comprimento de 0,03 m (3 cm), e sua massa é de 0,010 kg (10,0 g).
Para calcularmos a pressão exercida pela face inferior do cubo, aquela sobre a qual se apoia, utilizaremos a definição mais simples de pressão:
Como já sabemos, a força exercida pelo cubo é a força normal de compressão, que, no caso de uma superfície horizontal, é numericamente igual ao seu peso. Portanto:

02) Durante a execução de uma obra, um engenheiro deseja que a água saia de uma torneira com uma pressão máxima de 2,0 atm a fim de evitar possíveis danos ao sistema hidráulico. Para isso, qual deverá ser a mínima altura que as caixas d'águas devem ser instaladas a partir da altura dessa torneira?
Dados:
1 atm = 1,01.10⁵ Pa
g = 10 m/s²
d_água= 1000 kg/m³
Resolução:
Para calcularmos a altura mínima que as caixas d'água devam ser instaladas, é necessário lembrar que existe ar atmosférico no interior delas. Por isso, não basta calcularmos somente a pressão hidrostática da água, devemos levar em conta sua pressão absoluta por meio do Teorema de Stevin:
P = P₀ + d.g.h
Portanto, considerando a pressão absoluta igual a 2 atm (2 x 1,01.10⁵ Pa), teremos a seguinte resolução:

RESOLVIDOS - DENSIDADE
01) Uma solução cuja densidade é de 1150 g/L foi preparada, dissolvendo-se 160 g de NaOH em 760 cm³ de água. Determine respectivamente a massa da solução obtida e seu volume. (Dado: densidade da água = 1,0 g/cm³):
(A) 160 g e 0,14 mL.
(B) 760 g e 0,66 mL.
(C) 920 g e 0,8 mL.
(D) 160 g e 0,21 mL.
(E) 920 g e 800 mL.
Resolução:
A massa da solução (m) é dada pela soma da massa do soluto (m₁ = 160 g) com a massa do solvente (m₂). Assim, precisamos primeiro descobrir a massa da água:
d₂= m₂/v₂
m₂ = d₂. v₂
m₂ = 1,0 . 760
m₂ = 760 g
Agora descobrimos a massa da solução:
m = m₁ + m₂
m = 160 + 760
m = 920g
Agora falta descobrir o volume da solução:
d = m/v
v = m/d
v = 920/1150 L
v = 0,8 L = 800 mL
Alternativa: E

02) O leite é uma mistura de diferentes substâncias (proteínas, carboidratos, vitaminas, gordura, sais minerais e água) e, por meio da análise de sua composição e propriedades, é possível verificar a qualidade do leite. Uma análise simples é a medida da densidade, que deve estar entre os valores 1,028 e 1,034 g/L. Com base nisso, julgue os itens a seguir e assinale a única opção que está correta:
(A) No caso de o leite ser adulterado com a adição de água (d_água = 1,0 g/cm³), sua densidade será maior que os valores-padrão.
(B) No caso de o leite ser adulterado por retirada de gordura (utilizada na produção de manteiga), sua densidade será menor que os valores-padrão.
(C) A densidade do leite adulterado pode se situar entre os valores permitidos.
(D) A densidade da gordura do leite é aproximadamente 0,927 g/cm³, e a do leite desnatado é cerca de 1,035 g/cm³. Assim, um leite com 3,0% de gordura deverá ter uma densidade menor que o de um com 4,5% de gordura.
(E) A densidade da água oxigenada (solução de peróxido de hidrogênio) é de 1,45 g/cm³. No entanto, escândalos surgiram em torno de uma suposta adição de água oxigenada no leite. Nesse caso, a densidade do leite adulterado será menor que a dos valores-padrão.
Resolução:
A) Incorreta. Visto que a densidade da água é menor que a do leite, a sua adição ao leite deve diminuir a densidade.
B) Incorreta. A densidade será maior porque a gordura tem menor densidade entre as substâncias do leite, e a sua retirada implica o aumento da porcentagem das substâncias mais densas, aumentando a densidade do leite que sobrou.
C) Correta. Se ao leite for adicionada uma substância menos densa que ele, como a água, e houver a retirada de substâncias menos densas, como a gordura, esses dois frascos podem se compensar e a densidade do leite permanecer dentro dos valores permitidos.
D) Incorreta. Visto que a densidade da gordura do leite é menor que a densidade do leite, um leite que tiver mais gordura terá menor densidade.
E) Incorreta. Visto que a densidade da água oxigenada é maior que a do leite, a sua adição ao leite deve aumentar a densidade.
Alternativa: C

03) Qual a densidade em g/cm³ de uma solução de volume igual a 5 L e massa de 4000 g:
(A) 0,08
(B) 0,8
(C) 8
(D) 80
(E) 800
Resolução:
d = m/v
d = 4000g/5000cm³
d = 0,8 g/cm³
Alternativa: B

03) (UFPI) Em uma cena de um filme, um indivíduo corre carregando uma maleta tipo 007(volume de 20 dm³) cheia de barras de um certo metal. Considerando que um adulto de peso médio (70 kg) pode deslocar com uma certa velocidade, no máximo, o equivalente ao seu próprio peso, indique qual o metal, contido na maleta, observando os dados da tabela a seguir.
(Dado: 1 dm³ = 1L = 1 000 cm³.)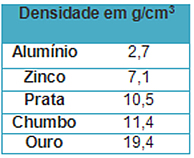
(A) Alumínio.
(B) Zinco.
(C) Prata.
(D) Chumbo.
(E) Ouro.
Resolução:
Achar o volume da mala em cm³:
V = 20 dm³ = 20 L = 20 000 cm³
Usando a fórmula da densidade (d = m/V), encontramos a massa de cada metal:
d = m/V
m = d . V
Alumínio Zinco Prata
m = 2,7 . 20 000 m = 7,1 . 20 000 m = 10,5. 20 000
m = 54 000 g m = 142 000 g m = 210 000 g
m = 54 kg m = 142 kg m = 210 kg
Chumbo Ouro
m = 11,4 . 20 000 m = 19,4 . 20 000
m = 228 000 g m = 388 000g
m = 228 kg m = 388 kg
Visto que o indivíduo só poderia correr com um peso menor que 70 kg, temos, então, que o metal mais adequado seria o Alumínio.
Alternativa: A

05) (UFMG) Em um frasco de vidro transparente, um estudante colocou 500 mL de água e, sobre ela, escorreu vagarosamente, pelas paredes internas do recipiente, 50 mL de etanol. Em seguida, ele gotejou óleo vegetal sobre esse sistema. As gotículas formadas posicionaram-se na região interfacial, conforme mostrado nesta figura: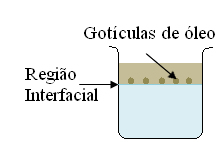
Considerando-se esse experimento, é correto afirmar que:
(A) a densidade do óleo é menor que a da água.
(B) a massa da água, no sistema, é 10 vezes maior que a de etanol.
(C) a densidade do etanol é maior que a do óleo.
(D) a densidade da água é menor que a do etanol.
Resolução:
A) Correto. O óleo é menos denso que a água, por isso, suas gotículas ficam acima da superfície da água.
B) Incorreto. A massa de cada um é encontrada por meio da fórmula da densidade. (d_água= 1,0 g/cm³, d_etanol= 0,79 g/cm³):
d = m/V → m = d . V
m_água = d . V m_etanol = d . V
m_água = 1,0 . 500 m_etanol = 0,79. 50
m_água = 500 gm_etanol = 39,5 g
Veja que a massa da água, no sistema, não é 10 vezes maior que a de etanol.
C) Incorreto. A densidade do etanol é menor que a do óleo, por isso, o óleo afunda em relação ao etanol.
D) Incorreto. A densidade da água é maior que a do etanol porque ela afunda em relação a ele.
Alternativa: A

06) (FESP) O volume de álcool etílico que devemos misturar com 80cm³ de água destilada para obtermos uma solução alcoólica de densidade 0,93 g/cm³ é (despreze a contração de volume que acompanha a mistura de álcool com água): (Dados: d _H2O = 1 g/cm³; d_C2H2OH = 0,79 g/cm³)
(A) 4 cm³.
(B) 40 cm³.
(C) 60 cm³.
(D) 70 cm³.
(E) 65 cm³.
Resolução:
Dados:
V_H2O = 80 cm³
d_H2O= 1 g/cm³
d_C2H2OH= 0,79 g/cm³
V_C2H2OH = ?
d = 0,93 g/cm³
V = 80 + V_C2H2OH
Aplicando e substituindo
d.V = d_H2O. V_H2O + d_C2H2OH. V_C2H2OH
0,93 (80 + V_C2H2OH) = 80.1 + 0,79.V_C2H2OH
0,14V_C2H2OH = 5,6
V_C2H2OH = 40 cm³
Alternativa: B

Mistura de líquidos
Quando dois líquidos imiscíveis são colocados em um recipiente em formato de U, pode-se aplicar a lei de Stevin para estabelecer uma relação entre as densidades e as alturas das colunas de líquido. Na imagem a seguir, dois líquidos com densidades D₁ e D₂ foram colocados em um recipiente.

As alturas das colunas de líquido são proporcionais às densidades dos fluidos.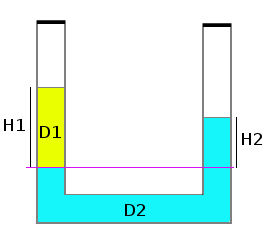
Aplicando a lei de Stevin e sabendo que pontos de mesma altura possuem mesma pressão, teremos:
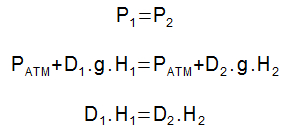Conclui-se que o produto das densidades pela altura da coluna de líquido deve ser igual para cada um dos fluidos dentro do recipiente. A igualdade será mantida se o líquido de menor densidade possuir a maior altura e vice-versa.

É possível escrever a pressão para dois pontos distintos da seguinte forma

PA = d g h_A
PB = d g h_B

RESOLVIDOS – VASOS COMUNICANTES
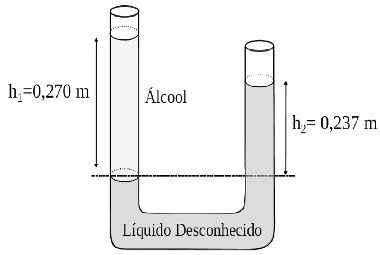
01) (Uncisal) Em um laboratório, as substâncias são identificadas no rótulo pelo nome e por algumas propriedades químicas. No intuito de descobrir qual a substância armazenada num frasco no qual o rótulo foi retirado, um estudante aplicado de física propôs um experimento. Foram colocados num sistema constituído por vasos comunicantes o líquido desconhecido e álcool. Como são líquidos imiscíveis, é possível estimar a densidade do líquido medindo a altura das colunas líquidas a partir da superfície de separação desses líquidos. Esses valores são mostrados na figura a seguir. Consultando a tabela com os valores das densidades de alguns líquidos, disponível nesse laboratório, é provável que o líquido desconhecido seja: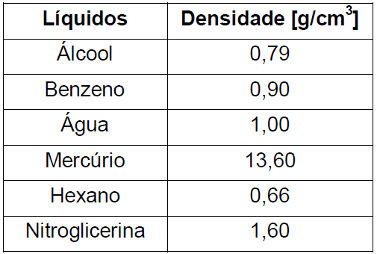
(A) a nitroglicerina.
(B) o hexano.
(C) o mercúrio.
(D) a água.
(E) o benzeno.
Resolução:
Aplicando a lei de Stevin para o caso dos vasos comunicantes, o produto das alturas das colunas de líquido, determinadas de um mesmo ponto, pela densidade dos líquidos deve ser igual. Assim, podemos escrever que:
ρ_ÁLCOOL. h₁ = ρ . h₂
0,79 . 0,270 = ρ . 0,237
0,2133 = ρ . 0,237
ρ = 0,9 g/cm³
O líquido desconhecido é o benzeno.
Alternativa: E

02) (Unifesp) O sistema de vasos comunicantes da figura contém água em repouso e simula uma situação que costuma ocorrer em cavernas: o tubo A representa a abertura para o meio ambiente exterior e os tubos B e C representam ambientes fechados, onde o ar está aprisionado.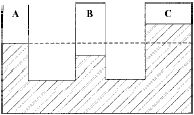
Sendo p_A a pressão atmosférica ambiente, p_B e p_C as pressões do ar confinado nos ambientes B e C, pode-se afirmar que é válida a relação:
(A) p_A = p_B > p_C.
(B) p_A> p_B = p_C.
(C) p_A > p_B > p_C.
(D) p_B > p_A > p_C.
(E) p_B > p_C > p_A.
Resolução:
Quanto maior a pressão sobre os líquidos, maiores serão os desníveis entre os vasos comunicantes. O nível mais baixo tem ação da maior pressão, logo:
p_B > p_A > p_C
Alternativa: D

03) As seguintes afirmações são feitas a respeito de dois líquidos de densidades diferentes colocados juntos em um tubo em formato de U.
I) A determinação da densidade ou altura das colunas de líquido é feita a partir da lei de Stevin.
II) A pressão atmosférica só fará diferença se pelo menos uma das extremidades do recipiente estiver fechada.
III) A menor coluna de líquido sempre será daquele que possui menor densidade.
IV) A pressão para pontos de mesma altura será a mesma.
Marque a alternativa correta.
(A) As afirmações I, III e IV são verdadeiras.
(B) As afirmações II e III são falsas.
(C) Todas as afirmações são verdadeiras.
(D) Somente I é verdadeira.
(E) As afirmações I, II e IV são verdadeiras.
Resolução:
I) Verdadeira: as análises feitas para os vasos comunicantes baseiam-se no cálculo da pressão de um líquido feito pela chamada lei de Stevin.
II) Verdadeira: se as duas extremidades estiverem abertas ou fechadas, a pressão atmosférica poderá ser desprezada.
III) Falsa: a menor coluna de líquido sempre será daquele que possui menor densidade.
IV) Verdadeira: a lei de Stevin mostra que pontos de mesma altura possuem mesma pressão.
Alternativa: E

ESTÁTICA DOS FLUÍDOS
Fluidos, são assim denominados os líquidos e os gases pelo fato de poderem se escoar com grande facilidade. Seu estudo teve início com Arquimedes e sua mecânica dos fluídos, responsável pelo estudo da hidrostática, força gerada por líquidos e gases. Personalidades como Torricelli, Stevin e Pascal também contribuíram muito para estes estudos.
Divisão da Mecânica dos Fluídos

A mecânica dos fluídos foi dividida em duas partes:

Fluído estática – estuda os fluidos em repouso, parados.

Fluído dinâmica – analisa os fluidos que estão em movimento.

Também são considerados os termos:

Hidrostática para Fluído estática.

Hidrodinâmica para Fluído dinâmica.

Densidade
Densidade é grandeza Física responsável pela medida da concentração da massa de uma substância em um determinado volume.

Define-se matematicamente como a razão entre a massa e o volume correspondentes da substância analisada.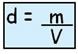
Onde:
d = densidade da substância
m = massa do corpo
V = volume do corpo

Observação:

A unidade de medida da densidade, mo Internacional de Unidades, é o quilograma por metro cúbico (kg/m³), embora as unidades mais utilizadas sejam o grama por centímetro cúbico (g/cm³) ou o grama por mililitro (g/mL). Para gases, ela costuma ser expressa em gramas por litro (g/L).

PRESSÃO
Pressão é definida pelo limite da relação de um ponto anterior com a área tendendo a zero.

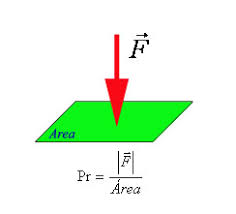
Ex: Um prego com ponta bem fina sendo facilmente penetrado na parede. Esse exemplo indica que mais importante que a força exercida é a área em que a força atua.

Portanto, a pressão é a divisão entre a intensidade da força F e a área S em que tal força é distribuída.

RESOLVIDOS – PRINCÍPIO DE PASCAL
01) (UERJ) Observe, na figura a seguir, a representação de uma prensa hidráulica, na qual as forças F₁ e F₂ atuam, respectivamente, sobre os êmbolos dos cilindros I e II.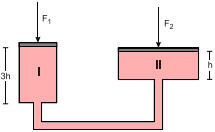
Admita que os cilindros estejam totalmente preenchidos por um líquido. O volume do cilindro II é igual a quatro vezes o volume do cilindro I, cuja altura é o triplo da altura do cilindro II. A razão entre as intensidades das forças F₂e F₁, quando o sistema está em equilíbrio, corresponde a:
(A) 12
(B) 6
(C) 3
(D) 2
Resolução:
Sabendo que o volume de um sólido geométrico é definido como sendo o produto da área da base pela altura, temos:
V₂ = 4.V₁
A₂h = 4.A₁3.h
A₂= 12 . A₁
Aplicando o Princípio de Pascal, temos:
F₁/A₁ = F₂/A₂
F₁/A₁ = F₂/12.A₁
F₁ = F₂/12
F₂/F₁ = 12
Alternativa: A

02) (Espcex) Um elevador hidráulico de um posto de gasolina é acionado por um pequeno êmbolo de área igual a 4 x 10^{– 4 m2}. O automóvel a ser elevado tem peso de 2 x 10 ⁴ N e está sobre o êmbolo maior, de área 0,16 m². A intensidade mínima da força que deve ser aplicada ao êmbolo menor para conseguir elevar o automóvel é de:
(A) 20 N
(B) 40 N
(C) 50 N
(D) 80 N
(E) 120 N
Resolução:
Aplicando o Princípio de Pascal, temos:
F_APLICADA/A_MENOR = Peso/ A_MAIOR
F/ 4 x 10^{– 4} = 2 x 10 ⁴/0,16
F/ 4 x 10^{– 4} = 12,5 x 10 ⁴
F = 4 x 10^{– 4} . 12,5 x 10 ⁴
F = 50 N
Alternativa: C

03) Uma prensa hidráulica é composta por dois cilindros de áreas A₁ e A₂. Um objeto de 1000 kg foi colocado sobre a maior área. Determine a força mínima necessária que deve ser aplicada sobre a menor área para que o objeto seja levantado. A área A₂ é o quíntuplo da área A_1.
Dado: Adote g = 10 m/s²
(A) 2000 N
(B) 4000 N
(C) 5000 N
(D) 800 N
(E) 1200 N
Resolução:
Aplicando o Princípio de Pascal, temos:
F₁/A₁ = F₂/A₂
A força 2 corresponde ao peso do objeto, logo:
F₂ = m.g
F₂ = 1000. 10
F₂ = 10000 N
Sabendo que A₂ = 5.A₁, temos:
F₁/A₁ = 10000/5A₁
F₁ = 10000/5
F₁ = 2000 N
Alternativa: A

04) A respeito do Princípio de Pascal, marque a alternativa correta.
(A) A pressão exercida sobre um líquido é maior na região de aplicação da força.
(B) A pressão exercida sobre um líquido é transmitida de forma integral a todos os pontos do líquido.
(C) Somente a pressão exercida sobre a água é transmitida de forma integral por todas as partes do líquido.
(D) Somente a pressão exercida sobre a água não é transmitida de forma integral por todas as partes do líquido.
(E) Todas as alternativas estão erradas.
Resolução:
O Princípio de Pascal diz que qualquer acréscimo de pressão sobre um líquido é transmitido integralmente para todos os seus pontos.
Alternativa: B

05) (UERJ-RJ) Algumas cafeteiras industriais possuem um tubo de vidro transparente para facilitar a verificação da quantidade de café no reservatório, como mostra a figura. Observe que os pontos A e B correspondem a aberturas na máquina.
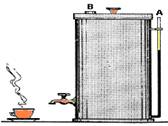Admita que a área da seção reta horizontal do reservatório seja 20 vezes maior do que a do tubo de vidro.
Quando a altura alcançada pelo café no tubo é x, a altura do café no interior do reservatório corresponde a:
(A) x
(B) x/2
(C) x/10
(D) x/20
(E) x/25
Resolução:
A pressão hidrostática é fornecida por Ph = d_café.g.h e observe que ela não depende das dimensões do tubo e da cafeteira e, como os pontos A e B estão abertos, a pressão nos dois é a mesma e ficam na mesma altura
Alternativa: A

06) (PUC-MG) A figura representa duas caixas d’água, abertas para o ar, interligadas por um cano com uma válvula de passagem. A caixa da esquerda está cheia. Quando a válvula é aberta, a caixa da direita começa a encher até que o nível da água nas duas caixas seja o mesmo.
É correto afirmar:
(A) Ao final do processo, a pressão no fundo da caixa à esquerda será menor que no início.
(B) Durante o processo, a velocidade de escoamento da água é constante.
(C) Ao final do processo, a pressão no fundo da caixa à direita será maior que a pressão no fundo da caixa à esquerda.
(D) Durante o processo, a velocidade de escoamento da água aumenta.
Resolução:
Quando você abre a válvula,a água flui da caixa da esquerda para a da direita até que elas tenham a mesma altura — a altura da caixa da esquerda diminui e consequentemente a pressão na base da mesma também diminui
Alternativa: A

EXERCÍCIOS RESOLVIDOS SEDUC-SP-2025

01) (Livro do aluno - SEDUC-SP-2025) Qual o valor do volume de um objeto constituído de prata cuja densidade é igual a 30 g/m³ e massa igual a 15 kg?

Resolução:

02) (Livro do aluno - SEDUC-SP-2025) Uma substância com massa igual a 10 kg ocupa um volume de 5 m³. Calcule a densidade absoluta dessa substância.

(A) 3 kg/m³

(B) 0,5 kg/m³

(D) 4 kg/m³

(E) 5 kg/m³

Resolução:

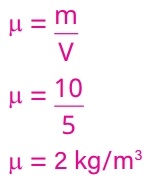
Alternativa: C

03) (Livro do aluno - SEDUC-SP-2025) Qual o valor da massa de um objeto constituído de ouro maciço cuja densidade é igual a 30 g/cm³ e volume igual a 5 m3?

(A) 5 kg

(B) 15 102, ·kg

(D) 15 105, · kg

(E) 1,5 kg

Resolução:

Alternativa: D

04) (Livro do aluno - SEDUC-SP-2025 - UPF 2013) Os chamados “buracos negros”, de elevada densidade, seriam regiões do Universo capazes de atrair matéria, que passaria a ter a densidade desses “buracos”. Se a Terra, com massa da ordem de 1024 kg, fosse absorvida por um “buraco negro” de densidade 1024 g/cm³, ocuparia um volume compatível ao:

(A) de um nêutron.

(B) de uma gota d’água.

(D) da Lua.

(E) do Sol.

Resolução:

Alternativa: C

05) (Livro do aluno - SEDUC-SP-2025 - FUVEST 1978) Uma chapa de cobre de 2 m², utilizada em um coletor de energia solar, é pintada com tinta preta cuja massa específica, após a secagem, é 1,7 g/cm³. A espessura da camada é da ordem de 5 µm (micrômetro). Qual é a massa de tinta seca existente sobre a chapa?

Resolução:

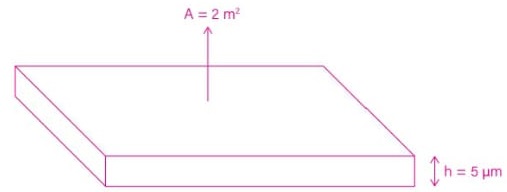
06) (Livro do aluno - SEDUC-SP-2025) A pressão exercida por uma coluna de água de 10 m de altura é igual a 1,0 atm. Um mergulhador encontra-se a uma profundidade H da superfície livre da água. A pressão absoluta sobre o mergulhador é de 5,0 atm. Determine a profundidade em que o mergulhador se encontra.

Resolução:

Como a pressão exercida por uma coluna de água de 10 m equivale a 1,0 atm, a profundidade em que o mergulhador se encontra é de 40 m.

07) (Livro do aluno - SEDUC-SP-2025) Calcule a pressão exercida por uma coluna de água de 2 m de altura, sabendo que a densidade da água é 1000 kg/m³ e que o valor da aceleração da gravidade local é de 9,8 m/s².

Resolução:

08) (Livro do aluno - SEDUC-SP-2025) Um recipiente aberto contém mercúrio até uma altura de 50 cm, em um local onde a aceleração da gravidade é de 9,8 m/s². Sabendo que a densidade do mercúrio é de 13 600 kg/m³, a pressão na superfície do mercúrio é mais próxima de:

(A) 6,7 . 10⁴ Pa

(B) 6,7 . 10⁵ Pa

(D) 6,7 . 10⁷ Pa

Resolução:

Alternativa:

09) (Livro do aluno - SEDUC-SP-2025 - ENEM 2020) Um mergulhador fica preso ao explorar uma caverna no oceano. Dentro da caverna, formou-se um bolsão de ar, como mostrado na figura, onde o mergulhador se abrigou.

Durante o resgate, para evitar danos a seu organismo, foi necessário que o mergulhador passasse por um processo de descompressão antes de retornar à superfície, para que seu corpo ficasse novamente sob pressão atmosférica.

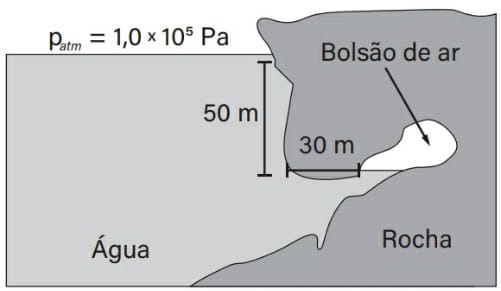
O gráfico mostra a relação entre os tempos de descompressão, recomendados para indivíduos nessa situação, e a variação de pressão.

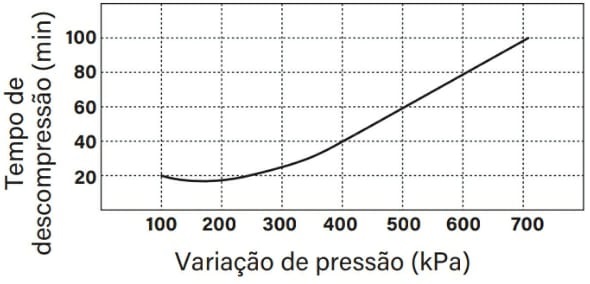
Considere que a aceleração da gravidade seja igual a 10 m.s^‑2 e que a densidade da água seja p = 1000 kg.m‑3. Em minutos, qual é o tempo de descompressão a que o mergulhador deverá ser submetido?

(A) 100

(B) 80

(D) 40

(E) 20

Resolução:

Para resolver essa questão, inicialmente, calcularemos a variação de pressão a que foi submetido o mergulhador e, com esse valor, determinaremos, utilizando o gráfico, o tempo de descompressão recomendado para essa situação. Para o cálculo da variação de pressão, desde a superfície da água até a posição do mergulhador, vamos utilizar a expressão matemática do teorema de Stevin. Assim, a variação de pressão é dada por: Δp = µ . g . ∆h

Portanto temos: Δp = µ . g . ∆h = 1000 . 10 . 50 = 500 kPa Analisando o gráfico, notamos que o intervalo de tempo de descompressão recomendado para esse mergulhador é de 60 min

Alternativa: C

10) (Livro do aluno - SEDUC-SP-2025 - EsFCEx 2022) As figuras mostram o fundo do mar de uma mesma região em dois momentos: na figura 1, em uma situação de maré alta e, na figura 2, em uma situação de maré baixa. Nas duas figuras, vê-se, ainda, uma pedra de dimensões desprezíveis em repouso no fundo do mar.

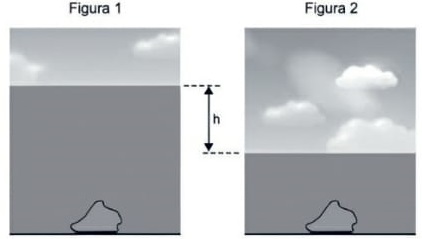
Considerando g = 10 m/s², a densidade da água do mar igual a 1 g/cm³ e sabendo que a diferença de pressão sobre a pedra, nas duas situações, é de 40 000 Pa, o desnível h, indicado na figura, é de:

(A) 1,4 m

(B) 0,4 m

(D) 4 m

Resolução:

Primeiro, vamos converter a unidade de densidade da água de g/cm³para kg/m³. Dessa forma, temos:

Alternativa: D

11) (Livro do aluno - SEDUC-SP-2025) Um vaso de flores, cuja forma encontra-se representada na figura, está cheio de água.

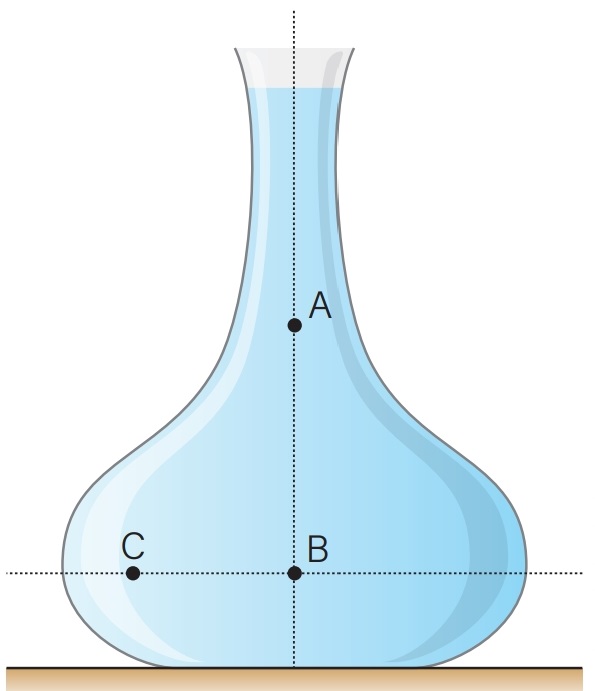
Três posições, A, B e C, estão indicadas na figura.

A relação entre as pressões PA, PB e PC exercidas pela água, respectivamente nos pontos A, B e C, pode ser descrita como:

(A) pA > pB > pC.

(B) pA > pB = pC.

(D) pA = pB < pC.

(E) pA < pB = pC

Resolução:

Observando a imagem, podemos notar que os pontos B e C estão no mesmo nível, indicando que P_B = P_C. Além disso, o ponto A está posicionado acima dos pontos B e C, o que implica que o ponto A está sujeito a uma pressão menor em comparação com os pontos B e C. Logo, a resposta correta para essa questão é P_A < P_B = P_C.

Alternativa: E

12) (Livro do aluno - SEDUC-SP-2025 - PUCRS 2023) A figura a seguir mostra dois recipientes A e B que contêm álcool (µ = 0,8 g/cm³) e glicerina (µ = 1,2 g/cm³), respectivamente.

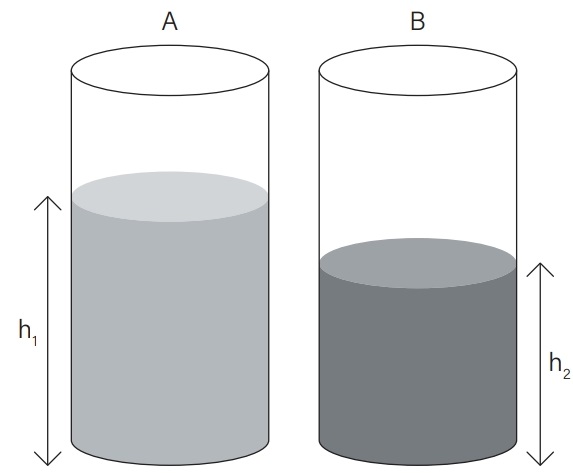
Para que a pressão exercida no fundo dos recipientes seja a mesma, a razão h1/h2deve ser igual a:

(A) 0,6

(B) 0,8

(D) 2,0

Resolução:

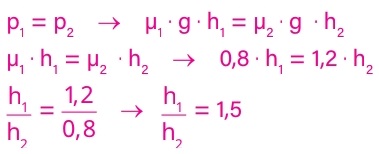
Alternativa: C

13) (Livro do aluno - SEDUC-SP-2025 - FASM 2017) O esquema representa a experiência feita por Torricelli. A cuba e o tubo contêm mercúrio líquido e têm como finalidade a medição da pressão atmosférica.

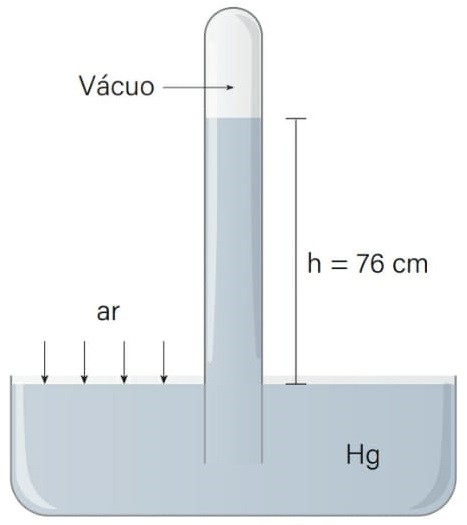
Verificou-se nessa experiência que, ao nível do mar, a altura da coluna de mercúrio dentro do tubo foi de 76 cm para uma pressão atmosférica de 10⁵ N/m² e uma aceleração da gravidade de 10 m/s².

Nessas mesmas condições, substituindo-se o mercúrio por um líquido de densidade absoluta 8 × 10³ kg/m³, a altura da coluna do líquido dentro do tubo será igual a:

(A) 125 cm

(B) 130 cm

(D) 135 cm

(E) 120 cm

Resolução:

Para a resolução desse exercício, devemos considerar que a pressão no ponto A (atmosférica) é igual à pressão no ponto B (devido ao líquido), ou seja: P_A = P_B

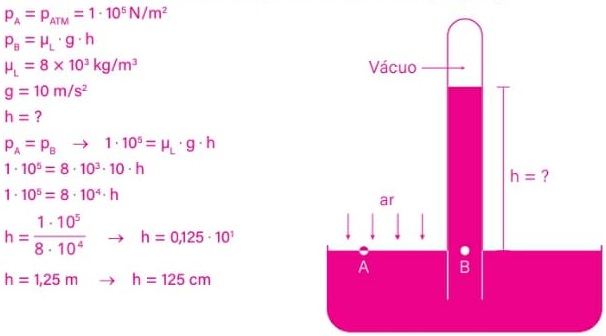
Alternativa: A

14) (Livro do aluno - SEDUC-SP-2025 - EsPCEx 2012) A pressão (P) no interior de um líquido homogêneo, incompressível e em equilíbrio, varia com a profundidade (X) de acordo com o gráfico abaixo.

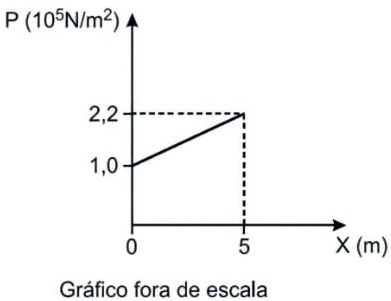
Considerando a aceleração da gravidade igual a 10 m/s², podemos afirmar que a densidade do líquido é de:

(A) 1,1 . 10⁵ kg/m³

(B) 6,0 . 10⁴ kg/m³

(D) 4,4 . 10³ kg/m³

(E) 2,4 . 10³ kg/m³

Resolução:

Segundo o gráfico, a pressão para a profundidade de 5 metros é de p = 2,2 . 10⁵N/m². Assim, com base no Teorema de Pascal, podemos dizer que:

Alternativa: E

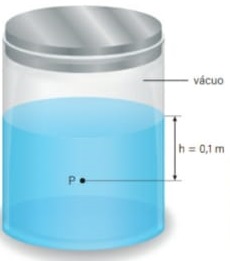
15) (Livro do aluno - SEDUC-SP-2025) No esquema apresentado, temos um líquido em equilíbrio dentro de um recipiente fechado por uma tampa. Admitamos que o espaço que o espaço entre a região embaixo da tampa e a superfície do líquido seja preenchido com vácuo e que a massa específica do líquido seja de 1000 kg/m³. Qual ao valor da pressão no ponto P a 0,1 m de profundidade? Use g = 10 m/s².

Resolução:

O valor da pressão no ponto P é equivalente à pressão exercida pela camada líquida até a profundidade de 0,1 m, então:

P = µ ∙ g ∙ h = 1000 ∙ 10 ∙ 0,1 = 1000 Pa

16) (Livro do aluno - SEDUC-SP-2025 - UNIOESTE 2024) Em 18 de junho de 2023, o submersível Titan, da empresa de expedições OceanGate, sofreu um acidente no mar do Atlântico Norte, Canadá, quando levava uma expedição de cinco pessoas para ver o local do naufrágio do navio Titanic. Segundo as investigações do acidente, o casco do submersível não suportou a alta pressão na profundidade de 2500 metros, sofrendo uma implosão que causou a morte dos tripulantes.

Se, no local do acidente, a relação da pressão em função da profundidade no mar é a mostrada na figura abaixo, indique o valor CORRETO da pressão em 3800 metros abaixo da superfície, profundidade onde se encontram os destroços do Titanic. Use g = 10 m/s² (aceleração da gravidade).

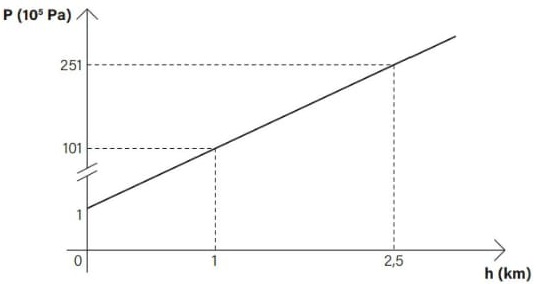
(A) 353 Pa

(B) 3,52 × 10⁵ Pa

(D) 350 × 10⁷ Pa

(E) 800 Pa

Resolução:

O valor da pressão sofrida por um ponto P qualquer na profundidade de 3800 metros é obtido pela soma da pressão hidrostática (da água) com a pressão atmosférica local. Sendo assim:

P_P = P_ÁGUA+ P_ATMOSFÉRICA

Pelo gráfico, notamos que, a cada 1000 metros de profundidade (1 km), temos o acréscimo de 101 ∙ 10⁵ Pa na pressão sofrida por um ponto P nessa situação. Do total dessa pressão, 100 ∙ 10⁵. Pa são devidos à pressão exercida pela água e 1 ∙ 10⁵ Pa, à ação da pressão atmosférica.

1 km → 100 ∙ 10⁵ Pa + 1 ∙ 10⁵ Pa (pressão atmosférica)

3,8 km → 380 ∙ 10⁵Pa + 1 ∙ 10⁵ Pa (pressão atmosférica)

Sendo assim, a pressão a 3800 metros de profundidade será:

P_P = 381 ∙ 10⁵ P_A → P_P = 3,81 ∙ 10⁷Pa

Alternativa: C

17) (Livro do aluno - SEDUC-SP-2025 - UEA 2021) Um dispositivo foi projetado para medir a velocidade do ar, baseando-se na diferença de pressão dentro de um tubo. Em determinada ocasião, conforme o ar em movimento entra pelo orifício direito do tubo, o êmbolo é empurrado para baixo, fazendo que o fluido no lado esquerdo do tubo suba 4 cm, como mostra a figura.

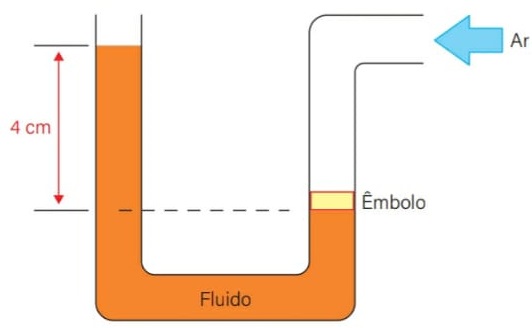
Sabendo que a densidade desse fluido é de 900 kg/m³, que a aceleração da gravidade é 10 m/s² e que o peso do êmbolo é desprezível, a diferença de pressão entre o nível do fluido na parte esquerda do tubo e o fluido sob o êmbolo, após ser empurrado para baixo, é de:

(A) 90 Pa

(B) 180 Pa

(D) 360 Pa

(E) 540 Pa

Resolução:

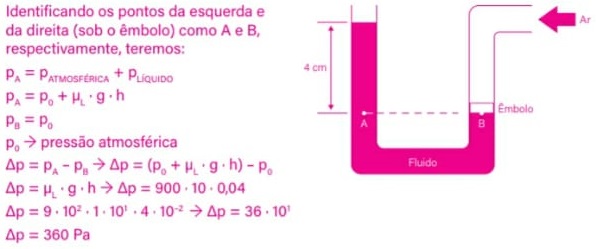
Alternativa: D

18) (Livro do aluno - SEDUC-SP-2025) Um tubo em U, aberto em ambos os ramos, contém dois líquidos imiscíveis em equilíbrio hidrostático, como mostra a figura. Calcule a densidade do líquido 2. Dados: 13 ‑ 1 6, / g cm .

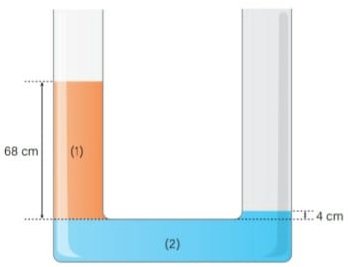
Resolução:

Para responder a essa questão, utilizaremos a seguinte expressão:

19) (Livro do aluno - SEDUC-SP-2025) Dois tubos em formato de U estão interligados e cheios de um líquido incompressível, conforme mostra a figura. Cada tubo tem um pistão que pode se mover verticalmente. O pistão menor tem área de 10 m², e o pistão maior tem área de 80 m².

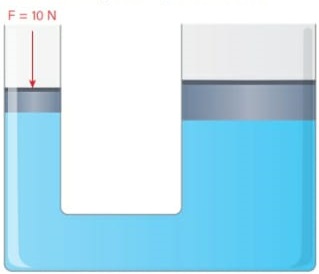
Sabendo que a intensidade da força aplicada no pistão menor é de 10 N, determine o valor da força transmitida para o pistão maior.

Resolução:

Para responder a essa questão, utilizaremos a seguinte expressão:

20) (Livro do aluno - SEDUC-SP-2025 - UERJ 2013 – Adaptada) Observe, na figura a seguir, a representação de uma prensa hidráulica na qual as forças F1

e F2 atuam, respectivamente, sobre os êmbolos dos cilindros I e II.

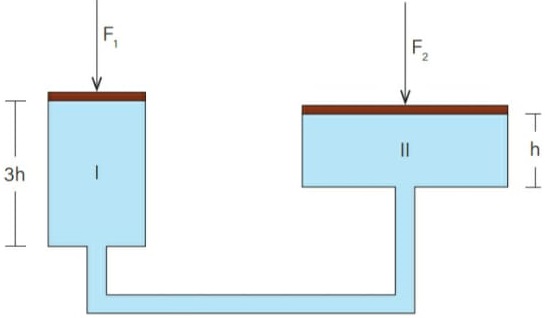
Admita que os cilindros estejam totalmente preenchidos por um líquido. O volume do cilindro II é igual a quatro vezes o volume do cilindro I, cuja altura é o triplo da altura do cilindro II.

A razão entre as intensidades das forças F2 e F1, quando o sistema está em equilíbrio, corresponde a:

(A) 12

(B) 6

(D) 4

(E) 2

Resolução:

Para resolvemos essa questão, precisamos recordar que o volume de um cilindro é determinado pelo produto entre a área da base pela altura. Assim, podemos dizer que:

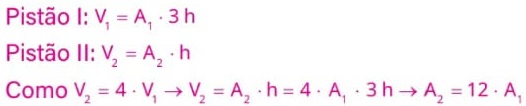
Agora que encontramos uma expressão que relaciona as áreas dos dois pistões, faremos:

Alternativa: A

21) (Livro do aluno - SEDUC-SP-2025) Um bloco com volume V_bloco = 0,83 m³ é colocado em um recipiente contendo um líquido. Sabendo que a densidade do líquido é μ_líquido = 2000 kg/m³, calcule a força de empuxo que o bloco sofre.

Resolução:

Considere g = 10m/s².

Para calcular o empuxo, faremos:

E = μ_f . f_d . g

O volume representado na equação é o volume do líquido deslocado, o qual também representa o volume do bloco, então, substituindo:

E = 2000 . 16 000 N

22) (Livro do aluno - SEDUC-SP-2025) Um bloco de madeira com densidade μ_bloco = 800 kg/m³ e volume V_bloco = 0,5 m³ é colocado em um tanque com água. Sabendo que a densidade da água é μ_{água =} 1000 kg/m³, calcule o empuxo que o bloco sofre.

Considere g = 10 m/s².

Resolução:

Para calcular o empuxo, faremos:

E = μ_f . f_d . g

E = 1000 . 0,5 . 10 = 5000 N

23)(Livro do aluno - SEDUC-SP-2025) Sabendo que a densidade da água é μ_água = 1000 kg/m³, calcule o empuxo que atua sobre a esfera. Considere π = 3 e g = 10 m/s².

Resolução:

Para calcular o empuxo, faremos:

E = μ_f . f_d . g

Mas, antes, precisaremos calcular o volume da esfera, então:

Substituindo, ficamos com:

E = 1000 . 0,004 . 10 = 40 N

24) (Livro do aluno - SEDUC-SP-2025 - UERJ 2016 – Adaptada) Uma barca para transportar automóveis entre as margens de um rio, quando vazia, tem volume igual a 100 m³ e massa igual a 4 . 10⁴ kg. Considere que todos os automóveis transportados tenham a mesma massa de 1,5 . 10³ kg e que a densidade da água seja de 10³ kg/m³. Qual o número máximo de automóveis que podem ser simultaneamente transportados pela barca?

Resolução:

Para que a barca flutue, o seu peso somado com o peso dos automóveis (P_total) deve ser igual ao empuxo:

E = P_total

Sendo m_c a massa de cada carro, m_b a massa da barca e n o número de automóveis, temos:

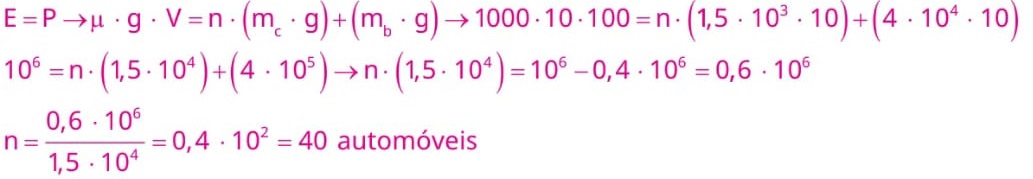
25) (Livro do aluno - SEDUC-SP-2025 - UFPR 2017 – Adaptada) Um objeto sólido com massa 600 g e volume 1 litro está parcialmente imerso em um líquido, de maneira que 80% do seu volume está submerso. Considerando a aceleração da gravidade igual a 10 m/s², determine a massa específica do líquido.

Resolução:

Para que o corpo flutue:

P = E

Como o volume que está submerso representa 80% do volume total, temos:

V_submerso = 0,8 . V . 1 = 0,8L

Substituindo, temos:

Continua...

topo