Professor Diminoi
INEQUACOES TRIGONOMETRICAS
Introdução
Quando encontramos função trigonométrica da incógnita ou função trigonométrica de alguma função da incógnita em pelo menos um dos membros de uma inequação, dizemos que esta inequação é trigonométrica.
Exemplos
1) sen x > 1/2 e sen2 x + tg 2 são inequações trigonométricas.
2) (sen 30º) . (x2 - 1) > 0
![]()
não são inequações trigonométricas.
Resolver uma inequação como f(x) < g(x), por exemplo, significa determinar o conjunto S dos números s, sendo s elemento do domínio de f e de g, tais que f(s) < g(s).
O conjunto S é chamado de conjunto solução da inequação e todo elemento de S é uma solução da inequação.
Assim, na inequação sen x > -1/2, os números![]() São algumas de suas soluções e os números
São algumas de suas soluções e os números![]() Não o são.
Não o são.
Resolução das inequações trigonométricas fundamentais
Quase todas as inequações trigonométricas, quando convenientemente tratadas e transformadas, podem ser reduzidas a pelo menos uma das inequações fundamentais. Vamos conhecê-las, a seguir, através de exemplos.
1º caso : sen x < sen a (sen x sen a)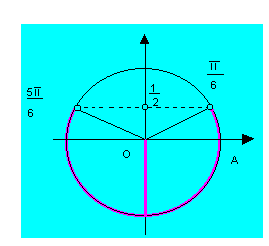 Por exemplo, ao resolvermos a inequação
Por exemplo, ao resolvermos a inequação![]() Encontramos, inicialmente,
Encontramos, inicialmente,![]() Que é uma solução particular no intervalo
Que é uma solução particular no intervalo![]() Acrescentando
Acrescentando![]() As extremidades dos intervalos encontrados, temos a solução geral em IR, que é:
As extremidades dos intervalos encontrados, temos a solução geral em IR, que é: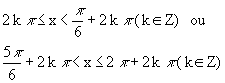
O conjunto solução é, portanto:
![]()
Por outro lado, se a inequação fosse
![]()
Então, bastaria incluir as extremidades de
![]()
E o conjunto solução seria:
![]()
2º caso: sen x > sen a (sen x sen a)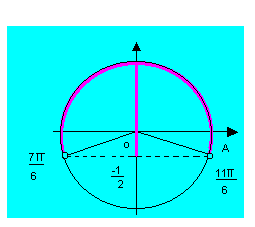 Por exemplo, ao resolvermos a inequação sen x > sem
Por exemplo, ao resolvermos a inequação sen x > sem
![]()
ou sen x > -1/2 encontramos, inicialmente,![]()
Que é uma uma solução particular no intervalo
![]()
Acrescentando
![]()
As extremidades dos intervalos encontrados, temos a solução geral em IR, que é:
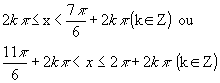
O conjunto solução é , portanto:
![]()
3º caso: cos x < cos a (cos x cos a)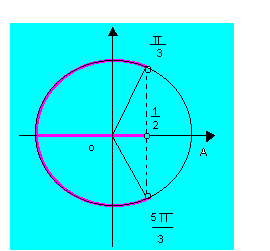 Por exemplo, ao resolvermos a inequação
Por exemplo, ao resolvermos a inequação
![]()
Encontramos, inicialmente,
![]()
Que é uma solução particular no intervalo
![]()
Acrescentando
![]()
As extremidades do intervalo encontrado, temos a solução geral em IR, que é:
![]()
O conjunto solução é, portanto:
![]()
Por outro lado, se a inequação fosse cos x cos
![]()
ou cos x![]() Então, bastaria incluir as extremidades de
Então, bastaria incluir as extremidades de
![]()
E o conjunto solução seria:
![]()
Resolução das inequações trigonométricas fundamentais (parte 2)
4º caso: cos x > cos a (cos x cos a)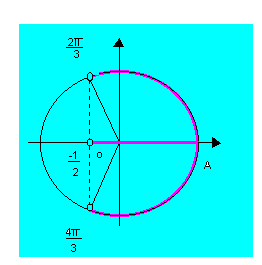 Por exemplo, ao resolvermos a inequação
Por exemplo, ao resolvermos a inequação
![]()
Encontramos, inicialmente,
![]()
Que é uma solução particular no intervalo
![]()
Acrescentando
![]()
As extremidades dos intervalos encontrados, temos o conjunto solução seguinte:
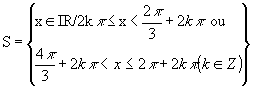
5º caso: tg x < tg a (tg x tg a)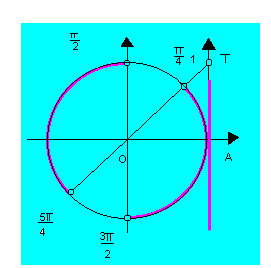 Por exemplo, ao resolvermos a inequação
Por exemplo, ao resolvermos a inequação
![]()
Encontramos, inicialmente,
![]()
Que é uma solução particular no intervalo
![]()
A solução geral em IR pode ser expressa por
![]()
O conjunto solução é, portanto:
![]()
6º caso: tg x > tg a ( tg x tg a)
Vamos estudar este último caso resolvendo a inequação tg x > tg
![]()
Exemplo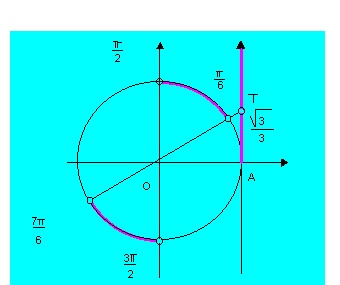
Então, na resolução da inequação
![]()
Encontramos, inicialmente
![]()
Que é uma solução particular no intervalo
![]()
A solução geral em IR pode ser expressa por
![]()
O conjunto solução é, portanto:
![]()
Continua ...






