Professor Diminoi
POTENCIAÇÃO
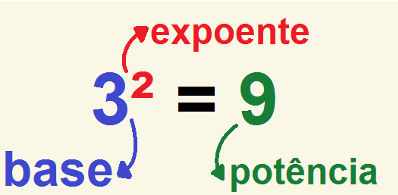
A potenciação (ou exponenciação) é uma das operações básicas no universo dos números naturais onde um dado número é multiplicado por ele mesmo, uma quantidade n de vezes.
Lembrando que para representar a soma de várias parcelas iguais, usamos a multiplicação, podemos recorrer à potenciação para expressar o produto de vários fatores iguais.
Propriedades das potências
Propriedades das potências podem ser usadas para ajudar no cálculo e na simplificação de expressões. As quatro operações matemática básicas são adição, subtração, multiplicação e divisão, entretanto, não são as únicas operações existentes.
Propriedades da potenciação
A potenciação possui oito propriedades mais importantes, com as quais é possível resolver quase todos os problemas envolvendo essa operação:
Expoente zero
Sempre que o expoente de uma potência for zero, independentemente do valor de sua base, o resultado dessa potência será igual a 1. Em outras palavras, sendo a pertencente ao conjunto dos números reais, com a ≠ 0:
a0 = 1
Expoente um
Sempre que o expoente de uma potência for 1, independentemente do valor de sua base, o resultado dessa potência sempre será igual ao valor da base. Em outras palavras, sendo a pertencente ao conjunto dos números reais, com a ≠ 0:
a1 = a
Potência de potência
Isso ocorre quando a base de uma potência é outra potência. Nesse caso, multiplicamos os expoentes e conservamos a base.
Assim, se a for pertencente ao conjunto dos números reais e diferente de zero, m e n pertencentes ao conjunto dos números naturais, teremos:
(an)m = an·m
Produto de potência de mesma base
Conserva-se a base e soma-se ou subtrai-se os expoentes.
Exemplos:
am . an = am + n
Divisão de potência de mesma base
Devemos conservar a base e subtrair os expoentes.
Exemplo:
am / an = am - n
Base negativa (observe cada caso)
Quando a base e negativa e o expoente é impar o resultado é sempre negativo.
(-2)3 = -8
Quando a base e negativa e o expoente é par, o resultado é sempre positivo.
(-2)2 = 4
Potência de potência
Nesse caso, devemos conservar a base e multiplicar os expoentes.
Exemplo:
(am)n = am . n
Potência de um produto
Devemos atribuir o expoente aos fatores do produto.
Exemplo:
(a . b)n = an . bn
Divisão de potência de mesmo expoente
Numa divisão com expoente devemos elevar tanto o numerador como denominador ao expoente.
Exemplos:
a) (a/b)n = na / bn
b) (5/3)3 = 53 / 33 = 125 / 27
Multiplicação de potência om o mesmo expoente.
Quando multiplicamos um expoente com a mesma expoente podemos conservar o expoente e multiplicar as bases.
Exemplo:
(an . bn) = ( a . b)n
(32 . 22) = (3 . 2)2 = 62 = 36
Exemplos:
(a) 23 . 2-2 = 23 + (-2) = 21
(b) 5-3 . 2-3 = (5 . 2)-3 = 10-3
(c) 52 / 5-5 = 52-(-3) = 52 + 3 = 55
(d) 5-2 / 3-2 = (5/3)-2 = (3/5)2 = 9/25
(e) (32)-1 = 32 . (-1) = 3-2 = (1/3)2 = 1/9
Expoentes negativos
Quando um expoente é negativo, seu sinal poderá ser invertido desde que, para isso, a base da potência também seja invertida. Assim, caso a pertença aos números reais, e n seja pertencente aos números naturais e diferente de zero, teremos:
a-n = ( 1/a)n
Potência com expoente fracionário
Quando o expoente é fracionário, podemos transformar essa potência em uma radiciação.
![]()
Exemplo:
![]()
Potências com expoente racional
Caso uma potência apresente base a e expoente m/n, ela poderá ser reescrita como a raiz enésima de a elevado a m. Assim, matematicamente, teremos:
![]()
Quadrados perfeitos
Vamos calcular os quadrados dos primeiros números naturais:
0² = 0
1² = 1
2² = 4
3² = 9
4² = 16
5² = 25
6² = 36
7² = 49
Os números : 0,1,4,9,16,25,36,49,..........chamam-se quadrado perfeito. Somente esses números possuem raiz quadrada exata em IN.
QUESTÕES RESOLVIDAS
01) Simplificando a expressão (a3 · b-7 · a2) / (a2 · b-4)2, encontraremos:
(A) a/b
(B) ab
(C) b
(D) a²b
Resolução:
Letra B. Usando as propriedades de multiplicação de potência de mesma base, potência de potência e divisão de potência de mesma base, temos que:
(a³ . b-7 · a²) / (a² . b-4)²
(a3 + 2 . b-5 ) / (a22 . b-4 . 2)
(a5 · b-7 ) / (a4 . b-8)
a5-4 · b-7-(-8)
a1 . b-7+8
a1 . b1
a . b
Alternativa: B
02) (IFG) O valor da expressão aritmética abaixo é equivalente a:
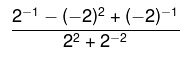
(A) 8/17
(B) -8/17
(C) 16/17
(D) -16/17
Resolução:
Resolvendo primeiro o numerador, temos que:
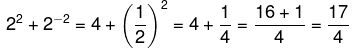
Agora vamos resolver o denominador:
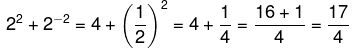
Como temos uma divisão do numerador pelo denominador, vamos multiplicar pelo inverso da segunda fração:
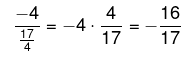
Alternativa: D
03) Ao término de uma avalição de matemática os colegas da classe estavam discutindo o resultado de uma questão que pedia para calcular 323/5 – 272/3. Entre os diferentes resultados comentados por eles, o correto é
(A) (1)1/15
(B) −1.
(C) 51/2
(D) 51/15
Resolução:
Fatorando 32 e 27 respectivamente, têm-se ( 25 )3/5 – (33 )2/3
Aplicando a propriedade da potência de potência temos 215/5 – 36/3
Simplificando as frações dos expoentes obtêm-se 23 − 32 = 8 − 9 = −1.
Alternativa: B
04) Qual o valor da expressão abaixo?
![]()
(A) 3
(B) 32
(C) 10,2
(D) 4996
(E) 0,72
Resolução:
Sabemos que
23 = 8
38 = 6561
54 = 652
Assim, 6561 – 652 = 5936 (numerador)
44 = 256
203 = 8000
Assim, 256 + 8000 = 8256 (denominador)
Fazendo a divisão do numerador pelo denominador temos:
5936 / 8256 = 0,72
Alternativa: E
05) valor da expressão 21/4 . 23/4 + 31/3 . 33/2 é:
(A) 2 3 + 3
(B) 11
(C) 13
(D) 85
Resolução:
Observa-se que se têm uma expressão numérica na qual cada parcela é um produto de potência de mesma base com expoentes fracionários. Primeiramente devemos aplicar a propriedade do produto de potências de mesma base, calcular a potenciação resultante e, em seguida, resolver a adição correspondente.
2(1+3) /4 + 3(1+3) /2
21 + 32
2 + 9 = 11
Alternativa B
07) (UFRGS - 2013) Um adulto humano saudável abriga cerca de 100 bilhões de bactérias, somente em seu trato digestivo. Esse número de bactérias pode ser escrito como
(A) 109
(B) 1010
(C) 1011
(D) 1012
(E) 1013
Resolução:
Um bilhão é a mesma coisa que mil milhões, ou seja, 1000 . 1 000 000 = 1 000 000 000.
100 bilhões é igual a 100 . 1 000 000 000 = 100 000 000 000.
Números grandes como o dessa questão podem ser escritos em notação científica, cuja escrita segue o padrão N . 10n, onde N é um número menor que 10 e maior ou igual a 1. Já o expoente da base 10 é o número de casas decimais que a vírgula "andou" para obtermos o valor de N.
Observe que para chegar até ao número 11 foi preciso "andar" 11 casas decimais. Portanto, temos a potência 1011 como resultado.
Alternativa: C
08) (Senai) Considerando que cada aula dura 50 minutos, o intervalo de tempo de duas aulas seguidas, expresso em segundos, é de:
(A) 3,0 . 10²
(B) 3,0 . 10³
(C) 3,6 . 10³
(D) 6,0 . 10³
(E) 7,2 . 10³
Alternativa: D
09) (ENEM) A gripe é uma infecção respiratória aguda de curta duração causada pelo vírus influenza. Ao entrar no nosso organismo pelo nariz, esse vírus multiplica-se, disseminando-se para a garganta e demais partes das vias respiratórias, incluindo os pulmões. O vírus influenza é uma partícula esférica que tem um diâmetro interno de 0,00011 mm.

Em notação científica, o diâmetro interno do vírus influenza, em mm, é
(A) 1,1 × 10-1
(B) 1,1 × 10-2
(C) 1,1 × 10-3
(D) 1,1 × 10-4
(E) 1,1 × 10-5
Alternativa: D
RADICIAÇÃO

É a operação matemática inversa à potenciação.
Enquanto a potenciação é uma multiplicação na qual todos os fatores são iguais, a radiciação procura descobrir que fatores são esses, dando o resultado dessa multiplicação
Propriedades da radiciação
A raiz enésima de um número elevado a n é igual a esse mesmo número:
![]()
Índice e expoente do radicando podem ser multiplicados ou divididos pelo mesmo número. Assim, dados os números reais a, m, n e p, teremos:
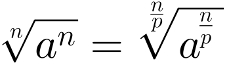
Para simplificar a raiz de uma raiz, basta multiplicar seus índices. Matematicamente, isso pode ser representado da seguinte forma:
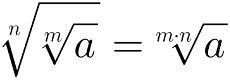
A raiz enésima do produto é igual ao produto das raízes enésimas:
![]()
A raiz enésima da razão é igual à razão das raízes enésimas, ou seja:
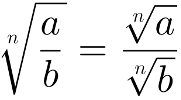
Exemplo:
Escreva na forma simplificada a raiz quadrada de 360.
Vamos realizar a fatoração de 360 utilizando o método das divisões sucessivas.
360|2→ 2 é o menor número primo que divide 360;
180|2→ 2 é o menor número primo que divide 180;
90|2 → 2 é o menor número primo que divide 90;
45|3 → 3 é o menor número primo que divide 45;
15|3 → 3 é o menor número primo que divide 15;
5|5 → 5 é o menor número primo que divide 5.
1|
Sendo assim, temos que 360= 2 · 2 · 2 · 3 · 3 · 5.
Como o nosso objetivo é simplificar uma raiz quadrada, vamos agrupar esses fatores de 2 em 2, logo, podemos reescrever 200 como:
360= 2² . 2 . 3² . 5
Assim, podemos reescrever a raiz de 360, utilizaremos a primeira propriedade para simplificar a raiz quadrada, o que significa que os termos que estão elevados ao quadrado sairão do radical, e os que não estão permanecem dentro do radical:
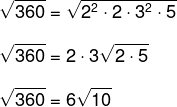
QUESTÕES RAIZ QUADRADA
01) Decomponha os números abaixo em fatores primos e encontre as suas respectivas raízes.
a) √625
Resolução:
625|5
125|5
25|5
5|5
1|
![]()
b) √100
Resolução:
100|2
50|2
25|5
5|5
1|
![]()
c) √81
Resolução:
81|3
27|3
9|3
3|3
1|
![]()
02) (Cefet/RJ 2014) Por qual número devemos multiplicar o número 0,75 de modo que a raiz quadrada do produto obtido seja igual a 45?
(A) 2700
(B) 2800
(C) 2900
(D) 3000
Resolução:
A área de um quadrada é igual ao lado ao quadrado, então, para encontrar o valor do lado, vamos calcular a raiz quadrada da área do terreno.
Para calcular a raiz quadrada de 196, vamos fatorar esse número:
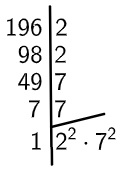
Então, temos que:
![]()
Alternativa: C
05) O valor da expressão algébrica a seguir é: √4+√16 – √25 ×√9
(A) – 9.
(B) – 6.
(C) – 5.
(D) – 4.
(E) – 2.
Resolução:
Resolvendo a expressão, temos que:
√4+√16 – √25 ×√9
2 + 4 – 5 × 3
6 – 15
– 9
Alternativa: A
06) Qual é a raiz quadrada de 5184?
(A) 42
(B) 58
(C) 68
(D) 72
(E) 88
Resolução:
Fatorando 5184, temos que:

Então, podemos fazer o seguinte cálculo:
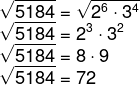
Alternativa: D
07) (Ethos concursos) A raiz quadrada de um número é uma importante operação matemática, assim como a adição, a subtração, a multiplicação e a divisão. Somente alguns números possuem raiz quadrada, são aqueles considerados quadrados perfeitos. Sendo assim, calcule a raiz quadrada de 625 e assinale a alternativa CORRETA.
(A) 35
(B) 24
(C) 25
(D) 17
(E) 49
Resolução:
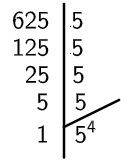
Então, temos que:
√625 = √54
√625 = 5²
√625 = 25
Alternativa: C
08) Sabendo que √x = 9, então o valor da terça parte de x é:
(A) 81
(B) 72
(C) 36
(D) 27
(E) 9
Resolução:
√x = 9
√x² = 9²
x = 81
Alternativa: A
09) (PM Piauí 2009 – Nucepe) A expressão √18 + √50 é equivalente:
(A) 2√2
(B) 3√2
(C) 8√2
(D 15√2
(E) 8√3
Resolução
Vamos fatorar os números dentro dos radicais:
18 = 2.3²
50 = 2.5²
Resolvendo a expressão:
√18 + √50
√(2.3²) + √(2.5²)
3√2 + 5√2
8√2
Resposta: C
Continuação ...
Continua...






