Professor Diminoi

ELETRICIDADE

A Eletricidade é a área da Física responsável pelo estudo de fenômenos associados a cargas elétricas. O termo eletricidade originou-se da palavra eléktron, que é derivada do nome grego âmbar. 

O que são os raios?
As nuvens de tempestades, chamadas de cumulonimbus, são carregadas de partículas elétricas. Quando há um acúmulo excessivo delas, ocorre a perda da capacidade isolante e surgem as descargas elétricas que formam os raios.

O que acontece quando o avião é atingido por um raio durante o voo?
Ao sobrevoar uma região com tempestade, o avião corre o risco de ser atingido por um raio. Quando isso acontece, a barulho e a luz gerados pelo raio pode causar apreensão nos passageiros. Embora pareça algo extremamente crítico para o voo, as aeronaves são fabricadas para aguentar o impacto de uma descarga elétrica sem sofrer danos nem colocar em risco a segurança do voo.
Segundo o engenheiro sênior Edward J. Rupke, em artigo publicado no site Scientific American, estima-se que, em média, um avião comercial em operação nos Estados Unidos seja atingido pelo menos uma vez por ano por um raio.

Benjamin Franklin -   Em 15 de junho, Franklin pode ter realizado o experimento da pipa na Filadélfia, com sucesso ao extrair faíscas de uma nuvem. A experiência não foi escrita com crédito até a divulgação por Joseph Priestley. Cientistas, como Georg Wilhelm Richmann, foram eletrocutados em testes seguintes ao experimento de Franklin.
.
Neste sentido se convém dizer que Ben Franklin não descobriu a eletricidade anexando chave à pipa durante tempestade em 1752. Na realidade, a eletricidade já havia sido descoberto anos antes. O próprio Franklin se tornou interessado ao fenômeno elétrico no ano de 1746. Na prática durante a experiência estava apenas tentando provar que o raio era de natureza elétrica, conforme afirma o The Franklin Institute.


Modelo atômico / Modelo de Rutherford-Bohr – Se assemelha ao modelo do Sistema Solar, eu que o Sol ocupa o centro do Sistema e os planetas giram em torno dele. Por essa razão também é chamado de modelo planetário de átomo.

Segundo esse modelo, cada átomo tem duas regiões:

Núcleo - É a região central do átomo onde ficam os prótons (carga positiva +) e os nêutrons (não possuem carga)

Eletrosfera - É a região em torno do núcleo no qual orbitam os elétrons (canga negativa -).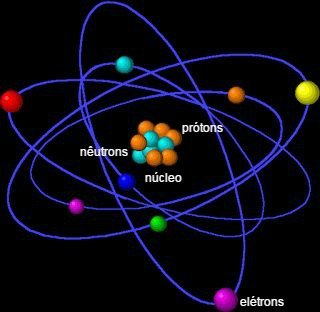
Atração e repulsão – Cargas de sinais diferentes se atraem e cargas de sinais iguais se repelem.
         
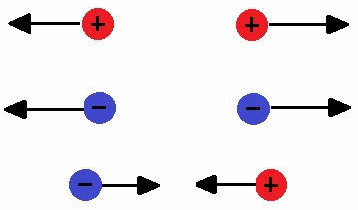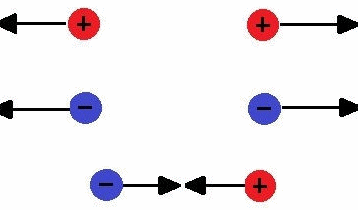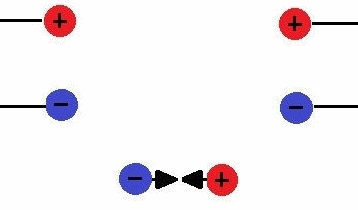
Carga elétrica É a propriedade das partículas subatômicas que determina as interações eletromagnéticas dessas. Matéria eletricamente carregada produz, e é influenciada por, campos eletromagnéticos. A unidade de carga elétrica no SI (Sistema Internacional de Unidades): ampère segundo (A.s) , unidade também denominada coulomb (C).
Q = quantidade de carga (C)
n = quantidade (números) de elétrons
e = 1,6 . 10^-19C  (carga elementar do elétron (-) ou do próton (+))

Os submúltiplos do Coulomb - Quando falamos em 1,0C (Coulomb), em relação à quantidade de energia, devemos saber que essa energia é totalmente elevada em um simples ponto material. Para que possamos reprimir essa energia, precisaríamos de uma esfera metálica bem grande, por causa da repulsão que existe entre as cargas. Consequentemente os submúltiplos do Coulomb tiveram que ser usados de forma experimental.

Submúltiplos do Coulomb
1 microcoulomb 1µC = 10^-6C
1 nanocoulomb 1nC = 10^-9C
1 picocoulomb 1 pC = 10^-12C

Observação: normalmente, em livros ou em simulados, nunca vêm escritos os prefixos micros, nano ou pico sempre irá encontrar da seguinte forma:
1 µ = 10^-6
1n = 10^-9
1p = 10^-12

RESOLVIDA - CARAGA ELÉTRICA
01) Usando a quantização das cargas elétricas, representada pela fórmula anterior, podemos calcular qual deve ser a quantidade de elétrons, em falta ou em excesso, necessária para produzir uma carga elétrica total de 1,0 C em um corpo:
Resolução:
Q = n . e
Q = 1,0 = n .  1,6 .  10^-19
n =        1, 0       
        1,6 . 10^-19
n = 6,25 . 10¹⁸ elétrons

02) Durante um processo de eletrização, um corpo recebe uma quantidade de 2,0.10¹⁵ elétrons, tornando-se eletricamente carregado, com carga elétrica de:

(A) 3,2.10^-4 C
(B) 1,6.10^-18 C
(C) 3,2.10^-5 C
(D) 0,32.10^-5 C
(E) 320.10^-1 C
Resolução:
Q = n . e
Q = 2,0 . 10¹⁵ . 1,6 .  10^-19
Q = 3,25 . 10^-4 C

03) Um corpo apresenta 1,2.10³ elétrons a menos que prótons. Determine o sinal e o módulo da carga elétrica desse corpo.

(A) Negativa, 0,92.10^-13 C
(B) Positiva, 1,92.10^-13 C
(C) Negativa, 1,92.10^-16 C
(D) Positiva, 1,92.10^-16 C
(E) Negativa, 1,6.10^-14 C
Resolução:
Q = n . e
Q = 1,2 . 10³ . 1,6 .  10^-19
Q = 1,92 . 10^-16 C
Alternativa: D

04) Determine qual é a quantidade de elétrons que precisam ser retirados de um corpo para que sua carga elétrica seja de 6,4 C.

(A) 4,0.10¹⁵ elétrons
(B) 4,0.10¹⁹ elétrons
(C) 2,5.10¹⁸ elétrons
(D) 3,5.10²¹ elétrons
(E) 1,6.10¹² elétrons
Resolução:
Q = n . e
6,4 = n . 1,6 .  10^-19
n =       6,4     
        1,6 . 10^-16 C
n = 1,0 . 10¹⁹ elétrons
Alternativa: B

05) (Unitau-SP) Uma esfera metálica tem carga elétrica negativa de valor igual a 3,2 . 10^-4 C. Sendo a carga do elétron igual a 1,6 10^-19 C, pode-se concluir que a esfera contém:

(A) 2 . 10¹⁵elétrons
(B) 200 elétrons
(C) um excesso de 2. 10¹⁵elétrons
(D) 2 . 10¹⁰ elétrons
(E) um excesso de 2 . 10¹⁰ elétrons
Resolução:
Q = n . e
3,2 . 10 ^-4 = n . 1,6 . 10^-19
n = 3,2 . 10^-4
       1,6 . 10^-19
n = 2 . 10¹⁵ elétrons
Como o corpo tem carga elétrica negativa, ele possui excesso de elétrons.
Alternativa: C

07) Calcule a carga elétrica de um corpo que possui excesso de 24 . 10¹² elétrons. Considere o módulo da carga elementar igual a 1,6 . 10^-19 C.
Resolução:
Q = n . e
Q = 24 . 10¹² . ( - 1,6 . 10^-19)
Q =  - 38,4 .10^-7 C

07) Julgue os itens a seguir:

1 - Um corpo que tem carga positiva possui mais prótons do que elétrons;
2 - Dizemos que um corpo é neutro quando ele possui o mesmo número de prótons e de elétrons;
3 -O núcleo do átomo é formado por elétrons e prótons.

Estão corretas as afirmativas:

(A) 1 e 2 apenas
(B) 2 e 3 apenas
(C) 1 e 3 apenas
(D) 1, 2 e 3
(E) nenhuma.
Resolução:
Afirmativa 1 – correta. Quando um corpo perde elétrons, ele passa a ter maior número de prótons, portanto fica com carga positiva.
Afirmativa 2 – correta. Os corpos neutros possuem a mesma quantidade de prótons e de elétrons.
Afirmativa 3 – incorreta. O núcleo atômico é formado por prótons e nêutrons.
Alternativa: A.

08) Calcule a carga de um corpo que possui 5.10¹⁹ prótons e 4.10¹⁹ elétrons.
Resolução:
Para calcular a carga elétrica de um corpo, utiliza-se a seguinte expressão, considerando que a carga elementar possui o valor de 1,6 . 10^-19C:
Q = n . e
Q = (5.1019- 4.1019).1,6.10-19
Q = 1019. 1,6.10-19
Q = 1,6 C

ELETRIZAÇÃO

É o processo pelo qual os corpos perdem ou ganham elétrons.
Observação: um corpo não ganha nem perde prótons, mas elétrons.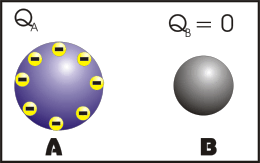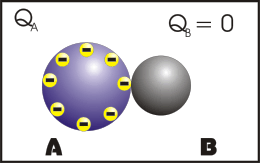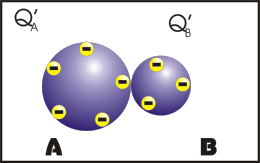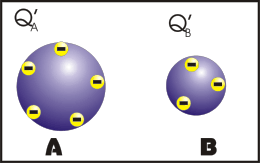
Eletrização por Atrito
esse processo, os corpos se tocam e são atritados (esfregados) após a ocorrência desse atrito, os coros ficam com cargas de módulos iguais em intensidade, porém de sinais contrários.
Eletrização por Contato
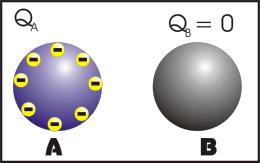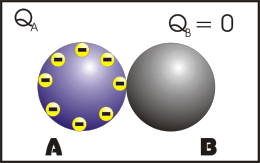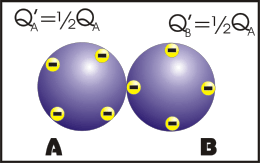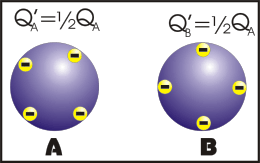
Nesse processo, os corpos se tocam e após o contato, os corpos ficam com cargas de mesmo sinal e se os corpos forem exatamente idênticos, eles irão ter o mesmo módulo de carga elétrica.

Observação: a primeira animação (eletrização) ocorre entre corpos de tamanhos diferentes e a segunda animação (eletrização) ocorre entre corpos de tamanhos iguais (corpos idênticos). Apos observar atentamente este processo que comentário você fará?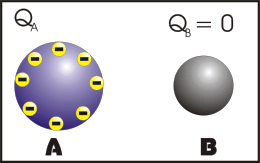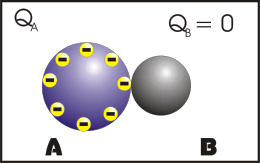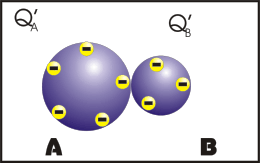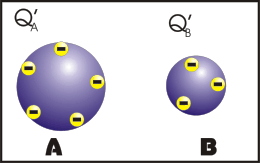
 
Eletrização por Indução
Nesse processo, os corpos não se tocam, apenas ficam próximos um do outro portanto, não ocorrem transferência de eletros de um corpo para o outro. Enquanto os corpos estiverem próximos um do outro ocorre um deslocamento de cagas no interior de cada corpo e ao se afastarem o deslocamento se desfaz ficando os corpos com cargas de sinais diferentes.

Quantidade de carga elétrica

Q = n . e

Q = a carga elétrica total de um corpo (C)
n = o número de elétrons perdidos ou recebidos
e = a carga elementar (1,6 . 10-19 C).

RESOLVIDAS / PROCESSO DE ELETRIZAÇÃO
09) (UFRGS) Uma carga negativa Q é aproximada de uma esfera condutora isolada, eletricamente neutra. A esfera é, então, aterrada com um fio condutor. Assinale a alternativa que preenche corretamente as lacunas do enunciado abaixo, na ordem em que aparecem.
Se a carga Q for afastada para bem longe enquanto a esfera está aterrada, e, a seguir, for desfeito o aterramento, a esfera ficará ________ . Por outro lado, se primeiramente o aterramento for desfeito e, depois, a carga Q for afastada, a esfera ficará ________ .

(A) eletricamente neutra – positivamente carregada
(B) eletricamente neutra – negativamente carregada
(C) positivamente carregada – eletricamente neutra
(D) positivamente carregada – negativamente carregada
(E) negativamente carregada – positivamente carregada
Resolução:
Se a carga Q for afastada para bem longe enquanto a esfera está aterrada, e, a seguir, for desfeito o aterramento, a esfera ficará eletricamente neutra. Por outro lado, se primeiramente o aterramento for desfeito e, depois, a carga Q for afastada, a esfera ficará positivamente carregada.
Alternativa: A

10) Quando um corpo exerce sobre o outro uma força elétrica de atração, pode-se afirmar que:

(A) um tem carga positiva e o outro, negativa.
(B) pelo menos um deles está carregado eletricamente.
(C) um possui maior carga que o outro.
(D) os dois são condutores.
(E) pelo menos um dos corpos conduz eletricidade .
Resolução:
Alternativa correta: letra “b”, pois para ocorrer à aproximação entre os corpos, pelo menos um deles precisa estar eletrizado.
Alternativa: B

11) (UFRGS - 2014) Considere dois balões de borracha, A e B. O balão B tem excesso de cargas negativas; o balão A, ao ser aproximado do balão B, é repelido por ele. Por outro lado, quando certo objeto metálico isolado é aproximado do balão A, este é atraído pelo objeto.
Assinale a alternativa que preenche corretamente as lacunas do enunciado abaixo, na ordem em que aparecem.
A respeito das cargas elétricas líquidas no balão A e no objeto, pode-se concluir que o balão A só pode _______ e que o objeto só pode _______ .

(A) ter excesso de cargas negativas – ter excesso de cargas positivas
(B) ter excesso de cargas negativas – ter excesso de cargas positivas ou estar eletricamente neutro
(C) ter excesso de cargas negativas – estar eletricamente neutro
(D) estar eletricamente neutro – ter excesso de cargas positivas ou estar eletricamente neutro
(E) estar eletricamente neutro – ter excesso de cargas positivas
Resolução:
Alternativa: b) ter excesso de cargas negativas – ter excesso de cargas positivas ou estar eletricamente neutro
Quando dois corpos estão carregados eletricamente com cargas de sinais contrários, ao se aproximarem surgirá entre eles uma força de atração.
Ao contrário, se suas cargas tiverem mesmo sinal, a força será de repulsão. Quando um corpo neutro se aproxima de um corpo eletrizado, a força entre eles será de atração, independente do sinal da carga.
Sendo assim, como o balão A foi repelido pelo balão B, sua carga será igual a de B, ou seja, possui excesso de cargas negativas.
Agora que sabemos a carga do balão A, podemos descobrir a carga do objeto. Como a força é atrativa, então temos duas possibilidades: o objeto pode ser neutro ou apresentar carga contrária do balão A.
Desta forma, o objeto pode estar neutro ou carregado positivamente.
Alternativa: B

12) (Enem - 2010) Duas irmãs que dividem o meso quarto de estudos combinaram de comprar duas caixas com tampas para guardarem seus pertences dentro de suas caixas, evitando, assim, a bagunça sobre a mesa de estudos. Uma delas comprou uma metálica, e a outra, uma caixa de madeira de área e espessura lateral diferentes, para facilitar a identificação. Um dia as meninas foram estudar para a prova de Física e, ao se acomodarem na mesa de estudos, guardaram seus celulares ligados dentro de suas caixas. Ao longo desse dia, uma delas recebeu ligações telefônicas, enquanto os amigos da outra tentavam ligar e recebiam a mensagem de que o celular estava fora da área de cobertura ou desligado.
Para explicar essa situação, um físico deveria afirmar que o material da caixa, cujo telefone celular não recebeu as ligações é de

(A) madeira, e o telefone não funcionava porque a madeira não é um bom condutor de eletricidade.
(B) metal, e o telefone não funcionava devido à blindagem eletrostática que o metal proporcionava.
(C) metal, e o telefone não funcionava porque o metal refletia todo tipo de radiação que nele incidia.
(D) metal, e o telefone não funcionava porque a área lateral da caixa de metal era maior.
(E) madeira, e o telefone não funcionava porque a espessura desta caixa era maior que a espessura da caixa de metal.
Resolução:
O metal, e o telefone não funcionava devido à blindagem eletrostática que o metal proporcionava.
Os materiais metálicos são bons condutores de cargas, sendo assim, em uma caixa de metal os elétrons livres ficarão distribuídos na sua parte externa.
Dentro da caixa o valor do campo elétrico é nulo. Este fato é chamado de blindagem eletrostática e foi comprovado por Michael Faraday, em uma experiência que ficou conhecida como gaiola de Faraday.
Alternativa: B

13) (UFPel) Em relação à eletrização de um corpo, analise as afirmativas a seguir.
I. Se um corpo neutro perder elétrons, ele fica eletrizado positivamente;
II. Atritando-se um bastão de vidro com uma flanela, ambos inicialmente neutros, eles se eletrizam com cargas iguais;
III. O fenômeno da indução eletrostática consiste na separação de cargas no induzido pela presença do indutor eletrizado;
IV. Aproximando-se um condutor eletrizado negativamente de outro neutro, sem tocá-lo, este permanece com carga total nula, sendo, no entanto, atraído pelo eletrizado.
V. Um corpo carregado pode repelir um corpo neutro.
Estão corretas
(A) apenas a I, a II e a IV.
(B) apenas a I, a III e a IV.
(C) apenas a I, a IV e a V.
(D) apenas a II e a IV.
(E) apenas a II, a III e a V.
Resolução:
II – ERRADA. Após a eletrização por atrito, os corpos atritados sempre adquirem cargas de sinais opostos.
Alternativa: B

14) A respeito dos processos de eletrização, marque a alternativa incorreta:
(A) Após a eletrização por contato, os corpos terão cargas elétricas de mesmo sinal.
(B) Na eletrização por indução, o corpo que inicia o processo já eletrizado é denominado de (indutor.
(C) Ao atritar duas canetas compostas de polietileno, ambas ficam eletrizadas negativamente.
(D) A série triboelétrica é aplicada à eletrização por atrito.
(E) Após a eletrização por indução, o corpo induzido apresenta carga elétrica de sinal oposto à carga do indutor.
Resolução:
Só ocorre eletrização por atrito com a fricção de objetos constituídos de materiais diferentes.
Alternativa: C

15) Um estudante atrita um pente de plástico em seu cabelo e aproxima-o de um filete de água, que imediatamente se encurva na direção do pente. Marque a alternativa que explica de forma correta o motivo pelo qual isso ocorre.
(A) O fenômeno é possível porque a água é um condutor universal.
(B) Após o atrito, o pente adquire a mesma carga elétrica da água, por isso, o filete é atraído.
(C) As cargas elétricas em excesso no pente atraem as cargas de mesmo sinal da água, fazendo com que o filete sofra deflexão.
(D) As cargas elétricas em excesso no pente atraem as cargas de sinal oposto da água, fazendo com que o filete sofra deflexão.
(E) Todas as alternativas estão incorretas.
Resolução:
Após o atrito, o pente fica eletrizado. Aproximando-o da água, as cargas de sinal oposto que compõem o líquido são atraídas pelo pente, o que causa uma leve deflexão do fio de água.
Alternativa: D

16) Se um corpo neutro é colocado em contato com um corpo eletrizado negativamente, ou seja, com excesso de elétrons, pode-se afirmar que:
(A) Ele permanece neutro;
(B) Adquire carga positiva;
(C) Adquire carga negativa;
(D) Neutraliza eletricamente o outro corpo.
Resolução:
Quando um corpo neutro é colocado em contato com um corpo carregado eletricamente, as cargas do corpo carregado passam para o neutro. Dessa forma, ambos ficam carregados com cargas iguais. No caso do exercício, como se trata de excesso de elétrons, após o contato, ambos ficarão com carga negativa.
Alternativa: C

17) (UFMT – MG) Da palavra grega elektron derivam os termos eletrização e eletricidade, entre outros. Analise as afirmativas sobre alguns conceitos da eletrostática.
I. A carga elétrica de um sistema eletricamente isolado é constante, isto é, conserva-se.
II. Um objeto neutro, ao perder elétrons, fica eletrizado positivamente;
III. Ao se eletrizar um corpo neutro, por contato, este fica com carga de sinal contrário à daquele que o eletrizou.
É correto o contido em:
(A) I apenas.
(B) I e II, apenas.
(C) I e III, apenas.
(D) II e III, apenas.
(E) I, II e III.
Resolução:
e acordo com o princípio da conservação de cargas, a soma algébrica das cargas elétricas de um sistema isolado é constante. Portanto, I está correta.
Um corpo é neutro quando possui a mesma quantidade de prótons e elétrons. Quando um objeto neutro perde elétrons, ele passa a ter mais prótons, ou seja, excesso de cargas positivas. Pode-se concluir então que ele fica eletrizado positivamente. Assim, II também está correta.
Quando um corpo neutro é eletrizado por contato, ele adquire carga de mesmo sinal à do corpo que o eletrizou. Tendo por base esse conceito, a alternativa III é incorreta.
Alternativa: B

18) (Livro do Aluno - SEDUC/2026 - (FUVEST 2021) Dois balões negativamente carregados são utilizados para induzir cargas em latas metálicas, alinhadas e em contato, que, inicialmente, estavam eletricamente neutras.

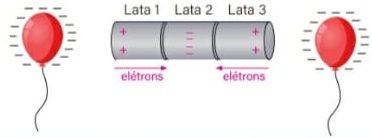
Note e anote: o contato entre dois objetos metálicos permite a passagem de cargas elétricas entre um e outro. Suponha que o ar no entorno seja um isolante perfeito.
Conforme mostrado na figura, os balões estão próximos, mas jamais chegam a tocar as latas. Nessa configuração, as latas 1, 2 e 3 terão, respectivamente, carga total:

(A) 1: zero; 2: negativa; 3: zero.
(B) 1: positiva; 2: zero; 3: positiva.
(C) 1: zero; 2: positiva; 3: zero.
(D) 1: positiva; 2: negativa; 3: positiva.
(E) 1: zero; 2: zero; 3: zero.
Resolução:
A carga total do sistema, antes das trocas de cargas entre os corpos, era de:
Q1 + Q2 + Q3 = - 2 μC + 5 μC - 4 μC = -1μC
Após trocarem cargas entre si, temos:
Q’1 = 1 μC e Q’2 = 3 μC.
Assim, como o sistema é eletricamente isolado, vamos calcular o valor de Q’3:
Q’1 + Q’2 + Q’3 = -1μC
Q’3 = -5 μC
O problema também pede a quantidade de elétrons recebida ou cedida pelo corpo 2. Assim, temos:
Q = ± n ∙ e
-2 ∙ 10-6 C = n · (-1,6 ∙ 10-19 C)
n = 1,25 ∙ 1013 elétrons
Alternativa: B

19) (Livro do Aluno - SEDUC/2026 - (UNICENTRO 2017) Três corpos eletrizados inicialmente com carga Q1 = -2 μC, Q2 = 5 μC e Q3 = -4 μC localizam-se em um sistema eletricamente isolado.
Após trocarem cargas entre si, os corpos 1 e 2 apresentam as cargas
Q'1 = 1 μC e Q'2 = 3 μC, respectivamente.
Qual a carga final do corpo 3 (Q'3)?
Qual o número de elétrons cedidos ou recebidos pelo corpo 2?
(Dado 1 μC = 10^-6 C)

(A) -2 μC e 1,50 . 10¹³ elétrons.
(B) -5 μC e 1,25 . 10¹³ elétrons.
(C) 2 μC e 1,25 . 10¹³ elétrons.
(D) -3 μC e 1,75 . 10¹³ elétrons.
(E) 1 μC e 1,25 . 10¹³ elétrons.
Resolução:
A eletrização de um corpo é o desequilíbrio entre as cargas positivas (prótons) e as cargas negativas (elétrons) que ele possui. Nesse caso, como o corpo apresenta carga positiva (+Q), então ele possui mais prótons que elétrons.
Alternativa: B

20) (Livro do Aluno - SEDUC/2026 - (UECE 2011) Um condutor elétrico metálico, de formato irregular e isolado, está carregado com uma carga positiva total +Q. Pode-se afirmar corretamente que a carga +Q:

(A) é a somatória das cargas dos prótons que compõem o condutor.
(B) é o saldo do balanço entre as cargas dos prótons e dos elétrons que compõem o condutor.
(C) está distribuída uniformemente por todo o condutor, exceto pela sua superfície.
(D) está distribuída uniformemente por toda a superfície externa do condutor
Resolução:
Os elétrons livres é que se movimentam entre um corpo e outro, desequilibrando o balanço entre as cargas de cada um dos corpos.
Alternativa: D

21) (Livro do Aluno - SEDUC/2026 - (ENEM 2020)

Por qual motivo ocorre a eletrização ilustrada na tirinha?

(A) Troca de átomos entre a calça e os pelos do gato.
(B) Diminuição do número de prótons nos pelos do gato.
(C) Criação de novas partículas eletrizadas nos pelos do gato.
(D) Movimentação de elétrons entre a calça e os pelos do gato.
(E) Repulsão entre partículas elétricas da calça e dos pelos do gato.
Alternativa: D

22) (Livro do Aluno - SEDUC/2026 - (VUNESP 2012) Indução eletrostática é o fenômeno no qual pode-se provocar a separação de cargas em um corpo neutro pela aproximação de um outro já eletrizado.
O condutor que está eletrizado é chamado indutor e o condutor no qual a separação de cargas ocorreu é chamado induzido. A figura mostra uma esfera condutora indutora positivamente eletrizada induzindo a separação de cargas em um condutor inicialmente neutro.

Analisando a figura e sobre o processo de eletrização por indução, são feitas as seguintes afirmações:

I Para eletrizar o corpo neutro por indução, deve-se aproximar o indutor, conectar o induzido à terra, afastar o indutor e, finalmente, cortar o fio terra.
II Para eletrizar o corpo neutro por indução, deve-se aproximar o indutor, conectar o induzido à terra, cortar o fio terra e, finalmente, afastar o indutor.
III Na situação da figura, a conexão do induzido à terra, com o indutor nas suas proximidades, faz com que prótons do induzido escoem para a terra, por repulsão.
IV No final do processo de eletrização por indução, o corpo inicialmente neutro e que sofreu indução, adquire carga de sinal negativo.

Está correto, apenas, o contido em:

(A) II.
(B) I e III.
(C) I e IV.
(D) II e IV.
(E) II, III e IV.
Alternativa: B

23) (Livro do Aluno - SEDUC/2026 - (PUC-RJ 2015) Dois bastões metálicos idênticos estão carregados com a carga de 9,0 μC. Eles são colocados em contato com um terceiro bastão, também idêntico aos outros dois, mas cuja carga líquida é zero. Após o contato entre eles ser estabelecido, afastam-se os três bastões.

Qual é a carga líquida resultante, em μC, no terceiro bastão?

(A) 3,0
(B) 4,5
(C) 6,0
(D) 9,0
(E) 18
Resolução:
Dois dos bastões apresentam 9 μC de carga cada um e o terceiro não está carregado (carga igual a zero), portanto, a carga total é de +9 μC + 9 μC + 0 = 18 μC.
O enunciado afirma que os bastões são idênticos e metálicos, portanto são condutores.
Dessa forma, a carga total se distribuiu uniformemente entre os três bastões quando eles foram colocados em contato.
Sendo assim, cada bastão adquiriu uma carga de
18 μC = 6,0 μC
   6
Alternativa: C

BLINDAGEM ELETROSTÁTICA

Ocorre quando o excesso de cargas em um condutor distribui-se uniformemente em sua superfície e o campo elétrico em seu interior fica nulo. ... A blindagem eletrostática foi comprovada, em 1936, por Michael Faraday (1821-1867) através de um experimento que ficou conhecido como a gaiola de Faraday.

Essa blindagem também ficou conhecida por gaiola de Faraday e esse efeito é muito utilizado em nosso dia a dia. Como exemplos podemos citar os carros e aviões, que atuam como gaiolas de Faraday, nos protegendo caso sejamos atingidos por uma descarga elétrica, contrariando o pensamento popular de que os pneus do carro é que fazem essa proteção. Construções também são feitas utilizando blindagem eletrostática, a fim de proteger equipamentos eletrônicos.

Observação: essa blindagem pode ser vista facilmente, para isso pegue um celular ou um rádio ligado e embrulhe-o em papel alumínio. O alumínio vai agir como a gaiola de Faraday, o celular e o rádio poderão perder o sinal.

Eletrostática
Refere-se ao comportamento das cargas elétricas em repouso e seu estudo engloba os processos de eletrização, campo elétrico, força eletrostática e potencial elétrico.
Poder das pontas (para-raios)
Uma ponta é uma região muito curva. E como a eletricidade se acumula mais nas regiões mais curvas, quando um corpo eletrizado tem uma ponta, nela há grande acúmulo de carga elétrica. Numa ponta a densidade elétrica é sempre maior do que nas regiões não pontudas.

Com as pontas se dão os três fatos seguintes:
1 -  Uma ponta sempre se eletriza mais facilmente do que uma região não pontuda;
2 - Se um corpo já está eletrizado, uma ponta perde carga elétrica mais facilmente do que as regiões não pontudas; por este motivo é difícil manter-se eletrizado um corpo que possua pontas;
3 -  Se um corpo está eletrizado, uma ponta tem sobre os outros corpos uma ação muito mais forte do que as regiões não pontudas.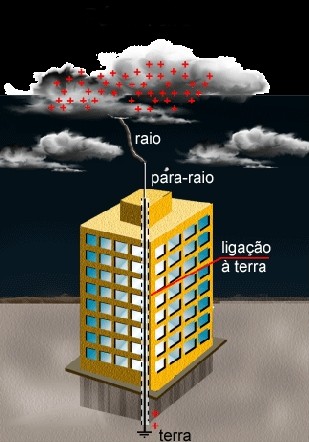
 
RAIO / RELÃMPAGO / TROVÃO / PARA-RAIOS
Em um dia de muita chuva estamos sujeitos aos trovões e raios que podem ser extremamente perigosos para nossa integridade física. Tentaremos esclarecer algumas dúvidas e também mitos sobre o aparecimento de raios e trovões, e ainda os para-raios.

Os raios são descargas elétricas que, segundo o (Inpe), matam cerca de 200 pessoas e trazem prejuízos de US$ 200 milhões a cada ano. Todos os dias alguém é atingido por um raio. Um raio, relâmpago ou corisco é talvez a mais violenta manifestação da natureza. 

125 milhões de volts
200 mil amperes
25 mil graus centígrados

Raios atingindo o solo. Embora nem sempre sejam alcançados tais valores, mesmo um raio menos potente ainda tem energia suficiente para matar, ferir, incendiar, quebrar estruturas, derrubar árvores e abrir buracos ou valas no chão.

Ao redor da Terra caem cerca de 100 raios por segundo. No Brasil, nas regiões Sudeste e Sul, a incidência é de 25 milhões de raios anualmente, sendo a maior quantidade, no período de dezembro a março, que corresponde à época das chuvas de verão.

Relâmpago e Trovão
Durante a formação de uma tempestade, verifica-se que ocorre uma separação de cargas elétricas, ficando as nuvens mais baixas eletrizadas negativamente, enquanto as nuvens mais altas se eletrizam positivamente. 

Quando isso acontece, o ar torna-se condutor e uma enorme centelha elétrica ( relâmpago ) salta de uma nuvem para outra ou de uma nuvem para a Terra.
 
Para-raios
Os para-raios foram inventados por Benjamin Franklin no século XVIII. Assim, ele suspeitou q eu os raios eram nada mais que enormes centelhas que saltavam entre nuvens e, consequentemente, entre nuvens e a superfície terrestre. 

Conhecendo o poder das pontas, Benjamin Franklin teve então a idéia de construir um dispositivo de proteção contra os efeitos desastrosos dos raios.

Poder das Pontas
Um fenômeno também interessante, relacionado com o conceito de rigidez dielétrica denomina-se poder das pontas. Este fenômeno ocorre porque, em um condutor eletrizado a carga tende a se acumular nas regiões pontiagudas. 

TESTES - PODER DAS PONTAS / RIGIDEZ DIELÉTRICA

24) (Enem PPL 2018) Em uma manhã ensolarada, uma jovem vai até um parque para acampar e ler. Ela monta sua barraca próxima de seu carro, de uma árvore e de um quiosque de madeira. Durante sua leitura, a jovem não percebe a aproximação de uma tempestade com muitos relâmpagos.
A melhor maneira de essa jovem se proteger dos relâmpagos é

(A) entrar no carro.
(B) entrar na barraca.
(C) entrar no quiosque.
(D) abrir um guarda-chuva.
(E) ficar embaixo da árvore.
Resolução:
O carro, por ser um recinto fechado, tem comportamento mais aproximado ao de um condutor em equilíbrio eletrostático (gaiola de Faraday), sendo desprezíveis a intensidade do vetor campo elétrico no seu interior e a diferença de potencial entre dois pontos do seu interior.
Alternativa: A

25) (Enem, 2010) Duas irmãs que dividem o mesmo quarto de estudos combinaram de comprar duas caixas com tampas para guardarem seus pertences dentro de suas caixas, evitando, assim, a bagunça sobre a mesa de estudos.
Uma delas comprou uma metálica, e a outra, uma caixa de madeira de área e espessura lateral diferentes, para facilitar a identificação.
Um dia as meninas foram estudar para a prova de Física e, ao se acomodarem na mesa de estudos, guardaram seus celulares ligados dentro de suas caixas. Ao longo desse dia, uma delas recebeu ligações telefônicas, enquanto os amigos da outra tentavam ligar e recebiam a mensagem de que o celular estava fora da área de cobertura ou desligado.
Para explicar essa situação, um físico deveria afirmar que o material da caixa, cujo telefone celular não recebeu as ligações é de

(A) madeira e o telefone não funcionava porque a madeira não é um bom condutor de eletricidade.
(B) metal e o telefone não funcionava devido à blindagem eletrostática que o metal proporcionava.
(C) metal e o telefone não funcionava porque o metal refletia todo tipo de radiação que nele incidia.
(D) metal e o telefone não funcionava porque a área lateral da caixa de metal era maior.
(E) madeira e o telefone não funcionava porque a espessura desta caixa era maior que a espessura da caixa de metal.
Resolução:
No interior de um condutor (caixa metálica) em equilíbrio eletrostático, as cargas distribuem-se na superfície externa do condutor, anulando o campo elétrico no seu interior. Esse fenômeno é conhecido como blindagem eletrostática.
Alternativa: B

26) (Enem PPL 2022) Para reduzir a poluição atmosférica gerada pela emissão de fumaça por grandes indústrias, utilizam-se precipitadores eletrostáticos. Sua função é suprimir os gases poluentes antes que sejam lançados para a atmosfera. A figura ilustra um precipitador constituído, basicamente, por uma entrada e uma saída de gases e por um fio grosso de cobre, conectado a uma fonte de tensão. O acúmulo de cargas no fio de cobre induz a polarização das partículas poluentes. Os gases poluídos são injetados pela entrada de gases, e os gases sem poluentes são lançados na atmosfera pela saída do precipitador.
No precipitador eletrostático, as partículas poluentes são

(A) atraídas e se acumulam no fio carregado.
(B) decompostas em moléculas não poluentes
(C) ionizadas e podem ser lançadas na atmosfera.
(D) repelidas pelo fio carregado e se acumulam na parede do tubo.
Alternativa: A

27) O poder das pontas é uma consequência da forma como as partículas portadoras de carga elétrica se distribuem na superfície de um condutor. Em um dado condutor carregado, em equilíbrio eletrostático, pode-se afirmar que, em relação ao restante da superfície, nas pontas:

(A) A quantidade e a densidade de cargas são sempre maiores.
(B) A quantidade e a densidade de cargas são sempre menores.
(C) A quantidade e a densidade de cargas são sempre iguais.
(D) A quantidade de cargas é sempre menor, mas a densidade de cargas é sempre maior.
(E) A quantidade de cargas é sempre maior, mas a densidade de cargas é sempre menor.
Resolução:
Em um condutor carregado, as cargas tendem a se aproximar das pontas, fazendo com que, naquela região, tenha uma maior quantidade e densidade de cargas.
Alternativa: A

28) (Enem 2020) Há muitos mitos em relação a como se proteger de raios, cobrir espelhos e não pegar em facas, garfos e outros objetos metálicos, por exemplo. Mas, de fato, se houver uma tempestade com raios, alguns cuidados são importantes, como evitar ambientes abertos. Um bom abrigo para proteção é o interior de um automóvel, desde que este não seja conversível.

Qual o motivo físico da proteção fornecida pelos automóveis, conforme citado no texto?

(A) Isolamento elétrico dos pneus.
(B) Efeito de para-raios da antena.
(C) Blindagem pela carcaça metálica.
(D) Escoamento da água pela lataria.
(E) Aterramento pelo fio terra da bateria.
Alternativa: C

29) (Enem 2018 PPL) Em uma manhã ensolarada, uma jovem vai até um parque para acampar e ler. Ela monta sua barraca próxima de seu carro, de uma árvore e de um quiosque de madeira. Durante sua leitura, a jovem não percebe a aproximação de uma tempestade com muitos relâmpagos.

A melhor maneira de essa jovem se proteger dos relâmpagos é

(A) A entrar no carro.
(B) entrar na barraca.
(C) entrar no quiosque.
(D) abrir um guarda-chuva.
(E) ficar embaixo da árvore.
Alternativa: A

30) Os objetos listados na coluna à esquerda abaixo se relacionam com propriedades listadas na coluna à direita.

1 - pára-raios
2 - gaiola metálica
3- pilha seca
( ) força eletromotriz
( ) blindagem eletrostática
( ) poder das pontas

De cima para baixo, a numeração correta da coluna da direita em correlação com a da esquerda é:

(A) 3, 2, 1
(B) 1, 2, 3
(C) 3, 1, 2
(D) 2, 3, 1
(E) 2, 1, 3
Resolução:
Na ordem, a pilha é uma representação de uma fonte de força eletromotriz. A gaiola metálica é uma representação da gaiola de faraday, demonstrando a blindagem eletrostática. Por fim, o para raios demonstra o poder das pontas.
Alternativa: A

31) (UFF-RJ) Considere a seguinte experiência: “Um cientista construiu uma grande gaiola metálica, isolou-a da Terra e entrou nela. Seu ajudante, então, eletrizou a gaiola, transferindo-lhe grande carga”. Pode-se afirmar que:

(A) O cientista nada sofreu, pois, o potencial da gaiola era menor que o de seu corpo
(B) O cientista nada sofreu, pois, o potencial de seu corpo era o mesmo que o da gaiola
(C) Mesmo que o cientista houvesse tocado no solo, nada sofreria, pois, o potencial de seu corpo era o mesmo que o do solo
(D) O cientista levou choque e provou com isso a existência da corrente elétrica
Resolução:
Como o cientista está dentro de uma gaiola de faraday ele não vai sofrer nada devido ao fato de não haver diferença de potencial no interior.
Alternativa: B

32) (AFA-RJ) Durante tempestade, um raio atinge um avião em vôo. Pode-se afirmar que a tripulação:

(A) não será atingida, pois aviões são obrigados a portar um pára-raios em sua fuselagem.
(B) será atingida em virtude de a fuselagem metálica ser boa condutora de eletricidade.
(C) será parcialmente atingida, pois a carga será homogeneamente distribuída na superfície interna do avião.
(D) não sofrerá dano físico, pois a fuselagem metálica atua como blindagem.
Resolução:
A descarga elétrica ocorrida irá eletrizar o avião — porém, como sua fuselagem é metálica (bom condutor), essas cargas irão se distribuir na superfície externa, não causando danos aos passageiros. A fuselagem atua como blindagem para o seu conteúdo.
Alternativa: D

33) (UFRGS-RS) A figura abaixo representa, em corte, três objetos de formas geométricas diferentes, feitos de material bom condutor, que se encontram em repouso. Os objetos são ocos, totalmente fechados, e suas cavidades internas se acham vazias. A superfície de cada um dos objetos está carregada com carga elétrica estática de mesmo valor Q.

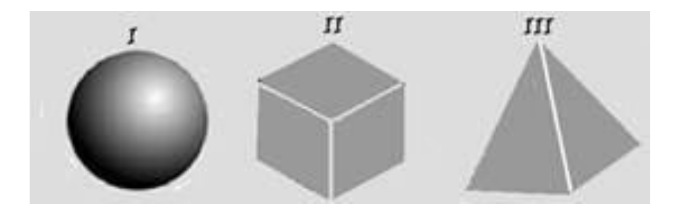
Em quais desses objetos o campo elétrico é nulo em qualquer ponto da cavidade interna?

(A) Apenas em I.
(B) Apenas em II.
(C) Apenas em I e II.
(D) Apenas em II e III.
(E) Em I, II e III.
Resolução:
O campo elétrico é nulo nos pontos internos de um condutor eletrizado e em equilíbrio, independentemente da sua forma.
Alternativa: E

34) (UFV, 1996) Durante uma tempestade, um raio atinge um ônibus que trafega por uma rodovia.

Pode-se afirmar que os passageiros:

(A) não sofrerão dano físico em decorrência deste fato, pois os pneus de borracha asseguram o isolamento elétrico do ônibus.
(B) serão atingidos pela descarga elétrica, em virtude da carroceria metálica ser boa condutora de eletricidade.
(C) serão parcialmente atingidos, pois a descarga será homogeneamente distribuída na superfície interna do ônibus.
(D) não sofrerão dano físico em decorrência deste fato, pois a carroceria metálica do ônibus atua como blindagem.
(E) não serão atingidos, pois os ônibus interurbanos são obrigados a portar um para-raios em sua carroceria.
Resolução:
O ônibus funciona como uma gaiola de Faraday, mantendo toda a eletrização na lataria do veículo.
Alternativa: D

35) (UFRN, 2003) Mauro ouviu no noticiário que os presos do Carandiru, em São Paulo, estavam comandando, de dentro da cadeia, o tráfico de drogas e fugas de presos de outras cadeias paulistas, por meio de telefones celulares. Ouviu também que uma solução possível para evitar os telefonemas, em virtude de ser difícil controlar a entrada de telefones no presídio, era fazer uma blindagem das ondas eletromagnéticas, usando telas de tal forma que as ligações não fossem completadas. Mauro ficou em dúvida se as telas eram metálicas ou plásticas. Resolveu, então, com seu celular e o telefone fixo de sua casa, fazer duas experiências bem simples.

1ª - Mauro lacrou um saco plástico com seu celular dentro. Pegou o telefone fixo e ligou para o celular. A ligação foi completada.
2ª - Mauro repetiu o procedimento, fechando uma lata metálica com o celular dentro. A ligação não foi completada.

O fato de a ligação não ter sido completada na segunda experiência, justifica-se porque o interior de uma lata metálica fechada

(A) permite a polarização das ondas eletromagnéticas diminuindo a sua intensidade.
(B) fica isolado de qualquer campo magnético externo.
(C) permite a interferência destrutiva das ondas eletromagnéticas.
(D) fica isolado de qualquer campo elétrico externo.
Resolução:
No interior de uma lataria, pela superfície ser de um material condutor, configurou-se a gaiola de Faraday.
Alternativa: D

36) (UEG, 2007) Os recentes motins em presídios brasileiros chamaram a atenção de modo geral para a importância das telecomunicações na operação de estruturas organizacionais. A necessidade de se impossibilitar qualquer tipo de comunicação, no caso de organizações criminosas, tornou-se patente. Embora existam muitos sistemas de comunicação móvel, o foco centrou-se em celulares, em virtude de suas pequenas dimensões físicas e da facilidade de aquisição e uso. Várias propostas foram colocadas para o bloqueio das ondas eletromagnéticas ou de rádio. A primeira delas consiste em envolver o presídio por uma “gaiola de Faraday”, ou seja, “embrulhá-lo” com um material que seja bom condutor de eletricidade ligado à terra. Uma segunda proposta era utilizar um aparelho que gerasse ondas eletromagnéticas na mesma faixa de frequência utilizada pelas operadoras de telefonia móvel. Essas ondas seriam espalhadas por meio de antenas, normalmente instaladas nos muros do presídio.

Acerca das informações contidas no texto acima, julgue a validade das afirmações a seguir.

I. Uma “gaiola de Faraday” é uma blindagem elétrica, ou seja, uma superfície condutora que envolve uma dada região do espaço e que pode, em certas situações, impedir a entrada de perturbações produzidas por campos elétricos e/ou magnéticos externos.
II. A eficiência da “gaiola de Faraday” depende do comprimento de onda das ondas eletromagnéticas da telefonia celular, pois isso definirá as dimensões da malha utilizada em sua construção.
III. A segunda proposta citada no texto é a geração de ondas nas mesmas frequências utilizadas pelas operadoras de telefonia móvel. Com isso, através de interferências destrutivas, compromete-se a comunicação entre a ERB (torre celular ou estação de rádio) e o telefone.

Assinale a alternativa CORRETA:

(A) Apenas as afirmações I e II são verdadeiras.
(B) Apenas as afirmações I e III são verdadeiras.
(C) Apenas as afirmações II e III são verdadeiras.
(D) Todas as afirmações são verdadeiras.
Resolução:
Todas as alternativas estão corretas em suas descrições.
Alternativa: D

37) (CFTMG G1, 2011) O eletroscópio da figura, eletrizado com carga desconhecida, consiste de uma esfera metálica ligada, através de uma haste condutora, a duas folhas metálicas e delgadas. Esse conjunto encontra-se isolado por uma rolha de cortiça presa ao gargalo de uma garrafa de vidro transparente, como mostra a figura.

Sobre esse dispositivo, afirma-se:

I. As folhas movem-se quando um corpo neutro é aproximado da esfera sem tocá-la.
II. O vidro que envolve as folhas delgadas funciona como uma blindagem eletrostática.
III. A esfera e as lâminas estão eletrizadas com carga de mesmo sinal e a haste está neutra.
IV. As folhas abrem-se ainda mais quando um objeto, de mesma carga do eletroscópio, aproxima-se da esfera sem tocá-la.

Estão corretas apenas as afirmativas

(A) I e II.
(B) I e IV.
(C) II e III.
(D) III e IV.
Resolução:
I. Correta: haverá indução;
II. Errada: para haver blindagem, o material deve ser condutor;
III. Errada: a carga distribui-se por todo o material condutor;
IV. Correta: haverá indução.
Alternativa: B

38) (FGV, 2018) A gaiola de Faraday é um curioso dispositivo que serve para comprovar o comportamento das cargas elétricas em equilíbrio. A pessoa em seu interior não sofre descarga

Dessa experiência, conclui-se que o campo elétrico no interior da gaiola é

(A) uniforme e horizontal, com o sentido dependente do sinal das cargas externas.
(B) nulo apenas na região central onde está a pessoa.
(C) mais intenso próximo aos vértices, pois é lá que as cargas mais se concentram.
(D) uniforme, dirigido verticalmente para cima ou para baixo, dependendo do sinal das cargas externas.
(E) inteiramente nulo.
Resolução:
A gaiola de Faraday ilustra o fenômeno no qual as cargas elétricas se distribuem pela superfície externa de um condutor isolado em equilíbrio eletrostático, sendo nulo o campo elétrico em seu interior.
Alternativa: E

39) (AFA-RJ) Durante tempestade, um raio atinge um avião em vôo.
Pode-se afirmar que a tripulação:
(A) não será atingida, pois aviões são obrigados a portar um pára-raios em sua fuselagem.
(B) será atingida em virtude de a fuselagem metálica ser boa condutora de eletricidade.
(C) será parcialmente atingida, pois a carga será homogeneamente distribuída na superfície interna do avião.
(C) não sofrerá dano físico, pois a fuselagem metálica atua como blindagem.
Resolução:
A descarga elétrica ocorrida irá eletrizar o avião  —  porém, como sua fuselagem é metálica (bom condutor), essas cargas irão se distribuir na superfície externa, não causando danos aos passageiros. A fuselagem atua como blindagem para o seu conteúdo.
Alternativa: D

40) (UFBA) Aviões com revestimento metálico, voando em atmosfera seca, podem atingir elevado grau de eletrização, muitas vezes evidenciado por um centelhamento para a atmosfera, conhecido como fogo-de-santelmo.
Nessas circunstâncias é correto afirmar:
(01) A eletrização do revestimento dá-se por indução.
(02) O campo elétrico no interior do avião causado pela eletrização do revestimento, é nulo.
(04) A eletrização poderia ser evitada se o avião fosse revestido com material isolante.
(08) O centelhamento ocorre preferencialmente nas partes pontiagudas do avião.
(16) O revestimento metálico não é uma superfície equipotencial, pois, se o fosse, não haveria centelhamento.
(32) Dois pontos quaisquer no interior do avião estão a um mesmo potencial, desde que não haja outras fontes de campo elétrico.
Resolução:
(01) Falsa  —  a eletrização ocorre por atrito.
(02) Verdadeira  —  as cargas elétricas ficam distribuídas pela superfície do condutor, seja ele oco ou maciço (blindagem eletrostática), e consequentemente, o campo elétrico no seu interior é nulo.
(04) Falsa  —  os isolantes também podem ser eletrizados por atrito.
(08) Verdadeira  —  o campo elétrico criado nas partes pontiagudas de um condutor eletrizado, pode assumir valores extremamente altos e provocar um fenômeno eletrostático denominado poder das pontas, que consiste na troca de cargas elétricas entre as pontas do corpo eletrizado e o meio isolante que o envolve.
(16) Falsa  — o potencial elétrico é o mesmo em todos os pontos da superfície de um condutor em equilíbrio eletrostático, portanto a superfície é eqüipotencial.
(32) Verdadeira Internamente o potencial elétrico é constante e igual ao potencial na superfície.
R: [02 + 08 + 32] =4 2

41) (UEM-PR) Uma esfera metálica de raio R, isolada, está carregada com uma carga elétrica Q. Seja r a distância do centro da esfera a qualquer ponto dentro (r < R) ou fora (r > R) da esfera.
Nessas condições, assinale o que for correto:
(01) A carga elétrica se distribui uniformemente em toda a massa da esfera.
(02) O campo elétrico e o potencial elétrico são constantes no interior da esfera.
(04) Para r > R, o campo elétrico é inversamente proporcional ao quadrado da distância e tem direção perpendicular à superfície da esfera.
(08) As eqüipotenciais associadas ao campo elétrico da esfera, para r > R, são superfícies esféricas concêntricas com a esfera e igualmente espaçadas.
(16) O potencial elétrico é uma grandeza escalar, enquanto o campo elétrico é uma grandeza vetorial.
Dê como resposta a soma dos números que precedem as afirmativas corretas.
Resolução:
R: [02+04+16] = 22

42) (FMTM-MG) A seção transversal de um condutor em equilíbrio eletrostático carregado positivamente tem uma forma de pêra, conforme mostra a figura. Considere dois pontos A e B em sua superfície e as seguintes informações a seu respeito:
I. A e B estão submetidos ao mesmo potencial.
II. O vetor campo elétrico tem a mesma intensidade em A e B.
III. O vetor campo elétrico  resultante no interior do condutor é nulo.
Das afirmativas acima:
(A) Apenas II está correta.                 
(B) Apenas II e III estão corretas.        
(C) Apenas I e II estão corretas.
(D) Apenas I e III estão corretas.       
(E) I, II e III estão corretas.
Resolução:
I. Verdadeira — todos os pontos internos e da superfície possuem o mesmo potencial.
II. Falsa — é mais intenso em B (ponta)
III. Verdadeira
Alternativa: D

43) (UFMT) Indique a aplicação tecnológica do conceito demonstrado por Faraday, na primeira metade do século XIX, na experiência  conhecida como gaiola de Faraday.
(A) Isolamento térmico do conteúdo de garrafas térmicas.
(B) Atração dos raios em tempestades por pára-raios.
(C) Isolamento elétrico promovido pela borracha dos pneus de veículos.
(D) Recobrimento com material isolante em cabos utilizados para transporte de energia elétrica.
(E) Bloqueio para chamadas de telefone celular em penitenciárias.
Resolução:
Se uma penitenciária fosse envolvida por uma malha metálica, onde os “buracos” tivessem dimensões menores de 15 cm, não haveria a penetração de campos elétricos em seu interior, tornando-a blindada a ondas eletromagnéticas na faixa da telefonia móvel (da ordem de 1.800MHz). No entanto, isso não é feito pelo alto custo, preferindo-se a utilização da interferência, emitindo-se ondas nessa faixa de freqüência com intensidade muito maior.
Alternativa: E

44) (PUC-MG) Em dias secos e com o ar com pouca umidade, é comum ocorrer o choque elétrico ao se tocar em um carro ou na maçaneta de uma porta em locais onde o piso é recoberto por carpete. Pequenas centelhas elétricas saltam entre as mãos das pessoas e esses objetos. As faíscas elétricas ocorrem no ar quando a diferença de potencial elétrico atinge o valor de 10.000V numa distância de aproximadamente 1 cm.
 A esse respeito, marque a opção CORRETA.
(A) A pessoa toma esse choque porque o corpo humano é um bom condutor de eletricidade.
(B) Esse fenômeno é um exemplo de eletricidade estática acumulada nos objetos.
(C) Esse fenômeno só ocorre em ambientes onde existem fiações elétricas como é o caso dos veículos e de ambientes residenciais e comerciais.
(D) Se a pessoa estiver calçada com sapatos secos de borracha, o fenômeno não acontece, porque a borracha é um excelente isolante elétrico.
Resolução:
O atrito da pele das pessoas com objetos isolantes (lã, flanela, papel, plástico) tornam a pele eletrizada  —  em dias normais, esse excesso de cargas é descarregado no contato com o próprio ar  —  porém, em dias secos, esse processo torna-se muito lento, acumulando cargas estáticas  —  no contato com objetos, principalmente metálicos, ocorre uma brusca descarga, que é o choque elétrico
Alternativa: B

45) (UCPEL-RS) Considere as afirmativas abaixo.
I. A força entre duas cargas elétricas em equilíbrio eletrostático independe do meio onde essas cargas estão imersas.
II. Dois bastões de alumínio, um neutro e outro carregado positivamente, são postos em contato e, em seguida, afastados um do outro. Após o afastamento, o que estava neutro perdeu elétrons.
III. Dois corpos de mesmo material, inicialmente neutros, são atritados. Ambos se eletrizam com carga de mesmo sinal.
IV. Numa superfície equipotencial, as linhas de força serão sempre perpendiculares a qualquer ponto da superfície.
V. Para uma esfera metálica carregada positivamente, o campo elétrico no seu interior é constante e maior que zero.
Das afirmações acima, pode-se concluir que

(A) II e IV estão corretas.                     
(B) I, III e V estão corretas.                            
(C) todas estão corretas.
(D) todas estão incorretas.                       
(E) I, II, IV e V estão corretas.
Resolução:
I. Falsa — essa força é fornecida por F=KQq/d² e K é uma constante que depende do meio onde as cargas estão imersas.
II. Correta — depois do contato o bastão neutro ficou com carga positiva, ou seja, perdeu elétrons.
III. Falsa  —  só se eletrizam se forem de materiais diferentes e na eletrização por atrito terão sempre cargas de mesmo módulo mas sinais contrários.
IV. Correta — Define-se superfície equipotencial de um campo elétrico a qualquer superfície em cujos pontos o potencial elétrico é constante.
Estas superfícies têm duas propriedades importantes:
1a – A força elétrica durante o deslocamento de uma carga elétrica puntiforme sobre uma superfície equipotencial é nula.
2a – As superfícies equipotenciais são perpendiculares às linhas de força ou linhas de campo elétrico e, conseqüentemente, perpendiculares ao vetor campo elétrico e à qualquer ponto da superfície. .
V. Falsa — o campo elétrico em seu interior é nulo  —  é o potencial elétrico que é constante.
Alternativa: A

ELETRODINÂMICA

Eletrodinâmica - É a parte da Eletricidade responsável pelo estudo das cargas elétricas em movimento. O foco dessa área é a corrente elétrica e os componentes de circuitos elétricos, como capacitores e resistores.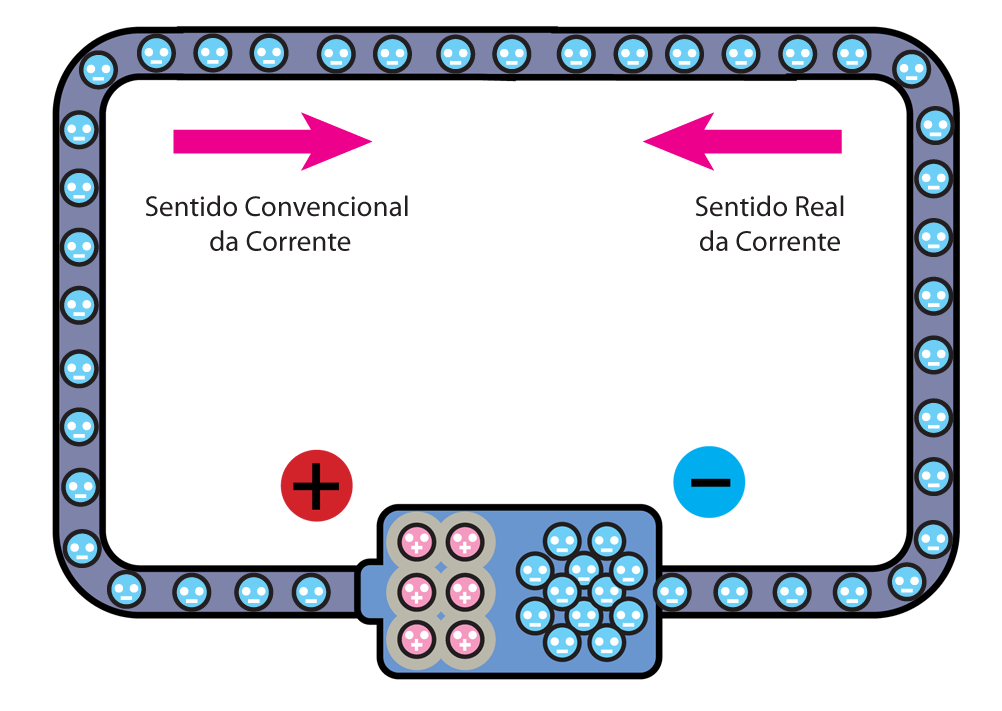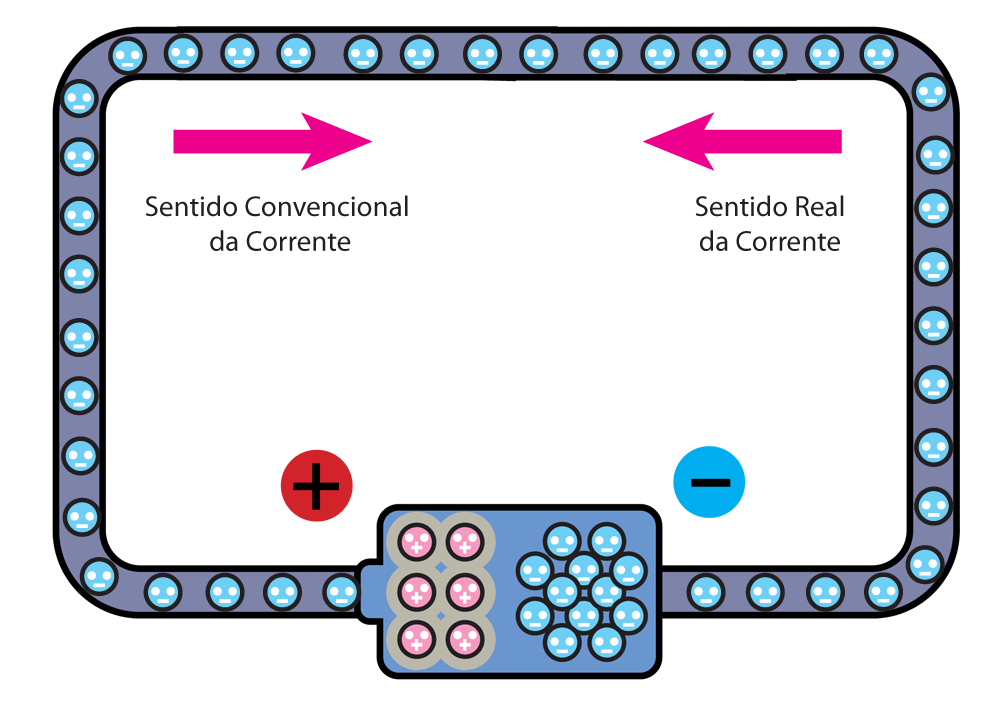
Eletromagnetismo - Estuda a relação entre os fenômenos elétricos e magnéticos, tais como campo magnético produzido por cargas elétricas em movimento e campo elétrico produzido pela variação de fluxo magnético.
Energia elétrica – É a energia armazenada ou distribuída na forma elétrica. No SI: a mesma da energia, o joule (J).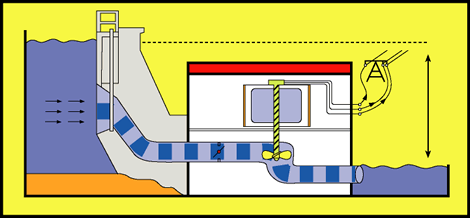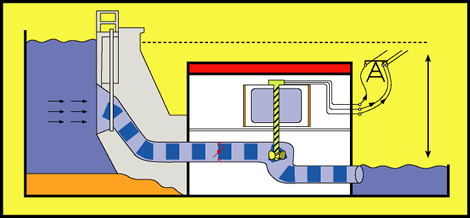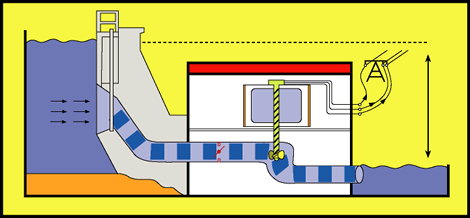
Usina Hidroelétrica
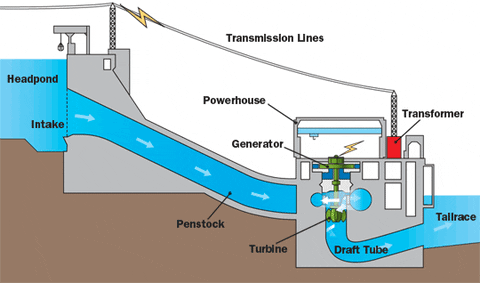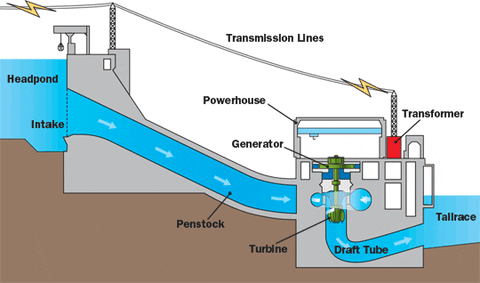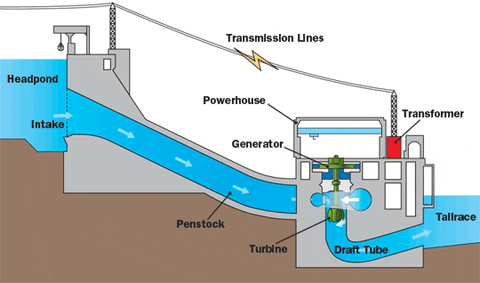Energia Solar

CORRENTE ELÉTRICA
Corrente elétrica - É o movimento ordenado de elétrons no interior de um condutor.
Sentido do campo elétrico X sentido da força elétrica sobres os elétrons:

Intensidade da corrente elétrica - É dada pela razão entre a quantidade Q de carga elétrica transportada que atravessa um secção transversal reta do condutor e o intervalo de tem..t dessa travessia.
   
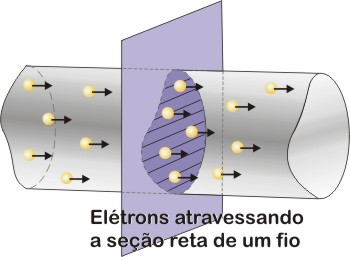
DIFERENÇAS ENTRE CORRENTE ALTERNADA (AC) E CORRENTE DIRETA (DC)
Impresso em algum local da superfície dos aparelhos elétricos residenciais é possível encontrar as inscrições AC, DC e 60Hz.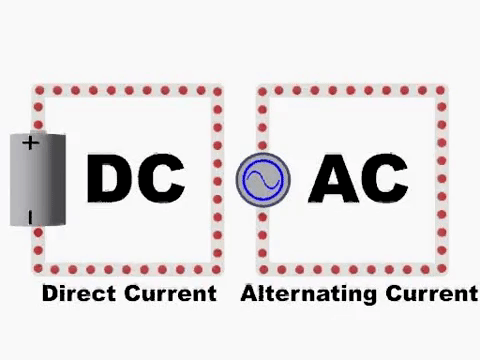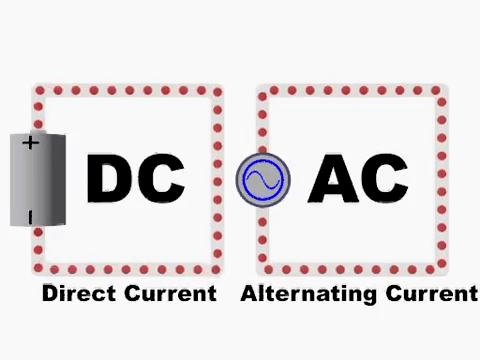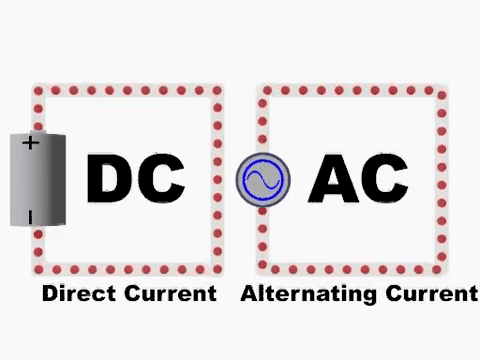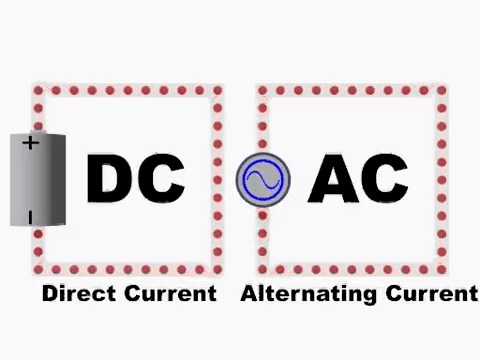
O que é eletricidade DC e AC?
As siglas AC e DC são provenientes das siglas da língua inglesa para alternating current e direct current e correspondem à corrente alternada (AC) e corrente contínua (DC), respectivamente. A principal diferença entre as correntes AC e DC é a direção em que os elétrons se movimentam.

Contínua – É aquela que mantém seu sentido constante, como, por exemplo, as correntes estabelecidas por baterias de carros e pilhas.


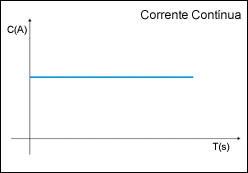
AC significa AlternatingCurrent (corrente alternada) - Em um circuito AC, a corrente ora circula em um sentido, ora em outro. Hz ou hertz significa repetições por segundo. Por isso, o valor 60 Hz indica que a corrente elétrica fornecida nas tomadas de nossa casa oscila sessenta vezes por segundo.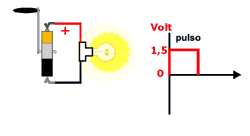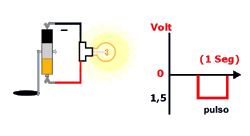
Alternada – É o tipo de corrente fornecida por usinas hidrelétricas, cuja intensidade e sentido variam periodicamente, usada em residências.
Miliampère (mA) Corrente elétrica

Nanoampère (nA) = 10⁶
Microampère (µA) = 10³
Miliampère (mA) = 1
Ampère (A) = 10^-3
Kiloampère (kA) = 10^-6
Megaampère (MA) = 10.10^-10
Gigaampère (GA) = 10.10^-13
Abaampère (aA) = 10^-4
Coulumb por segundo (C/s) = 10^-3

INTESIDADE DA CORRENTE ELÉTRICA

i = ΔQ
      Δt

i = corrente elétrica (A)
ΔQ = quantidade de carga (C)
Δt = tempos (s)

RESOLVIDOS - CORRENTE ELÉTRICA
46) (U.E. Londrina-PR) Pela secção reta de um condutor de eletricidade passam 12,0 C a cada minuto. Nesse condutor, a intensidade da corrente elétrica, em ampères, é igual a:

 (A) 0,08
(B) 0,20
(C) 5,00
(D) 7,20
(E) 120
Resolução:
i = Δq
      Δt    
i = 12
     60
i = 0,2 A
Alternativa: B

47) Assinale a alternativa que apresenta corretamente a unidade utilizada para determinar a corrente elétrica de acordo com o sistema internacional de unidades (SI):

(A) Volt - V
(B) Watt - W
(C) Coulomb - C
(D) Coulomb vezes segundo – C.s
(E) Ampére - A
Resolução:
A unidade de corrente elétrica utilizada no sistema internacional de unidades (SI) é o Ampére. Uma corrente elétrica de módulo igual a 1,0 A transporta, através de um corpo condutor, uma carga elétrica de 1,0 C durante o intervalo de tempo de 1,0 s.
Alternativa: E

48) Durante 2,0 s são transportados 0,5 C de carga elétrica em um corpo condutor. Determine a corrente elétrica formada nesse corpo.

(A) 2,5 A
(B) 1,0 A
(C) 0,25 A
(D) 2,0 A
(E) 0,5 A
Resolução:
A fórmula de corrente elétrica é dada pela equação abaixo:
i = Δq
      Δt    
Portanto, podemos calcular a corrente elétrica nesse condutor da seguinte forma:
i =  0,5
      2,0
i = 0,25 A
Alternativa: C

49) Uma corrente elétrica de 0,15 A é formada em um fio condutor durante o intervalo de tempo de 2 minutos. Determine o módulo da carga elétrica que atravessou o fio durante esse tempo.

 (A) 18 C
(B) 0,30 C
(C) 0,075 C
(D) 13,33 C
(E) 15 C
Resolução:
Para calcularmos a quantidade de carga que atravessou o fio, usamos a fórmula da corrente elétrica mostrada abaixo:
i = Δq
      Δt    
No entanto, para fazermos o cálculo da quantidade de carga, é necessário que todas as unidades estejam expressas em unidades do SI. Nesse caso, o intervalo de tempo será de 120 segundos, uma vez que cada minuto tem 60 segundos de duração. O cálculo é mostrado abaixo:
0,15 =  ΔQ
            120
ΔQ = 18 C
Alternativa: A

50) Calcule o tempo necessário, em segundos, para que uma corrente elétrica de 2,0 A transporte uma carga elétrica total de 10,0 C.

(A) 0,2 s
(B) 20,0 s
(C) 5,0 s
(D) 12,0 s
(E) 10,0 s
Resolução:
Para calcularmos o tempo necessário para os 10,0 C de carga serem transportados, utilizamos a fórmula de corrente elétrica abaixo:
i = Δq
      Δt    
Substituindo os valores informados no enunciado do exercício, teremos a seguinte resolução:
2,0 = 10,0
           Δt
2,0 Δt = 10,0
Δt = 5,0 s
Alternativa: C

51) )UFRGS 1993/62) Selecione a alternativa que completa corretamente as lacunas nas seguintes afirmações:

I - Para ligar um aparelho elétrico de 120 V em uma residência onde a tensão da rede elétrica é de 220 V, usa-se um transformador. Esse transformador funciona porque a corrente elétrica é .......... .
II - Ao ligar-se um conjunto de lâmpadas de filamento coloridas para iluminar um pinheirinho de Natal, uma delas "queimou" (rompeu o filamento). Como as demais lâmpadas continuaram acesas, conclui-se que elas estão ligadas em .......... .
III - Quando se precisa aumentar a temperatura de um ferro elétrico de passar roupas, gira-se o botão do resistor no sentido em que a sua resistência elétrica .......... .

(A) contínua - série - aumenta
(B) contínua - série - diminui
(C) alternada - série - aumenta
(D) alternada - paralelo - aumenta
(E) alternada - paralelo - diminui
Resolução:
Para resolver a questão, vamos analisar cada uma das afirmações e preencher as lacunas corretamente.
I - Para ligar um aparelho elétrico de 120 V em uma residência onde a tensão da rede elétrica é de 220 V, usa-se um transformador. Esse transformador funciona porque a corrente elétrica é .......... .
Um transformador é um dispositivo que funciona com corrente elétrica alternada. Ele é usado para aumentar ou diminuir a tensão elétrica. Portanto, a corrente elétrica deve ser alternada.
II - Ao ligar-se um conjunto de lâmpadas de filamento coloridas para iluminar um pinheirinho de Natal, uma delas "queimou" (rompeu o filamento). Como as demais lâmpadas continuaram acesas, conclui-se que elas estão ligadas em .......... .
Se uma lâmpada queima e as outras continuam acesas, isso indica que as lâmpadas estão ligadas em paralelo. Em uma ligação em série, se uma lâmpada queima, todas as outras apagam.
III - Quando se precisa aumentar a temperatura de um ferro elétrico de passar roupas, gira-se o botão do resistor no sentido em que a sua resistência elétrica .......... .
Para aumentar a temperatura de um ferro elétrico, a resistência elétrica deve diminuir. Isso ocorre porque, de acordo com a Lei de Ohm V = R . i, se a resistência diminui e a tensão  permanece constante, a corrente  aumenta, resultando em maior dissipação de energia na forma de calor.
Alternativa: E

52) Determine a intensidade da corrente elétrica em um fio que tem sua secção reta atravessada por 5.10²⁰ elétrons a cada segundo. Dados: e = 1,6.10^-19 C.

(A) 60 A
(B) 80 A
(C) 30 A
(D) 50 A
Resolução:
Vamos utilizar a fórmula da corrente elétrica que leva em conta a quantização da carga elétrica.
i = n . e
       Δt
i = 5 . 10²⁰ . 1,6 . 10^-19
                  1
i = 80 A
Alternativa: B

53) Determine a intensidade da corrente elétrica que percorre um fio condutor cuja resistência elétrica é igual 0,005 Ω e que está sujeito a uma diferença de potencial de 10V.

(A) 2 mA
(B) 2 kA
(C) 50 mA
(D) 0,5 kA
Resolução:
Para resolver a questão, é necessário usar a 1ª lei de ohm.
U = R . i
10 = 0,0005 . i
i =    10  
     0,0005
i = 2000 A ou 2kA
Alternativa: B

54)  Determine qual é a potência elétrica dissipada em forma de calor em um fio de resistência elétrica igual a 0,025 Ω, percorrido por uma corrente elétrica de 20,0 A.

(A) 10 W
(B) 0,25 W
(C) 0,5 W
(D) 5,0 W
Resolução:
Para resolver o exercício, devemos fazer o cálculo da potência elétrica dissipada:
P = R . i²
P = 0,025 . 20²
P = 10W
Alternativa: A

55) (UEL-PR) Em relação à corrente elétrica, considere as afirmativas a seguir.
I – A corrente elétrica é uma grandeza escalar, definida como a razão entre a variação da quantidade de carga elétrica que flui em um meio em um intervalo de tempo.
II – A corrente elétrica convencional descreve o fluxo de cargas elétricas positivas.
III – Os elétrons fluem no interior dos metais com a velocidade da luz.
IV – O campo elétrico é o responsável por fazer cargas elétricas se movimentarem em um circuito elétrico.

(A) Somente as afirmativas I e II são corretas.
(B) Somente as afirmativas I e III são corretas.
(C) Somente as afirmativas III e IV são corretas.
(D) Somente as afirmativas I, II e IV são corretas.
(E) Somente as afirmativas II, III e IV são corretas.
Resolução:
Correto: A quantidade de cargas que atravessa uma seção de um condutor por unidade de tempo determina a corrente elétrica. Matematicamente:
I = Q/t
Correto: O sentido por convenção considera as partículas positivas, ainda que a corrente real seja determina pelo movimento das cargas negativas.
Errado: As cargas elétricas no interior de um condutor não se movem a velocidade da luz.
Correto: É o campo elétrico que produz a diferença de potencial (ddp) que proporcionará o movimento das partículas.
Alternativa: D

56) (UNIFESP-SP) Uma das grandezas que representa o fluxo de elétrons que atravessa um condutor é a intensidade da corrente elétrica, representada pela letra i. Trata-se de uma grandeza

(A) vetorial, porque a ela sempre se associa um módulo, uma direção e um sentido.
(B) escalar, porque é definida pela razão entre grandezas escalares: carga elétrica e tempo.
(C) vetorial, porque a corrente elétrica se origina da ação do vetor campo elétrico que atua no interior do condutor.
(D) escalar, porque o eletromagnetismo só pode ser descrito por grandezas escalares.
(E) vetorial, porque as intensidades das correntes que convergem em um nó sempre se somam vetorialmente.
Resolução:
Alínea b) escalar, porque é definida pela razão entre grandezas escalares: carga elétrica e tempo.
Para definir corrente elétrica a unidade de medida é o Ampere, sendo uma medida escalar, por não haver necessidade de determinação de direção e sentido.
O Ampere i é determinado pela divisão entre a carga e o tempo, duas grandezas escalares.
Alternativa: B

57) (UFRS-RS) O gráfico da figura representa a intensidade da corrente elétrica i em um fio condutor, em função do tempo transcorrido t.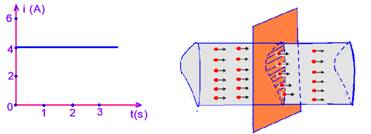
Calcule a carga elétrica Q que passa por uma seção do condutor nos dois primeiros segundos.
Resolução:
Quando o gráfico for i x t, a quantidade de carga é igual a área do gráfico. 

58) (UNIFOR-CE) Um circuito eletrônico foi submetido a um pulso de corrente indicada no gráfico.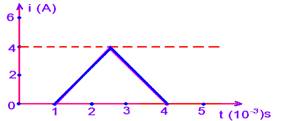
Durante esse pulso, a carga elétrica que fluiu no circuito, em coulombs, foi igual a:
(A) 1,3 . 10^-3
(B) 2,6 . 10^-3
(C) 3,0 . 10^-3
(D) 6,0 . 10^-3
(E) 1,2 . 10^-2
Resolução:
Quando o gráfico for i x t, a quantidade de carga é igual a área do gráfico. 

59) (UEL-PR) O gráfico mostra, em função do tempo t, o valor da corrente elétrica i através de um condutor.
Sendo Q a carga elétrica que circulou no intervalo de tempo de 0 a 4,0, a carga elétrica que circulou no intervalo de tempo de 4,0s a 8,0s foi:
(A) 0,25Q
(B) 0,40Q
(C) 0,5Q
(D) 2,0Q
(E) 4,0Q
Resolução:
Quando o gráfico for i x t, a quantidade de carga é igual a área do gráfico. 

CONDUTORES E ISOLANTES

Condutores – Os corpos considerados condutores elétricos possuem excesso de elétrons em sua camada de valência, que é a última camada a receber elétrons em um átomo.
De modo geral, os metais são excelentes condutor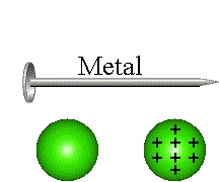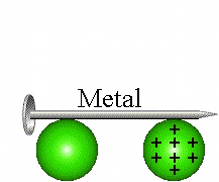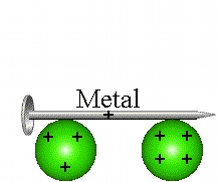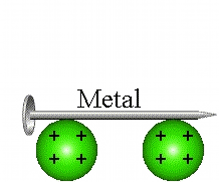es elétricos.
 Isolantes - Eles são também chamados de dielétricos. Os elétrons que formam esses materiais não têm facilidade de movimentação, tendo em vista a forte ligação entre eles e o núcleo atômico. Isopor, borracha, madeira seca, vidro, entre outros, são exemplos de materiais isolantes elétricos.
Semicondutores - Os materiais denominados de semicondutores possuem propriedades elétricas intermediárias entre condutores e isolantes. 

O silício e o germânio são exemplos de materiais com essa característica.
Supercondutores
Os supercondutores são materiais que oferecem baixíssimas resistências à passagem de corrente elétrica

O que são condutores?

Os condutores são materiais elétricos que conduzem as cargas elétricas com o mínimo de resistência quando submetidos a uma diferença de potencial elétrico (tensão elétrica, como pilhas, baterias ou tomadas. 

Isso acontece devido à enorme presença de elétrons em sua camada de valência (última camada do átomo a receber elétrons), denominados elétrons livres, que apresentam uma baixa força de atração com o núcleo do seu átomo, o que concede grande liberdade de movimento dos elétrons (corrente elétrica através do condutor.


O que são bons e males condutores
A propriedade condutividade elétrica é o que determina se um condutor é considerado bom ou mal.

Bons condutores: são aqueles que conduzem melhor a eletricidade, já que possuem valores maiores de condutividade elétrica do que outros materiais. Por exemplo, a prata é considerada o melhor condutor, já que apresenta uma condutividade elétrica de 6,8⋅10⁷(Ω⋅m⁾⁻¹.

Males condutores:  são aqueles que conduzem pior a eletricidade, já que possuem valores menores de condutividade elétrica do que outros materiais.

Por exemplo, a borracha é considerada um dos piores condutores, já que apresenta uma condutividade elétrica de 1,1⋅10⁻¹⁵(Ω⋅m⁾⁻¹.


Características dos condutores
Os condutores são caracterizados pelas propriedades físicas condutividade elétrica e resistividade elétrica, que variam com a resistência elétrica, a temperatura e as dimensões do condutor.

Sendo assim, os condutores possuem elevada condutividade elétrica, uma propriedade que indica o quanto o material facilita no deslocamento das cargas elétricas.

Ela é calculada pela fórmula:

σ =   L
          R⋅A

σ = condutividade elétrica do material, medida em (Ω⋅m)⁻¹ ou siemens por metro (S/m)
L = comprimento do condutor, medido em metros (m)
R = resistência elétrica, medida em Ohm (Ω)
A = área de secção transversal do condutor, medida em (m²)

A resistividade elétrica também é calculada pelo inverso da condutividade elétrica:

ρ = 1
      σ

ρ = resistividade elétrica do material, medida em (Ω⋅m)
σ = condutividade elétrica do material, medida em (Ω⋅m)⁻¹)

Eles também possuem baixa resistividade elétrica, uma propriedade que indica o quanto o material resiste ao deslocamento de cargas elétricas, calculada pela fórmula:

ρ = R⋅A
       L

Os condutores são tipificados em sólidos, líquidos ou gasosos.

Condutores sólidos: Os condutores sólidos, ou condutores metálicos, são aqueles caracterizados pela facilidade em doar elétrons e pelo deslocamento dos elétrons livres, que são atraídos pelo polo positivo e repelidos pelo polo negativo, conduzindo rapidamente a energia.

Condutores líquidos: Os condutores líquidos, ou condutores eletrolíticos, são aqueles caracterizados pelo deslocamento dos ânios (íon negativos) e dos cátions (íons positivos) em sentidos opostos, gerando uma corrente elétrica e, consequentemente, energia.

Condutores gasosos: Os condutores gasosos, ou condutores de terceira classe, são aqueles caracterizados pelo deslocamento dos ânions (íon negativos) para o polo positivo e dos cátions (íons positivos) para o polo negativo, gerando energia por meio das suas colisões.

Exemplos de condutores
- No estado sólido: prata, cobre, alumínio, ouro, aço, alumínio, ferro.
- No estado líquido: sódio, mercúrio, cálcio, potássio, soluções básicas ácidas ou salinas.
- No estado gasoso: todos os gases que podem ser ionizados (aqueles que ganham ou perdem elétrons).

Semicondutores: Os materiais semicondutores são materiais sólidos que apresentam uma condutividade elétrica intermediária, fazendo com que eles se comportem ora como isolantes, ora como condutores de acordo com as condições ambientais, como temperatura e estado elétrico.
 
60) A respeito da condutividade elétrica e térmica dos materiais, marque a alternativa correta:

(A) Somente os metais podem conduzir eletricidade e calor.
(B) Em hipótese alguma, um dielétrico pode conduzir corrente elétrica ou calor.
(C) Os metais destacam-se como bons condutores elétricos porque possuem excesso de prótons em sua estrutura atômica.
(D) Os materiais que são isolantes elétricos possuem alta condutividade elétrica.
(E) Um material é melhor condutor que outro quando possuir valor de condutividade elétrica maior.
Resolução:
Quanto maior o valor da condutividade elétrica de um material, melhor condutor elétrico ele será.
Alternativa: E

61) Em uma experiência de laboratório, você precisa escolher um material para realizar fios elétricos. Qual dos materiais a seguir é considerado um condutor elétrico eficaz, permitindo a passagem de corrente? Assinale a alternativa que apresenta a resposta correta.

(A) Alumínio.
(B) Cobre.
(C) Aço.
(D) Vidro.
(E) Plástico.
Alternativa: B

62) Um estudante está estudando sobre a diferença entre condutores e isolantes. Ele anota que, em geral, os materiais que facilitam a passagem de corrente são chamados de condutores. Qual das alternativas abaixo representa um isolante comum, usado frequentemente na eletricidade? Assinale a alternativa correta.

(A) Plástico.
(B) Madeira.
(C) Cobre.
(D) Alumínio.
Alternativa: A

FORÇA ENTRE CARGAS ELÉTRICAS

Fórmula da lei de Coulomb
De acordo com a sua lei, a força entre duas partículas eletricamente carregadas é diretamente proporcional ao módulo de suas cargas e é inversamente proporcional ao quadrado da distância entre elas.

F_e = |Q1| . |Q2|
       d²

F = força (N)
k = constante eletrostática no vácuo (9 . 10⁹N . m2/C² )
|Q1| = módulo da carga 1 (C)
|Q2| = módulo da carga 2 (C)
d = distância entre as cargas (m)

Na fórmula acima, k₀ é uma constante de proporcionalidade chamada de constante eletrostática do vácuo, seu módulo é aproximadamente de 9,0.10⁹ N.m²/C². 

Sentido da força elétrica
Atração: cargas de sinais diferentes se atraem.
Repulsão: cargas de mesmo sinal se repelem.

Gráfico da lei de Coulomb
A lei de Coulomb estabelece que a força elétrica entre duas partículas carregadas é inversamente proporcional ao quadrado da distância existente entre elas. Dessa forma, se duas cargas elétricas encontram-se a uma distância d e passarem a encontrar-se à metade dessa distância (d/2), a força elétrica entre elas deverá ser aumentada em quatro vezes (4F):

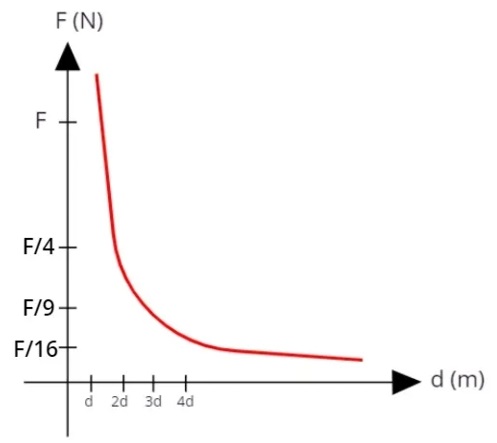
QUESTÕES RESOLVIDAS
62) Duas partículas eletricamente carregadas, com cargas de 1,0 μC e 2,0 mC, são separadas no vácuo a uma distância de 0,5 m. Determine o módulo da força elétrica existente entre as cargas.
Resolução:
F = k . Q . q
           d²

F = (9, 0. 10⁹)  . (1,0. 10^-6) . (2,0 .10^-3)
                            (0,5)²

F = 18. 10,0^{9 -6 -3}
             0,25

F = 18 . 10⁰
          0,25

F = 72 N

63) (SEDUC – Livro do Aluno/2026) (FAG 2014) Duas pequenas esferas estão, inicialmente, neutras eletricamente. De uma das esferas são retirados 5,0 . 10¹⁴, ⋅ elétrons, que são transferidos para a outra esfera. Após essa operação, as duas esferas são afastadas de 8,0 cm, no vácuo.
Dados:
Carga elementar e = 1,6 . 10^-19C,
Constante eletrostática no vácuo k₀ = 9,0.10⁹ N.m²/C²
A força de interação elétrica entre as esferas será de:

 (A) atração e intensidade 7,2 . 10⁵ N.
(B) atração e intensidade 9,0 . 10³ N.
(C) atração e intensidade 6,4 . 10³N.
(D) repulsão e intensidade 7,2 . 10³ N.
(E) repulsão e intensidade 9,0 . 10³ N.
Resolução:
Inicialmente, as esferas estão descarregadas, portanto, não há força de interação elétrica entre elas.
Após a transferência de elétrons de uma esfera para a outra, a esfera que ganhou elétrons se eletrizou negativamente, e o módulo da carga adquirida por ela será igual à carga de cada elétron (carga elementar) multiplicada pela quantidade de elétrons que ela perdeu:
q1 = n . e
q1 = 5,0 . 10¹⁴ . 1,6 . 10^-19C
q1 = 8,0 . 10^-5C.
Pelo princípio da conservação de carga, a esfera que perdeu os elétrons se eletri­zou positivamente com a mesma carga.
q2 = 8,0 . 10^-5 C
O enunciado nos dá o valor da constante eletrostática e da distância entre as cargas.
Dessa forma, temos todas as informações para calcular a força de interação elétrica entre as esferas:
q1 = 8,0 . 10^-5C
q2 = 8,0 . 10^-5 C
d = 8,0 cm = 8 . 10^-2 m
Sabendo que as cargas elétricas das esferas têm sinais opostos, podemos concluir que a força de interação entre as esferas será atrativa.
Para que haja coerência entre as unidades de medida, é importante trabalhar com todas as unidades no Sistema Internacional de Unidades (S.I.). Por isso, a distância d precisou ser convertida de centímetros (cm) para metros (m).
Dessa forma, podemos aplicar esses valores na Lei de Coulomb para determinar a intensidade da força elétrica entre as esferas:
Fe = k . q1 . q2
               d²

Fe = 9,0.10⁹ N.m²/C² . 8,0 . 10^-5 . 8,0 .10^-5
                                         (3,0 . 10^-9 m)²

 Fe = 9,0.10⁹ . 64,0 . 10^-10
                       64 . 10^-4

Fe = 9,0.10⁹ . 10^-10 . 10⁴
Fe = 9,0.10³ N
Alternativa: B

64) (SEDUC – Livro do Aluno/2026) (FAG 2018) Duas partículas de cargas elétricas q1 = 4,0 . 10^-16 C, e q2 = 6,0 . 10^-16 C, estão separadas no vácuo por uma distância de 3,0 . 10^-9 m. Sendo k₀ = 9,0.10⁹ N.m²/C², a intensidade da força de interação entre elas, em newtons, é de:

(A) 1,2 . 10^-5
(B) 1,8 . 10^-4
(C) 2,0 . 10^-4
(D) 2,4 . 10^-4
(E) 3,0 . 10^-3
Resolução:
Fe = k . q1. q2
             d²

Fe = 9,0.10⁹ N.m²/C² . 4,0 . 10^-16 C . 6,0 . 10^-16 C
                                           (3,0 . 10^-9 m)²

Fe = 9,0.10⁹ N.m²/C² . 24,0 . 10^-32 C²
                                     9,0 . 10^-18 m²

Fe = 216,0 . 10^-23
         9,0 . 10^-18 

Fe = 24 . 10^-5 N
Fe = 2,4 . 10^-4 N
Alternativa: D


65) SEDUC – Livro do Aluno/2026) (PUC-RJ 2018) Duas cargas elétricas idênticas estão separadas por uma distância d e, nessa condição, em cada uma delas atua uma força de módulo F.
Ao dobrar a distância entre as cargas, qual é a nova força atuante em cada carga?

(A) F/4
(B) F/2
(C) F
(D) 2F
(E) 4F
Resolução:
Inicialmente as duas cargas idênticas q1e q2 estão separadas por uma distância d. Portanto, a força de interação elétrica que atua entre elas é:
F_f = k . q1. q2
             d²
Após serem afastadas para o dobro da distância (2d), a força de interação elétrica entre elas tam­bém muda. Vamos chamar esse novo valor de F_f (força final):
F_f = k . q1. q2   
           (2d)²

F_f = k . q1. q2
              4d²
Note que F_f pode ser escrita como:
F_f = k . q1. q2
              4d²

F_f = 1 (k . q1. q2 / d²)
       4         
Portanto:
F_f = F/4
Alternativa: A

05) (SEDUC – Livro do Aluno/2026) (UFPE 2000) O gráfico abaixo representa a força F entre duas cargas pontuais positivas de mesmo valor, separadas pela distância r.

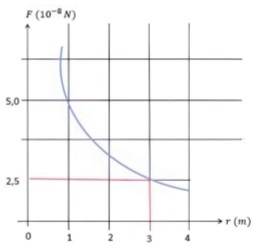
Considere k₀ = 9,0.10⁹ N.m²/C², e determine o valor das cargas, em unidades de 10^-9 C.

(A) 1,0
(B) 2,0
(C) 3,0
(D) 4,0
(E) 5,0
Resolução
Ao analisarmos o gráfico, podemos concluir que, na distância de d = 3 m, a força entre as cargas é de F = 2,5 .10^-8 N.
Sabendo que as cargas são positivas e têm o mesmo valor, então q1 = q2. Vamos chamar esse valor de q.
O enunciado nos dá o valor da constante eletrostática: k₀ = 9,0.10⁹ N.m²/C².
Desta forma, podemos substituir esses valores na lei de Coulomb:
F = k . q1. q2
             d²

2,5  . 10^-8 = 9 . 10⁹ . q . q
                                    3²

2,5  . 10^-8 = 9 . 10⁹ . q . q
                                    9
2,5 . 10^-8 = 10⁹ . q²

q2 = 2,5 . 10^-8
            10⁹

q2 = 2,5 . 10^-8 . 10^-9
q2 = 2,5 . 10^-17
q2 = 2,5 . 10^-18
q = √25 . 10^-18
q = 5 . 10^-9 C
Alternativa: E

06) (SEDUC – Livro do Aluno/2026) (VUNESP 2015) Em um experimento de eletrostática, um estudante dispunha de três esferas metálicas idênticas, A, B e C, eletrizadas, no ar, com cargas elétricas 5Q, 3Q e –2Q, respectivamente.

Utilizando luvas de borracha, o estudante coloca as três esferas simultaneamente em contato e, depois de separá-las, suspende A e C por fios de seda, mantendo-as próxi­mas. Verifica, então, que elas interagem eletricamente, permanecendo em equilíbrio estático a uma distância d uma da outra.
Sendo k a constante eletrostática do ar, assinale a alternativa que contém a correta re­presentação da configuração de equilíbrio envolvendo as esferas A e C e a intensidade da força de interação elétrica entre elas.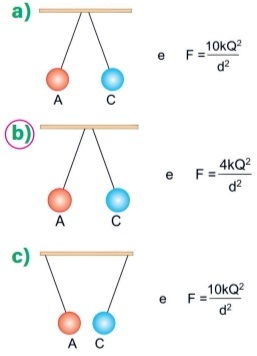


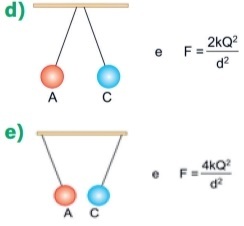
Resolução:
O problema apresenta três esferas metálicas idênticas, A, B e C, inicialmente com cargas diferentes:
Q_A = 5Q, Q_B = 3Q e QC = -2Q
Estas esferas são colocadas simultaneamente em contato.
Como elas são metálicas (portanto condutoras) e idênticas, ao serem colocadas em contato, as
cargas se distribuíram igualmente entre as três esferas.
Utilizando o princípio da conservação da carga elétrica:
Q _{antes do contato} = Q _{depois do contato}
Q _{antes do contato} = QA + QB + QC = 5Q + 3Q – 2Q = 6Q
Logo:
Q _{depois do contato} = 6Q
Depois do contato, como a carga se distribuiu igualmente nas três esferas, então a carga de cada esfera pode ser calculada:
QA = QB = QC = 6Q = 2Q
                              3
Sabendo o valor da carga de cada esfera, podemos calcular o módulo da força de interação eletros­tática entre as esferas A e C utilizando a lei de Coulomb:
F = k . Q . Q
            d²
Sendo QA = QC = 2Q
F = k . 2Q . 2Q
              d²

F = 4k . Q²
              d²
Para saber qual é a alternativa correta, podemos pensar que as cargas das esferas A e C são po­sitivas. Portanto, a força eletrostática entre elas é de repulsão.

07) (SEDUC – Livro do Aluno/2026) (PUC-RJ 2018) Duas cargas elétricas +Q e +4Q estão fixas sobre o eixo x, respectiva­mente nas posições x = 0,0 m e x = 1,0 m.
Uma terceira carga é posicionada entre as duas, sobre o eixo x, tal que se encontra em equilíbrio eletrostático.

Qual é a posição da terceira carga, em m?

(A) 0,25
(B) 0,33
(C) 0,40
(D) 0,50
(E) 0,66
Resolução:
Observe o esquema representando a situação. Vamos chamar a carga +Q de Q1 e posicioná-la em x = 0,0 m e a carga +4Q de Q2 e colocá-la na posição x= 1,00 m. Chamaremos a terceira carga de Q3.
A força que a carga Q1 exerce na carga Q3 chamaremos de F13 e a força que a carga Q2 exerce na carga Q3 chamaremos de F23

O enunciado não diz se a carga Q3 é positiva ou negativa e isso não influenciará na resolução da questão, porém, para elaborar o esquema, vamos considerar a carga Q3 como positiva, de forma que as forças F₁₃ e F₂₃ sejam repulsivas.

Como a distância total entre Q1 e Q2 é 1,00 m, podemos descrever a distância entre Q1 e Q3 com x e a distância entre Q3 e Q2 com 1,00 − x.

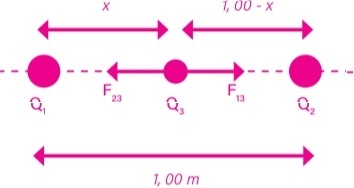
Para que a carga Q₃ fique em equilíbrio eletros­tático, a força resultante que atua sobre ela deve ser nula. Portanto, F₁₃ = F₂₃.

Vamos então escrever a expressão de F₁₃ e F₂₃ :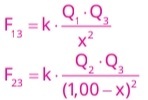

Igualando as expressões: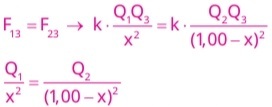

A partir do enunciado, podemos concluir que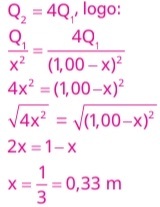

Alternativa: B

82) (PUC-MG) Duas cargas elétricas puntiformes são separadas por uma distância de 4,0 cm e se repelem mutuamente com uma força de 3,6 × 10^-5 N. Se a distância entre as cargas for aumentada para 12,0 cm, a força entre as cargas passará a ser de:

(A) 1,5 × 10^-6 N                               
(B) 4,0 × 10^-6 N                   
(C) 1,8 × 10^-6 N                       
(C) 7,2 × 10^-6 N
(E) 0,2 × 10^-6 N
Resolução
F = k . Q₁ . Q₂
             d²
F . d² = k . Q₁ . Q₂
F' d'² = k . Q₁ . Q₂
F' . d'² = F. d² 

F' = F. d²
              d'² 

F' = 3,6 × 10^-5 . (4 × 10^-2)² 
                (12 × 10^-2)²

F' = 3,6 × 10^-5 . 4 × 10^-2. 4 × 10^-2
             12 × 10^-2 . 12 × 10^-2
F' = 3,6 × 10^-5
          (3 × . 3 

F' = 0,4 × 10^-5
F' = 4 × 10^-6 N

83) (UF JUIZ DE FORA) Duas esferas igualmente carregadas, no vácuo, repelem-se mutuamente quando separadas a uma certa distância. Triplicando a distância entre as esferas, a força de repulsão entre elas torna-se: 

(A) 3 vezes menor
(B) 6 vezes menor
(C) 9 vezes menor
(D) 12 vezes menor
(E) 9 vezes maior 
Resolução
F = (k . Q₁ . Q₂)
              d²

F' = (k . Q₁ . Q₂)
             (3d)²

F' = (k . Q₁ . Q₂)
              9d²
F' = F
       9
F' é 9 vezes menor que F

84) Entre duas partículas eletrizadas, no vácuo, e a uma distância d, a força de interação eletrostática tem intensidade F. Se dobrarmos as cargas das duas partículas e aumentarmos a separação entre elas para 2d, ainda no vácuo, qual a intensidade F' da nova força de interação eletrostática?

(A) F' = 4 . F
(B) F' = F/2
(C) F' = 2 . F
(D) F' = F/4
(E) F' = F
Resolução
F = (k . Q₁ . Q₂)
             d²

F' = (k . 2Q₁ . 2Q₂)
               (2d)²

F' = 4.(k . Q₁ . Q₂)
                4d²

F' = (k . Q₁ . Q₂)
              d²
F' = F

85) As cargas Q₁ e Q₂ estão separadas pela distância (d) e se repelem com força (F). Calcule a intensidade da nova força de repulsão (F') se a distância for reduzida à metade e dobrada a carga Q₁.

(A) F' = 4 . F
(B) F' = 2 . F
(C )F' = 8 . F
(D) F' = 6 . F
(E) F' = 10 . F
Resolução
F = (k . Q₁ . Q₂)
              d²

F' = (k . 2Q₁ . Q₂)
             (d / 2)²

F' = (k . 2Q₁ . Q₂)
             (d² / 4)

F' = 4.(k . 2Q₁ . Q₂)
              d²

F' = 8.(k . Q₁ . Q₂)
              d²
F' = 8F

CAMPO ELÉTRICO

Campo elétrico: o que é, como calcular, força e potencial elétrico
O campo elétrico desempenha a função de transmissor das interações entre cargas elétricas, podendo ser de afastamento ou de aproximação, de acordo com o sinal da carga que o produziu.
Observamos que na região onde existe um campo elétrico, surgirá uma força sobre uma carga puntiforme de prova que for introduzida em algum ponto deste campo. Esta força poderá ser de repulsão ou de atração.

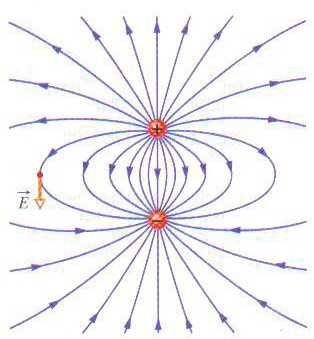
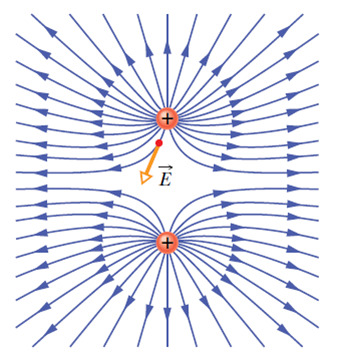
- Uma carga fixa positiva gera um campo, ao seu redor, de afastamento.
- Uma carga fixa negativa gera um campo, ao seu redor, de aproximação

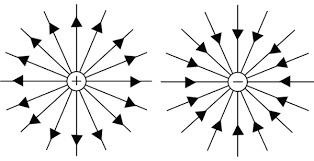
Fórmula do Campo Elétrico
Quando uma carga puntiforme eletrizada está fixa em um ponto,https://img.comunidades.net/pro/professordiminoi/3Aa_fsdervca3red.jpg ao seu redor irá surgir um campo elétrico. A intensidade deste campo depende do meio onde a carga está inserida e poderá ser encontrada através da seguinte fórmula:

E = k . |Q|
           d²

E = intensidade do campo elétrico (N/C)
k₀ = constante eletrostática no vácuo (9.10⁹ N.m²/C²)
|Q| = módulo da carga (C)
d = distância entre a carga e um ponto do campo (m)

Intensidade do Campo Elétrico
O valor da intensidade do campo elétrico pode ser encontrado através da seguinte fórmula:

E = k₀ . |Q|
      d²

E = campo elétrico (N/C)
F = força elétrica (F)
q =  carga elétrica (m)

No Sistema Internacional de Unidade, a intensidade do campo elétrico é medido em Newton por Coulomb (N/C), a força em Newton (N) e a carga elétrica em Coulomb (C).

Vetor Campo Elétrico
Ao campo elétrico associamos uma grandeza vetorial chamada vetor campo elétrico. Como o próprio nome indica, trata-se de uma grandeza vetorial que possui módulo, direção e sentido.


Sentido do Vetor Campo Elétrico

A força elétrica e o vetor campo elétrico possuem mesma direção. Entretanto, convencionamos que terão mesmo sentido quando a carga de prova for positiva, e sentido contrário quando a carga de prova for negativa.

 - Uma carga fixa positiva gera um campo, ao seu redor, de afastamento.
- Uma carga fixa negativa gera um campo, ao seu redor, de aproximação.
 

Linhas de Força
Podemos representar o campo elétrico através de linhas orientadas segundo o sentido do vetor campo elétrico. Chamadas linhas de força, são tangentes ao vetor campo elétrico em cada ponto.

A intensidade do campo elétrico é maior quanto mais próximas estiverem as linhas de campo e menos intenso nas regiões mais afastadas.

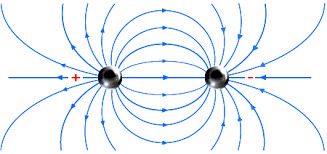
Campo Elétrico Uniforme
Quando em uma região do espaço existe um campo elétrico onde o vetor associado a ele apresenta mesma intensidade, mesma direção e mesmo sentido em todos os pontos, esse campo elétrico é chamado uniforme.

Este tipo de campo é obtido com a aproximação de duas placas condutoras planas e paralelas eletrizadas com cargas de mesmo valor absoluto e sinais contrários.

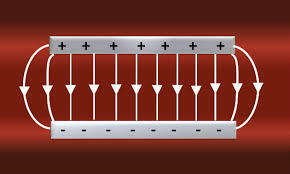
Força Elétrica - Lei de Coulomb
Na natureza existem as forças de contato e as forças de campo. As forças de contato só agem quando os corpos se tocam. A força de atrito é um exemplo de força de contato.

Força Elétrica
A força elétrica, a força gravitacional e a força magnética são forças de campo, pois agem sem a necessidade que os corpos estejam em contato.
A Lei de Coulomb, formulada pelo físico francês Charles Augustin de Coulomb (1736-1806) no final do século XVIII, foca nos estudos sobre a interação eletrostática entre partículas eletricamente carregadas:

“A força de ação mútua entre dois corpos carregados tem a direção da linha que une os corpos e sua intensidade é diretamente proporcional ao produto das cargas e inversamente proporcional ao quadrado da distância que as separa”.

A unidade de medida das cargas elétricas, é Coulomb (C), em homenagem ao físico pelas suas contribuições aos estudos da eletricidade. Assim, para calcular a força entre as cargas:

F = k_e . |Q1|. |Q2|
       d²

F = força (N)
k_e = constante eletrostática (no vácuo seu valor é igual a 9 . 10⁹ Nm² /C²)
q1 e q2 = cargas elétricas (C)
d = distância entre as cargas (m)

A força que surge da interação entre cargas será de atração quando as cargas apresentarem sinais contrários, e de repulsão, quando as tiverem sinais iguais.


Potencial Elétrico
O potencial elétrico, medido em Volts (V), é definido como o trabalho da força elétrica sobre uma carga eletrizada no deslocamento entre dois pontos.
Considerando dois pontos A e B e o valor do potencial no ponto B nulo, então o potencial será dado por:

V_A = τAB
           q

V_A = Potencial elétrico no ponto A (V)
τAB =  trabalho para deslocar uma carga do ponto A ao ponto B (J)
q = Carga elétrica (C)
 

Diferença de Potencial em um campo elétrico uniforme
Quando temos um campo elétrico uniforme, podemos encontrar a diferença de potencial entre dois pontos através da fórmula:

U = V_A – V_B = E . d

U = diferença de potencial (V)
V_A = potencial no ponto A (V)
V_B = potencial no ponto B (V)
E =  campo elétrico (N/C ou V/m)
d = distância entre as superfícies equipotenciais, ou seja, superfícies com mesmo potencial (m)


QUESTÕES RESOLVIDAS
97) (Livro do Aluno SEDC/2026) O gráfico representa a intensidade do campo elétrico gerado por uma carga puntiforme fixa no vácuo em função da distância da carga.

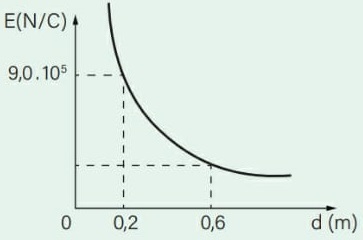
Considere k = 9, 0 .10⁹.N.m²/C².

a) Calcule o valor do módulo da carga Q que origina o campo.

Resolução:

 Analisando o gráfico, percebemos que, a uma distância d = 0,2m, a intensidade do campo elétrico é E = 9, 0 .10⁹.N. m²/C².
O enunciado fornece o valor da constante eletrostática k = 9, 0 .10⁹.N.m²/C².
Substituindo esses valores na expressão matemática que descreve a intensidade do campo elétrico:

E = k . |Q|
             d²

E = 9, 0 .10⁹ =   |Q|
                        (0,2)²

E = 9, 0 .10⁹ = |Q|
                        4,10^-1

|Q| = 4,10^-1 . 9, 0 .10⁵
                     9, 0 .10⁹

|Q| = 4μC

b) Determine a intensidade do campo elétrico a uma distância de 60 cm da carga.

Resolução:
Sabendo o valor do módulo da carga |Q| = 4 . 10^-6, conhecendo a distância (60cm) e o valor da constante eletrostática k = 9, 0 .10⁹.N.m²/C², podemos calcular o valor da intensidade campo elétrico neste ponto.

Inicialmente precisamos converter a distância de centímetros (cm) para metros (m).
d = 60 cm = 0,6 m. Substituindo os valores na expressão do campo elétrico:

E = k . |Q|
           d²

E = 9, 0 .10⁹ = |Q|
                        (0,2)²

E = 9, 0 .10⁹ = 4 . 10⁶ = 36 . 10³
                         (0,6)²     36. 10^-2

E = 1,0 .10⁵ N/C

98) (Livro do Aluno SEDC/2026) (UNAERP 2019) Uma carga de prova de 60 mC quando colocada em um campo elétrico, no ponto P, recebe uma força resultante de módulo igual a 0,15 N. Podemos afirmar que
o valor do campo elétrico neste ponto é, em N/C:

(A) 0,02
(B) 0,16
(C) 0,20
(D) 1,60
(E) 2,50
Resolução:
q = 60 . 10^-3 C
F = 0,15N
Logo:
0,15 N = E. 60 10^-3 C

E =     0,15N    = 0,0025 . 10³ = 2,50 N
       60 . 10^-3 C
Alternativa: E

99) (Livro do Aluno SEDC/2026) (UEMG 2019) Fundado em 2002 pelo Prêmio Nobel Carl Wieman, o projeto PhET Simulações Interativas da Universidade de Colorado Boulder (EUA) cria simulações interativas gratuitas de matemática e ciências. As simulações PhET baseiam-se em extensa pesquisa em educação e envolvem os alunos através de um ambiente intuitivo, onde os alunos aprendem através da exploração e da descoberta.
A figura a seguir foi obtida pelo PhET, sendo que duas partículas A e B, eletricamente carregadas, foram colocadas em uma determinada região do espaço.

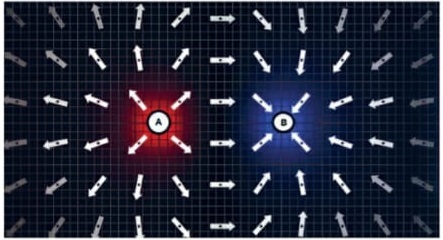
As setas indicam a direção e o sentido das linhas de força do vetor campo elétrico do sistema.
A respeito das cargas elétricas A e B do esquema anterior, é CORRETO afirmar que:

(A) ambas são eletricamente positivas.
(B) ambas são eletricamente negativas.
(C) B é eletricamente positiva e A é negativa.
(D) A é eletricamente positiva e B é negativa.
Resolução:
A figura mostra que as linhas de força do vetor campo elétrico estão apontando “para fora” da partícula A, portanto, podemos concluir que a partícula A é eletricamente positiva.
Da mesma forma, vemos que as linhas de campo estão apontando “para dentro” da partícula carregada B, logo, chegamos à conclusão de que ela é eletricamente negativa.
Alternativa: D

100) (Livro do Aluno SEDC/2026) (IFRR 2020) A intensidade do vetor campo elétrico, num ponto situado a 5 cm de uma carga elétrica puntiforme igual a 2 μC, no vácuo, onde k = 9, 0 .10⁹.N. m²/C², é:

(A) 7,2 . 10⁶ N/C.
(B) 4,8 . 10⁶ N/C.
(C) 6,5 . 10⁶ N/C.
(D) 3,6 . 10⁶ N/C.
(E) 8,4 . 10⁶ N/C.
Resolução:
|Q| = 2 μC = 2 ⋅ 10^-6 C
d = = 5 cm = 5 . 10^-2 m
k =  9 . 10⁹ Nm²/C
Substituindo estes valores na expressão do campo elétrico:
E = k . |Q|
             d²

E = 9 . 10⁹ . 2 . 10^-6
                   (5 . 10)^-2

E =   18 . 10³
       25 . 10^-4

E = 0,75 . 10⁷
E = 0,75 . 10⁶N/C
Alternativa: D

101) (Livro do Aluno SEDC/2026) (VUNESP 1994) A figura 1 representa uma carga elétrica pontual positiva no ponto P e o vetor campo elétrico no ponto 1, devido a essa carga.

No ponto 2, a melhor representação para o vetor campo elétrico, devido à mesma carga em P, será: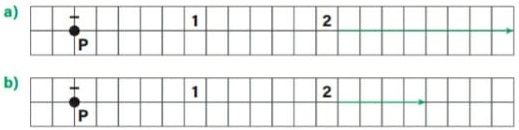

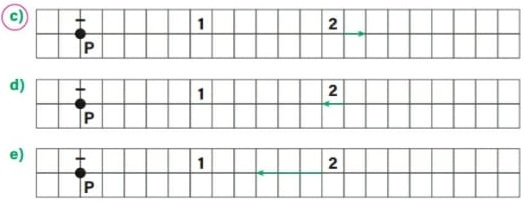
Resolução:
O enunciado indica que a carga em P é positiva, logo o campo aponta para fora e as alternativas D e E são incorretas. Pela figura, o ponto 1 está a 6 unidades de P e o ponto 2 a 12, ou seja, o dobro da distância. Como o campo é inversamente proporcional ao quadrado da distância, sua intensidade cai 4 vezes: se no ponto 1 vale 4, no ponto 2 vale 1.
Alternativa: C

102) (Livro do Aluno SEDC/2026) (PUC-RS 2006) A quantização da carga elétrica foi observada por Millikan em 1909. Nas suas experiências, Millikan mantinha pequenas gotas de óleo eletrizadas em equilíbrio vertical entre duas placas paralelas também eletrizadas, como mostra a figura a seguir. Para conseguir isso, regulava a diferença de potencial entre essas placas alterando, consequentemente, a intensidade do campo elétrico entre elas, de modo a equilibrar a força da gravidade.

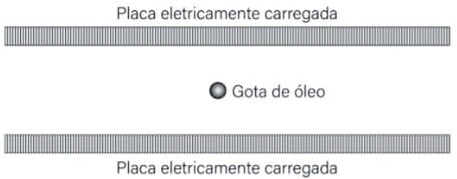
Suponha que, em uma das suas medidas, a gota tivesse um peso de 2,4 . 10^-13 N e uma carga elétrica positiva de 4,8 . 10^-19 C.
Desconsiderando os efeitos do ar existente entre as placas, qual deveria ser a intensidade e o sentido do campo elétrico entre elas para que a gota ficasse em equilíbrio vertical?

(A) 5.0 . 10⁵ N/ C, para cima.
(B) 5,0 . 10⁴ N/ C, para cima.
(C) 4 8 . 10⁵ N/C, para cima.
(D) 2,0 . 10⁵ N/C, para baixo.
(E) 2,0 . 10⁶ N/C, para baixo.
Resolução:
F_e = E . |q|
2,4 . 10^-13 N = E . 4,8 . 10^-19 C

E = 2,4 . 10^-13
       4,8 . 10^-19

E = 0,5 . 10⁶
E = 5 . 10⁵ N/C
Como a carga é positiva, a força elétrica tem o mesmo sentido do campo. Como a força atua para cima, concluímos que o campo aponta para cima.
Alternativa: A

103) (Livro do Aluno SEDC/2026) (FAMERP 2020) Nas ciências, muitas vezes, se inicia o estudo de um problema
fazendo uma aproximação simplificada. Um desses casos é o estudo do comportamento da membrana celular devido à distribuição do excesso de íons positivos e negativos em torno dela. A figura mostra a visão geral de uma célula e a analogia entre o modelo biológico e o modelo físico, o qual corresponde a duas placas planas e paralelas, eletrizadas com cargas elétricas de tipos opostos.

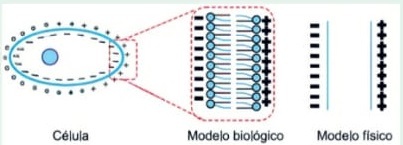
Com base no modelo físico, considera-se que o campo elétrico no interior da membrana celular tem sentido para:

(A) fora da célula, com intensidade crescente de dentro para fora da célula.
(B) dentro da célula, com intensidade crescente de fora para dentro da célula.
(C) dentro da célula, com intensidade crescente de dentro para fora da célula.
(D) fora da célula, com intensidade constante.
(E) dentro da célula, com intensidade constante.
Resolução:
O modelo físico da membrana celular, apresentado no enunciado da questão, simplifica a membrana como duas placas paralelas eletrizadas com cargas opostas (positivas fora e negativas dentro).
O campo elétrico sempre aponta “para fora” das cargas positivas e “para dentro” das cargas negativas; então, o campo no interior da membrana vai do exterior (região positiva) para o interior (região negativa) da célula.
A intensidade do campo elétrico na região central entre as placas é constante, ou seja, não varia de ponto a ponto.
Com base no modelo físico, portanto, considera-se que o campo elétrico no interior da membrana celular tem sentido para dentro da célula, com intensidade constante.
Alternativa: E

104) (Livro do Aluno SEDC/2026) (UFMG 1995) Um ponto P está situado à mesma distância de duas cargas, umapositiva e outra negativa, de mesmo módulo. A opção que representa corretamente a direção e o sentido do campo elétrico criado por essas cargas, no ponto P, é:

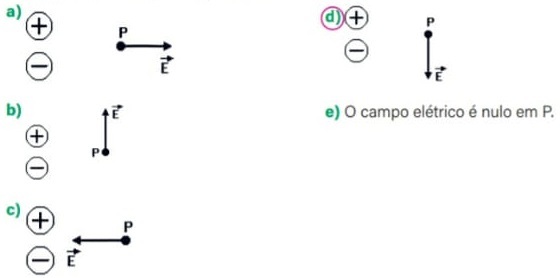
Resolução:
O vetor campo elétrico resultante (E), criado por estas duas cargas, é dado pela somatória dos vetores campo elétrico criados por cada carga (E ₊ e E₋):
E = E₊ + E_-
Lembrando que o vetor campo elétrico aponta “para fora” da carga positiva e “para dentro” da carga negativa, o esquema a seguir representa a soma vetorial dos campos elétricos E₊ e E₋
Portanto, podemos ver que a direção e o sen­tido do campo elétrico resultante, criado pelas cargas positiva e negativa, é vertical e apontado para baixo.

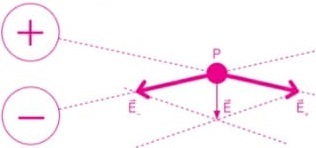
Alternativa: D

105) (Livro do Aluno SEDC/2026) (MACKENZIE 1997) As cargas puntiformes q₁ = 20 μC e q₂ = 64 μC estão fixas no vácuo (k _9, 0 .10⁹.N. m²/C²), respectivamente nos pontos A e B.

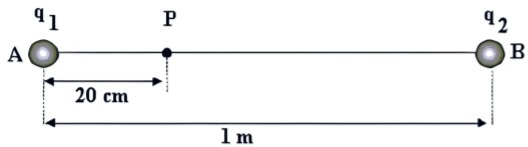
O campo elétrico resultante no ponto P tem intensidade de:

(A) 3,0 . 10⁶ N/C
(B) 3,6 . 10⁶ N/C
(C) 4,0 . 10⁶ N/C
(D) 4,5 . 10⁶ N/C
(E) 5,4 . 10⁶ N/C
Resolução:
O vetor campo elétrico resultante (E), criado por estas duas cargas, é dado pela somatória dos vetores campo elético criados pelas cargas (E₁ e E₂):
E = E₁ + E₂
Como ambas as cargas geradoras são positivas, tanto o vetor E₁ quanto o vetor E₂ apontarão “para fora” de suas respectivas cargas geradoras.
Portanto, temos a somatória de dois vetores na mesma direção, porém em sentidos opostos.

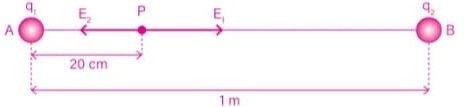
Vamos calcular a intensidade do vetor campo elétrico gerado por carga no ponto P:
q = 20μC = 20 . 10^-6 C
E₁ = k_o . q1
               q2

E₁ = 9,0 .10⁹ . 20 .10^-6
                       (-0,2)²

E₁ = 9,0 . 10⁹ . 20 .10^-6
                           0,04

E₁ = 9,0 .10⁹ . 20 .10^-6
                         4 .10^-2    

E₁ = 9,0 .10⁹ . 5,0 .10^-4
E₁ = 45,0 . 10⁵ N/C
q2 =  64μC
q2 =  64 .10^-6 C
d2 = 1 m – 02 m = 0,8m

E₂ = k_o . q2
               q2
 
E₂ = 9,0 .10⁹ . 64 .10^-6
                       (-0,8)² 

E₂ = 9,0 . 10⁹ . 64 .10^-6
                         64 . 10^-2 

E₂ = 9,0 .10⁹ . 64 .10^-6

                         4 .10^-2    

E₂ = 9,0 10⁵ N/C
Podemos perceber que o vetor campo elétrico E1 é maior que o vetor campo elétrico E2 no ponto P.
Estando E1 e E2 na mesma direção, mas em sentidos opostos, então:

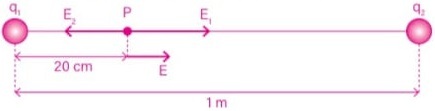
E = E₁ – E₂
E = 45,0 .10⁵ N/C – 9,0 . 10⁵ N/C
E = 3,6 . 10⁶ N/C
Alternativa: B

106) (Livro do Aluno SEDC/2026) (FPS 2017) Duas cargas elétricas pontuais de mesmo valor Q_A =  Q_B =  − 10^-19 C são fixadas nos vértices A e B do triângulo equilátero de lado igual a 10⁻⁶ m, como ilus­trado na figura a seguir.

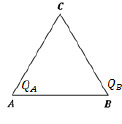
Qual a direção e sentido do vetor campo elétrico resultante no vértice C?

Resolução:
O vetor campo elétrico resultante (E) criado por essas duas cargas no ponto C é dado pela somató­ria dos vetores campo elétrico criados por cada uma das cargas (E_A e E_B): E = E_A = + E_B
Como ambas as cargas são negativas, o vetor campo elétrico tem direção e sentido “para dentro” das cargas.

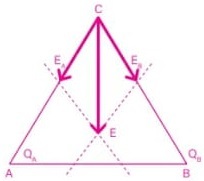
Como as distâncias entre as cargas Q_A e Q_B são iguais em relação ao vértice C e suas cargas também são iguais, então as intensidades dos vetores E_A e E_B são iguais.
Alternativa: D

107) (Livro do Aluno SEDC/2026) (FUVEST 2005) Três grandes placas P₁, P₂ e P₃, com, respectivamente, cargas +Q, -Q e +2Q, geram campos elétricos uniformes em certas regiões do espaço. As figuras a seguir mostram, cada uma, intensidade, direção e sentido dos campos criados pelas respectivas placas P₁, P₂ e P₃, quando vistas de perfil.

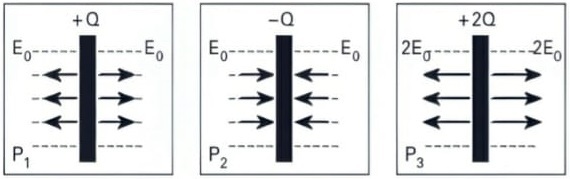
Colocando-se as placas próximas, separadas pela distância D indicada, o campo elé­trico resultante, gerado pelas três placas em conjunto, é representado por:

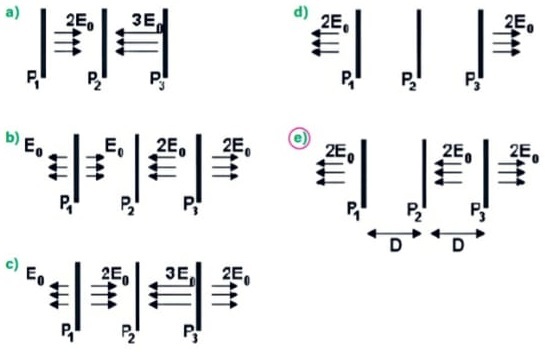
Resolução:
Para resolver essa questão vamos traçar o campo elétrico gerado por cada uma das placas, inde­pendentemente, nas quatro regiões. Como as placas são grandes e estão próximas, podemos considerar os campos gerados por cada uma delas como campos constantes.
Os vetores acima são os vetores campo elétrico gerados pela placa P₁, de intensidade E₀; os vetores do meio são os vetores campo elétrico gerados pela placa P₂, de intensidade E₀; e os vetores abaixo são os vetores campo elétrico gerados pela placa P₃ de intensidade 2E₀ :

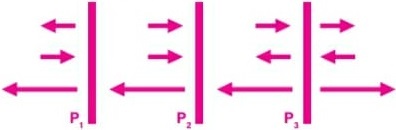
Realizando a soma desses vetores em cada uma das quatro regiões, obtemos o resultado:

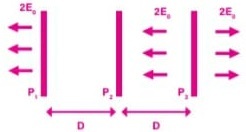
Alternativa: E

108) (Livro do Aluno SEDC/2026) (NEM 2020) Há muitos mitos em relação a como se proteger de raios, cobrir espelhos e não pegar em facas, garfos e outros bjetos metálicos, por exemplo. Mas, de fato, se houver uma tempestade com raios, alguns cuidados são importantes, como evitar ambientes abertos. Um bom abrigo para proteção é o interior de um automóvel, desde que este não seja conversível.

Qual o motivo físico da proteção fornecida pelos automóveis, conforme citado no texto?

(A) Isolamento elétrico dos pneus.
(B) Efeito de para-raios da antena.
(C) Blindagem pela carcaça metálica.
(D) Escoamento da água pela lataria.
(E) Aterramento pelo fio terra da bateria.
Resolução:
A carcaça do automóvel, sendo feita de material condutor, atua como uma gaiola de Faraday, garantindo que o campo elétrico em seu interior seja sempre nulo. As cargas elétricas se distribuem na superfície da carcaça do automóvel de forma a neutralizar os campos elétricos externos. Essa blindagem eletrostática eficaz é o que torna o interior de um automóvel fechado um local seguro durante uma tempestade com raios.
Alternativa: C

109) (Livro do Aluno SEDC/2026) (ENEM 2024) Em um experimento de laboratório, duas barras metálicas, A e B, são carregadas com cargas opostas e imersas em óleo. Farelo de milho é jogado sobre o óleo e, após um certo tempo, o farelo assume o formato das linhas de campo elétrico entre as barras. A figura representa a vista superior desse experimento.

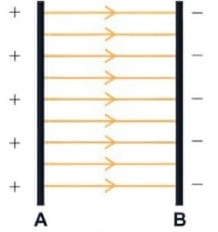
Ao repetir o experimento colocando um cilindro metálico oco entre as placas, o es­quema que representa o formato das linhas de campo assumido pelo farelo é:

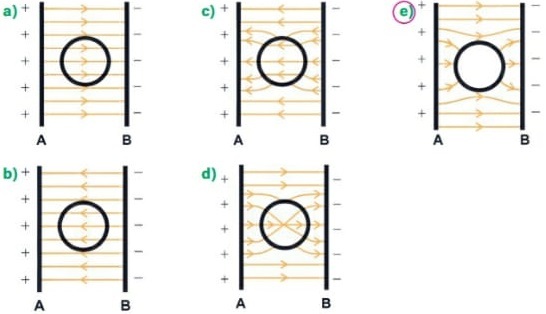
Resolução:
Quando um condutor fechado é introduzido em uma região com um campo elétrico externo, as cargas elétricas dentro do condutor se redistribuem devido à influência desse campo. Essa redistri­buição ocorre de forma que as cargas se organizam na superfície do condutor de maneira a gerar um campo elétrico interno que neutraliza exatamente o campo elétrico externo. Como resultado, o campo elétrico resultante no interior do condutor é anulado, portanto, não há linhas de campo elétrico dentro do condutor em equilíbrio eletrostático.
Alternativa:

RESUMO – POTENCIAL ELÉTRICO

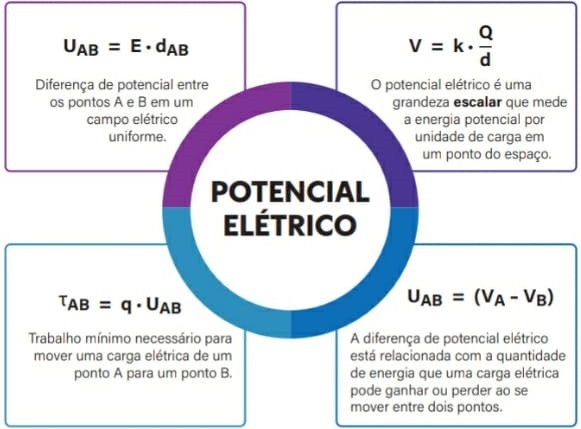
110) (Livro do Aluno SEDC/2026) (UFAM 2016) A figura a seguir mostra a configuração das linhas de força de duas superfícies equipotenciais de um campo elétrico uniforme de intensidade.

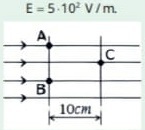
Se uma carga puntiforme q C = + 01,_μé colocada no ponto A, assinale a alternativa INCORRETA.

(A) O trabalho da força elétrica que atua na carga puntiforme não depende da trajetória que liga o ponto A com o ponto C e vale 5 . 10^-6 J .
(B) A diferença de potencial elétrico entre os pontos A e C vale 50V.
(C) Nenhum trabalho é realizado pela força elétrica ao deslocar a carga puntiforme do ponto A para o ponto B.
(D) O potencial elétrico é uma grandeza escalar associada a cada ponto do campo elé­trico, de modo que o potencial elétrico no ponto B é maior que o potencial elétrico no ponto C.
(E) O potencial elétrico é uma grandeza vetorial associada a cada ponto do campo elé­trico, de modo que o potencial elétrico nos pontos A e B tem o mesmo valor.
Resolução:
Para resolver esta questão, analisaremos cada uma das alternativas:
O trabalho da força elétrica que atua na carga puntiforme não depende da trajetória que liga o ponto A com o ponto C. Essa afirmação é verdadeira.
O trabalho realizado pela força elétrica pode ser calculado pela expressão:
τ_AC = q . U_AV
O enunciado fornece o valor da carga:
q = +0,1 τC = 0,1 ⋅ 10^-6 C
Porém o valor da diferença de potencial (U) não é dado.
O enunciado fornece o valor do campo elétrico:
E = 5 . 10² V/M
O valor da distância pode ser obtido a partir da figura:
d = 10 cm = o,1 m
Lembrando que a distância deve ser medida sempre na direção das linhas de força.
Logo, a diferença de potencial entre os pontos A e C é:
U = 5 . 10⁵ V/m . 0,1 m
U = 50 V
Agora que descobrimos o valor da diferença de potencial, podemos calcular o traba­lho realizado pela força elétrica:
τ_AC = q . U_AV = 0,1 . 10^-6 . 50
τ_AC = 5 . 10-6 J
Podemos concluir, portanto, que a alternativa A é CORRETA.
Alternativa B
Conforme calculamos anteriormente, a diferença de potencial U entre os pontos A e C é igual a 50V.
Logo, a alternativa B também é CORRETA.
Alternativa C
Pela figura podemos notar que os pontos A e B estão sobre uma superfície equipo­tencial (superfície perpendicular à direção das linhas de força), o que significa que o potencial elétrico é o mesmo nesses dois pontos. Dessa forma, não há diferença de potencial entre esses dois pontos.
Logo, o trabalho realizado pela força elétrica ao deslocar a carga puntiforme do ponto A para o ponto B é nulo.
Portanto, a alternativa C também é CORRETA.
Alternativa D

A primeira parte da alternativa: “O potencial elétrico é uma grandeza escalar asso­ciada a cada ponto do campo elétrico” é verdadeira.
Aplicando a ideia de que quanto mais se avança no sentido das linhas de força do campo elétrico, menor será o potencial elétrico, e analisando a figura, percebemos que o ponto C está à frente do ponto B (em relação ao sentido das linhas de força). Portanto o potencial elétrico em C é menor que o potencial elétrico em B.
Logo, a alternativa D também é CORRETA.
Alternativa E
A alternativa E inicia afirmando que o potencial elétrico é uma grandeza vetorial. Essa afirmação é falsa, dado que o potencial elétrico é uma grandeza escalar.
A segunda parte da alternativa “o potencial elétrico nos pontos A e B tem o mesmo valor” é verdadeira, dado que os pontos A e B estão situados na mesma superfície equipotencial.
Porém, como a primeira parte da alternativa apresenta uma afirmação falsa, então a alternativa está INCORRETA.

112) (Livro do Aluno SEDC/2026) (INATEL 2019) Na figura a seguir, estão dispostas, no vácuo, três cargas elétricas de intensidade q_A = -2μ_C, q_B = 4μC e qC = -1μC.

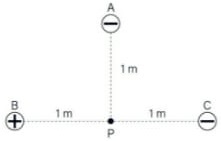
Qual das alternativas representa o potencial elétrico resultante no ponto P? Dado: k= 9, 0 .10⁹.N. m²/C²

(A) 20 10³ V
(B) 9 10³ V
(C) - 9 . 10³ V
(D) - 20 10³ V
(E) 0 V
Resolução:
Para calcular o potencial elétrico no ponto P, é preciso primeiro calcular o potencial que cada uma das cargas gera no ponto P independentemente.
Potencial que a carga A gera no ponto P:
q_A = - 2μ  = -2 . 10^-6 C
d_A = 1 m
k₀ = 9,0 . 10 Nm²/C
Aplicando:
V = k . |Q|
             D

V_A = ko . qA = 9,0 .10⁹ . (-2 . 10^-6)
                dA                              1

V_A = - 18 .10³ V
Potencial que a carga B gera no ponto P:
V_A = ko . qB = 9,0 .10⁹ . 4 . 10^-6
               qB                              1

V_B = 36 .10³ V
Potencial que a carga C gera no ponto P:
V_A = ko . qC = 9,0 .10⁹ . (-1 . 10^-6)
                qC                              1

V_C = - 96 .10³ V
O potencial resultante no ponto P (VP) é a soma algébrica dos potenciais gerados por cada carga neste ponto:
V_P = Va + V_B + V_C
V_P = (- 18 . 1^-3) + (36 . 10³) + (-9 . 10³)
V_P = 9 .10³ V
Alternativa: B

113) (Livro do Aluno SEDC/2026) (FUVEST 2013) Um raio proveniente de uma nuvem transportou para o solo uma carga de 10 C sob uma diferença de potencial de 100 milhões de volts.  A energia liberada por esse raio é:
Note e anote: 1 310 7 _J__kWh = _ −

(A) 30_MWh.
(B) 3 MWh.
(C) 300 kWh
(D) 30 kWh
(E) 3 kWh
Resolução:
A energia liberada pelo raio equivale ao trabalho realizado pela força elétrica para transportar a carga da nuvem (A) até o solo (B). Portanto, podemos calcular essa energia por meio de:
τAB = q . U_AB
q = 10 C
U_AB = 100 . 10⁶ . V = 10⁸ V
τAB = 10 . 10⁸
τAB = 10⁹ J
Como trabalhamos com as unidades do SI, então obtivemos o resultado em joule (J).
Porém, as alternativas apresentam o resultado em MWh (Megawatt-hora) ou kWh (quilowatt-hora).
Portanto, é necessário converter o resultado obtido para as unidades indicadas.
O enunciado fornece a relação entre joule (J) e kilowatt-hora (kWh):
1J = 3 . 10^-7 kWh
τAB = 10⁹ J = 10⁹ . 3 .10^-7 = 3 .10² kWh
τAB = 300 kWh
Alternativa: C

114) (Livro do Aluno SEDC/2026) (FUVEST 2008 – Adaptada) Duas pequenas esferas iguais, A e B, carregadas, cada uma, com uma carga elétrica Q igual a – 4,8 . 10^-9  C, estão fixas e com seus centros separados por uma distância de 12 cm.

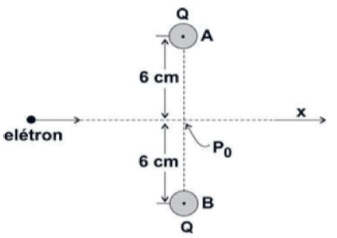
Calcule o potencial elétrico V, em volts, criado pelas duas esferas no ponto P0.
Note e anote: k = 9,0 . 10⁹ Nm²/C²
Resolução:
Calculando o potencial elétrico no ponto P₀:
V = VA + VB = k . Q + k . Q = 2 k .Q
                             D         d            d 

V = 2 .  9 . 10⁹ . (- 4,8  . 10^-9)
                     6 . 10^-2

V = - 1,440V

115) (Livro do Aluno SEDC/2026) (VUNESP 2008) A figura é a intersecção de um plano com o centro C de um condutor esférico e com três superfícies equipotenciais ao redor desse condutor.

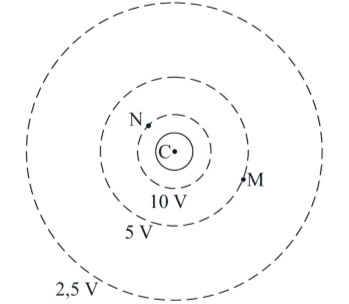
Uma carga de 1,6 .10^-19 Cé levada do ponto M ao ponto N. O trabalho realizado para deslocar essa carga foi de:

(A) 3,2 . 10^-20 J
(B) 16,0 . 10^-19 J
(C) 8,0 . 10^-19 J
(D) 4,0 . 10^-19 J
(E) 3,2 . 10^-18
Resolução:
A carga foi deslocada do ponto M onde o potencial elétrico é:
V_M = 5 V
Até o ponto N, onde o potencial elétrico é:
V_N = 10 V
A diferença de potencial não depende do caminho que a carga percorreu.
Podemos calcular a diferença de potencial (U) entre os dois pontos desta forma:
U = (V_N – V_N) = 5 V – 10V = - 5V
O enunciado nos fornece o valor da carga:
q = 1,6 . 10^-19 C
Com tais dados, podemos calcular o trabalho realizado:
τMN = q . U
τMN = 1,6 . 10^-19 . (-5)
τMN = - 8. 10-¹⁹ J
O enunciado pede o trabalho realizado para deslocar essa carga. Notamos que a carga está se deslocando de va­lores de menor potencial para valores de maior potencial, o que representa um movimento forçado. Portanto, o agente que deslocou a carga teve que realizar um trabalho positivo de mesmo valor.
Logo: τMN = - 8. 10-¹⁹ J
Alternativa: C


116) (Livro do Aluno SEDC/2026) (UERJ 2018) Na ilustração, estão represen­tados os pontos I, II, III e IV em um campo elétrico uniforme.

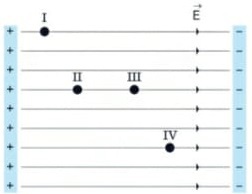
Uma partícula de massa desprezível e carga positiva adquire a maior energia potencial elétrica possível se for colocada no ponto:

(A) I
(B) II
(C) III
(D) IV
Resolução:
Alternativa: A

117) (Livro do Aluno SEDC/2026) (UNICAMP 2022) As máscaras de proteção N95 e PFF2 se tornaram ferramentas importantes no combate à disseminação do novo coronavírus durante a pandemia da covid-19. Essas máscaras possuem fibras compostas de um material com campo elétrico permanente e são capazes de realizar uma filtragem eletrostática das partícu­las ou gotículas dispersas no ar.
Considere um campo elétrico uniforme de módulo E = 4,0 . 10^-2 V/M, em uma região do espaço.

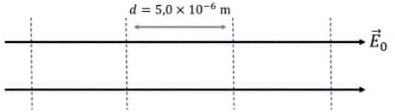
A diferença de potencial elétrico entre duas linhas tracejadas paralelas entre si e perpendiculares à direção desse campo elétrico, separadas por uma distân­cia d, conforme mostra a figura a seguir, é igual a:

(A) 1,6 . 10^-10 V
(B) 2,0 . 10^-7 V
(C) 08, 10^-6 V
(D) 1,2 .10^-4 V
Resolução:
O enunciado afirma que o campo elétrico é uniforme.
A diferença de potencial em um campo elétrico uniforme é dada pela expressão:
U = E . d
O enunciado fornece o valor do campo elétrico:
E₀ = 4,0 . 10^-2