Professor Diminoi
FUNÇÃO LOGARÍTMICA
A função logarítmica de base a é definida como f (x) = loga x, com a real, positivo e a ≠ 1. A função inversa da função logarítmica é a função exponencial.
O logaritmo de um número é definido como o expoente ao qual se deve elevar a base a para obter o número x, ou seja: Exemplos
Exemplos
- f (x) = log3 x
- g (x) =
- h (x) = log10 x = log x
Domínio da função logaritmica
ara que a função seja contínua, por definição, o domínio de uma função logarítmica é o conjunto dos números reais positivos diferentes de zero, isso significa que x sempre será um número positivo, o que faz com que o gráfico da função restrinja-se ao primeiro e segundo quadrantes.
Gráfico da função logarítmica
Existem duas possibilidades de comportamento para o gráfico de uma função logarítmica, podendo ser crescente ou decrescente. Um gráfico é conhecido como crescente quando à medida que o valor de x aumenta, o valor de f(x) também aumenta, e como decrescente quando à medita que o valor de x aumenta, o valor de f(x) diminui.
Para verificar se a função é crescente ou decrescente, é necessário analisar o valor da base do logaritmo:
Dada a função f(x) = logax
- Se a > 1 → f(x) é crescente. (Quando a base do logaritmo é um número maior que 1, a função é crescente.)
- Se 0 < a < 1 → f(x) é decrescente. (Quando a base do logaritmo é um número entre 0 e 1, então a função é decrescente.)
Função crescente
Para construção do gráfico, vamos atribuir valores para x e encontrar o correspondente em y.
Exemplo:
f(x) = log2x
Marcando-se os pontos no plano cartesiano, é possível realizar-se a representação gráfica. Como a base era maior que 1, então é possível perceber que o gráfico da função comporta-se de forma crescente, ou seja, quanto maior o valor de x, maior será o valor de y.
Como a base era maior que 1, então é possível perceber que o gráfico da função comporta-se de forma crescente, ou seja, quanto maior o valor de x, maior será o valor de y.
Função decrescente
Para realizar a construção, utilizaremos o mesmo método feito anteriormente.
Exemplo:
![]()
Encontrando alguns valores numéricos na tabela, teremos:
Realizando a marcação dos pares ordenados no plano cartesiano, encontraremos a seguinte curva: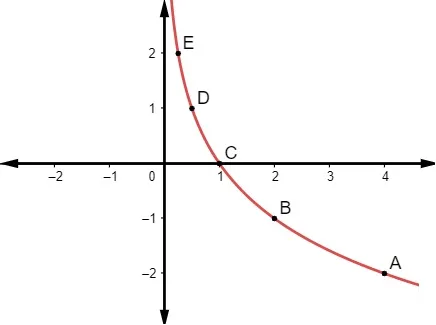
É importante perceber que quanto maior o valor de x, menor será sua imagem y, o que torna esse gráfico decrescente de uma função logarítmica. Isso ocorre porque a base é um número entre 0 e 1
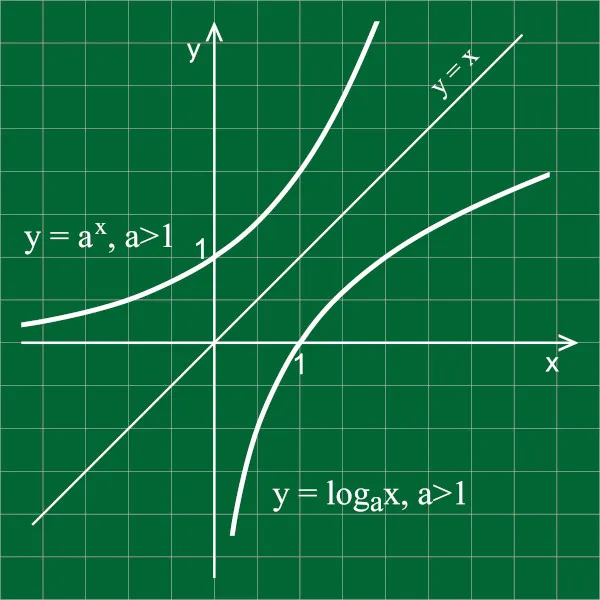
Função logarítmica e função exponencial
Essa relação é bastante importante para compreender-se o comportamento das funções. Acontece que tanto a função logarítmica quanto a função exponencial são inversíveis, ou seja, admitem inversa, além disso, a função logarítmica é a inversa da função exponencial e vice-versa, veja:
Para encontrar a lei de formação e o domínio e contradomínio da função inversa, precisamos, primeiramente, inverter o domínio e o contradomínio.
Se a função logarítmica, como vimos, vai dos R*+ → R, então a função inversa terá domínio e contradomínio R → R*+, além disso, vamos inverter a lei de formação.
y = logax
Para inverter, trocamos x e y de lugar, e isolamos o y, então teremos:
x = logay
Aplicando a exponencial de a dos dois lados, temos que:
ax = alogay
ax = y → função exponencial
A função logarítmica é a inversa da função exponencial
QUESTÕES COMENTADAS
01) (Enem) A Escala e Magnitude de Momento (abreviada como MMS e denotada como MW), introduzida em 1979 por Thomas Haks e Hiroo Kanamori, substituiu a Escala de Richter para medir a magnitude dos terremotos em termos de energia liberada. Menos conhecida pelo público, a MMS é, no entanto, a escala usada para estimar as magnitudes de todos os grandes terremotos da atualidade. Assim como a escala Richter, a MMS é uma escala logarítmica. MW e M0 se relacionam pela fórmula:![]() Em que M0 é o momento sísmico (usualmente estimado com base nos registros de movimento da superfície, por meio dos sismogramas), cuja unidade é o dina⋅cm. O terremoto de Kobe, acontecido no dia 17 de janeiro de 1995, foi um dos terremotos que causaram maior impacto no Japão e na comunidade científica internacional. Teve magnitude MW = 7,3.
Em que M0 é o momento sísmico (usualmente estimado com base nos registros de movimento da superfície, por meio dos sismogramas), cuja unidade é o dina⋅cm. O terremoto de Kobe, acontecido no dia 17 de janeiro de 1995, foi um dos terremotos que causaram maior impacto no Japão e na comunidade científica internacional. Teve magnitude MW = 7,3.
Mostrando que é possível determinar a medida por meio de conhecimentos matemáticos, qual foi o momento sísmico M0?
(A) 10-5,10
(B) 10-0,73
(C) 1012,00
(D) 1021,65
(E) 1027,00
Resolução:
Para encontrar o M0, vamos substituir o valor da magnitude dado na questão:
Alternativa: E
02) (Enem 2019 – PPL) Um jardineiro cultiva plantas ornamentais e as coloca à venda quando atingem 30 centímetros de altura. Esse jardineiro estudou o crescimento de suas plantas, em função do tempo, e deduziu uma fórmula que calcula a altura em função do tempo, a partir do momento em que a planta brota do solo até o momento em que ela atinge sua altura máxima, de 40 centímetros. A fórmula é h = 5·log2 (t + 1), em que t é o tempo contado em dia, e h, a altura da planta em centímetro.
A partir do momento em que uma dessas plantas é colocada à venda, em quanto tempo, em dias, ela alcançará sua altura máxima?
(A) 63
(B) 96
(C) 128
(D) 192
(E) 255
Resolução:
t1 o tempo que a planta leva para atingir h1 = 30 cm
t2 o tempo que a planta leva para atingir h2 = 40 cm
Queremos encontrar o intervalo de tempo entre h1 = 30 cm e h2 = 40 cm. Para isso, vamos substituir cada um deles na lei de formação, e fazer a diferença entre t2 e t1.
Encontrando t1:
Agora vamos encontrar o valor de t2:
O tempo t é a diferença t2 – t1 = 255 – 63 = 194.
Alternativa: D
03) Seja f(x) = log2x e g(x) = log3 x a lei de formação de duas funções f(x) e g(x), então o valor de f(8) – g (9) é igual a:
(A) 0.
(B) 1.
(C) 2.
(D) –1.
(E) – 2.
Resolução:
Calculando f(8), temos que:
f(8) = log2 8
f(8) = 3
Agora calculando g(9):
g(9) = log39
g(9) = 2
Por fim, a diferença entre elas é 3 – 2 = 1.
Alternativa: B
04) Analisando o gráfico da função: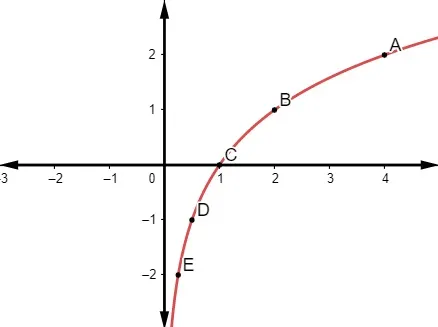 Podemos afirmar que a sua lei de formação é:
Podemos afirmar que a sua lei de formação é:
(A) f(x) = 2x
(B) f(x) = logx + 2
(C) f(x) = log2x
(D)f(x) = – 2x
(E) f(x) = log x²
Resolução:
Analisando o comportamento da função, ela é uma função logarítmica. Note que o ponto (2,1) pertence ao gráfico, então:
f(x) = logax
f(2) = loga2
1 = loga2
Aplicando a definição de logaritmo, temos que:
a1= 2
a = 2
Como a base é 2, então a função é:
f(x) = log2x
Alternativa: C
06) Podemos ver a seguir a representação de uma função logarítmica: Com base em seu gráfico, sabendo que essa função é uma função do tipo f(x) = logb x, então o valor da base b é:
Com base em seu gráfico, sabendo que essa função é uma função do tipo f(x) = logb x, então o valor da base b é:
(A) 1
(B) 2
(C) 4
(D) – 2
(E) 1/2
Resolução:
Analisando o gráfico, sabemos que f(4) = – 2. Então, temos que:
f(4) = logb 4
– 2 = logb 4
Aplicando a definição de logaritmo:
Alternativa: E
07) Sobre a função logarítmica, julgue as afirmativas a seguir:
I → O domínio da função logarítmica é o conjunto dos números reais.
II → A função logarítmica é crescente quando a sua base é maior que 1.
III → A função logarítmica é decrescente quando sua base é negativa.
(A) Somente a I é verdadeira.
(B) Somente a II é verdadeira.
(C) Somente a III é verdadeira.
(D) Somente a II e a III são verdadeiras.
(E) Somente a I e a II são verdadeiras.
Resolução:
I → Falsa, pois o domínio é formado pelos números reais positivos.
II → Verdadeira. Se a base é maior que 1, a função é crescente.
III → Falsa. A base não pode ser negativa. Para que a função seja decrescente, sua base precisa ser um número maior que 0 e menor que 1.
Alternativa: B
08) (Uerj) O número, em centenas de indivíduos, de um determinado grupo de animais, x dias após a liberação de um predador no seu ambiente, é expresso pela seguinte função:![]() Após cinco dias da liberação do predador, o número de indivíduos desse grupo presentes no ambiente será igual a:
Após cinco dias da liberação do predador, o número de indivíduos desse grupo presentes no ambiente será igual a:
(A) 3.
(B) 4.
(C) 300.
(D) 400.
Resolução:
Calculando f(5), temos que:
Agora resolvendo o logaritmo, temos que:
O valor encontrado está em centenas de pessoas, logo há 3 centenas, ou seja, 300.
Alternativa: C
09) Durante os estudos sobre o crescimento de uma determinada árvore, foi possível modelar o crescimento dela no decorrer do tempo por meio da função A(t) = 1 + log3 (5 + t), em que t é o tempo em anos e A(t) é a altura em metros. Sendo assim, podemos afirmar que altura dessa árvore, após 4 anos, será de:
(A) 1 metro.
(B) 2 metros.
(C) 2 metros e meio.
(D) 3 metros.
(E) 3 metros e meio.
Resolução:
A(t) = 1 + log3 (5 + t)
A(4) = 1 + log3 (5 + 4)
A(4) = 1 + log3 (9)
A(4) = 1 + 2
A(4) = 3
Alternativa: D
10) Em uma determinada cidade, o número de nascimentos, no decorrer dos anos, está sempre crescendo. Para compreender melhor essa relação, os matemáticos modelaram uma função que dá a expectativa da quantidade que crianças que vão nascer para um determinado ano.
N(t) = 900 ·log2 (t – 1999)3 , em que t > 1999. De acordo com essa função, supondo que o comportamento seja exatamente o previsto, nascerão 5.400 crianças no ano de:
(A) 2002.
(B) 2003.
(C) 2004.
(D) 2005.
(E) 2006.
Resolução:
Dada a função:
N(t) = 900 ·log2 (t – 1999)3
Queremos que:
900 ·log2 (t – 1999)3 = 5400
Utilizando a propriedade do logaritmo:
900 ·3 log2 (t – 1999) = 5400
2700 log2 (t – 1999) = 5400
log2(t – 1999) = 5400 : 2700
log2 (t – 1999) = 2
Utilizando a definição de logaritmo:
2² = t – 1999
4 = t – 1999
4 + 1999 = t
2003 = t
Alternativa: B
12) O tempo, em minutos, que um medicamento leva para fazer efeito em uma pessoa é dado pela função:![]() Considere que x é a idade e f(x) é o tempo em minutos.
Considere que x é a idade e f(x) é o tempo em minutos.
Em um paciente que possui 30 anos, o tempo necessário para que esse remédio faça efeito é de:
(Use log 2 = 0,3.)
(A) 2 minutos e 70 segundos.
(B) 2 minutos e 42 segundos.
(C) 3 minutos e 26 segundos.
(D) 5 minutos.
(E) 7 minutos e 30 segundos.
Resolução:
Calculando f(30):
Agora vamos converter a parte decimal em segundos. Sabemos que 0,7 · 60 = 42, ou seja, 2 minutos e 42 segundos.
Alternativa: B
13) (Unesp) A expectativa de vida em anos, em uma região, de uma pessoa que nasceu a partir de 1900 no ano x ( x ≥ 1900) é dada por L(x)=12·(199log10x - 651). Considerando Log2 = 0,3, uma pessoa dessa região que nasceu no ano 2000 tem expectativa de viver:
(A) 48,7 anos.
(B) 54,6 anos.
(C) 64,5 anos.
(D) 68,4 anos.
(E) 72,3 anos.
Resolução:
L(x) = 12·(199log10x – 651)
L(2000) = 12·(199log102000 - 651)
L(2000) = 12·[199log10(1000·2) - 651]
L(2000) = 12·[199(log101000+ log102) - 651]
L(2000) = 12·[199·(3+ 0,3) - 651]
L(2000) = 12·[199·(3,3) - 651]
L(2000) = 12·[656,7 - 651]
L(2000 )=12·5,7
L(2000) = 68,4 anos
Alternativa: D
14) O volume de um reservatório em função do tempo é dado em litros pela função:![]() Considere que t ≥ 1, e t é dado em dias e V(t) é dado em litros. Sendo assim, após quantos dias o volume da piscina será de 284 litros?
Considere que t ≥ 1, e t é dado em dias e V(t) é dado em litros. Sendo assim, após quantos dias o volume da piscina será de 284 litros?
(A) 12 dias
(B) 14 dias
(C) 15 dias
(D) 16 dias
(E) 17 dias
Resolução:
Sabemos que V(t) = 284, então:
Alternativa: E
15) A solução real da equação logaritmica -1 = log5[ 2x/(x + 1) ] é
Resolução: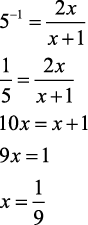
Se log10(2x – 5) = 0, então x vale:
FUNÇÃO TRIGONOMETRICA
As funções trigonométricas são consideradas funções angulares e são utilizadas para o estudo dos triângulos e em fenômenos periódicos. Podem ser caracterizadas como razão de coordenadas dos pontos de um círculo unitário.
As funções consideradas elementares são:
- Seno: f(x) = sen x
- Cosseno: f(x) = cos x
- Tangente: f(x) = tg x
Gráfico da função trigonométrica seno: f(x) = sen (x + 2) Gráfico da função trigonométrica cosseno: f(x) = cos (x + 2)
Gráfico da função trigonométrica cosseno: f(x) = cos (x + 2) Gráfico da função tangente: f(x) = tg (x + 2)
Gráfico da função tangente: f(x) = tg (x + 2)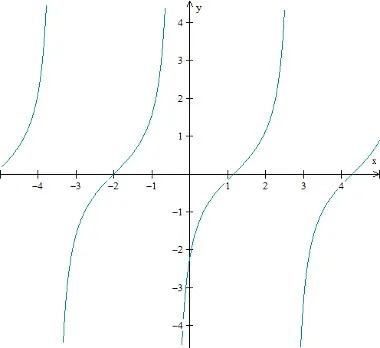
17 - Função RAIZ
O que determina o domínio da função raiz é o termo n que faz parte do expoente. Se n for ímpar, o domínio (x) será o conjunto dos números reais; se n for par, o domínio (x) será somente os números reais positivos. Isso porque, quando o índice é par, o radicando (termo que fica dentro da raiz) não pode ser negativo.
Fórmula geral da função raiz
f(x) = x 1/n
f(x) = Imagem
x = domínio/ base
1/n = expoente
Gráfico da função raiz: f(x) = (x)1/2
FUNÇÕES TRIGONOMÉTRICAS
Funções trigonométricas são três: a função seno, a função cosseno e a função tangente. Elas relacionam o valor do ângulo com o valor da razão trigonométrica.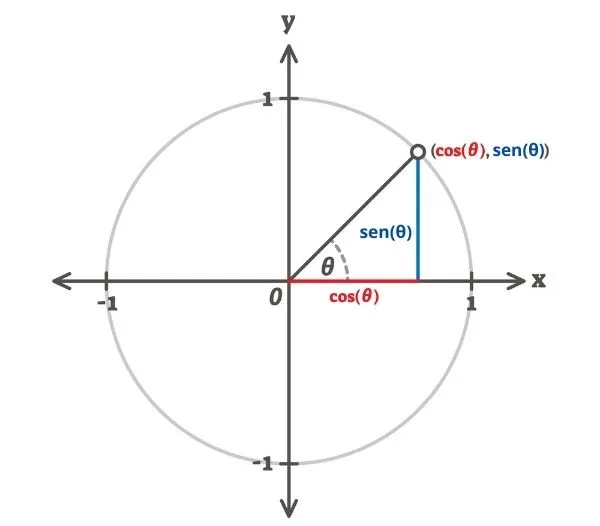
As funções trigonométricas são as funções sebo, cosseno e tangente. Todas as funções trigonométricas relacionam o valor do ângulo em graus ou radianos com o valor da razão trigonométrica, relação essa que pode ser feita por meio do estudo do ciclo trigonométrico.
Com o estudo individual de cada uma das funções trigonométricas, é possível fazer a representação gráfica, estudar o sinal da função para cada um dos quadrantes, entre outras características importantes.
Quais são as funções trigonométricas?
As funções trigonométricas mais usuais são a função seno, a função cosseno e a função tangente. O estudo delas está ligado ao ciclo trigonométrico.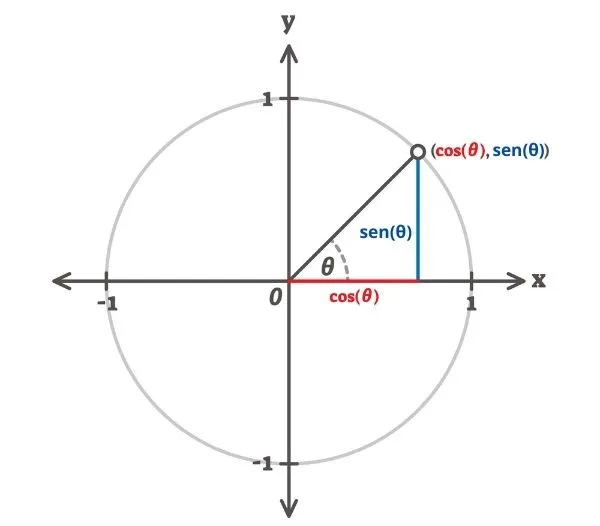
Ciclo trigonométrico
Para cada valor de ângulo, há um único valor para o seno e para o cosseno. As funções trigonométricas nada mais são que a relação entre o ângulo e o valor da razão trigonométrica para esse ângulo. Vale lembrar que o valor desse ângulo pode ser dado em radianos ou em graus e que o valor do seno e do cosseno é sempre um número real entre -1 e 1. Valor do seno e do cosseno para os principais ângulos
Valor do seno e do cosseno para os principais ângulos
Note na imagem que, para cada ângulo, o cosseno e o seno admitem um valor. É com base no estudo de cada uma das funções trigonométricas que observamos a relação entre o valor do ângulo e o valor da razão trigonométrica.
Função cosseno
A função cosseno é a função f : R → R, cuja lei de formação é f(x) = cos (x). Como o cosseno de um ângulo é sempre um número entre 1 e -1, então, -1 ≤ cos (x) ≤ 1.
Domínio
O domínio da função cosseno é o conjunto dos números reais, pois não existe nenhuma restrição para o valor de x, em que x é o ângulo em radianos. Para todo número real, é possível encontrar o valor de cos(x), então, Df = R.
Imagem
Sabemos que o contradomínio da função cosseno é o conjunto dos números reais, entretanto, quando analisamos a imagem da função, é possível perceber que ela é sempre um valor maior ou igual a -1 e menor ou igual a 1, pois o ciclo trigonométrico tem raio 1, então, o maior valor que a função cosseno pode assumir é 1, e, analogamente, o menor valor que ela pode assumir é -1. Im = [-1, 1]
Gráfico da função cosseno
O gráfico da função cosseno está contido entre as retas y = -1 e y = 1. Vale lembrar que isso acontece porque a imagem da função é sempre um número entre -1 e 1 e possui parte crescente e parte decrescente, como podemos ver a seguir: Gráfico da função cosseno
Gráfico da função cosseno
Fazendo a correspondência do valor do ângulo com o valor da razão trigonométrica, é possível perceber que o gráfico possui um comportamento cíclico, ou seja, o comportamento sempre se repete de forma periódica. O gráfico da função cosseno é conhecido como cossenoide.
Sinal
Sabemos que, no ciclo trigonométrico, o cosseno possui valores positivos no I e IV quadrantes. O primeiro quadrante está entre 0º e 90º, e o quarto quadrante está entre 270º e 360º. Em radianos, a função é positiva para valores de x entre 0 e π/2 e entre 3π/2 e 2π.
A função cosseno possui valores negativos no II e III quadrantes, ou seja, o ângulo está entre 90º e 270º. Em radianos, para que a função cosseno seja negativa, x está entre π/2 e 3π/2. Sinal da função cosseno
Sinal da função cosseno
Período da função cosseno
O gráfico da função cosseno tem um período de 2π. Analisando, é possível perceber que o gráfico está contido no intervalo de 0 a 2π. Para valores anteriores ou posteriores a esse intervalo, o gráfico se repete.
Paridade
A função cosseno é considerada uma função par, pois há uma simetria no gráfico em relação ao eixo y. Quando uma função é considerada par, temos que f (x) = f (-x), ou seja, cos (x) = cos (-x).
Arcos notáveis da função cosseno
Vejamos o valor do cosseno para os principais ângulos:
Arcos notáveis da função cosseno
Função seno
A função cosseno é a função f : R → R, cuja lei de formação é f(x) = sen (x). Como o seno de um ângulo, assim como o cosseno, é sempre um número entre 1 e -1, então, -1 ≤ sen (x) ≤ 1.
Domínio
O domínio da função seno é o conjunto dos números reais. A função f(x) = sen (x) está definida para todos os números reais, então, Df = R.
Imagem
A imagem da função seno possui valor máximo em f(x) = 1 e valor mínimo quando f(x) = -1. Então, a imagem da função é o intervalo real [-1, 1].
Gráfico da função seno
O gráfico da função seno é limitado também pelas retas horizontais y = -1 e y = 1. O comportamento é parecido com o da função seno periódico, tendo intervalos crescentes e intervalos decrescentes.
Observe a representação gráfica da função seno no plano cartesiano a seguir:
Gráfico da função seno O gráfico da função seno também é periódico e é conhecido como senoide.
O gráfico da função seno também é periódico e é conhecido como senoide.
Sinal
Diferentemente da função cosseno, a função seno possui valores positivos nos quadrantes I e II primeiro, ou seja, para ângulos entre 0º e 180°. Em radianos, a função é positiva para valores entre 0 e π.
A função seno possui valores negativos no III e IV quadrantes, ou seja, o ângulo está entre 180º e 360º. Em radianos, para que a função seno seja negativa, x está entre π e 2π.
 Sinal da função seno
Sinal da função seno
Período da função cosseno
O gráfico da função seno tem um período de 2π. Isso significa que, posteriormente ou anteriormente ao intervalo de 0 a 2π, o gráfico é periódico, ou seja, repete-se.
Paridade
A função seno é considerada uma função ímpar, pois há uma simetria no gráfico em relação à bissetriz dos quadrantes ímpares. Quando uma função é considerada ímpar, temos que f (x) = -f (x), ou seja, sen (-x) = -sen (x).
Arcos notáveis da função seno
Vejamos o valor do seno para os principais ângulos:
Arcos notáveis da função seno.
Função tangente
Sabemos que a tangente é a razão entre o seno e o cosseno. Diferentemente das duas funções trigonométricas anteriores, a função tangente não possui valor de máximo nem valor de mínimo. Além disso, existem restrições para o domínio, mas a lei de formação da função tangente é f(x) = tan(x).
Domínio
A função tangente possui restrições para o seu domínio, como ela é formada pela razão entre o seno e o cosseno, não existem valores para tangente quando cos(x) = 0. Pesando no ciclo trigonométrico de 0º a 360º, a função tangente não está definida para os ângulos de 90º e 270º, pois são os valores em que o cosseno é igual a 0. Quando há ângulos maiores que uma volta completa, todos aqueles em que o valor de cosseno é 0 não fazem parte do domínio da função cosseno.
Imagem
Diferentemente da função seno e da função cosseno, a imagem da função tangente é o conjunto dos números reais, ou seja, ela não é limitada e não possui valor de máximo nem de mínimo. Im = R
Gráfico da função tangente
A função tangente também é periódica como as funções seno e cosseno, ou seja, ela sempre se repete. Quando comparamos:
Gráfico da função tangente.
Sinal
A função tangente possui valor positivo para os quadrantes ímpares, ou seja, I e III quadrantes. Para ângulos entre 0º e 90º e ângulos entre 180º e 270º, a função possui valores positivos. Em radianos, o valor de x tem que estar entre 0 e π/2 ou π e 3π/2.
Gráfico da função tangente
Período
O período da função tangente também é diferente das funções seno e cosseno. O período da função tangente é π.
Paridade
A função tangente é uma função ímpar, pois tan(-x) = -tan(x), logo, há uma simetria no gráfico em relação à origem do plano cartesiano.
Arcos notáveis da função tangente
Vejamos o valor da tangente para os principais ângulos:
Arcos notáveis da função tangente.
FUNÇÕES TRIHONOMÉTRICAS - COMENTADAS
25) Uma função trigonométrica possui lei de formação igual a f(x) = 2cos(x) – 1. O valor numérico dessa função quando x = π/3 é:
(A) -2
(B) -1
(C) 0
(D) 1
(E) 2
Resolução:
Queremos o valor de f(x) para x = π/3, então, temos que:
Alternativa: C
26) Dada a função f(x) = 3sen(4x) + 6, com domínio e contradomínio nos números reais, podemos afirmar que o conjunto imagem dessa função é:
(A) [-4, 4]
(B) [-4, 6]
(C) [6, 3]
(D) [3, 9]
(E) ]-∞, ∞[
Resolução:
Sabemos que sen(x) está sempre entre -1 e 1, então, para calcular o mínimo da funções, temos que sen(x) = -1.
f(x) = 3 · (-1) + 6
f(x) = -3 + 6
f(x) = 3
Agora, o máximo da função é quando sen(x) = 1:
f(x) = 3 · 1 + 6
f(x) = 3 + 6
f(x) = 9
Alternativa: D
27) Uma função de A → B possui lei de formação igual a:![]() Podemos afirmar que o menor valor que essa função pode ter assim é:
Podemos afirmar que o menor valor que essa função pode ter assim é:
(A) -2
(B) -1
(C) 0
(D) 1
(E) 2
Resolução:
Analisando o denominador, sabemos que ele sempre será positivo, já que cos(x) será sempre menor que 1.
Então, para encontrar o menor valor possível da função, vamos dividir 2 pelo maior número possível.
Nesse caso, admitindo cos(x) = -1, temos que:
Assim, o menor valor possível para essa função é 1.
Alternativa: D
28) Seja f(x) = 1 + 2sen(x), qual deve ser o valor de x, sabendo que ele é um ângulo do 1º quadrante, que faz com que f(x) = 2:
(A) π
(B) π/2
(C) π/3
(D) π/4
(E) π/6
Resolução:
Dada a função f(x) 1 + 2sen(x), sabemos que:
1 + 2sen(x) = 2
2sen(x) = 2 – 1
2sen(x) = 1
sen(x) = 1/2
Queremos encontrar o ângulo do 1º quadrante cujo o valor de seu seno é ½. Nesse caso, trata-se de um ângulo notável que é o ângulo de 30º, que, em radianos, corresponde ao arco π/6.
Alternativa: E
29) Analise as afirmativas a seguir sobre as funções trigonométricas:
I → A função tangente possui imagem no conjunto [-1, 1].
II → A função cosseno e a função seno são periódicas.
III → O conjunto imagem da função trigonométrica y = sen(x) + cos(x) é [-1, 1].
Marque a alternativa correta:
(A) Somente a afirmativa I é verdadeira.
(B) Somente a afirmativa II é verdadeira.
(C) Somente a afirmativa III é verdadeira.
(D) Todas as afirmativas são verdadeiras.
Resolução:
I. Falsa. Diferentemente das funções seno e cosseno, a imagem da função tangente não é limitada entre -1 e 1, podendo ser qualquer número real.
II. Verdadeira. Sabemos que a função cosseno é periódica, pois ela possui período igual a 2π.
III. Falsa. O maior valor da imagem da função é quando sen(x) = 1, ou seja, y = 1 + 3 = 4. O menor valor da imagem da função é quando sen(x) = -1, ou seja, y = -1 + 3 = 2. Assim, a imagem da função seria o conjunto [2, 4].
Alternativa: B
30) (Enem) Segundo o Instituto Brasileiro de Geografia e Estatística (IBGE), produtos sazonais são aqueles que apresentam ciclos bem definidos de produção, consumo e preço. Resumidamente, existem épocas do ano em que a sua disponibilidade nos mercados varejistas ora é escassa, com preços elevados, ora é abundante, com preços mais baixos, o que ocorre no mês de produção máxima da safra.
A partir de uma série histórica, observou-se que o preço P, em reais, do quilograma de certo produto sazonal pode ser descrito pela função![]() Onde x representa o mês do ano, sendo x = 1 associado ao mês de janeiro, x = 2 ao mês de fevereiro, e assim sucessivamente, até x = 12 associado ao mês de dezembro.
Onde x representa o mês do ano, sendo x = 1 associado ao mês de janeiro, x = 2 ao mês de fevereiro, e assim sucessivamente, até x = 12 associado ao mês de dezembro.
Na safra, o mês de produção máxima desse produto é
(A) janeiro.
(B) abril.
(C) junho.
(D) julho.
(E) outubro.
Resolução:
A safra tem seu valor máximo quando o preço é o mínimo possível, e, para isso, o menor valor que o cosseno pode assumir é -1. Ainda, o ângulo que faz com que cos(a) = -1 é a = π, então, temos que:
Alternativa: D
31) (Enem 2017) Raios de luz solar estão atingindo a superfície de um lago formando um ângulo x com a sua superfície, conforme indica a figura.
Em determinadas condições, pode-se supor que a intensidade luminosa desses raios, na superfície do lago, seja dada aproximadamente por I(x) = k · sen(x), sendo k uma constante, e supondo-se que X está entre 0° e 90º. Quando x = 30º, a intensidade luminosa se reduz à qual percentual de seu valor máximo?
Quando x = 30º, a intensidade luminosa se reduz à qual percentual de seu valor máximo?
(A) 33%
(B) 50%
(C) 57%
(D) 70%
(E) 86%
Resolução:
No intervalo de 0º a 90º, a função seno tem seu maior valor quando x = 90º, então, temos que:
i = k · sen(90º)
i = k · 1
i = k
Agora, quando x = 30º, temos que:
i = k · sen(30º)
i = k · 1/2
i = k/2
Como, com 30º, a intensidade é a metade de k, então ela se reduziu a 50% do seu valor máximo.
Alternativa: B
32) (Enem 2018) Em 2014 foi inaugurada a maior roda-gigante do mundo, a High Roller, situada em Las Vegas. A figura representa um esboço dessa roda-gigante, no qual o ponto A representa uma de suas cadeiras: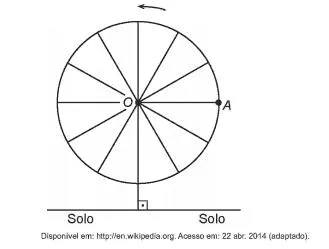 A partir da posição indicada, em que o segmento OA se encontra paralelo ao plano do solo, rotaciona-se a High Roller no sentido anti-horário, em torno do ponto O. Sejam o ângulo determinado pelo segmento OA em relação à sua posição inicial, e f a função que descreve a altura do ponto A, em relação ao solo, em função de t. Após duas voltas completas, f tem o seguinte gráfico:
A partir da posição indicada, em que o segmento OA se encontra paralelo ao plano do solo, rotaciona-se a High Roller no sentido anti-horário, em torno do ponto O. Sejam o ângulo determinado pelo segmento OA em relação à sua posição inicial, e f a função que descreve a altura do ponto A, em relação ao solo, em função de t. Após duas voltas completas, f tem o seguinte gráfico: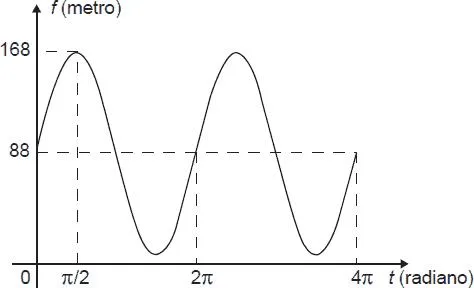 A expressão da função altura é dada por:
A expressão da função altura é dada por:
(A) f(t) = 80sen(t) + 88
(B) f(t) = 80cos(t) + 88
(C) f(t) = 88cos(t) + 168
(D) f(t) = 168sen(t) + 88cos(t)
(E) f(t) = 88sen(t) + 168cos(t)
Resolução:
Sabemos que f(π/2) = 168, que é o máximo da função. A função trigonométrica que tem esse comportamento com máximo em π/2 é a função seno, logo, a função possui lei de formação igual a:
f(t) = X + Y sen(t)
Quando t = 0 e f(t) = 88:
f(0) = X + Ysen(0)
88 = X + Y · 0
88 = X
Conhecendo o valor de X, note que f(π/2) = 168:
f(π/2) = 88 + Ysen(π/2)
168 = 88 + Y · 1
168 – 88 = Y
80 = Y
Então, a lei de formação da função altura é f(t) = 80 + 88sen(t).
Alternativa: A
33) (Furb) Considere o gráfico a seguir: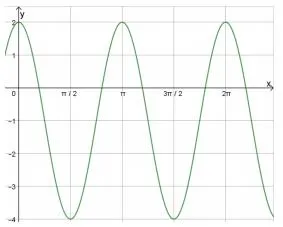 Pode-se afirmar que a função que está representada nesse gráfico é:
Pode-se afirmar que a função que está representada nesse gráfico é:
(A) y = 3cos(2x) – 1
(B) y = cos(2x) + 2
(C) y = 2cos(2x) – 4
(D) y = 3cos(x/2) – 1
(E) y = 2cos(x/2) – 4
Resolução:
Analisando a função, sabemos que:
y = Acos(kx) + B
Sabemos que o ponto (0, 2) pertence ao gráfico, então, temos que:
2 = Acos(k0) + B
2 = Acos(0) + B
2 = A + B
Sabemos que o menor valor que cos(kx) pode assumir é -1, e, quando cos(kx) = -1, temos que f(x) = -4.
-4 = A (-1) + B
-4 = -A + B
Então, temos duas equações:
A + B = 2
-A + B = -4
Realizando a soma dessas equações, temos que:
0A + 2B = -2
2B = -2
B = -2 : 2
B = -1
Como A + B = 2 e B = -1, então, temos que:
A + (-1) = 2
A – 1 = 2
A = 2 + 1
A = 3
Então, a lei de formação é:
y = 3cos(kx) – 1
Por fim, para encontrar o valor de k, temos que x = π, então, y = 2, logo, temos que:
2 = 3cos(kπ) – 1
2 + 1 = 3cos(kπ)
3 = 3cos(kπ)
3 : 3 = cos(kπ)
1 = cos(kπ)
Sabemos que cos(2π) = 1, então, temos que:
kπ = 2π
k = 2
Assim, a lei de formação da função é:
y = 3cos(2x) – 1
Alternativa: A
34) Conhecendo a função trigonométrica y = 2cos²(x) – √2sen(x), o valor da função quando x = π/4 é:
(A) -2
(B) -1
(C) 0
(D) 1
(E) 2
Resolução:
Substituindo x por π/4, temos que:
Alternativa: C
35) Durante a análise de uma função, Kárita encontrou uma função trigonométrica, e ficou em dúvida entre as funções f(x) = sen(x); f(x) = cos(x); e f(x) = tg(x).
I → A função possui imagem [-1, 1].
II → A função é trigonométrica e possui período igual a 2π.
III → O valor numérico da função f(π/2) = 1.
A função descrita por ela é:
(A) uma função seno
(B) uma função cosseno
(C) uma função tangente
(D) uma função cotangente
(E) uma função exponencial
Resolução:
Analisando as informações dadas, sabemos que as funções trigonométricas que satisfazem a afirmativa I e II são a seno e a cosseno, pois ambas são periódicas e também possuem imagem entre [-1, 1].
Para diferenciar entre as duas funções, utilizamos a afirmativa III. A função trigonométrica que possui valor f(π/2) = 1 é a função f(x) = sen(x).
Alternativa: A
36) Das alternativas a seguir, marque aquela que possui a lei de formação de uma função trigonométrica:
(A) f(x) = logx
(B) f(x) = ex
(C) f(x) = 2cos(x) – 4
(D) f(x) = 4x + senπ
(E) f(x) = 2x + 3
Resolução:
A alternativa que contém uma função trigonométrica é a C, pois note que somente nela há uma razão trigonométrica cujo o ângulo é a variável x.
Alternativa: C
37) (Enem 2017) Em um mês, uma loja de eletrônicos começa a obter lucro já na primeira semana. O gráfico representa o lucro (L) dessa loja desde o início do mês até o dia 20. Mas esse comportamento se estende até o último dia, o dia 30. A representação algébrica do lucro(L) em função do tempo (t) é:
A representação algébrica do lucro(L) em função do tempo (t) é:
(A) L(t) = 20t + 3 000
(B) L(t) = 20t + 4 000
(C) L(t) = 200t
(D) L(t) = 200t - 1 000
(E) L(t) 200t + 3 000
Resolução
Analisando o gráfico e sabendo que ele se comporta como uma reta, o gráfico de uma função polinomial do primeiro grau possui lei de formação f(x) = ax + b. Nesse caso, trocando a letras, podemos descrever por:
L(t) = at + b
É possível ver no gráfico que, se t = 0 e L(0) = - 1000, temos que b = - 1000.
Agora, quando t = 20 e L(20) = 3000, substituindo na lei de formação, temos que:
3000 = a·20 - 1000
3000+1000 = 20a
4000 = 20a
4000 : 20 = a
a = 200
A lei de formação da função é:
L(t) = 200t – 1000
Alternativa: D
38) (Enem 2011) Um satélite de telecomunicações, t minutos após ter atingido sua órbita, está a r quilômetros de distância do centro da Terra. Quando r assume seus valores máximo e mínimo, diz-se que o satélite atingiu o apogeu e o perigeu, respectivamente. Suponha que, para esse satélite, o valor de r em função de t seja dado por:![]() Um cientista monitora o movimento desse satélite para controlar o seu afastamento do centro da Terra. Para isso, ele precisa calcular a soma dos valores de r, no apogeu e no perigeu, representada por S.
Um cientista monitora o movimento desse satélite para controlar o seu afastamento do centro da Terra. Para isso, ele precisa calcular a soma dos valores de r, no apogeu e no perigeu, representada por S.
O cientista devera concluir que, periodicamente, S atinge o valor de:
(A) 12 765 km.
(B) 12 000 km.
(C) 11 730 km.
(D) 10 965 km.
(E) 5 865 km.
Resolução
Considere rm e rM, respectivamente, como r mínimo e r máximo. Sabemos que, em uma divisão, quanto maior o denominador, menor será o resultado e que o maior valor que a função cosseno pode assumir é 1, então faremos cos(0,06t) = 1 para calcular o perigeu, ou seja, rm.
Agora, sabemos que o menor valor que a função cosseno pode assumir é – 1 e, quanto menor for o denominador, maior será o resultado de r, logo o rM é calculado por:
Por fim, a soma das distâncias percorridas é dada por:
S = 6900 + 5100 = 12 000
Alternativa: B
Continua...





