PP-M-1ª-2ºBIM-2023

Professor Diminoi
PROVA PAULISTA - MATEMÁTICA - 1º BIM - 2ª SÉRIE

01) (Prova Paulista – 1ª Serie EM)  Chiquinho aplicou a quantia de R $500,00 a juros simples durante 6 meses. A taxa de aplicação foi de 5% ao mês. O montante obtido foi de:
(A) R$ 650,00.
(B) R$ 700,00.
(E) R$ 750,00.
(D) R$ 800,00.
(E) R$ 850,00

02) (Prova Paulista – 1ª Serie EM)  O capital em reais, que deve ser aplicado à taxa mensal de juros simples de 5% , por 4 meses, para se obter juros de R$ 400,00 é igual a,
(A) R$ 1.600,00
(B) R$ 1.800,00
(C) R$ 2.000,00
(D) R$ 2.400,00
(E) R$ 2.500,00

03) (Prova Paulista – 1ª Serie EM-ENEM 2012)  Arthur deseja comprar um terreno de Cléber, que lhe oferece as seguintes possibilidades de pagamento:
Opção 1: Pagar à vista, por R$ 55 000,00;
Opção 2: Pagar a prazo, dando uma entrada de R$ 30 000,00, e mais uma prestação de R$ 26 000,00 para dali a 6 meses.
Opção 3: Pagar a prazo, dando uma entrada de R$ 20 000,00, mais uma prestação de R$ 20 000,00, para dali a 6 meses e outra de R$ 18 000,00 para dali a 12 meses da data da compra.
Opção 4: Pagar a prazo dando uma entrada de R$ 15 000,00 e o restante em 1 ano da data da compra, pagando R$ 39 000,00.
Opção 5: pagar a prazo, dali a um ano, o valor de R$ 60 000,00.
Arthur tem o dinheiro para pagar à vista, mas avalia se não seria melhor aplicar o dinheiro do valor à vista (ou até um valor menor) em um investimento, com rentabilidade de 10% ao semestre, resgatando os valores à medida que as prestações da opção escolhida fossem vencendo.
Após avaliar a situação do ponto de vista financeiro e das condições apresentadas, Arthur concluiu que era mais vantajoso financeiramente escolher a opção:
(A) Opção 1.
(B) Opção 2.
(C) Opção 3.
(D) Opção 4.
(E) Opção 5.
 
04) (Prova Paulista – 1ª Serie EM)  Um empréstimo no valor de R$ 2.000,00 é concedido à taxa de juros compostos de 10% ao ano, a ser reembolsado em 5 anos de acordo com o SAC.
Determine o valor total do finaciament.
(A) R$ 4.500,00.
(B) R$ 3.500,00.
(C) R$3.000,00.
(D) R$ 2.600,00.
(E) R$ 1.800,00.

05) (Prova Paulista – 1ª Serie EM)  Dentre os números 2.501, 4.235, 1.536, 4.057, 30.597 e 41.500, quantos têm o algarismo 5 ocupando a ordem das centenas?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5

06) (Prova Paulista – 1ª Serie EM-ENEM 2016) O ábaco é um antigo instrumento de cálculo que usa notação posicional de base dez para repre-sentar números naturais.
Ele pode ser apresen-tado em vários modelos, um deles é formado por hastes apoiadas em uma base. Cada haste corresponde a uma posição no sistema decimal e nelas são colocadas argolas; a quantidade de argolas na haste representa o algarismo daque-la posição. Em geral, colocam-se adesivos abaixo das hastes com os símbolos U, D, C, M, DM e CM que correspondem, respectivamente, a unidades, dezenas, centenas, unidades de milhar, dezenas de milhar e centenas de milhar, sempre começando com a unidade na haste da direita e as demais ordens do número no siste-ma decimal nas hastes subsequentes (da direita para esquerda), até a haste que se encontra mais à esquerda.
Entretanto, no ábaco da figura, os adesivos não seguiram a disposição usual.
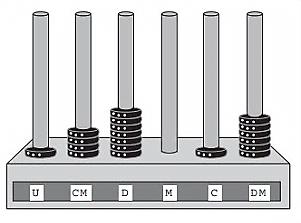Nessa disposição, o número que está representado na figura é:
(A) 46 171
(B) 147 016
(C) 171 064
(D) 460 171
(E) 610 741

07) (Prova Paulista – 1ª Serie EM)  No sistema de numeração decimal, um número tem dois algarismos, sendo y o algarismo das unidades e x o algarismos das dezenas. Se colocarmos o algarismo a direita desse número, sua decomposição será:
Número: xy
Novo número: xy2
(A) x + y + 2
(B) 200 + 10·y + x
(C) 100·x + 10·y + 2
(D) 100·y + 10·x + 2
(E) 200.x.y

08) (Prova Paulista – 1ª Serie EM)  Seu Arthur deseja cercar com tela de arame, um canteiro que tem as medidas indicadas na figura abaixo.
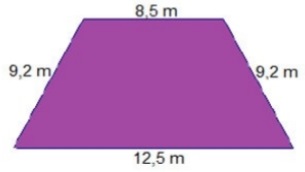Se cada metro custa R$ 3,00, quanto Seua Authur va gastar
(A) R$ 39,40
(B) R$ 116,20
(C) R$ 117,20
(D) R$ 118,20
(E) R$ 161,00

09) (Prova Paulista – 1ª Serie EM)  Fernando fez uma maquete de dois comprimentos de sua casa e usou pedaços retangulares de madeira com as seguintes dimensões, conforme a figura abaixo.
O perímetro dessa figura é
(A) 21,2 cm.
(B) 20,2 cm.
(C) 15,6 cm
(D) 15,2 cm.
(E) 12,6 cm.

10) (Prova Paulista – 1ª Serie EM)  Três cartões retangulares e com as mesmas dimensões foram colocados lado a alado e sem sobreposição, como mostra a figura abaixo.
Qual é a medida de perímetro de retângulo formado pelos três cartões?
(A) 864
(B) 288
(C) 216
(D) 192
(E) 168

11) (Prova Paulista – 1ª Serie EM)  Para incentivar a prática de atividades físicas, a Associação dos Moradores do Bairro Morada Feliz decidiu construir uma pista para caminhada, composta por um retângulo e duas semicircunferências de raio igual a 30 metro, como mostra a figura a seguir.
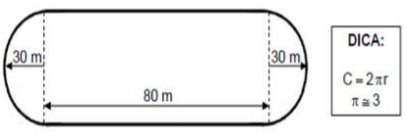Considere que uma pessoa caminhe 10 voltas completas por essa pista. A distância aproximada, em metros, que essa pessoa terá caminhado será de:
(A) 3400
(B) 3300
(C) 3200
(D) 3100
(E) 3000

12) (Prova Paulista – 1ª Serie EM)  O Sistema Decimal é o mais utilizado atualmente para medir comprimentos  e distâncias. Em algumas atividades, porém é possível a utilização de diferentes unidades de medidas. Um exemplo disso pode ser observando no quadro.
Assim, um pé, em polegadas, equivale a
(A) 0,1200
(B) 0,3048
(C) 1,0800
(D) 12,0000
(E) 36,0000

13) (Prova Paulista – 1ª Serie EM)  A informação pode evitar doenças: “Para evitar a contaminação da água pela fossa, deve-se construí-la distante, no mínimo, 20 metros do poça de água.” Observando o esquema abaixo, podemos concluir que a construção da fossa e do poço está:
Realize os cálculos necessários para responder e considere Tg 30º = 0,6.
(A) incorreta, pois a distância do poço à fossa é de 15m.
(B) correta, pois a distância do poço à fossa é de 20m.
(C) correta, pois a distância do poço à fossa é de 22m.
(D) correta, pois a distância do poço à fossa é de 25m.
(E) incorreta, pois a distância do poço à fossa é de 29m.

14) (Prova Paulista – 1ª Serie EM -SARESP 2007) Nos triângulos retângulos representados na figur, qual é a medida da tangente do ângulo β?
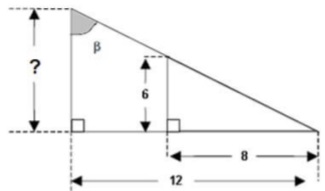(A) 3/5
(B) 3/2
(C) 4/3
(D) 4/5
(E) 5/4

15) (Prova Paulista – 1ª Serie EM)  (Saresp 2007) Para medir a distância que o separava de uma grande árvore, Beto caminhou 200 metros em uma direção perpendicular à linha imaginária que o unia à árvore. Em seguida, mediu o ângulo entre a direção em que andou e a linha imaginária que, agora, o unia à árvore, encontrando
60º.
Nessas condições, a distância inicial entre Beto e a árvore era de aproximadamente
(A) 346 m
(B) 200 m
(C) 172 m
(D) 114 m
(E) 100 m

16) (Prova Paulista – 1ª Serie EM - SARESP – 2009) A forma geométrica espacial que pode ser associada à planificação abaixo é
(A) Um cilindro.
(B) Uma pirâmide de base pentagonal.
(C) Um prisma de base pentagonal.
(D) Um paralelepípedo.
(E) Um cubo.

17) (Prova Paulista – 1ª Serie EM)  A figura seguinte mostra um modelo de sombrinha muito usado em países orientais.
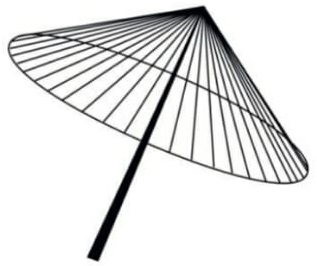Esta figura é uma representação de uma superfície de revolução chamada de
(A) Pirâmide.
(B) Semiesfera.
(C) Cilindro.
(D) Tronco de cone.
(E) Cone.

18) (Prova Paulista – 1ª Serie EM – ENEM 2012)  Um forro retangular de tecido traz em sua etiqueta a informação de que encolherá após a primeira lavagem mantendo, entretanto, seu formato. A figura a seguir mostra as medidas originais do forro e o tamanho do encolhimento (x) no comprimento e (y) na largura. A expressão algébrica que representa a área do forro após ser lavado é (5 – x) (3 – y).
Nestas condições, a área perdida do forro, após a primeira lavagem, será expressa por
(A) 2xy
(B) 15 − 3x
(C) 15 − 5y
(D) −5y − 3x
(E) 5y + 3x − xy

19) (Prova Paulista – 1ª Serie EM - SARESP) Um bombeiro sobe uma escada de 15 m de comprimento, que forma um ângulo de 60° com o solo. Usando 0,87 como valor aproximado de sen 60°, assinale a alternativa que mostra a altura aproximada que o bombeiro está do solo, quando chega ao topo escada.
(A) 10,23 m
(B) 12,14 m
(C) 13,05 m
(D) 14,55 m
(E) 15 m

20) (Prova Paulista – 1ª Serie EM - Enem - 2007) Para se calcular a distância entre duas árvores, representadas pelos pontos A e B, situados em margens opostas de um rio, foi escolhido um ponto C arbitrário, na margem onde se localiza a árvore A. As medidas necessárias foram tomadas, e os resultados obtidos foram os seguintes:
AC = 70 m, BAC = 62º e ACB = 74º. Sendo cos 28º = 0,88, sen 74º = 0,96 e sen 44º = 0,70, podemos afirmar que a distância entre as árvores é:
(A) 48 metros
(B) 78 metros
(C) 85 metros
(D) 96 metros
(E) 102 metros

GABARITO
01A – 02C – 03D – 04D – 05D – 06D – 07C – 08D – 09A – 10E – 11A – 12D – 13D – 14C – 15A – 16C – 17E – 18E – 19C – 20D.