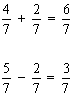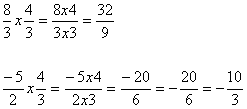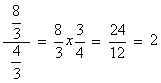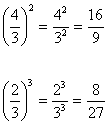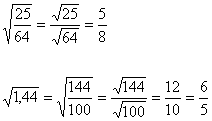EF II - FRACAO

Professor Diminoi
FRACOES

O que é uma fração?
O símbolo a/b significa a:b, sendo a e b números naturais e b diferente de zero.
Exemplo
A fração 8/2 é igual a 8:2. Neste caso, 8 é o numerador e 2 é o denominador. Efetuando a divisão de 8 por 2, obtemos o quociente 4. Assim, 8/2 é um número natural e 8 é múltiplo de 2.
Durante muito tempo, os números naturais foram os únicos conhecidos e usados pelos homens. Depois começaram a surgir questões que não poderiam ser resolvidas com números naturais. Então surgiu o conceito de número fracionário.

O significado de uma fração
Algumas vezes, a/b é um número natural. Outras vezes, isso não acontece. Neste caso, qual é o significado de a/b?
Uma fração envolve a seguinte ideia: dividir algo em partes iguais. Dentre essas partes, consideramos uma ou algumas, conforme nosso interesse.

Exemplo:
Roberval comeu 3/4 de um chocolate. Isso significa que, se dividíssemos o chocolate em 4 partes iguais, Roberval teria comido 3 partes:
Na figura acima, as partes pintadas seriam as partes comidas por Roberval, e a parte branca é a parte que sobrou do chocolate.

Como se lê uma fração
A nomenclatura de uma fração pode ser dividida em dois grupos:
- o primeiro compreende os denominadores iguais a 2, 3, 4, 5, 6, 7, 8, 9, 10, 100, 1000.
- o segundo compreende os denominadores que não pertencem ao primeiro grupo, como 12, 20, 51.

Para denominadores iguais a 2, 3, 4, 5, 6, 7, 8, 9, 10, 100, 1000, a leitura das frações fica da seguinte forma:

Segundo grupo: considerando que o denominador seja qualquer outro número, acrescentamos na sua leitura a palavra “avos”. 


Classificação das frações
Fração própria: o numerador é menor que o denominador:


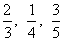
Fração imprópria: o numerador é maior ou igual ao denominador.


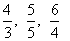
Fração aparente: o numerador é múltiplo do denominador.


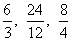
Frações equivalentes
Frações equivalentes são frações que representam a mesma parte do todo.

Exemplos


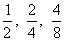
Para encontrar frações equivalentes, devemos multiplicar o numerador e o denominador por um mesmo número natural, diferente de zero.
Obtendo frações equivalentes à fração 1/2.


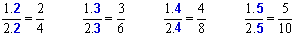
Simplificação de frações
Uma fração equivalente a 9/12, com termos menores, é 3/4. A fração 3/4 foi obtida dividindo-se ambos os termos da fração 9/12 pelo fator comum 3. Dizemos que a fração 3/4 é uma fração simplificada de 9/12.
A fração 3/4 não pode ser simplificada, por isso é chamada de fração irredutível.
A fração 3/4 não pode ser simplificada porque 3 e 4 não possuem nenhum fator comum.

Números fracionários
Seria possível substituir a letra x por um número natural que torne a sentença abaixo verdadeira?
5 . x = 1
Substituindo x, temos:
x por 0, temos: 5.0 = 0
x por 1, temos: 5.1 = 5

Portanto, substituindo x por qualquer número natural, jamais encontraremos o produto 1. Para resolver esse problema, temos que criar novos números. Assim, surgem os números fracionários.

Observacao: Toda fração equivalente representa o mesmo número fracionário.

Portanto, uma fração m/n (n diferente de zero) e todas frações equivalentes a ela representam o mesmo número fracionário m/n.
Resolvendo agora o problema inicial, concluímos que x = 1/5, pois:


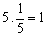
Adição e subtração de números fracionários

Caso 1: Denominadores iguais
Para somar frações com denominadores iguais, basta somar os numeradores e conservar o denominador.
Para subtrair frações com denominadores iguais, basta subtrair os numeradores e conservar o denominador.

Exemplos:


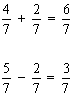
Caso 2: Denominadores diferentes
Para somar frações com denominadores diferentes, uma solução é obter frações equivalentes, de denominadores iguais ao mmc dos denominadores das frações.

Exemplo de somar as frações

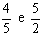
Obtendo o mmc dos denominadores temos mmc(5,2) = 10.

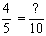
(10:5).4 = 8

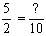
(10:2).5 = 25


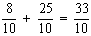
Resumindo: utilizamos o mmc para obter as frações equivalentes e depois somamos normalmente as frações, que já terão o mesmo denominador, ou seja, utilizamos o caso 1.

Multiplicação e divisão de números fracionários
Na multiplicação de números fracionários, devemos multiplicar numerador por numerador, e denominador por denominador, assim como é mostrado nos exemplos abaixo:

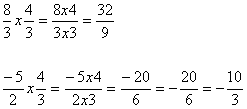
Na divisão de números fracionários, devemos multiplicar a primeira fração pelo inverso da segunda, como é mostrado no exemplo abaixo:


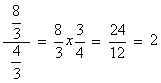
Potenciação e radiciação de números fracionários
Na potenciação, quando elevamos um número fracionário a um determinado expoente, estamos elevando o numerador e o denominador a esse expoente, conforme  os exemplos abaixo:

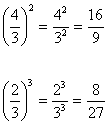
Na radiciação, quando aplicamos a raiz quadrada a um número fracionário, estamos aplicando essa raiz ao numerador e ao denominador, conforme o exemplo abaixo:



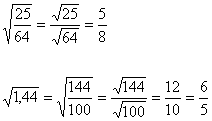
Continua...