POLINÔMIOS
Professor Diminoi
EXPRESSÕES NUMÉRICAS
As expressões algébricas são aquelas expressões matemáticas que possuem números e letras, também conhecidas como variáveis. Utilizamos as letras para representar valores desconhecidos ou até mesmo para analisar o comportamento da expressão de acordo com o valor dessa variável. As expressões algébricas são bastante comuns no estudo das equações e na escrita de fórmulas da Matemática e áreas afins.
Caso a expressão algébrica possua um único termo algébrico, ela é conhecida como monômio; quando possui mais de um, é chamada de polinômio. É possível também calcular operações algébricas, que são as operações entre expressões algébricas.
O que é uma expressão algébrica?
Definimos como expressão algébrica uma expressão que contém letras e números, separados por operações básicas da Matemática, como a adição e a multiplicação. As expressões algébricas são de grande importância para o estudo mais avançado da Matemática, tornando possível o cálculo de valores desconhecidos nas equações ou até mesmo o estudo de funções. Vejamos alguns exemplos de expressões algébricas:
a) 2x²b + 4ay² + 2
b) 5m³n8
c) x² +2x - 3
As expressões algébricas recebem nomes particulares dependendo da quantidade de termos algébricos que possuem.
Monômios
Uma expressão algébrica é conhecida como monômio quando ela possui somente um termo algébrico. Um termo algébrico é aquele que possui letras e números separados apenas por uma multiplicação entre eles.
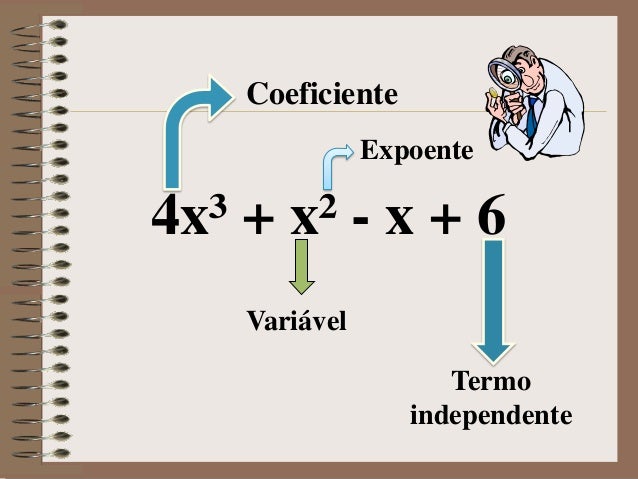
Um monômio é dividido em duas partes: o coeficiente, que é o número que está multiplicando a letra, e a parte literal, que é a variável com o seu expoente.
Exemplos:
a) 2x³ → coeficiente é igual a 2 e a parte literal é igual a x³.
b) 4ab → coeficiente é igual a 4 e a parte literal é igual a ab.
c) m²n → coeficiente é igual a 1 e a parte literal é igual a m²n.
Quando as partes literais de dois monômios são iguais, eles são conhecidos como monômios semelhantes.
Exemplos:
a) 2x³ e 4x³ são semelhantes.
b) 3ab² e -7ab² são semelhantes.
c) 2mn e 3mn² não são semelhantes.
d) 5y e 5x não são semelhantes.
 Observação: As divisões por variáveis não são consideradas monômios, mas sim frações algébricas.
Observação: As divisões por variáveis não são consideradas monômios, mas sim frações algébricas.
Polinômios
 Quando a expressão algébrica possui muitos termos algébricos, ela é conhecida como polinômio. Um polinômio nada mais é do que a soma ou a diferença entre monômios. É bastante comum o uso de polinômios no estudo de equações e funções, ou na geometria analítica, para descrever as equações de elementos da geometria.
Quando a expressão algébrica possui muitos termos algébricos, ela é conhecida como polinômio. Um polinômio nada mais é do que a soma ou a diferença entre monômios. É bastante comum o uso de polinômios no estudo de equações e funções, ou na geometria analítica, para descrever as equações de elementos da geometria.
Exemplos:
a) 2x² + 2x + 3
b) 2ab – 4ab² + 2a - 4b + 1
c) 5mn - 3
d) 4y² + x³ – 4x + 8
Simplificação de expressões algébricas
Em uma expressão algébrica, quando há termos semelhantes, é possível realizar a simplificação dessa expressão por meio de operações com os coeficientes dos termos semelhantes.
Exemplo:
5xy² + 10x – 3xy + 4x²y – 2x²y² + 5x – 3xy + 9xy² – 4x²y + y
Para simplificar, vamos identificar os termos semelhantes, ou seja, termos que possuem mesma parte literal.
5xy² + 10x – 3xy + 4x²y – 2x²y² + 5x – 3xy + 9xy² – 5x²y
Realizaremos as operações entre os termos semelhantes, então:
5xy² + 9xy² = 14xy²
10x + 5x = 15x
-3xy – 3xy = -6xy
4x²y -5x²y = -1x²y= -x²y
O termo -2x²y² não possui nenhum termo semelhante a ele, logo a expressão algébrica simplificada será:
-2x²y² + 14xy² + 15x – 6xy -x²y
Operações algébricas
Realizar adição ou subtração de expressões algébricas nada mais é do que simplificar a expressão, portanto só é possível operar com os termos algébricos que são semelhantes. Já na multiplicação, é necessário utilizar a propriedade distributiva entre os termos, conforme os exemplos a seguir:
Exemplo de adição:
(2x² + 3xy – 5) + (3x² – xy + 2)
Como é uma adição, podemos simplesmente remover os parênteses, sem alterar nenhum dos termos:
2x² + 3xy – 5 + 3x² – xy + 2
Agora vamos simplificar a expressão:
5x² +2xy – 3
Exemplo de subtração:
(2x² + 3xy – 5) – (3x² – xy + 2)
Para remover os parênteses, é necessário inverter o sinal de cada termo algébrico da segunda expressão:
2x² + 3xy – 5 –3x² + xy – 2
Agora vamos simplificar a expressão:
– x² + 4xy – 7
Exemplo de multiplicação:
(2x² + 3xy – 5) ( 3x² – xy + 2)
Aplicando a propriedade distributiva, encontraremos:
6x4 – 2x³y + 4x² + 9x³y – 3x²y² +6xy – 15x² – 5xy + 10
Agora vamos simplificar a expressão:
6x4 + 7x³y – 11x² –3x²y² + xy + 10
Valor numérico das expressões algébricas
Quando conhecemos o valor da variável de uma expressão algébrica, é possível encontrar o seu valor numérico. O valor numérico da expressão algébrica nada mais é do que o resultado final quando substituímos a variável por um valor.
Exemplo:
Dada a expressão x³ + 4x² + 3x – 5, qual é o valor numérico da expressão quando x = 2.
Para calcular o valor da expressão, vamos substituir o x por 2.
2³ + 4 · 2² + 3 · 2 – 5
8 + 4 · 4 + 6 – 5
8 + 16 + 6 – 5
30 – 5
25
Exercícios resolvidos
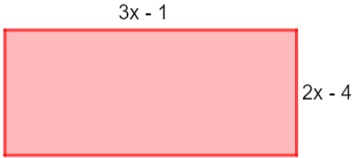
01) A expressão algébrica que representa o perímetro do retângulo a seguir é:
 (A) 5x – 5
(A) 5x – 5
(B) 10x – 10
(C) 5x + 5
(D) 8x – 6
(E) 3x – 2
Resolução:
Para calcular o perímetro, vamos somar os quatro lados. Sabendo que os lados paralelos são iguais, temos que:
P = 2(2x – 4) + 2 (3x – 1)
P = 4x – 8 + 6x – 2
P = 10x – 10
Alternativa: B.
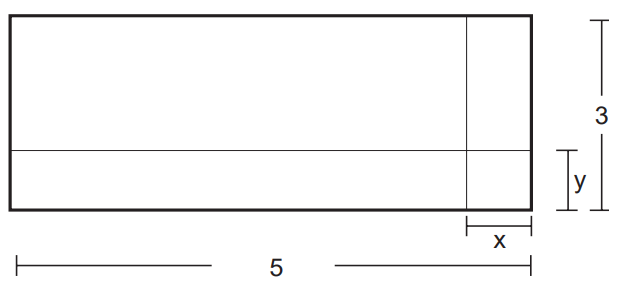
02) (ENEM) Um forro retangular de tecido traz em sua etiqueta a informação de que encolherá após a primeira lavagem, mantendo, entretanto, seu formato. A figura a seguir mostra as medidas originais do forro e o tamanho do encolhimento (x) no comprimento e (y) na largura. A expressão algébrica que representa a área do forro após ser lavado é (5 – x) (3 – y).
 Nessas condições, a área perdida do forro, após a primeira lavagem, será expressa por:
Nessas condições, a área perdida do forro, após a primeira lavagem, será expressa por:
(A) 2xy
(B)15 – 3x
(C) 15 – 5y
(D) -5y – 3x
(E) 5y + 3x – xy
Resolução:
Para calcular a área de um retângulo, calculamos a área encontrando o produto entre a base e a altura do retângulo. Analisando a parte perdida do forro, é possível dividi-la em dois retângulos, mas existe uma região que pertence aos dois retângulos, logo vamos ter que subtrair a área dessa região.
O retângulo maior tem base 5 e altura y, logo sua área é dada por 5y. O outro triângulo possui base x e altura 3, então sua área é dada por 3x. A região que pertence aos dois retângulos simultaneamente tem base x e altura y, então, como ela está sendo contada nos dois retângulos, vamos subtraí-la da soma das áreas. Assim, a área perdida é dada pela expressão algébrica:
5y + 3x – xy
Alternativa: B
BINÔMIOS
Os binômios são aqueles polinômios que possuem apenas dois monômios, separados por uma operação de adição ou subtração.
Exemplos:
a) 2x + 4y
b) a² – b²
c) 3ab + 5c
TRINÔMIOS
Por fim, os trinômios são os polinômios que têm em sua expressão a aparição de três monômios (ou termos), separados pela expressão de soma ou subtração.
Exemplos:
a) x³ + 4y + 5
b) 2ab + 4c – 10d
c) 2a + 2b + 5c
GRAU DO POLIÔMIO
Os polinômios possuem diferentes graus, podendo ser reconhecidos por meio dos expoentes apontados em suas variáveis literais. Para encontrar o grau de um polinômio, deve-se somar os expoentes das letras de cada termo. A maior soma corresponderá ao grau do polinômio em questão.
Exemplos:
3x³ + y
Na expressão acima, o primeiro termo do polinômio (que, neste caso, é um binômio) tem expoente equivalente a 3. O segundo termo tem expoente de 1. Como 3 é maior que 1, dizemos que o polinômio em questão tem grau 3.
3x²y + 5x³y³ – xy²
Na soma dos expoentes de cada termo, temos:
a) 3x²y, somando 2 + 1, temos 3;
b) 5x³y³, somando 3 + 3, temos 6;
c) xy², somando 1 + 2, temos 3.
Como a soma dos expoentes é maior no segundo termo do polinômio, seu grau é 6.
OPERAÇÃO COM POLINÔMIOS
Ao tratarmos de polinômios, podemos aplicar diversas operações, como adição, subtração, multiplicação e divisão.
Redução e multiplicação de termos semelhantes - Quando existem termos semelhantes entre os polinômios, é possível realizar-se a redução de seus termos na adição e ou subtração de dois polinômios. É possível também multiplicar dois polinômios por meio da propriedade distributiva. Já a divisão é realizada pelo método de chaves. Dizemos que é inteira porque não pode constar a presença de variáveis dentro de radicais ou mesmo em denominadores de frações.

ADIÇÃO E SUBTRAÇÃO
Adição
1º) (–2x² + 5x – 2) + (–3x³ + 2x – 1) (eliminar os parênteses realizando o jogo de sinal)
2º) –2x² + 5x – 2 – 3x³ + 2x – 1 (reduzir os termos semelhantes)
3º) –2x² + 7x – 3x³ – 3 (ordenar de forma decrescente de acordo com a potência)
4º) –3x³ – 2x² + 7x – 3
Subtração
1º) (–2x² + 5x – 2) – (–3x³ + 2x – 1) (eliminar os parênteses realizando o jogo de sinal)
2º) –2x² + 5x – 2 + 3x³ – 2x + 1 (reduzir os termos semelhantes)
3º) –2x² + 3x – 1 + 3x³ (ordenar de forma decrescente de acordo com a potência)
4º) 3x³ – 2x² + 3x – 1
Multiplicação de polinômio por polinômio
Para efetuarmos a multiplicação de polinômio por polinômio, devemos utilizar a propriedade distributiva.
Exemplo:
(x – 1) . (x2 + 2x – 6)
1º) x.x2 + x.2x – x.6 + (-1).x2 + (-1).2x – (-1).6
2º) x³ +2x² – 6x – x² – 2x + 6
Reduzindo os termos semelhantes.
x³ + x² – 8x + 6
Multiplicação de polinômios
Leva completamente em conta a propriedade distributiva dos polinômios, popularmente conhecida como “chuveirinho”. Para utilizar esse recurso, é só multiplicar cada monômio do primeiro polinômio por todos os monômios do segundo polinômio, sempre levando em consideração os sinais de cada resultado.
Exemplo:
(3x2 – 5x + 8) . (-2x + 1)
– 6x3 + 3x2 + 10x2 – 5x – 16x + 8
– 6x3 + 13x2 – 21x +8
Observe que, na multiplicação de variáveis (letras) iguais, repete-se e soma-se cada um dos expoentes.
Exemplos:
(2x + a) . (2x -4a)
2x . 2x – 2x . 4a + a . 2x – a . 4a
4x² – 6xa – 4ª²
Divisão com polinômios
Na divisão de polinômios, é utilizado o chamado método chave, da mesma maneira que fazemos com números inteiros.
Exemplos:
Na divisão de P(x) = x³ + 7x² + 15x + 9 pelo polinômio D(x) = x + 1, o primeiro é o dividendo e o segundo é o divisor, sendo o Q(x) o quociente. O primeiro passo é buscar um monômio que, se for multiplicado pelo termo de grau mais alto do divisor, apresente o termo de grau mais alto do dividendo. Para a operação acima, esse monômio é x².
Após encontrá-lo, multiplique-o pelo divisor, colocando o resultado sob o dividendo, assim como fazemos para a divisão de números inteiros.
Exemplo:
x³ + 7x² + 15x + 9 : x + 1 = x²
x² . (x + 1) à x³ + x²
O resultado dessa multiplicação é, então, subtraído do dividendo, de modo que os sinais devem ser trocados. Assim:
x³ + 7x² + 15x + 9 – x³ – x²
Aqui, o resultado fica em 0 + 6x² +15x + 9, pois devemos “descer” na operação todos os termos que não foram subtraídos dessa vez. Agora, o procedimento é repetido até que o resto tenha menor grau que o divisor. Então, na sequência dessa operação, temos como resultado x² + 6x + 9.
Fatoração com polinômios
Fatoração é um processo matemático que busca representar números ou expressões como produtos de fatores. Quando escrevemos um polinômio como o resultado da multiplicação de outros polinômios, geralmente conseguimos expressar esse resultado de maneira mais simplificada.
Existem alguns tipos de fatoração de polinômios, que explicaremos a seguir.
Fator comum em evidência
Esse tipo de fatoração é usado quando existe um fator recorrente em todos os termos do polinômio. Pode conter números e letras, sendo assim colocado à frente dos parênteses. Dentro desses parênteses, fica o resultado da divisão de cada termo pelo fator comum.
Observação: o “passo a passo” desse tipo de fatoração se dá em 3 etapas, sendo:
Identificar algum número que divida todos os coeficientes do polinômio e as letras que se repetem em cada um dos termos;
Colocar os fatores comuns, sejam eles números ou letras, na frente dos parênteses, em evidência;
Colocar dentro dos parênteses o resultado da divisão de cada fator identificado do polinômio pelo que está na frente dos parênteses. Para letras, utiliza-se a regra da divisão de potências que possuem mesma base.
Exemplos - 1:
Como expressar a forma fatorada de 12x + 6y – 9z?
Primeiramente, identificamos que todos os coeficientes podem ser divididos por 3 e que não há nenhuma letra repetida. Na sequência, coloca-se 3 na frente dos parênteses, dividindo todos os termos por esse número e colocando o resultado da operação dentro dos parênteses.
Assim, temos que:
12x + 6y – 9z = 3(4x +2y – 3z)
Como fatorar o polinômio 2a2b + 3a3c – a4?
Na primeira etapa, verificamos que não há nenhum número que seja capaz de dividir, ao mesmo tempo, 2, 3 e 1. Assim, nenhum número é colocado à frente dos parênteses.
Na sequência, podemos perceber que a letra “a” se repete em cada um dos termos do polinômio. Portanto, o fator comum será a², já que este é o menor expoente de “a” no polinômio. Assim, dividimos cada termo do polinômio por a², tendo como:
2a2 b : a2 = 2a2 – 2 b = 2b
3a3c : a2 = 3a3 – 2 c = 3ac
a4 : a2 = a2
Por fim, coloca-se a² na frente dos parênteses e o resultado da divisão dentro deles, tendo como resultado da fatoração:
2a2b + 3a3c – a4 = a2 (2b + 3ac – a2)
Exemplo -2:
Considere o retângulo:
 Observe que a área do retângulo azul mais a área do retângulo verde resultam no retângulo maior. Vamos analisar cada uma dessas áreas:
Observe que a área do retângulo azul mais a área do retângulo verde resultam no retângulo maior. Vamos analisar cada uma dessas áreas:
AAZUL = b · x
AVERDE = b · y
AMAIOR = b · (x + y)
Assim, temos que:
AMAIOR = AAZUL + AVERDE
b (x + y) = bx + by
01) Para fatorar a expressão: 12x + 24y.
Resolução:
Nota-se que 12 é o fator em evidência, uma vez que ele aparece em ambas as parcelas, assim, para determinar os números que vão no interior dos parênteses, basta dividir cada parcela pelo fator em evidência.
12x / 12 = x
24y / 12 = 2y
12x + 24y = 12 . (x + 2y)
02) Para fatorar a expressão 21ab2 – 70a2b.
Resolução:
Do mesmo modo, inicialmente, determina-se o fator em evidência, isto é, o fator que se repete nas parcelas. Veja que da parte numérica temos o 7 como fator comum, uma vez que ele é o único que divide ambos os números.
Agora, em relação à parte literal, veja que se repete somente o fator ab, logo, o fator em evidência é: 7ab.
21ab2 – 70a2b = 7ab (3b – 10a)
Fatoração por agrupamento
A fatoração por agrupamento é decorrente da fatoração por evidência, a única diferença é que, em vez de termos um monômio como fator comum ou fator em evidência, teremos um polinômio.
Exemplo:
Considere a expressão (a + b) · xy + (a + b) · wz2
Resolução:
Observe que o fator comum é o binômio (a + b), logo, a forma fatorada da expressão anterior é:
(a + b) · (xy + wz2)
Diferença entre dois quadrados
Considere dois números a e b, quando temos a diferença do quadrado desses números, isto é, a2 – b2, então podemos escrevê-los como sendo o produto da soma pela diferença, ou seja:
a2 – b2 = (a + b) · (a – b)
03) Para fatorar a expressão x2 – y2.
Resolução:
Podemos utilizar a diferença entre dois quadrados, logo:
x2 – y2 = (x + y) · (x – y)
04) Para fatorar 2.0202 – 2.0192.
Resolução:
Podemos utilizar a diferença entre dois quadrados, logo:
2.0202 – 2.0192 = (2.020 + 2.019) · (2.020 – 2.019)
2.0202 – 2.0192 = 4.039 · 1
2.0202 – 2.0192 = 4.039
Trinômio do quadrado perfeito
Considere o quadrado seguinte de lado (a + b) e observe as áreas dos quadrados e retângulos formados em seu interior.
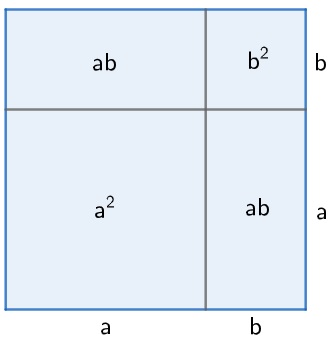 Veja que a área do quadrado maior é dada por (a + b)2, mas, por outro lado, a área do quadrado maior pode ser obtida pela soma dos quadrados e retângulos do seu interior, assim:
Veja que a área do quadrado maior é dada por (a + b)2, mas, por outro lado, a área do quadrado maior pode ser obtida pela soma dos quadrados e retângulos do seu interior, assim:
(a + b)2 = a2 + ab + ab + b2
(a + b)2 = a2 + 2ab + b2
(a + b)2 = a2 + 2ab + b2
De maneira análoga, temos que:
(a – b)2 = a2 – 2ab + b2
05) Considere a expressão x2 + 12x + 36.
Resolução:
Para fatorar uma expressão desse tipo, basta identificar o coeficiente da variável x e o coeficiente independente, e comparar com a fórmula dada, veja:
x2 + 12x + 36
a2 + 2ab + b2
Fazendo as comparações, veja que x = a, 2b = 12 e b2 = 36; das igualdades, temos que b = 6, assim a expressão fatorada é:
x2 + 12x + 36 = (x + 6)2
Trinômio do segundo grau
Considere o trinômio ax2 + bx + c. A sua forma fatorada pode ser encontrada utilizando suas raízes, ou seja, os valores de x que zeram tal expressão. Para determinar os valores que zeram tal expressão, basta resolver a equação ax2 + bx + c = 0 utilizando o método que achar conveniente. Aqui ressaltamos o método mais conhecido como Método de Bhaskara .
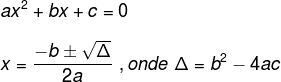 A forma fatorada do trinômio ax2 + bx + c é:
A forma fatorada do trinômio ax2 + bx + c é:
ax2 + bx + c
a · (x – x1) · (x – x2)
06) Considere a expressão x2 + x – 20.
Resolução:
O primeiro passo é determinar as raízes da equação x2 + x – 20 = 0.
Assim a forma fatorada da expressão x2 + x – 20 é:
(x – 4) · (x + 5) cubo da diferença entre dois números
O cubo da diferença entre dois números a e b é dado por:
(a – b)3 = (a – b) · (a – b)2
(a – b)3 = (a – b) · (a2 – 2ab + b2) cubo da soma de dois números
De maneira análoga, temos que (a + b)3 = (a + b) · (a + b)2 , logo:
(a + b)3 = (a + b) · (a2 + 2ab + b2)
A fatoração é um instrumento que facilita a resolução das expressões algébricas.
07) (Cefet-MG) Sendo o número n = 6842 – 6832, a soma dos algarismos de n é:
(A) 14
(C) 15
(C) 16
(D) 17
(E) 18
Resolução
Alternativa d. Para determinar a soma dos algarismos de n, inicialmente fatorarmos a expressão, uma vez que calcular os quadrados e, em seguida, realizar a subtração geram trabalho desnecessário. Fatorando a expressão utilizando a diferença entre dois quadrados, temos:
n = 6842 – 6832
n = (684 + 683) · (684 – 683)
n = 1.367 · 1
n = 1.367
Portanto, a soma dos algarismos de n é dada por 1 + 3 + 6 + 7 = 17
Alternativa: D
08) (Insper-SP modificada) Determine o valor da expressão:
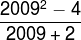 (A) 1007
(A) 1007
(C) 2000
(C) 2007
(D) 2010
(E) 2107
Resolução
Com a intenção de facilitar a notação, vamos nomear a = 2.009 e b = 2. Lembre-se de que 22 = 4, assim temos que:
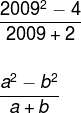 Veja que, no numerador da fração, temos a diferença entre dois quadrados, logo, podemos escrever a2 – b2 = (a + b) (a – b).
Veja que, no numerador da fração, temos a diferença entre dois quadrados, logo, podemos escrever a2 – b2 = (a + b) (a – b).
Logo:
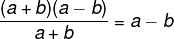 a – b = 2009 – 2 = 2007.
a – b = 2009 – 2 = 2007.
Alternativa: C
Polinômios incompletos
O polinômio será incompleto quando faltar algum número na sua sequência de expoentes.
Exemplo:
x5+ 5 . x1– 2 . x0
A forma completa desse polinômio seria: 3. x5 + 0 . x4 – 0 . x3 + 0 . x2 + 5 . x1 – 2 . x0.
Faltaram os expoentes em relação à variável x: x4, x3 e x2. Por esse motivo, o polinômio é incompleto.
Grau de um polinômio com apenas uma variável
Quando o polinômio possuir apenas uma variável, o grau será dado pelo maior expoente. Exemplo:
a) x³ + x² + 10x – 5 possui grau 3;
b) x10– x9+ 50 possui grau 10.
Grau dos Polinômios
O grau de um polinômio é dado pelos expoentes da parte literal. Para encontrar o grau de um polinômio devemos somar os expoentes das letras que compõem cada termo. A maior soma será o grau do polinômio.
Exemplos
a) 2x3+ y
O expoente do primeiro termo é 3 e do segundo termo é 1. Como o maior é 3, o grau do polinômio é 3.
b) 4 x2y + 8x3y3- xy4
Grau do polinômio com mais de uma variável: Quando o polinômio possui mais do que uma variável, para saber o seu grau, devemos somar os expoentes de cada monômio. A maior soma de expoentes determinará o grau. Exemplo:
3 + 12 . x . y – 2 . x . y2
Grau do monômio: x1 . Y1 → 1 + 1 = 2
Grau do monômio: x . y2 → 1 + 2 = 3
Da soma de expoentes de cada monômio, obtivemos que: para (x . y), o grau é 2; e para (x . y2), o grau é 3. Sendo assim, o polinômio (3 + 12 . x . y – 2 . x . y2) é de terceiro grau.
Soma os expoentes de cada termo:
a) 4x2y = 2 + 1 = 3
b) 8x3y3= 3 + 3 = 6
c) xy4= 1 + 4 = 5
Valor numérico dos polinômios
Exemplo 1
Qual o valor numérico do polinômio p(x )= x² -2x + 5 para x =2.
Como vimos na definição, devemos pegar o valor 2 e substituir no lugar de x, formando assim p(2).
.png)
Resposta: o valor numérico do polinômio p(x) = x²-2x + 5 quando x = 2 é 5.
Exemplo 1
Calcule o p(1), p(0) e p(3) do seguinte polinômio.
.png)
Para p(0) temos que x=0, então:
.png)
Para p(3), faremos x=3 e calcularemos o valor do polinômio com este valor de x.
.jpg)
Observação: Um polinômio pode ter vários valores numéricos, afinal a variável x pode assumir diversos valores.
09) Observe os polinômios a seguir. (a) 3abcd2, (b) 3a + bc - d2 e (c) 3ab - cd2 e classifique-os e São monômios, binômios e trinômios, respectivamente:
(A) (b) monômio. (c) trinômio e (c) binômio
(B) (a) monômio. (a) trinômio e (c) binômio
(C) (a) monômio. (b) trinômio e (c) binômio
(D) (b) monômio. (a) trinômio e (c) binômio
(E) (a) monômio. (c) trinômio e (c) binômio
Resolução:
(a) monômio. (b) trinômio e (c) binômio
Alternativa: C
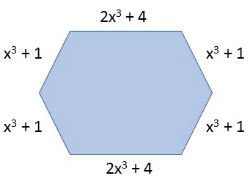
10) Qual o valor do perímetro da figura abaixo:
 (A) 8x + 12
(A) 8x + 12
(B) 12 – 8x
(C) 12 – 8x2
(D) 8x + 122
(E) 8x3 + 12
Resolução:
O perímetro da figura é encontrado somando-se todos os lados.
2x3 + 4 + 2x3 + 4 + x3 + 1 + x3 + 1 + x3 + 1 + x3 + 1 = 8x3 + 12
Alternativa: E
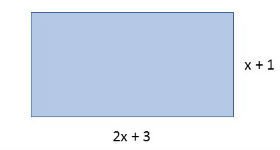
11) Encontre a área da figura:
 (A) 2x + 5x + 3
(A) 2x + 5x + 3
(B) 2x2 + 5x + 3
(C) 2x2 + 5x
(D) 2x2 + 5x2 + 3
(E) 2x2 + 5x2 + 9
Resolução:
A área do retângulo é encontrada multiplicando-se a base pela altura.
(2x + 3) . (x+1) = 2x2 + 5x + 3
Alternativa: B
12) Fatorando p polinômios 8ab + 2a2b - 4ab2 temos:
(A) 2ab (4 + a - 2b)
(B) 2ab (4 + a - 2b)2
(C) 2ab2 (4 + a - 2b)
(D) 2ab2 (4 + a – b)
(E) 2ab (4 + a)
Resolução:
Como existem fatores comuns, fatorar colocando esses fatores em evidência: 2ab (4 + a - 2b)
Alternativa: A
13) Fatorando o polinômio 25 + 10y + y2 temos:
(A) (52+y)2
(B) 5+y
(C) (5+y2)2
(D) (5+y)
(E) (5+y)2
Resolução:
Trinômio quadrado perfeito: (5+y)2
Alternativa: E
14) Fatorando o polinômio 9 - k2 temos:
(A) (3 - k) . (3 + k)
(B) (3 + k) . (3 - k)
(C) (3 + k) . (3 + k)
(D) (3 - k) . (3 - k)
(E) 32 + k2
Resolução:
Diferença de dois quadrados: (3 + k) . (3 - k)
Alternativa: B
15) Temos que a raiz do polinômio p(x) = x² – mx + 6 é igual a 6. Calcule o valor de m.
(A) 7
(B) 30
(C) 6
(D) 8
(E) 0
Resolução:
p(x) = x² – mx + 6
p(6) = 0
6² – m . 6 + 6 = 0
36 – 6m + 6 = 0
– 6m = – 42 . (–1)
6m = 42
m = 42/6
m = 7
O valor de m que satisfaz as condições informadas é 7.
Alternativa: A
16) (Guarda Civil SP) Considere o polinômio: p(x) = 4x4 + 3x3 – 2x2 + x + k . Sabendo que P(1) = 2, então o valor de P(3) é:
(A) 386.
(B) 405.
(C) 324.
(D) 81.
(E) 368.
Resolução:
Como P(1) = 2:
P(1) = 4.1 + 3.1 – 2.1 + 1 + k = 2
4 + 3 – 2 + 1 + k = 2
6 + k = 2
k = 2 – 6
k = – 4
O polinômio será P(x) = 4x4 + 3x³ – 2x² + x – 4
Calculando P(3):
P(x) = 4x4 + 3x³ – 2x² + x – 4
P(3) = 4.34 + 3.3³ – 2.3² + 3 – 4
P(3) = 4.81 + 3.27 – 2.9 + 3 – 4
P(3) = 324 + 81 – 18 + 3 – 4
P(3) = 386
Alternativa: A
17) (RFB 2009 – Esaf). Se um polinômio f for divisível separadamente por (x – a) e (x – b) com a ≠ b, então f é divisível pelo produto entre (x–a) e (x–b). Sabendo-se que 5 e -2 são os restos da divisão de um polinômio f por (x – 1) e (x + 3), respectivamente, então o resto da divisão desse polinômio pelo produto dado por (x – 1) e (x + 3) é igual a:
(A) 13x/4 + 7/4
(B) 7x/4 – 13/4
(C) 7x/4 + 13/4
(D) -13x/4 – 13/4
(E) -13x/4 – 7/4
Resolução:
Primeiramente, o resto da divisão de um polinômio P(x) por (x-a) é igual a P(a).
Dividindo o polinômio f pelo polinômio de grau 2, resultado do produto (x-1).(x+3). Observe que o resto deve ter grau 1 ou 0 (se divisão exata).Vamos chamar o resto de ax + b.
Temos::
P(1) = 5 (5 é o resto da divisão de f por x-1)
P(-3) = -2 (-2 é o resto da divisão de f por x+3)
Daí,
a.1 + b = 5
a.(-3) + b = -2
Subtraindo a equação 1 pela equação 2, temos:
4a = 7
a = 7/4
Substituindo “a” na equação 1, temos:
7/4 + b = 5
b = 5 – 7/4
b = 13/4
Concluímos que o resto é ax + b = (7/4).x + 13/4
Alternativa: C
18) (Prefeitura de Terra de Areia RS – Objetiva) Assinalar a alternativa que
apresenta o resultado do polinômio abaixo: 2x(5x + 7y) + 9x(2y)
(A) 10x + 14xy + 18yx
(B) 6x² + 21xy
(C) 10x² + 32xy
(D) 10x² + 9y
(E) 22x + 9y
Resolução
2x(5x + 7y) + 9x(2y)
2x.5x + 2x.7y + 9x.2y
10x² + 14xy + 18xy
10x² + 32xy
Resposta: C
19) (UP) Sabe-se que o resto da divisão de um polinômio P(x) por binômio do tipo (x – a) é P(a). Qual é o resto da divisão de P(x) = 5x³ – 5x² + 5 por (x + 1)?
(A) -1
(B) 5
(C) 1
(D) -5
Resolução
Observe que o binômio (x + 1) possui a = -1.
Calculando o valor de P(a):
P(x) = 5x³ – 5x² + 5
P(-1) = 5(-1)³ – 5(-1)² + 5
P(-1) = 5.(-1) – 5.1 + 5
P(-1) = -5 – 5 + 5
P(-1) = -5
Alternativa: D
20) Seja o polinômio P(x) 5x5 + 2x4 + x3 – 4x2 + x + k, sabendo que P(1) = 5, então calcule P(3).
(A) 1371
(B) 371
(A) 2372
(D) 371
(E) 130
Resolução:
Sabendo que P(1) = 5, então o valor de k é:
P(1) = 5 . 15 + 2 . 14 + 13 – 4 . 12 + 1 + k = 5
5 + 2 + 1 – 4 + 1 + k = 5
5 + k = 5
k = 5 – 5
k = 0
Agora que já temos o valor de k, então podemos calcular P(3)
Assim,
P(3) = 5 . 243 + 2 . 81 + 27 – 4 . 9 + 3 + 0
P(3) = 1215 + 162 + 27 – 36 + 3
P(3) = 1407 – 36
P(3) = 1371
Alternativa: A
21) Faça a adição e subtração dos seguintes polinômios: P(x) = 2x³ + 4x + 2 e Q(x) = – x³ + x – 3. Respectivamente.
(A) 3x³ + 3x + 5 e x³ + 5x – 1
(B) ) x³ + 5x e 3x³ + 3x + 5
(C) x³ + 5x – 1 e 3x³ + 3x + 5
(D) ) x³ + 5x – 1 e 3x³ + 3x
(E) ) x³ + 5x – 1 e 3x³ + 3x3
Resolução:
Temos que:
Adição:
P(x) + Q(x) = 2x³ + 4x + 2 + (- x³ + x – 3 )
P(x) + Q(x) = 2x³ – x³ + 4x + x + 2 – 3
P(x) + Q(x) = x³ + 5x – 1
Subtração:
P(x) – Q(x) = (2x³ + 4x + 2) – (- x³ + x – 3 )
P(x) – Q(x) = 2x³ + 4x + 2 + x³ – x + 3
P(x) – Q(x) = 2x³ + x³ + 4x – x + 2 + 3
P(x) – Q(x) = 3x³ + 3x + 5
Alternativa: C
22) Considere os polinômios: P(x) = x² – 3x + 9 e Q(x) = -2x + 3. Realize a multiplicação entre estes polinômios.
(A) – 2x2 + 9x² – 27x2 + 27
(B) – 2x + 9x – 27x + 27
(C) – 2x³ + 9x² – 27x
(D) 2x³ + 9x² – 27x + 27
(E) – 2x³ + 9x² – 27x + 27
Resolução:
Temos que:
(P . Q)(x) = (x² – 3x + 9) . (-2x + 3)
(P . Q)(x) = – 2x³ + 3x² + 6x² – 9x – 18x + 27
(P . Q)(x) = – 2x³ + 9x² – 27x + 27
Alternativa: E
23) (Avaliação da Aprendizagem em Processo – 3º E.M.) Determine o valor de k na equação algébrica 2𝑥3 − 4𝑥2 − 2𝑥 + 𝑘 = 0 sabendo que uma de suas raizes é igual a 1.
(A) -4
(B) 0
(C) 1
(D) 4
(E) 9
Resolução:
Basta fazer a divisão substituindo “x” por 1 e aparentemente não tem maiores dificuldades com a execução.
Alternativa: D
24) (Avaliação da Aprendizagem em Processo – 3º E.M.) Dada a equação do 3º grau 𝑥3 + 2𝑥2 − 5𝑥 − 6 = 0 a adição de suas três raizes é igual a:
(A) -3
(B) -1
(C) -2
(D) 0
(E) 1
Resolução:
Além de calcular corretamente as três raízes da equação o aluno compreendeu o que foi solicitado na questão.
Alternativa: C
25) (Avaliação da Aprendizagem em Processo – 3º E.M.) Calcule o volume do sólido representado na figura abaixo
 (A) 𝒙𝟑 − 𝟑𝒙 − 𝟐
(A) 𝒙𝟑 − 𝟑𝒙 − 𝟐
(B) 𝑥 − 3𝑥3 – 2
(C) 𝑥3 − 3𝑥2 − 2
(D) 𝑥2 − 3𝑥3 − 2
(E) 𝑥3 − 3𝑥 + 2
Resolução:
O aluno realizou corretamente o produto das três dimensões do paralelepípedo.
Alternativa: A
26) (Avaliação da Aprendizagem em Processo – 3º E.M.) O polinômio obtido pela divisão do polinômio 2𝑥2 − 5𝑥 − 12 pelo binômio 𝑥 − 4 é:
(A) 0,5𝑥 − 4,25
(B) 2𝑥 − 9
(C) 𝟐𝒙 + 𝟑
(D) 2𝑥 2 − 4𝑥 − 16
(E) 2𝑥 2 − 6𝑥 − 8
Resolução:
Observe a técnica para divisão de polinômios e fique atento à solução.
Alternativa: C
27) (Avaliação da Aprendizagem em Processo – 3º E.M O quociente do polinômio 6𝑥 3 − 2𝑥 2 + 𝑥 + 1 pelo binômio 3𝑥 − 6 tem resto igual a:
(A) 0
(B) 2
(C) 10
(D) 25
(E) 43
Resolução:
Alternativa: E
28) (EAM – Aprendiz de marinheiro) Analise a figura a seguir:
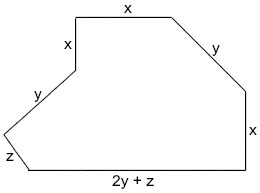 Suponha que o terreno comprado por um proprietário tenha a forma da figura acima e suas medidas sejam representadas, em unidades de comprimento, pelas variáveis X, Y e Z. A expressão algébrica que representa o perímetro desse terreno é:
Suponha que o terreno comprado por um proprietário tenha a forma da figura acima e suas medidas sejam representadas, em unidades de comprimento, pelas variáveis X, Y e Z. A expressão algébrica que representa o perímetro desse terreno é:
(A) 2x + 3y + z
(B) 3x + 4y + 2z
(C) 3x + 3y + z
(D) 3x + 2y + 3z
(E) 4x + 3y + 2z
Resolução:
Para determinamos a expressão algébrica que representa o perímetro, devemos somar todos os lados da figura geométrica que representa o terreno.
x + y + x + 2y + z + z + y + x =
Devemos agrupar os termos semelhantes, ou seja, os que possuem mesma variável.
= x + x + x + y + 2y + y + z + z =
Faça a redução dos termos semelhantes operando os coeficientes.
= 3 x + 4y + 2z
Alternativa: B
29) (EAM – Aprendiz de marinheiro) Reduzindo-se os termos semelhantes da expressão b(a - b) + (b + a) (b - a) - a(b - a) + (b - a)2, obtém-se:
(A) (a – b)2
(B) (a + b)2
(C) b2 – a2
(D) a2 – b2
(E) a2 + b2
Resolução:
b(a - b) + (b + a) (b - a) - a(b - a) + (b – a)2 =
Efetue os produtos pela propriedade distributiva:
= ba – b2 + b2 – ab + ab – a2 – ab +a2 + b2 – 2ba + a2 =
Agrupe os termos semelhantes:
= ba – ab + ab – ab – 2ba – b2 + b2 + b2 – a2 +a2+ a2 =
Faça a redução dos termos semelhantes operando os coeficientes / números:
= - 2 ba + b2 + a2 =
Organizando os termos:
= + a2 - 2 ba + b2 =
Fatore a expressão:
= (a - b)2
Alternativa: A
30) Resolva: (y2 + 4y – 5) + (– 3y2 + 12y – 1).
Resolução:
(y2 + 4y – 5) + (– 3y2 + 12y – 1) =
Tiremos os termos de dentro dos parênteses:
= y2 + 4y – 5 – 3y2 + 12y – 1 =
Agora agrupemos os termos semelhantes:
= y2 – 3y2 + 4y + 12y – 5 – 1 =
Basta reduzir os termos semelhantes operando os coeficientes / números.
= – 2y2 + 16y – 6
32) Subtraia x2 + 12x – 9 por – 8x2 + 7x – 1
Resolução:
(x2 + 12x – 9) - (– 8x2 + 7x– 1) =
Tiremos os termos de dentro dos parênteses fazendo o jogo de sinal para: - (– 8x2 + 7x– 1)
= x2 + 12x – 9 + 8x2 – 7x + 1 =
Agrupemos os termos semelhantes:
= X2 + 8x2 + 12x – 7x – 9 + 1 =
Basta reduzir os termos semelhantes operando os coeficientes / números.
= 9x2 + 5x - 8
Raiz do polinômio
Tomando um polinômio qualquer cujo resultado seja 0, por exemplo 2x3 + 4x2 – 2x, a raiz desse polinômio assumirá um valor b caso, e somente se, esse polinômio obtiver valor zero quando b = x.
31) Sabendo-se que –3 é raiz de P(x) = x³ + 4x² - ax + 1, calcule o valor de a.
Resolução:
Como foi dito que -3 é raiz do polinômio, devemos inserir -3 no lugar de x e igualar o polinômio a zero a fim de obter o valor de a.
(-3)3 + 4(-3)2 + -a(-3) + 1 = 0
-27 + 36 + 3a + 1 = 0
-26 + 36 = -3a
10 = -3a
a = -10/3















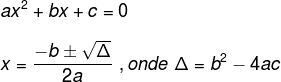
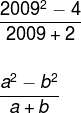
.png)
.png)
.jpg)



